② 中煤科工集团西安研究院有限公司, 陕西西安 710077
② Xi'an Research Institute of China Coal Techno-logy and Engineering Group, Xi'an, Shaanxi 710077, China
磁法勘探是最早应用于地质调查的地球物理勘探方法。作为一种成熟的勘探方法,它具有经济、高效、便捷等特点,因而被广泛应用于矿产勘查和地质调查。然而,在异常圈定和构造划分时,难以从原始磁异常中直接识别地质体的参数信息,大多情况下需基于当地地磁场磁化角度进行化极或其他处理,才能够获取有用信息[1-5]。Nabighian[6]推导并证明了二维磁解析信号振幅不受斜磁化影响,之后解析信号技术在磁异常处理中得到广泛的应用[7-11],并推广到三维磁异常解释[12-13]。虽然解析信号对于三维磁异常解释具有一定指导作用,但其依旧会受斜磁化影响[14]。Verduzco等[15]提出了tilt梯度的水平导数模法,在二维磁异常处理中,该方法不仅不受磁化方向的影响,相比于解析信号法,其分辨率更高;但在三维磁异常数据处理中,这种方法同样需要先进行化极处理。Wijns等[16]基于水平导数与解析信号的比值提出了Theta Map法,并应用于低纬度地区磁异常体的边界识别中,获得了良好的应用效果,但该方法在中纬度地区需考虑磁化角度影响,直接使用效果较差。邰振华等[17]针对Theta Map法的优缺点提出了伪总梯度余弦值法,提高了原方法的识别能力和抗干扰能力,但仍不适合于斜磁化磁异常的解释。磁梯度张量可以提供更丰富的异常信息,近年来被广泛应用于磁异常解释,获得了较为良好的应用效果[18-24]。
对于二维磁场数据,利用解析信号或者tilt梯度的水平导数模可直接进行异常解释,但三维磁异常的解释往往需要化极处理。然而,当磁测工区纬度低、存在强剩磁或范围较大时,磁异常化极存在较大难度。本文在tilt梯度的基础上提出了一种受磁化方向影响更小的三维磁异常识别方法,并通过理论模型及实例数据说明了新方法的有效性及实用性。
1 基本原理Tilt角[2]是一种从位场一阶导数推导而来、可以均衡不同异常强度的位场数据处理方法,其理论公式为
| $ \mathrm{TILT} = \arctan \frac{\frac{\partial T}{\partial z}}{\sqrt{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial y}\right)^{2}}} $ | (1) |
式中T表示磁异常。
将式(1)的分母拆分为
| $ \theta^{x} = \arctan \left(\frac{\partial T}{\partial z} / \frac{\partial T}{\partial x}\right) $ | (2) |
| $ \theta^{y} = \arctan \left(\frac{\partial T}{\partial z} / \frac{\partial T}{\partial y}\right) $ | (3) |
由式(2)和式(3)可以分别得到θx在x方向的导数和θy在y方向的导数
| $ \theta_{x}^{x} = \frac{\partial \theta^{x}}{\partial x} = \frac{\frac{\partial T}{\partial x} \frac{\partial^{2} T}{\partial x \partial z}-\frac{\partial T}{\partial z} \frac{\partial^{2} T}{\partial x^{2}}}{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}} $ | (4) |
| $ \theta_{y}^{y} = \frac{\partial \theta^{y}}{\partial y} = \frac{\frac{\partial T}{\partial y} \frac{\partial^{2} T}{\partial y \partial z}-\frac{\partial T}{\partial z} \frac{\partial^{2} T}{\partial y^{2}}}{\left(\frac{\partial T}{\partial y}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}} $ | (5) |
根据式(4)和式(5)可知,θxx与θyy的单位均为m-1,并不具备磁异常及其导数异常的物理意义。为此,对式(4)和式(5)的分母进行均方根处理
| $ \theta_{x}^{x \mathrm{S}} = \frac{\frac{\partial T}{\partial x} \frac{\partial^{2} T}{\partial x \partial z}-\frac{\partial T}{\partial z} \frac{\partial^{2} T}{\partial x^{2}}}{\sqrt{\left(\frac{\partial T}{\partial x}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}}} $ | (6) |
| $ \theta_{y}^{y \mathrm{S}}=\frac{\frac{\partial T}{\partial y} \frac{\partial^{2} T}{\partial y \partial z}-\frac{\partial T}{\partial z} \frac{\partial^{2} T}{\partial y^{2}}}{\sqrt{\left(\frac{\partial T}{\partial y}\right)^{2}+\left(\frac{\partial T}{\partial z}\right)^{2}}} $ | (7) |
此时,θxxS和θyyS的单位为nT/m2, 具有磁异常二阶导数的物理意义,也与公式中使用的导数阶次一致。θxxS和θyyS可以分别突出三维磁异常体在x和y方向上的信息特征,因此,可利用二者组合识别磁性体
| $ \theta^{\mathrm{THS}} = \sqrt{\left(\theta_{x}^{x \mathrm{S}}\right)^{2}+\left(\theta_{y}^{y \mathrm{S}}\right)^{2}} $ | (8) |
式中θTHS为改进tilt梯度的水平导数模。当地质体为(近似)棱柱体状时,其极大值对应场源边界;当地质体为(近似)球体时,则对应场源中心;当地质体为(近似)岩脉状时,则对应场源的中心走向。
2 理论模型试验为了验证新方法的应用效果,设计了一个磁化倾角和磁化偏角不同的复杂模型(表 1,图 1)。其中,异常体①、⑤为球体,异常体②和④为棱柱体,异常体③为垂直岩脉,所有异常体的磁化强度均设为1A/m。图 1为网格间距为0.1 km的组合模型理论磁异常,可以看出斜磁化下的磁异常与地质体无明显的对应关系。
|
|
表 1 模型参数 |

|
图 1 组合模型体的正演磁异常 图中圈码代表异常体编号,黑色线条表示异常体边界,黑色“+”表示球心位置。图 2同 |
|
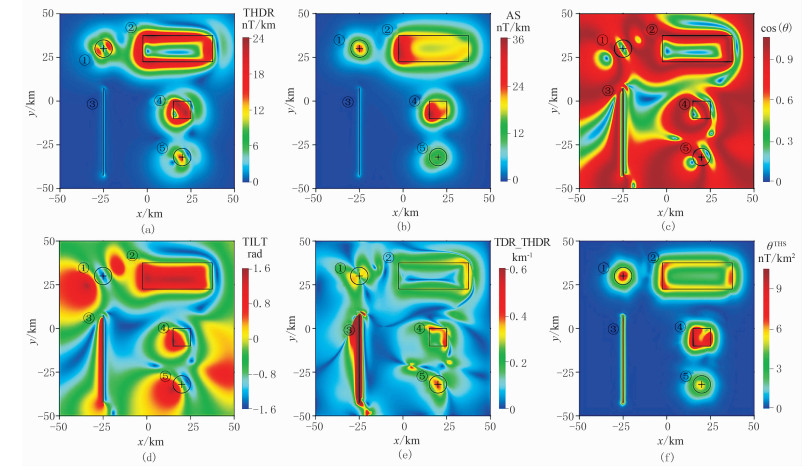
图 2 不同方法对组合模型磁异常的处理结果 (a)水平总梯度;(b)解析信号;(c)cos(θ);(d)tilt梯度;(e)tilt梯度的水平导数模;(f)改进tilt梯度的水平导数模 |
为了说明本文方法的优越性,选用水平总梯度(THDR)[1]、解析信号(AS)[12]、Theta Map(cos(θ))[16]、tilt梯度(TILT)[2]及水平导数模(TDR_THDR)[15]等常用的数据处理方法进行模拟对比分析,各算法的表达式为
| $ \left\{ \begin{array}{l} {\rm{THDR}} = \sqrt {{{\left( {\frac{{\partial T}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial T}}{{\partial y}}} \right)}^2}} \\ {\rm{AS}} = \sqrt {{{\left( {\frac{{\partial T}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial T}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial T}}{{\partial z}}} \right)}^2}} \\ \cos \left( \theta \right) = {\rm{THDR/AS}}\\ {\rm{TIL}}{\rm{T}} = \arctan \left( {\frac{{\partial T}}{{\partial z}}/{\rm{THDR}}} \right)\\ {\rm{TD}}{{\rm{R}}_-}{\rm{THDR}} = \sqrt {{{\left( {\frac{{\partial \theta }}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial \theta }}{{\partial y}}} \right)}^2}} \end{array} \right. $ | (9) |
图 2是常规方法和新方法对磁异常的处理结果。从图 2a可以看出,水平总梯度可以较好地识别规模较大的棱柱体②的边界,对棱柱体④的边界也有一定展示,但识别的边界位置与实际位置偏差较大,对其他异常体的识别效果也较差。作为一种边界识别手段,水平梯度模对磁化角度敏感。前人的研究表明,该方法不能直接应用于原始磁异常[25]。图 2b是解析信号的计算结果,由图可见该方法可以较好地检测到球体①的质心位置及棱柱体②的边界位置,但对岩脉③识别模糊,对棱柱体④的边界识别存在部分缺失,对球体⑤的质心识别位置存在较大偏差。从图 2c可以看出,Theta Map法可以识别棱柱体②的边界及岩脉③的位置,对棱柱体④识别的边界存在较大偏差,无法识别球体①和⑤,另外还在异常体外产生了很多虚假信息。图 2d是tilt梯度的计算结果,可以看出,tilt梯度可以有效均衡磁异常,突出弱异常,但是无法准确识别五个异常体的边界或者中心位置,受磁化角度的影响严重,因此,tilt梯度并不适合用于斜磁化磁异常的直接解释。图 2e是tilt梯度水平导数模的处理结果,可见该方法较好地反映出棱柱体②的边界位置和棱柱体④的部分边界,还可以较好地反映岩脉③的位置及球体⑤的质心水平位置,但无法识别球体①的质心位置。另外,该方法还会产生一些虚假异常,而这些虚假信息在实际资料处理易被看作是有用信号,从而获得错误的解释。图 2f是本文方法的识别结果,可以看出,对于磁化方向不同、几何形状不同的异常体,本文方法可以有效识别长方体异常体②和④的边界位置、球体①和⑤的中心位置及岩脉③的位置。
3 实际资料应用为了验证本文方法的实用性,对中国内蒙古塔木素地区的航磁数据进行处理与解释。图 3为研究区的地质概况图,可以看出,研究区整体划分为两部分:西北部的火山岩分布区和中部及东南部的沉积岩分布区,在沉积岩分布区内还零星分布着火山岩,部分沉积层中也含有火山岩成分。火山岩一般具有较强的磁性,尤其闪长岩磁性更明显;沉积岩一般无磁性或磁性较弱,但含有火成岩成分的沉积岩也表现出一定的磁性。另外,图 3中还展示了地震解译的断裂构造及断裂倾向,这些地质和地震资料为方法试验提供了较好的对比依据。

|
图 3 内蒙古塔木素地区地质图 图中蓝色虚线圈闭代表重点研究区域 |
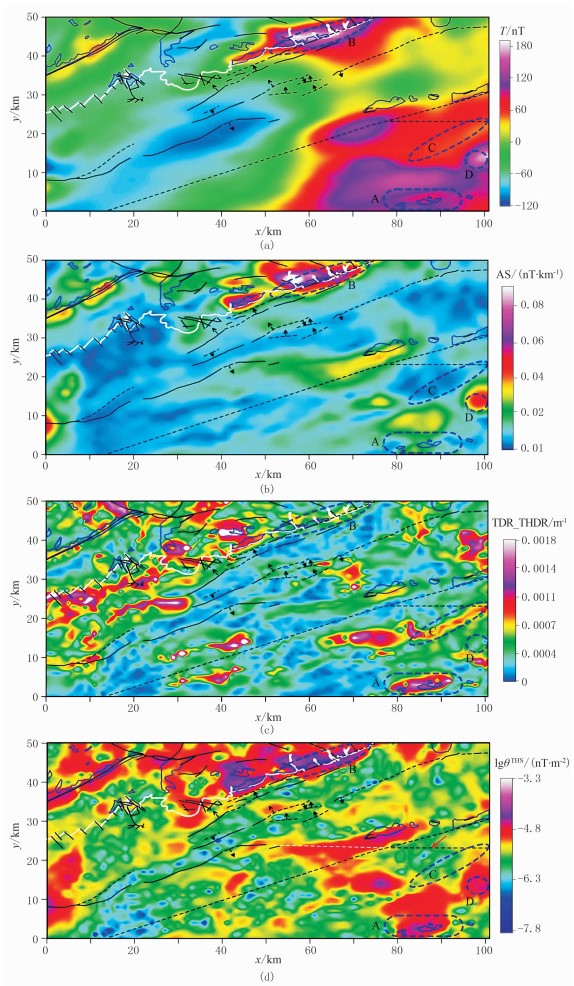
图 4a为网格间距为1km的航磁异常图,可见研究区北部及东南地区以高磁异常为主,西南部为磁异常低值区,磁异常的高低分布与地质图中的火山岩和沉积岩分布并无明显的对应关系,可能是原始磁异常受磁化角度影响导致的。为了提高磁场数据的地质解释能力,选择受磁化角度影响较小的解析信号和tilt梯度的水平导数模及本文提出的改进tilt梯度水平导数模对磁异常进行处理,计算结果分别见图 4b、图 4c和图 4d。解析信号(图 4b)整体表现为西北高和中部及东南部低的特征,与地质图中的火山岩与沉积岩分布均有良好的对应性。中部及东南部还存在局部高值,可能是火山岩或含火山岩成分的沉积岩引起的,但解析信号对弱信号的识别能力较差,异常细节模糊。tilt梯度的水平导数模(图 4c)获得了丰富的异常细节信息,异常圈闭走向与地质单元分布及断裂构造走向具有一定的相关性,但计算结果中可能存在虚假信息,例如在西部火山岩与沉积岩的分界线以南,tilt梯度水平导数模的信号强弱与地质体的磁性高低相反。改进tilt梯度水平导数模(图 4d)获得了较为丰富的异常细节信息,看起来是对解析信号中弱信号的强化,但相对解析信号还获得了更多的异常信息。
|
图 4 实际航磁数据计算结果 (a)原始磁异常;(b)解析信号;(c)tilt梯度的水平导数模;(d)改进tilt梯度的水平导数模 图中黑色实线和虚线代表已知断裂和地震解释断裂,黑色箭头代表地震解释断裂的倾向,深蓝色实线圈闭代表磁性相对较强的地质单元,白色实线代表西北火山岩地区与沉积岩地区的分界线,蓝色虚线代表重点研究区域,白色虚线代表根据θTHS解释的断裂带 |
为了更为详细地对比三种方法的效果,进一步分析一些详细的异常特征,选定图 3中蓝色虚线圈定的A、B、C、D等4个区域。A区内存在花岗岩、闪长岩等高磁性物质,沉积岩乌兰苏海组(K2w)因含有火山岩成分也具有一定磁性,因此A区相对周围的沉积岩应表现出高磁异常,tilt梯度的水平导数模和改进tilt梯度水平导数模可以有效识别,但解析信号仅反映出了少量的局部信息,仅在地表出露的火山岩上方显示出较弱的异常;B区为火山岩分布区,以闪长岩为主,因此也是一个高磁异常区。解析信号和改进tilt梯度水平导数模的识别效果较好,均展示出大面积的高值区,但tilt梯度的水平导数模不仅异常信号较弱,且反映的火山岩分布范围远小于实际分布范围;C区地表主要是第四系沉积,解析信号和改进tilt梯度水平导数模均无明显的信号显示,而tilt梯度的水平导数模却展示了一条东北走向的带状异常,很可能是虚假信息;D区地表为第四系沉积,解析信号与改进tilt梯度水平导数模均表现出高值异常,推断地下存在着隐伏高磁性岩体,然而tilt梯度的水平导数模却没有明显的异常显示。
上述对比分析结果表明,解析信号可以较好地识别规模较大、埋深较浅的磁性体,但对弱磁异常识别能力欠佳;tilt梯度的水平导数模可以获得丰富的异常细节信息,但存在虚假异常;改进tilt梯度的水平导数模则弥补了上述两种方法的不足,获得了更丰富、准确的异常细节信息。
由于改进tilt梯度的水平导数模具有更强的异常识别效果,下面依据该方法的处理结果进行简单的地质解释。
对比改进tilt梯度水平导数模的处理结果(图 4d)与地质图(图 3)可以发现,在沉积岩分布区内,断裂构造附近,改进tilt梯度水平导数模都表现出明显的异常,且这些异常信号恰出现在构造倾向方向上。因此认为断裂构造带是磁性物质来源的一个通道,即改进tilt梯度水平导数模图上具有一定走向的异常圈闭应与断裂带有关,以此为特征可以进行隐伏断裂带的推断,如图 4d中部的白色虚线可认为是前人推断的断裂带(红色箭头指示)在西侧的延续。在研究区东南部,高值区范围远大于地表零星分布的火山岩或含有火山成分沉积岩的分布范围,因此推断地下存在大规模的隐伏高磁性岩体,甚至地表零星分布的火山岩在地下可能是连通的,这有待后续研究的证实。
4 结束语强剩磁情况下磁异常体的解释一直是磁法勘探的一个难点,本文在tilt梯度法的基础上,推导了一种新的三维磁异常解释方法——改进tilt梯度的水平导数模。该方法无需化极处理,可以较好地反映地质体的实际平面位置。模型试验表明,相对于其他常用的磁异常数据处理方法,改进tilt梯度的水平导数模可以更准确、清晰地反映异常体的边界或质心的平面位置,且处理结果不会引入虚假信息。在中国内蒙古塔木素地区的航磁资料应用中,本文方法获得了更丰富、准确且清晰的异常细节信息,与已知地质资料、地震解译结果吻合较好,有效佐证了方法的适用性。
| [1] |
Cordell L.Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin[C].30th Field Conference New Mexico Geological Society, 1979, 59-64.
|
| [2] |
Miller H G, Singh V. Potential field tilt:a new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(1): 213-217. |
| [3] |
马龙, 孟军海, 付强, 等. 独立分量分析在重磁数据处理中的应用[J]. 石油地球物理勘探, 2017, 52(6): 1344-1353. MA Long, MENG Junhai, FU Qiang, et al. Application of independent component analysis in gravity and magnetic data processing[J]. Oil Geophysical Prospecting, 2017, 52(6): 1344-1353. |
| [4] |
王彦国, 张凤旭, 刘财, 等. 位场垂向梯度最佳自比值的边界检测技术[J]. 地球物理学报, 2013, 56(7): 2463-2472. WANG Yanguo, ZHANG Fengxu, LIU Cai, et al. Edge detection in potential fields using optimal auto-ratio of vertical gradient[J]. Chinese Journal of Geophysics, 2013, 56(7): 2463-2472. |
| [5] |
英高海, 姚长利, 郑元满, 等. 基于磁异常的边界特征增强方法对比研究[J]. 地球物理学报, 2016, 59(11): 4383-4398. YING Gaohai, YAO Changli, ZHENG Yuanman, et al. Comparative study on methods of edge enhancement of magnetic anomalies[J]. Chinese Journal of Geophysics, 2016, 59(11): 4383-4398. DOI:10.6038/cjg20161137 |
| [6] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:Its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [7] |
Hsu S K. Depth to magnetic source using the generali-zed analytic signal[J]. Geophysics, 1998, 63(6): 1947-1957. DOI:10.1190/1.1444488 |
| [8] |
Bastani M, Pedersen L B. Automatic interpretation of magnetic dike parameters using the analytical signal technique[J]. Geophysics, 2001, 66(2): 551-561. DOI:10.1190/1.1444946 |
| [9] |
Salem A, Ravat D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data[J]. Geophysics, 2003, 68(6): 1952-1961. DOI:10.1190/1.1635049 |
| [10] |
Ma G, Du X. An improved analytic signal technique for the depth and structural index from 2D magnetic anomaly data[J]. Pure and Applied Geophysics, 2012, 169(6): 2193-2200. |
| [11] |
Cooper G R J. Using the analytic signal amplitude to determine the location and depth of thin dikes from magnetic data[J]. Geophysics, 2015, 80(1): J1-J6. DOI:10.1190/geo2014-0061.1 |
| [12] |
Roeat W R, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal[J]. Geophy-sics, 1992, 57(1): 116-125. |
| [13] |
Hsu S K, Sibuet J C, Shyu C T. High-resolution detection of geologic boundaries from potential-field anomalies:An enhanced analytic signal technique[J]. Geophysics, 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [14] |
Li X. Understanding 3D analytic signal amplitude[J]. Geophysics, 2006, 71(2): L13-L16. DOI:10.1190/1.2184367 |
| [15] |
Verduzco B, Fairhead J D, Green C M. New insights into magnetic derivatives for structural mapping[J]. The Leading Edge, 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [16] |
Wijns C, Perez C, Kowalczyk P. Theta map:Edge detection in magnetic data[J]. Geophysics, 2005, 70(4): L39-L43. DOI:10.1190/1.1988184 |
| [17] |
邰振华, 张凤旭, 刘国兴, 等. 基于差分求导的伪总梯度余弦值法的位场边界检测[J]. 石油地球物理勘探, 2014, 49(4): 807-814. TAI Zhenhua, ZHANG Fengxu, LIU Guoxing, et al. Potential field edge detection based on difference derivative with cosine of pseudo total gradient[J]. Oil Geophysical Prospecting, 2014, 49(4): 807-814. |
| [18] |
Pedersen L B, Rasmussen T M. The gradient tensor of potential field anomalies:Some implications on data collection and data processing of maps[J]. Geophy-sics, 1990, 55(12): 1558-1566. |
| [19] |
Schmidt P, Clark D, Leslie K, et al. GETMAG:a SQUID magnetic tensor gradiometer for mineral and oil exploration[J]. Exploration Geophysics, 2004, 35(1): 297-305. |
| [20] |
Schmidt P W, Clark D A. The magnetic gradient tensor:Its properties and uses in source characterization[J]. The Leading Edge, 2006, 25(1): 75-78. DOI:10.1190/1.2164759 |
| [21] |
Beiki M, Clark D A, Austin J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics, 2012, 77(6): J23-J37. DOI:10.1190/geo2011-0437.1 |
| [22] |
马国庆, 李丽丽, 杜晓娟. 磁张量数据的边界识别和解释方法[J]. 石油地球物理勘探, 2012, 47(5): 815-821. MA Guoqing, LI Lili, DU Xiaojuan. Boundary detection and interpretation by magnetic gradient tensor data[J]. Oil Geophysical Prospecting, 2012, 47(5): 815-821. |
| [23] |
张恒磊, Marangoni Y R, 左仁广, 等. 改进的各向异性标准化方差探测斜磁化磁异常源边界[J]. 地球物理学报, 2014, 57(8): 2724-2731. ZHANG Henglei, Marangoni Y R, ZUO Renguang, et al. The improved anisotropy normalized variance for detecting non-vertical magnetization anomalies[J]. Chinese Journal of Geophysics, 2014, 57(8): 2724-2731. |
| [24] |
周文纳, 杜晓娟, 李吉焱. 重力数据的平面全张量梯度角度边界识别方法[J]. 石油地球物理勘探, 2013, 48(6): 1009-1015. ZHOU Wenna, DU Xiaojuan, LI Jiyan. Gravity data edge identification using plane full tensor gradient angle[J]. Oil Geophysical Prospecting, 2013, 48(6): 1009-1015. |
| [25] |
王万银. 位场总水平导数极值位置空间变化规律研究[J]. 地球物理学报, 2010, 53(9): 2257-2270. WANG Wanyin. Spatial variation law of the extreme value positions of total horizontal derivative for potential field data[J]. Chinese Journal of Geophysics, 2010, 53(9): 2257-2270. DOI:10.3969/j.issn.0001-5733.2010.09.027 |



 罗潇, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
罗潇, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: