定向井开采借助定向随钻电磁波测量仪器,使钻头按照设计的轨迹钻进,井轨迹包括垂直段、倾斜段及水平段,增加了油层卸油面积、减少了单位面积开采井数量,提高了油气综合开采效益,因此成为目前较受关注的油气勘探及开采技术[1-3]。定向井作业需要精确地控制井眼钻进轨迹[4-11],期望钻头始终在储层中钻进。这是由于储层岩性较泥岩更稳定,钻头在储层中钻进能够最大程度地保证井眼的稳定性,并使初始产量和持续产量稳定。合理的井眼布置可以延迟井出水和气窜,从而更加高效地开采油气藏。为了更好地开采定向井,现代地质导向钻井技术利用随钻测井(Logging While Drilling,LWD)资料及时、准确地划分已钻地层、预测待钻进地层、实时控制仪器沿期望轨迹钻进,大大提高了油气采收率。
定向井中倾斜段及水平段的仪器轴线与地层不垂直,测井环境处于非对称状态,地层电导率呈各向异性分布,水平电阻率不等于垂直电阻率,给地质导向测井解释带来一定困难。杨锦舟等[12]通过研究轴向发射线圈倾斜接收线圈系结构对比了方位随钻仪器的定向探测范围与电阻率随钻仪器的探测深度。魏宝君等[13]在水平层状地层中,采用并矢格林函数法计算了地质导向电磁波随钻测井仪器的定向探测特性。Wang等[14]研究了三维各向异性地层中的随钻测井响应特性,在数值计算时将磁场强度分量置于矩阵边上,为得到对称的系数矩阵,需对计算区域进行均匀离散化。Newman等[15]阐述了径向层状各向异性地层中的电性响应特性。史晓峰[16]研究了层状倾斜地层中的随钻电磁波仪器定向响应特性,分析了地层界面处的响应曲线变化特征,在水平井中利用测井数据进行地层分层及钻前预测井眼轨迹。
本文基于轴向发射、倾斜接收线圈系地质导向随钻电磁波测井仪器,采用三维有限元法分析仪器在大斜度井中的定向响应特性。针对井眼成像测井在低井斜角时的测量精度较低、受井眼环境影响较大,提出由定向地质导向信号获得低井斜角的方法。
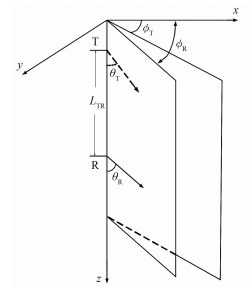
1 定向测量信号定义及其数值计算 1.1 定向测量信号为进行地质导向,斜线圈的设计方法被用于随钻测量仪器,从而使仪器能够识别地层界面、及时调整井眼走向(即地质导向)、识别地层的电性各向异性信息。在电阻率测量时电磁波测量仪器采用单发、双收的三线圈系结构,测量响应为两个接收线圈的幅值比和相位差。当随钻电磁波仪器用于地质导向时采用单发、单收的双线圈系结构,接收线圈测量信号经过处理后反映地层边界及方位等地质导向信息。图 1为倾斜线圈系示意图,地层坐标系为x、y、z。研究基于单发、单收线圈系结构,发射、接收线圈磁矩共面,且与仪器轴向(也为地层界面法向)z方向的夹角分别为θT和θR,方位角分别为ϕT和ϕR。倾斜天线系发射天线T与接收天线R选择相同的磁矩平面方位角,令ϕT = ϕR = ϕ。仪器旋转时方位角随之变化,接收线圈处的感应电动势也随之改变,且受方位角、地层界面等影响。
|
图 1 倾斜线圈系示意图 |
倾斜线圈系的磁偶极子源可等效为一个垂直磁偶极子源和一个水平磁偶极子源的叠加,如Mx与Mz的叠加(或My与Mz的叠加)。倾斜线圈的接收信号也等效为水平方向与垂直方向的接收信号的叠加,如x与z(或y与z)方向的接收信号的叠加。为讨论方便,推导在x、y、z三个方向上发射磁偶极子源及在三个方向均能接收到信号的一般情况。此时,接收线圈共能接收到具有9个分量的磁场张量信号。
在地层坐标系下,磁场可表示为
| $ \mathit{\boldsymbol{\bar {\bar H}}} = \left( {\begin{array}{*{20}{c}} {{H_{xx}}}&{{H_{xy}}}&{{H_{xz}}}\\ {{H_{yx}}}&{{H_{yy}}}&{{H_{yz}}}\\ {{H_{zx}}}&{{H_{zy}}}&{{H_{zz}}} \end{array}} \right) $ | (1) |
式中Hij表示在j(j = x,y,z)方向接收到的i(i = x,y,z)方向的磁偶极子源产生的磁场信号。
由式(1)可知,接收线圈在每个方向上均可接收到x、y、z三个方向磁偶极子源产生的磁场信号。x方向上的磁场为
| $ \begin{array}{l} {H_x} = {M_{\rm{T}}}\left( {{H_{xx}}\sin {\theta _{\rm{T}}}\cos \phi + {H_{yx}}\sin {\theta _{\rm{T}}}\sin \phi + } \right.\\ \;\;\;\;\;\;\;\;\left. {{H_{zx}}\cos {\theta _{\rm{T}}}} \right) \end{array} $ | (2) |
同理, y、z方向上的磁场分别为
| $ \begin{array}{l} {H_y} = {M_{\rm{T}}}\left( {{H_{xy}}\sin {\theta _{\rm{T}}}\cos \phi + {H_{yy}}\sin {\theta _{\rm{T}}}\sin \phi + } \right.\\ \;\;\;\;\;\;\;\;\left. {{H_{zy}}\cos {\theta _{\rm{T}}}} \right) \end{array} $ | (3) |
| $ \begin{array}{l} {H_z} = {M_{\rm{T}}}\left( {{H_{xz}}\sin {\theta _{\rm{T}}}\cos \phi + {H_{yz}}\sin {\theta _{\rm{T}}}\sin \phi + } \right.\\ \;\;\;\;\;\;\;\;\left. {{H_{zz}}\cos {\theta _{\rm{T}}}} \right) \end{array} $ | (4) |
根据接收线圈倾角求得接收线圈处的总磁场强度
| $ {H_{\rm{R}}} = {H_x}\sin {\theta _{\rm{R}}}\cos \phi + {H_y}\sin {\theta _{\rm{R}}}\sin \phi + {H_z}\cos {\theta _{\rm{R}}} $ | (5) |
将式(2)~式(4)代入式(5),得
| $ \begin{array}{l} {H_{\rm{R}}} = \frac{{{M_{\rm{T}}}\left[ {2{H_{zz}}\cos {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}} + \left( {{H_{xx}} + {H_{yy}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}} \right]}}{2} + \\ \;\;\;\;\;\;\;{M_{\rm{T}}}\left( {{H_{xz}}\cos {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}} + {H_{zx}}\sin {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}}} \right)\cos \phi + \\ \;\;\;\;\;\;\;{M_{\rm{T}}}\left( {{H_{yz}}\cos {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}} + {H_{zy}}\sin {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}}} \right)\sin \phi + \\ \;\;\;\;\;\;\;\frac{{{M_{\rm{T}}}\left( {{M_{xx}} - {M_{yy}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}\cos 2\phi }}{2} + \\ \;\;\;\;\;\;\;\frac{{{M_{\rm{T}}}\left( {{M_{xy}} + {M_{yx}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}\sin 2\phi }}{2} \end{array} $ | (6) |
式中MT = ITATNT为线圈源磁矩,其中IT为发射电流强度, AT为发射线圈面积, NT为发射线圈匝数。
求出HR后,由法拉第电磁感应定律可求出感应电动势为
| $ \begin{array}{l} U = - {\rm{i}}\omega \mu {H_{\rm{R}}}{N_{\rm{R}}}{A_{\rm{R}}} = {a_0} + {a_1}\cos \phi + {b_1}\sin \phi + \\ \;\;\;\;\;\;{a_2}\cos 2\phi + {b_2}\sin 2\phi \end{array} $ | (7) |
其中
| $ \begin{array}{l} {a_0}\left( {{\theta _{\rm{T}}},{\theta _{\rm{R}}}} \right)\\ \;\;\;\; = {U_{zz}}\cos {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}} + \frac{{\left( {{U_{xx}} + {U_{yy}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}}}{2} \end{array} $ | (8) |
| $ {a_1}\left( {{\theta _{\rm{T}}},{\theta _{\rm{R}}}} \right) = {U_{zx}}\sin {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}} + {U_{xz}}\cos {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}} $ | (9) |
| $ {b_1}\left( {{\theta _{\rm{T}}},{\theta _{\rm{R}}}} \right) = {U_{zy}}\sin {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}} + {U_{yz}}\cos {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}} $ | (10) |
| $ {a_2}\left( {{\theta _{\rm{T}}},{\theta _{\rm{R}}}} \right) = \frac{{\left( {{U_{xx}} - {U_{yy}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}}}{2} $ | (11) |
| $ {b_2}\left( {{\theta _{\rm{T}}},{\theta _{\rm{R}}}} \right) = \frac{{\left( {{U_{xx}} + {U_{yy}}} \right)\sin {\theta _{\rm{T}}}\sin {\theta _{\rm{R}}}}}{2} $ | (12) |
式中:ω为发射线圈中交变电流的角频率;μ为磁导率;NR为接收线圈匝数;AR为接收线圈面积;Uij表示在j(j = x,y,z)方向接收到的i(i = x,y,z)方向的磁偶极子源产生的感应电动势。
在常规的随钻测量仪器中,所有线圈平面均与仪器轴垂直,即θT = θR = 0。此时, a0≠0, a1、b1、a2、b2均为零,感应电动势不再是ϕ的函数,此时仪器测量信号不能反映方位信息。
若发射线圈和接收线圈中有一个相对仪器轴向倾斜,即θT≠0或θR≠0,则a0≠0、a1≠0、b1≠0、a2 = 0、b2 = 0,此时,感应电动势为ϕ的函数,仪器测量信号中包含了方位信息。
若发射线圈和倾斜线圈磁矩方向均为非轴向,则a0、a1、b1、a2、b2均不为零,可以计算水平电导率及垂直电导率,从而识别地层电性各向异性。
为了既充分利用现有的轴向线圈测量地层电参数,同时能够实现地质导向,目前的地质导向电磁波传播随钻测井仪器均采用发射线圈磁矩方向为轴向、接收线圈磁矩方向为非轴向的布置方式,即θT = 0、θR≠0。同时,假设仪器在xoz平面内钻进,即Hyz = Hzy = 0,则只有a0≠0及a1≠0。此时,接收线圈接收到的感应电动势为
| $ U = {a_0} + {a_1}\cos \phi $ | (13) |
定义地质导向响应信号包括定向幅度衰减信号和定向相移信号,可由ϕ = 0°和ϕ = 180°时的测量信号定义地质导向信号。对于单侧布置发射—接收线圈对,定向幅度定义为
| $ \begin{array}{l} {A_{{\rm{tt}}}} = \\ \;\;\; - 10\lg \frac{{{{\left[ {{\mathop{\rm Re}\nolimits} \left( {{a_0} + {a_1}} \right)} \right]}^2} + {{\left[ {{\mathop{\rm Im}\nolimits} \left( {{a_0} + {a_1}} \right)} \right]}^2}}}{{{{\left[ {{\mathop{\rm Re}\nolimits} \left( {{a_0} - {a_1}} \right)} \right]}^2} + {{\left[ {{\mathop{\rm Im}\nolimits} \left( {{a_0} - {a_1}} \right)} \right]}^2}}} \end{array} $ | (14) |
定向相移定义为
| $ {\rm{PS}} = {\tan ^{ - 1}}\frac{{{\mathop{\rm Im}\nolimits} \left( {{a_0} + {a_1}} \right)}}{{{\mathop{\rm Re}\nolimits} \left( {{a_0} + {a_1}} \right)}} - {\tan ^{ - 1}}\frac{{{\mathop{\rm Im}\nolimits} \left( {{a_0} - {a_1}} \right)}}{{{\mathop{\rm Re}\nolimits} \left( {{a_0} - {a_1}} \right)}} $ | (15) |
式(14)、式(15)中Re(·)、Im(·)分别表示取实部和虚部。
对于对称补偿布置的发射—接收线圈对,其地质导向信号定义为两对单个发射—接收线圈对的地质导向信号之和。
Schlumberger公司推出的具有较深探测深度的PeriScope15是新一代应用较为成熟的地质导向随钻电磁波测量仪器。该仪器在常规随钻测井仪器的基础上增加了倾斜或者横向线圈,探测深度较常规随钻仪器更大,具备较强的地质导向能力和方位探测能力,实现了对未钻进地层边界的距离和方向的钻前预测。该仪器作定向测量用的线圈有轴向布置发射线圈及两个倾斜接收线圈,倾斜接收线圈磁矩方向与仪器轴向的夹角分别为-45°和45°。定向测量提供22in(0.56m)、34in(0.864m)、84in(2.134m)及96in(2.438m)等4个源距及2MHz、40kHz和100kHz等3个频率的定向相移和定向幅度测量。水平布置发射线圈T6测量地层各向异性电阻率。
1.2 数值计算本文采用三维有限元法[17-21]分析仪器在大斜度井中的定向响应特性,推导了地质导向电磁波测井响应三维有限元泛函求解方程。在边界条件处理时,基于Paulsen提出的思路,在不连续性边界两侧引入两倍的节点施加连续性边界条件的方法[22]。根据变分原理,电、磁场求解方程分别为
| $ \begin{gathered} F\left( \mathit{\boldsymbol{E}} \right) = \frac{1}{2}\iiint_V {\left\{ {\frac{1}{{{\mu _{\text{r}}}}}\left( {\nabla \times \mathit{\boldsymbol{E}}} \right) \cdot \left( {\nabla \times \mathit{\boldsymbol{E}}} \right) + } \right.} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{s}{{{\mu _{\text{r}}}\varepsilon _{\text{r}}^2}}{{\left[ {\nabla \cdot \left( {{\varepsilon _{\text{r}}}\mathit{\boldsymbol{E}}} \right) + \frac{{\nabla \cdot \mathit{\boldsymbol{J}}}}{{{\text{i}}\omega {\varepsilon _0}}}} \right]}^2} - k_0^2{\varepsilon _{\text{r}}}\mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{E}}} \right\}{\text{d}}V + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\iint_S {\left[ {\frac{{{\gamma _{\text{e}}}}}{2}\left( {\mathit{\boldsymbol{\hat n}} \times \mathit{\boldsymbol{E}}} \right) \cdot \left( {\mathit{\boldsymbol{\hat n}} \times \mathit{\boldsymbol{E}}} \right) + \mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{U}}} \right]{\text{d}}S} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;{\text{i}}{k_0}{Z_0}\iiint_V {\mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{J}}{\text{d}}V} \hfill \\ \end{gathered} $ | (16) |
| $ \begin{gathered} F\left( \mathit{\boldsymbol{H}} \right) = \frac{1}{2}\iiint_V {\left\{ {\frac{1}{{{\varepsilon _{\text{r}}}}}\left( {\nabla \times \mathit{\boldsymbol{H}}} \right) \cdot \left( {\nabla \times \mathit{\boldsymbol{H}}} \right) + } \right.} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{s}{{{\mu _{\text{r}}}\varepsilon _{\text{r}}^2}}{{\left[ {\nabla \cdot \left( {{\mu _{\text{r}}}\mathit{\boldsymbol{H}}} \right)} \right]}^2} - k_0^2{\mu _{\text{r}}}\mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{H}}} \right\}{\text{d}}V + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\iint_S {\left[ {\frac{{{\gamma _{\text{h}}}}}{2}\left( {\mathit{\boldsymbol{\hat n}} \times \mathit{\boldsymbol{H}}} \right) \cdot \left( {\mathit{\boldsymbol{\hat n}} \times \mathit{\boldsymbol{H}}} \right) + \mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{V}}} \right]{\text{d}}S} - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\iiint_V {\mathit{\boldsymbol{H}}\left( {\nabla \times \frac{1}{{{\varepsilon _{\text{r}}}}}\mathit{\boldsymbol{J}}} \right){\text{d}}V} \hfill \\ \end{gathered} $ | (17) |
式(16)、式(17)中:E为电场强度;H为磁场强度;J为外加电流或源电流;εr、μr分别为相对介电常数和相对磁导率;k0为复波数;γe、γh分别为电场、磁场边界条件耦合系数;s为惩罚因子,用于消除解的散度,减少伪解;ε0为介电常数;
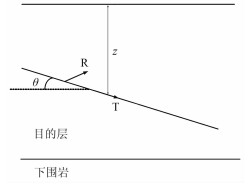
为更好地进行地质导向,要求仪器在尽量远的距离能够发现地层边界,从而尽早调整仪器钻进方向,即要求具有较大的定向探测深度。为此,可适当降低发射频率并增大发射—接收源距。本文采用三维有限元法分析仪器在大斜度井中的定向响应特性,发射频率为100kHz,源距为96in(2.438m),线圈系分别为单侧布置及对称布置,仪器在地层中以不同倾角θ倾斜钻进地层(图 2)。
|
图 2 斜井地层模型示意图 T为轴向发射线圈, R为倾斜接收线圈, z为仪器与地层边界距离 |
测井时,在发射线圈中通入交变电流,以此作为激励源。根据全电流定律,交变电流在井眼周围地层中将会产生一次交变电磁场。由电磁感应定律可知,变化的磁场产生电场。一次场在地层中产生以发射源为中心的涡流,变化的电场又产生磁场,因此,环形涡流建立二次电磁场,接收线圈接收二次场信号。环形涡流的大小是地层电导率的函数,接收线圈中的接收信号也是地层电导率的函数。
当存在地层界面时,一次场在地层中产生的涡流以不同角度穿越层边界。根据电磁波传播理论,时变的入射波在介质分界面处产生时变的电荷并作为新的波源。新波源产生的电磁波分别向边界两侧传播,与电流流入同侧但方向相反的波为反射波,穿过界面流入另一侧的波为折射波或透射波。透射波的传播方向与入射角及地层界面两侧介质特性有关。
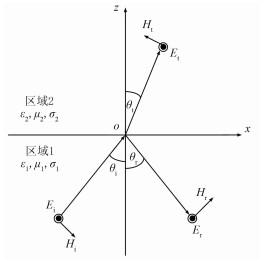
基于地质沉积规律,测井理论研究中一般将所探测地层简化为层状模型。为研究地层界面两侧电磁波传播特性,假设入射波从介电常数为ε1、磁导率为μ1、电导率为σ1的各向同性区域1斜入射进入介电常数为ε2、磁导率为μ2、电导率为σ2的各向同性区域2中。如图 3所示,在三维直角坐标系下,令xoy坐标面与地层界面重合,地层界面法向为z方向,为研究方便,选择入射面为xoz面,则场量与y无关。
|
图 3 有耗介质中的平面波斜入射 E、H分别为电、磁场强度的振幅,下标i、r、t分别代表入射波、反射波、透射波 |
在电磁波传播理论中,如果发射线圈源的尺寸与其波长相比很小,可将发射源视为偶极子源。采用倾斜线圈系时,可将发射源近似为与仪器轴向呈一定角度的磁偶极子源(点源)。倾斜磁偶极子源可分解为垂直磁偶极子源和水平磁偶极子源,线圈倾斜角度不同,水平方向和垂直方向上磁偶极子源的强度不同。设线圈磁矩方向与仪器轴的夹角为θT,则MV = MTcosθT, MH = MTsinθT。MT、MV和MH分别为发射线圈磁矩、垂直磁偶极子源磁矩及水平磁偶极子源磁矩。
根据电磁波传播理论,任意方向的磁偶极子源产生的电磁波可分解为TM(transverse magnetic)波和TE(transverse electric)波。TE波定义为电场向量垂直于入射面的线性极化波,TM波定义为电场向量平行于入射面的线性极化波。TE波和TM波可分别研究。
在区域1中,直角坐标系下的Maxwell方程可写为
| $ {H_x} = - \frac{1}{{{\text{i}}\omega {\mu _1}}}\frac{\partial }{{\partial z}}{E_y} $ | (18) |
| $ {H_z} = - \frac{1}{{{\text{i}}\omega {\mu _1}}}\frac{\partial }{{\partial x}}{E_y} $ | (19) |
| $ \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}} + {\omega ^2}{\mu _1}{\varepsilon _1}} \right){E_y} = 0 $ | (20) |
| $ {E_x} = - \frac{1}{{{\text{i}}\omega {\varepsilon _1}}}\frac{\partial }{{\partial z}}{H_y} $ | (21) |
| $ {E_z} = - \frac{1}{{{\text{i}}\omega {\varepsilon _1}}}\frac{\partial }{{\partial x}}{H_y} $ | (22) |
| $ \left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}} + {\omega ^2}{\mu _1}{\varepsilon _1}} \right){H_y} = 0 $ | (23) |
式(18)~式(20)为TE波方程,式(21)~式(23)为TM波方程,其中式(20)和式(23)为齐次Helmholtz方程。式中:Ex、Ey、Ez分别为x、y、z方向上的电场分量;Hx、Hy、Hz分别为x、y、z方向上的磁场分量;ω = 2πf, f为发射频率。
为研究电磁波在地层中的传播特性,需要求解给定边界条件下的波动方程。磁偶极子源产生的电磁波在纵向和横向上同时传播,此时可在柱坐标系下求解波动方程,可认为柱面波是沿各种角度传播的平面波的叠加。
柱坐标系(ρ, φ, z)下的波动方程为
| $ \left[ {\frac{1}{\rho }\frac{\partial }{{\partial \rho }}\left( {\rho \frac{\partial }{{\partial \rho }}} \right) + \frac{1}{{{\rho ^2}}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} + {k^2}} \right]u\left( {\rho ,\varphi } \right) = 0 $ | (24) |
其解可表示为
| $ u\left( {\rho ,\varphi } \right) = {H_n}\left( {k\rho } \right){{\text{e}}^{{\text{i}}m\varphi }} $ | (25) |
式中Hn(kρ)为n阶Hankel函数; m为不同角度平面波的个数。
假设磁偶极子源位于坐标系原点,地层界面位于z = d1处。波动方程的解可写为TE波和TM波的叠加。设EiTM、ErTM及EtTM分别为TM波入射波、反射波及透射波的振幅, EiTE、ErTE及EtTE分别为TE波入射波、反射波及透射波的振幅。则区域l中磁场及电场的解为
| $ {E_{lz}} = \int_{ - \infty }^{ + \infty } {{\text{d}}{k_\rho }\left( {E_{l{\text{i}}}^{{\text{TM}}}{{\text{e}}^{{\text{i}}{k_{lz}}z}} + E_{l{\text{r}}}^{{\text{TM}}}{{\text{e}}^{ - {\text{i}}{k_{lz}}z}}} \right)H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){C_n}\left( \varphi \right)} $ | (26) |
| $ \begin{array}{l} {E_{l\rho }} = \int_{ - \infty }^{ + \infty } {{\rm{d}}{k_\rho }\frac{{{\rm{i}}{k_{lz}}}}{{{k_\rho }}}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} - E_{l{\rm{r}}}^{{\rm{TM}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right)} \times \\ \;\;\;\;\;\;\;\;H_n^{{{\left( 1 \right)}^\prime }}\left( {{k_\rho }\rho } \right){C_n}\left( \varphi \right) + \\ \;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {{\rm{d}}{k_\rho }\frac{{{\rm{i}}\omega {\mu _1}}}{{k_\rho ^2\rho }}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} + E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right)} \times \\ \;\;\;\;\;\;\;\;H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){{S'}_n}\left( \varphi \right) \end{array} $ | (27) |
| $ \begin{array}{l} {E_{l\varphi }} = \int_{ - \infty }^{ + \infty } {{\rm{d}}{k_\rho }\frac{{{\rm{i}}{k_{lz}}}}{{k_\rho ^2\rho }}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} - E_{l{\rm{r}}}^{{\rm{TM}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right)} \times \\ \;\;\;\;\;\;\;\;H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){{C'}_n}\left( \varphi \right) + \\ \;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {{\rm{d}}{k_\rho }\frac{{ - {\rm{i}}\omega {\mu _1}}}{{{k_\rho }}}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} + E_{l{\rm{r}}}^{{\rm{TM}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right)} \times \\ \;\;\;\;\;\;\;\;H_n^{{{\left( 1 \right)}^\prime }}\left( {{k_\rho }\rho } \right){S_n}\left( \varphi \right) \end{array} $ | (28) |
| $ {H_{lz}} = \int_{ - \infty }^{ + \infty } {{\rm{d}}{k_\rho }\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} + E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right)H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){S_n}\left( \varphi \right)} $ | (29) |
| $ \begin{array}{l} {H_{l\rho }} = \int_{ - \infty }^{ + \infty } {\rm{d}} {k_\rho }\frac{{{\rm{i}}{k_{lz}}}}{{{k_\rho }}}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} - E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right) \times \\ \;\;\;\;\;\;\;\;\;H_n^{{{\left( 1 \right)}^\prime }}\left( {{k_\rho }\rho } \right){S_n}\left( \varphi \right) + \\ \;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {\rm{d}} {k_\rho }\frac{{ - {\rm{i}}\omega {\varepsilon _1}}}{{k_\rho ^2\rho }}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} + E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right) \times \\ \;\;\;\;\;\;\;\;\;H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){{C'}_n}\left( \varphi \right) \end{array} $ | (30) |
| $ \begin{array}{l} {H_{l\varphi }} = \int_{ - \infty }^{ + \infty } {\rm{d}} {k_\rho }\frac{{{\rm{i}}{k_{lz}}}}{{k_\rho ^2\rho }}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} - E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right) \times \\ \;\;\;\;\;\;\;\;\;H_n^{\left( 1 \right)}\left( {{k_\rho }\rho } \right){{S'}_n}\left( \varphi \right) + \\ \;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {\rm{d}} {k_\rho }\frac{{{\rm{i}}\omega {\varepsilon _1}}}{{{k_\rho }}}\left( {E_{l{\rm{i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{lz}}z}} + E_{l{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{lz}}z}}} \right) \times \\ \;\;\;\;\;\;\;\;\;H_n^{{{\left( 1 \right)}^\prime }}\left( {{k_\rho }\rho } \right){C_n}\left( \varphi \right) \end{array} $ | (31) |
式中:Hn(1)′(kρρ)为n阶第一类Hankel函数对kρρ的导数;Sn(n)、Cn(φ)以及Hankel函数的阶数n取决于磁偶极子源的类型,即为垂直磁偶极子源时, n = 0,为水平磁偶极子源时, n = 1。
将所有的场量及矢量微分算子分为横向分量和纵向分量两部分,横向分量以下标H表示,纵向分量以下标V表示,即
| $ \nabla = \mathit{\boldsymbol{x}}\frac{\partial }{{\partial x}} + \mathit{\boldsymbol{y}}\frac{\partial }{{\partial y}} + \mathit{\boldsymbol{z}}\frac{\partial }{{\partial z}} = {\nabla _{\rm{H}}} + \mathit{\boldsymbol{z}}\frac{\partial }{{\partial z}} $ | (32) |
x、y、z分别为x、y、z三个方向的单位矢量。
则Maxwell方程中的两个旋度方程可表示为
| $ \left( {{\nabla _{\rm{H}}} + \mathit{\boldsymbol{z}}\frac{\partial }{{\partial z}}} \right) \times \left( {{\mathit{\boldsymbol{E}}_{\rm{H}}} + {\mathit{\boldsymbol{E}}_{\rm{V}}}} \right) = {\rm{i}}\omega \mu \left( {{\mathit{\boldsymbol{H}}_{\rm{H}}} + {\mathit{\boldsymbol{H}}_{\rm{V}}}} \right) $ | (33) |
| $ \left( {{\nabla _{\rm{H}}} + \mathit{\boldsymbol{z}}\frac{\partial }{{\partial z}}} \right) \times \left( {{\mathit{\boldsymbol{H}}_{\rm{H}}} + {\mathit{\boldsymbol{H}}_{\rm{V}}}} \right) = - {\rm{i}}\omega \varepsilon \left( {{\mathit{\boldsymbol{E}}_{\rm{H}}} + {\mathit{\boldsymbol{E}}_{\rm{V}}}} \right) $ | (34) |
把横向分量和纵向分量分开后有
| $ {\rm{i}}\omega \mu {\mathit{\boldsymbol{H}}_{\rm{H}}} = {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{E}}_{\rm{V}}} + \mathit{\boldsymbol{z}} \times \frac{{\partial {\mathit{\boldsymbol{E}}_{\rm{H}}}}}{{\partial z}} $ | (35) |
| $ - {\rm{i}}\omega \varepsilon {\mathit{\boldsymbol{E}}_{\rm{H}}} = {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{H}}_{\rm{V}}} + \mathit{\boldsymbol{z}} \times \frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{H}}}}}{{\partial z}} $ | (36) |
| $ {\rm{i}}\omega \mu {\mathit{\boldsymbol{H}}_{\rm{V}}} = {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{E}}_{\rm{H}}} $ | (37) |
| $ - {\rm{i}}\omega \varepsilon {\mathit{\boldsymbol{E}}_{\rm{V}}} = {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{H}}_{\rm{H}}} $ | (38) |
由于
| $ {\mathit{\boldsymbol{E}}_{\rm{H}}} = \frac{1}{{{\omega ^2}\mu \varepsilon - k_{\rm{H}}^2}}\left( {{\nabla _{\rm{H}}}\frac{{\partial {\mathit{\boldsymbol{E}}_{\rm{V}}}}}{{\partial z}} + {\rm{i}}\omega \mu {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{H}}_{\rm{V}}}} \right) $ | (39) |
| $ {\mathit{\boldsymbol{H}}_{\rm{H}}} = \frac{1}{{{\omega ^2}\mu \varepsilon - k_{\rm{H}}^2}}\left( {{\nabla _{\rm{H}}}\frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{V}}}}}{{\partial z}} + {\rm{i}}\omega \mu {\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{E}}_{\rm{V}}}} \right) $ | (40) |
在区域2(无源区域)中
| $ {\mathit{\boldsymbol{E}}_{\rm{H}}}\left( {{k_\rho }} \right) = \frac{1}{{k_\rho ^2}}\left[ {{\nabla _{\rm{H}}}\frac{\partial }{{\partial z}}{\mathit{\boldsymbol{E}}_{\rm{V}}}\left( {{k_\rho }} \right) + {\rm{i}}\omega {\mu _2}{\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{H}}_{\rm{V}}}\left( {{k_\rho }} \right)} \right] $ | (41) |
| $ {\mathit{\boldsymbol{H}}_{\rm{H}}}\left( {{k_\rho }} \right) = \frac{1}{{k_\rho ^2}}\left[ {{\nabla _{\rm{H}}}\frac{\partial }{{\partial z}}{\mathit{\boldsymbol{H}}_{\rm{V}}}\left( {{k_\rho }} \right) + {\rm{i}}\omega {\varepsilon _2}{\nabla _{\rm{H}}} \times {\mathit{\boldsymbol{E}}_{\rm{V}}}\left( {{k_\rho }} \right)} \right] $ | (42) |
边界条件要求在交界面z = d1处电场和磁场切向连续。对于TM波,有
| $ {k_{{\rm{2V}}}}E_{{\rm{2i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = {k_{1{\rm{V}}}}\left( {E_{{\rm{1i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} - E_{{\rm{1r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) $ | (43) |
| $ {\varepsilon _2}E_{{\rm{2i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = {\varepsilon _1}\left( {E_{{\rm{1i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} + E_{{\rm{1r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) $ | (44) |
对于TE波,有
| $ {k_{{\rm{2V}}}}E_{{\rm{2i}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = {k_{1{\rm{V}}}}\left( {E_{{\rm{1i}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} - E_{{\rm{1r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) $ | (45) |
| $ {\mu _2}E_{{\rm{12}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = {\mu _1}\left( {E_{{\rm{1i}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} + E_{{\rm{1r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) $ | (46) |
在区域1中,有
| $ \begin{array}{l} E_{{\rm{2i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = \frac{1}{2}\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} + \frac{{{k_{{\rm{1V}}}}}}{{{k_{{\rm{2V}}}}}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {E_{{\rm{1i}}}^{{\rm{TM}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} + R_{12}^{{\rm{TM}}}E_{1{\rm{r}}}^{{\rm{TM}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) \end{array} $ | (47) |
| $ \begin{array}{l} E_{{\rm{2i}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{2V}}}}{d_2}}} = \frac{1}{2}\left( {\frac{{{\mu _1}}}{{{\mu _2}}} + \frac{{{k_{{\rm{1V}}}}}}{{{k_{{\rm{2V}}}}}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {E_{{\rm{1i}}}^{{\rm{TE}}}{{\rm{e}}^{{\rm{i}}{k_{{\rm{1V}}}}{d_2}}} + R_{12}^{{\rm{TE}}}E_{1{\rm{r}}}^{{\rm{TE}}}{{\rm{e}}^{ - {\rm{i}}{k_{{\rm{1V}}}}{d_2}}}} \right) \end{array} $ | (48) |
其中
| $ R_{12}^{{\rm{TM}}} = \frac{{1 - \frac{{{\varepsilon _1}{k_{{\rm{2V}}}}}}{{{\varepsilon _2}{k_{{\rm{1V}}}}}}}}{{1 + \frac{{{\varepsilon _1}{k_{{\rm{2V}}}}}}{{{\varepsilon _2}{k_{{\rm{1V}}}}}}}}\;\;\;\;\;\;\;R_{12}^{{\rm{TE}}} = \frac{{1 - \frac{{{\mu _1}{k_{{\rm{2V}}}}}}{{{\mu _2}{k_{{\rm{1V}}}}}}}}{{1 + \frac{{{\mu _1}{k_{{\rm{2V}}}}}}{{{\mu _2}{k_{{\rm{1V}}}}}}}} $ |
施加垂直磁偶极子源时只产生TE波,施加水平磁偶极子源时,可同时产生TM波和TE波。
可见,电磁波在有耗介质中传播时,地层界面两侧的反射、透射现象与入射角、透射角及地层界面两侧电导率有关。不同的仪器与地层界面距离、不同的发射-接收源距及在地层界面不同位置点处的入射角均不同。对于相同的入射角,地层界面两侧的电导率对比度不同时,透射角也不同。因此,有耗介质中地层界面两侧涡流流动特性非常复杂,当仪器以不同角度穿越地层界面时,由于边界效应,定向响应特性曲线变化也非常复杂。
3 仿真分析 3.1 各向同性目的层定向响应特性假设三层模型的上、下围岩及目的层电阻率分别为2、1、4Ω·m,目的层厚度为6m,工作频率为100kHz。仪器以不同角度穿过目的层时,单侧布置线圈对及对称布置线圈对的定向幅度及定向相移如图 4所示(h为仪器在目的层中的深度)。由图 4可见:

|
图 4 仪器以不同角度穿过三层各向同性地层的定向测量信号 (a)单个线圈对定向幅度特性;(b)对称线圈对定向幅度特性;(c)单个线圈对定向相移特性;(d)对称线圈对定向相移特性 |
(1) 围岩与目的层的相对位置不同,地质导向响应信号的符号也不同。当目的层位于围岩下方时,地质导向信号为正;当目的层位于围岩上方时,地质导向信号为负。仪器穿过目的层中点时,定向响应信号会穿过零点后改变极性。因此,极性可以在钻井时指导仪器的钻进方向。
(2) 在远离地层界面时定向响应信号很小,当仪器穿过目的层中点时,定向响应信号会穿过零点后改变极性。围岩与目的层界面处定向响应信号呈现峰值,由此可以判断地层界面的位置。
(3) 无论仪器是从围岩向目的层钻进还是从目的层向围岩钻进,定向响应信号的符号不发生变化,响应曲线的单调变化趋势也相同。
(4) 单侧布置发射-接收线圈对的定向幅度曲线的峰值出现在地层边界处,从而可以判断地层界面位置;且随着地层相对倾角变化,地层界面附近的定向响应曲线出现较大分离(图 4a)。
(5) 采用对称布置线圈对测量时,在地层界面处,定向幅度曲线出现峰值且随着地层倾角变化,曲线除峰值幅值大小不同有分离外,基本不受地层相对倾角影响(图 4b)。
(6) 当以约90°的倾角穿过目的层时,由于边界效应的影响,单侧布置发射—接收线圈对定向响应信号在地层边界处不再是单调变化的曲线,可能会出现双峰现象,且边界两侧地层电导率对比度不同,边界效应的影响也不同(图 4c),这个现象给测井解释带来困难。采用对称布置线圈对测量(即采用对称补偿后),响应曲线简单(图 4d)。
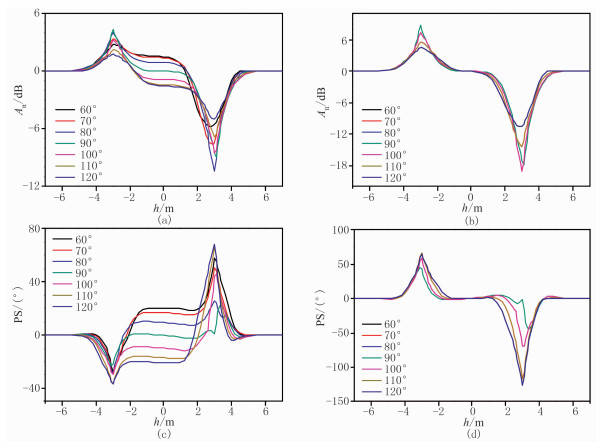
3.2 各向异性目的层定向响应特性在地层模型中,设目的层厚度为6m,定向幅度衰减特性如图 5所示。由图可见:
|
图 5 仪器以不同角度穿过三层各向异性地层的定向测量信号 (a)单个线圈对定向幅度;(b)对称线圈对定向幅度;(c)单个线圈对定向相移;(d)对称线圈对定向相移目的层电阻率:RH=4Ω·m,RV=20Ω·m。上、下围岩电阻率分别为2、1Ω·m |
(1) 采用单侧布置的线圈对测量时,在目的层中,定向响应信号为井斜角的函数,偏离零值。除了尖峰相对层界面发生平移外,在目的层的中间,响应值由于受各向异性的影响也不再是零。当相对倾角小于90°时信号零点更靠近目的层的下界面;当相对倾角大于90°时信号零点靠近目的层上界面;当相对倾角等于90°时,对相对倾角和各向异性不敏感。由于地层电导率等参数的准确值未知,采用单侧布置线圈对测量时,测量结果容易导致错误的地质导向(图 5a、图 5c)。
(2) 采用对称布置的线圈对后,地层倾角变化只对地层界面处的定向响应信号影响较大,远离地层边界时(在目的层中)其响应值仍接近零值,对地层各向异性不再敏感,响应特性曲线简单。这说明采用对称布置发射—接收线圈对(即采用对称补偿后)可以消除或减小相对倾角和各向异性的大部分影响,只有在界面处的尖峰幅度仍受这些因素影响(图 5b、图 5d)。
考虑到很多情况下地层都呈各向异性,且相对倾角一般不等于90°,为进行定向钻井,必须要区分定向响应曲线特征是受地层边界影响还是受地层各向异性影响。因此,在大斜度井中进行定向钻井时,应该采用对称布置线圈对进行测量。把两对单发、单收线圈对的定向测量结果叠加在一起,在接近地层边界时只对相对倾角敏感。在离地层界面较远时,定向响应信号受各向异性和相对倾角影响较小,定向响应曲线简单。这也是开发对称组合仪器的主要原因。
3.3 低井斜角测量通常,通过地质构造图和井眼成像可以获得井斜角。地质构造图能够提供较大范围内的地质构造信息。井眼成像能够得到井眼内的地层构造信息并成像,精度高于地质构造图。但是,当井斜角较小时,由于受井眼影响,井眼成像测量精度较低。本文提出了由定向测量数据实时获取低井斜角信息的方法。以仪器深度h为横坐标,以定向响应信号与井斜角的比值W为纵坐标,绘出定向响应特性曲线。图 6为低井斜角时厚度为6m的各向异性目的层、各向同性围岩层定向响应。由图可见:当地层相对倾角小于20°时,无论发射—接收线圈对是否对称布置,定向响应曲线呈线性变化且基本重叠在一起,即地层倾角增大(或减小)一定倍数,相应的定向响应信号也相应增大(或减小)相同的倍数。因此,在低井斜角测量时,只需要知道某个地层倾角时的定向响应信号值,可根据实际测量得到的定向响应信号测量值按比例换算出井斜角,即地质导向信号对井斜角探测具有很好的灵敏性,利用该方法测量低井斜角精度高且实时性好。当目的层厚度超过6m时,不能得到上述结论。保持上、下围岩及目的层电导率不变,当目的层厚度为10m时,绘出定向响应特性曲线。图 7为低井斜角时厚度为10m的各向异性目的层、各向同性围岩层定向响应。由图可见,定向响应信号与地层倾角的比值曲线不再呈线性变化且不重叠,相互分离,分析响应曲线特征可判断仪器在地层中的位置,从而进行地质导向。
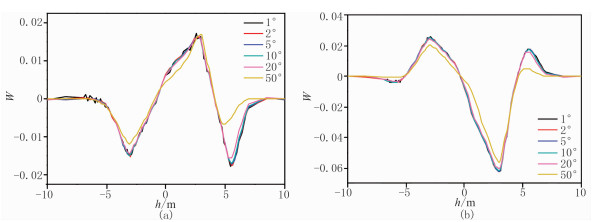
|
图 6 低井斜角时厚度为6m的各向异性目的层、各向同性围岩层定向响应 (a)单个线圈对;(b)对称线圈对RH=5Ω·m,RV=10Ω·m,上、下围岩电阻率分别为2、1Ω·m,仪器水平钻穿三层地层,地层相对倾角或井斜角分别取1°、2°、5°、10°、20°及50°, f=100kHz。W的量纲为dB/(°), 下同 |
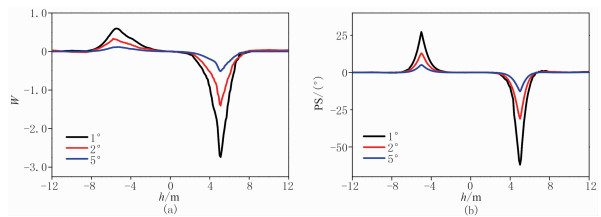
|
图 7 低井斜角时厚度为10m的各向异性目的层、各向同性围岩层定向响应 (a)定向幅值信号;(b)定向相移信号RH=5Ω·m,RV=10Ω·m,上、下围岩电阻率分别为2、1Ω·m,仪器水平钻穿三层地层,地层相对倾角或井斜角分别取1°、2°、5°, f=100kHz |
本文研究了地质导向电磁波测量仪器的响应特性。在大斜度井模型中,通过数值模拟分析了目的层分别为各向同性和各向异性、地层相对倾角变化时的定向响应。研究发现:由定向响应信号的变化可获得地层界面的位置及方位信息,由定向响应信号的正、负可判断围岩层与目的层的相对位置。为减小或消除地层倾角和地层各向异性对定向响应的影响,应该采用对称布置线圈对进行测量。把两对单发、单收线圈对的定向测量结果叠加在一起,在接近地层边界时只对相对倾角敏感。在距地层界面较远时,定向响应信号受各向异性和相对倾角影响较小,定向响应曲线简单。研究结果可对实际钻井测量提供理论指导。
此外,数值仿真了地层相对倾角小于20°时的定向测量响应,研究了由定向响应数据获取低井斜角的方法。结果表明:当目的层厚度不超过6m时,地质导向信号对低井斜角探测具有很好的灵敏性。这种通过定向地质导向信号获得低井斜角的方法弥补了井眼成像的不足,具有较高的测量精度,并且极具实时性。
| [1] |
黄世军, 康博韬, 程林松, 等. 海上普通稠油油藏多层合采层间干扰定量表征与定向井产能预测[J]. 石油勘探与开发, 2015, 42(4): 488-495. HUANG Shijun, KANG Botao, CHENG Linsong, et al. Quantitative characterization of interlayer interference and productivity prediction of directional wells in the multilayer commingled production of ordinary offshore heavy oil reservoirs[J]. Petroleum Exploration and Development, 2015, 42(4): 488-495. |
| [2] |
屈亚光, 安桂荣, 周文胜, 等. 层状砂岩油藏水平井与定井适应性探讨[J]. 断块油气田, 2013, 20(2): 216-220. QU Yaguang, AN Guirong, ZHOU Wensheng, et al. Discussion on adaptability of horizontal well and directional well in stratified sandstone reservoir[J]. Fault-Block Oil & Gas Field, 2013, 20(2): 216-220. |
| [3] |
赵兵. 定向井井眼轨迹不确定性分析[J]. 录井工程, 2012, 23(3): 45-48. ZHAO Bing. Uncertainty analysis of hole trajectory in directional well[J]. Mud Logging Engineering, 2012, 23(3): 45-48. DOI:10.3969/j.issn.1672-9803.2012.03.011 |
| [4] |
Wang T, Roland C, Eric H, et al.Real-time formation imaging, dip, and azimuth while drilling from compensated deep directional resistivity[C].SPWLA 48th Annual Logging Symposium, 2007.
|
| [5] |
Zhou J Q. On the depth of investigation-achieving deeper investigation with shorter source-receiver spacing[J]. Petrophysics, 2009, 50(5): 427-429. |
| [6] |
Ai-Haiari A.Proactive geosteering in thin reservoir bounded by anhydrite in Saudi Aribia[C].International Petroleum Conference, 2009.
|
| [7] |
Khadija A.Shallow azimuthal measurements a step towards 3D petrophysical evaluation in thin reservoirs[C].SPE Abu-Duabi International Petroleum Exhibition and Conference, 2010.
|
| [8] |
Michael B, Roland C.Real-time proactive optimal well placement using geo-signal and deep images[C].Offshore Technology Conference, 2010.
|
| [9] |
霍进, 宋渝新, 张一军, 等. PeriScope随钻测井技术在克拉玛依油田水平井开发中的应用[J]. 新疆石油地质, 2008, 29(2): 238-239. HUO Jin, SONG Yuxin, ZHANG Yijun, et al. Application of LWD PeriScope to horizontal well development in Karamay oil field[J]. Xinjiang Petroleum Geology, 2008, 29(2): 238-239. |
| [10] |
Nedhal Al-Musharfi, Radhey B, Mahbub A, et al.Real-time reservoir characterization and geosteering using advanced high resolution LWD resistivity imaging[C].SPE Annual Technical Conference and Exhibition, 2010, 19-22.
|
| [11] |
Khadija A.Reservoir characterization, fracture map-ping, and well placement using a suite of logging-while drilling images with multiple resolutions in a marginal, middle-east carbonate reservoir[C].SPE Reservoir Characterization and Simulation Conference and Exhibition, 2011, 9-11.
|
| [12] |
杨锦舟, 马哲, 林楠. PeriScope15方位定向电阻率测量仪的功能与特点[J]. 录井工程, 2009, 20(4): 53-56. YANG Jinzhou, MA Zhe, LIN Nan. Functions and features of Periscope15 azimuthal orientation resistivity measuring instrument[J]. Mud Logging Engineering, 2009, 20(4): 53-56. DOI:10.3969/j.issn.1672-9803.2009.04.013 |
| [13] |
魏宝君, 田坤, 张旭, 等. 定向电磁波传播随钻测量基本理论及其在地质层界面预测中的应用[J]. 地球物理学报, 2010, 53(10): 2507-2515. WEI Baojun, TIAN Kun, ZHANG Xu, et al. Physics of directional electromagnetic propagation measurements-while-drilling and its application for forecasting formation boundaries[J]. Chinese Journal of Geophy-sics, 2010, 53(10): 2507-2515. DOI:10.3969/j.issn.0001-5733.2010.10.024 |
| [14] |
Wang T, Sheng F. 3-D electromagnetic anisotropy modeling using finite differences[J]. Geophysics, 2001, 66(5): 1386-1398. DOI:10.1190/1.1486779 |
| [15] |
Newman G A, Alumbaugh D L. Three dimensional induction logging problems, Part 2:A finite difference solution[J]. Geophysics, 2002, 67(2): 484-491. DOI:10.1190/1.1468608 |
| [16] |
史晓峰. 水平井中随钻电阻率测量仪定位和预测地层界面的方法[J]. 测井技术, 2006, 30(2): 119-121. SHI Xiaofeng. Methods for orientation of formation layerings and formation boundary prediction with LWD resistivity logs in HZ wells[J]. Well Logging Technology, 2006, 30(2): 119-121. DOI:10.3969/j.issn.1004-1338.2006.02.006 |
| [17] |
刘立辉, 李建海, 孙莹频, 等. 时域属性法薄互层预测[J]. 石油地球物理勘探, 2017, 52(6): 1261-1268. LIU Lihui, LI Jianhai, SUN Yingpin, et al. Thin inter-bed prediction with time and frequency attributes[J]. Oil Geophysical Prospecting, 2017, 52(6): 1261-1268. |
| [18] |
欧阳芳, 戴世坤, 张钱江, 等. 层状单轴各向异性介质中长导线源电磁响应的快速计算[J]. 石油地球物理勘探, 2016, 51(5): 1012-1020. OUYANG Fang, DAI Shikun, ZHANG Qianjiang, et al. A fast calculation method for electromagnetic fields generated by finite-length wire source in stratified uniaxial anisotropic medium[J]. Oil Geophysical Prospecting, 2016, 51(5): 1012-1020. |
| [19] |
曹辉, 王绪本, 何展翔, 等. 水平层状介质条件下的井地电磁场响应计算[J]. 石油地球物理勘探, 2012, 47(2): 338-343. CAO Hui, WANG Xuben, HE Zhangxiang, et al. Calculation of borehole-to-surface electromagnetic responses on horizontal stratified earth medium[J]. Oil Geophysical Prospecting, 2012, 47(2): 338-343. |
| [20] |
杨振威, 冯磊, 赵宁, 等. 多重网格法二维Helmholtz方程解算及其在电磁法正演模拟中的应用[J]. 石油地球物理勘探, 2017, 52(1): 167-172. YANG Zhengwei, FENG Lei, ZHAO Ning, et al. Calculating 2D Helmholtz equation based on multigrid method and application in magnetotelluric modeling[J]. Oil Geophysical Prospecting, 2017, 52(1): 167-172. |
| [21] |
于新娟, 刘迪仁, 蔡明, 等. 围岩对井间电磁测井的影响[J]. 石油地球物理勘探, 2011, 46(4): 654-656. YU Xinjuan, LIU Diren, CAI Ming, et al. Influence of neighboring rock on cased crosswell electromagnetic logging[J]. Oil Geophysical Prospecting, 2011, 46(4): 654-656. |
| [22] |
金建铭, 王建国. 电磁场有限元方法[M]. 陕西西安: 西安电子科技大学出版社, 1998.
|



 解茜草, 陕西省西安市雁塔区电子二路18号西安石油大学电子工程学院仪器系, 710065。Email:
解茜草, 陕西省西安市雁塔区电子二路18号西安石油大学电子工程学院仪器系, 710065。Email: