② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
③ 油气资源与勘探技术教育部重点实验室, 湖北武汉 430100;
④ 长江大学地球物理与石油资源学院, 湖北武汉 430100;
⑤ 中冶集团武汉勘察研究院有限公司, 湖北武汉 430080;
⑥ 中国石化胜利油田分公司物探技术研究院, 山东东营 257022
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China;
③ Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Wuhan, Hubei 430100, China;
④ College of Geophysics & Oil Resources, Yangtze University, Wuhan, Hubei 430100, China;
⑤ Wuhan Surveying-Geotechnical Research Institute Co. Ltd., MCC, Wuhan, Hubei 430080, China;
⑥ Research Institute of Geophysics, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257022, China
岩性识别是储层评价的一个重要环节,是油藏描述、实时钻井监控及求取储层参数的基础。直接对岩心进行实验测量是识别岩性最准确的方法,但时间与经费消耗巨大,在实际应用中受到限制。测井曲线包含丰富的储层信息,如何快速、低耗利用测井资料获取地层岩性信息越来越受到研究人员的重视。Busch等[1]、Doveton[2]提出基于测井曲线交会的地层岩性经典识别技术,并迅速得到推广应用。然而随着勘探难度的不断加大,交会图法暴露出较大的局限性,许多学者提出了新的解决方案,岩性识别技术得到了长足的发展。刘爱疆等[3]将多元统计学中的主成分分析法(PCA)应用于碳酸盐岩岩性识别,潘保芝等[4]将因子分析法成功应用于火成岩岩性的识别,但都是针对特定岩性;Samuel等[5]、吴磊等[6]利用神经网络对岩性进行了有效识别,但由于黑盒效应,无法控制与分析模型的中间过程;张翔等[7]、吴施楷等[8]利用支持向量机进行岩性分类,但支持向量机需要寻找最优的分界样本,样本的选择不当会影响识别效果;葛新民等[9]借助核函数方法和时频分析理论,建立了一套基于核主成分分析(KPCA)与小波能谱分析的复杂储层油水界面的识别方法;陈钢花等[10]利用粒子群算法对支持向量机的核函数进行优化,提高了对复杂砂砾岩体的识别精度,验证了粒子群算法寻优性能。
东营凹陷董集洼陷的浊积岩类型多样、纵向岩性变化大、次生成岩作用改造明显,具有极强的非均质性,测井参数之间非线性关系严重,传统的交会图法及常规主成分分析法均不能得到精确的识别结果,是该区的研究难点[11-12]。
为解决该难题,综合前人的研究思路,采用核主成分分析方法,利用基于动态惯性权重系数的粒子群算法构建合理的核函数变换矩阵,通过核函数把原始测井数据从输入空间投影到高维线性特征空间,在高维线性特征空间中进行主成分分析,选取能够代表大部分测井信息的核主成分进行交会分析,建立了一种快速有效的浊积岩岩性识别方法。
1 方法原理 1.1 主成分分析法原理主成分分析是在保证样本数据信息损失最小的前提下,运用降维的思想将多个指标问题转换为较少的新的指标问题,并且这些新的指标既互不相关,又能综合反映原指标所包含信息的一种分析方法[13-14]。PCA运算实际上是一种确定一个坐标系统的正交变换,在这个新的坐标系统下,变换数据点的方差沿新的坐标轴得到了最大化,这些坐标轴经常被称为是主成分[15]。PCA的具体计算过程如下。
(1) 假定存在p个样本,每个样本含有n个变量,即X′i = (x′1i,x′2i,…,x′ni)T(i = 1,2,…,p),那么样本矩阵为
| $ \mathit{\boldsymbol{X'}} = \left( {\begin{array}{*{20}{c}} {{{x'}_{11}}}& \cdots &{{{x'}_{1p}}}\\ \vdots & \ddots & \vdots \\ {{{x'}_{n1}}}& \cdots &{{{x'}_{np}}} \end{array}} \right) = \left[ {{{\mathit{\boldsymbol{X'}}}_1},{{\mathit{\boldsymbol{X'}}}_2}, \cdots ,{{\mathit{\boldsymbol{X'}}}_p}} \right] $ | (1) |
为避免不同变量的数量级和量纲的影响,需要将原始数据标准化变换为X。变换公式为
| $ {x_{ij}} = \frac{{{{x'}_{ij}} - {{\bar x'}_i}}}{{S_i^2}} $ | (2) |
式中:x′i为样本第i行平均值;Si2为原始样本矩阵第i行方差。
(2) 计算经过标准化变换后的样本矩阵相关系数矩阵
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}}\\ {}& \vdots &{}&{}\\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nn}}} \end{array}} \right] = \frac{{{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}}}{{p - 1}} $ | (3) |
式中
| $ {r_{ij}} = \frac{{\sum\limits_{k = 1}^p {{x_{ik}}} \cdot {x_{jk}}}}{{p - 1}}\quad i,j = 1,2, \cdots ,n $ | (4) |
(3) 利用雅可比变换求出相关系数矩阵R的特征方程非负特征根,并按大小进行排列λi(λ1>λ2>…>λn>0)。通过施密特正交化方法单位正交化其特征向量
| $ \left\{\begin{aligned} \boldsymbol{a}_{1} &=\left(a_{11}, a_{21}, \cdots, a_{n 1}\right)^{\mathrm{T}} \\ \boldsymbol{a}_{2} &=\left(a_{12}, a_{22}, \cdots, a_{n 2}\right)^{\mathrm{T}} \\ & \vdots \\ \boldsymbol{a}_{n} &=\left(a_{1 n}, a_{2 n}, \cdots, a_{n n}\right)^{\mathrm{T}} \end{aligned}\right. $ | (5) |
(4) 计算样本的主成分变量,以表示原样本的线性组合
| $ \boldsymbol{F}=\boldsymbol{A X} $ | (6) |
即
| $ F_{i j}=\sum\limits_{k=1}^{n} a_{i k} x_{k j} $ | (7) |
(5) 利用特征值累积贡献度确定m的值,即当前m个主分量的方差和占全部总方差的比例超过0.85时,选取前m(m < n)个主分量表示原样本[16]。由此,变量的数目由n个减少为m个,从而起到降维的作用。
1.2 核主成分分析法原理利用主成分分析可以较好地处理变量间的线性关系,但处理非线性关系时会导致各主成分的贡献率过于分散,不能找到能够有效代表原样本的综合变量,处理效果较差[17]。
核方法是一类有效处理非线性问题的方法,通过非线性映射Ф,将低维输入空间每一个X = (X1,X2,…,Xp)(Xi∈Rn,i = 1,2,…,p)中不可分的数据映射到高维特征空间Y,即
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}:\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}^n} \to \mathit{\boldsymbol{Y}}}\\ {\mathit{\boldsymbol{X}} \to \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\bf{X}})} \end{array}} \right. $ | (8) |
在高维特征空间中进行数据处理,使输入空间中不可分的数据在高维特征空间中变得可分,再在高维特征空间采用主成分分析进行特征提取,解决原样本空间中样本数据线性不可分的问题[18-19]。
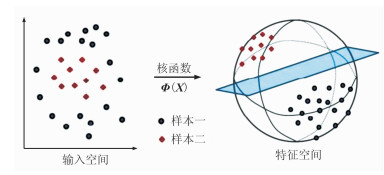
图 1为利用核主成分分析解决非线性问题的效果。如图所示,样本一和样本二在低维的输入空间中线性不可分,而通过简单的非线性映射函数Ф,可在高维的特征空间中实现样本分离。
|
图 1 KPCA实现样本分离的原理示意图 |
利用核主成分分析计算过程如下。
假设待处理的数据已经零均值化,在高维特征空间Y中利用协方差矩阵
| $ \mathit{\boldsymbol{C}} = \frac{1}{p}\sum\limits_{j = 1}^p \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \left( {{\mathit{\boldsymbol{X}}_j}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_j}} \right) $ | (9) |
构建特征方程寻找非零特征值λ和特征向量v∈Y,即
| $ \lambda \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{Cv}} $ | (10) |
根据Mercer条件,存在如下的核函数矩阵[20]
| $ \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_i}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right) \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right) $ | (11) |
且在空间Y中任一特征向量都可以由该空间中的所有样本线性表示,则
| $ \mathit{\boldsymbol{v}} = \sum\limits_{i = 1}^p {{\alpha _i}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} $ | (12) |
式(10)可变换为
| $ \lambda \sum\limits_{i = 1}^p {{\alpha _i}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} = \frac{1}{p}\sum\limits_{i = 1}^p {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_j}} \right)} \sum\limits_{i = 1}^p {{\alpha _i}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} $ | (13) |
等式两边同时乘以ФT(Xk),并联合式(9)可得
| $ \begin{array}{*{20}{c}} {\lambda \sum\limits_{i = 1}^p {{\alpha _i}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_k}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} = \frac{1}{p}\sum\limits_{i = 1}^p {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_k}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right)} \times }\\ {\sum\limits_{i = 1}^p {{\alpha _i}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{X}}_i}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} } \end{array} $ | (14) |
即
| $ \lambda \mathit{\boldsymbol{K\alpha }} = \frac{1}{p}{\mathit{\boldsymbol{K}}^2}\mathit{\boldsymbol{\alpha }} $ | (15) |
式中:K为p×p维的核函数矩阵;α为包含α1、α2、…、αp的列向量。
由于K是满足Mercer条件的实正定函数,所以式(15)可化简为
| $ p\lambda \mathit{\boldsymbol{\alpha }} = \mathit{\boldsymbol{K\alpha }} $ | (16) |
上式的非负特征根可以利用雅可比变换求出,并通过施密特正交化方法单位正交化其特征向量。
对于输入空间中某一个样本Xj (j = 1,2,…,p),利用非线性映射得到特征空间Y的像Φ(Xj),那么它在特征空间Y中的主成分可以表示为在子特征空间向量上vk的投影
| $ {\mathit{\boldsymbol{v}}_k} \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right) = \sum\limits_{i = 1}^p {{\alpha _i}\left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_i}} \right) \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right)} \right]} $ | (17) |
然而,利用核方法的内积运算把样本数据从低维空间映射到高维特征空间,虽然方便了非线性特征的提取,但是随着维数的增加,计算量也随之增加,甚至会出现“维数灾难”。所以要利用核函数取代内积运算来避免“维数灾难”[21-22]。
目前常用的有多项式核函数、径向基(高斯)核函数、神经网络核函数。
(1) 多项式核函数为
| $ \boldsymbol{K}\left(\boldsymbol{X}_{i}, \boldsymbol{X}_{j}\right)=\left[b\left(\boldsymbol{X}_{i}, \boldsymbol{X}_{{j}}\right)+c\right]^{d} $ | (18) |
式中:b、c为常数系数;d为多项式核的阶次。
(2) 径向基(高斯)核函数为
| $ \boldsymbol{K}\left(\boldsymbol{X}_{i}, \boldsymbol{X}_{j}\right)=\exp \left(-\frac{\left\|\boldsymbol{X}_{i}-\boldsymbol{X}_{j}\right\|^{2}}{2 \sigma}\right) $ | (19) |
式中σ是参数,它决定了输入变量在学习算法中被缩放的程度。
(3) 神经网络核函数为
| $ \boldsymbol{K}\left(\boldsymbol{X}_{i}, \boldsymbol{X}_{j}\right)=\tanh \left[s\left(\boldsymbol{X}_{i}, \boldsymbol{X}_{j}\right)+c\right] $ | (20) |
式中: tanh为双曲正切函数;s、c是根据先验知识指定的参数。
将内积用核函数替换, 则式(17)变为
| $ {\mathit{\boldsymbol{v}}_k} \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{X}}_j}} \right) = \sum\limits_{i = 1}^p {{\alpha _i}} \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) $ | (21) |
所以借助核函数就可以在高维特征空间中对样本进行主成分分析[23]。
上述推导过程均是在Ф(X)进行中心化处理后进行的,但在实际应用中并不知道Ф(X)的显式表达,也就无法对其中心化,所以要使用对角化后的Kc来代替K进行上述求解过程。Kc的表达式为[24]
| $ {\mathit{\boldsymbol{K}}_{\rm{c}}} = \mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{l}}_\rho }\mathit{\boldsymbol{K}} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{l}}_p} + {\mathit{\boldsymbol{l}}_p}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{l}}_p} $ | (22) |
式中:lp为p×p的矩阵,其每一个元素都是1/p。
1.3 粒子群算法优化原理粒子群算法的基本思想是通过群体中个体之间的协作和信息共享寻找最优解,是基于对鸟群觅食行为的生物仿真模拟,目前已被广泛应用于函数优化、模糊系统控制等领域[25]。
在粒子群算法中,惯性权重w是最重要的参数,较大的w有利于提高算法的全局搜索能力,而较小的w会增强算法的局部搜索能力。为了平衡传统粒子群算法的全局搜索能力和局部寻优能力,本文采用自适应的动态惯性权重系数公式,具体为
| $ w = \left\{ {\begin{array}{*{20}{c}} {{w_{\min }} - \frac{{\left( {{w_{\max }} - {w_{\min }}} \right)\left( {f - {f_{\min }}} \right)}}{{{f_{{\rm{avg}}}} - {f_{{\rm{min}}}}}}}&{f \le {f_{{\rm{avg}}}}}\\ {{w_{\max }}}&{f > {f_{{\rm{avg}}}}} \end{array}} \right. $ | (23) |
式中:wmax、wmin分别表示w的最大值和最小值;f为粒子当前的目标函数值;favg和fmin分别表示当前所有粒子的平均和最小目标函数值。
基于自适应的动态惯性权重粒子群算法简单、容易实现并且没有太多参数的调节,适用于核主成分分析中的核函数参数的优选[26]。
2 实例研究 2.1 地质概况董集洼陷位于西段东营凹陷北部,在沙三中段沉积时期,董集洼陷接受的南北两个方向的物源供给,发育多套浊积岩,这些浊积岩被沙三中段的深湖相暗色泥岩包裹,形成自生自储的岩性油藏。根据研究区的岩心资料,沙三中段沉积时期的岩石类型主要为深灰色的泥岩、灰质泥岩、浅灰色的细砂岩、灰色的灰质砂岩、褐色的油页岩。研究区的浊积岩主要包括砂岩与泥岩、砂岩与灰质泥岩、灰质砂岩与泥岩、灰质砂岩与灰质泥岩及砂岩与油页岩等5种岩性组合方式[27]。
2.2 样本参数选择测井曲线包含多个参数,每个参数对岩性都有不同的区分度,但若选取的测井参数过多,往往会增加分析过程的复杂性。基于前人经验和测井响应原理,选取自然伽马(GR)、声波时差(AC)、补偿中子孔隙度(CNL)、密度(DEN)、原状地层电阻率(RT)值作为输入样本参数X′ = [GR,AC,CNL,DEN,RT]。
选择研究区W9井的沙三中段4层(Es3z4)的测井数据作为研究样本,进行单位长度为0.125m的数据重采样,得到230个样本,对样本数据进行异常值处理,去除无效参数,最终确定用于分析的样本个数为203。不同岩性测井数据的均值和中值统计结果如表 1所示。
|
|
表 1 不同岩性测井数据统计结果 |
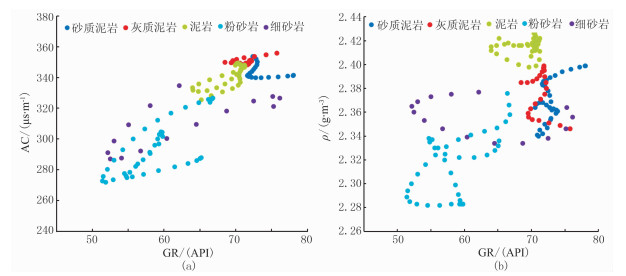
根据测井数据统计可知,砂质泥岩、灰质泥岩的测井曲线具有高GR、高AC、中CNL、中DEN、中RT即“两高、三中”的响应特征;细砂岩、粉砂岩表现为低GR、低AC、低CNL、高DEN、高RT即“三低、两高”的特征;泥岩显示为高GR、高AC、高CNL、低DEN、低RT即“三高、二低”特征。通过对不同岩性测井值的统计,发现五种岩性的测井响应特征存在一定差异,适合采用多元统计学方法进行分析[28]。
2.3 核函数及其参数的选择为了选取合适的核函数,对样本进行试验。试验发现,选取神经网络核函数来构造KPCA核变换矩阵时,对参数的选择较为苛刻,易造成病态核矩阵,生成负的特征向量从而导致模型构建失败;而径向基核函数和多项式核函数的正定性较好,参数的选择区间较广,容错率较高。
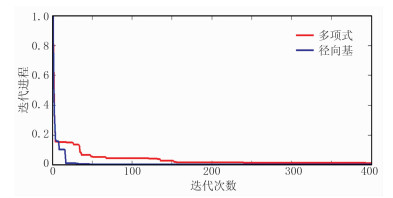
对径向基核函数和多项式核函数运算性能进行进一步的试验对比(将迭代进程归一化为0和1,1为开始,0为结束),对比结果如图 2所示。从图中可以看出,相对于多项式核函数,径向基核函数只用了较少的迭代次数和运算时间就完成了迭代进程,运算效率高,且函数需要确定的参数只有一个,模型构建较为容易。通过以上试验分析,选取径向基核函数作为核主成分分析的核函数。
|
图 2 两种不同核函数的运算效率对比 |
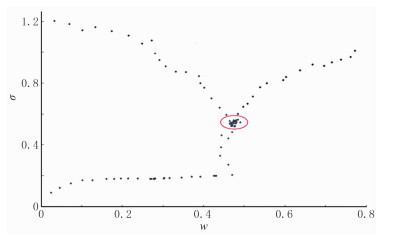
为了确定径向基核函数的核参数σ,避免人工选择的误差以及提高识别效率,采用基于动态惯性权重的粒子群算法对σ进行优选。粒子群的运动轨迹如图 3所示,可以看出,在迭代初期粒子扩散到全区在较大范围内搜索最优解,随着迭代次数的增加,惯性权重也在发生改变,整个粒子群不断向最优的位置靠近聚集,在迭代后期锁定了全局最优解的位置,得到核函数参数的最优解大约为0.6(图中红圈处)。
|
图 3 粒子群的运动轨迹 |
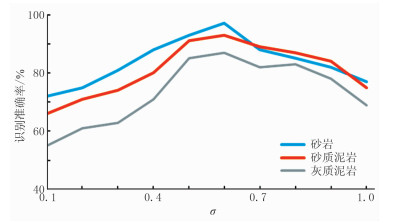
为了验证该方法选取σ的可行性,分别选取不同的σ值对标准井中较难识别的三种岩性进行识别,结果如图 4所示。从图中可以看出,随着σ取值的改变,三种岩性的识别准确率也在改变,在σ值为0.6时,三种岩性的识别准确率均达到最高,验证了该方法的准确性。
|
图 4 σ的取值对识别结果的影响分析 |
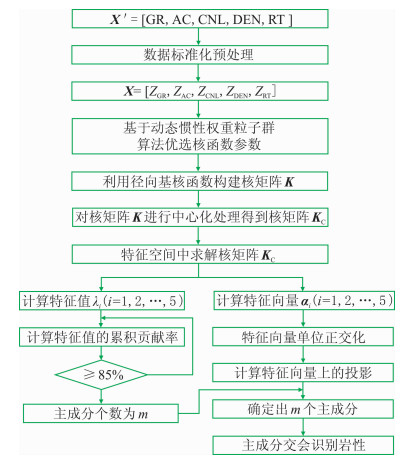
(1) 数据的标准化预处理。对选取的p个测井数据(每个测井数据包含n个参数)进行标准化预处理,克服数据间量纲和数量级的差别,以保证分析结果的客观性和准确性。
(2) 核函数参数优选。基于动态惯性权重的粒子群算法对σ进行优选,避免人工选择的误差以及提高识别的准确率。
(3) 计算并修正核矩阵。利用确定最优核参数的径向基核函数构建核矩阵K,并将核矩阵进行中心化修正得到Kc。
(4) 高维空间中核矩阵分解。在选定的核函数的作用下,通过雅可比迭代计算修正后的核矩阵Kc的特征值和对应的特征向量,并利用施密特正交化方法单位正交化其特征向量,得到α1、a2、…、αn。
(5) 计算特征值的累积贡献率B1、B2、…、Bm, 根据给定的提取效率h,如果Bm≥h,则提取m个特征分量。
(6) 高维空间中的主成分提取。计算已修正的核矩阵在提取出的特征向量上的投影,得到m个主成分。
(7) 主成分交会识别岩性。根据得到的前两个主成分进行交会分析,确定每种岩性在主成分坐标系中的分布区间[29]。
2.5 计算过程在对输入参数X′进行分析之前,先对样本数据进行标准化,使每个测井参数变量的均值为0,方差为1,标准化后的样本为X。
对标准化后的样本数据分别进行主成分分析和核主成分分析(流程如图 5所示),并对得到的各主成分的特征值及方差贡献率进行比较(表 2)。
|
图 5 基于核主成分分析的岩性识别流程 |
|
|
表 2 PCA和KPCA的特征值贡献率比较 |
从表 2中可以看出,经过主成分分析计算得到的第一主成分F1的方差贡献率只有40.13%,贡献率并不理想;第二主成分F2的方差贡献率也仅有21.44%,主成分F1和F2方差之和只占到总方差的61.57%,原有变量的信息损失较大。经过核主成分分析计算后仅第一主成分F1的方差贡献率就达到86.31%,第一主成分F1和第二主成分F2方差贡献率之和占到总方差93.83%,有效地保留了原有样本变量的信息。
3 应用效果及实例分析图 6为常规测井交会图法对研究区的浊积岩识别结果,可以看出,该方法的识别精度较低,很难区分所有岩性。
|
图 6 常规测井交会图法岩性识别 (a)AC与GR;(b)DEN与GR |
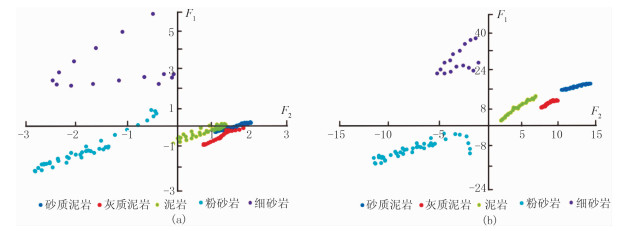
图 7a为由主成分变换方程计算的F1和F2交会图,图 7b为由核主成分变换方程计算的F1和F2交会图。可以看出,主成分分析法对细砂岩和粉砂岩区分度很高,但对泥岩、灰质泥岩、砂质泥岩的区分度并不理想;而核主成分分析可以有效区分泥岩、灰质泥岩、砂质泥岩、粉砂岩和细砂岩,岩性识别精度明显提高。
|
图 7 两种方法主成分岩性交会识别对比 (a)主成分分析;(b)核主成分分析 |
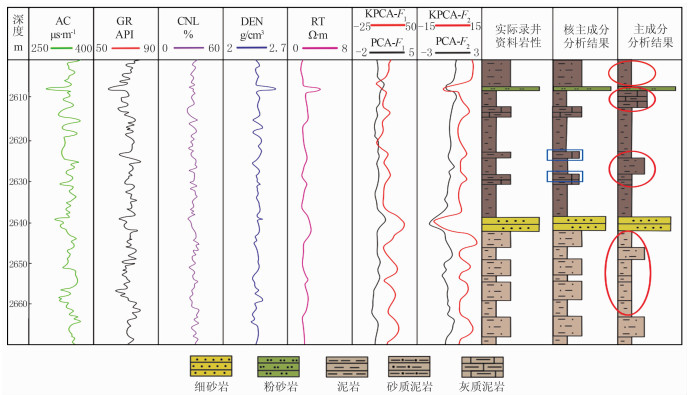
分别运用核主成分分析法和主成分分析法对研究区的W9井进行连续测井剖面的岩性解释,结果如图 8所示。从图中可以看出,在量纲一致的条件下,KPCA法的F1、F2分量曲线垂向上变化程度更加剧烈,不同岩性之间的差异性更加明显,对于岩性的区分更加敏感。根据实际录井资料,W9井2600~ 2670m深度区间里共出现20个不同的岩性段。PCA法可以有效识别细砂岩和粉砂岩段,但是对泥岩、灰质泥岩、砂质泥岩段的误判率很高,20个岩性段误判8个(见图中红色圆圈处),岩性识别率仅为60%;KPCA法解释结果与实际录井资料较为吻合,只是将2622~2624m和2627~2629m处的砂质泥岩误判为灰质泥岩,20个岩性段仅误判2个(图中蓝色方框处),岩性识别准确率达到90%,在浊积岩地区进行岩性识别效果良好。
|
图 8 研究区W9井两种方法测井岩性解释结果对比 |
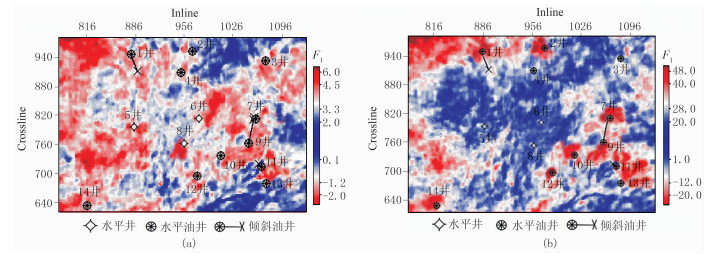
对区内的多口井应用KPCA法和PCA法进行岩性识别后预测了该区的沙三中段4层有利储层的分布,结果如图 9所示。研究区砂岩的F1值分布区域大致为-20~-12和40~48,从图中可以看出,KPCA法预测结果在钻井处与实际测井资料吻合度更高,更精细地刻画了储层的分布范围,符合该区储层的分布规律。
|
图 9 两种方法储层平面预测结果对比 (a)PCA;(b)KPCA。亮色表示有利储层区域 |
(1) 东营凹陷董集洼陷浊积岩岩性复杂多变,基于粒子群算法以及核函数理论,采用核主成分分析法能有效地从多种测井参数中提取突出岩性特征的主成分分量,实现了降维处理。
(2) 利用核主成分分析法算出的第一主成分和第二主成分变量进行交会分析,能够有效地识别泥岩、灰质泥岩、砂质泥岩、细砂岩和粉砂岩,岩性识别精度明显高于常规测井交会图法和主成分分析法。
(3) 多口井实际资料的识别结果与录井资料符合程度较高,为后续的储层评价奠定了基础。
| [1] |
Busch J M, Fortney W G, Berry L N. Determination of lithology from well logs by statistical analysis[J]. SPE Formation Evaluation, 1987, 2(4): 412-418. DOI:10.2118/14301-PA |
| [2] |
Doveton J H.Geologic Log Analysis Using Computer Methods[M].AAGP, Tulsa, 1994.
|
| [3] |
刘爱疆, 左烈, 李景景, 等. 主成分分析法在碳酸盐岩岩性识别中的应用——以YH地区寒武系碳酸盐岩储层为例[J]. 石油与天然气地质, 2013, 34(2): 192-196. LIU Aijiang, ZUO lie, LI Jingjing, et al. Application of principal component analysis in carbonate lithology identification:a case study of the Cambrian carbonate reservoir in YH field[J]. Oil & Gas Geology, 2013, 34(2): 192-196. |
| [4] |
潘保芝, 李舟波, 付有升, 等. 测井资料在松辽盆地火成岩岩性识别和储层评价中的应用[J]. 石油物探, 2009, 48(1): 48-52. PAN Baozhi, LI Zhoubo, FU Yousheng, et al. Application of logging data in lithology identification and reservoir evaluation of igneous rock in Songliao basin[J]. Geophysical Prospecting for Petroleum, 2009, 48(1): 48-52. DOI:10.3969/j.issn.1000-1441.2009.01.008 |
| [5] |
Samuel J R, Fang J H, Karra C L, et al. Determination of lithology from well logs using a neural network[J]. AAPG Bulletin, 1992, 76(5): 731-739. |
| [6] |
吴磊, 徐怀民, 季汉成. 基于交会图和多元统计法的神经网络技术在火山岩识别中的应用[J]. 石油地球物理勘探, 2006, 41(1): 81-86. WU Lei, XU Huaimin, JI Hancheng. Application of neural networks technique based on crossplot and multielement statistics to recognition of volcanic rocks[J]. Oil Geophysical Prospecting, 2006, 41(1): 81-86. DOI:10.3321/j.issn:1000-7210.2006.01.016 |
| [7] |
张翔, 肖小玲, 严良俊, 等. 基于模糊支持向量机方法的岩性识别[J]. 石油天然气学报, 2009, 31(6): 115-118. ZHANG Xiang, XIAO Xiaoling, YAN Liangjun, et al. Lithologic identification based on fuzzy support vector machines[J]. Journal of Oil and Gas Technology, 2009, 31(6): 115-118. DOI:10.3969/j.issn.1000-9752.2009.06.021 |
| [8] |
吴施楷, 曹俊兴. 基于连续限制玻尔兹曼机的支持向量机岩性识别方法[J]. 地球物理学进展, 2016, 31(2): 821-828. WU Shikai, CAO Junxing. Lithology identification method based on continuous restricted Boltzmann machine and support vector machine[J]. Progress in Geo-physics, 2016, 31(2): 821-828. |
| [9] |
葛新民, 范卓颖, 范宜仁, 等. 基于核主成分-小波能谱分析的复杂储层油水界面预测[J]. 中南大学学报(自然科学版), 2015, 46(5): 1747-1753. GE Xinmin, FAN Zhuoying, FAN Yiren, et al. Oil/water contact prediction of complex reservoir using kernel principal component analysis and wavelet po-wer spectrum analysis[J]. Journal of Central South University (Science and Technology), 2015, 46(5): 1747-1753. |
| [10] |
陈钢花, 王军, 程探探, 等. 粒子群算法在砂砾岩体岩性识别中的应用[J]. 测井技术, 2015, 39(2): 171-174. CHEN Ganghua, WANG Jun, CHENG Tantan, et al. Application of particle swarm optimization to glute-nite lithology identification[J]. Well Logging Techno-logy, 2015, 39(2): 171-174. |
| [11] |
于正军. 灰质背景下浊积岩储层地震响应特征及识别方法——以东营凹陷董集洼陷为例[J]. 油气地质与采收率, 2014, 21(2): 95-97. YU Zhengjun. Seismic response characteristics and recognition method of turbidity under carbonate depositional environment:a case in Dongji sag of Dongying sag[J]. Petroleum Geology and Recovery Efficiency, 2014, 21(2): 95-97. DOI:10.3969/j.issn.1009-9603.2014.02.024 |
| [12] |
周游, 高刚, 桂志先, 等. 灰质发育背景下识别浊积岩优质储层的技术研究——以东营凹陷董集洼陷为例[J]. 物探与化探, 2017, 41(5): 899-906. ZHOU You, GAO Gang, GUI Zhixian, et al. Study on the identification of turbidite high-quality reservoirs under gray background:a case study in Dongji sag of Dongying depression[J]. Geophysical and Geochemical Exploration, 2017, 41(5): 899-906. |
| [13] |
杨兆栓, 林畅松, 尹宏, 等. 主成分分析在塔中地区奥陶系鹰山组碳酸盐岩岩性识别中的应用[J]. 天然气地球科学, 2015, 26(1): 54-59. YANG Zhaoshuan, LIN Changsong, YIN Hong, et al. Application of principal component analysis in carbo-nate lithology identification of the Ordovician Ying-shan formation in Tazhong area[J]. Natural Gas Geoscience, 2015, 26(1): 54-59. |
| [14] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |
| [15] |
赵京, 李立明. 基于主成分分析法和核主成分分析法的机器人全域性能综合评价[J]. 北京工业大学学报, 2014, 40(12): 1763-1769. ZHAO Jing, LI Liming. Comprehensive evaluation of robotic global performance based on principal component analysis and kernel principal component analysis[J]. Journal of Beijing University of Technology, 2014, 40(12): 1763-1769. DOI:10.11936/bjutxb2014121763 |
| [16] |
殷俊, 周静波, 金忠. 基于余弦角距离的主成分分析与核主成分分析[J]. 计算机工程与应用, 2011, 47(3): 9-12. YIN Jun, ZHOU Jingbo, JIN Zhong. Principal component analysis and kernel principal component analysis based on co-sine angle distance[J]. Computer Engineering and Applications, 2011, 47(3): 9-12. DOI:10.3778/j.issn.1002-8331.2011.03.003 |
| [17] |
郑静静, 王延光, 杜磊, 等. 基于概率核主成分分析的属性优化方法及其应用[J]. 石油地球物理勘探, 2014, 49(3): 567-571. ZHENG Jingjing, WANG Yanguang, DU Lei, et al. Attribute optimization based on the probability kernel principal component analysis[J]. Oil Geophysical Prospecting, 2014, 49(3): 567-571. |
| [18] |
印兴耀, 孔国英, 张广智. 基于核主成分分析的地震属性优化方法及应用[J]. 石油地球物理勘探, 2008, 43(2): 179-183. YIN Xingyao, KONG Guoying, ZHANG Guangzhi. Seismic attributes optimization based on kernel principal component analysis (KPCA) and application[J]. Oil Geophysical Prospecting, 2008, 43(2): 179-183. DOI:10.3321/j.issn:1000-7210.2008.02.011 |
| [19] |
陈斌, 陆从德, 刘光鼎. 基于核主成分分析的时间域航空电磁去噪方法[J]. 地球物理学报, 2014, 57(1): 295-302. CHEN Bin, LU Congde, LIU Guangding. A denoising method based on kernel principal component analysis for airborne time domain electromagnetic data[J]. Chinese Journal of Geophysics, 2014, 57(1): 295-302. |
| [20] |
胡嘉蕊, 吕震宙. 基于核主成分分析的多输出模型确认方法[J]. 北京航空航天大学学报, 2017, 43(7): 1470-1480. HU Jiarui, LYU Zhenzhou. Model validation method with multivariate output based on kernel principal component analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7): 1470-1480. |
| [21] |
潘新朋, 张广智, 印兴耀. 岩石物理驱动的储层裂缝参数与物性参数概率地震反演方法[J]. 地球物理学报, 2018, 61(2): 683-696. PAN Xinpeng, ZHANG Guangzhi, YIN Xingyao. Probabilistic seismic inversion for reservoir fracture and petrophysical parameters driven by rock-physics models[J]. Chinese Journal of Geophysics, 2018, 61(2): 683-696. |
| [22] |
Schölkopf B, Smola A, Muller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. DOI:10.1162/089976698300017467 |
| [23] |
Schölkopf B, Smola A, Muller K R. Kermel principal component analysis[J]. Advances in Kernel Methods-Support Vector Learning, 2009, 27(4): 555-559. |
| [24] |
Jolliffe I T.Principal Component Analysis[M].Springer-Verlag, Berlin, 2002, 20-24.
|
| [25] |
程国建, 郭瑞华. PSO-LSSVM分类模型在岩性识别中的应用[J]. 西安石油大学学报(自然科学版), 2010, 25(1): 96-99. CHENG Guojian, GUO Ruihua. Application of PSO-LSSVM classification model in logging lithology reco-gnition[J]. Journal of Xi'an Shiyou University (Na-tural Science Edition), 2010, 25(1): 96-99. DOI:10.3969/j.issn.1673-064X.2010.01.022 |
| [26] |
马海, 王延江, 胡睿, 等. 测井岩性识别新方法研究[J]. 地球物理学进展, 2009, 24(1): 263-269. MA Hai, WANG Yanjiang, HU Rui, et al. A novel method for well logging lithologic identification[J]. Progress in Geophysics, 2009, 24(1): 263-269. |
| [27] |
戴世立. 徐家围子断陷营城组火山岩岩性、储层岩石物理弹性参数特征分析[J]. 石油地球物理勘探, 2018, 53(1): 122-128. DAI Shili. Volcanic lithology and reservoir identification based elastic wave characteristics analysis in Yingcheng Formation, Xujiaweizi Depression[J]. Oil Geophysical Prospecting, 2018, 53(1): 122-128. |
| [28] |
刘毅, 陆正元, 吕晶, 等. 主成分分析法在泥页岩地层岩性识别中的应用[J]. 断块油气田, 2017, 24(3): 360-363. LIU Yi, LU Zhengyuan, LYU Jing, et al. Application of principal component analysis method in lithology identification for shale-formation[J]. Fault-Block Oil & Gas Field, 2017, 24(3): 360-363. |
| [29] |
关涛. 基于交会图和贝叶斯聚类分析法的岩性识别方法[J]. 科学技术与工程, 2013, 13(4): 976-979. GUAN Tao. Method of lithololgic identification based on crossplot and Bayseian cluster analysis algorithm[J]. Science Technology and Engineering, 2013, 13(4): 976-979. DOI:10.3969/j.issn.1671-1815.2013.04.029 |



 高刚, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院, 430100。Email:
高刚, 湖北省武汉市蔡甸区大学路111号长江大学地球物理与石油资源学院, 430100。Email: