② 中海石油(中国)有限公司深圳分公司, 广东深圳 518067;
③ 油气藏地质及开发工程国家重点实验室, 四川成都 610059;
④ 成都理工大学地球物理学院, 四川成都 610059
② Shenzhen Branch, CNOOC, Shenzhen, Guangdong 518067, China;
③ State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu, Sichuan 610059, China;
④ Geophysical Institute, Chengdu University of Technology, Chengdu, Sichuan 610059, China
随着石油工业从增加产量转向价值优化,石油行业对储层预测的精度要求越来越高。由于储层的渗流能力反映储层品质,因此在评价中、深层优质储层时,不能仅考虑孔隙度参数,而要同时兼顾渗透率、流体性质等其他因素。但迄今为止,人们还基本停留在通过研究渗透率的地震响应特征评价储层[1-2],而很难基于地震资料反演渗透率或预测储层。因此,近年来人们将目光逐渐由渗透率转向储层流体的可动性,如流体流度属性可很好地表征流体的可动性。有人[3-5]以渗流理论为基础首次推导了饱和流体弹性介质波动方程,并证明该方程与试井分析中常用的Frenkel-Gassmann-Biot多孔弹性模型、压力扩散模型[6]相关,最终得到饱和流体储层低频域反射系数渐近表达式,认为低频反射系数正比于流体流度(Fluid Mobility,又称迁移率)、岩石体积密度、地震信号频率的平方根。Goloshubin等[7-8]应用流体流动性和散射机制,推导出与地震频率相关的流体流度属性,并用该属性预测储层中流体的流动能力和渗透率。Chen等[9]基于实际地震资料的流体流度属性识别流体,取得了较好的效果。张生强等[10]基于高分辨率反演谱分解近似计算流体流度属性,进一步提高了流体流度属性剖面的分辨率。其中高分辨率反演谱分解使用稀疏反演算法将地震资料投影到分频子波库,再将所得结果进行重排,从而得到一个稀疏的时频谱, 其实质仍是一种分频方法。
由于在流体流度属性计算过程中,需要计算地震数据的瞬时振幅谱,不同时频分析方法获得的流体流度属性剖面的分辨率存在差异,进而影响储层预测精度。因此为提高储层预测精度,有必要选择时频分析方法以获得高分辨流体流度属性剖面。小波变换(WT)继承和发展了短时傅里叶变换局部化的思想,同时能够提供一个随频率改变的“时—频”窗口,是信号时频分析的较理想工具,但小波变换的结果是时间—尺度谱,而非时频谱。为此,Stockwell等[11]提出了S变换,S变换不仅反映信号在频率域的变化,而且可以实现无损重构。为了使窗函数更灵活,人们又提出了广义S变换,如陈学华等[12-14]引入了两个调节参数λ、p,可根据实际地震资料分解尺度的需要灵活调节,以使地震资料的分辨率达到所需的分析尺度。与小波变换相比,S变换、广义S变换等引入信号频率参数控制窗口尺度,其变换结果是更为直观的时间—频率谱,便于分析信号的频率特征。受测不准原理的制约,以上变换的时频谱分辨率仍然有限。Wigner-Ville分布作为一种非线性时频分析方法,摆脱了测不准原理的制约,但对于复杂信号会产生交叉项干扰[15]。Lu等[16-17]提出反褶积短时傅里叶变换,不仅提高了时、频分辨率,且减少了交叉项干扰。朱恒等[18]首次利用反褶积短时傅里叶变换提取单频剖面预测薄储层。张懿疆等[19]首次利用反褶积广义S变换分析薄储层的低频伴影,取得较好的效果。本文利用反褶积广义S变换提取流体流度属性,通过仿真试验和实例试算验证了方法的有效性和实用性。
1 方法原理 1.1 流体流度属性的定义及提取方法Korneev等[3]、Silin等[4]、Goloshubin等[8]推导了饱和流体介质在低频域地震响应的反射系数线性渐近表达式。平面纵波在干岩石与饱含流体弹性介质界面上的反射系数为
| $ R = {R_0} + {R_1}(1 + {\rm{i}})\sqrt {\frac{{\kappa {\rho _{\rm{b}}}}}{\eta }\omega } $ | (1) |
式中:i为虚数单位;R0和R1是实系数,为反映岩石和流体特性的函数,包括孔隙度、密度和弹性系数信息;κ为储层渗透率;η为流体黏滞系数;ρb为储层内流体的密度;ω为低频地震信号的角频率。
将式(1)对ω求导,得
| $ \frac{{{\rm{d}}R}}{{{\rm{d}}\omega }} = \frac{{{R_1}(1 + {\rm{i}})}}{2}\sqrt {\frac{{{\rho _{\rm{b}}}}}{\omega }} \sqrt {\frac{\kappa }{\eta }} $ | (2) |
Goloshubin等[7]在低频渐近分析理论的基础上提出了成像属性的概念,即
| $ A(x, y) = \frac{{{\rm{d}}R\left( {{\omega _{{\rm{low}}}}} \right)}}{{{\rm{d}}\omega }} \sim \frac{{{\rm{d}}a\left( {{\omega _{{\rm{low}}}}} \right)}}{{{\rm{d}}\omega }} $ | (3) |
式中:R(ωlow)为低频反射系数;a(ωlow)为低频端地震振幅;~代表等价关系;x、y为储层的横向坐标。令
| $ A(x, y) \approx C{\left( {\frac{\kappa }{\eta }} \right)^{\frac{1}{2}}} = C{m^{\frac{1}{2}}} $ | (4) |
式中
| $ m = \frac{\kappa }{\eta } \sim \frac{1}{{{C^2}}}{\left( {\frac{{{\rm{d}}a}}{{{\rm{d}}\omega }}} \right)^2} $ | (5) |
Silin等[4-5]指出,当含流体孔隙介质其结构属性值在合理范围内时,依赖频率的地震反射系数在低频端达到峰值,而对地震数据进行瞬时谱分解后,单频瞬时振幅或能量能准确地刻画该频率的地震反射振幅或能量,且利用具有高分辨率和良好时频局部化性能的时频分析方法可减少薄互层调谐对地震瞬时振幅计算结果的影响。因此,文中依据文献[9]、[10]的近似计算流体流度属性的方法,对地震资料的低频成分进行时频分析获得
在求取流体流度属性过程中,需要求取峰值频率,Silin等[5]在推导纵波入射渗透地层的反射理论公式时,获得了快纵波反射共振峰值频率
| $ {f_{\max }} = \frac{\kappa }{{2\pi \eta {H^2}}}\frac{{2M}}{{\gamma \beta + \gamma {K^2}}} $ | (6) |
式中:H为目的层厚度;
| $ {K_{{\rm{sg}}}} = \frac{{{K_{\rm{g}}}}}{{1 - \phi }} $ |
| $ {K_{{\rm{fg}}}} = \frac{{{K_{\rm{g}}}}}{{1 - \frac{K}{{{K_{\rm{g}}}}}}} $ |
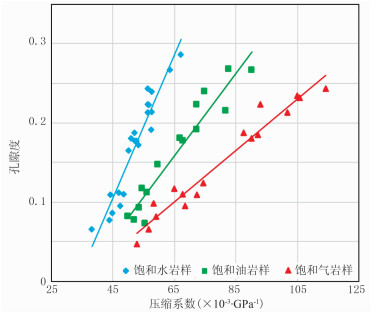
式中:Ksg和Kfg分别为骨架的体应变和流体压力变化造成的基质颗粒压缩,把颗粒体应变与骨架应力、流体压力联系起来;Kg为基质体积模量;ϕ为孔隙度;K为干岩石体积模量。以上各参数中,Kg最难求取。为此,本文采用贺锡雷[20]的LRM线性拟合法求取Kg。通过对Biot-Gassmann流体替换方程进行合理改造,可获得其近似公式。考虑到难以直接由测井资料获得骨架模量或干岩石模量以及孔隙结构明显影响岩石有效弹性模量等因素,将含有孔隙结构信息的干岩石椭球包体近似公式引入流体替换方程近似式,与常规计算岩石基质模量的方法相比,LRM法简单易行且精度较高。图 1为根据南海A区岩石物理参数得到的压缩系数(体积模量的倒数)—孔隙度交会图。根据LRM方法可知,压缩系数为截距B(在负半轴,取绝对值)与斜率A的比值。表 1是据A区54块岩样计算的压缩系数及拟合系数A、B。由表可见,岩样饱和不同流体求出的压缩系数基本是一致的,在实际计算过程中取平均值即可。
|
图 1 压缩系数—孔隙度交会图 三条直线分别由三组数据拟合而成,系数A、B分别为所拟合直线的斜率与截距 |
|
|
表 1 据A区54块岩样计算的压缩系数 |
陈学华等[12-13]引入高斯窗函数的调节参数λ>0、p>0,通过调节λ、p改变高斯窗随频率的变化趋势,从而灵活地分析、处理具体信号。对于信号x(t),其广义S变换可表示为
| $ {\mathop{\rm GST}\nolimits} (\tau , f) = \int_{ - \infty }^\infty x (t)\frac{{\lambda |f{|^p}}}{{\sqrt {2\pi } }}{{\rm{e}}^{\frac{{ - {\lambda ^2}{f^{2\beta }}{{(\tau - t)}^2}}}{2}}}{{\rm{e}}^{ - {\rm{i}}2\pi ft}}{\rm{d}}t $ | (7) |
式中:τ为用于确定分析时窗的时间位移;f为频率。
广义S变换谱为原始信号与高斯窗各自的Wigner-Ville分布的二维褶积,即
| $ \begin{array}{l} {{\mathop{\rm SPEC}\nolimits} _x}{\left| {{{{\mathop{\rm GST}\nolimits} }_x}(t, f)} \right|^2} = \int {\int_{ - \infty }^\infty {{\rm{WV}}{{\rm{D}}_x}} } (u, v) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{WV}}{{\rm{D}}_h}(t - u, f - v){\rm{d}}u{\rm{d}}v \end{array} $ | (8) |
式中:WVDx为原始信号x(t)的Wigner-Ville分布(简写为Wx );WVDh为高斯窗h(u)的Wigner-Ville分布(简写为Wh)。本文采用非线性的迭代复原反褶积算法——Lucy-Richardson反褶积算法[16-17]计算广义S变换谱,其表达式为
| $ W_x^ - (k + 1) = W_x^ - (k)\left( {{W_h}*\frac{{{S_x}}}{{{W_h} \otimes W_x^ - (k)}}} \right) $ | (9) |
式中:k+1是目前的迭代次数;
首先利用合成信号验证广义S变换、反褶积短时傅里叶变换、反褶积广义S变换的时频分析效果。合成信号x(t)为由3个线性信号叠加而成的时变信号,即
| $ x(t) = \left\{ \begin{array}{l} \cos \left[ {2\pi \cdot \left( {\frac{{20}}{{512}}} \right)} \right]t\;\;\, 0 \le t \le \frac{{512}}{3}\\ \cos \left[ {2\pi \cdot \left( {\frac{{60}}{{512}}} \right)} \right]t\;\;\, \frac{{512}}{3} < t \le \frac{{1024}}{3}\\ \cos \left[ {2\pi \cdot \left( {\frac{{100}}{{512}}} \right)} \right]t\;\;\, \frac{{1024}}{3} < t \le 512 \end{array} \right. $ | (10) |
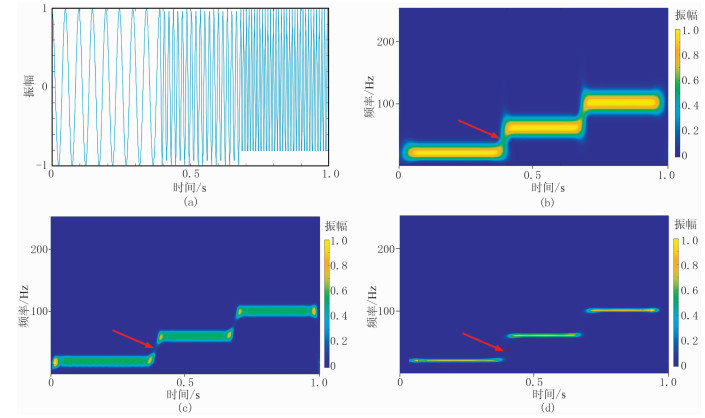
图 2为合成信号及利用不同分析方法得到的时频谱。由图可见:利用广义S变换得到的时频谱中频率发生突变的位置(红色箭头所示)不清晰(图 2b);对信号做反褶积短时傅里叶变换得到的时频分布的边界相对清楚(图 2c),但仍不明显;对信号做反褶积广义S变换得到的时频分布(图 2d)较好地区分了不同频率成分的信号,显示出较高的时频分辨率与时频聚集性。
|
图 2 合成信号及利用不同分析方法得到的时频谱 (a)合成信号;(b)广义S变换时频谱;(c)反褶积短时傅里叶变换时频谱;(d)反褶积广义S变换时频谱 |
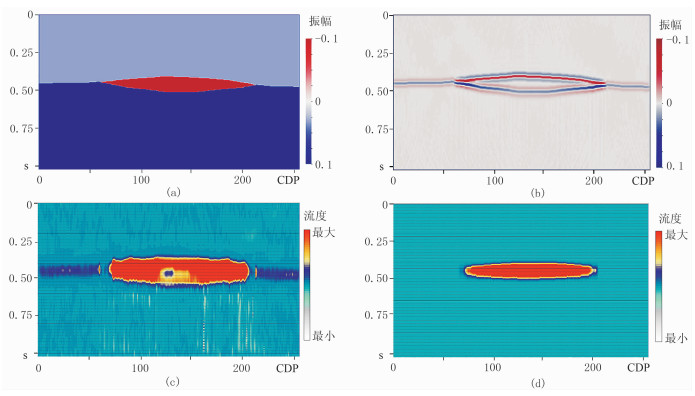
利用黏滞—弥散波动方程进行数值模拟,该方程是一种考虑流体黏滞性和弥散性的声波方程,可以很好地体现含流体储层对不同频率地震波的衰减特性[21-23]。图 3为透镜体储层模型及由不同方法得到的流体流度属性剖面。由图可见:基于反褶积短时傅里叶变换得到的储层流体流度剖面中目的层的高流体流度属性区域与透镜体位置不完全对应(图 3c);基于反褶积广义S变换得到的储层流体流度剖面中高流体流度属性区域与透镜体的位置较为一致,尤其对透镜体储层两侧尖灭点刻画较好,验证了方法的高分辨率特性(图 3d)。
|
图 3 透镜体储层模型及由不同方法得到的流体流度属性剖面 (a)透镜体储层模型;(b)合成地震记录;(c)基于反褶积短时傅里叶变换得到的储层流体流度;(d)基于反褶积广义S变换得到的储层流体流度。图a中包含一个薄透镜体储层,红色区域为含气层,其他区域为干层 |
为了进一步验证文中方法的实效性,从南海A区的地震数据中提取了流体流度属性。该区位于南海北部陆坡前缘,处于长源富砂珠江组下方,是深水勘探的有利地区,已发现多个油气田和具有潜在商业价值的含油气构造。工区内储层纵波速度约为3500~4200m/s,地震资料主频为25~30Hz,砂体平均厚度约为30m。地温梯度、埋深、成岩作用类型及强度共同控制砂岩储集性能的优劣。研究区优质储层埋深变化较大,主要分布范围为1000~3000m,地温梯度G分布范围为3~7℃/100m。在低地温梯度条件下(G<4℃/100m),储层原生、次生孔隙发育,渗透率较大,即使埋深达3000m时孔隙度也可达到15%,渗透率可达数十毫达西;在中、高地温梯度(G≥4℃/100m)条件下,储层次生孔隙发育、原生孔隙次之,形成中孔、低渗储层。工区横向地温梯度及纵向埋深差异造成强烈的储层物性非均质性,致使储层物性评价面临巨大挑战。
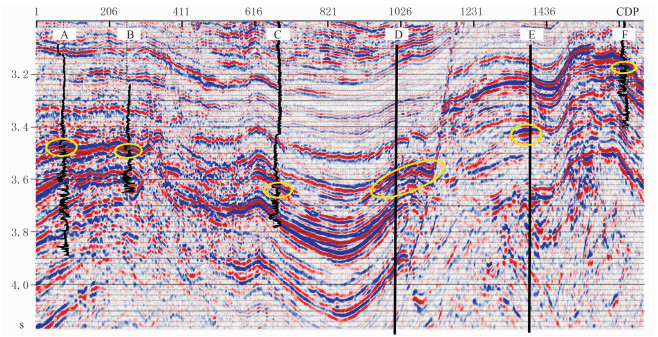
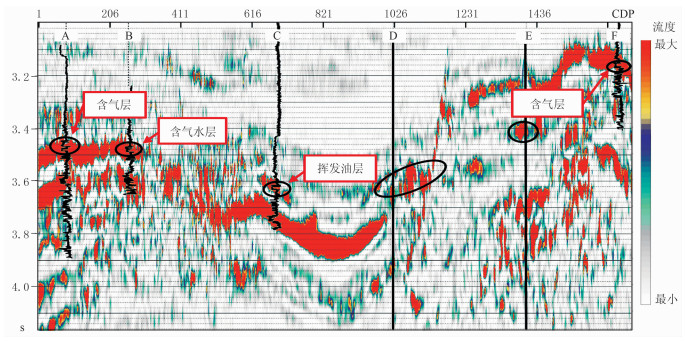
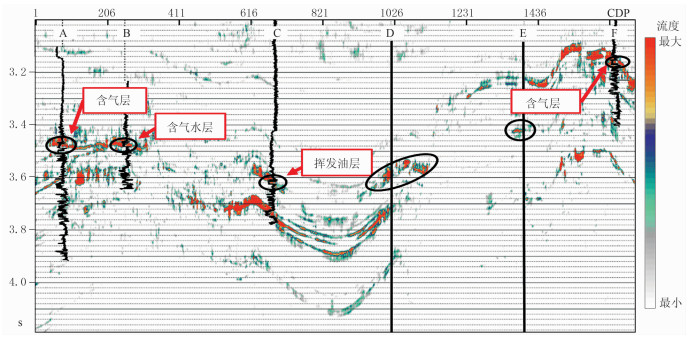
图 4为A—B—C—D—E—F井连井地震剖面,图 5、图 6分别为利用广义S变换和反褶积广义S变换获得的流体流度属性剖面。由图可见:由于流体在砂岩中的流动性较高,对应于高流度属性值(图 5、图 6);基于广义S变换的流体流度属性剖面虽然在储层位置呈流体流度属性高值,但高值区域的储层厚度大于井中解释的储层厚度(椭圆区域所示),即剖面的分辨率不高(图 5);基于反褶积广义S变换的流体流度属性剖面高值区与储层解释结果吻合很好,具有较高的分辨率(图 6)。
|
图 4 A—B—C—D—E—F井连井地震剖面 A、B、C和F井为已钻井,均钻遇储层(黄色椭圆位置),储层分别为含气层、含气水层、挥发油层和含气层;D、E井为待钻井。井曲线为伽马曲线,伽马曲线异常低值区域指示砂岩储层,高值区域指示泥岩,图 5、图 6同 |
|
图 5 广义S变换获得的流体流度属性剖面 黑色椭圆位置呈流体流度属性高值,指示储层物性及连通性较好 |
|
图 6 反褶积广义S变换获得的流体流度属性剖面 黑色椭圆位置呈流体流度属性高值,指示储层物性及连通性较好,但反映的储层厚度略小于图 5 |
(1) 与广义S变换相比,反褶积广义S变换的时频分辨率与频率聚集性进一步提高,适合处理具有时变特征的地震数据。
(2) Goloshubin流体流度属性与储层渗透率和流体黏滞系数具相关性,在理论上表征了储层流体的活动能力。实例分析展示了由地震数据得到的流体流度属性预测储层的可行性。
(3) 精确获取地震频率信息是获得高精度流体流度属性的关键,不同时频分析方法获得的流体流度属性剖面的分辨率存在一定差异,本文通过引入反褶积广义S变换,提高了流体流度属性剖面的分辨率。
尚需指出,流体流度属性目前在流体性质识别方面上存在一定缺陷,因此需结合其他方法(如叠前反演或AVO分析)评价储层。
| [1] |
Rubino J G, Velis D R, Holliger K. Permeability effects on the seismic response of gas reservoirs[J]. Geophysical Journal International, 2012, 189(1): 448-468. DOI:10.1111/gji.2012.189.issue-1 |
| [2] |
陈程, 文晓涛, 郝亚矩, 等. 基于White模型的砂岩储层渗透率特性分析[J]. 石油地球物理勘探, 2015, 50(4): 723-729. CHEN Cheng, WEN Xiaotao, HAO Yaju, et al. Sandstone reservoir permeability characteristics analysis based on White model[J]. Oil Geophysical Prospecting, 2015, 50(4): 723-729. |
| [3] |
Korneev V A, Silin D B, Goloshubin G M, et al.Seismic imaging of oil production rate[C].SEG Technical Program Expanded Abstracts, 2004, 23: 1476-1479.
|
| [4] |
Silin D and Goloshubin G M.A Low-frequency As-ymptotic Model of Seismic Reflection from a High Permeability Layer[R].Lawrence Berkeley National Laboratory Report, Berkeley, California, USA, 2009.
|
| [5] |
Silin D, Goloshubin G M. An asymptotic model of seismic reflection from a permeable layer[J]. Transport in Porous Media, 2010, 83(1): 233-256. DOI:10.1007/s11242-010-9533-8 |
| [6] |
Gassmann F. Uber die elastizitat poroser medien[J]. Veirteljahrsschrift der Naturforschenden Gesellschaft in Zzirich, 1951, 96: 1-23. |
| [7] |
Goloshubin G, Vanschuyver C, Korneev V, et al. Reservoir imaging using low frequencies of seismic reflections[J]. The Leading Edge, 2006, 25(5): 527-531. DOI:10.1190/1.2202652 |
| [8] |
Goloshubin G, Silin D, Vingalov V, et al. Reservoir permeability from seismic attribute analysis[J]. The Leading Edge, 2008, 27(3): 376-381. DOI:10.1190/1.2896629 |
| [9] |
Chen X H, He Z H, Zhu S X, et al. Seismic low-frequency-based calculation of reservoir fluid mobility and its applications[J]. Applied Geophysics, 2012, 9(3): 326-332. DOI:10.1007/s11770-012-0340-6 |
| [10] |
张生强, 韩立国, 李才, 等. 基于高分辨率反演谱分解的储层流体流度计算方法研究[J]. 石油物探, 2015, 54(2): 142-149. ZHANG Shengqiang, HAN Liguo, LI Cai, et al. Computation method for reservoir fluid mobility based on high-resolution inversion spectral decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 142-149. DOI:10.3969/j.issn.1000-1441.2015.02.004 |
| [11] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum:the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [12] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008, 43(5): 530-534. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-efficient time-frequency spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geophysical Prospecting, 2008, 43(5): 530-534. DOI:10.3321/j.issn:1000-7210.2008.05.008 |
| [13] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN Xuehua, HE Zhenhua, Huang Deji, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [14] |
陈学华, 贺振华, 文晓涛, 等. 低频阴影的数值模拟与检测[J]. 石油地球物理勘探, 2009, 44(3): 298-303. CHEN Xuehua, HE Zhenhua, Wen Xiaotao, et al. Numeric simulation and detection of low frequency sha-dow[J]. Oil Geophysical Prospecting, 2009, 44(3): 298-303. DOI:10.3321/j.issn:1000-7210.2009.03.010 |
| [15] |
Martin W, Flandrin P. Wigner-Ville spectral analysis of nonstationary processes[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 2003, 33(6): 1461-1470. |
| [16] |
Lu W K, Zhang Q. Deconvolutive short-time Fourier transform spectrogram[J]. IEEE Signal Processing Letters, 2009, 16(7): 576-579. DOI:10.1109/LSP.2009.2020887 |
| [17] |
Lu W K, Li F Y. Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram[J]. Geophysics, 2013, 78(2): V43-V51. DOI:10.1190/geo2012-0125.1 |
| [18] |
朱恒, 文晓涛, 金炜龙, 等. 基于反褶积短时傅立叶变换的油气检测[J]. 地球物理学进展, 2015, 30(5): 2354-2359. ZHU Heng, WEN Xiaotao, JIN Weilong, et al. Oiland gas detection based on deconvolutive short-time Fourier transform[J]. Progress in Geophysics, 2015, 30(5): 2354-2359. |
| [19] |
张懿疆, 文晓涛, 刘婷, 等. 基于反褶积广义S变换的地震频谱成像方法研究[J]. 科学技术与工程, 2017, 17(15): 12-18. ZHANG Yijiang, WEN Xiaotao, LIU Ting, et al. Seismic spectral imaging method based on deconvolutive generalized S-transform[J]. Science Technology and Engineering, 2017, 17(15): 12-18. DOI:10.3969/j.issn.1671-1815.2017.15.002 |
| [20] |
贺锡雷.烃类预测的岩石物理基础和地震孔隙度反演[D].四川成都: 成都理工大学, 2012.
|
| [21] |
胡军辉, 文晓涛, 杨小江, 等. 基于叠前黏滞-弥散波动方程的数值模拟[J]. 石油地球物理勘探, 2014, 49(4): 708-714. HU Junhui, WEN Xiaotao, YANG Xiaojiang, et al. Numerical simulation based on prestack diffusive-viscous wave equation[J]. Oil Geophysical Prospecting, 2014, 49(4): 708-714. |
| [22] |
胡军辉, 文晓涛, 许艳秋, 等. 利用黏滞-弥散波动方程理论进行油水识别[J]. 石油地球物理勘探, 2016, 51(3): 556-564. HU Junhui, WEN Xiaotao, XU Yanqiu, et al. Oil-water recognition based on diffusive-viscous wave equation[J]. Oil Geophysical Prospecting, 2016, 51(3): 556-564. |
| [23] |
李世凯, 文晓涛, 阮韵淇, 等. 基于黏滞-弥散理论的含气砂岩数值模拟与分析[J]. 石油地球物理勘探, 2017, 52(4): 752-759. LI Shikai, WEN Xiaotao, RUAN Yunqi, et al. Sandstone gas reservoir simulation and analysis based on diffusive-viscous theory[J]. Oil Geophysical Prospecting, 2017, 52(4): 752-759. |



 张懿疆 四川省成都市成华区二仙桥东三路1号成都理工大学油气藏地质及开发工程国家重点实验室, 610059。Email:
张懿疆 四川省成都市成华区二仙桥东三路1号成都理工大学油气藏地质及开发工程国家重点实验室, 610059。Email: