利用地震数据时频分析[1-3]进行储层预测的应用非常广泛,这些方法通过分析地震数据频谱的振幅谱,利用含流体储层高频衰减、低频阴影的特征辅助进行流体检测以及薄互层识别,并取得了较好的应用效果。相位谱也是地震信号频谱分析中非常重要的组成部分。目前,研究人员主要用相位信息辅助进行地层结构的解释,如通过瞬时相位信息识别超剥线、计算薄层厚度等[4-5],但对于相位谱的进一步应用显得不足,特别是针对地震数据中相位信息分解与重构的研究几乎是空白,主要原因是相位谱不太直观,并且对相位谱的有效应用有一定的难度。因此,如何从地震数据中有效地提取相位信息并进行分析是地震数据频率域处理的难点,也是今后研究的热点。
以高分辨率谱估计方法[6]为基础,选择合适的窗函数,逐点提取地震道的时频信息,针对相位谱信息,在[-180°, 180°]区间设定待重构的相位值及相位容许误差,并将设定值以外的相位信息置为零,再进行傅里叶反变换,即可得到分相位重构后的地震道。该地震道只包含设定相位的信息,实现了地震数据的分相位重构。该方法能用于地震数据的处理和解释,可以根据需要在不同的相位内分析地震数据,实现薄层或特殊反射体的有效识别,具有广泛的应用前景。
1 分相位重构方法原理 1.1 基于反演的谱估计谱估计的目的是得到地震数据的振幅谱和相位谱,这些振幅谱和相位谱包含了丰富的信息,进而可以进行储层预测。目前常用的谱估计方法包括短时傅里叶变换[7]、小波变换[8]、S变换[9]、匹配追踪分解[10]等,这些方法在石油勘探中得到了广泛的应用。
本文采用基于反演理论[11-13]的谱估计方法(Inversion based Spectral Analysis, ISA)实现地震信号的谱估计,与其他的谱估计方法相比,ISA方法具有更高的分辨率和稳定性。
考虑下面的正演方程
| $ \mathit{\boldsymbol{Fm}} = \mathit{\boldsymbol{d}} $ | (1) |
式中:m表示待求的频率系数向量;d表示加窗的地震数据;F表示不同频率的三角函数构成的矩阵
| $ F(t, f) = \cos (2\pi ft) + {\rm{i}}\sin (2\pi ft) $ | (2) |
式中:t表示时间;f表示频率;i为虚数单位。
为了提高时频估计结果的稳定性和分辨率,可以通过Hilbert[14-15]变换将d转换成复数的形式
| $ \mathit{\boldsymbol{d}} = {\mathit{\boldsymbol{d}}_{\rm{r}}} + {\rm{i}}{\mathit{\boldsymbol{d}}_{\rm{i}}} $ | (3) |
式中:dr表示d的实部;di表示d的虚部。
从式(1)中可以看出,已知观测数据d和正演矩阵F,求m,这是一个典型的反问题,实际应用中,式(1)往往是超定的,一般可以通过最小二乘法求解
| $ {\mathit{\boldsymbol{m}}_{\rm{e}}} = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (4) |
式中:me为最小二乘反演结果;FT表示F的共轭转置矩阵。
与其他地震反演过程[16-19]类似,为了提高式(4)求解的稳定性,需要加入约束信息[20],进一步得到
| $ {\mathit{\boldsymbol{m}}_{\rm{e}}} = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}} + \alpha \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (5) |
式中:α为常数;I表示单位对角矩阵。此时的me即为ISA结果。在加入αI约束分量后,对于信噪比较低、时间段较短的地震数据的谱估计会有更好的效果,可以提高求解过程的稳定性和分辨率。进一步将ISA的分析结果表示为
| $ {\mathit{\boldsymbol{F}}_{\rm{d}}}(f, t) = {\rm{ISA}}(\mathit{\boldsymbol{d}}) $ | (6) |
ISA只是一种谱估计的方法,为了得到时频谱,需要逐点对地震数据进行ISA分析。以待分析点为中心,对待分析信号加窗函数,目的是提取待分析点前后的若干点,窗函数可以有效减小频谱能量泄漏,窗函数可以加在时域上,也可以加在频域上,但在时域上加窗更为普遍。实际应用的窗函数主要包括:①幂窗(如矩形、三角形、梯形等);②三角函数窗(如汉宁窗、海明窗等);③指数窗(如高斯窗等)。文中使用的是汉宁窗,汉宁窗适用于非周期性的连续信号,地震数据实际上就是一种非周期性的连续信号。一般设定窗函数的时间长度为主频的倒数,如主频为25Hz,则窗长为40ms,具体可根据分相位重构的效果进行判断。
在通过ISA方法得到地震数据的时频谱Fd(f, t)后,时变振幅谱和相位谱的计算公式如下
| $ \left\{ \begin{array}{l} A(f, t) = \sqrt {{\left\{ {{\mathop{\rm real}\nolimits} \left[ {{\mathit{\boldsymbol{F}}_d}(f, t)} \right]} \right\}}^2} + {{\left\{ {{\mathop{\rm imag}\nolimits} \left[ {{\mathit{\boldsymbol{F}}_d}(f, t)} \right]} \right\}}^2} \\ P(\theta , t) = \frac{\arctan \frac{\text{imag}\left[ {{\mathit{\boldsymbol{F}}}_{d}}(f,t) \right]}{\text{real}\left[ {{\mathit{\boldsymbol{F}}}_{d}}(f,t) \right]}\times {{180}^{{}^\circ }}}{\pi } \end{array} \right. $ | (7) |
式中:A(f, t)表示地震数据的振幅谱;P(θ, t)表示地震数据的相位谱;θ表示相位;imag(·)表示求虚部;real(·)表示求实部。
进一步将振幅谱和相位谱统一表示为
| $ B(f, \theta , t) = \{ A(f, t), P(\theta , t)\} $ | (8) |
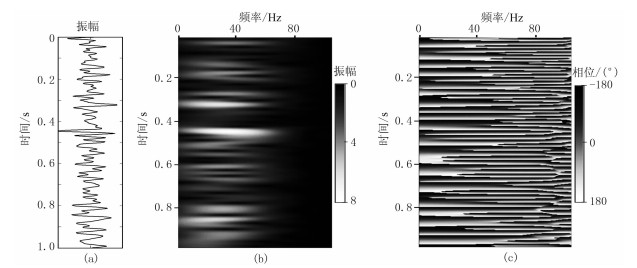
图 1为某一地震数据及其ISA时频分析结果。从图中可以看出,ISA时频分析结果具有较高的频率分辨率,并且相位谱在频率方向也比较平稳,说明该方法具有较高的相位分辨率和稳定性。
|
图 1 地震信号及其ISA分析结果 (a)原始地震道; (b)时频振幅谱; (c)时频相位谱 |
分相位数据的重构是方法的核心,设定相位值
| $ {{P}_{r}}\in [-{{180}^{{}^\circ }},\text{ }{{180}^{{}^\circ }}\text{ }\!\!]\!\!\text{ } $ | (9) |
式中Pr表示待重构的相位值。
由于实际地震数据中含有各种噪声,其瞬时相位谱复杂多变,很难得到较稳定的相位信息,往往呈现斜线、折线、震荡等特点,无法准确地提取所设定的相位值的相位信息。因此,为了保证相位重构后地震数据的稳定性,除了先要设定待重构的相位值外,还需要给定相位容许误差
| $ \left| {P(\theta , t) - {P_r}} \right| < {\varepsilon _b} $ | (10) |
式中εb表示相位容许误差,即当某一时刻的瞬时相位信息与设定的相位值之差的绝对值小于相位容许误差时,就保留该时刻的频谱信息;否则就将该时刻时频谱的实部和虚部都置为零,即只保留设定的待重构相位值的频率信息,其他相位所对应的频率信息都去除。
相位容许误差的大小可以通过试算法得到,给定若干相位容许误差,分别对数据进行分相位重构,并对重构结果进行分析,选择合适的相位容许误差。
用待重构的相位值Pr及相位容许误差εb对相位信息进行处理,然后在频谱的一定频率范围内进行傅里叶反变换,即可得到分相位重构后的地震数据,公式如下
| $ {D^\prime }\left( {{\theta _{{P_r}}}, t} \right) = {\mathop{\rm IFFT}\nolimits} \left\{ {\left[ {B\left( {f, {\theta _{{P_r}}}, t} \right)} \right]} \right\}_{{f_1}}^{{f_2}} $ | (11) |
式中:D′(θPr, t)表示重构后只包含指定相位信息的地震数据;θPr表示某一指定的相位值;f1、f2表示反变换所用的频率范围,一般令f1为0、f2为奈奎斯特频率(fN)[21],当f1>0、f2<fN时,该方法可实现带通分相位重构。对时频谱沿着时间轴逐点进行上述操作,即可完成整个地震道的分相位重构。地震数据分相位重构方法流程如图 2所示。

|
图 2 方法流程图 |
将[-180°, 180°]区间所有分相位重构后地震数据集合,就得到了相位道集。相位道集是相位分解与分重构中一个非常重要的概念,为了进一步说明,假设θ只取[-180°, 180°]区间的整数,定义下面的数据集合
| $ \begin{array}{l} {D^\prime }(\theta , t) = \left[ {{D^\prime }\left( {{\theta _{ -{{180}^{{}^\circ }}}}, t} \right), \cdots , {D^\prime }\left( {{\theta _{{{{0}^{{}^\circ }} }}}, t} \right), \cdots } \right., \\ \;\;\;\;\;\;\;\;\;\;\;\;{D^\prime }\left( {{\theta _{{{{180}^{{}^\circ }}}}}, t} \right)]\\ \end{array} $ | (12) |
式中:D′(θ, t)为相位道集;D′(θ-180°, t)为-180°相位的地震数据,依此类推。
相位道集的纵坐标表示时间,横坐标表示相位,包含了[-180°, 180°]区间的相位信息。相位道集的一个重要性质是将相位道集的数据叠加,可无损恢复原始地震数据,即
| $ D(t) = {D^\prime }(t) = \int_{-{{180}^{{}^\circ }}}^{{{180}^{{}^\circ }}}{{{{D^\prime }} (\theta , t){\rm{d}}\theta}} $ | (13) |
式中:D(t)表示地震数据;D′(t)表示将相位道集叠加后的地震数据。
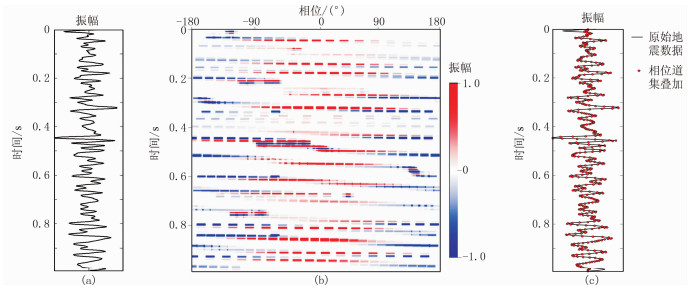
图 3为一个地震道的分相位重构效果。相位道集也称为分相位体,与分频体的概念类似,所有频率的分频体叠加,可无损恢复地震数据;同理,分相位体叠加,亦可无损恢复地震数据。图 3c中两条曲线几乎重合,说明了本文提出的分相位重构方法的准确性。
|
图 3 地震数据分相位重构 (a)地震道; (b)相位道集; (c)重构后地震道 |
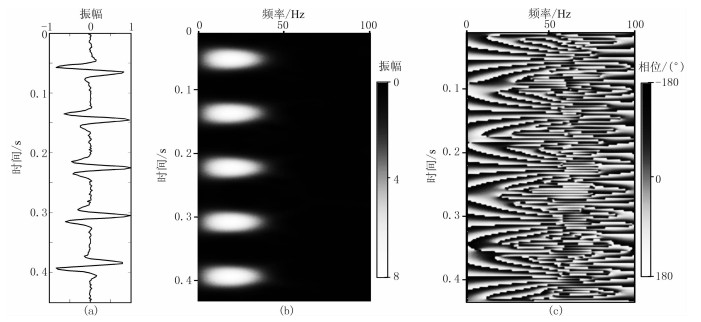
图 4a为一个合成信号,由5个不同相位的信号组成,从左到右分别为-90°、-40°、0°、40°、90°相位,并加入信噪比为4:1的噪声。用ISA方法对其进行时频分解,得到其时频振幅谱(图 4b)和时频相位谱(图 4c),可以看出这5个子信号的振幅谱一样,主频都是25Hz左右,带宽也基本一样,但是相位谱却明显不同。
|
图 4 合成信号及其ISA分析结果 (a)不同相位合成信号; (b)时频振幅谱; (c)时频相位谱 |
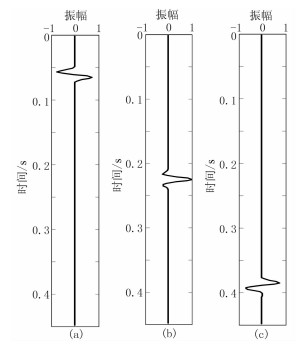
对该信号进行指定相位的重构,重构-90°、0°、90°相位分量的信号,如图 5所示。-90°相位分量只包含了合成信号中-90°相位分量的成分,波形特征为从波谷到波峰的变化;0°相位分量只包含了合成信号中0°相位分量的成分,波形特征为近似对称,一个主瓣外加两个旁瓣;90°相位分量只包含了合成信号中90°相位分量的成分,波形特征为从波峰到波谷的变化。通过对比可以看出,这3个相位分量信号与原始合成信号相应分量信号的波形基本一致,时间位置相同,说明了本文提出的分相位重构方法的有效性和准确性。
|
图 5 合成信号分相位重构 (a)-90°相位分量; (b)0°相位分量; (c)90°相位分量 |
实际应用中地震数据的长度应大于一个波长,为了保证分相位重构过程的稳定性和准确性,要求地震资料的信噪比大于4:1。在完成一维地震数据的分相位重构后,对地震数据进行道循环,即可完成三维地震数据的分相位重构。对于三维地震数据的分相位重构,相位容许误差的设定非常重要,相位容许误差过大,会包含过多的待重构相位以外的信息,相位容许误差过小,相位重构后地震数据的连续性会很差。一般来说,相位容许误差的设置原则是,在保证指定相位重构后剖面连续性的情况下,尽量减小相位容许误差。
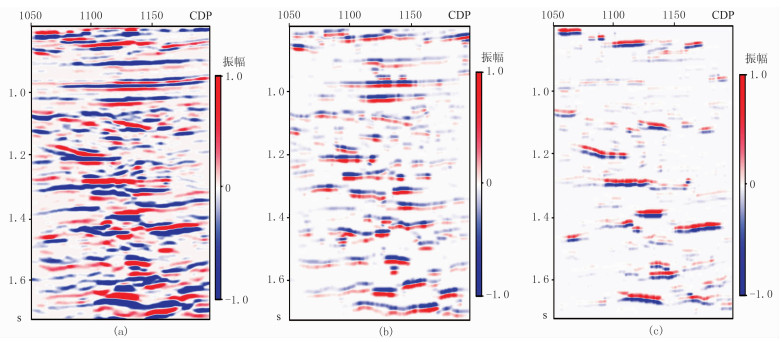
图 6为二维地震数据分相位重构结果,该数据摘自文献[6],通过图像处理技术转为SEGY格式。从图中可见,通过应用本文方法,地震亮点反射被放大聚焦,同时分辨率也得到了提高,并且不同相位分量地震剖面所表现出的地震同相轴以及亮点的形态不一样。对于零相位的地震资料,当储层波阻抗大于上下围岩时,一般对应着90°相位分量地震数据;当储层波阻抗小于上下围岩时,一般对应着-90°相位分量地震数据。实际过程中需结合研究区储层的速度分析结果对相位重构结果进行综合应用。
|
图 6 地震数据分相位重构 (a)原始地震数据; (b)-90°相位分量地震数据; (c)90°相位分量地震数据 |
如何从地震数据中有效地提取相位信息,并进一步分析处理,是目前地震数据频率域分析的热点和难点之一。本文实现了地震数据的分相位重构,进而可以得到不同相位分量的地震数据,这些不同相位分量的数据可以从不同的角度反映地质体的特征,从而更好地凸显地质异常体。下一步将开展分相位重构方法的实际应用研究。相信相位分析方法在岩性以及地层类油气藏储层预测中将发挥重要的作用。
| [1] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [2] |
Castagna J P, Sun S, Siegfried R, et al. Instantaneous spectral analysis:detection of low-frequency shadows associated with hydrocarbon[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [3] |
刘力辉, 李建海, 孙莹频, 等. 时频属性法薄互层预测[J]. 石油地球物理勘探, 2017, 52(6): 1261-1268. LIU Lihui, LI Jianhai, SUN Yingpin, et al. Thin inter-bed prediction with time and frequency attributes[J]. Oil Geophysical Prospecting, 2017, 52(6): 1261-1268. |
| [4] |
蔡涵鹏, 龙浩, 贺振华, 等. 基于地震数据瞬时相位谱的地层厚度估算[J]. 天然气地球科学, 2014, 25(4): 575-581. CAI Hanpeng, LONG Hao, HE Zhenhua, et al. Thickness estimation from instantaneous phase spectrum of post stack seismic data[J]. Natural Gas Geoscience, 2014, 25(4): 575-581. |
| [5] |
王鹏, 胡向阳, 魏水建. 基于改进的相位目标函数估算薄层厚度[J]. 石油地球物理勘探, 2018, 53(1): 178-185. WANG Peng, HU Xiangyang, WEI Shuijian. Thin bed thickness estimation based on an improved phase objective function[J]. Oil Geophysical Prospecting, 2018, 53(1): 178-185. |
| [6] |
Castagna J, Oyem A, Portniaguine O, et al. Phase decomposition[J]. Interpretation, 2016, 4(3): SN1-SN10. DOI:10.1190/INT-2015-0150.1 |
| [7] |
王祝文, 向旻, 刘菁华, 等. 基于分数阶Fourier变换的声波测井全波列特征时频分析[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1553-1559. WANG Zhuwen, XIANG Min, LIU Jinghua, et al. Time-frequency analysis for full waveform characterristics of acoustic logging based on fractal Fourier transform[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(5): 1553-1559. |
| [8] |
王西文, 刘全新, 高静怀, 等. 地震资料在小波域的分频处理与重构[J]. 石油地球物理勘探, 2001, 36(1): 78-85. WANG Xiwen, LIU Quanxin, GAO Jinghuai, et al. Frequency-shared processing and reconstitution of seismic data in wavelet domain[J]. Oil Geophysical Prospecting, 2001, 36(1): 78-85. DOI:10.3321/j.issn:1000-7210.2001.01.012 |
| [9] |
刘晗, 张建中, 黄忠来. 基于同步挤压S变换的地震信号时频分析[J]. 石油地球物理勘探, 2017, 52(4): 689-695. LIU Han, ZHANG Jianzhong, HUANG Zhonglai. Time-frequency analysis of seismic data using synchro-squeezing S transform[J]. Oil Geophysical Prospecting, 2017, 52(4): 689-695. |
| [10] |
Puryear C I, Tai S, Castagna J P, et al.Comparison of frequency attributes from CWT and MPD spectral decompositions of a complex turbidite channel model[C].SEG Technical Program Expanded Abstracts, 2008, 27: 393-397.
|
| [11] |
Puryear C I, Tai S, Castagna J P, et al. Constrained least-squares spectral analysis:Application to seismic data[J]. Geophysics, 2012, 77(5): V143-V167. DOI:10.1190/geo2011-0210.1 |
| [12] |
Portniaguine O, Castagna J P.Inverse spectral decomposition[C].SEG Technical Program Expanded Abstracts, 2004, 23: 1786-1789.
|
| [13] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. DOI:10.1190/1.1444596 |
| [14] |
刘柏森, 卢志茂, 申丽然, 等. 基于希尔伯特-黄变换的低信噪比语音端点检测[J]. 吉林大学学报(工学版), 2011, 41(3): 844-848. LIU Bosen, LU Zhimao, SHEN Liran, et al. Voice activity detection with low signal-to-noise ratio based on Hilbert-Huang transform[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(3): 844-848. |
| [15] |
梁岳, 顾汉明, 姚知铭. 改进的希尔伯特-黄变换在储层预测中的应用[J]. 石油物探, 2016, 55(4): 606-615. LIANG Yue, GU Hanming, YAO Zhiming. The application of improved Hilbert-Huang transform in reservoir prediction[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 606-615. DOI:10.3969/j.issn.1000-1441.2016.04.016 |
| [16] |
杨培杰.地震子波盲提取与非线性反演[D].山东东营: 中国石油大学(华东), 2008. YANG Peijie.Seismic Wavelet Blind Extraction and Non-linear Inversion[D].China University of Petroleum(East China), Dongying, Shandong, 2008. |
| [17] |
杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演[J]. 地球物理学报, 2008, 51(6): 1876-1882. YANG Peijie, YIN Xingyao. Non-linear quadratic programming Bayesian prestack inversion[J]. Chinese Journal of Geophysics, 2008, 51(6): 1876-1882. DOI:10.3321/j.issn:0001-5733.2008.06.030 |
| [18] |
Hampson D P. AVO inversion, theory and practice[J]. Geophysics, 1991, 56(6): 39-42. |
| [19] |
李坤, 印兴耀, 宗兆云, 等. 基于快速匹配追踪的混合域地震稀疏反演方法[J]. 中国石油大学学报(自然科学版), 2018, 42(1): 50-59. LI Kun, YIN Xingyao, ZONG Zhaoyun, et al. Seismic sparse inversion in mixed-domain utilizing fast ma-tching pursuit algorithm[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2018, 42(1): 50-59. DOI:10.3969/j.issn.1673-5005.2018.01.006 |
| [20] |
杨培杰, 王长江, 毕俊凤, 等. 可变点约束叠前流体因子直接提取方法[J]. 地球物理学报, 2015, 58(6): 2188-2200. YANG Peijie, WANG Changjiang, BI Junfeng, et al. Direct extraction of the fluid factor based on variable point-constraint[J]. Chinese Journal of Geophysics, 2015, 58(6): 2188-2200. |
| [21] |
程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2013.
|



 杨培杰 山东省东营市聊城路2号中国石化胜利油田分公司勘探开发研究院, 257015。Email:
杨培杰 山东省东营市聊城路2号中国石化胜利油田分公司勘探开发研究院, 257015。Email: