② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580;
③ 中国石油化工股份有限公司胜利油田分公司物探研究院, 山东东营 257022
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China;
③ Geophysical Research Institute, Shengli Oil Field Branch Co., SINOPEC, Dongying, Shandong 257022, China
石油和天然气为重要的战略资源,随着国民经济的发展,油气需求量逐渐增大,油气勘探目标逐渐从构造油气藏转向岩性油气藏[1],薄层及薄互层逐渐成为勘探工作的重点。砂体厚度小、横向连通性差、难以确定沉积尖灭位置等因素增大了薄层和薄互层的识别难度[2],特别是当目标储层上、下存在高阻层时,较强的波阻抗差在地震剖面上呈强反射[3],屏蔽了目标砂层的弱反射信息,难以确定薄储层的尖灭线位置。地层尖灭线是控制油气成藏的重要因素,对于油气勘探、开发评价具有重要意义[4]。在一定的地域范围内,通常地层的结构特征变化不大,在地震剖面上同相轴的横向连续性较好[5],其反射子波的振幅、频率、相位等属性保持相对一致。因此根据这种特征利用匹配追踪稀疏理论拾取和剥离强反射干扰,进而削弱强反射对薄层砂体有效反射信息的屏蔽作用。
Mallat等[6]提出的匹配追踪算法(Matching Pursuit)根据信号局部结构特征构建超完备的字典原子库,在一组能够适应各种时频特性的原子上将信号展开,最终利用有限个原子稀疏表示原始信号,实现信号的自适应分解。Liu等[7-8]提出了动态匹配追踪算法的概念,在每次迭代过程中参与內积运算的时频原子随信号的局部瞬时属性发生变化,提高了信号的分解效率。匹配追踪算法在各领域得到广泛应用。宋维琪等[9]将复数子波匹配追踪算法应用于储层预测领域,可较好地识别薄层砂体信息;杨昊等[10]利用匹配追踪算法自动提取薄层顶、底反射系数,定量预测薄层厚度;张繁昌等[11]研究了基于匹配追踪瞬时谱计算的砂体尖灭线识别方法,并用于检测三角洲沉积砂体的尖灭线;李海山等[12]采用贪婪匹配追踪算法分离煤层强反射;李坤等[13]利用匹配追踪算法识别流体、刻画储层边界,减少了反演流程,且反演结果与测井资料保持一致。
基于以上研究背景,本文采用动态匹配追踪算法识别强反射,通过得到的最佳匹配强反射的子波剥离强反射。考虑到传统的瞬时频率运算结果存在负频率现象且易受噪声影响,即当计算结果出现负频率时,只能进行时频原子频率属性的全局搜索,并不是真正意义上的动态搜索[14]。为此,本文引进局部频率计算模式用于约束动态匹配追踪算法最优原子的搜索范围,其频率计算结果合理,可以确定最佳匹配强反射的地震子波。通过构建含高阻层的地质模型和实际资料验证了方法的可行性。
1 匹配追踪强反射识别与分离方法 1.1 基于局部频率约束的动态匹配追踪算法传统的匹配追踪算法是一种贪婪算法[15],通过创建超完备的时频原子库,对时移、频率和相位参数进行全局扫描,以寻找最佳相关的匹配原子,但该算法每一次迭代的內积运算量大,对信号的分解效率极低。动态匹配追踪算法将信号的瞬时特征作为先验信息约束匹配原子的搜索范围[16],以先验信息创建动态子波库,使每一次迭代的內积运算量大为减小,极大地提高了分解效率。传统方法以瞬时频率确定最优原子搜索范围,而瞬时频率是瞬时相位对时间的导数,计算结果存在“负频率”现象,且受噪声干扰大,计算结果极不稳定。当频率计算结果不合理时,只能对时频原子的频率属性进行全局搜索,并不是真正意义上的动态搜索。为此,本文将局部频率算法用于动态匹配追踪算法,根据整形光滑理论,利用差分算子综合某数据点邻域内的频率值,计算得到该数据点的频率属性信息,局部频率计算结果合理、稳定,抗噪性较强, 因此可以直接用于确定最优时频原子的搜索邻域。
连续信号x(t)的复地震道为[17]
| $ c(t) = x(t) + {\rm{i}}h(t) = A(t){{\rm{e}}^{{\rm{i}}\varphi (t)}} $ | (1) |
式中:h(t)为x(t)的Hilbert变换;A(t)为地震道包络;φ(t)为信号的瞬时相位。
传统的瞬时角频率ω(t)是瞬时相位φ(t)的时间变化率[18],即
| $ \begin{array}{l} \omega (t) = {\varphi ^\prime }(t) = {\mathop{\rm Im}\nolimits} \left[ {\frac{{{c^\prime }(t)}}{{c(t)}}} \right] = \frac{{x(t){h^\prime }(t) - {x^\prime }(t)h(t)}}{{{x^2}(t) + {h^2}(t)}}\\ \;\;\;\;\;\;\;\; = \frac{{u(t)}}{{v(t)}} \end{array} $ | (2) |
引入Fomel[19]的局部角频率ωloc的计算策略
| $ {\omega _{{\rm{loc}}}} = {\left[ {{\lambda ^2}\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{V}} - {\lambda ^2}\mathit{\boldsymbol{I}}} \right)} \right]^{ - 1}}\mathit{\boldsymbol{SU}} $ | (3) |
式中:λ为平滑尺度因子;I为单位向量;S为整形正则化算子[20];U和V分别为u(t)和v(t)组成的向量矩阵。
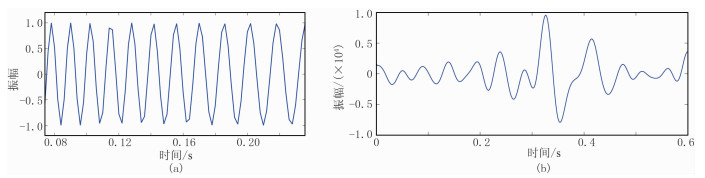
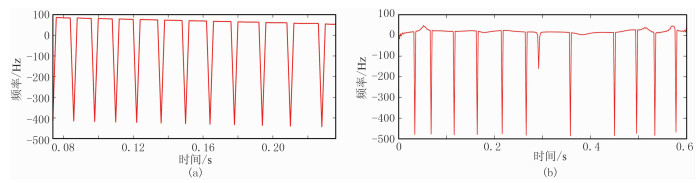
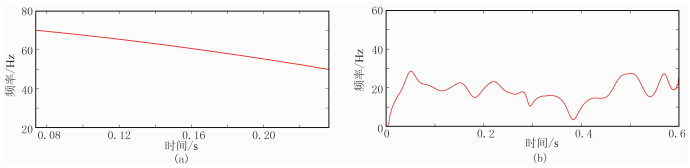
为了验证局部频率计算结果的合理性,设计两个用于对比的瞬时频率与局部频率信号(图 1)。图 2为线性调谐信号与实际地震信号的瞬时频率。由图可见,由于瞬时频率是相位对时间的导数,计算结果出现很多“负频率”现象,利用负频率奇异点不能直接确定动态匹配追踪频率参数搜索范围,需要进行全局扫描,因此不是真正意义上的动态搜索方式。图 3为线性调谐信号与实际地震信号的局部频率。由图可见,线性调谐信号的局部频率计算结果与理论值一致(图 3a),实际地震信号的局部频率计算结果较为合理(图 3b),在理论范围内不存在“负频率”现象,可以用于确定最佳匹配原子的频率参数。
|
图 1 线性调谐信号(a)与实际地震信号(b) 图a的频率由70Hz向50Hz减小 |
|
图 2 线性调谐信号(a)与实际地震信号(b)的瞬时频率 |
|
图 3 线性调谐信号(a)与实际地震信号(b)的局部频率 |
首先确定最大包络振幅的时间位置u0,即为此次迭代搜索的中心,进而得到该时间位置u0处的局部角频率ω0和相位φ0,以此创建匹配搜索的先验信息点α0(u0, ω0, φ0),并设定相邻控制参数的间隔Δα,得到最佳匹配原子的搜索范围γ′=[α0-nΔα, α0+nΔα](n为正整数, α为时频原子的三个控制参数u、ω和φ, Δα为相邻控制参数α的间隔),即得到迭代搜索的动态字典原子库D′={gγ′(t)}(D′∈D, gγ′(t)为时频原子), D为过完备字典原子库。
假定第1次迭代需要扫描动态字典原子库中的m个时频原子
| $ \begin{array}{l} \mathop g\limits_{i = 1, \cdots , {m^{\gamma '}}} = \left\{ {{u_0}, {\omega _i} \in \mathit{\boldsymbol{U}}\left[ {\omega \left( {{u_0}} \right), {\delta _\omega }} \right]} \right., \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varphi _i} \in \mathit{\boldsymbol{U}}\left[ {\varphi \left( {{u_0}} \right), {\delta _\varphi }} \right]\} \end{array} $ | (4) |
式中:u0为每个最佳匹配子波的搜索中心位置处的时间;ω(u0)和φ(u0)分别为搜索中心位置处信号的瞬时角频率和相位信息;U[ω(u0), δω]、U[φ(u0), δφ]分别为角频率和相位的搜索邻域, δω、δφ为相应参数搜索半径。
第1次迭代与信号最佳相关的时频原子gγ1(t)满足
| $ \left| {\left\langle {f, {g_{{\gamma _1}}}} \right\rangle } \right| = \mathop {\sup }\limits_{i = 1, \cdots , m} \left| {\left\langle {f, {g_{{\gamma _i}}}} \right\rangle } \right| $ | (5) |
则信号f被表示为沿gγ1(t)方向的分量和残差分量,即
| $ f = \left\langle {f, {g_{{\gamma _1}}}} \right\rangle {g_{{\gamma _1}}} + {{\rm{R}}^1}f $ | (6) |
式中R1f为第一次迭代后的残差信号。按上述方式依次迭代下去,直至达到预设的迭代次数和残差阈值,则迭代停止。若经过n次迭代后,完成对信号的分解过程,最终将信号表示为n个最佳匹配原子的线性组合
| $ f = \sum\limits_{i = 1}^n {\left\langle {{{\rm{R}}^{i - 1}}f, {g_{{\gamma _i}}}} \right\rangle } {g_{{\gamma _i}}} + {{\rm{R}}^n}f $ | (7) |
式中:Ri-1f为i-1次迭代后的残差信号;Rnf为n次迭代后的残差信号,当i=1时, R0f为原始信号。
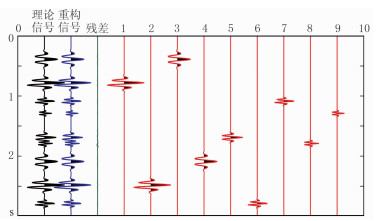
利用9个Morlet小波合成理论信号,基于局部频率约束的匹配追踪算法迭代分解理论信号,图 4为无噪声理论信号的迭代分解过程。由图可见,每一次迭代优选出一个最佳匹配的原子,经过9次迭代后,重构信号与理论信号高度吻合,残差曲线为零值。为验证本文提出的匹配追踪算法的抗噪性,对理论合成信号进行加噪,在信噪比为5:1的情况下,对加噪信号迭代分解,图 5为加噪理论信号的迭代分解过程。由图可见,基于局部频率约束的匹配追踪算法对信号的迭代分解过程稳定,经过9次迭代后,得到9个最佳匹配原子重构理论信号,残差曲线基本为噪声信号,证明该算法具有一定抗噪性。
|
图 4 无噪声理论信号的迭代分解过程 |

|
图 5 加噪理论信号的迭代分解过程 |
在对原始数据进行强反射识别与分离时,可以利用层位约束或一定的时窗范围内信号包络振幅最大位置拾取强反射具体位置。通过求取强反射时间位置的复地震道的局部频率、瞬时相位信息,构建局部反射特征波形库,利用式(5)搜索最佳相关的子波作为强反射子波。在对实际数据进行强反射剥离前,需要先确定强反射剥离的强度[21],即
| $ \frac{1}{M}\left\| {{d_N} - \xi \times {d_{{\rm{strong}}}}} \right\|_2^2 = \frac{1}{N}\left\| {{d_M}} \right\|_2^2 $ | (8) |
式中:dN为强反射时窗内地震数据能量, dM为背景时窗内地震数据能量, N和M分别代表其时窗内地震数据的采样点数;ξ为强反射压制参数;dstrong为拾取的强反射地震数据。
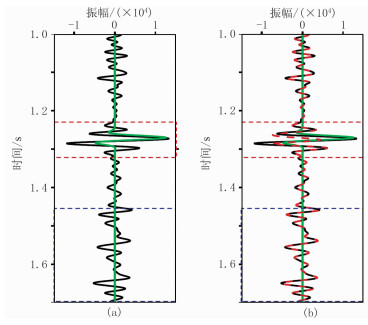
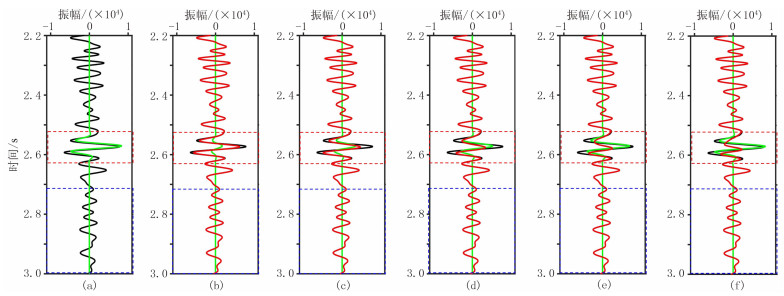
图 6为去除强反射前、后记录。根据压制强反射的能量均衡原则(式8),认为使去除强反射后的平均能量(红色虚线框)与背景能量(蓝色虚线框)基本保持一致的ξ为最佳强反射压制系数,能够达到较为理想的强反射压制效果(图 6b)。图 7为M区不同ξ的单道处理结果。为了满足能量均衡原则(式8),即使去除强反射后的平均能量(红色虚线框内)与地震数据背景能量(蓝色虚线框内)保持一致,通过对比选取ξ=0.6为最佳强反射压制系数,以此系数对实际地震数据进行强反射剥离,能够较为理想地压制强反射并突显目标储层弱反射信息(图 7d)。
|
图 6 去除强反射前(a)、后(b)记录 红色虚线框为含强反射的时窗,蓝色虚线框为选取的背景能量时窗,黑线为原始地震记录,绿线为根据强反射分析后拾取的最佳匹配子波,红线为去强反射后的地震记录 |
|
图 7 M区不同ξ的单道处理结果
(a)原始地震记录;(b)ξ=0.2;(c)ξ=0.4;(d)ξ=0.6;(e)ξ=0.8;(f)ξ=1.0 红色虚线框为含强反射的时窗,蓝色虚线框为选取的背景能量时窗,黑线为一道原始地震记录,绿线为利用基于局部频率约束的动态匹配追踪算法得到的最佳强反射子波,红线为去强反射后的单道地震记录 |
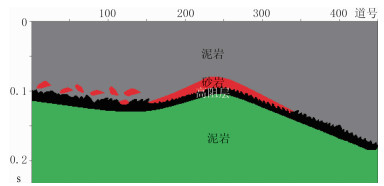
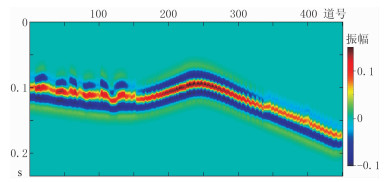
将本文提出的基于优化局部频率约束的动态匹配追踪强反射识别与分离方法用于模型数据的处理,以验证方法可靠性。构建含高阻层的理论地质模型(图 8),利用28Hz的Morlet小波合成理论模型的正演地震记录(图 9),可见由于受高速层的影响,顶部薄砂体的有效反射信息被强反射淹没,难以识别上覆砂体真正的形态和位置。图 10为由本文方法识别和剥离强反射后的地震记录。由图可见,明显地削弱了强干扰的影响,能够恢复上覆薄砂岩的地震响应。为了更清晰地看出强反射对砂体特征识别的影响,图 11和图 12分别为去除强反射前、后的地震道集。由图可见,剥离强反射后突显了砂体形态特征,有助于对储层进行精细描述,为后续地震数据处理提供了有效的数据基础(图 12)。
|
图 8 理论地质模型 模型顶部(灰色)和底部(绿色)为大套泥岩(平均速度为4300m/s,密度为2.7g/cm3),中部(黑色)为因泥岩脱水形成的高阻层(平均速度为4700m/s,密度为2.8g/cm3),高阻层上覆薄层砂岩(红色,平均速度为4350m/s,密度为2.5g/cm3) |
|
图 9 理论模型的正演地震记录 |
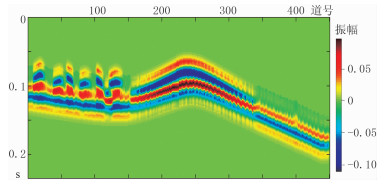
|
图 10 由本文方法识别和剥离强反射后的地震记录 |
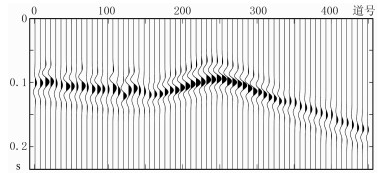
|
图 11 模型原始正演道集 |
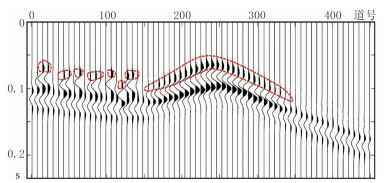
|
图 12 去除强反射后的地震道集 |
A区位于济阳坳陷,该区存在多级不整合,利于发育与不整合有关的油藏。实际地震资料存在典型的不整合反射特征,为准确描述岩性圈闭提供了基础数据。由于该区储层倾角小、储层厚度小且目的层上、下存在高阻抗体,地震反射特征不能真实反映不整合圈闭的地质特征。为了准确地拾取砂体反射特征信息,有必要识别与分离强反射。
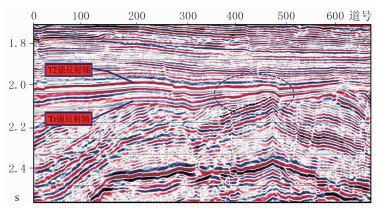
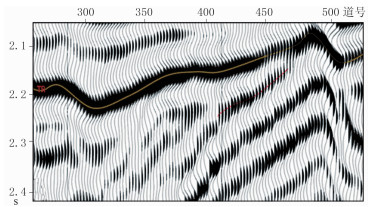
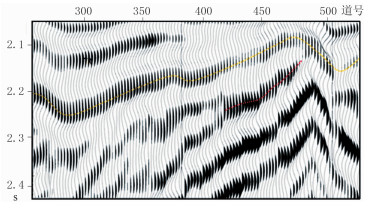
图 13为原始地震记录。由图可见,砂岩尖灭反射信息淹没于上覆高速层强反射中,难以识别真正的砂体尖灭点。考虑到强反射记录具有很好的横向连续性,利用本文提出方法将T2和Tr强反射从工区实际数据中剥离,从剥离后的地震记录(图 14)上可见,砂体的反射信息得到突显。从去除强反射前、后的地震道集上也能明显地看到:由于Tr强反射与砂体反射干涉、叠加,无法准确识别砂体尖灭位置(图 15);剥离Tr和T2强反射后砂体尖灭反射信息更清楚(图 16)。因此,高速层强反射识别与剥离技术为砂体尖灭识别提供了可靠的数据。
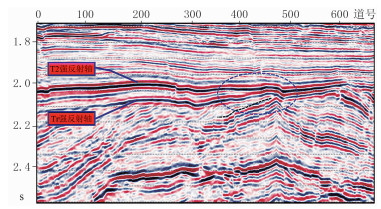
|
图 13 原始地震记录 强反射下存在砂岩储层(黑色虚线),蓝色椭圆框内为砂体尖灭位置 |
|
图 14 去除强反射的地震记录 |
|
图 15 原始地震道集 |
|
图 16 去除强反射的地震道集 |
为削弱目标储层上、下高阻层形成的强反射干扰影响,本文提出了基于局部频率约束的动态匹配追踪强反射识别与分离方法。考虑到瞬时频率计算结果存在“负频率”现象,认为其不适用于作为时频原子的频率搜索参数,本文提出局部频率计算模式,计算结果较为合理,将其作为构建动态子波库的控制参数。利用强反射位置处的局部频率和瞬时相位信息作为先验信息,构建动态反射特征波形库,以此搜索最佳匹配强反射子波,通过单道测试确定强反射压制系数,以保证剥离强反射后的均衡能量与背景能量一致,有助于拾取目标储层的反射信息,最终实现储层的精细描述。通过构建含高阻层的模型数据验证了基于局部频率约束的动态匹配追踪强反射识别和分离方法的可行性,并将该方法应用于实际地震数据,削弱了强反射干扰影响,突显了弱反射信息。
| [1] |
凌云研究组. 应用振幅的调谐作用探测地层厚度小于1/4波长地质目标[J]. 石油地球物理勘探, 2003, 38(3): 268-274. LING Yun Research Group. Application of amplitude tuning in surveying geologic target thickness less than 1/4 wavelength[J]. Oil Geophysical Prospecting, 2003, 38(3): 268-274. DOI:10.3321/j.issn:1000-7210.2003.03.011 |
| [2] |
Widess M B. How thin is a thin bed?[J]. Geophysics, 1973, 38(6): 1176-1180. DOI:10.1190/1.1440403 |
| [3] |
张在金, 张军华, 李军, 等. 煤系地层地震强反射剥离方法研究及低频伴影分析[J]. 石油地球物理勘探, 2016, 51(2): 376-383. ZHANG Zaijin, ZHANG Junhua, LI Jun, et al. A method for stripping coal seam strong reflection and low-frequency shadow analysis[J]. Oil Geophysical Prospecting, 2016, 51(2): 376-383. |
| [4] |
赵卫军, 支东明, 党玉芳, 等. 准噶尔盆地陆西地区侏罗系西山窑组顶界不整合结构特征及其与油气关系[J]. 新疆地质, 2007, 25(1): 92-95. ZHAO Weijun, ZHI Dongming, DANG Yufang, et al. Trait of unconformity structure and its relation with oil and gas at Xishanyaozu in Jurassic at Luxi Area in Junggar Basin[J]. Xinjiang Geology, 2007, 25(1): 92-95. DOI:10.3969/j.issn.1000-8845.2007.01.018 |
| [5] |
张志敏.青南洼陷古近系地震沉积学研究[D].山东东营: 中国石油大学(华东), 2009. ZHANG Zhimin.The Study of Seismic Sedimentology of Paleogene in Qing-Nan Sag[D].China University of Petroleum(East China), Dongying, Shandong, 2009. |
| [6] |
Mallat S G, Zhang Z. Matching-pursuit with time frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [7] |
Liu J, Wu Y, Han D, et al.Time-frequency decomposition based on Ricker wavelet[C].SEG Technical Program Expanded Abstracts, 2004, 23: 1937-1940.
|
| [8] |
Liu J, Marfurt K J.Matching pursuit decomposition using Morlet wavelets[C].SEG Technical Program Expanded Abstracts, 2005, 24: 786-789.
|
| [9] |
宋维琪, 朱卫星, 孙英杰. 复数子波匹配追踪算法识别薄层砂体[J]. 地球物理学进展, 2007, 22(6): 1796-1801. SONG Weiqi, ZHU Weixing, SUN Yingjie. Identify bed layer sandbody by complex wavelet matching algorithm[J]. Progress in Geophysics, 2007, 22(6): 1796-1801. DOI:10.3969/j.issn.1004-2903.2007.06.018 |
| [10] |
杨昊, 郑晓东, 李劲松, 等. 基于匹配追踪的薄层自动解释方法[J]. 石油地球物理勘探, 2013, 48(3): 429-435. YANG Hao, ZHENG Xiaodong, LI Jinsong, et al. Thin-bed automatic interpretation based on matching pursuit[J]. Oil Geophysical Prospecting, 2013, 48(3): 429-435. |
| [11] |
张繁昌, 李传辉, 印兴耀. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82-88. ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J]. Oil Geophysical Prospecting, 2012, 47(1): 82-88. |
| [12] |
李海山, 杨午阳, 田军, 等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探, 2014, 49(5): 866-870. LI Hhaishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014, 49(5): 866-870. |
| [13] |
李坤, 印兴耀, 宗兆云. 基于匹配追踪谱分解的时频域FAVO流体识别方法[J]. 石油学报, 2016, 37(6): 777-786. LI Kun, YIN Xingyao, ZONG Zhaoyun. Time-frequency-domain FAVO fluid discrimination method based on matching pursuit spectrum decomposition[J]. Acta Petrolei Sinica, 2016, 37(6): 777-786. |
| [14] |
张繁昌, 刘汉卿, 张立强, 等. 复数道动态匹配追踪算法的改进[J]. 石油地球物理勘探, 2016, 51(1): 183-189. ZHANG Fanchang, LIU Hanqing, ZHANG Liqiang, et al. Improved complex-trace dynamic matching pursuit algorithm[J]. Oil Geophysical Prospecting, 2016, 51(1): 183-189. |
| [15] |
邓志文, 赵贤正, 陈雨红, 等. 自适应波形多道匹配追踪断层识别技术[J]. 石油地球物理勘探, 2017, 52(3): 532-537. DENG Zhiwen, ZHAO Xianzheng, CHEN Yuhong, et al. Fault identification based on multichannel adaptive waveforms matching pursuit[J]. Oil Geophysical Prospecting, 2017, 52(3): 532-537. |
| [16] |
李传辉.地震信号快速匹配追踪分解及瞬时谱分析[D].山东青岛: 中国石油大学(华东), 2012. LI Chuanhui.Fast Matching Pursuit Decomposition and Instantaneous Spectral Analysis of Seismic Signals[D].China University of Petroleum(East China), Qingdao, Shandong, 2012. |
| [17] |
Taner M T, Koehler F, Sheriff R E. Complex seismic trace analysis[J]. Geophysics, 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
| [18] |
Barnes A E. The calculation of instantaneous frequency and instantaneous bandwidth[J]. Geophysics, 1992, 57(11): 1520-1524. DOI:10.1190/1.1443220 |
| [19] |
Fomel S. Local seismic attributes[J]. Geophysics, 2007, 72(3): A29-A33. DOI:10.1190/1.2437573 |
| [20] |
Fomel S. Shaping regulation in geophysical-estimation problems[J]. Geophysics, 2007, 72(2): R29-R36. DOI:10.1190/1.2433716 |
| [21] |
Candes E J. Ridgelets and the representation of mutilated Sobolev functions[J]. SIAM Journal on Mathematical Analysis, 2001, 33(2): 347-368. DOI:10.1137/S003614109936364X |



 印兴耀 山东省青岛市黄岛区长江西路中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀 山东省青岛市黄岛区长江西路中国石油大学(华东)地球科学与技术学院, 266580。Email: