② 东方地球物理公司研究院库尔勒分院, 新疆库尔勒 841001;
③ 东方地球物理公司研究院, 河北涿州 072751;
④ 中国石油塔里木油田公司勘探开发研究院, 新疆库尔勒 841000
② Korla Branch, GRI, BGP Inc., CNPC, Korla, Xinjiang 841001, China;
③ GRI, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China;
④ Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
岩石物理模型是储层地质特性与地球物理特性之间的桥梁,用于建立储层物性与弹性参数之间的关系[1]。岩石物理模型分为两类:一是基于波动力学推导得到的理论模型及相应的近似模型,如K-T、Xu-White模型等[2-4];二是利用实验数据拟合得到的经验模型,如Wyllie时间平均方程等[5]。理论模型的物理意义明确、理论依据充足,能够更好地反映弹性参数与物性之间的关系。
储层物性反演需要以岩石物理模型为基础,由地球物理弹性参数预测储层物性参数[6-10]。但由于理论模型的非线性特征较强,导致大多数物性反演方法利用复杂的非线性优化算法迭代求解,如共轭梯度法、马氏链蒙特卡洛法、模拟退火法等[11-16],此类算法多解性强且计算量巨大。针对岩石物理模型的非线性问题,Grana[17]采用一阶泰勒级数展开法线性化近似岩石物理模型,并通过正演与反演方法分析经验模型、颗粒介质模型和等效介质模型的近似结果,取得了一定效果;印兴耀等[18]和Tian等[19]采用泰勒级数展开法线性化近似Xu-White模型,并通过纵、横波速度正演验证结果的有效性。前人研究成果表明,基于泰勒级数展开法线性化近似岩石物理模型具有一定的可行性,在已知点附近的精度较高,但在距已知点较远处,难以保证精度。因而该方法适用于岩相单一、物性较均匀的地层,对于岩相复杂多样、非均质性较强的地层则不适用。
在前人研究基础上,本文提出基于岩相约束的Xu-White模型线性化近似方法,使之适用于非均质性较强的砂泥岩地层,并以叠前弹性反演成果为基础,实现储层物性线性化反演。该方法在模型试算及实际测试中,均表现出较好的应用效果。
1 Xu-White模型线性化近似方法与改进 1.1 Xu-White模型非线性原因分析1995年,Xu等[3]在K-T模型的基础上,应用微分等效介质理论推导出新公式计算砂泥岩地层的纵、横波速度等弹性参数,该公式被命名为Xu-White模型。该模型是基于砂岩与泥岩的孔隙扁率具有显著差异这一基本条件得到的,目前普遍应用于砂泥岩地层中。其计算可分为四个部分[3-4]。
(1) 将孔隙空间区分为泥岩柔性孔隙与砂岩刚性孔隙两部分,应用K-T模型计算干岩石体积模量与剪切模量
| $ \begin{array}{l} {K_{{\rm{dry}}}} - {K_{{\rm{ma}}}} = \frac{1}{3}\left( {{K_{\rm{i}}} - {K_{{\rm{ma}}}}} \right)\frac{{3{K_{{\rm{dry}}}} + 4{\mu _{{\mathop{\rm ma}\nolimits} }}}}{{3{K_{{\rm{ma}}}} + 4{\mu _{{\mathop{\rm ma}\nolimits} }}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{S_{\rm{c}}}{T_{iijj}}\left( {{\alpha _{\rm{c}}}} \right) + \left( {1 - {S_{\rm{c}}}} \right){T_{iijj}}\left( {{\alpha _{\rm{s}}}} \right)} \right] \end{array} $ | (1) |
| $ \begin{array}{l} {\mu _{{\rm{dry}}}} - {\mu _{{\rm{ma}}}}\\ \;\;\; = \frac{{{\mu _{\rm{i}}} - {\mu _{{\rm{ma}}}}}}{5}\frac{{6{\mu _{{\rm{dry}}}}\left( {{K_{{\rm{ma}}}} + 2{\mu _{{\rm{ma}}}}} \right) + {\mu _{{\rm{ma}}}}\left( {9{K_{{\rm{ma}}}} + 8{\mu _{{\rm{ma}}}}} \right)}}{{5{\mu _{{\rm{ma}}}}\left( {3{K_{{\rm{ma}}}} + 4{\mu _{{\rm{ma}}}}} \right)}} \times \\ \;\;\;\;\;\;\;\left\{ {{S_{\rm{c}}}\left[ {{T_{ijij}}\left( {{\alpha _{\rm{c}}}} \right) - \frac{{{T_{iijj}}\left( {{\alpha _{\rm{c}}}} \right)}}{3}} \right] + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {1 - {S_{\rm{c}}}} \right)\left[ {{T_{ijij}}\left( {{\alpha _{\rm{s}}}} \right) - \frac{{{T_{iijj}}\left( {{\alpha _{\rm{s}}}} \right)}}{3}} \right]} \right\} \end{array} $ | (2) |
式(1)和式(2)中:Kdry、Kma和Ki分别为干岩石、岩石骨架和孔隙填充物的体积模量; μdry、μma和μi为相应的剪切模量;Sc为岩石骨架中的泥岩含量;αs为砂岩刚性孔隙扁率, αc为泥岩柔性孔隙扁率;Tiijj、Tijij是从张量函数Tijkl推导而来[20],与Ki、μi、αs、αc和饱和岩石的泊松比等参数有关。
(2) 应用微分等效介质理论,令ϕ为岩石总孔隙度,对式(1)、式(2)做进一步推导,得到
| $ \begin{aligned}(1-\phi) \frac{\mathrm{d} K_{\mathrm{dry}}}{\mathrm{d} \phi}=& \frac{1}{3}\left(K_{\mathrm{i}}-K_{\mathrm{dry}}\right)\left[S_{\mathrm{c}} T_{i i j j}\left(\alpha_{\mathrm{c}}\right)+\right.\\ &\left(1-S_{\mathrm{c}}\right) T_{i i j j}\left(\alpha_{\mathrm{s}}\right) ] \end{aligned} $ | (3) |
| $ \begin{array}{l}{(1-\phi) \frac{\mathrm{d} \mu_{\mathrm{dry}}}{\mathrm{d} \phi}} \\ {\quad=\frac{1}{5}\left(\mu_{\mathrm{i}}-\mu_{\mathrm{dry}}\right)\left\{S_{\mathrm{c}}\left[T_{i j i j}\left(\alpha_{\mathrm{c}}\right)-\frac{T_{i i j j}\left(\alpha_{\mathrm{c}}\right)}{3}\right]+\right.} \\ {\left(1-S_{\mathrm{c}}\right)\left[T_{i j i j}\left(\alpha_{\mathrm{s}}\right)-\frac{T_{i j j}\left(\alpha_{\mathrm{s}}\right)}{3}\right] \}}\end{array} $ | (4) |
式(3)和式(4)为耦合非线性微分方程,求解过程非常复杂。但对于干岩石模量计算, Ki、μi取值为零,且泊松比可近似为常数。因此,可通过式(3)、式(4)得到干岩石模量简化计算式
| $ K_{\mathrm{dry}}=K_{\mathrm{ma}}(1-\phi)^{p} $ | (5) |
| $ \mu_{\mathrm{dry}}=\mu_{\mathrm{ma}}(1-\phi)^{q} $ | (6) |
其中
| $ p = \frac{1}{3}\left[ {{S_{\rm{c}}}{T_{iijj}}\left( {{\alpha _{\rm{c}}}} \right) + \left( {1 - {S_{\rm{c}}}} \right){T_{iijj}}\left( {{\alpha _{\rm{s}}}} \right)} \right] $ | (7) |
| $ \begin{array}{l} q = \frac{1}{5}\left\{ {{S_{\rm{c}}}\left[ {{T_{ijij}}\left( {{\alpha _{\rm{c}}}} \right) - \frac{{{T_{iijj}}\left( {{\alpha _{\rm{c}}}} \right)}}{3}} \right] + } \right.\\ \;\;\;\;\;\left. {\left( {1 - {S_{\rm{c}}}} \right)\left[ {{T_{ijij}}\left( {{\alpha _{\rm{s}}}} \right) - \frac{{{T_{iijj}}\left( {{\alpha _{\rm{s}}}} \right)}}{3}} \right]} \right\} \end{array} $ | (8) |
(3) 在求得干岩石模量基础上,利用Gassmann方程计算饱和流体岩石体积模量与剪切模量。取Kf为孔隙流体的体积模量,可采用Reuss平均方程获得
| $ \frac{1}{K_{\mathrm{f}}}=\frac{S_{\mathrm{w}}}{K_{\mathrm{w}}}+\frac{1-S_{\mathrm{w}}}{K_{\mathrm{hc}}} $ | (9) |
式中:Sw为饱和流体岩石孔隙中的含水饱和度;Kw和Khc分别为孔隙中地层水、碳氢混合物的体积模量。饱和流体岩石体积模量(Ksat)与剪切模量(μsat)通过
| $ {K_{{\rm{sat}}}} = {K_{{\rm{dry}}}} + \frac{{{{\left( {1 - \frac{{{K_{{\rm{dry}}}}}}{{{K_{{\rm{ma}}}}}}} \right)}^2}}}{{\frac{\phi }{{{K_{\rm{f}}}}} + \frac{{1 - \phi }}{{{K_{{\rm{ma}}}}}} - \frac{{{K_{{\rm{dry}}}}}}{{K_{{\rm{ma}}}^2}}}} $ | (10) |
| $ {\mu _{{\rm{sat}}}} = {\mu _{{\rm{dry}}}} $ | (11) |
计算得到。取ρ为饱和流体岩石的等效密度,则
| $ \begin{array}{l} \rho = \phi \left[ {{\rho _{\rm{w}}}{S_{\rm{w}}} + {\rho _{{\rm{hc}}}}\left( {1 - {S_{\rm{w}}}} \right)} \right] + \\ \;\;\;\;\;\;\left( {1 - \phi } \right)\left[ {{\rho _{\rm{s}}}\left( {1 - {S_{\rm{c}}}} \right) + {\rho _{\rm{c}}}{S_{\rm{c}}}} \right] \end{array} $ | (12) |
式中:ρw和ρhc分别为孔隙中地层水、碳氢混合物的密度;ρs和ρc分别为岩石骨架中砂岩颗粒和泥岩颗粒密度。
(4) 结合式(10)~式(12)求取饱和流体岩石纵、横波速度
| $ {V_{\rm{P}}} = \sqrt {\frac{{{K_{{\rm{sat}}}} + \frac{4}{3}{\mu _{{\rm{sat}}}}}}{\rho }} $ | (13) |
| $ {V_{\rm{S}}} = \sqrt {\frac{{{\mu _{{\rm{sat}}}}}}{\rho }} $ | (14) |
在上述计算过程中,式(5)和式(6)中分别出现了指数系数p和q的形式,式(13)和式(14)中出现了平方根的形式,这四式是导致Xu-White模型非线性特征的主要原因, p和q与数值2之间的大小关系是决定岩石物理模型非线性强弱的关键因素。
p、q与岩石矿物模量、孔隙填充物体积模量、砂岩孔隙扁率、泥岩孔隙扁率及泥质含量相关。其中前四项为固定值,可通过岩石物理建模得到,泥质含量具空变特征,导致空间不同位置处的模型非线性特征不同。为研究p、q与泥质含量的关系,设定其他参数固定不变,泥质含量按照20%的间隔在0~100%范围变化。考虑不同地质条件的影响,构建泥岩与砂岩孔隙扁率比参数(αc/αs)[4],建立指数系数与孔隙扁率比关系图(图 1)。

|
图 1 不同泥质含量的指数系数—孔隙扁率比关系图 (a)系数p随αc/αs变化;(b)系数q随αc/αs变化 |
一般情况下,孔隙扁率比参数值远小于1, p、q随泥质含量增大急剧增大。图 1的不同泥质含量的模型曲线中,泥质含量从0至100%的线性变化分别对应p的最大值为2.7、22.4、43.1、63.8、84.5、105.2,对应q的最大值为2.8、17.4、33.1、48.6、64.2、79.8。可以看出,当泥质含量为0时, p、q略大于2,岩石物理模型为近线性特征;随着泥质含量增加, p、q急剧增大,导致岩石物理模型为强非线性特征[4, 21-23]。
1.2 Xu-White模型线性化近似方法当前的岩石物理模型线性化近似方法采用泰勒级数展开、去除高阶项之后得到一阶近似结果。将该方法应用于Xu-White模型,对于由n个样点组成的计算道,可将Xu-White模型正演过程写成
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{m}} \right) + \mathit{\boldsymbol{e}} $ | (15) |
其中
| $ \mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {{V_{\rm{P}}}}\\ {{V_{\rm{S}}}}\\ \rho \end{array}} \right],\mathit{\boldsymbol{m}} = \left[ {\begin{array}{*{20}{c}} \phi \\ {{S_{\rm{c}}}}\\ {{S_{\rm{W}}}} \end{array}} \right] $ | (16) |
式(15)和式(16)中:d为VP、VS和ρ组成的3n×1阶矩阵;m为ϕ、Sc和SW组成的3n×1阶矩阵;f为Xu-White模型函数;e为误差向量。
基于该非线性模型进行反演,需应用复杂的迭代优化算法,此类算法多解性强,且计算量巨大。为此,对式(15)中的Xu-White模型函数f采用泰勒级数展开,保留一阶项,得到线性近似式
| $ \mathit{\boldsymbol{d}} \cong \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{m}}_0}} \right) + {\mathit{\boldsymbol{J}}_{{\mathit{\boldsymbol{m}}_0}}}\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_0}} \right) + \mathit{\boldsymbol{e}} $ | (17) |
其中
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {V_{\rm{P}}}}}{{\partial \phi }}}&{\frac{{\partial {V_{\rm{P}}}}}{{\partial {S_{\rm{c}}}}}}&{\frac{{\partial {V_{\rm{P}}}}}{{\partial {S_{\rm{W}}}}}}\\ {\frac{{\partial {V_{\rm{S}}}}}{{\partial \phi }}}&{\frac{{\partial {V_{\rm{S}}}}}{{\partial {S_{\rm{c}}}}}}&{\frac{{\partial {V_{\rm{S}}}}}{{\partial {S_{\rm{W}}}}}}\\ {\frac{{\partial \rho }}{{\partial \phi }}}&{\frac{{\partial \rho }}{{\partial {S_{\rm{c}}}}}}&{\frac{{\partial \rho }}{{\partial {S_{\rm{w}}}}}} \end{array}} \right] $ | (18) |
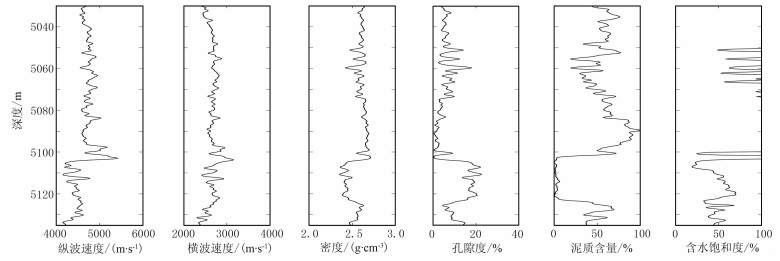
式(17)中Jm0为模型函数f在已知点m0处的雅可比矩阵,可直接调用数学函数进行数值求解。反演过程中,将m0设置为属性均值,可由测井数据统计得到。为研究Xu-White模型线性近似效果,选择塔里木盆地哈得逊油田的W1井进行分析,该井包含实测纵波速度、横波速度与密度曲线,通过计算得到孔隙度、泥质含量与含水饱和度曲线如图 2所示。
|
图 2 W1井实测弹性曲线与计算物性曲线 |
通过测井资料统计与实验数据分析结果,给定各矿物组分和流体的岩石物理基本参数(表 1),并基于Xu-White模型开展岩石物理建模。由岩心薄片扫描电镜结果获得砂岩、泥岩孔隙扁率的初始参考值[24-25]。通过调整孔隙扁率,使计算纵、横波速度与实测纵、横波速度达到最佳拟合[6],最终确定适用于本区的砂岩、泥岩孔隙扁率分别为0.172、0.027。
|
|
表 1 岩石物理基本参数 |
以岩石物理建模参数为基础,利用Xu-White模型的线性化近似(式(17)),分别开展模型及实测曲线的正演分析。模型分析中有3组18个正演模型,第一组包含6个正演模型,反映不同泥质含量、相同饱和度条件下纵、横波速度随孔隙度变化规律;第二组反映不同孔隙度、相同饱和度条件下纵、横波速度随泥质含量变化规律;第三组反映不同孔隙度、相同泥质含量条件下纵、横波速度随含水饱和度变化规律。
图 3a和图 3b为第一组正演模型,反映纵、横波速度随孔隙度变化规律,由图可见,在泥质含量较小的条件下,Xu-White模型与其线性近似后的正演结果基本吻合。但随泥质含量增加,在孔隙度低值段与高值段,差异性逐渐明显。说明泥质含量越大,模型非线性特征越强,采用泰勒级数一阶近似的正演结果与Xu-White模型出现较大偏差。

|
图 3 Xu-White模型与线性近似式正演结果对比 (a)不同泥质含量条件下纵波速度随孔隙度变化,含水饱和度为100%;(b)不同泥质含量条件下横波速度随孔隙度变化,含水饱和度为100%;(c)不同孔隙度条件下纵波速度随泥质含量变化,含水饱和度为100%;(d)不同孔隙度条件下横波速度随泥质含量变化,含水饱和度为100%;(e)不同孔隙度条件下纵波速度随含水饱和度变化,泥质含量为50%;(f)不同孔隙度条件下横波速度随含水饱和度变化,泥质含量为50% |
图 3c和图 3d为第二组正演模型,除孔隙度为零时表现为近线性特征,其他模型的非线性特征基本一致,说明孔隙度变化对模型非线性特征的影响较小。
图 3e和图 3f为第三组正演模型,趋势一致且呈线性变化,说明含水饱和度基本不影响模型非线性特征。
综上所述,泥质含量是影响Xu-White模型非线性特征的主要因素,泥质含量越大时,模型非线性特征越强(与图 1的分析结论完全吻合);具有强非线性特征的岩石物理模型不能直接开展线性化近似,需要改进方法、提高精度。因此,利用反映泥质含量的自然伽马曲线划分岩相,针对不同岩相分别采用不同的孔隙度、泥质含量及饱和度均值进行泰勒级数一阶近似,可改善储层线性近似效果。
1.3 岩相约束的Xu-White模型线性化近似方法利用反映泥质含量的自然伽马曲线划分岩相并作为约束条件,形成多个具有相似非线性特征的研究层段,实现强、弱非线性层段分离。岩相模型的建立可概括为两个步骤:第一步,对测井曲线进行标准化处理,利用自然伽马曲线确定泥岩基线,进而划分出砂岩相与泥岩相;第二步,以地震层位为格架、地震波形为约束,利用单井岩相曲线进行井间插值(本文采用反距离加权插值算法)得到岩相模型体。岩相模型精度主要取决于地震格架的合理性、地震波形的保真度与参与曲线内插井的个数。
在不同的岩相内,由实际数据统计得到孔隙度参数的上、下限,用于确定研究范围、找准均值点m0的位置,可有效改善线性化近似效果。在砂泥岩条件下,可假设岩石孔隙在不同组分中分布均匀,岩石总孔隙由砂岩基质孔隙和泥岩孔隙两部分组成,即
| $ \phi = \left( {1 - {S_{\rm{c}}}} \right){\phi _{\rm{s}}} + {S_{\rm{c}}}{\phi _{\rm{c}}} $ | (19) |
式中ϕsϕc分别为砂岩、泥岩孔隙度。根据不同组分孔隙度变化范围,可计算岩石总孔隙度上、下限。
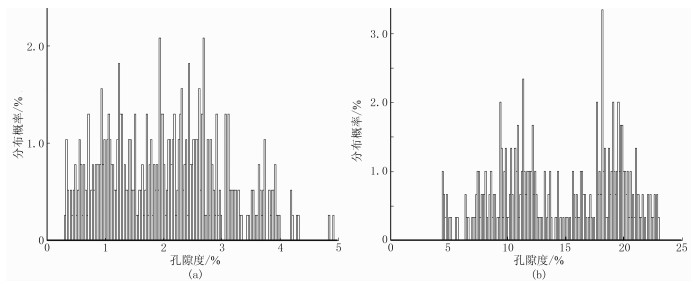
相比于砂岩基质,泥岩孔隙度变化范围较小。如图 4所示的W1井泥岩相孔隙度变化范围为0~5%,砂岩相孔隙度变化范围为5%~25%。结合图 3a、图 3b分析可知,泥质含量较低的岩相内的非线性特征较弱,限定孔隙度范围并精确确定物性均值m0后,表现出近线性特征;泥质含量较高的岩相内虽然非线性特征较强,但是孔隙度范围大幅收窄并精确确定m0后,其表现出弱非线性特征,此时的线性化近似成果精度可得到大幅提高。
|
图 4 W1井分岩相孔隙度统计分析 (a)泥岩相;(b)砂岩相 |
通过式(19)计算得到岩石孔隙度上、下限,在此范围内精确确定不同泥质含量条件下的物性均值m0,对图 3第一组正演模型开展岩相约束的Xu-White模型线性化近似。
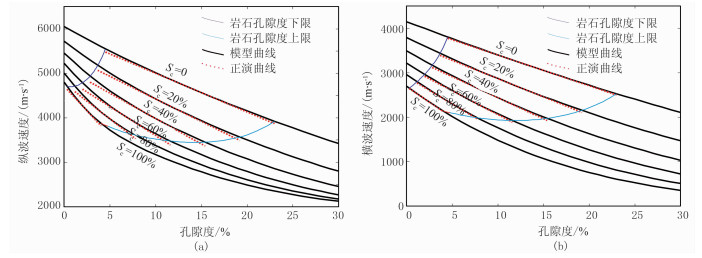
由图 5可见,在W1井岩石孔隙度上、下限范围内,泥质含量越大,岩石有效孔隙变化范围越小。在有效孔隙范围内,模型的非线性特征整体减弱。Xu-White模型和线性近似正演结果的吻合程度较高,预测效果得到改善。表明岩相约束岩石物理模型线性化近似方法可行、有效。
|
图 5 不同泥质含量条件下Xu-White模型与岩相约束线性近似正演结果对比 (a)纵波速度随孔隙度变化;(b)横波速度随孔隙度变化 |
因此,在常规线性化近似方法式(17)的基础上,提出岩相约束的Xu-White模型线性化近似方程
| $ \mathit{\boldsymbol{d}} \cong \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}} \right)}\\ {\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}} \right)} \end{array}} \right] + \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}}{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}\\ {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}}}{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}} \end{array}} \right] + \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}}}\\ {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}}}} \end{array}} \right]\mathit{\boldsymbol{m}} $ | (20) |
式中:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{\bf{0}}&{\bf{0}}&{\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{A}}&{\bf{0}}&{\bf{0}}&{\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}}&\mathit{\boldsymbol{A}}&{\bf{0}}&{\bf{0}}&{\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}} \end{array}} \right] $ | (21) |
其中I为单位阵,而
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&0&0&0&0\\ 0& \cdots &0&0&0\\ 0&0&{{a_i}}&0&0\\ 0&0&0& \cdots &0\\ 0&0&0&0&{{a_n}} \end{array}} \right] $ | (22) |
式(22)中设定A中对角线元素ai为计算道中序号为i的样点位置处的岩相系数,砂岩相中ai=1,泥岩相中ai=0。
将该方法用于实测曲线近似分析,效果如图 6所示,蓝、黑、红色曲线分别为实测、Xu-White正演及线性化近似结果。由图可见,岩相约束的方法提高了线性化近似结果与Xu-White正演结果的吻合程度,进一步验证了该方法的有效性,为后续实现储层物性线性化反演奠定了基础。

|
图 6 岩石物理模型线性化近似效果 (a)常规线性近似; (b)岩相约束线性近似 |
基于岩相约束的Xu-White模型线性化近似式(20),采用贝叶斯理论构建储层物性线性化反演目标函数。令
| $ \mathit{\boldsymbol{d'}} = \mathit{\boldsymbol{d}} - \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}} \right)}\\ {\mathit{\boldsymbol{f}}\left( {{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}} \right)} \end{array}} \right] - \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}}{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}\\ {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}}}{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{C}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{s}}}}}}\\ {{\mathit{\boldsymbol{J}}_{{{\mathit{\boldsymbol{\bar m}}}_{\rm{c}}}}}} \end{array}} \right] $ |
则式(20)可简写为线性化形式
| $ \mathit{\boldsymbol{d'}} = \mathit{\boldsymbol{Gm}} + \mathit{\boldsymbol{e}} $ | (23) |
假设式(23)中的误差项e与模型参数m均服从高斯分布,依据贝叶斯理论[26-27],基于式(23)可构建后验概率密度分布函数近似式
| $ \begin{array}{l} P\left( {\mathit{\boldsymbol{m}}\left| {\mathit{\boldsymbol{d'}}} \right.} \right) \cong {\rm{const}} \times \\ \;\;\;\;\exp \left[ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{d'}} - \mathit{\boldsymbol{Gm}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}^{ - 1}\left( {\mathit{\boldsymbol{d'}} - \mathit{\boldsymbol{Gm}}} \right)} \right] \times \\ \;\;\;\;\exp \left[ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_0}} \right)}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_0}} \right)} \right] \end{array} $ | (24) |
式中:const为常量系数;Ce、Cm分别为误差项e和模型参数m的协方差矩阵,与m0共同作为先验信息(均由测井数据统计得到)约束求解过程,得到概率最大值。该过程一般通过求解下式最小值的方式实现,即
| $ \begin{array}{l} \mathit{\boldsymbol{L}} = {\left( {\mathit{\boldsymbol{d'}} - \mathit{\boldsymbol{Gm}}} \right)^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}^{ - 1}\left( {\mathit{\boldsymbol{d'}} - \mathit{\boldsymbol{Gm}}} \right) + \\ \;\;\;\;\;\;{\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_0}} \right)^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_0}} \right) \end{array} $ | (25) |
令
| $ \begin{array}{l} \mathit{\boldsymbol{m}} = {\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}^{ - 1}\mathit{\boldsymbol{G}} + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}^{ - 1}\mathit{\boldsymbol{d'}} + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}{\mathit{\boldsymbol{m}}_0}} \right)\\ \;\;\;\; = {\mathit{\boldsymbol{m}}_0} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_m}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_e}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{d'}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_0}} \right) \end{array} $ | (26) |
式(25)的求解过程可看作最小二乘拟合过程,式(26)得到的解析解则为最小二乘最优估计值,即最终的反演结果。依式(24)推导反演参数协方差矩阵,用于分析反演结果的不确定性。即
| $ \begin{array}{l} {{\mathit{\boldsymbol{C'}}}_\mathit{\boldsymbol{m}}} = {\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}^{ - 1}\mathit{\boldsymbol{G}} + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}} \right)^{ - 1}} = {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}} - {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}\mathit{\boldsymbol{G}} \times \\ \;\;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{e}}}} \right)^{ - 1}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}} \end{array} $ | (27) |
反演参数协方差矩阵Cm′对角线元素对应m中各变量的方差,该值越大,反演结果的不确定性越大。
2.2 反演效果为验证线性化储层物性反演方法的可行性及有效性,分别采用哈得逊油田一维测井数据W1(如图 2)与过该井的二维反演剖面进行测试。基于W1井所建立的岩石物理模型,将纵、横波速度与密度曲线作为输入,应用上述反演方法反演孔隙度、泥质含量及含水饱和度。反演过程采用岩相约束的孔隙度、泥质含量、含水饱和度等先验物性数据,在岩相内选择数据,统计数值范围并计算数据均值,依据岩相内均值计算结果分别设定砂岩、泥岩段待反演物性参数m0。
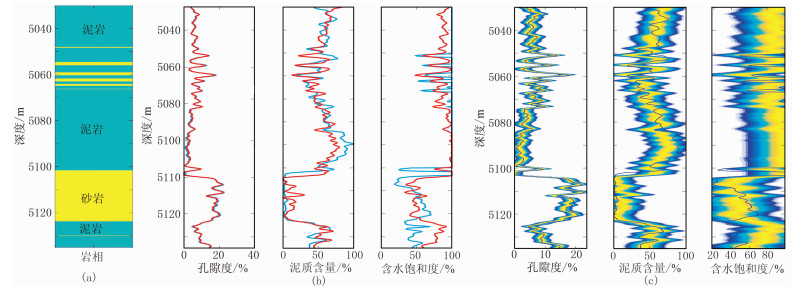
图 7a为单井岩相曲线,用于约束反演过程。由图 7b可见实测曲线与反演结果趋势基本一致,只在局部细节有所差异,差异主要是由模型线性化近似方法、岩石物理建模精度和测井物性曲线计算精度等共同导致。图 7c为反演结果的不确定性分析,蓝色曲线为实测曲线,背景颜色为每个样点对应的后验概率密度分布。概率密度函数服从高斯分布,均值为样点位置处的反演结果。方差值为对应的反演参数协方差矩阵对角线元素,由式(27)求取。方差值越大,概率密度分布范围越大,反演结果不确定性越大。由图可见,后验方差从小到大依次为孔隙度、泥质含量和含水饱和度,说明孔隙度不确定性最小,反演精度最高;泥质含量次之;含水饱和度不确定性较大,反演精度较低。
|
图 7 W1井储层物性线性化反演效果 (a)单井岩相划分;(b)反演结果对比,蓝线为实测曲线,红线为反演结果;(c)反演结果不确定性分析 |
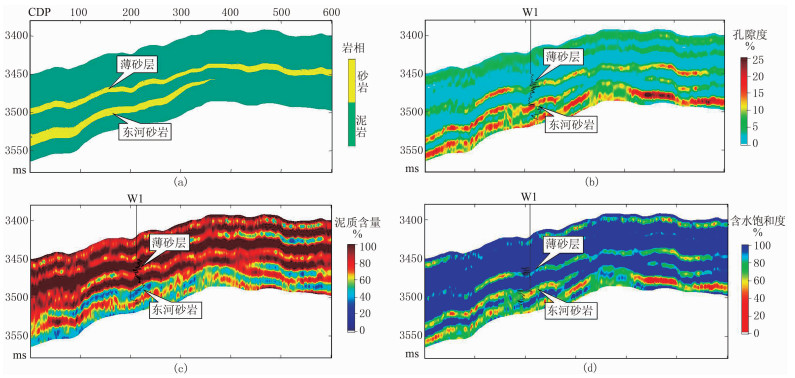
基于叠前同步反演得到的纵、横波速度及密度等弹性参数,采用岩相约束的储层物性线性化反演方法,求取孔隙度、泥质含量与含水饱和度等物性参数,过W1井储层物性反演结果如图 8所示。W1井在目的层系钻遇薄砂层与东河砂岩两套储层,且东河砂岩储层物性明显好于薄砂层,与孔隙度、泥质含量反演结果相吻合。为进一步验证反演效果,提取井点位置处的反演曲线(图 9)进行分析。
|
图 8 过W1井储层物性反演剖面
(a)岩相;(b)孔隙度;(c)泥质含量;(d)含水饱和度 黑色曲线为对应测井物性曲线 |
|
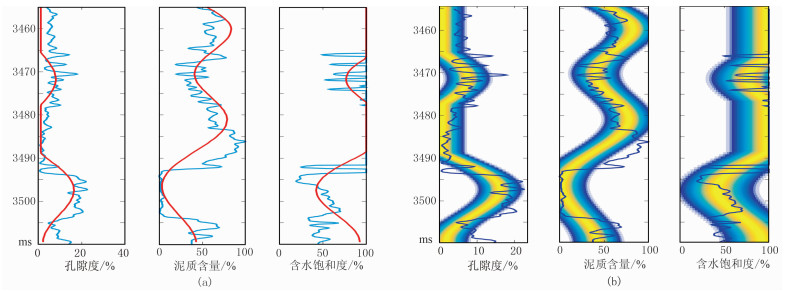
图 9 W1井点位置线性反演效果 (a)反演结果对比,蓝、红曲线分别为实测曲线与反演结果;(b)反演结果不确定性分析 |
由图 9a可见,实测曲线与反演结果趋势基本一致,细节差异主要由地震资料分辨率所致。图 9b为不确定性分析结果,孔隙度、泥质含量不确定性相对较小,可靠程度较高,而含水饱和度反演不确定性相对较大。综合分析表明,反演结果对储层物性具有一定指示作用。
3 结论针对Xu-White模型开展的正演分析表明,泥质含量为0时,该模型为近线性特征;随着泥质含量增加,模型的非线性强度快速增大;泥质含量的大小是决定模型非线性强弱的关键因素。利用反映泥质含量的自然伽马曲线划分岩相,在不同岩相内确定实际数据分布范围并求取储层物性均值进行泰勒级数一阶近似,可大幅改善岩石物理模型线性化近似的精度。
本文提出基于岩相约束的岩石物理模型线性化近似和反演方法,实现了Xu-White模型线性化求解储层物性参数的反演过程,主要有四个步骤:①利用测井曲线建立岩相模型;②利用泰勒级数展开方法,分岩相线性化近似Xu-White模型;③依据贝叶斯理论分岩相建立储层物性参数反演目标函数,并利用最小二乘优化算法得到孔隙度、泥质含量与含水饱和度反演结果;④通过不确定性分析,验证反演结果的可信程度。该方法在模型试算及实际测试中,均取得了较高质量的反演结果,对孔隙度、泥质含量和含水饱和度等储层物性参数具有一定指示作用。
| [1] |
马淑芳, 韩大匡, 甘利灯, 等. 地震岩石物理模型综述[J]. 地球物理学进展, 2010, 25(2): 460-471. MA Shufang, HAN Dakuang, GAN Lideng, et al. A review of seismic rock physics models[J]. Progress in Geophysics, 2010, 25(2): 460-471. DOI:10.3969/j.issn.1004-2903.2010.02.012 |
| [2] |
Kuster G T, Toksöz M N. Velocity and attenuation of seismic waves in two-phase media, Part 1:Theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [3] |
Xu S Y, White R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/gpr.1995.43.issue-1 |
| [4] |
Robert G K, Xu S Y. An approximation for the Xu-White velocity model[J]. Geophysics, 2002, 67(5): 1406-1414. DOI:10.1190/1.1512786 |
| [5] |
Wyllie M R J. Elastic wave velocities in heterogeneous and porous media[J]. Geophysics, 1956, 21(1): 41-70. DOI:10.1190/1.1438217 |
| [6] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN Xingyao, LIU Xinxin. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. DOI:10.3969/j.issn.1000-1441.2016.03.001 |
| [7] |
Yin X Y, Zong Z Y, Wu G C. Research on seismic fluid identification driven by rock physics[J]. Science China:Earth Sciences, 2015, 58(2): 159-171. DOI:10.1007/s11430-014-4992-3 |
| [8] |
杨志芳, 曹宏. 地震岩石物理研究进展[J]. 地球物理学进展, 2009, 24(3): 893-899. YANG Zhifang, CAO Hong. Review of progress in seismic rock physics[J]. Progress in Geophysics, 2009, 24(3): 893-899. DOI:10.3969/j.issn.1004-2903.2009.03.011 |
| [9] |
姜仁, 曾庆才, 黄家强, 等. 岩石物理分析在叠前储层预测中的应用[J]. 石油地球物理勘探, 2014, 49(2): 322-328. JIANG Ren, ZENG Qingcai, HUANG Jiaqiang, et al. Application of rock physics analysis in pre-stack seismic reservoir prediction[J]. Oil Geophysical Prospecting, 2014, 49(2): 322-328. |
| [10] |
方兴, 孙夕平, 张明, 等. 基于AVO流体反演的储层孔隙度预测技术[J]. 石油地球物理勘探, 2012, 47(3): 469-472. FANG Xing, SUN Xiping, ZHANG Ming, et al. Re-servoir porosity prediction based on AVO fluid inversion[J]. Oil Geophysical Prospecting, 2012, 47(3): 469-472. |
| [11] |
杨培杰. 砂泥岩储层孔隙度和含水饱和度同步反演[J]. 地球物理学报, 2018, 61(2): 673-682. YANG Peijie. Porosity and water saturation simultaneous inversion for sand-mudstone reservoir[J]. Chinese Journal of Geophysics, 2018, 61(2): 673-682. |
| [12] |
李志勇, 钱峰, 胡光岷, 等. 储层弹性与物性参数地震叠前同步反演的确定性优化方法[J]. 地球物理学报, 2015, 58(5): 1706-1716. LI Zhiyong, QIAN Feng, HU Guangmin, et al. Pre-stack seismic joint inversion of reservoir elastic and petrophysical parameters using deterministic optimization method[J]. Chinese Journal of Geophysics, 2015, 58(5): 1706-1716. |
| [13] |
Sen M K, Stoffa P L. Global Optimization Methods in Geophysical Inversion[M]. Cambridge University Press, 2013.
|
| [14] |
Aster R C, Borchers B, Thurber C H. Parameter Estimation and Inverse Problems[M]. Academic Press, 2012.
|
| [15] |
Grana D, Rossa E D. Probabilistic petrophysical pro-perties estimation integrating statistical rock physics with seismic inversion[J]. Geophysics, 2010, 75(3): O21-O37. DOI:10.1190/1.3386676 |
| [16] |
Larsen A L, Ulvmoen M, Omre H, et al. Bayesian lithology/fluid prediction and simulation on the basis of a Markov-chain prior model[J]. Geophysics, 2006, 71(5): R69-R78. DOI:10.1190/1.2245469 |
| [17] |
Grana D. Bayesian linearized rock-physics inversion[J]. Geophysics, 2016, 81(6): D625-D641. DOI:10.1190/geo2016-0161.1 |
| [18] |
印兴耀, 化世榜, 宗兆云. 基于线性近似的微分等效介质方程解耦方法[J]. 石油地球物理勘探, 2016, 51(2): 281-287. YIN Xingyao, HUA Shibang, ZONG Zhaoyun. A decoupling approach for differential equivalent equations based on linear approximation[J]. Oil Geophysical Prospecting, 2016, 51(2): 281-287. |
| [19] |
Tian L, Hua S B, Yin X Y.A decoupling approach for differential equivalent equations based on linear approximation[C].Extended Abstracts of 78th EAGE Conference & Exhibition, 2016, Tu13.
|
| [20] |
Wu T T. The effect of inclusion shape on the elastic moduli of a two-phase material[J]. International Journal of Solids and Structures, 1966, 2(1): 1-8. DOI:10.1016/0020-7683(66)90002-3 |
| [21] |
郑旭桢, 王涛, 刘钊, 等. 泥岩基质弹性参数对Xu-White模型横波速度估算的影响[J]. 石油地球物理勘探, 2017, 52(5): 990-998. ZHENG Xuzhen, WANG Tao, LIU Zhao, et al. Influence of clay elastic parameters on S-wave velocity estimation based on Xu-White model[J]. Oil Geophysical Prospecting, 2017, 52(5): 990-998. |
| [22] |
刘致水, 孙赞东, 董宁, 等. 一种修正的Kuster-Toksöz岩石物理模型及应用[J]. 石油地球物理勘探, 2018, 53(1): 113-121. LIU Zhishui, SUN Zandong, DONG Ning, et al. A modified Kuster-Toksöz rock physics model and its application[J]. Oil Geophysical Prospecting, 2018, 53(1): 113-121. |
| [23] |
贺锡雷, 林凯, 张祖豪, 等. 孔隙度和孔隙结构对储层特性影响的定量比较[J]. 石油物探, 2018, 57(2): 179-184. HE Xilei, LIN Kai, ZHANG Zuhao, et al. Quantitative comparison of the influence of porosity and pore structure on reservoir characteristics[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 179-184. DOI:10.3969/j.issn.1000-1441.2018.02.002 |
| [24] |
韩如冰, 刘强, 江同文, 等. 钙质隔夹层特征、成因及分布——以塔里木盆地哈得油田东河砂岩为例[J]. 石油勘探与开发, 2014, 41(4): 428-437. HAN Rubing, LIU Qiang, JIANG Tongwen, et al. Feature, origin and distribution of calcareous interlayers:A case of Carboniferous Donghe sandstone in Hade Oil Field, Tarim Basin, NW China[J]. Petro-leum Exploration and Development, 2014, 41(4): 428-437. |
| [25] |
刘清俊, 于炳松, 周芳芳, 等. 阿克库勒凸起东河砂岩成岩作用与成岩相[J]. 西南石油大学学报(自然科学版), 2011, 33(5): 54-62. LIU Qingjun, YU Bingsong, ZHOU Fangfang, et al. Diagenesis and diagenetic facies of Donghe sandstone of Akekule uplift in Tarim Basin[J]. Journal of Southwest Petroleum University(Science & Techno-logy Edition), 2011, 33(5): 54-62. DOI:10.3863/j.issn.1674-5086.2011.05.009 |
| [26] |
Albert T. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2005.
|
| [27] |
田军, 吴国忱, 宗兆云. 鲁棒性AVO三参数反演方法及不确定性分析[J]. 石油地球物理勘探, 2013, 48(3): 443-449. TIAN Jun, WU Guochen, ZONG Zhaoyun. Robust three-term AVO inversion and uncertainty analysis[J]. Oil Geophysical Prospecting, 2013, 48(3): 443-449. |



 凌东明 新疆维吾尔自治区库尔勒市302信箱东方地球物理公司研究院库尔勒分院, 841001。Email:
凌东明 新疆维吾尔自治区库尔勒市302信箱东方地球物理公司研究院库尔勒分院, 841001。Email: