对于油气地震勘探,需建立较精确的近地表模型以消除地表起伏及近地表速度异常对反射信号的影响,特别是对于山地等复杂探区,近地表模型的精度直接决定了最终的成像效果[1-2]。由于初至旅行时的稳健性及旅行时层析的高效性,目前利用初至旅行时层析反演进行近地表建模是应用最广泛的方法。近地表模型通常用于静校正[3]、深度域建模[4]等处理流程。
经典的初至层析反演方法基于射线追踪方程,在反演中需要显式计算炮点到检波点的旅行时及射线路径[5],本文将这类经典的初至层析反演方法称为基于射线追踪方程的初至层析反演方法。反演中通常采用两种方式求取旅行时及射线路径:①采用两点射线追踪[6]或类似方法同时求取旅行时及射线路径;②采用波前追踪类方法,如基于程函方程的有限差分类方法[7-8]、基于线性旅行时假设的线性旅行时插值方法[9]、基于图理论的最短路径方法[10]等,该类方法需在求解得到初至时间场的基础上从检波点开始反向追踪得到射线路径[9, 11-12]。反演通常采用反向投影[13]、最小二乘奇异值分解(LSQR)[11]、同时迭代重构(SIRT)[14]等方法。基于射线追踪方程的层析反演方法已在实际生产中广泛应用,目前主要研究方向是如何与波形反演等精度较高的反演方法相结合[15-16]。
除了上述经典算法外,还存在一类层析反演算法,本文将其称为基于程函方程的层析反演方法。该类方法仅需要计算初至时间场而不需要计算射线路径,借助伴随状态方法[17]求取模型更新量。该类方法最早由Sei等[18]于1994年提出,近年来得益于波形反演的兴起,伴随状态方法为地球物理学家所熟知,进而开展了广泛的研究。Leung等[19]、Taillandier等[20]、谢春等[21]采用快速扫描方法进行初至旅行时层析;Huang等[22]利用该方法进行透射及反射旅行时层析;Benaichouche等[23]、李勇德等[24]讨论了该类层析方法中预处理方法对层析的影响;Waheed等[25]将该类方法用于各向异性介质的初至旅行时层析。
虽然两类方法已得到了广泛研究,但目前还没有从理论及数值测试上进行系统的对比分析。本文首先基于统一的反演框架从方法原理上对两种方法进行了详细的对比分析,并做了定性的评价;然后通过一个数值测试实例,对两种方法的反演精度、计算效率、内存占用等情况进行了定量的对比分析。
1 方法原理及对比分析 1.1 层析反演基本理论旅行时层析通过迭代反演寻找正演旅行时与观测旅行时最优拟合的模型,若不考虑正则化项,L2模的目标函数可写为
| $ O(\mathit{\boldsymbol{m}}) = \frac{1}{2}\sum\limits_{s = 1}^{{n_s}} {{{\left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right]}^{\rm{T}}}} \left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right] $ | (1) |
式中:m为模型介质参数向量;ns为总炮数;tscal为在当前介质模型m下第s炮对应所有检波点处的正演初至时间;tsobs为在第s炮观测记录上通过拾取得到的初至时间。
将目标函数在m0处展开且只保留至二阶项,可整理为
| $ \begin{array}{l} O(\mathit{\boldsymbol{m}}) \approx O\left( {{\mathit{\boldsymbol{m}}_0}} \right) + {\left[ {{{\left. {\frac{{\partial O(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}}}} \right|}_{\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{m}}_0}}}} \right]^{\rm{T}}}\delta \mathit{\boldsymbol{m}} + \\ \frac{1}{2}{\rm{ \mathit{ δ} }}{\mathit{\boldsymbol{m}}^{\rm{T}}}{\left. {\frac{{{\partial ^2}O(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}\partial {\mathit{\boldsymbol{m}}^{\rm{T}}}}}} \right|_{\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{m}}_0}}}{\rm{ \mathit{ δ} }}\mathit{\boldsymbol{m}} \end{array} $ | (2) |
通常将目标函数相对于介质参数的一阶导数称为梯度,即
| $ \mathit{\boldsymbol{g = }}\frac{{\partial O(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}}} $ | (3) |
将目标函数相对于介质参数的二阶导数称为Hessian矩阵,即
| $ \mathit{\boldsymbol{H}} = \frac{{{\partial ^2}O(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}\partial {\mathit{\boldsymbol{m}}^{\rm{T}}}}} $ | (4) |
由于求取目标函数最小,需要求取目标函数的驻点,即g=0的点。对式(2)求导并将其设为零,可得
| $ {\left. \mathit{\boldsymbol{H}} \right|_{{\mathit{\boldsymbol{m}}_0}}}{\rm{ \mathit{ δ} }}\mathit{\boldsymbol{m}} = - {\left. \mathit{\boldsymbol{g}} \right|_{{\mathit{\boldsymbol{m}}_0}}} $ | (5) |
| $ {\rm{ \mathit{ δ} }}\mathit{\boldsymbol{m}} = - {({\left. \mathit{\boldsymbol{H}} \right|_{{\mathit{\boldsymbol{m}}_0}}})^{ - 1}}{\left. \mathit{\boldsymbol{g}} \right|_{{\mathit{\boldsymbol{m}}_0}}} $ | (6) |
式(6)为在当前模型m0下对应模型更新量的显式表示。利用δm更新当前模型参数m0并将其作为下次迭代的初始模型,可实现非线性反演。当目标函数小于给定的阈值时,停止迭代,得到最终的反演模型。
由于Hessian矩阵的逆很难直接求取,通常通过迭代反演的方式求取式(5)所示的线性方程,此时反演方法通常称为高斯—牛顿法。对于尺度较大的问题,Hessian矩阵H的求取非常耗时且存储困难,通常需要对其进行近似处理。若将Hessian矩阵近似为一单位矩阵,则退化为最速梯度方法;若将Hessian矩阵近似为对角或带限矩阵,则退化为预处理的最速梯度方法。
1.2 基于射线追踪方程的初至层析反演对基于射线追踪方程的初至层析反演,需要求取每个炮检对的射线路径,在得到射线路径之后,可将初至时间表示为
| $ {t_{s, r}} = \sum\limits_{i = 1}^{{n_m}} {{m_i}} l_{s, r}^i $ | (7) |
式中:nm为模型离散网格总数;mi为第i个网格内的慢度;ls, ri为第s炮、第r个接收点对应射线在第i个网格内射线段的长度。可将其写成矩阵的形式
| $ \mathit{\boldsymbol{t}}_s^{{\rm{ cal }}}(\mathit{\boldsymbol{m}}) = {\mathit{\boldsymbol{L}}_s}(\mathit{\boldsymbol{m}})\mathit{\boldsymbol{m}} $ | (8) |
式中Ls(m)为正演算子,包含了不同检波点对应射线路径在网格内的长度。由于正演算子同样是介质参数m的函数,即计算初至时间tscal与介质参数m为非线性关系。
假设每次迭代的模型更新量不大,不足以引起射线路径的剧烈变化,即∂Ls(m)/∂m=0。利用该假设,将式(8)代入式(1),利用式(3)可求得一阶梯度为
| $ \mathit{\boldsymbol{g}} = \sum\limits_{s = 1}^{{n_s}} {\mathit{\boldsymbol{L}}_s^{\rm{T}}} \left( {{\mathit{\boldsymbol{L}}_s}\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right) $ | (9) |
利用式(4)可求得二阶Hessian矩阵为
| $ \mathit{\boldsymbol{H}} = \sum\limits_{s = 1}^{{n_s}} {\mathit{\boldsymbol{L}}_s^{\rm{T}}} {\mathit{\boldsymbol{L}}_s} $ | (10) |
若利用对角元素近似Hessian矩阵,并将其代入式(6),通过整理可得到反向投影算法的基本公式
| $ \delta {m_i} = \frac{{\sum\limits_s {\sum\limits_r {\rm{ \mathit{ δ} }} } {t_{s, r}}l_{s, r}^i}}{{\sum\limits_s {\sum\limits_r {{{\left( {l_{s, r}^i} \right)}^2}} } }} $ | (11) |
式中δts,r为第s炮的第r个检波点处的初至旅行时残差。
将式(9)和式(10)代入式(5),整理可得
| $ \sum\limits_s {{\mathit{\boldsymbol{L}}_s}} {\rm{ \mathit{ δ} }}\mathit{\boldsymbol{m}} = \sum\limits_s {\rm{ \mathit{ δ} }} {\mathit{\boldsymbol{t}}_s} $ | (12) |
式中δts=Lsm-tsobs为第s炮对应的旅行时残差。式(12)为线性方程,对应式(5),基于射线追踪方程的初至层析反演通常是在一次非线性迭代的内部通过求解式(12)实现与高斯—牛顿法相同的效果。根据求取式(12)方法的不同而发展了一系列不同的方法,如LSQR法[11]、SIRT法[14]等,多为数值求解线性方程组算法。
1.3 基于程函方程的初至层析反演基于程函方程的初至层析反演方法直接采用程函方程而不是射线追踪方法作为反演中的正演方法。各向同性介质中初至旅行时的传播满足程函方程,利用迎风有限差分进行离散之后的形式为
| $ \begin{array}{l} \left( {{\mathit{\boldsymbol{D}}_x}{\mathit{\boldsymbol{t}}_s}} \right)\left( {{\mathit{\boldsymbol{D}}_x}{\mathit{\boldsymbol{t}}_s}} \right) + \left( {{\mathit{\boldsymbol{D}}_y}{\mathit{\boldsymbol{t}}_s}} \right)\left( {{\mathit{\boldsymbol{D}}_y}{\mathit{\boldsymbol{t}}_s}} \right) + \left( {{\mathit{\boldsymbol{D}}_z}{\mathit{\boldsymbol{t}}_s}} \right)\left( {{\mathit{\boldsymbol{D}}_z}{\mathit{\boldsymbol{t}}_s}} \right)\\ = {\mathop{\rm diag}\nolimits} (\mathit{\boldsymbol{m}})\mathit{\boldsymbol{m}} \end{array} $ | (13) |
满足初始条件
| $ \mathit{\boldsymbol{t}}_s^{\rm{ }}({\mathit{i}_\mathit{s}}) = 0 $ | (14) |
式中:ts为第s炮对应的所有网格点上的初至时间;Dx、Dy、Dz分别为x、y、z方向的迎风差分矩阵;diag(m)为将慢度向量的元素放在对角位置形成的对角矩阵;is为第s炮震源网格序号。本文利用基于快速匹配方法的迎风差分方法[26]求解式(13)。
对ts作用观测系统算子P后,可提取检波点位置处的初至时间tscal
| $ \mathit{\boldsymbol{t}}_s^{{\rm{cal}}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{t}}_s} $ | (15) |
将式(15)代入式(1),利用式(3)可求得一阶梯度为
| $ \mathit{\boldsymbol{g}} = \frac{{\partial O(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}}} = \sum\limits_{s = 1}^{{n_s}} {{{\left( {\frac{{\partial \mathit{\boldsymbol{t}}_s^{{\rm{cal}}}}}{{\partial \mathit{\boldsymbol{m}}}}} \right)}^{\rm{T}}}} \left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right] $ | (16) |
式中
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{t}}_s^{{\rm{cal}}}}}{{\partial \mathit{\boldsymbol{m}}}} = \mathit{\boldsymbol{P}}\left[ {{\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_x}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_x} + {\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_y}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_y} + } \right.\\ {\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_z}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_z}{]^{ - 1}}{\mathop{\rm diag}\nolimits} (\mathit{\boldsymbol{m}}) \end{array} $ | (17) |
将式(17)代入式(16), 可得一阶梯度为
| $ \begin{array}{l} \mathit{\boldsymbol{g}} = \sum\limits_{s = 1}^{{n_s}} {{\mathop{\rm diag}\nolimits} (\mathit{\boldsymbol{m}})} \left[ {{\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_x}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_x}^{\rm{T}} + {\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_y}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_y}^{\rm{T}} + } \right.\\ {\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_z}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_z}^T{]^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right] \end{array} $ | (18) |
由于很难直接求解上式中矩阵的逆,对于单炮梯度可通过有限差分方法求解如下方程得到
| $ \begin{array}{l} \left[ {{\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_x}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_x}^{\rm{T}} + {\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_y}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_y}^{\rm{T}} + } \right.{\mathop{\rm diag}\nolimits} \left( {{\mathit{\boldsymbol{D}}_z}{\mathit{\boldsymbol{t}}_s}} \right){\mathit{\boldsymbol{D}}_z}^T] \times \\ {[{\mathop{\rm diag}\nolimits} (\mathit{\boldsymbol{m}})]^{ - 1}}{\mathit{\boldsymbol{g}}_s} = {\mathit{\boldsymbol{P}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right] \end{array} $ | (19) |
式(19)是Taillandier等[20]的连续形式偏微分方程式(13)的离散形式。本文对式(19)采用迎风差分方法求解。
利用式(4)可求取Hessian矩阵为
| $ \mathit{\boldsymbol{H}} = \sum\limits_{s = 1}^{{n_s}} {{{\left( {\frac{{\partial \mathit{\boldsymbol{t}}_s^{{\rm{cal}}}}}{{\partial \mathit{\boldsymbol{m}}}}} \right)}^{\rm{T}}}} \frac{{\partial \mathit{\boldsymbol{t}}_s^{{\rm{cal}}}}}{{\partial \mathit{\boldsymbol{m}}}} $ | (20) |
由于式(17)中存在矩阵的逆,通常无法直接求解。将式(20)代入式(5),通过整理可获取其等价的形式为
| $ \sum\limits_{s = 1}^{{n_s}} {{{\left. {\frac{{\partial \mathit{\boldsymbol{t}}_s^{{\rm{cal}}}}}{{\partial \mathit{\boldsymbol{m}}}}} \right|}_{{\mathit{\boldsymbol{m}}_0}}}} {\rm{ \mathit{ δ} }}\mathit{\boldsymbol{m}} - \left[ {\mathit{\boldsymbol{t}}_s^{{\rm{cal}}}\left( {{\mathit{\boldsymbol{m}}_0}} \right) - \mathit{\boldsymbol{t}}_s^{{\rm{obs}}}} \right] = 0 $ | (21) |
若在每次非线性迭代内部迭代求解式(21)即为高斯—牛顿法。若只保留Hessian矩阵对角元素,则为预处理的最速下降方法。
1.4 对比分析上文基于相同的目标函数,在统一的反演框架下分别推导了基于射线追踪方程与程函方程初至旅行时层析迭代反演的基础公式。详细对比两者的理论推导过程,两类方法具有如下共性。
(1) 具有相同的理论基础。理论初至旅行时的计算均采用基于高频近似的射线理论进行;初至旅行时反演采用统一的目标函数,且均可在统一的反演框架下推导迭代反演的基本公式。
(2) 具体反演算法之间具有对应性。基于射线追踪方程方法中的反向投影算法与基于程函方程方法的预处理最速下降方法是对应的;基于射线追踪方程方法中的LSQR、SIRT等与基于程函方程方法中的高斯—牛顿算法是对应的。对应方法之间可产生相近的效果。
由于两者在理论上的相似性,两者具有相似的分辨率以及处理复杂问题的能力,如两者均无法解决速度反转等复杂探区的问题。
两种方法在理论上具有如下的主要区别。
(1) 二者所基于的正演算子不同。前者基于射线追踪方程,即旅行时为沿射线路径对慢度的积分;后者基于程函方程,即利用有限差分等数值解法通过求解程函方程得到检波点处的初至时间。
(2) 二者求取或构造目标函数相对于介质参数一阶梯度及二阶Hessian矩阵的方式不同。对于前者,可利用不同网格内射线段长度显式地构建一阶及二阶导数所对应的矩阵(式(9)、式(10)),直观且物理意义明确;对于后者,只能通过隐式数值求解偏微分方程(式(19))得到单炮所对应的梯度,对于Hessian矩阵则很难显式地进行构建,只能通过间接的方式考虑Hessian矩阵的影响,物理意义相对不明确。
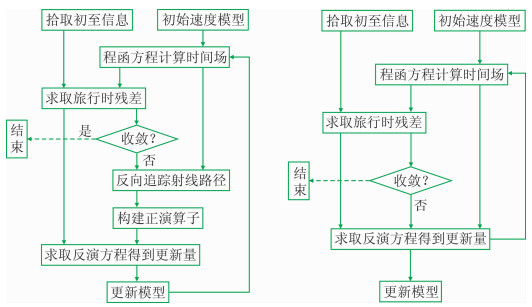
基于理论上的异同,结合具体实现细节(如图 1所示两种方法的反演流程对比),在实际应用中,基于射线追踪方程的初至层析反演方法具有如下优势。
|
图 1 两种层析反演方法反演流程对比 (a)基于射线追踪方程;(b)基于程函方程 |
(1) 反演过程中针对性处理更为灵活。可利用已知的射线路径计算射线角度、射线密度等信息,可利用这些信息在反演的过程中进行针对性处理。
(2) 丰富的质控方法。将射线路径、射线角度、射线密度等利用图形化的方式进行显示,可对最终的反演方法进行有效的质控,如可检查射线是否到达模型边界、根据射线密度判断不同部位反演模型的可靠程度等。
基于程函方程的初至层析反演方法具有如下优势。
(1) 避免了射线路径的计算以及由于射线路径计算引入的误差。由于初至旅行时只考虑最小时间且由于地表起伏可能引起的散射,实际处理中很少直接进行显式的射线追踪,而是在利用程函方程计算得到初至时间场的基础上通过从检波点处反向追踪得到射线路径。不管是采用梯度方法[7]还是线性旅行插值方法[9],均基于局部近似,求取射线路径存在一定误差,特别是在地表起伏等复杂近地表条件下。若采用基于射线追踪方程的层析反演,需显式进行射线路径的求取,在增加计算量的同时也在反演过程中也引入了部分误差。由于不需要进行射线路径的求取,因此基于程函方程的层析反演有效地避免了这个问题。
(2) 计算效率及占用内存大小主要受模型大小的影响,与检波点个数基本无关。在基于程函方程层析反演内部,主要利用有限差分求解式(13)、式(19)和式(21),这些方程的计算效率及所需内存的大小仅与所用模型的大小有关,与检波点的个数无关。
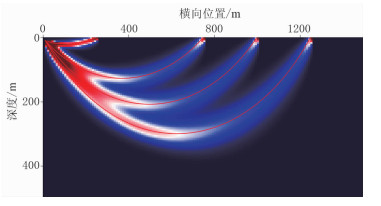
(3) 如图 2所示,基于程函方程的层析反演方法核函数具有一定的宽度,在复杂区域反演效果略好。核函数代表空间任一位置一个散射点对走时变化的影响[27-28],决定了梯度的形态。主要受差分算子的影响,基于程函方程的层析反演其核函数具有一定的宽度,类似于有限频效应,在复杂区域理论上具有更好的反演效果。
|
图 2 两种反演方法核函数对比 背景图片为基于程函方程层析反演的核函数;红色实线为射线路径,为基于射线追踪方法对应的核函数 |
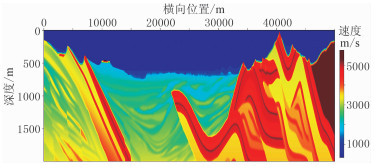
为了对比两种方法在反演精度、计算效率、内存占用等方面的差异,选用Amoco静校正基准测试模型(图 3)进行数值测试。该模型包含了大部分常见的近地表地质构造,如高速层出露、局部高速、低速异常体、浅层低速层、近地表复杂构造及极浅层低速体等,可进行较全面的对比分析。由于常规近地表建模通常的反演深度大约在1km左右,图 3所示模型是对原有模型在深度方向进行压缩之后的结果,在保留原有模型复杂性的同时使其深度与常规近地表问题一致。
|
图 3 Amoco静校正基准测试模型 |
两种反演方法内部的正演算子均通过数值求解程函方程实现,具体采用基于快速匹配追踪的迎风差分算法[26]。对于基于射线追踪方程的层析反演,在通过求解程函方程获取时间场之后由检波点位置开始沿初至时间场的负梯度方向追踪射线路径,最后计算每条射线所经过网格内射线段的长度来构建式(7)中对应的正演算子[13]。基于程函方程的层析反演采用预处理的最速梯度方法,预处理算子采用与Benaichouche等[23]、李勇德等[24]相同的形式,式(19)对应的方程采用迎风有限差分方法进行求解;基于射线追踪方程的层析反演方法采用与最速梯度法对应的反向投影算法。除以上差别外,两种反演方法均采用相同的处理方式,数值试验时也选用相同的参数。
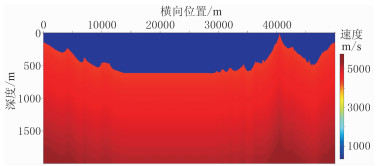
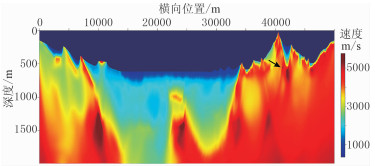
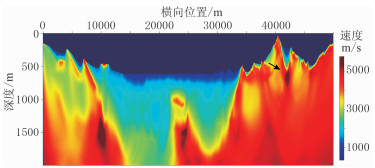
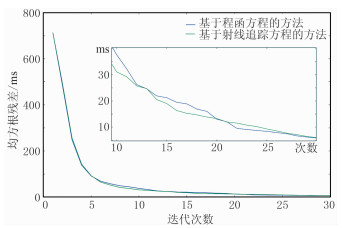
以25m为间隔在地表均匀布置共1998炮,每炮最大炮检距为7500m,检波点间距为20m。采用数值正演方法为层析反演生成合成数据。选用图 4所示线性递增模型为初始模型,地表速度为4500m/s,速度随深度变化梯度为0.5,在模型底部速度约为5500 m/s。图 5为基于射线追踪方程的层析反演结果,图 6为基于程函方程的层析反演结果。对比图 5与图 6可知,从整体形态上来说,两种反演结果基本一致,高速层出露、局部高速、低速异常体、浅层低速层、极浅层低速体等近地表地质构造均得到较好的反演。由于射线层析分辨率的限制,模型右侧复杂构造区域均未取得理想的效果。从反演细节上来说,由于基于程函方程的层析反演其核函数是带限的,即具有类似有限频的特性,反演结果更加稳定,特别是在复杂构造区域,如图 5黑色箭头所示区域,基于射线追踪方程的层析反演结果存在局部的高速异常,但在基于程函方程的层析反演结果中不存在这类高速异常。从反演精度上来说,两类方法具有相似的反演精度,在局部细节上基于程函方程的层析反演方法略优。由图 7的两种方法残差曲线对比可知,两者具有相似的收敛效率。
|
图 4 初始模型 |
|
图 5 基于射线追踪方程的层析反演结果 |
|
图 6 基于程函方程的层析反演结果 |
|
图 7 两种方法反演残差曲线对比 |
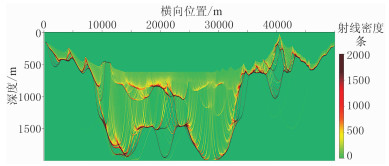
图 8为基于射线追踪方程层析反演最后一次迭代的射线密度,利用射线密度可分析不同区域速度反演的可靠性。由于基于程函方程的层析反演没有射线密度的概念,因此缺少类似的质控图件。
|
图 8 基于射线追踪方程层析反演最后迭代的射线密度 |
为了在内存占用、计算效率等方面对两种方法进行更全面的对比,设计了四种不同的观测系统进行测试。由前面的理论分析可发现,基于射线追踪方程层析反演的一个主要特点是其内存占用、计算效率等均是与检波点个数相关的。基于这个主要差别,在固定总炮数、最大炮检距的基础上通过设置不同的检波点间距(5、10、20、40m)模拟不同的观测系统。测试环境为Linux集群,操作系统为企业版Red Hat 6.4,CPU为Intel(R) Xeon(R) CPU E5-2670(2.60GHz),编译器为Intel icpc。程序源代码采用C++编写,内部采用MPI并行处理。数值测试共用7个节点,每个节点有30个线程,每次层析反演迭代30次。
在不同观测系统下内存占用(单进程对应内存占用)及运行时间对比如图 9所示,可以看出:①基于程函方程的层析反演内存占用及计算时间与检波点个数无关,只与当前模型的大小有关;②基于射线追踪方程的层析反演占用内存及计算时间均是检波点个数的函数,检波点个数越多,占用内存越大、计算时间越长;③当检波点较密时,如宽方位、高密度等观测数据,基于程函方程的层析反演方法在内存占用、计算效率等具有较大优势;当检波点稀疏时,基于射线追踪方程的层析反演方法具有更大的优势。
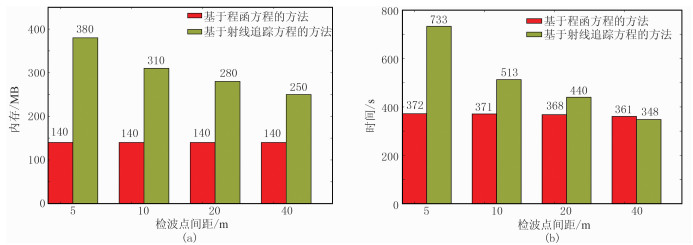
|
图 9 两种方法在不同检波点间距下内存占用(a)和运行时间(b)对比 |
本文在统一的反演框架下推导了两种层析方法的基本公式,在理论上对两种方法的主要差别进行了定性的分析;通过理论数值测试,对两种方法在反演精度、计算效率等方面进行了定量的分析。基于以上的分析,可以得出如下结论:
(1) 两种方法在理论上具有对应性,可在统一的反演框架下导出,且不同迭代反演方法之间均具有对应关系,主要的差别是由于反演中正演算子的不同引起;
(2) 当基于射线追踪方程的方法采用反向投影反演方法、基于程函方程的方法采用与之对应的最速梯度方法反演方法时,两者具有相近的反演精度,基于程函方程的反演方法核函数具有类似有限频的特性,在复杂构造中的反演更加稳定;
(3) 计算效率及内存占用是两者的主要差别。对于基于射线追踪方程的层析反演方法,计算效率等依赖于检波点个数,在检波点特别稀疏时具有优势;对于基于程函方程的层析反演方法,其主要依赖于模型大小,在检波点间距较小时具有优势;
(4) 基于射线追踪方程的层析反演方法具有射线密度等质控手段,是一个主要的优势。
鉴于目前宽方位、高密度数据的大量采集,建议在实际中以应用基于程函方程的层析反演方法为主;在层析反演过程中选用部分炮进行射线追踪以指导、控制反演过程并生成射线密度等质控图件,从而充分利用不同方法之间的优势。
| [1] |
高秦, 陈超群, 王智茹, 等. 多方法静校正融合技术在鄂尔多斯盆地黄土塬区中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 38-44. GAO Qin, CHEN Chaoqun, WANG Zhiru, et al. Multiple statics fusion in loess tablelands, Ordos Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 38-44. |
| [2] |
李素闪, 程元方, 刘建红, 等. 火成岩发育区静校正技术与应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 45-49. LI Sushan, CHENG Yuanfang, LIU Jianhong, et al. Static corrections for igneous rock areas[J]. Oil Geophysical Prospecting, 2017, 52(S2): 45-49. |
| [3] |
Zhu X, Sixta D, Angstman B. Tomostatics:Turning-ray tomography+static corrections[J]. The Leading Edge, 1992, 11(12): 15-23. DOI:10.1190/1.1436864 |
| [4] |
Carney B J.Building Velocity Models for Steep-dip Prestack Depth Migration through First Arrival Tra-veltime Tomography[D]. Virginia Polytechnic Institute and State University, Blacksburg, 2000.
|
| [5] |
Stewart R R. Exploration Seismic Tomography:Fundamentals[M]. SEG, 1991.
|
| [6] |
Bulant P. Two-point ray tracing in 3-D[J]. Pure and Applied Geophysics, 1996, 148(3-4): 421-447. DOI:10.1007/BF00874574 |
| [7] |
Vidale J E. Finite-difference calculation of traveltimes in three dimensions[J]. Geophysics, 1990, 55(5): 521-526. DOI:10.1190/1.1442863 |
| [8] |
Noble M, Gesret A, Belayouni N. Accurate 3-D finite difference computation of traveltimes in strongly he-terogeneous media[J]. Geophysical Journal International, 2014, 199(3): 1572-1585. DOI:10.1093/gji/ggu358 |
| [9] |
Zhang J, Huang Y, Song L P, et al. Fast and accurate 3-D ray tracing using bilinear traveltime interpolation and the wave front group marching[J]. Geophysical Journal International, 2011, 184(3): 1327-1340. DOI:10.1111/gji.2011.184.issue-3 |
| [10] |
Zhang J, Toksoz M N. Nonlinear refraction traveltime tomography[J]. Geophysics, 1998, 63(5): 1726-1737. DOI:10.1190/1.1444468 |
| [11] |
Zelt C A, Barton P J. Three-dimensional seismic re-fraction tomography:A comparison of two methods applied to data from the Faeroe Basin[J]. Journal of Geophysical Research Atmospheres, 1998, 103(B4): 7187-7210. DOI:10.1029/97JB03536 |
| [12] |
苗贺, 孙建国, 王蕤, 等. 基于Chebyshev多项式的三维射线追踪[J]. 石油地球物理勘探, 2018, 53(3): 462-468. MIAO He, SUN Jianguo, WANG Rui, et al. 3D tra-veltime ray tracing based on Chebyshev polynomials[J]. Oil Geophysical Prospecting, 2018, 53(3): 462-468. |
| [13] |
Hole J A. Nonlinear high-resolution three-dimensional seismic travel time tomography[J]. Journal of Geophysical Research:Solid Earth, 1992, 97(B5): 6553-6562. DOI:10.1029/92JB00235 |
| [14] |
Yang Y, Qin K, Zhang D, et al. Improvement of SIRT algorithm in near-surface seismic tomography[J]. Journal of Wuhan University, 2009, 55(2): 201-205. |
| [15] |
Liu Z Y and Zhang J. Joint traveltime, waveform, and waveform envelope inversion for near-surface imaging[J]. Geophysics, 2017, 82(4): R235-R244. DOI:10.1190/geo2016-0356.1 |
| [16] |
Sun M, Zhang J, Zhang W, et al.Alternating traveltime tomography and waveform inversion for near-surface imaging[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 2596-2600.
|
| [17] |
Plessix R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 167(2): 495-503. |
| [18] |
Sei A, Symes W W.Gradient calculation of the travel time cost function without ray-tracing[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1351-1354
|
| [19] |
Leung S, Qian J. An adjoint state method for three-dimensional transmission traveltime tomography using first-arrivals[J]. Communications in Mathematical Sciences, 2006, 4(1): 249-266. DOI:10.4310/CMS.2006.v4.n1.a10 |
| [20] |
Taillandier C, Noble M, Chauris H, et al. First-arrival traveltime tomography based on the adjoint-state method[J]. Geophysics, 2009, 74(6): WCB1-WCB10. DOI:10.1190/1.3250266 |
| [21] |
谢春, 刘玉柱, 董良国, 等. 伴随状态法初至波走时层析[J]. 石油地球物理勘探, 2014, 49(5): 877-883. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival traveltime tomography based on the adjoint state method[J]. Oil Geophysical Prospecting, 2014, 49(5): 877-883. |
| [22] |
Huang J W, Bellefleur G. Joint transmission and reflection traveltime tomography using the fast swee-ping method and the adjoint-state technique[J]. Geophysical Journal International, 2012, 188(2): 570-582. DOI:10.1111/gji.2012.188.issue-2 |
| [23] |
Benaichouche A, Noble M, Gesret A.First arrival tra-veltime tomography using the fast marching method and the adjoint state technique[C]. Extended Abstracts of 77th EAGE Conference & Exhibition, 2015, Tu N10209.
|
| [24] |
李勇德, 董良国, 刘玉柱. 一种新的预条件伴随状态法初至波走时层析[J]. 地球物理学报, 2017, 60(10): 3934-3941. LI Yongde, DONG Liangguo, LIU Yuzhu. First arrival traveltime tomography based on a new preconditioned adjoint-state method[J]. Chinese Journal of Geophysics, 2017, 60(10): 3934-3941. DOI:10.6038/cjg20171021 |
| [25] |
Waheed U B, Flagg G, Yarman C E. First-arrival tra-veltime tomography for anisotropic media using the adjoint-state method[J]. Geophysics, 2016, 81(4): R147-R155. DOI:10.1190/geo2015-0463.1 |
| [26] |
[CM(71.98mm]Sethian J A.A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences of the United States of America, 1996, 93(4): 1591-1595. http://med.wanfangdata.com.cn/Paper/Detail/PeriodicalPaper_PM11607632
|
| [27] |
江燕, 陈晓非. 有限频与射线层析成像比较研究综述[J]. 地球物理学进展, 2011, 26(5): 1566-1575. JIANG Yan, CHEN Xiaofei. Review on the comparative study between finite-frequency tomography and ray-theoretical tomography[J]. Progress in Geophy-sics, 2011, 26(5): 1566-1575. DOI:10.3969/j.issn.1004-2903.2011.05.008 |
| [28] |
刘小民, 邬达理, 梁硕博, 等. 潜水波胖射线走时层析速度反演及其在深度偏移速度建模中的应用[J]. 石油物探, 2017, 56(5): 718-726. LIU Xiaomin, WU Dali, LIANG Shuobo, et al. Diving wave tomography velocity inversion using fat ray in prestack depth migration[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 718-726. DOI:10.3969/j.issn.1000-1441.2017.05.012 |



 郭振波, 河北省涿州市华阳东路东方地球物理公司科技园, 072751。Email:
郭振波, 河北省涿州市华阳东路东方地球物理公司科技园, 072751。Email: