长期以来海洋地震以拖揽观测系统为主,这种方法在海洋石油勘探过程中发挥了重要的作用。以墨西哥湾为代表的海上成熟探区,随着开发程度的深入,钻井平台、海底管线等生产设备密布,拖揽地震采集面临的施工难度越来越大。同时,这种方法自身也存在诸多缺陷,如观测方位受限、炮检距较短、噪声严重等,所以人们一直在寻求新的海洋地震数据采集方法。海底地震(Ocean Bottom Seismic,OBS)数据采集始于1965年,并于1984年实现了海底压力检波器和速度检波器的同时观测;20世纪90年代开始了海底多分量地震观测, 同期开展了面向油田开发的时移地震[1]。与海面拖缆地震观测相比,OBS具有如下优势:①由于观测时四分量检波器全部沉放到海底,由潮汐、海面波浪等引起的环境噪声对观测数据几乎没有影响,较常规拖缆数据具有更高的信噪比;②检波器与海底直接接触, 在海底可以观测到包括压力分量在内的4个分量地震数据;③由于检波器固定在海底, 震源船摆脱了拖缆的影响,可在360°全方位任意激发, 能够得到长排列、全方位的地震数据;④OBS,特别是海底节点(Ocean Bottom Node, OBN)观测方式具有良好的可重复性, 是理想的时移地震观测方法。
随着地震勘探向深海的延伸,水深超过2000m的探区比比皆是,海底电缆收放非常困难。OBN摆脱了电缆的束缚,依赖GPS定位系统和自带的动力系统,能够准确到达预设位置。现阶段受节点成本、放置和回收速度等因素的影响,采集中实用的OBN观测系统都是用相对稀少的节点接收高密度炮点激发的方式[2-4]。OBN观测系统的节点太少,造成地震数据空间采样不足,且传统反射波对海底及浅层覆盖存在盲区,而现有成像方法是建立在反射波理论基础上的,故不能解决上述问题。
White等[5]指出检波点端海水一阶多次波(下行波)与传统反射波(上行波)相比具有相同的振幅、相反的极性,因此下行波完全可以作为有效信息进行地震成像。在处理苏格兰东北部Foinaven油田的OBC资料时,Godfrey等[6]首先提出了镜像成像的概念,研究思路是以海平面为镜面,把海底对称映射到海面以上,形成虚拟的镜像海底,在镜像海底上对下行波进行成像,极大地改善了OBC数据的成像效果。随后Ebrom等[7]、Ronen等[8]、Pica等[9]及Muijs等[10]分别展示了此方法在不同区域实际数据中的应用效果。
本文首先推导海底地震上、下行波反射轨迹的数学表达式,并分别图示两种地震波共检波点数据的覆盖范围;然后研究海底地震上、下行波Kirchhoff叠前时间偏移旅行时的计算公式,展示镜像偏移理论在时间域成像算法的实现细节。旅行时计算需要用到海平面、实际海底、镜像海底等基准面上的均方根速度,并据此推导了不同基准面均方根速度换算公式。最后用模型数据验证了本文方法的正确性。
1 海底地震波场特征图 1是OBS观测示意图。在上、下行波的反射点处分别应用Snell定理,即反射角等于入射角, 得到

|
图 1 OBS观测示意图 图中h表示炮点到检波点的水平距离;dr表示检波点深度;Ru、Rd分别表示上行、下行波的反射点,其偏离检波点的水平距离分别为hur、hdr;蓝色和黑色箭头线段分别表示上行波和下行波的射线路径 |
| $ \frac{{h - {h_{{\rm{ur}}}}}}{d} = \frac{{{h_{{\rm{ur}}}}}}{{d - {d_{\rm{r}}}}} $ | (1) |
| $ \frac{{h - {h_{{\rm{dr}}}}}}{d} = \frac{{{h_{{\rm{dr}}}}}}{{d + {d_{\rm{r}}}}} $ | (2) |
整理式(1)和式(2),得到
| $ {h_{{\rm{ur}}}} = h\frac{{d - {d_{\rm{r}}}}}{{2d - {d_{\rm{r}}}}} $ | (3) |
| $ {h_{{\rm{dr}}}} = h\frac{{d + {d_{\rm{r}}}}}{{2d + {d_{\rm{r}}}}} $ | (4) |
式(3)和式(4)分别是OBS地震上、下行波反射点偏离检波点的水平距离的计算公式。式(3)中,当地下某一层位深度d趋向于dr时,hur趋向于0,即地下反射点逐渐变浅,反射点横向位置向检波点无限靠近;当d趋向于无穷大时,hur趋向于炮检距的一半,即地下反射点逐渐变深,反射点横向位置向炮检中心点无限靠近。图 2是根据式(3)绘制的海底地震共接收点数据上行波覆盖范围示意图。图中包括了三个接收点,每个接收点接收n炮的地震数据,两条黑色曲线中间范围为中间共接收点道集数据的覆盖范围。覆盖范围形似一口大钟,在海底只覆盖接收点所在位置,随着深度的逐渐加深,覆盖范围逐渐向传统地震共中心点位置靠近。

|
图 2 OBS共接收点数据上行波覆盖范围示意图 图中两条红色虚线分别表示中间接收点位置按照传统拖缆地震计算的第1炮和第n炮的中心点位置;两条黑色曲线分别是中间检波点对应第1炮和第n炮地震道的反射点轨迹;左右两口蓝色“大钟”是相邻共接收点道集数据的覆盖范围;红色区域是上行波的照明盲区 |
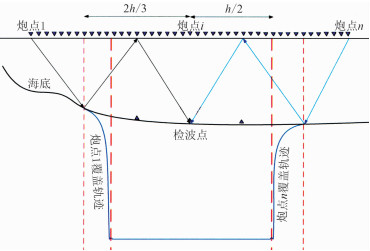
式(4)中,当d趋向于dr时,hdr趋向于炮检距的2/3倍,即地下反射点逐渐变浅,反射点横向位置向2/3倍炮检距无限靠近;当d趋向于无穷大时,hdr趋向于炮检距的一半,即地下反射点逐渐变深,反射点横向位置向中心点无限靠近。图 3是根据式(4)绘制的海底地震共接收点数据下行波反射点覆盖范围示意图。图中有三个接收点,为了图示清晰只绘制了中间共接收点道集数据的覆盖范围。由图可见,每一道地震数据覆盖轨迹是横向范围介于h/2~2h/3的一条曲线,一个共接收点道集数据覆盖海底下蓝色线条之间的范围,好似一个“烧杯”。
|
图 3 图 3 OBS共接收点数据下行波覆盖范围示意图 图中两组垂直粗、细红色虚线分别表示中间接收点位置按照传统拖缆地震计算的第1炮和第n炮的1/2和2/3炮检距位置 |
通过对式(3)和式(4)及图 2和图 3的详细分析,可以看出OBS数据具有以下特征。
(1) 在浅层,上、下行波对地下介质的照明范围存在很大差别,随着深度的增大,上、下行波反射点都向炮检中心点靠拢。
(2) 上行波对浅层存在覆盖盲区[11],利用这类地震波无法对海底及浅层正确成像。现阶段受到采集成本的限制,检波点间距设置太大,加大了浅层覆盖盲区。
(3) 下行波对浅层介质无覆盖盲区,对海底照明范围比上行波宽2/3~0倍(随反射深度增加而变化)炮检距。用下行波进行成像能够极大地改善海底和浅层的成像效果。
(4) OBS采集时炮点与检波点高差为数十米到数千米,这必然导致同一地震道不同样点是来自地下不同横向位置的反射信息,彻底颠覆了常规地震共中心点假设的前提,因此基于共中心点理论的所有处理方法将不适用于OBS数据,必须研究相应的成像理论。
(5) OBS上行波对地下不同区域覆盖次数变化剧烈。
2 海底地震Kirchhoff叠前时间偏移方法实际地震数据处理流程中,Kirchhoff叠前偏移是最常用的成像方法,该方法包括走时计算和振幅处理两个关键步骤。其中旅行时代表地震波传播的运动学特征,其计算精度直接决定地震构造成像的正确性。海底地震采集的炮点与检波点的高程差使常规处理流程中很多技术不再适应,Kirchhoff叠前时间偏移也不例外[12-17]。但该方法是逐道、单样点独立计算,其成像正确与否的关键是对每一个地震样点根据上、下行波传播的实际路径正确计算旅行时间。
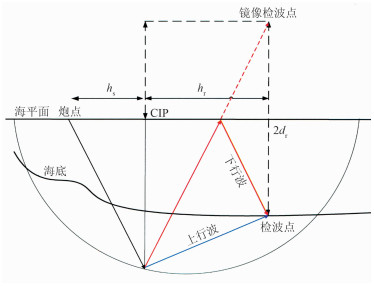
2.1 旅行时计算方法图 4所示为OBS上、下行波叠前时间偏移旅行路径示意图,图中的镜像检波点就是检波点以海平面为镜面的镜像位置,CIP表示共成像点位置。由图可见,炮点激发的地震波场经地下界面反射最终被接收点接收。上行波路径由两段组成,即炮点→反射点→检波点,下行波路径由三段组成,即炮点→反射点→海面→检波点。根据简单几何推导可知下行波传播路径等同于其镜像路径(炮点→反射点→镜像检波点)。由于传统积分法叠前时间偏移旅行时计算由上、下行波两段组成,用下行波镜像路径代替其真实路径研究叠前时间偏移正好与传统旅行时的计算类似。下行波旅行时间为
|
图 4 OBS上、下行波叠前时间偏移旅行时计算示意图 |
| $ t = {t_{\rm{s}}} + {t_{\rm{r}}} = \sqrt {t_0^2 + \frac{{h_{\rm{s}}^2}}{{v_{{\rm{rms}}}^2}}} + \sqrt {{{\left( {{t_0} + \frac{{{d_{\rm{r}}}}}{{{v_{\rm{m}}}}}} \right)}^2} + \frac{{h_{\rm{r}}^2}}{{v_{{\rm{rms}}1}^2}}} $ | (5) |
上行波旅行时为
| $ t = {t_{\rm{s}}} + {t_{\rm{r}}} = \sqrt {t_0^2 + \frac{{h_{\rm{s}}^2}}{{v_{{\rm{rms}}}^2}}} + \sqrt {{{\left( {{t_0} - \frac{{{d_{\rm{r}}}}}{{{v_{\rm{m}}}}}} \right)}^2} + \frac{{h_{\rm{r}}^2}}{{v_{{\rm{rms2}}}^2}}} $ | (6) |
式中:hs表示炮点到成像点的水平距离;hr表示检波点到成像点的水平距离;t0表示以海平面为基准面的成像时间;vm表示海水速度;vrms表示以海平面为基准面的均方根速度;vrms1表示镜像海底基准面的均方根速度;vrms2表示海底基准面的均方根速度;ts表示炮点端旅行时;tr表示检波点端旅行时。
无论式(5)还是式(6),炮点端旅行时与常规地震方法的计算公式完全相同,但检波点端旅行时的计算存在两点差异:一是对于成像时间基准面校正,式(5)用正项dr/vm将成像时间基准面由海平面校正到镜像检波点位置,式(6)用负项dr/vm将成像时间基准面由海平面校正到实际检波点位置;二是关于均方根速度的差异,式(5)在计算检波点端旅行时时用vrms1,而式(6)用的是vrms2。
2.2 均方根速度处理策略无论式(5)还是式(6),都要用到两个基准面的速度,下行波用到海平面和镜像海底基准面的均方根速度,上行波用到了海平面和实际海底基准面的均方根速度。这种对速度的要求限制了式(5)和式(6)的适用性。为了使本文所述方法实用化,正确处理式(5)和式(6)中的均方根速度是无法回避的。
均方根速度实质上是一种等效速度,其量值与基准面的高程密切相关。对于相同的地下结构,基准面高程不同,其均方根速度值也不同。
根据Dix公式,基准面为海平面的均方根速度和层速度的转换式为
| $ v_{{\rm{rms}}}^2 = \frac{{\sum\limits_{i = 1}^n {v_{{\rm{in}}{{\rm{t}}_i}}^2} \Delta {t_i}}}{{{t_n}}} $ | (7) |
式中:vinti表示第i层的层速度;Δti表示地震波在第i层的垂直传播时间;tn表示地震波在n层介质中垂直传播的总时间。
令dm表示速度参考点位置处的海水深度。镜像海底基准面与海平面相比,相当于在海面以上增加一层,其层速度为海水速度vm,垂直反射时间为dm/vm,可根据下式计算该基准面上的均方根速度vrms1
| $ v_{{\rm{rms}}1}^2 = \frac{{v_{\rm{m}}^2\frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}} + \sum\limits_{i = 1}^n {v_{{\rm{in}}{{\rm{t}}_i}}^2} \Delta {t_i}}}{{{t_n} + \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} $ | (8) |
联合求解式(7)和式(8)可以得到vrms1与vrms的转换公式
| $ v_{{\rm{rmsl}}}^2 = v_{{\rm{rms}}}^2\frac{{{t_n}}}{{{t_n} + \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} + \frac{{{v_{\rm{m}}}{d_{\rm{m}}}}}{{{t_n} + \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} $ | (9) |
式(7)还可以表示为
| $ v_{{\rm{rms}}}^2 = \frac{{v_{\rm{m}}^2\frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}} + \sum\limits_{i = 2}^n {v_{{\rm{in}}{{\rm{t}}_i}}^2} \Delta {t_i}}}{{{t_n}}} $ | (10) |
海底基准面与海平面相比相当于去掉海水层,可根据下式计算该基准面上的均方根速度
| $ v_{{\rm{rms}}2}^2 = \frac{{\sum\limits_{i = 2}^n {v_{{\rm{in}}{{\rm{t}}_i}}^2} \Delta {t_i}}}{{{t_n} - \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} $ | (11) |
联合求解式(10)和式(11)可以得到海底基准面均方根速度与vrms的转换公式
| $ v_{{\rm{rms}}2}^2 = v_{{\rm{rms}}}^2\frac{{{t_n}}}{{{t_n} - \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} - \frac{{{v_{\rm{m}}}{d_m}}}{{{t_n} - \frac{{{d_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} $ | (12) |
根据式(9)能够把vrms转换到vrms1,然后计算式(5)中下行波检波点端的旅行时。同样,根据式(12)能够把vrms转换到vrms2,计算式(6)中上行波检波点端的旅行时。
虽然利用式(9)和式(12)能实现速度基准面的转化,但是由于海底地震数据不满足常规地震勘探共中心点的假设,因此不能直接用常规速度分析方法得到vrms。
常规资料叠前时间偏移处理用叠加速度作为初始速度,经过几次叠前时间偏移—反动校正—叠加速度分析的循环迭代,可以得到准确的均方根速度。对OBS来说,式(5)和式(6)中成像时间tn基准面为海平面,叠前时间偏移成像结果CIP道集位于海平面上,该道集完全消除了炮检点不在同一基准面的影响,速度分析可以继续使用叠前时间偏移循环迭代的思路,初始速度用区域背景速度即可。即使无法得到背景速度,笔者用常速度1500m/s作为初始速度,经过两次叠前时间偏移循环迭代进行试算,最终也能收敛到精确的均方根速度vrms。
2.3 加权函数振幅处理就是对地震波传播过程中由于几何扩散而损失的能量进行补偿,使成像结果的地震振幅只与地层反射系数相关。长期以来学者们一直追求真振幅偏移,提出了不同的振幅加权理论[18-21],这些加权函数都有共同缺点:表达式非常复杂,计算量很大。Kirchhoff积分法在偏移实现中,加权函数的计算处于循环的内核部分,如果使用精确的加权函数公式计算权系数,将会使计算成本成倍增加,严重影响这类成像方法的实用性。
遵循Bleistein等[21]的理论,在常速介质假设前提下,Zhang等[18]推导了一系列满足不同工区类型、数据类型的近似权系数表达式,其中三维共炮检距域加权系数为
| $ w = \frac{z}{{{v^2}}}\left( {\frac{{{t_{\rm{s}}}}}{{{t_{\rm{r}}}}} + \frac{{{t_{\rm{r}}}}}{{{t_{\rm{s}}}}}} \right)\left( {\frac{1}{{{t_{\rm{r}}}}} + \frac{1}{{{t_{\rm{s}}}}}} \right) $ | (13) |
可简化为
| $ w = \frac{{8z}}{{{v^2}\left( {{t_{\rm{s}}} + {t_{\rm{r}}}} \right)}} $ | (14) |
式中:z表示成像深度;v表示速度。
在常速介质情况下,双程成像时间T0与成像深度存在如下关系
| $ z = \frac{{{T_0}v}}{2} $ | (15) |
因此式(13)也可表示为
| $ w = \frac{{{T_0}}}{{2v}}\left( {\frac{{{t_{\rm{s}}}}}{{{t_{\rm{r}}}}} + \frac{{{t_{\rm{r}}}}}{{{t_{\rm{s}}}}}} \right)\left( {\frac{1}{{{t_{\rm{r}}}}} + \frac{1}{{{t_{\rm{s}}}}}} \right) $ | (16) |
同样式(14)也可表示为
| $ w = \frac{{4{T_0}}}{{v\left( {{t_{\rm{s}}} + {t_{\rm{r}}}} \right)}} $ | (17) |
虽然式(16)是在常速介质的假设下推导出来,但大多数情况下尚能取得理想的成像效果。对海底地震下行波数据进行成像时,继续沿用式(16)的加权函数表达式。但是对上行波成像时,在海底附近tr会向零值逼近,式(16)的加权系数会出现极大值,故改用简化公式(17)作为其权函数计算公式。
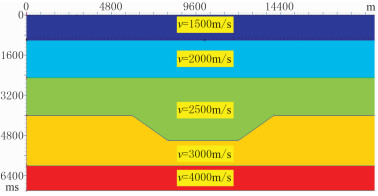
3 模型数据验证为了验证本文方法,设计图 5所示地质模型。共4个反射界面,除了第3个界面为地堑构造外,其他皆为水平界面。如果选第1层顶界面为0时刻参考面,则根据式(7)计算的各层均方根速度依次为1500、1782、2022~2109、2312~2236m/s,各界面理论垂直反射时间分别为1333、2833、4033~4833、5333~5500ms。
|
图 5 二维地质模型 |
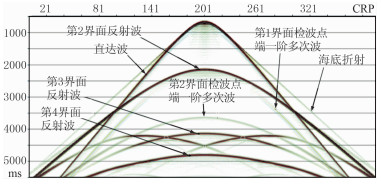
模型长度为20000m。炮点放置在第一层顶界面(模拟海面),炮间距为50m,共401炮。四分量检波器放置在第一层底界面(模拟海底),检波点距为200m,共101个检波点。炮点从左到右依次激发,每一炮激发时全部101个检波器同时记录地震波场。图 6是第51个共接收点(模型中间位置)道集P分量数据,图中标记了各个波组的地震属性。从图中除了能观测到直达波、折射波以及各个层位的反射波外,来自海水自由表面的一阶多次波也清晰可见。
|
图 6 第51个共接收点道集P分量数据 |
理论上海底地震资料处理步骤包括:海水速度和潮汐校正、炮点端气泡压制、多次波压制、上下行波场分离、成像等[22-29]。为了排除其他处理环节对测试结论的影响,不对原始数据做任何处理,直接用P分量作为叠前时间偏移的输入数据,测试结果虽然包含一些干扰波,但这样可以最大限度保证测试结论的客观性。
图 7是该模型第51共检波点P分量叠前时间偏移剖面。上行波叠前时间偏移采用式(6)旅行时计算方法,用式(12)计算检波点端均方根速度;下行波叠前时间偏移采用式(5)旅行时计算方法,用式(9)计算检波点端均方根速度。由于未对原始波场进行分离,上行波成像结果中包含下行波,同样下行波成像结果中也含有上行波,所以两种波的成像结果均存在很强的干扰波。由图可见,第1层上行波只成像1个点,下行波成像很宽,其宽度约为模型长度的2/3倍;上行波第2层成像宽度变宽,但是没有达到下行波的成像宽度;上、下行波第3层成像结果几乎相同。本模型单个共检波点道集数据成像结果与图 2和图 3中上、下行波照明范围理论分析结果完全相同。

|
图 7 第51共检波点上行波(上)和下行波(下)P分量叠前时间偏移剖面 图中红、蓝、粉色椭圆分别标记模型第一、二、三界面成像结果 |
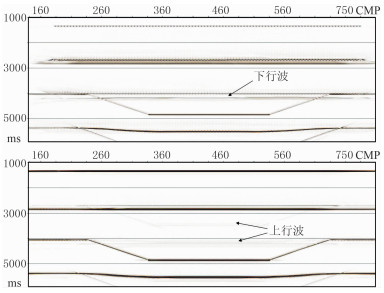
图 8是该模型中间100个共检波点P分量叠前时间偏移成像剖面。宏观来看两种地震波都能够使模型所有层位正确成像,各层位成像时间以及第3层构造拐点位置与图 5模型完全吻合。图 8中上、下行波剖面都存在较强的干扰波,这是由于没有进行波场分离,用上行波成像时下行波相当于干扰波,反之亦然。分析剖面细节可以发现,下行波较上行波成像剖面具有以下三方面优势:①下行波成像剖面横向范围更宽;②上行波对第1层成像结果呈间断状,而下行波成像结果连续很好;③下行波比上行波在浅层的成像结果信噪比高,下行波对浅层横向照明更加均匀,这是成像信噪比高的原因。
|
图 8 模型正演数据上行波(上)和下行波(下)叠前时间偏移剖面 |
常规海洋拖缆地震数据处理过程中,海水多次波被当作噪声压制。本文介绍的海底地震叠前时间偏移方法采用检波点端一阶海水多次波进行成像,首先在理论上证明了这类地震波对海底和浅层能够提供更宽、更均匀的照明,然后推导了新的Kirchhoff叠前时间偏移旅行时计算公式及相应的速度转化公式,并对上、下行波地震振幅的处理方法进行了描述。理论模型数据试算结果表明:下行波与上行波成像结果相比,不仅浅层成像效果改善更明显,同时扩展了横向成像范围。对海底地震数据用多次波替代反射波进行地震成像,可极大改善地下构造的成像效果,具有广阔的应用前景。
| [1] |
耿建华, 董良国, 马在田, 等. 海底节点长期地震观测:油气田开发与CO2地质封存过程监测[J]. 地球科学进展, 2011, 26(6): 669-677. GENG Jianhua, DONG Liangguo, MA Zaitian, et al. Ocean bottom nodes time-lapse seismic survey for monitoring oil and gas production and CO2 geological storage[J]. Advances in Earth Science, 2011, 26(6): 669-677. |
| [2] |
Holloway A, Grant D, Watts G, et al.The future of deepwater ocean bottom seismic: Are flying nodes the next big step?[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 115-119.
|
| [3] |
Gestel J, Heureux E, Sandschaper J.Atlantis "Beyond 4D" ocean bottom nodes acquisition design[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 125-129.
|
| [4] |
Sergio G, Russell E. Mirror imaging of OBS data[J]. First Break, 2007, 25(11): 37-42. |
| [5] |
White J E, Lindsay R B. Seismic waves:Radiation, transmission, and attenuation[J]. Physics Today, 1967, 20(2): 74-75. DOI:10.1063/1.3034162 |
| [6] |
Godfrey R J, Kristiansen P, Armstrong B, et al.Imaging the Foinaven ghost[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 1333-1355.
|
| [7] |
Ebrom D, Li X, Sukup D. Facilitating technologies for permanently instrumented oil fields[J]. The Leading Edge, 2000, 19(3): 282-285. DOI:10.1190/1.1438592 |
| [8] |
Ronen S, Comeaux L, and Miao X G.Imaging downgoing waves from ocean bottom stations[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 963-967.
|
| [9] |
Pica A, Manin M, Granger P Y, et al.3D SRME on OBS data using waveform multiple modelling[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2659-2663.
|
| [10] |
Muijs R, Robertsson J O, Holliger K. Prestack depth migration of primary and surface-related multiple reflections, Part Ⅰ:Imaging[J]. Geophysics, 2007, 72(2): S59-S69. DOI:10.1190/1.2422796 |
| [11] |
Barr F J, Sanders J I.Attenuation of water-column reverberations using pressure and velocity detectors in a water-bottom cable[C]. SEG Technical Program Expanded Abstracts, 1989, 8: 653-656.
|
| [12] |
陈浩林, 张保庆, 秦学彬, 等. 海上OBC地震勘探高精度潮汐校正方法[J]. 石油地球物理勘探, 2014, 49(增刊1): 1-4. CHEN Haolin, ZHANG Baoqing, QIN Xuebin, et al. High resolution tide correction method for seismic OBC prospecting[J]. Oil Geophysical Prospecting, 2014, 49(S1): 1-4. |
| [13] |
程元方, 李素闪, 张文栋, 等. 海底电缆资料处理关键技术及其应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 26-31. CHENG Yuanfang, LI Sushan, ZHANG Wendong, et al. Key techniques for OBC data processing[J]. Oil Geophysical Prospecting, 2017, 52(S2): 26-31. |
| [14] |
贺兆全, 张保庆, 刘原英, 等. 双检理论研究及合成处理[J]. 石油地球物理勘探, 2011, 46(4): 522-528. HE Zhaoquan, ZHANG Baoqing, LIU Yuanying, et al. Response characteristics of dual-sensor and their application in OBC data processing[J]. Oil Geophysical Prospecting, 2011, 46(4): 522-528. |
| [15] |
刘帅, 季晓慧, 卢俊, 等. CPU与GPU协同并行的多分量地震数据各向异性叠前时间偏移[J]. 石油地球物理勘探, 2019, 54(1): 65-72. LIU Shuai, JI Xiaohui, LU Jun, et al. Multi-component anisotropy prestack time migration based on collaborative parallel computing with CPU and GPU[J]. Oil Geophysical Prospecting, 2019, 54(1): 65-72. |
| [16] |
吴丹, 龚仁彬, 王从镔, 等. 最小二乘叠前时间偏移在地震数据规则化中的应用[J]. 石油地球物理勘探, 2019, 54(1): 36-44. WU Dan, GONG Renbin, WANG Congbin, et al. Seismic data regularization via least-squares prestack time migration[J]. Oil Geophysical Prospecting, 2019, 54(1): 36-44. |
| [17] |
钟广见, 刘大锰, 冯常茂, 等. OBS纵波资料镜像叠前时间偏移处理[J]. 热带海洋学报, 2014, 33(3): 46-51. ZHONG Guangjian, LIU Dameng, FENG Changmao, et al. Mirroring pre-stack time migration processing for OBS P-wave data[J]. Journal of Tropical Oceano-graphy, 2014, 33(3): 46-51. DOI:10.3969/j.issn.1009-5470.2014.03.007 |
| [18] |
Zhang Y, Gray S, Young J.Exact and approximate weights for Kirchhoff migration[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 1036-1039.
|
| [19] |
Dellinger J, Gray S, Murphy G, et al.Efficient two and one-half dimensional true-amplitude migration[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 1540-1543.
|
| [20] |
Schleicher J, Tygel M, Hubral P. 3-D true amplitude finite-offset migration[J]. Geophysics, 1993, 58(8): 1112-1126. DOI:10.1190/1.1443495 |
| [21] |
Bleistein N, Cohen J and Stockwell J.Mathematics of Multidimensional Seismic Inversion[R]. Summer School in Mathematical Geophysics, Stanford University, 1998.
|
| [22] |
Beal E, Salo E, Corcoran C.Lessons from the deep processing ocean bottom seismic data[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3679-3684.
|
| [23] |
Pacal E, Stewart R, Baysal E, et al.Seismic imaging with ocean-bottom nodes(OBN): mirror migration technique[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4039-4043.
|
| [24] |
Alerini M, Traub B. Prestack depth imaging of ocean-bottom node data[J]. Geophysics, 2009, 74(6): 57-63. |
| [25] |
Muijs R, Robertsson J O, Holliger K. Prestack depth migration of primary and surface-related multiple reflections, Part Ⅱ:Identification and removal of resi-dual multiples[J]. Geophysics, 2007, 72(2): 71-76. DOI:10.1190/1.2424544 |
| [26] |
Duan Y, Sava P.Elastic reverse-time migration with OBS multiples[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 4071-4074.
|
| [27] |
Xia G, Clarke R, Etgen J, et al.OBS multiple attenuation with application to the deep water GOM Atlantis OBS nodes data[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2654-2658.
|
| [28] |
Amundsen L, Ikelle L, Robertsson J, et al.Wavefield decomposition of seabed node marine recordings[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 146-150.
|
| [29] |
Jiang Z, Yu J, Schuster G T, et al. Migration of multiples[J]. The Leading Edge, 2005, 24(3): 315-318. DOI:10.1190/1.1895318 |



 王狮虎, 河北省涿州市华阳东路东方地球物理公司科技园区, 072751。Email:
王狮虎, 河北省涿州市华阳东路东方地球物理公司科技园区, 072751。Email: