② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
地震波场数值模拟是已知地下介质结构和参数,基于射线理论或波动方程理论模拟地震波在地下传播的一种技术。主要有有限元法、有限差分法和伪谱法等。近年来,学者们逐渐提出了一些新的数值模拟方法,如傅里叶积分法[1-2]、一步外推法[3-4]和低秩近似法[5-7]等。
有限差分法因其具有计算效率高、内存占用小、方便实现等优点,被广泛应用于地震波波动方程数值模拟[8-10]。Alterman等[11]最先提出层状介质二阶弹性波方程的离散数值解,其实质就是均匀介质的数值解。Boore[12]提出非均匀介质二阶弹性波有限差分法,Kelly等[8]对这一方法进行了改进。Madariaga[13]提出一阶速度—应力弹性波方程交错网格的有限差分法,Virieux[14-15]将交错网格法用于P-SV和SH波速度—应力方程的数值模拟。Levander[16]在Madariaga方法的基础上提出四阶精度交错网格有限差分法,提高了数值模拟的稳定性。Graves[17]将交错网格有限差分应用于三维弹性波介质。Moczo等[18]推导了纵横波的稳定性条件,并指出阶数越小频散越严重。Kristek等[19]提出了三维空间四阶速度—应力交错网格有限差分算法,有效压制了数值频散,提高了数值模拟精度。国内许多学者对于有限差分法进行了大量研究,如:刘洋等[20]提出任意偶数阶精度差分格式;董良国等[21]基于交错网格提出时间四阶、空间高阶有限差分法,实现一阶弹性波方程高精度数值求解;殷文等[22]在频率域实现了有限差分法,在提高模拟精度的同时很好地压制了频散;杨庆节等[23]在董良国等[21]研究的基础上优化了差分格式,提高了算法的稳定性和精度;杜启振等[24]联合高阶有限差分法和伪谱法共同求解声波方程,针对复杂介质的数值模拟有较好的稳定性。
目前应用最广泛的是Virieux[15]、Levander[16]的交错网格有限差分法,不仅可以对流体—固体耦合介质进行建模,且能够适应于高泊松比介质(包括流体),同时将密度的空间分布以及变化考虑在内,对于非均匀弹性介质下地震波传播建模是一个非常不错的选择。然而交错网格有限差分法面临内存需求量大、计算效率低的问题[25-27]。为此,Di Bartolo等[28]提出等效交错网格法,实现了二阶变密度声波方程的数值模拟,该方法精度与交错网格的正演模拟精度一致,从数学上也能够证明二者之间的等价性,且在存储上的优势非常明显,二维情况下内存占用量仅相当于交错网格法的三分之一。
受Di Bartolo等[28]研究的启发,本文应用准规则网格(Quasi-regular grid,QRG)正演算法模拟非均匀弹性介质地震波传播。首先给出各向同性非均匀弹性介质下通常使用的一阶速度—应力弹性波方程和二阶位移弹性波方程,在特殊假设条件下分析二者与经典二阶均匀弹性波位移方程的联系;然后回顾了QRG与交错网格剖分算法,在此基础上提出弹性波QRG高阶有限差分算法,分析不同算法的内存占用情况,以体现QRG法的优越性;从数学角度证明了QRG法和交错网格法在模拟弹性波传播过程中的等价性,并给出不同震源的加载方式以及边界条件和稳定性条件;最后采用简单层状模型和复杂Marmousi-2模型进行数值模拟,通过与交错网格法和规则网格法的对比,验证QRG法对非均匀介质数值模拟的准确性及适用性。
1 弹性波波动方程二维弹性波传统二阶位移—应力方程为
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right)\\ \frac{{{\partial ^2}w}}{{\partial {t^2}}} = \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}} \right)\\ {\tau _{xx}} = \left( {\lambda + 2\mu } \right)\frac{{\partial u}}{{\partial x}} + \lambda \frac{{\partial w}}{{\partial z}} + {f_x}\\ {\tau _{zz}} = \left( {\lambda + 2\mu } \right)\frac{{\partial w}}{{\partial z}} + \lambda \frac{{\partial u}}{{\partial x}} + {f_z}\\ {\tau _{xz}} = \mu \left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right) + {f_{xz}} \end{array} \right. $ | (1) |
式中:u和w分别为x、z方向的位移波场;λ和μ为弹性介质中的拉梅常数;ρ为介质密度;τxx和τzz表示正应力;τxz表示切应力;fx、fz和fxz是震源项。
将式(1)中应力分量代入位移分量中,就得到各向同性非均匀二阶位移弹性波方程
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \frac{1}{\rho }\frac{\partial }{{\partial x}}\left[ {\lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial u}}{{\partial x}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{1}{\rho }\frac{\partial }{{\partial z}}\left[ {\mu \left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right] + {s_x}\\ \frac{{{\partial ^2}w}}{{\partial {t^2}}} = \frac{1}{\rho }\frac{\partial }{{\partial z}}\left[ {\lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial w}}{{\partial z}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{1}{\rho }\frac{\partial }{{\partial x}}\left[ {\mu \left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right] + {s_z} \end{array} \right. $ | (2) |
式中sx和sz为纯位移方程震源项。需要注意的是,在离散情况下,加载震源方式不同会导致二阶方程与二阶位移—应力方程模拟结果不同。
在弹性介质均匀假设条件下,式(2)退化为经典的二阶弹性波位移方程
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {t^2}}} = v_{\rm{P}}^2\left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial x\partial z}}} \right) + v_{\rm{S}}^2\left( {\frac{{{\partial ^2}u}}{{\partial {z^2}}} - \frac{{{\partial ^2}w}}{{\partial x\partial z}}} \right) + {s_x}\\ \frac{{{\partial ^2}w}}{{\partial {t^2}}} = v_{\rm{P}}^2\left( {\frac{{{\partial ^2}u}}{{\partial x\partial z}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) + v_{\rm{S}}^2\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}} - \frac{{{\partial ^2}u}}{{\partial x\partial z}}} \right) + {s_z} \end{array} \right. $ | (3) |
式中vP和vS分别表示纵、横波速度,与拉梅常数的关系为
规则网格法是地震波传播模拟最常用的有限差分法,具体思想是对均匀假设下的弹性波方程(式(3))中的连续偏导数项应用中心差分近似得到离散的近似表达式。因为均匀假设不涉及弹性参数和密度的空间变化,显然该方法仅在假定模型参数变化忽略不计或只考虑运动学的情况下满足精度要求,是一种利用规则网格剖分得到一个稳定的解析近似解的方法。在规则网格法中位移被限制在空间步长为Δx、Δz和时间间隔为Δt的每个离散点上,然后通过泰勒级数展开,并用已知的中心差分算子来近似弹性波方程的时空连续偏导项。
以位移水平分量为例,时间二阶导数差分近似为
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}}\left| {_{i,k}^n} \right. = \frac{{u_{i,k}^{n + 1} - 2u_{i,k}^n + u_{i,k}^{n - 1}}}{{\Delta {t^2}}} $ | (4) |
式中ui, kn是在nΔt时刻、离散位置(iΔx,kΔz)处的位移分量。在时间递推过程中,计算(n+1)Δt时刻波场需同时储存nΔt与(n-1)Δt两个时间片。式(4)中时间导数的差分精度为二阶,也可以可以推广至更高阶,处理手段是增加时间片或者时空转嫁的方法[29-30],但会相应增加计算量。
对于空间导数,二阶有限差分近似为
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {x^2}}}\left| {_{i,k}^n} \right. = \frac{{u_{i + 1,k}^n - 2u_{i,k}^n + u_{i - 1,k}^n}}{{{h^2}}}\\ \frac{{{\partial ^2}u}}{{\partial x\partial z}}\left| {_{i,k}^n} \right. = \frac{{u_{i + 1,k + 1}^n - u_{i + 1,k - 1}^n - u_{i - 1,k + 1}^n + u_{i - 1,k - 1}^n}}{{{{\left( {2h} \right)}^2}}} \end{array} \right. $ | (5) |
式中假设Δx=Δz=h。从式(5)可知,在同一方向的二阶导数融合了半网格的思想,空间步长是h,而混合求导项的空间步长必须是2h。
2.2 交错网格法Virieux[15]的交错网格法是通过建立半网格进行中心差分运算,实现对非均匀弹性波方程进行数值求解。例如空间二阶精度差分格式可表示为
| $ \frac{{\partial u}}{{\partial x}}\left| {_{i,k}^n} \right. = \frac{{u_{i + \frac{1}{2},k}^n - u_{i - \frac{1}{2},k}^n}}{h} $ | (6) |
类似地,对于时间的中心差分运算也采用半网格思想,具体的递推流程如图 1所示。经典交错网格提出后最先是应用于弹性波一阶速度—应力方程

|
图 1 弹性介质交错网格模拟示意图 左图表示速度场和应力场随时间的递推;中图是速度场和密度的网格剖分;右图是应力场和拉梅参数网格剖分 |
| $ \left\{ \begin{array}{l} \frac{{\partial {v_x}}}{{\partial t}} = \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right)\\ \frac{{\partial {v_z}}}{{\partial t}} = \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}} \right)\\ \frac{{\partial {\tau _{xx}}}}{{\partial t}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {v_x}}}{{\partial x}} + \lambda \frac{{\partial {v_z}}}{{\partial z}}\\ \frac{{\partial {\tau _{zz}}}}{{\partial t}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {v_z}}}{{\partial z}} + \lambda \frac{{\partial {v_x}}}{{\partial x}}\\ \frac{{\partial {\tau _{xz}}}}{{\partial t}} = \mu \left( {\frac{{\partial {v_z}}}{{\partial x}} + \frac{{\partial {v_x}}}{{\partial z}}} \right) \end{array} \right. $ | (7) |
式中vx、vz为弹性波场x、z方向速度分量。
2.3 准规则网格法受Di Bartolo等[28]等效交错网格法启发,本文提出QRG高阶有限差分法,利用交错网格对位移分量剖分,实现非均匀介质弹性波场数值模拟。该方法是建立在二阶位移方程之上,实际上该方程与一阶速度—应力方程是等价的,等价的基础是位移与速度满足
| $ \left\{ \begin{array}{l} {v_x} = \frac{{\partial u}}{{\partial t}}\\ {v_z} = \frac{{\partial w}}{{\partial t}} \end{array} \right. $ | (8) |
将式(8)代入一阶速度—应力方程(式(7)),则转换为二阶位移—应力方程(式(1))。虽然二阶位移—应力方程的时间离散并没有落在半网格上,即无半时间网格,但是空间离散仍然采用交错网格法剖分。
图 2为QRG法与交错网格法网格剖分对比,可以看出,在二维情况下,交错网格法需要存储应力(τxx、τzz、τxz)、位移(u、w)共5个变量场,而QRG法只需存储2个位移场(u、w);在三维情况下,交错网格法需要存储应力(τxx、τyy、τzz、τxy、τyz、τxz)、位移(u、v、w)共9个变量场,而QRG法只需存储3个位移场(u、v、w),因此QRG法内存占用更少。

|
图 2 交错网格与准规则网格剖分对比 |
QRG法剖分下的任意阶差分格式为
| $ \frac{\partial }{{\partial x}}\left( {b\frac{{\partial u}}{{\partial x}}} \right)_{i,k}^n = \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i + l - \frac{1}{2},k}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i + m + l - 1,k}^n - u_{i - m + l,k}^n} \right)} } \right] - \\ b_{i - l + \frac{1}{2},k}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i + m - l,k}^n - u_{i - m - l + 1,k}^n} \right)} } \right] \end{array} \right\}} $ | (9) |
| $ \frac{\partial }{{\partial x}}\left( {b\frac{{\partial w}}{{\partial z}}} \right)\left| {_{i,k}^n} \right. = \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i + l - \frac{1}{2},k}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + l - \frac{1}{2},k + m - \frac{1}{2}}^n - w_{i + l - \frac{1}{2},k - m + \frac{1}{2}}^n} \right)} } \right]\\ - b_{i - l + \frac{1}{2},k}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i - l + \frac{1}{2},k + m - \frac{1}{2}}^n - u_{i - l + \frac{1}{2},k - m + \frac{1}{2}}^n} \right)} } \right] \end{array} \right\}} $ | (10) |
| $ \frac{\partial }{{\partial z}}\left( {b\frac{{\partial w}}{{\partial x}}} \right)\left| {_{i,k}^n} \right. = \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i,k + l - \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + m - \frac{1}{2},k + l - \frac{1}{2}}^n - w_{i - m + \frac{1}{2},k + l - \frac{1}{2}}^n} \right)} } \right]\\ - b_{i,k - l + \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + m - \frac{1}{2},k - l + \frac{1}{2}}^n - w_{i - m + \frac{1}{2},k - l + \frac{1}{2}}^n} \right)} } \right] \end{array} \right\}} $ | (11) |
| $ \frac{\partial }{{\partial z}}\left( {b\frac{{\partial u}}{{\partial z}}} \right)\left| {_{i,k}^n} \right. = \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i,k + l - \frac{1}{2}}^n\left( {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i,k + m + l - 1}^n - u_{i,k - m + l}^n} \right)} } \right)\\ - b_{i,k - l + \frac{1}{2}}^n\left( {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i,k + m - 1}^n - u_{i,k - m - l + 1}^n} \right)} } \right) \end{array} \right\}} $ | (12) |
| $ \frac{\partial }{{\partial z}}\left( {b\frac{{\partial w}}{{\partial z}}} \right)\left| {_{i + \frac{1}{2},k + \frac{1}{2}}^n} \right. = \\ \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i + \frac{1}{2},k + l}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + \frac{1}{2},k + m + l - \frac{1}{2}}^n - w_{i + \frac{1}{2},k - m + l + \frac{1}{2}}^n} \right)} } \right]\\ - b_{i + \frac{1}{2},k + 1 + l}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + \frac{1}{2},k + m - l + \frac{1}{2}}^n - w_{i + \frac{1}{2},k - m + l + \frac{1}{2}}^n} \right)} } \right] \end{array} \right\}} $ | (13) |
| $ \frac{\partial }{{\partial z}}\left( {b\frac{{\partial u}}{{\partial x}}} \right)\left| {_{i + \frac{1}{2},k + \frac{1}{2}}^n} \right. = \\ \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i + \frac{1}{2},k + l}^n\left[ {\sum\limits_{m = 1}^N {{a_n}\left( {u_{i + m,k + l}^n - u_{i + m + 1,k + l}^n} \right)} } \right]\\ - b_{i + \frac{1}{2},k - l + 1}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {u_{i + m,k - l + 1}^n - u_{i - m + 1,k - l + 1}^n} \right)} } \right] \end{array} \right\}} $ | (14) |
| $ \frac{\partial }{{\partial x}}\left( {b\frac{{\partial u}}{{\partial z}}} \right)\left| {_{i + \frac{1}{2},k + \frac{1}{2}}^n} \right. = \\ \frac{1}{{{h^2}}}\sum\limits_{l = 1}^N {{a_l}\left\{ {\begin{array}{*{20}{l}} {b_{i + l,k + \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_{\rm{m}}}\left( {u_{i + l,k + m}^n - u_{i + l,k - m + 1}^n} \right)} } \right]}\\ { - b_{i - l + 1,k + \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_{\rm{m}}}\left( {u_{i - l + 1,k + m}^n - u_{i - l + 1,k - m + 1}^n} \right)} } \right]} \end{array}} \right\}} $ | (15) |
| $ \frac{\partial }{{\partial x}}\left( {b\frac{{\partial w}}{{\partial x}}} \right)\left| {_{i + \frac{1}{2},k + \frac{1}{2}}^n} \right. = \\ \frac{1}{{{h^3}}}\sum\limits_{l = 1}^N {{a_l}\left\{ \begin{array}{l} b_{i + l,k + \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + m + l - \frac{1}{2},k + \frac{1}{2}}^n - w_{i - m + l + \frac{1}{2},k + \frac{1}{2}}^n} \right)} } \right]\\ - b_{i + 1 - l,k + \frac{1}{2}}^n\left[ {\sum\limits_{m = 1}^N {{a_m}\left( {w_{i + m - l + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - m - l + \frac{3}{2},k + \frac{1}{2}}^n} \right)} } \right] \end{array} \right\}} $ | (16) |
式中:al和am是差分系数(表 1);2N为差分阶次;b为空间导数项对应的拉梅常数。
|
|
表 1 任意阶差分系数 |
式(9)~式(16)中位移分量的下标是严格按照图 2中准规则网格剖分方法给出的;式(9)~式(12)对应非均匀弹性波位移水平分量,其下标与正三角形一一对应;式(13)~式(16)对应位移垂直分量,其下标对应于倒三角形。
从效率角度来说,QRG法计算复杂度要高于交错网格法,纯位移弹性波方程式(2)中位移u、w的空间二阶偏导数项共为10项,而式(7)中,速度和应力的空间一阶导数同样10项。如果内层差分阶数和外层差分阶数相同的情况下,
以弹性波方程的水平分量为例,式(2a)忽略震源项可表示为
| $ \begin{array}{*{20}{c}} {\rho \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \frac{\partial }{{\partial x}}\left[ {\lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial u}}{{\partial x}}} \right] + }\\ {\frac{\partial }{{\partial z}}\left[ {\lambda \left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right]} \end{array} $ | (17) |
为方便书写,选用空间二阶精度近似,则式(17)QRG差分格式为
| $ \begin{array}{l} u_{i,k}^{n + 1} - 2u_{i,k}^n + u_{i,k}^{n - 1}\\ \;\;\;\;\; = \frac{{\Delta {t^2}}}{{{\rho _{i,k}}{h^2}}}\left[ {{{\left( {\lambda + 2\mu } \right)}_{i + \frac{1}{2},k}}\left( {u_{i + 1,k}^n - u_{i,k}^n} \right) - } \right.\\ \;\;\;\;\;\;\;\;{\left( {\lambda + 2\mu } \right)_{i - \frac{1}{2},k}}\left( {u_{i,k}^n - u_{i - 1,k}^n} \right) + \\ \;\;\;\;\;\;\;\;{\lambda _{i + \frac{1}{2},k}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i + \frac{1}{2},k - \frac{1}{2}}^n} \right) - \\ \;\;\;\;\;\;\;\;{\lambda _{i - \frac{1}{2},k}}\left( {w_{i - \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right) + \\ \;\;\;\;\;\;\;\;{\mu _{i,k + \frac{1}{2}}}\left( {u_{i,k + 1}^n - u_{i,k}^n} \right) - \\ \;\;\;\;\;\;\;\;{\mu _{i,k + \frac{1}{2}}}\left( {u_{i,k}^n - u_{i,k - 1}^n} \right) + \\ \;\;\;\;\;\;\;\;{\mu _{i,k + \frac{1}{2}}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k + \frac{1}{2}}^n} \right) - \\ \;\;\;\;\;\;\;\;\left. {{\mu _{i,k + \frac{1}{2}}}\left( {w_{i + \frac{1}{2},k - \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right)} \right] \end{array} $ | (18) |
二阶位移—应力方程(式(1))交错网格差分格式为
| $ \left\{ \begin{array}{l} u_{i,k}^{n + 1} - 2u_{i,k}^n + u_{i,k}^{n - 1}\\ \;\;\;\; = \frac{1}{{{\rho _{i,k}}}}\frac{{\Delta {t^2}}}{h}\left( {\tau _{x{x_{i + \frac{1}{2},k}}}^n - \tau _{x{x_{i - \frac{1}{2},k}}}^n + \tau _{x{z_{i,k + \frac{1}{2}}}}^n - \tau _{x{z_{i,k - \frac{1}{2}}}}^n} \right)\\ w_{i + \frac{1}{2},k + \frac{1}{2}}^{n + 1} - 2w_{i + \frac{1}{2},k + \frac{1}{2}}^n + w_{i + \frac{1}{2},k + \frac{1}{2}}^{n - 1} = \frac{1}{{{\rho _{i + \frac{1}{2},k + \frac{1}{2}}}}}\frac{{\Delta t}}{h} \times \\ \;\;\;\;\;\;\;\left( {\tau _{x{z_{i + 1,k + \frac{1}{2}}}}^n - \tau _{x{z_{i,k + \frac{1}{2}}}}^n + \tau _{x{x_{i + \frac{1}{2},k + 1}}}^n - \tau _{x{x_{i + \frac{1}{2},k}}}^n} \right) \end{array} \right. $ | (19a) |
| $ \left\{ \begin{array}{l} \tau _{x{x_{i + \frac{1}{2},k}}}^n = \frac{1}{h}\left[ {{{\left( {\lambda + 2\mu } \right)}_{i + \frac{1}{2},k}}\left( {u_{i + 1,k}^n - u_{i,k}^n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\lambda _{i + \frac{1}{2},k}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right)} \right]\\ \tau _{z{z_{i + \frac{1}{2},k}}}^n = \frac{1}{h}\left[ {{{\left( {\lambda + 2\mu } \right)}_{i + \frac{1}{2},k}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\lambda _{i + \frac{1}{2},k}}\left( {u_{i + 1,k}^n - u_{i,k}^n} \right)} \right]\\ \tau _{x{z_{i,k + \frac{1}{2}}}}^n = \frac{1}{h}\left[ {{\mu _{i,k + \frac{1}{2}}}\left( {u_{i,k + 1}^n - u_{i,k}^n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\lambda _{i,k + \frac{1}{2}}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k + \frac{1}{2}}^n} \right)} \right] \end{array} \right. $ | (19b) |
将式(19)中的应力项代入水平位移项中,整理可得
| $ \begin{array}{l} u_{i,k}^{n + 1} - 2u_{i,k}^n + u_{i,k}^{n - 1}\\ = \frac{1}{{{\rho _{i,k}}}}\frac{{\Delta {t^2}}}{{{h^2}}}\left[ {{{(\lambda + 2\mu )}_{i + \frac{1}{2},k}}\left( {u_{i + 1,k}^n - u_{i,k}^n} \right) + } \right.\\ {\lambda _{i + \frac{1}{2},k}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i + \frac{1}{2},k - \frac{1}{2}}^n} \right) - \\ {(\lambda + 2\mu )_{i - \frac{1}{2},k}}\left( {u_{i,k}^n - u_{i - 1,k}^n} \right) - \\ {\lambda _{i - \frac{1}{2},k}}\left( {w_{i - \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right) + {\mu _{i,k + \frac{1}{2}}}\left( {u_{i,k + 1}^n - u_{i,k}^n} \right) + \\ {\mu _{i,k + \frac{1}{2}}}\left( {w_{i + \frac{1}{2},k + \frac{1}{2}}^n - w_{i - \frac{1}{2},k + \frac{1}{2}}^n} \right) - {\mu _{i,k + \frac{1}{2}}}\left( {u_{i,k}^n - u_{i,k - 1}^n} \right) - \\ \left. {{\mu _{i,k + \frac{1}{2}}}\left( {w_{i + \frac{1}{2},k - \frac{1}{2}}^n - w_{i - \frac{1}{2},k - \frac{1}{2}}^n} \right)} \right] \end{array} $ | (20) |
对式(20)应用加法交换律即得到与QRG法差分格式(式(18))完全相同的结果,上述结果在空间任意阶差分格式、推广至三维的差分格式均成立。垂直分量的推导过程与之类似,不再赘述。
4 震源、稳定性和边界条件QRG法震源的加载需要考虑其网格剖分的特殊性。二阶位移—应力方程整理为二阶方程的过程中,对二阶位移—应力方程所加载的震源进行了一次空间求导运算,以位移水平分量为例
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \frac{1}{\rho }\left[ {\frac{{\partial \left( {{{\tau '}_{xx}} + {f_x}} \right)}}{{\partial x}} + \frac{{\partial \left( {{{\tau '}_{xz}} + {f_{xz}}} \right)}}{{\partial z}}} \right] $ | (21) |
式中τ′xx和τ′xz是式(1)中的不包括震源项的正应力和切应力。数学上直接将f分离得到离散条件下的震源项
| $ {s_x} = \frac{1}{\rho }\left( {\frac{{\partial {f_x}}}{{\partial x}} + \frac{{\partial {f_{xz}}}}{{\partial z}}} \right) $ | (22) |
通常正演模拟加载的是点震源,在空间坐标可以表达为f×δ(i,k),则震源的空间导数为
| $ \frac{{\partial {f_x}}}{{\partial x}} = \frac{{{\rm{ \mathit{ ?} }}\left( {i,k} \right)}}{{\Delta x}}\left( {{f_{{x_{i + \frac{1}{2},k}}}} - {f_{{x_{i - \frac{1}{2},k}}}}} \right) = 0 $ | (23) |
由上式可知,对f作中心差分求导为零值,因此在数值模拟中,二阶纯位移方程无法得到与位移—应力在应力上加载震源模拟的结果。鉴于此,选择将震源加载在位移分量上,其物理意义可以这样描述:对空间一点加力,使该点位移产生响应并等效于力源,位移响应即为新的震源加载在该点,这样就避免震源对空间求导。因此,规则网格法、QRG法和交错网格法同时加载位移震源模拟结果是相同的。
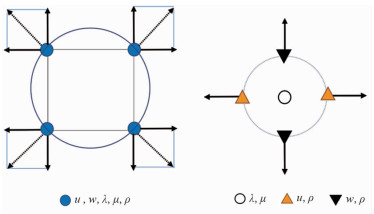
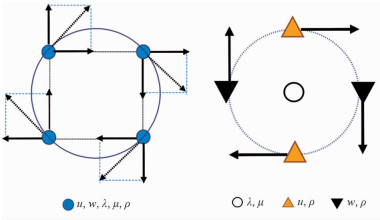
对于经典规则网格法的位移加载震源,通常有四点法和八点法,而QRG法因为网格剖分不同,所以震源加载的方式也会有所不同。以四点法为例,图 3和图 4是两种方法纵波震源、横波震源的加载方式对比示意图,规则网格法震源中虚线表示水平和垂直方向加载位移的合成,由于QRG法的位移是相互交错排列,因此加载方式与规则网格不同。
|
图 3 规则网格法(左)与准规则网格法(右)纵波震源加载示意图 |
|
图 4 规则网格法(左)与准规则网格法(右)横波震源加载示意图 |
图 5和图 6分别是QRG法不同的震源波场。因为QRG法的震源加载在位移上,所以纵波/横波震源加载过程中,会因为网格的离散导致残留的横波/纵波存在,该问题在规则网格法震源加载中同样存在。对于这种情况可以采用二阶位移—应力方程和二阶纯位移方程相互耦合的方法[31]在应力上加载震源,得到干净的纵波/横波波场,如图 7所示。

|
图 5 纵波源波场水平分量(a)与垂直分量(b)对比 |

|
图 6 横波源波场水平分量(a)与垂直分量(b)对比 |

|
图 7 二阶位移—应力方程和二阶纯位移方程耦合算法示意图 |
之前证明了QRG法与交错网格法的等价性,因此QRG法的稳定性条件与交错网格法一致[21]。对于有限模型空间造成的人工反射问题,QRG法与规则网格法加载方式类似,通常会采用吸收边界条件来模拟无限介质,常见的方法有波动方程分解法[32]、旁轴近似法[33]、阻尼衰减法[34]、完全匹配层吸收边界[35],本文采用完全匹配层吸收边界条件。
5 数值模拟结果及分析 5.1 层状模型首先通过简单模型验证QRG法的正演精度。层状模型(图 8)尺寸为1500m×1000m,其中第二层与第三层纵、横波速度相同,但密度相差很大;震源是主频为20Hz雷克子波,位于(750m,0m)处,空间步长统一为5m,时间采样间隔为0.4ms。

|
图 8 层状模型 |
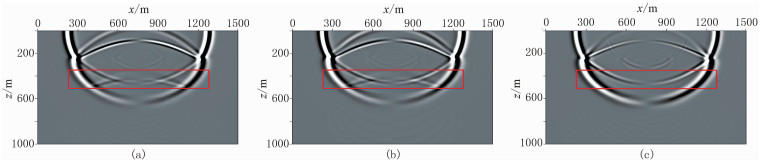
图 9为层状介质模型交错网格法、QRG法和规则网格法模拟的0.4s波场快照,可以看出,交错网格法和QRG法对于密度异常界面能够产生反射、透射波,而规则网格法模拟忽略了密度参数信息(式(3)),不能有效识别密度界面,表明交错网格法和QRG法有更高的模型参数利用率。图 10为抽取接收点位于x=500m和x=1000m的水平分量地震记录,可见:三种方法模拟记录中直达波(0.2s)与一次反射波(0.4~1.6s)的旅行时信息基本一致,说明模型参数的空间变化对于波的旅行时影响微乎其微;QRG法和交错网格法相位信息基本吻合,振幅略微有些许差异,是由计算过程中误差累积造成的;二者与规则网格对比差异很大,主要体现在反射波的相位与振幅信息,是介质的非均匀性造成的。对式(2)进行简单数学变换可得
|
图 9 层状介质模型不同方法模拟的0.4s波场快照 (a)交错网格法;(b)QRG法;(c)规则网格法 |

|
图 10 层状模型不同方法模拟的水平分量地震记录对比 (a)接收点位于x=500m;(b)接收点位于x=1000m |
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {t^2}}} = \left[ {\frac{{\lambda + 2\mu }}{\rho }\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{\lambda }{\rho }\frac{{{\partial ^2}w}}{{\partial x\partial z}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{\mu }{\rho }\left( {\frac{{{\partial ^2}w}}{{\partial x\partial z}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right] + {s_x} + \\ \underbrace {\frac{1}{\rho }\frac{{\partial \lambda }}{{\partial x}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + \frac{2}{\rho }\frac{{\partial \mu }}{{\partial x}}\frac{{\partial u}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial \mu }}{{\partial z}}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)}_{{A_u}}\\ \frac{{{\partial ^2}w}}{{\partial t}} = \left[ {\frac{\lambda }{\rho }\frac{{{\partial ^2}u}}{{\partial x\partial z}} + \frac{{\lambda + 2\mu }}{\rho }\frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{\mu }{\rho }\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial x\partial z}}} \right) + {s_z} + \\ \underbrace {\frac{1}{\rho }\frac{{\partial \lambda }}{{\partial z}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + \frac{2}{\rho }\frac{{\partial \mu }}{{\partial z}}\frac{{\partial w}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial \mu }}{{\partial x}}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)}_{{A_w}} \end{array} \right. $ | (24) |
对比上式与式(3)可知,非均匀介质弹性波方程位移分量比均匀介质下方程多出了关于拉梅常数的导数项Au和Aw,直达波是从炮点沿第一层介质直接传播至检波点,该过程满足介质均匀假设,即拉梅常数导数为0,因此QRG法的直达波模拟结果与规则网格法结果一致。在层状模型中,介质的非均匀性主要体现在在弹性间断面上,而在层间介质仍然满足均匀假设,因此Au和Aw仅对界面处的反射、透射波的振幅和相位产生影响,而不改变旅行时信息。
图 11为图 10的局部放大显示(0.3~0.8s),可见0.35~0.45s处第一界面的交错网格法和QRG法的反射波旅行时、相位和振幅基本一致,在0.5~0.6s处第二界面的反射波旅行时和相位基本吻合、振幅有所差异。而规则网格法除了旅行时信息与前二者吻合,相位和振幅均偏小。在0.6~0.7s处交错网格法和QRG法可见纯密度界面的反射波信息,而在规则网格法记录中观察不到。
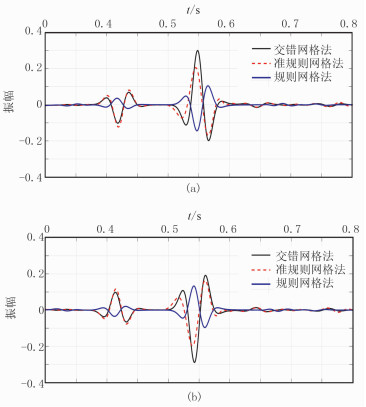
|
图 11 图 10局部放大显示 (a)接收点位于x=500m;(b)接收点位于x=1000m |
综上所述,相比于规则网格法,QRG法能够较准确地模拟非均匀弹性介质下的地震波传播,其旅行时、相位及振幅信息均与交错网格法模拟结果基本一致,在兼具模拟精度和节省内存的考虑下,QRG法在振幅上的微弱差异完全可以接受。
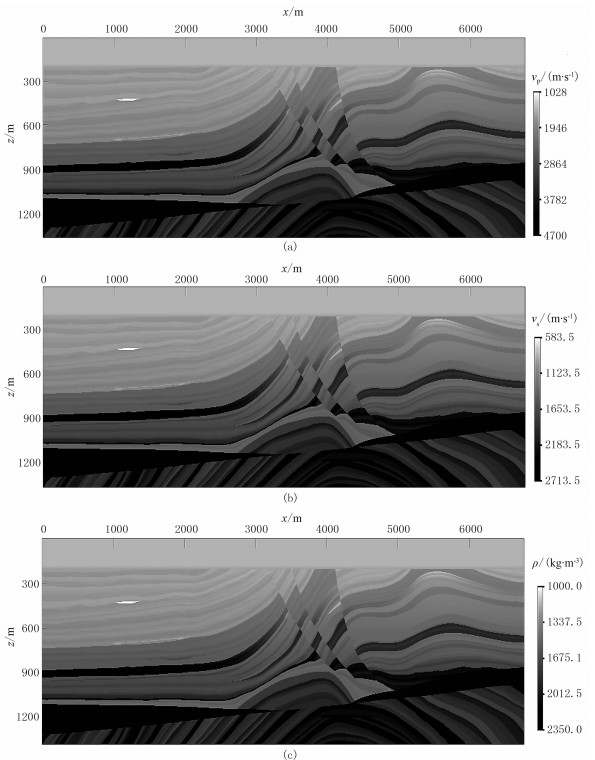
5.2 Marmousi-2模型采用复杂Marmousi-2模型(图 12)验证本文方法对复杂模型的适用性和稳定性。模型尺寸为6800m×1400m,空间步长为5m;震源采用主频为20Hz的雷克子波,时间采样间隔为0.4ms,震源位于(3400m,0m)处;检波器均匀布置在模型表面,间隔为5m。
|
图 12 Mamoursi-2模型 (a)纵波速度;(b)横波速度;(c)密度 |
图 13为Marmousi-2模型采用QRG法和交错网格法模拟的0.6s时刻水平分量波场快照,图 14为垂直分量波场快照,两种方法的时空差分精度均为时间二阶和空间十阶。波场信息完整且无明显频散,证明QRG法对复杂模型数值模拟稳定性良好,从波场快照可见本文QRG法对复杂模型模拟结果非常稳定。

|
图 13 Mamoursi-2两种方法模拟的0.6s水平分量波场快照 (a)交错网格法;(b)QRG法 |

|
图 14 Mamoursi-2两种方法模拟的0.6s垂直分量波场快照 (a)交错网格法;(b)QRG法 |
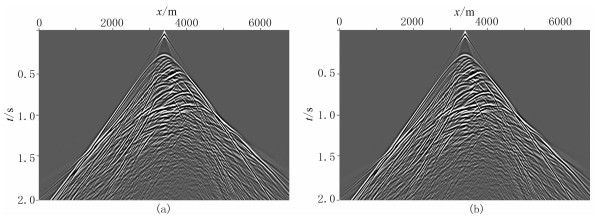
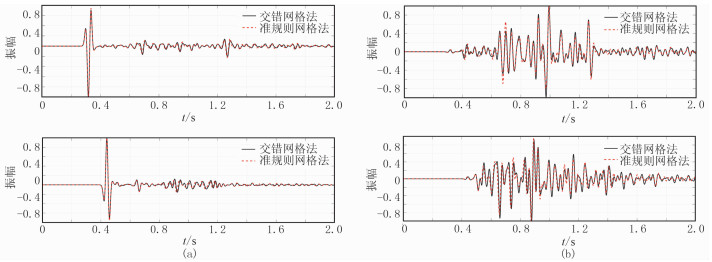
图 15为两种方法模拟的水平分量道集,图 16为两种方法模拟的垂直分量道集,从两种方法模拟记录结果可见,QRG与交错网格法的模拟精度基本一致。图 17为两种方法模拟结果的单道水平及垂直分量对比,可见对复杂的Marmousi-2模型,两种方法模拟的地震信号旅行时、相位和波形信息基本一致。

|
图 15 Mamoursi-2两种方法模拟水平分量的道集 (a)交错网格法;(b)QRG法 |
|
图 16 Mamoursi-2两种方法模拟垂直分量的道集 (a)交错网格法;(b)QRG法 |
|
图 17 Marmousi-2两种方法模拟的水平(a)及垂直(b)分量记录对比 上:接收点位于x=3000m;下:接收点位于x=4000m |
综上所述,本文提出QRG法高阶有限差分法在非均匀弹性介质复杂模型中的展示出良好的稳定性,同时通过与交错网格法结果的对比,体现了QRG法所具有的优势。
6 结论针对非均匀弹性介质中地震波传播正演模拟问题,本文提出一种新的QRG方法,对弹性波方程不同的位移分量采用交错的思想排列,并对位移分量做新的中心差分运算。通过算法分析和模型测试得到以下认识:
(1) 本文提出的QRG法与交错网格法具有相同的模拟精度,并且优于传统的规则法,同时具有良好的稳定性;
(2) QRG法在内存方面具有很大的优势,对同一个二维模型分别用QRG法和交错网格法做一次正演模拟,QRG法的内存使用量比交错法减少60%,如推广到三维,则减少66.7%;
(3) QRG法加载纵/横波震源会产生与规则网格法一样微弱的横/纵波残留,在一定误差允许范围内是可以忽略不计的。如果要得到干净的波场,可以通过交错网格法与QRG法相互耦合的方式解决这一问题。
QRG法计算量较大,如何引入一些优化系数方法降低计算复杂度,是今后的研究方向;另外,如何将QRG法应用到逆时偏移、最小二乘偏移以及全波形反演以提高地震偏移成像与反演的精度,也是今后的研究方向。
| [1] |
Song X, Fomel S. Fourier finite-difference wave pro-pagation[J]. Geophysics, 2011, 76(5): T123-T129. DOI:10.1190/geo2010-0287.1 |
| [2] |
Alkhalifah T. Residual extrapolation operators for efficient wavefield construction[J]. Geophysical Journal International, 2013, 193(2): 1027-1034. DOI:10.1093/gji/ggt040 |
| [3] |
Pestana R C, Stoffa P L. Time evolution of the wave equation using rapid expansion method[J]. Geophy-sics, 2010, 75(4): T121-131. |
| [4] |
Tessmer E. Using the rapid expansion method for accurate time-stepping in modeling and reverse-time migration[J]. Geophysics, 2011, 76(4): S177-S185. DOI:10.1190/1.3587217 |
| [5] |
Fomel S, Ying L, Song X. Seismic wave extrapolation using low rank symbol approximation[J]. Geophysical Prospecting, 2013, 61(3): 526-536. DOI:10.1111/gpr.2013.61.issue-3 |
| [6] |
Wu Z, Alkhalifah T. The optimized expansion based low-rank method for wavefield extrapolation[J]. Geophysics, 2014, 79(2): T51-T60. DOI:10.1190/geo2013-0174.1 |
| [7] |
Fang G, Fomel S, Du Q, et al. Low rank seismic-wave extrapolation on a staggered grid[J]. Geophysics, 2014, 79(3): T157-T168. DOI:10.1190/geo2013-0290.1 |
| [8] |
Kelly K R, Ward R W, Treitel S, et al. Synthetic seismograms:A finite-difference approach[J]. Geophy-sics, 1976, 41(1): 2-27. |
| [9] |
Robertsson J O A, Blanch J O, Symes W W, et al. Galerkin-wavelet modeling of wave propagation:Optimal finite-difference stencil design[J]. Mathematical and Computer Modelling, 1994, 19(1): 31-38. DOI:10.1016/0895-7177(94)90113-9 |
| [10] |
Robertsson J O A, Blanch J O, Symes W W. Visco-elastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [11] |
Alterman Z, Karal Jr F C. Propagation of elastic waves in layered media by finite difference methods[J]. Bu-lletin of the Seismological Society of America, 1968, 58(1): 367-398. |
| [12] |
Boore D M. Finite difference methods for seismic wave propagation in heterogeneous materials[J]. Methods in Computational Physics, 1972, 11: 1-37. |
| [13] |
Madariaga R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666. |
| [14] |
Virieux J. SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
| [15] |
Virieux J. P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 1203-1216. |
| [16] |
Levander A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [17] |
Graves R W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite diffe-rences[J]. Bulletin of the Seismological Society of America, 1996, 86(4): 1091-1106. |
| [18] |
Moczo P, Kristek J, Halada L. 3D fourth-order staggered-grid finite-difference schemes:Stability and grid dispersion[J]. Bulletin of the Seismological Society of America, 2000, 90(3): 587-603. DOI:10.1785/0119990119 |
| [19] |
Kristek J, Moczo P, Galis M. Stable discontinuous staggered grid in the finite-difference modelling of seismic motion[J]. Geophysical Journal International, 2010, 183(3): 1401-1407. DOI:10.1111/j.1365-246X.2010.04775.x |
| [20] |
刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟[J]. 石油地球物理勘探, 1998, 33(1): 1-10. LIU Yang, LI Chengchu, MOU Yongguang. Finite-difference numerical modeling of any even-order accuracy[J]. Oil Geophysical Prospecting, 1998, 33(1): 1-10. DOI:10.3321/j.issn:1000-7210.1998.01.001 |
| [21] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864. DONG Liangguo, MA Zaitian, CAO Jingzhong. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864. DOI:10.3321/j.issn:0001-5733.2000.06.015 |
| [22] |
殷文, 印兴耀, 吴国忱, 等. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 2006, 49(2): 561-568. YIN Wen, YIN Xingyao, WU Guochen, et al. The method of finite difference of high precision on elastic wave equations in the frequency domain and wavefield simulation[J]. Chinese Journal of Geophysics, 2006, 49(2): 561-568. DOI:10.3321/j.issn:0001-5733.2006.02.032 |
| [23] |
杨庆节, 刘财, 耿美霞, 等. 交错网格任意阶导数有限差分格式及差分系数推导[J]. 吉林大学学报(地球科学版), 2014, 44(1): 375-385. YANG Qingjie, LIU Cai, GENG Meixia, et al. Staggered grid finite difference scheme and coefficients deduction of any number of derivatives[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(1): 375-385. |
| [24] |
杜启振, 郭成锋, 公绪飞. VTI介质纯P波混合法正演模拟及稳定性分析[J]. 地球物理学报, 2015, 58(4): 1290-1304. DU Qizhen, GUO Chengfeng, GONG Xufei. Hybrid PS/FD numerical simulation and stability analysis of pure P-wave propagation in VTI media[J]. Chinese Journal of Geophysics, 2015, 58(4): 1290-1304. |
| [25] |
黄金强, 李振春, 黄建平, 等. TTI介质Lebedev网格高阶有限差分正演模拟及波型分离[J]. 石油地球物理勘探, 2017, 52(5): 915-927. HUANG Jinqiang, LI Zhenchun, HUANG Jianping, et al. Lebedev grid high-order finite-difference mode-ling and elastic wave-mode separation for TTI media[J]. Oil Geophysical Prospecting, 2017, 52(5): 915-927. |
| [26] |
高正辉, 孙建国, 孙章庆, 等. 基于完全匹配层构建新方法的2.5维声波近似方程数值模拟[J]. 石油地球物理勘探, 2016, 51(6): 1128-1133. GAO Zhenghui, SUN Jianguo, SUN Zhangqing, et al. 2.5D acoustic approximate equation numerical simulation with a new construction method of the perfect matched layer[J]. Oil Geophysical Prospecting, 2016, 51(6): 1128-1133. |
| [27] |
梁文全, 王彦飞, 杨长春. 声波方程数值模拟矩形网格有限差分系数确定法[J]. 石油地球物理勘探, 2017, 52(1): 56-62. LIANG Wenquan, WANG Yanfei, YANG Changchun. Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution[J]. Oil Geophysical Prospecting, 2017, 52(1): 56-62. |
| [28] |
Di Bartolo L, Dors C, Mansur W J. A new family offinite-difference schemes to solve the heterogeneous acoustic wave equation[J]. Geophysics, 2012, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
| [29] |
Dablain M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [30] |
李青阳, 吴国忱, 梁展源. 基于PML边界的时间高阶伪谱法弹性波场模拟[J]. 地球物理学进展, 2018, 33(1): 228-235. LI Qingyang, WU Guochen, LIANG Zhanyuan. Time domain high-order pseudo spectral method based on PML boundary for elastic wavefield simulation[J]. Progress in Geophysics, 2018, 33(1): 228-235. |
| [31] |
吴建鲁, 吴国忱, 王伟, 等. 基于等效交错网格的流固耦合介质地震波模拟[J]. 石油地球物理勘探, 2018, 53(2): 272-279. WU Jianlu, WU Guochen, WANG Wei, et al. Seismic forward modeling in fluid-solid media based on equi-valent staggered grid scheme[J]. Oil Geophysical Prospecting, 2018, 53(2): 272-279. |
| [32] |
Reynolds A C. Boundary conditions for the numerical solution of wave propagation problems[J]. Geophy-sics, 2012, 43(6): 155-165. |
| [33] |
Clayton R, Engquist B. Absorbing boundary condi-tions for acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540. |
| [34] |
Cerjan C, Dan K, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [35] |
Berenger J P. A perfectly matched layer for the ab-sorption of electromagnetic waves[J]. Physics of Plasmas, 1994, 114(2): 185-200. |



 吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266555。Email:
吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266555。Email: