② 青岛海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
③ 中国石油勘探开发研究院西北分院, 甘肃兰州 730020
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China;
③ Northwest Branch, Research Institute of Petro-leum Exploration & Development, PetroChina, Lanzhou, Gansu 730020, China
实际地球介质普遍具有黏弹性,地震波在实际介质中传播会产生衰减。地球介质的这种衰减特性可以用黏弹模型来描述[1]。
对于黏弹介质的地震波场模拟,国内外学者已经做了大量研究。Liu等[2]建立了线性黏弹流变学的理论框架,可以很好地解释实验观测到的地震波在地球介质中传播时的衰减现象;Day等[3]首次利用Padé近似方法将时间域的应力—应变褶积关系转换成微分形式,在二维时间域进行黏弹性介质数值模拟;Emmerich等[4]认为Padé近似方法存在计算效率低和数值模拟效果较差的缺点,在流变学模型的基础上提出了广义标准线性固体(Generalized Standard Linear Solid,GSLS)模型,并将其应用于标量波动方程的二维有限差分正演;Robertsson等[5-6]基于GSLS模型,推导了交错网格速度—应力有限差分格式,并对二维和三维黏弹介质进行了波场数值模拟与分析。Blanch等[7]针对时间域GSLS模型有限差分正演内存需求大、计算时间长的问题提出了τ方法,显著降低了存储空间要求,提高了计算效率;Bohlen[8]提出三维并行黏弹有限差分正演方法,使三维地震波场模拟的效率和规模大大提高;Saenger等[9]将旋转交错网格有限差分法用于模拟黏弹性介质中波的传播。杜启振等[10-11]先后采用有限元法、伪谱法和有限差分法对方位各向异性黏弹性介质中的波场进行模拟,分析了速度频散和衰减特征;牛滨华[12]详细介绍了黏弹性介质的理论及地震波在黏弹性介质中的传播特征;严红勇等[13]给出了适用于黏弹TTI介质的二维三分量一阶速度—应力方程,并采用旋转交错网格高阶有限差分实现了黏弹TTI介质的地震波场数值模拟;何兵红等[14]推导了基于傅里叶有限差分(FFD)算子的衰减介质地震单程波波场传播算子,通过空间—时间域与波数—频率域之间的转化实现了衰减介质地震波场数值模拟;罗文山等[15]基于常Q模型的应力—应变关系推导了时间域近似常Q黏滞波动方程的一阶速度—压力形式,能较好地描述地震波在黏滞介质中的衰减和频散;姚振岸等[16]对黏弹各向异性介质中不同震源机制的微地震波场特征进行了研究。
关于黏弹介质的研究还有很多[17-19],但这些研究主要是针对更高维度或更复杂的介质两种情况,而对黏弹机制数的研究较少。对于GSLS模型有限差分正演,通常使用的黏弹单元(常称为黏弹机制)数越多,精度越高,但相应的求解难度也越高,计算效率也越低。一般情况下,当Q值较小时需要使用较多的机制数才能得到较好的模拟效果,当Q值较高时仅使用较少的机制数便能得到较好的模拟效果。Zhu等[20]对GSLS模型正演中单机制数和三机制数的精确度做了调研,结果表明介质吸收衰减较弱时仅使用单机制数模拟就能达到较高的精度,介质吸收衰减较强而波传播距离很短时单机制数也能得到较好的模拟精度,因此一般情况下使用单机制模拟便可获得较好的结果,无需使用更多的黏弹机制数。但随着业界对精度的要求日益提高和近年来对近地表强吸收衰减影响的认识逐步加深[21-23],单机制的模拟精度已不能满足需求。Cai等[24]对不同机制数的模拟精度做了调研,并分析了变机制数正演的可行性。
本文基于GSLS模型有限差分正演提出了一种黏声波动方程变机制数有限差分正演方法,首先研究了不同机制数GSLS模型的地震波场正演模拟精度,然后对变机制数有限差分的适用性做了评估,最后实现地震波场交错网格有限差分数值模拟并对模拟结果进行了分析。
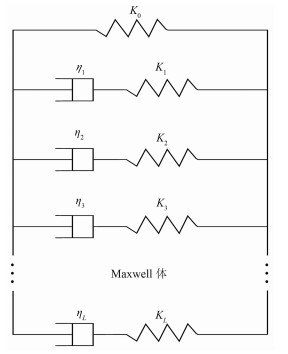
1 黏弹模型及其波动方程 1.1 GSLS衰减模型广义标准线性固体模型可以很好地模拟介质的衰减特性,图 1为L个Maxwell体(一个弹性元和一个牛顿黏滞元串联而成)与一弹性元并联组成的GSLS模型示意图。GSLS模型复模量可表示为[8]
|
图 1 GSLS衰减模型示意图 |
| $ M(\omega ) = {K_0}\left( {1 - L + \sum\limits_{l = 1}^L {\frac{{1 + {\rm{i}}\omega {\tau _{\varepsilon , l}}}}{{1 + {\rm{i}}\omega {\tau _{\sigma , l}}}}} } \right) $ | (1) |
式中:ω为角频率;K0为与Maxwell体并联的弹性元的弹性模量;Ki和ηi(l=1,2,…,L)分别为Maxwell体的
弹性模量和牛顿黏滞系数;τσ, l和τε, l分别为第l个Maxwell体的应力松弛时间和应变松弛时间,可表示为[25]
| $ {\tau _{\sigma , l}} = \frac{{{\eta _l}}}{{{K_l}}} $ | (2) |
| $ {\tau _{\varepsilon , l}} = \frac{{{\eta _l}}}{{{K_0}}} + \frac{{{\eta _l}}}{{{K_l}}} $ | (3) |
品质因子Q定义为[26]
| $ Q=\frac{\operatorname{RE}[M(\omega)]}{\operatorname{IM}[M(\omega)]} $ | (4) |
式中RE(·)和IM(·)分别表示求复数的实部和虚部。由式(1)和式(4)可得
| $ Q\left( {\omega , {\tau _{\sigma , l}}, \tau } \right) = \frac{{1 + \sum\limits_{l = 1}^L {\frac{{\tau {\omega ^2}\tau _{\sigma , l}^2}}{{1 + {\omega ^2}\tau _{\sigma , l}^2}}} }}{{\sum\limits_{l = 1}^L {\frac{{\tau \omega {\tau _{\sigma , l}}}}{{1 + {\omega ^2}\tau _{\sigma , l}^2}}} }} $ | (5) |
式中
| $ \tau = \frac{{{\tau _{\varepsilon , l}}}}{{{\tau _{\sigma , l}}}} - 1 $ | (6) |
当GSLS模型所用机制数L已知时,参数τσ, l、τ的最优值可由最小二乘反演得到
| $ J\left( {{\tau _{\sigma , l}}, \tau } \right) = \int_{{\omega _1}}^{{\omega _2}} {{{\left[ {{Q^{ - 1}}\left( {\omega , {\tau _{\sigma , l}}, \tau } \right) - {{\tilde Q}^{ - 1}}} \right]}^2}} {\rm{d}}\omega $ | (7) |
式中:ω1、ω2分别为计算时所用的起、止频率;
| $ \tau = \frac{1}{{\tilde Q}}\frac{{\sum\limits_{l = 1}^L {{I_0}} (l)}}{{\sum\limits_{l = 1}^L {{I_1}} (l) + \sum\limits_{l = 1}^{L - 1} {\sum\limits_{k = l + 1}^L {{I_2}} } (k, l)}} $ | (8) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{I_0}(l) = \frac{1}{{2{\tau _{\sigma , l}}}}\ln \left. {\left( {1 + {\omega ^2}\tau _{\sigma , l}^2} \right)} \right|_{{\omega _1}}^{{\omega _2}}}\\ {{I_1}(l) = \frac{1}{{2{\tau _{\sigma , l}}}}\left. {\left[ {{{\tan }^{ - 1}}\left( {\omega {\tau _{\sigma , l}}} \right) - \frac{{\omega {\tau _{\sigma , l}}}}{{1 + {\omega ^2}\tau _{\sigma , l}^2}}} \right]} \right|_{{\omega _1}}^{{\omega _2}}}\\ {{I_2}(k, l) = \frac{{{\tau _{\sigma , l}}{\tau _{\sigma , k}}}}{{\tau _{\sigma , l}^2 - \tau _{\sigma , k}^2}}\left. {\left[ {\frac{{{{\tan }^{ - 1}}\left( {\omega {\tau _{\sigma , l}}} \right)}}{{{\tau _{\sigma , l}}}} - \frac{{{{\tan }^{ - 1}}\left( {\omega {\tau _{\sigma , k}}} \right)}}{{{\tau _{\sigma , k}}}}} \right]} \right|_{{\omega _1}}^{{\omega _2}}} \end{array}} \right. $ | (9) |
式中“
有关黏弹波动方程的推导Robertsson等[6]已做过详细描述。二维黏声微分方程为
| $ \left\{ {\begin{array}{*{20}{c}} { - \dot P = {M_{\rm{R}}}\left[ {1 - \sum\limits_{l = 1}^L {\left( {1 - \frac{{{\tau _{\varepsilon , l}}}}{{{\tau _{\sigma , l}}}}} \right)} } \right]\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right) + \sum\limits_{l = 1}^L {{r_l}} }\\ \begin{array}{l} {{\dot r}_l} = \frac{1}{{{\tau _{\sigma , l}}}}{r_l} + {M_{\rm{R}}}\left[ {\frac{1}{{{\tau _{\sigma , l}}}}\left( {1 - \frac{{{\tau _{\varepsilon , l}}}}{{{\tau _{\sigma , l}}}}} \right)} \right]\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right)\;\;\;\;\\ 1 \le l \le L \end{array}\\ {{{\dot v}_x} = \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + {f_x}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {{{\dot v}_z} = \frac{1}{\rho }\frac{{\partial P}}{{\partial z}} + {f_z}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (10) |
式中:变量上面的点表示时间导数;P为压力;MR为介质松弛模量;rl为第l个Maxwell体的记忆变量;vx和vz分别为x方向和z方向的速度分量;ρ为密度;fx和fz分别为x方向和z方向施加的外力。
2 变机制数有限差分正演精度分析 2.1 数值解与解析解的对比为评估不同机制数黏声方程有限差分波场模拟的精度,本文首先计算二维均匀各向同性介质中黏声格林函数的解析解[27],然后将不同机制数黏声方程的模拟结果与解析解做对比。
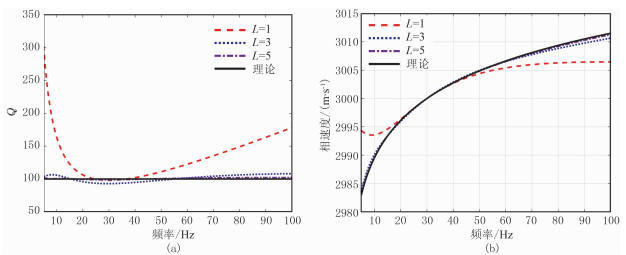
对于GSLS模型而言,使用的机制数越多,其对黏弹介质的描述就越准确。为研究不同机制数的模拟精度,建立一个均匀模型,Q值设置为100,震源是主频为30Hz为Ricker子波,频带为5~100Hz,参考频率(主频)处速度为3000m/s,密度为2.1g/cm3。采用时间二阶、空间八阶差分格式进行正演模拟,利用PML边界条件吸收边界反射。使用不同机制个数模拟的Q值曲线和相速度曲线如图 2所示。由图 2可见,单机制数(L=1)模拟的Q值只在参考频率附近与理论值较为接近,在低频和高频端都远大于理论值,三机制数(L=3)模拟的Q值在给定频带上都与理论值相差不大,五机制数(L=5)模拟的Q值在给定频带上与理论值几乎完全重合,表明GSLS模型使用的机制数越多其对黏弹介质的模拟就越准确。相速度曲线(图 2b)与Q值模拟曲线类似,即使用的机制数越多其模拟的相速度曲线越接近理论曲线。
|
图 2 Q=100时不同机制数的模拟结果 (a)Q值;(b)相速度 |
图 3为不同机制数黏声方程模拟结果随传播距离的变化。可以看出:当传播距离较近(500m)时,不同机制数的数值模拟结果都能与解析解相吻合;中传播距离(2500m)时单机制数和三机制数的模拟结果出现微小的误差;远传播距离(4500m)时各机制数的模拟结果都出现误差,但机制数越大误差越小。为衡量不同机制数波场模拟的准确性,计算模拟结果的均方根误差(RMSE)

|
图 3 Q=100时不同机制数有限差分模拟结果随传播距离的变化 (a)500m;(b)2500m;(c)4500m |
| $ E = \sqrt {\frac{{\sum\limits_{j = 1}^{{n_t}} {{{\left( {d_j^{\rm{n}} - d_j^{\rm{a}}} \right)}^2}} }}{{{n_t}}}} $ | (11) |
式中:nt为地震道采样点数;djn为有限差分模拟结果;dja为解析解。不同机制数模拟结果均方根误差值如表 1所示,可见机制数相同时波传播距离越远,误差越大;传播距离相同时使用的机制数越多,误差越小。因此,为了获得较高的计算精度,使用较大的机制数很有必要,但是随着机制数增加,正演的计算效率会相应降低。
|
|
表 1 不同机制数模拟结果均方根误差(Q=100) |
实际介质模拟中,模拟精度与机制数、Q值和波的传播距离有关。由上文可知基于GSLS模型的黏声波动方程有限差分正演使用的机制数越大,对地震波场的模拟就越准确,但相应的波动方程也越复杂,需要的存储空间也越多,计算效率也越低。为达到计算效率与计算精度的统一,需要根据所需要的模拟精度、Q值和波在该Q值区域传播的距离确定模拟时使用的机制数。具体研究思路为:
(1) 采用的不同机制个数对不同Q值、不同传播距离情况进行正演模拟;
(2) 将不同机制数的模拟结果分别与相应的解析解作对比,计算得出对应的模拟精度;
(3) 将不同机制数模拟结果的模拟精度与所需要的最低模拟精度进行比较,拟合得到不同机制数的适用范围。
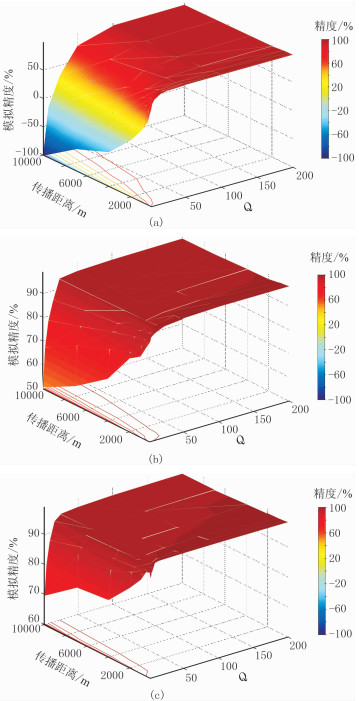
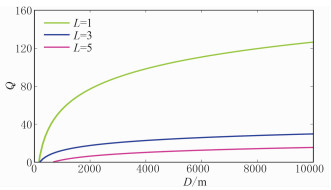
本文模拟精度设置为95%;Q值从2变化到200,涵盖强吸收介质和弱吸收介质的情况;波的传播距离从100m变化到10000m。震源设置为Ricker子波,主频为30Hz,频带为5~100Hz,参考频率处(主频)速度为3000m/s,密度为2.1g/cm3,采用时间二阶、空间八阶差分格式进行正演模拟,边界设置为PML条件。图 4展示了L=1、3、5时的模拟精度。由图可知三种机制数的模拟精度都随着传播距离减小而增大、随Q值增大而增大。L=1时的模拟精度在传播距离较大且Q值较小的时候出现负数情况,说明此时模拟的波场与实际波场相比出现了极大的波形畸变;L=3时的模拟精度在全区域大于50%并且大部分区域模拟精度在95%以上;L=5时的模拟精度在全区域大于70%并且绝大部分区域模拟精度都在95%以上。另外,模拟精度在传播距离和Q值组成的平面上的投影坐标值表示波传播一定的距离时满足特定精度所需的最小Q值,因此取不同机制数在模拟精度为95%时的投影点即可拟合得到不同机制数的模拟精度与Q值和波的传播距离的关系,如图 5所示。L=1、3和5满足模拟精度为95%时, 最小Q值和波的传播距离的关系分别为
|
图 4 模拟精度随Q值和传播距离变化 (a)L=1;(b)L=3;(c)L=5 |
| $ {Q_{\min }} = 30.937\ln D - 157.2\;\;\;\;\;\;L = 1 $ | (12) |
| $ {Q_{\min }} = 7.6039\ln D - 40.364\;\;\;\;\;\;L = 3 $ | (13) |
| $ {Q_{\min }} = 5.7302\ln D - 37.40\;\;\;\;\;\;L = 5 $ | (14) |
式中:Qmin为最小Q值;D为波的传播距离。因此在实际介质模拟中,控制精度为95%,在模型已知的情况下便可直接确定机制数。此外由图 5还可看出,当传播距离足够远、Q值又足够小时,L=5也不能满足模拟精度要求,此时应当使用更大的机制数,但此种情况实际中极其少见。
|
图 5 不同机制数模拟精度为95%时所需最小Q值与波的传播距离间的关系 |
黏声波动方程变机制数有限差分正演在不同Q值区域会使用不同机制数,因此在Q值发生变化的边界上,不同机制数黏声方程差分格式的差异不可避免地会引起人为的数值干扰。因此需对这种数值干扰进行定量分析,从而更好地评价方法的适用性。
设计一个尺寸为1000m×1000m的均匀模型,空间采样间隔Δx=Δz=5m,速度为2000m/s,密度为1.8g/cm3。为研究机制数变化引起的数值噪声的大小,以z=500m为分界面,界面以上采用L=1或3、界面以下采用L=3或5黏声方程进行波场模拟。震源采用Ricker子波,震源位于(500m,100m),主频为30Hz,时间步长为1ms,在z=400m的水平线上接收,间隔为5m;采用时间二阶、空间八阶差分格式及PML边界条件。
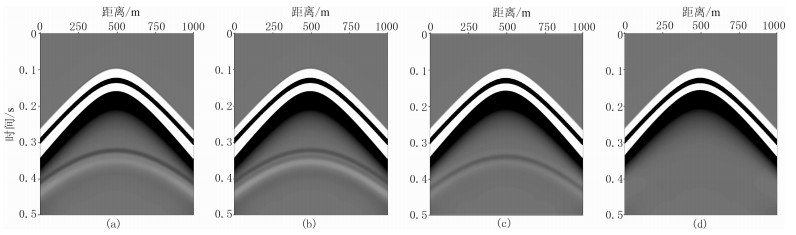
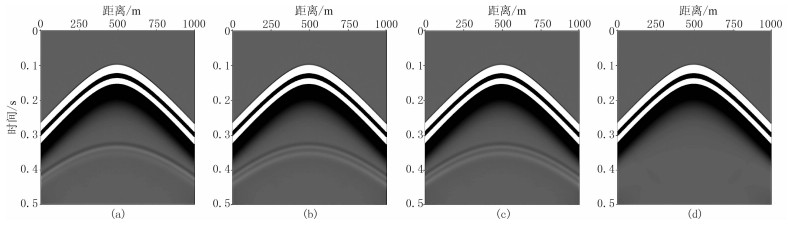
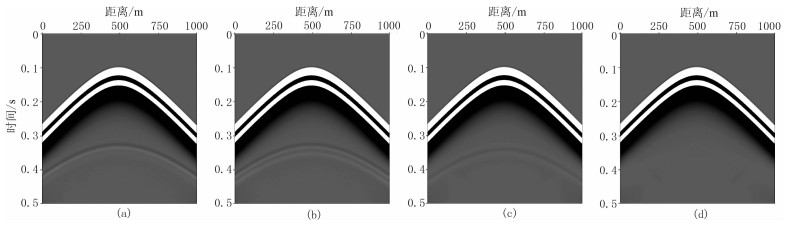
图 6~图 8分别为Q=20、60、100时均匀模型的变机制数正演结果。由图 6~图 8可以看出,变机制数模拟确实会引起数值噪声,但数值噪声非常小,只有把增益设置很大的时候才能看到数值反射。同时可以看出,Q值越大,机制数变化引起的数值干扰越小,Q值不变时,机制数由1变为5、由1变为3和由3变为5引入的数值干扰依次减小。
|
图 6 Q=20时变机制数正演记录 (a)界面上为1、下为3;(b)界面上为1、下为5;(c)界面上为3、下为5;(d)界面上、下均为5 |
|
图 7 Q=60时变机制数正演记录 (a)界面上为1、下为3;(b)界面上为1、下为5;(c)界面上为3、下为5;(d)界面上、下均为5 |
|
图 8 Q=100时变机制数正演记录 (a)界面上为1、下为3;(b)界面上为1、下为5;(c)界面上为3、下为5;(d)界面上、下均为5 |
为研究这些数值干扰对波场模拟的影响,本文将差分格式不同引起的数值干扰的大小与地下速度变化产生的反射波大小对应起来。首先提取这些数值干扰的振幅,然后保持模型其他参数不变,将z=500m以下的速度适当增大Δv后进行正演;提取正演记录中的反射波振幅与数值反射的振幅作对比,然后根据对比结果再调整速度增量(Δv)大小进行正演,直至反射波振幅和数值反射振幅相等。此时的速度增量与原速度的比值(Δv/v)即和数值噪声的影响相当,速度变化的大小反映数值干扰对波场模拟的影响大小。表 2为与数值干扰量级相当的反射波所对应的地层速度变化。可以看出,机制数变化相同时,Q值越小,数值干扰对波场模拟的影响越大,Q值相同时,机制数从1变到5引起的数值干扰最大,从1变到3次之,从3变到5最小。但不管是哪种情况,所引入的数值干扰在数量级上都比地下速度发生1%的扰动所产生的反射还要微弱,因此可以忽略不计,说明黏声波动方程变机制数有限差分正演方法具有很高的精度,可以较为精确地对地下复杂构造、细微岩性差异甚至流体变化引起的地震波场异常进行模拟。
|
|
表 2 与变机制数引起数值干扰相当的地层速度变化(%) |
由上文可知,在实际介质模拟中,L=5模拟结果在绝大多数情况下能保持很高的精度。因此,以L=5的模拟结果作为标准进行对比分析。
3.1 简单模型为了验证变机制数有限差分正演的效果,设计了一个大小为1000m×500m的简单层状模型,空间采样间隔Δx=Δz=1m,速度、密度和品质因子参数如表 3所示。其中各层品质因子根据岩性信息给出,例如Q=10模拟沙层,Q=40模拟含水沙层,Q=60模拟砂质胶泥层,Q=105模拟一般岩层。
|
|
表 3 层状模型参数 |
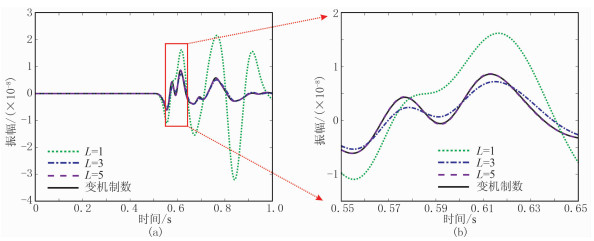
控制模拟精度为95%,震源采用Ricker子波,震源位于(500m,10m),主频为30Hz,时间步长为0.1ms,检波器位于模型顶界面,间隔为1m。采用时间二阶、空间八阶差分格式和PML边界条件对该模型做波场数值模拟。图 9是L=1、3、5和自适应变机制数的正演结果,四者的增益相同。从图 9可以看出,L=1模拟记录在小炮检距时能保持较高的精度,但当炮检距较大时其记录的振幅偏大,原因是L=1时模拟品质因子整体高于理论值很多,不能将介质的吸收特性描述准确;而L=3、5和变机制数的正演结果的初至、反射和多次波等主要特征差别很小,说明三者具有相似的精度。图 10为图 9中x=900m处的单道波形对比,可以看出L=1模拟结果的振幅误差超过实际振幅值的一倍,并且两个邻近波峰没能区分开来,说明L=1模拟不满足精度要求;L=3的模拟精度相较于L=1提高了很多,但波形还是出现了一些小的畸变;变机制数与L=5的模拟结果波形吻合较好。为进一步研究变机制数模拟结果的精度,将图 9c与图 9d数据相减,残差的最大振幅仅为图 9c数据最大振幅的0.0055%,因此可以认为变机制数和L=5具有相同的模拟精度。图 11为不同机制数模拟需要的计算时间,变机制数模拟效率比L=5提高了27.4%。

|
图 9 层状模型L不同时正演记录对比 (a)L=1;(b)L=3;(c)L=5;(d)变机制数 |
|
图 10 层状模型L不同时正演x=900m处单道对比(a)及其局部放大显示(b) |

|
图 11 层状模型不同L模拟计算时间对比 |
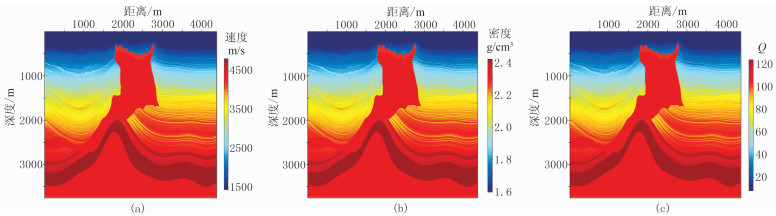
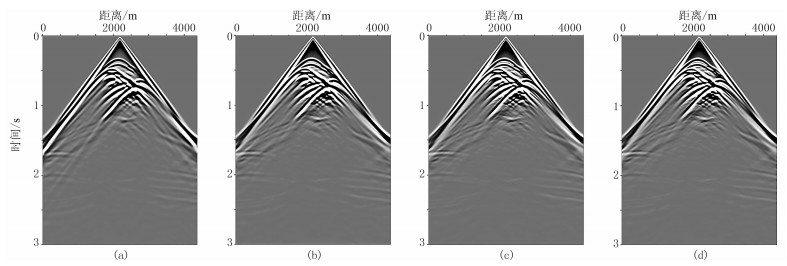
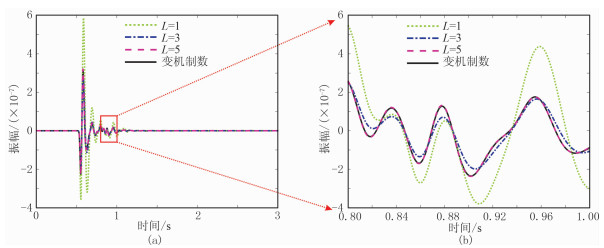
为更接近实际和检验算法的稳定性,建立一个SEAM模型,模型有751×876个网格点,网格间距Δx=Δz=5m。模型中存在连续和不连续的参数变化,如图 12所示,其中密度和品质因子模型根据速度模型给出。震源采用主频为30 Hz的Ricker子波,震源位于(2190m,20m),时间步长为0.5ms,检波器位于模型表面,间隔为5m,采用时间二阶、空间八阶差分格式,PML边界条件。图 13为L=1、3、5和变机制数的正演结果,四者的增益相同。L=1时的模拟结果在大炮检距时出现较大误差;L=3、5和变机制数模拟结果的初至、反射、折射、散射和多次波等主要特征差别很小,说明三者具有相似的精度。图 14为图 13中x=3000m的单道波形对比,L=1时对介质的吸收衰减特性描述不准确,其振幅明显偏大;L=3时模拟精度较高,但波形出现了一些小的畸变;而变机制数与L=5的道记录波形依旧吻合较好。
|
图 12 SEAM模型 (a)速度;(b)密度;(c)品质因子 |
|
图 13 SEAM模型L不同时正演记录对比 (a)L=1;(b)L=3;(c)L=5;(d)变机制数 |
|
图 14 SEAM模型L不同时正演x=3000m单道对比(a)及其局部放大显示(b) |
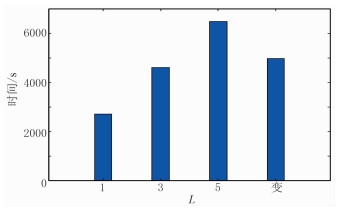
将图 13c与图 13d数据相减,残差的最大振幅仅为图 13c数据最大振幅的0.0038%,因此可以认为变机制和5机制具有相同的精度。图 15为不同机制数模拟的计算耗时,变机制模拟效率比L=5提高了23.25%。
|
图 15 SEAM模型不同L模拟计算时间对比 |
由以上结果可知,变机制数有限差分正演方法对复杂模型也能得到较精确的模拟结果,不仅具有与机制数L=5相同的模拟精度,并且计算效率约提高了四分之一。
4 结论随着业界对近地表研究的日益关注和对精度要求的日益提高,单机制GSLS模型有限差分正演已逐渐不能满足高精度地球物理研究的需要。本文基于GSLS模型有限差分正演,提出了一种变机制黏声波动方程有限差分正演方法,研究结果表明:
(1) 实际介质模拟中,模拟精度与机制数、Q值和波的传播距离有关。本文给出了机制数的选取方法。当控制在一定精度时,Q值和波的传播距离又是已知的情况下,利用本文给出的方法可直接确定机制数。
(2) 在Q值发生变化的边界上,不同机制数黏声方程差分格式的差异会引起人为的数值干扰。但这些数值干扰对波场模拟的影响极小,说明本文提出的黏声波动方程变机制数有限差分正演方法具有很高的精度,可以对地下复杂介质的细微结构引起的微弱波场异常进行精细模拟。
(3) 小机制数GSLS模型有限差分在介质吸收衰减较弱时能得到较高精度的模拟结果,而当介质吸收衰减较强时其正演结果会出现明显的振幅误差和波形畸变,无法满足信号分析等地球物理研究的精度要求;大机制数GSLS模型有限差分能得到高精度的模拟结果,但模拟时所需的存储空间大,计算效率低。变机制数GSLS模型有限差分针对不同模型自动选取机制数,因此对任意模型都能达到模拟精度与计算效率的统一。
尚需指出,本文仅研究了单机制数、三机制数和五机制数二维黏声波动方程有限差分正演,将其推广到三维黏弹介质是今后的研究方向。
| [1] |
Carcione J M. Wave propagation in anisotropic linear viscoelastic media:Theory and simulated wavefields[J]. Geophysical Journal International, 1990, 101(3): 739-750. DOI:10.1111/gji.1990.101.issue-3 |
| [2] |
Liu H P, Anderson D L, Kanamori H. Velocity dispersion due to anelasticity:implications for seismology and mantle composition[J]. Geophysical Journal International, 1976, 47(1): 41-58. DOI:10.1111/j.1365-246X.1976.tb01261.x |
| [3] |
Day S M, Bernard M J. Numerical simulation of atte-nuated wavefields using a Padé approximate method[J]. Geophysical Journal of the Royal Astronomical Society, 1984, 78(1): 105-118. DOI:10.1111/j.1365-246X.1984.tb06474.x |
| [4] |
Emmerich H, Korn M. Incorporation of attenuation into time-domain computations of seismic wave fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
| [5] |
Robertsson J O A, Blanch J O, Levander A, et al.3-D viscoelastic finite difference modeling[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 994-997.
|
| [6] |
Robertsson J O A, Blanch J O, Symes W W. Visco-elastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [7] |
Blanch J O, Robertsson J O A, Symes W W. Modeling of a constant Q:methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique[J]. Geophysics, 1995, 60(1): 176-184. DOI:10.1190/1.1443744 |
| [8] |
Bohlen T. Parallel 3-D viscoelastic finite difference seismic modelling[J]. Computers & Geosciences, 2002, 28(8): 887-899. |
| [9] |
Saenger E H, Bohlen T. Finite difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J]. Geophysics, 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [10] |
杜启振, 杨慧珠. 线性黏弹性各向异性介质速度频散和衰减特征研究[J]. 物理学报, 2002, 51(9): 2101-2108. DU Qizhen, YANG Huizhu. Velocity dispersion and attenuation in anisotropic linear viscoelastic media[J]. Acta Physica Sinica, 2002, 51(9): 2101-2108. DOI:10.3321/j.issn:1000-3290.2002.09.035 |
| [11] |
杜启振. 各向异性黏弹性介质伪谱法波场模拟[J]. 物理学报, 2004, 53(12): 4428-4434. DU Qizhen. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media[J]. Acta Physica Sinica, 2004, 53(12): 4428-4434. |
| [12] |
牛滨华. 黏弹性介质与地震波传播[M]. 北京: 地质出版社, 2007.
|
| [13] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN Hongyong, LIU Yang. Rotated staggered grid high order finite difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [14] |
何兵红, 吴国忱, 许冲. 基于FFD算子的衰减介质地震波模拟[J]. 石油地球物理勘探, 2014, 49(1): 153-160. HE Binghong, WU Guochen, XU Chong. Seismic wave simulation in attenuation medium based on FFD operator[J]. Oil Geophysical Prospecting, 2014, 49(1): 153-160. |
| [15] |
罗文山, 陈汉明, 王成祥, 等. 时间域黏滞波动方程及其数值模拟新方法[J]. 石油地球物理勘探, 2016, 51(4): 707-713. LUO Wenshan, CHEN Hanming, WANG Cheng-xiang, et al. A novel time-domain viscoacoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2016, 51(4): 707-713. |
| [16] |
姚振岸, 孙成禹, 谢俊法, 等. 黏弹TTI介质旋转交错网格微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(2): 253-263. YAO Zhen'an, SUN Chengyu, XIE Junfa, et al. Micro-seismic forward modeling in visco-elastic TTI media based on rotated staggered grid finite-difference method[J]. Oil Geophysical Prospecting, 2017, 52(2): 253-263. |
| [17] |
Talezer H. An accurate and efficient scheme for wave propagation in linear viscoelastic media[J]. Geophy-sics, 1990, 55(10): 1366-1379. |
| [18] |
杨仁虎, 常旭, 刘伊克. 基于非均匀各向同性介质的黏弹性波正演数值模拟[J]. 地球物理学报, 2009, 52(9): 2321-2327. YANG Renhu, CHANG Xu, LIU Yike. Viscoelastic wave modeling in heterogeneous and isotropic media[J]. Chinese Journal of Geophysics, 2009, 52(9): 2321-2327. DOI:10.3969/j.issn.0001-5733.2009.09.016 |
| [19] |
陈康, 吴国忱, 印兴耀, 等. 基于反射率法的TTI介质正演模拟[J]. 石油地球物理勘探, 2013, 48(5): 717-727. CHEN Kang, WU Guochen, YIN Xingyao, et al. The modeling based on the reflectivity method in TTImedia[J]. Oil Geophysical Prospecting, 2013, 48(5): 717-727. |
| [20] |
Zhu T, Carcione J M. Theory and modelling of constant-Q P-and S-waves using fractional spatial deri-vatives[J]. Geophysical Journal International, 2014, 196(3): 1787-1795. DOI:10.1093/gji/ggt483 |
| [21] |
Krohn C E, Murray T J. Shallow near-surface effects[J]. Geophysics, 2016, 81(5): T221-T231. DOI:10.1190/geo2016-0028.1 |
| [22] |
陈志德, 王成, 刘国友, 等. 近地表Q值模型建立方法及其地震叠前补偿应用[J]. 石油学报, 2015, 36(2): 188-196. CHEN Zhide, WANG Cheng, LIU Guoyou, et al. Modeling method of near-surface Q value and its seismic pre-stack compensation application[J]. Acta Petrolei Sinica, 2015, 36(2): 188-196. |
| [23] |
杨宇, 黄建平, 雷建设, 等. Lebedev网格黏弹性介质起伏地表正演模拟[J]. 石油地球物理勘探, 2016, 51(4): 698-706. YANG Yu, HUANG Jianping, LEI Jianshe, et al. Numerical simulation of Lebedev grid for viscoelastic media with irregular free-surface[J]. Oil Geophysical Prospecting, 2016, 51(4): 698-706. |
| [24] |
Cai R Q, Sun C Y, Wu D S, et al.Finite-difference numerical modeling with variable mechanism for viscoacoustic wave equation[C]. Extended Abstracts of 80th EAGE Conference & Exhibition, 2018, Tu P903.
|
| [25] |
Zener C M, Siegel S. Elasticity and Anelasticity of Metals[M]. Chicago, Illinois: University of Chicago Press, 1948.
|
| [26] |
O'Connell R J, Budiansky B. Measures of dissipation in viscoelastic media[J]. Geophysical Research Letters, 1978, 5(1): 5-8. DOI:10.1029/GL005i001p00005 |
| [27] |
Carcione J M, Dan K, Ronnie K. Wave propagation simulation in a linear viscoelastic medium[J]. Geophysical Journal of the Royal Astronomical Society, 1988, 93(2): 597-611. |



 孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: