随着准噶尔盆地油气勘探的持续深入,勘探目标更加复杂,希望更清晰地刻画断层、河道等地质目标体,这就对地震资料提出了更高精度要求。然而,准噶尔盆地特有的沙丘、戈壁、农田地貌与缺乏稳定潜水面的地震地质条件,导致了原始地震资料噪声发育、信噪比低,从而给后续的属性分析、波阻抗反演、裂缝预测等带来误差,严重影响构造解释和岩性识别[1-3]。包括FXY、小波变换、f-x滤波、KL变换、τ-p变换等的传统噪声压制方法[4-8],大多利用信号的空间相干特性,在增强同相轴连续性的同时,严重损伤尖灭、断层、不整合等地质异常体信息,模糊断层、河道等不连续结构特征,出现假像,最终影响地震资料精细解释。
现今主流处理解释软件系统大多采用三维空间预测滤波方法(FXY等)压制随机噪声[6-8]。准噶尔盆地前期地震资料处理也主要使用上述FXY方法,但该类方法均是假定在短距离内同相轴是线性的,以此提高强能量信号的信噪比,因此将会损伤弱能量的有效信号,降低空间分辨率,模糊断层、裂缝等线性相关性差的地质信息。
分离地震资料中有效信号与噪声的方法研究,一直是地震资料处理的热点之一[9-12]。Luo等[13]基于次序统计思想给出一种地震数据保边滤波算法,使用Kuwahara多窗分析技术计算当前分析点周围各子窗内数据的均值和方差,将最小方差对应子窗的均值作为当前点的滤波结果输出;AlBinHassan等[14]发展了这种保边滤波思想,给出了三维情况下的子窗剖分方法,将边缘保护平滑算法用于三维地震数据的保边滤波处理。这类基于次序统计的方法的缺点是容易对断裂带地震反射细节特征造成明显损伤,且固定尺寸的滤波窗口在处理强噪声干扰时常会引入滤波假象。
Fehmers等[15]提出将各向异性扩散滤波方法用于地震资料保边滤波处理,该方法利用梯度结构张量分析三维地震数据空间结构特征,为扩散滤波方程构造合适的扩散张量,并采用两种不同尺度梯度结构张量度量反射层不连续性,以此约束扩散滤波器在断层及其他地质异常体边缘的滤波程度;Lavialle等[16]发展了这种扩散滤波方法,提出专门用于保护和增强断层构造特征的滤波器。
以上采用的是各向异性扩散滤波方法,其缺点是通过不同的扩散张量构造扩散滤波方程,可操作性较差,且易导致扩散滤波的空间结构不明确,在特殊情况下还会引起多解性。
GeoEast处理解释系统是具有独立知识产权的地震资料采集、处理、解释一体化的综合性软件。该系统不仅在中国国内广泛应用,而且成为全球少数可为油气勘探开发提供全面技术支撑的软件系统[17-18],还具备友好的(用户)扩展研发平台。
为改善准噶尔盆地地震资料随机噪声压制效果,在GeoEast系统上开展了基于三维各向异性拉普拉斯滤波的随机噪声压制(简称3DALFRS)软件的研发。本方法核心思想是针对常规扩散滤波法在滤波处理时的不确定性,基于各向异性扩散滤波方程,推导出拉普拉斯滤波器模型;利用梯度结构张量技术估算地震同相轴方向和断层位置,并给出具有明确空间滤波结构的各向异性拉普拉斯滤波器。该方法对资料成像平滑区域进行各向同性的平滑处理,保留了传统方法的优点;对资料成像边缘区域进行各向异性处理,消除了传统方法的边缘模糊现象。准噶尔盆地实际资料处理结果表明,应用本文随机噪声压制方法保护了有效信号,地质体边缘特征更清晰,断层成像精度更高,为后续储层反演及构造精细解释等提供了可靠资料。
1 方法原理3DALFRS方法[19]在GeoEast上应用的基本思路是:首先对数据进行规则化处理,包括对不规则数据进行补道处理;再根据三维梯度结构张量估计地层方向并给出断层置信度;然后构造具有明确空间滤波结构的各向异性拉普拉斯滤波器(ANISO LAP),通过断层置信度调整三维空间中滤波器的形态,使其兼顾最大程度的滤波性能和有效的边缘保持、断层增强性能。
对于三维数据U,其梯度结构张量定义[20]为
| $ \mathit{\boldsymbol{J}}(\nabla U) = {L_P}*{\mathit{\boldsymbol{J}}_0}(\nabla U) = {L_P}*\left[ {\nabla U{{(\nabla U)}^{\rm{T}}}} \right] $ | (1) |
式中:LP为三维低通滤波函数,一般取尺度为ρ的高斯函数;
梯度结构张量
| $ \mathit{\boldsymbol{J}}(\nabla U) = \left( {{\mathit{\boldsymbol{v}}_1}{\mathit{\boldsymbol{v}}_2}{\mathit{\boldsymbol{v}}_3}} \right)\left( {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0\\ 0&{{\lambda _2}}&0\\ 0&0&{{\lambda _3}} \end{array}} \right){\left( {{\mathit{\boldsymbol{v}}_1}{\mathit{\boldsymbol{v}}_2}{\mathit{\boldsymbol{v}}_3}} \right)^{\rm{T}}} $ | (2) |
式中:v1、v2和v3为梯度结构张量的三个特征向量,构成一个局部正交坐标系,其中v1为梯度方向,而由v2和v3构成的平面平行于局部地层平面,且v3对应于局部地层反射能量变化最一致性方向;λ1≥λ2≥λ3≥0对应于梯度结构张量的三个非负特征值,它们反映了信号沿特征方向的平均能量变化程度。
利用梯度结构张量三个特征值给出的信息,定义地震数据中的线型结构置信度Cline和面型结构置信度Cplane为
| $ \left\{ {\begin{array}{*{20}{c}} {{C_{{\rm{ line }}}} = \frac{{{\lambda _2} - {\lambda _3}}}{{{\lambda _2} + {\lambda _3}}}}\\ {{C_{{\rm{ plane }}}} = \frac{{{\lambda _1} - {\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}} \end{array}} \right. $ | (3) |
在此基础上定义断层结构度参数
| $ {C_{{\rm{ fault }}}} = {C_{{\rm{ line }}}}\left( {1 - {C_{{\rm{ plane }}}}} \right) $ | (4) |
根据上述地层结构度参数,在地震同相轴线性延展区域,由于Cline→0且Cplane→1,使Cfault→0;在断层、裂缝等区域,由于Cline→1且Cplane→0,使Cfault→1。
(3) 构造各向异性拉普拉斯滤波器
| $ \begin{array}{l} {G^D}\left( {{\mathit{\boldsymbol{x}}_0}, \mathit{\boldsymbol{x}}} \right) = \exp \left\{ { - \frac{1}{2}\sum\limits_{i = 1}^3 {\frac{{{{\left[ {\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0}} \right) \cdot {\mathit{\boldsymbol{v}}_i}\left( {{\mathit{\boldsymbol{x}}_0}} \right)} \right]}^2}}}{{\sigma _i^2\left( {{\mathit{\boldsymbol{x}}_0}} \right)}}} } \right\}\\ = \exp \left[ { - \frac{{{{\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0}} \right)}}{{2\sigma _{\max }^2}}} \right] \end{array} $ | (5) |
式中:x=(x, y, t)为三维空间坐标,其中x和y分别表示三维地震数据体的CMPline和CMP,t表示采样时间位置;x0=(x0, y0, t0)为各向异性拉普拉斯滤波器中心位置;v1(x0)、v2(x0)和v3(x0)为空间位置x0处拉普拉斯滤波核函数的正交空间延展方向;σ1(x0)、σ2(x0)和σ3(x0)为该处拉普拉斯滤波函数沿相应方向的尺度参数。将拉普拉斯滤波核函数记为矩阵后,D为各向异性滤波张量,定义为
| $ \begin{array}{l} \mathit{\boldsymbol{D}} = \left[ {{\mathit{\boldsymbol{v}}_{\rm{1}}}{\rm{(}}{\mathit{\boldsymbol{x}}_{\rm{0}}}{\rm{)}}{\mathit{\boldsymbol{v}}_2}{\rm{(}}{\mathit{\boldsymbol{x}}_{\rm{0}}}{\rm{)}}{\mathit{\boldsymbol{v}}_3}{\rm{(}}{\mathit{\boldsymbol{x}}_{\rm{0}}}{\rm{)}}} \right] \times \\ \left( {\begin{array}{*{20}{c}} {{\sigma _1}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}&0&0\\ 0&{{\sigma _2}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}&0\\ 0&0&{{\sigma _3}\left( {{\mathit{\boldsymbol{x}}_0}} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_1}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}\\ {{\mathit{\boldsymbol{v}}_2}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}\\ {{\mathit{\boldsymbol{v}}_3}\left( {{\mathit{\boldsymbol{x}}_0}} \right)} \end{array}} \right) \end{array} $ | (6) |
根据地层结构自适应滤波的目的,构造如下形式的滤波器尺度参数
| $ \left\{ {\begin{array}{*{20}{c}} {{\sigma _1}\left( {{\mathit{\boldsymbol{x}}_0}} \right) = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {{\sigma _2}\left( {{\mathit{\boldsymbol{x}}_0}} \right) = {\sigma _{\min }} + \left[ {1 - {C_{{\rm{fault }}}}\left( {{\mathit{\boldsymbol{x}}_0}} \right)} \right]\left( {{\sigma _{{\rm{iso }}}} - {\sigma _{{\rm{min }}}}} \right)}\\ {{\sigma _3}\left( {{\mathit{\boldsymbol{x}}_0}} \right) = \frac{{\sigma _{{\rm{iso}}}^2}}{{{\sigma _2}\left( {{\mathit{\boldsymbol{x}}_0}} \right)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (7) |
式中:σmin是在断层、裂缝等地质体边界各向异性滤波核函数横跨边界的最小尺寸,用以保证在边界区域的最低滤波性能;σiso是在平坦地层区域各向同性的滤波核函数的最大尺寸,用以避免过大的各向同性滤波核函数压制局部地层的起伏变化。因此,在断层、裂缝等地层边缘区域,由于Cfault→1,故有σ2(x0)→σmin和σ3(x0)→σiso2/σmin,即拉普拉斯滤波核函数沿局部地层边缘方向拉伸为强各向异性的线条状形态,使滤波操作仅仅沿着地质体边界进行;而在反射同相轴延展良好的区域,由于Cfault→0,故有σ2(x0)→σiso和σ3(x0)→σiso,即拉普拉斯滤波核函数沿局部地层平面均匀拉伸为各向同性的圆饼状形态,使该区域的滤波程度最大化;对于同相轴内存在振幅平缓变化或同相轴有一定程度起伏的区域,由于0<Cfault<1,则拉普拉斯滤波核函数沿局部地层结构呈现弱各向异性形态,从而既保证这些区域的滤波性能,又不会造成对有效波振幅变化的压制或对地层几何形态的畸变。
图 1为3DALFRS方法应用流程图。首先对三维地震数据做规则化处理,采用三维梯度结构张量分别通过精确倾角估计和精细不连续度量,构造自适应拉普拉斯滤波器;在此基础上,将规则化处理后的三维数据直接通过拉普拉斯滤波器进行三维随机噪声压制处理,最后得到了三维保边滤波结果。
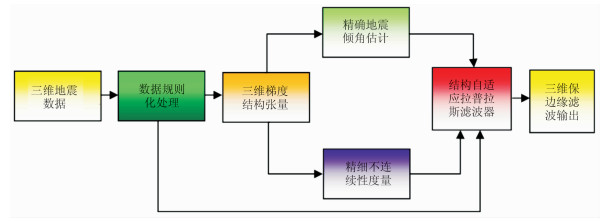
|
图 1 基于三维各向异性拉普拉斯滤波的噪声压制方法流程 |
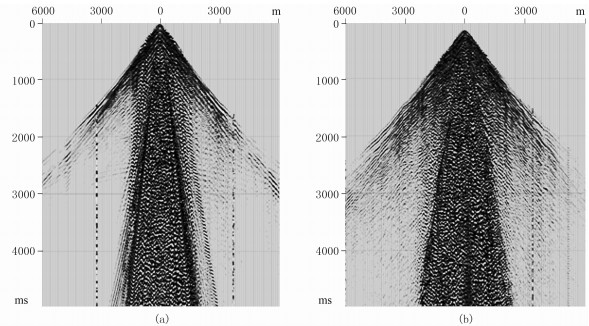
准噶尔盆地腹部的SNX井三维工区位于陆梁隆起西段的夏盐凸起,毗邻玛湖凹陷东斜坡,是近年油气勘探的重点区域。该区油气藏主要受构造控制,同时也存在岩性油气藏。勘探主要目的层为侏罗系、白垩系,要求查清构造形态,描述断裂发育特征,预测有利砂体发育带,落实岩性圈闭。工区地面海拔为280~400m,平均海拔约为340m(图 2),受近地表因素影响,原始资料信噪比低(图 3)。

|
图 2 研究区地表卫星照片 |
|
图 3 研究区两种典型地表(a、b对应图 2中的①、②)单炮记录 |
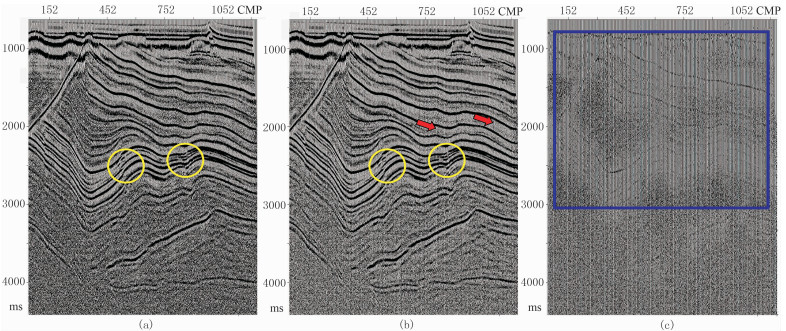
针对图 4a所示的原始模型数据,先后用FXY方法与3DALFRS方法做去噪对比试验,分别得到FXY方法和3DALFRS方法的去噪结果(图 4b、图 5a)及其去除的噪声数据(图 4c、图 5b,原始模型数据与处理后结果之差)。可见两种方法都压制了随机噪声(黄色椭圆框),但经3DALFRS方法压制后边缘及同相轴更清晰,同时还压制了异常道能量(红色双箭头所指);从噪声剖面看,FXY方法去除的噪声剖面中包含较多有效信号(蓝色矩形框内)。
|
图 4 原始模型数据(a)、FXY方法去噪结果(b)及其去除的噪声(c) |
|
图 5 模型数据3DALFRS方法去噪结果(a)及其去除的噪声(b) |
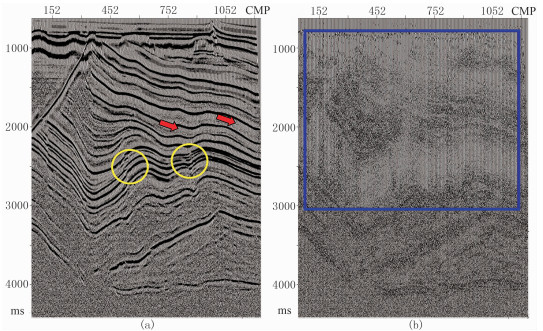
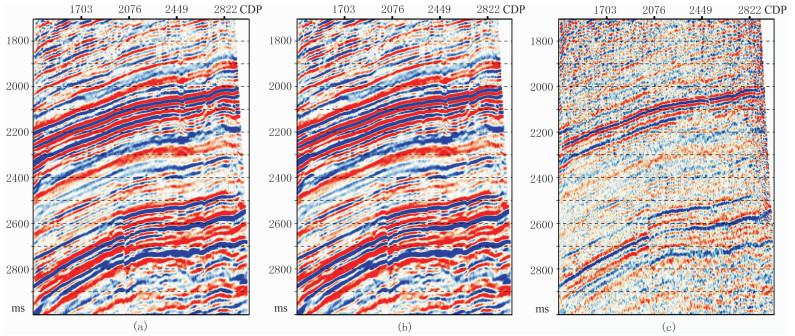
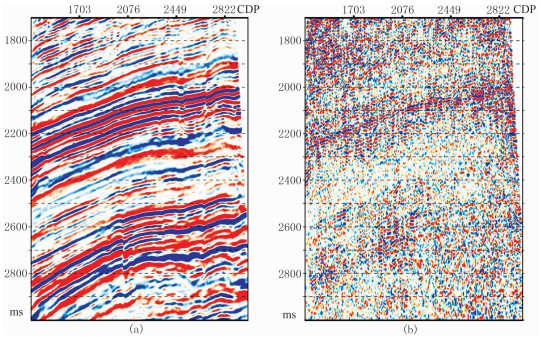
图 6a是SNX井区实际三维叠前时间偏移数据,先后用FXY方法与3DALFRS方法做去噪处理,分别得到FXY方法和3DALFRS方法去噪后剖面(图 6b、图 7a)及其噪声剖面(图 6c、图 7b,去噪前数据与处理后结果之差)。可见FXY方法在压制随机噪声的同时,对有效信号损伤明显,在噪声剖面(图 6c)中残留明显的有效波同相轴;而3DALFRS在压制随机噪声的同时,对有效波具有良好的保真性能,在噪声剖面中难觅有效信号踪迹。
|
图 6 去噪前实际叠前时间偏移数据(a)、FXY方法去噪后剖面(b)及其去除的噪声剖面(c) |
|
图 7 实际数据3DALFRS方法去噪后剖面(a)及其去除的噪声剖面(b) |
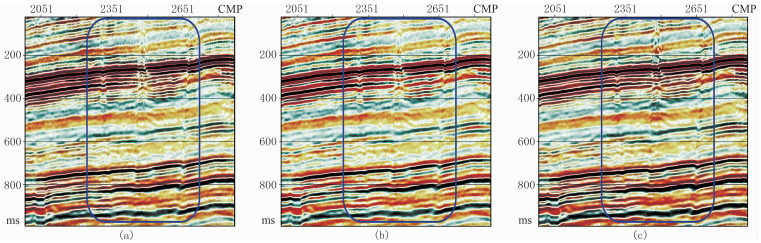
对比SNX井区三维叠前时间偏移资料与SN连片三维剖面(图 8),可见用3DALFRS方法做去噪处理后的剖面(图 8c)上,CMP2351~2651之间、时间400~800ms范围内反射层次更清晰、地层接触关系清楚、细节更丰富,整体信噪比大幅度提高。
|
图 8 去噪前叠前时间偏移数据(a)、FXY方法(b)及3DALFRS方法(c)去噪后剖面 |
从侏罗系西山窑组的相干属性平面图(图 9,等时切片)对比可见,SNX井区三维叠前时间偏移资料信噪比显著提高,为目的层精细目标识别和储层预测提供基础。实际应用结果表明,3DALFRS方法处理后(图 9c)噪声压制更干净,更利于断裂识别及储层精细预测。

|
图 9 去噪前叠前时间偏移数据(a)、FXY方法(b)及3DALFRS方法(c)等时切片 |
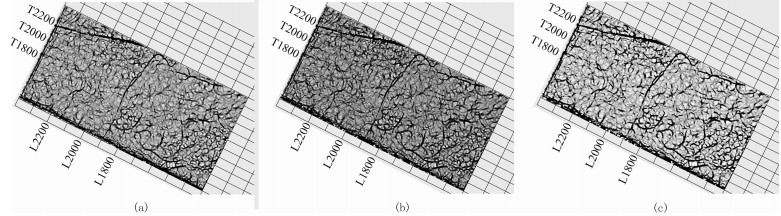
在小断裂成像方面,从SNX井区三维叠前时间偏移资料与SN连片三维主要目的层对比可知,目的层断裂识别能力有明显的改善:断裂组合样式更明确,剖面上断点更清晰干脆;平面上,通过提取沿层相干曲率属性(图 10),SNX井区三维主要目的层三工河组断裂展布规律更明确,小断裂边界更清晰(图 10c),更能满足小断裂识别和描述的精细地震解释需求。
|
图 10 去噪前叠前时间偏移数据(a)、FXY方法(b)及3DALFRS方法(c)沿层曲率切片 |
准噶尔盆地地震数据信噪比低,尤其是高密度采集通常采用可控震源激发时,因野外炮检点组合减少,带来了比常规地震资料更为严重的随机噪声,影响了资料品质。3DALFRS方法与业界常用的FXY方法去噪结果的对比表明,前者的残余噪声较微弱,断层、裂缝成像清晰,具有较好的保边性,提高了资料信噪比。即解决了常规噪声压制算法成像对平滑区域效果较好、但存在边缘模糊且残余噪声较大的问题;为解释提供更可靠的地震资料,也为后续在GeoEast系统上的软件研发积累了经验。通过新方法研究,总结形成一套成熟并适合准噶尔盆地高密度地震资料随机噪声压制方法及技术流程,大幅度提高地震数据质量,在准噶尔盆地不同地区均取得到较好应用效果。
| [1] |
苏爱芹, 郑宇霞, 魏广仁, 等. 复杂小断块综合研究技术[J]. 断块油气田, 2011, 18(4): 472-474. SU Aiqin, ZHENG Yuxia, WEI Guangren, et al. Integrated study technique of small complex fault block[J]. Fault-Block Oil & Gas Field, 2011, 18(4): 472-474. |
| [2] |
唐建华, 郭勇, 虞敏.准噶尔盆地腹部沙漠区低幅度构造和小断裂的正演模拟与识别[C]. CPS/SEG国际地球物理会议论文集, 2004, 507-510. TANG Jianhua, GUO Yong, YU Min.Forward mode-ling and identification of low amplitude structure in the hinterland desert area in the Zhunggar Basin[C]. Proceedings of 2004 CPS/SEG International Geophysical Conference, 2004, 507-510. http: //cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW200403001137.htm |
| [3] |
孙成田, 赵伟, 雷福平, 等. 多属性分析及断裂识别技术在酒泉盆地油气勘探中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 170-174. SUN Chengtian, ZHAO Wei, LEI Fuping, et al. Applications of multi-attribute analysis and fault identification approach in the oil and gas exploration of Jiu-quan Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 170-174. |
| [4] |
Harris P E, White R E. Improving the performance of f-x prediction filtering at low signal-to-noise ratios[J]. Geophysical Prospecting, 1997, 45(2): 269-302. DOI:10.1046/j.1365-2478.1997.00347.x |
| [5] |
Bekara M, van der Baan M. Local singular value decomposition for signal enhancement of seismic data[J]. Geophysics, 2007, 72(2): V59-V65. DOI:10.1190/1.2435967 |
| [6] |
李新祥, 李凤林.三维FXY预测滤波[C].中国地球物理学会第十届学术年会, 吉林长春, 1994, 397-398. LI Xinxiang, LI Fenglin.3-D FXY predictive filtering[C]. The 10th Annual Academic Annual Meeting of the China Geophysical Society, Changchun, Jilin, 1994, 397-398. http: //cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW199408001329.htm |
| [7] |
Michael K Chase著; 游有志译.应用三维空间预测滤波压制随机噪声//美国勘探地球物理学家学会第62届年会论文集[M].北京: 石油工业出版社, 1993, 461-463.
|
| [8] |
国九英, 周兴元, 杨慧珠. 三维f-x, y域随机噪音衰减[J]. 石油地球物理勘探, 1995, 30(2): 207-215. GUO Jiuying, ZHOU Xingyuan, YANG Huizhu. Atte-nuation of random noise in (f-x, y) domain[J]. Oil Geophysical Prospecting, 1995, 30(2): 207-215. |
| [9] |
贺振华, 黄德济. 裂缝油气藏地球物理预测[M]. 四川成都: 四川科技出版社, 2007: 136-168. HE Zhenhua, HUANG Deji. Fracture Reservoir Geo-physical Prediction[M]. Chengdu, Sichuan: Sichuan Technology Press, 2007: 136-168. |
| [10] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [11] |
刘宏杰, 蒋立, 张仲祜, 等. 基于能量差异的滑动扫描数据谐波压制方法[J]. 新疆石油地质, 2015, 36(1): 98-101. LIU Hongjie, JIANG Li, ZHANG Zhonghu, et al. Method for harmonic noise suppression of slip scan data based on energy difference[J]. Xinjiang Petro-leum Geology, 2015, 36(1): 98-101. |
| [12] |
刁瑞, 吴国忱, 尚新民, 等. 地面微地震有源噪声自动识别与匹配压制方法[J]. 石油地球物理勘探, 2018, 53(2): 311-319. DIAO Rui, WU Guochen, SHANG Xinmin, et al. Micro-seismic active noise automatic identification and ma-tching denoising[J]. Oil Geophysical Prospecting, 2018, 53(2): 311-319. |
| [13] |
Luo Y, Marhoon M, Al Dossary S, et al. Edge-preserving smoothing and applications[J]. The Leading Edge, 2002, 21(2): 136-158. DOI:10.1190/1.1452603 |
| [14] |
AlBinHassan N M, Luo Y, Al-Faraj M N. 3D edge-preserving smoothing and applications[J]. Geophy-sics, 2006, 71(4): P5-P11. |
| [15] |
Fehmers G C, Hocker C F W. Fast structural interpretation with structure-oriented filtering[J]. Geo-physics, 2003, 68(4): 1286-1293. |
| [16] |
Lavialle O, Pop S, Germain C, et al. Seismic fault preserving diffusion[J]. Journal of Applied Geophysics, 2007, 61(2): 132-141. DOI:10.1016/j.jappgeo.2006.06.002 |
| [17] |
黄德智, 毛锐强, 王庚, 等. 利用GeoEast系统处理低信噪比地震资料[J]. 石油地球物理勘探, 2014, 49(增刊1): 76-81. HUANG Dezhi, MAO Ruiqiang, WANG Geng, et al. Low-SNR seismic data processing by GeoEast[J]. Oil Geophysical Prospecting, 2014, 49(S1): 76-81. |
| [18] |
吴艳辉, 唐博文, 柯本喜, 等. GeoEast多次波压制技术在陆上地震资料处理中的应用[J]. 石油地球物理勘探, 2014, 49(增刊1): 93-98. WU Yanhui, TANG Bowen, KE Benxi, et al. Multiple elimination methods provided by GeoEast for land seismic data[J]. Oil Geophysical Prospecting, 2014, 49(S1): 93-98. |
| [19] |
王伟, 姜呈馥, 张丽霞, 等. 一种边界保持随机噪声衰减的各向异性拉普拉斯滤波技术[J]. 中国煤炭地质, 2015, 27(9): 61-66. WANG Wei, JIANG Chengfu, ZHANG Lixia, et al. An anisotropic Laplace filtering technology with edge random noise attenuation retaining[J]. Coal Geology of China, 2015, 27(9): 61-66. DOI:10.3969/j.issn.1674-1803.2015.09.15 |
| [20] |
Bakker P.Image Structure Analysis for Seismic Inter-pretation[D]. Technische Universiteit, Delft, the Netherlands, 2002.
|



 刘宏杰,新疆维吾尔自治区乌鲁木齐市北京北路397号中国石油新疆油田勘探开发研究院地球物理所,830013。Email:
刘宏杰,新疆维吾尔自治区乌鲁木齐市北京北路397号中国石油新疆油田勘探开发研究院地球物理所,830013。Email: