② 自然资源部中国地质调查局广州海洋地质调查局, 广东广州 510760
② Guangzhou Marine Geological Survey, Ministry of Natural resources, Guangzhou, Guangdong 510760, China
震源信号子波是反射地震勘探中重要的参数,在地震资料处理及后续很多环节中都起着关键作用,包括地震正演模拟、偏移成像、全波形反演、叠前叠后属性反演、多次波预测和多源数据合成处理等[1-8]。更为一般地说,震源信号是地震勘探信号系统的激励函数,也是地震波弹性波动方程中的源函数[9]。
研究震源信号的核心问题是获取震源信号子波。除了采集现场直接观测记录外,目前主要的方法有:①利用近场记录拟合[10-12];②通过专用软件模拟[13-17];③从地震数据本身提取[18]。地震数据采集受现场环境、仪器装备等因素影响,从现场直接观测震源子波十分困难。利用近场记录拟合时,因近场记录中常伴有干扰,拟合结果往往存在误差;在很多情况下地震数据中并没有近场记录,故该方法的使用受到限制。软件模拟方法受软件所使用理论模型、震源类型及环境参数等因素限制,模拟子波与实际子波存在差异。如果虑及检波器特性、仪器因素的影响,从地震数据中直接提取震源信号子波应更合理。随着数字信号处理理论、非线性理论、优化理论的发展,从反射地震数据中提取震源信号子波的方法从理论到实践都取得了巨大进展[19-20],如何消除反射地震数据中包含的地层信息对提取结果的影响是这类方法成败的关键。
反射勘探地震数据中的直达波,除了表层信息外,不含地下地层信息。如果表层介质是均匀的,则直达波沿直线路径传播。在海洋地震勘探中,震源的激发和数据的接收都是在水中进行,海水具有良好的均质性,地震数据中的直达波仅与震源信号、海面反射系数及海水声波速度有关,因此利用直达波提取震源信号子波是可行的,且无须考虑地层反射信息。
Oliveira[21]提出从地震资料直达波估算震源信号子波的方法,并与近场子波拟合的震源信号做分析对比;伍忠良等[22]从地震系统的滤波效应、直达波与鬼波传播路径及时间差、原始数据的处理对比和理论计算,分析了直达波和鬼波的综合效应;Koo等[3]研究了一种在拉普拉斯域全波形反演中利用全牛顿法直接从直达波估计震源子波的方法,可用于实际资料震源子波估计;陈礼等[23]基于深水可完整记录直达波的特点,在测线近道上应用通过直达波与海底反射波的组合得到统计子波的方法压制气泡效应;郑江龙等[24]在单道地震记录中利用从直达波提取地震子波进行相关滤波的方法有效地压制了干扰波;任婷等[25]基于深水地震资料利用直达波提取子波对数据进行确定性子波反褶积处理,以有效压制气泡效应。这些都从不同角度和层面针对从直达波中提取震源信号子波进行了一定程度的研究及应用。但如何建立震源信号与直达波之间通用的数学关系,进而给出从直达波提取震源信号子波的解析方法,是本文尝试深入、系统地研究的课题。
海洋地震资料中的直达波除了震源直达波能量外,还包括震源能量的水面反射波,后者即所谓震源鬼波,可看作是位于震源关于水面镜像点的虚震源的直达波。由于这两个直达波的传播路径不同,加之鬼波还经过水面的反射作用,二者的叠加效应随炮—检关系的变化而变化。另外,一般情况下炮检距远大于震源和电缆的沉放深度,直达波在接收点是大角度入射,研究直达波必须考虑地震记录系统的组合效应。显然,直达波不能直接作为震源信号子波使用。
本文依据气泡振荡理论和组合理论,通过推导震源及其虚震源的直达波时距曲线,考虑了震源和接收点组合情况,得到直达波与震源信号之间的关系式,并给出了频率域利用直达波计算震源信号远场子波的解析解。当地震数据接收位置满足震源远场条件时,利用地震数据中的直达波通过计算提取震源信号远场子波具有明显的可操作性和实际意义。实际地震资料处理效果表明,本文方法具有适用性强、抗干扰、计算精度高等特点。利用本文方法提取的地震子波,完全可用于后续的气泡压制、虚反射(鬼波)消除、多次波预测、波形反演、偏移成像等众多处理环节。
1 方法原理 1.1 理论基础海洋地震勘探最常用的是气枪阵列震源,气枪在水下激发产生的气泡快速膨胀形成弹性波能量。根据Keller等[26]提出的气泡振荡基础理论,气泡在水中被激起后形成一个反复膨胀←→收缩、幅度逐渐衰减的阻尼性振荡过程;同时,气泡本身也受水的浮力而自由上升,直至水面破裂。这种振荡过程产生一系列脉冲,其中第一次激发膨胀产生的脉冲叫初始脉冲或主脉冲,随后的多次振荡膨胀产生数次气泡脉冲,脉冲的周期与水的密度、静水压力、震源能量有关。设计不同脉冲周期的多个震源进行组合激发,使每个单独震源的初始高能脉冲正相干、而气泡脉冲为非正相干,就可达到增强初始脉冲、削弱气泡脉冲的效果。Ziolkowski等[27]和Parkes等[28]研究了气枪阵列特性,分析了单枪气泡之间存在的调谐、相干、连通三种关系,指出气泡在相干半径外其能量的互相作用呈现线性关系。对于某个检波点,记录到的多个单震源的调谐组合子波仅是每个震源子波振幅的简单叠加,即
| $ u(t) = \sum\limits_i {\frac{1}{{{r_i}}}} {n_i}\left( {t - \frac{{{r_i}}}{c}} \right) $ | (1) |
式中:u(t)表示位于检波点的震源信号的叠加信号;ni(t)表示单震源信号;ri表示检波点与单震源间的距离;c表示水中声波速度。
气泡激发的脉冲能量以弹性波方式在水中传播,遇到海面(海水与空气的界面)后形成反射,反射振幅满足Zoeppritz方程描述的AVO关系。郑晓东[29]对Aki等[30]提出的AVO近似公式进行了适当变换,利用射线参数统一了不同相态介质界面上入射波与反射波、透射波之间的关系公式。水与空气界面上的反射系数为
| $ {R_0}(p) = - \frac{{{\rho _{\rm{w}}}c\sqrt {1 - {a^2}{p^2}} - {\rho _{\rm{a}}}a\sqrt {1 - {c^2}{p^2}} }}{{{\rho _{\rm{w}}}c\sqrt {1 - {a^2}{p^2}} + {\rho _{\rm{a}}}a\sqrt {1 - {c^2}{p^2}} }} $ | (2) |
式中:p是射线参数;ρw、ρa是水和空气的密度;a是空气中声波速度;θ是入射角。由于ρwc≫ρaa,则R0绝对值约等于1。受风浪等因素影响,实际海面是不平整的,地震波在粗糙海面除了反射还会发生散射,散射波场只有一部分与反射波相干叠加,因此实际反射系数绝对值应小于1。
Jovanovich等[31]根据波浪谱的高斯分布及散射理论,推导出粗糙海面均方根波高幅值与海面反射系数之间的关系
| $ R(\alpha , \omega ) = {R_0}\exp \left[ { - 2{{\left( {\omega \sigma \frac{{\cos \alpha }}{c}} \right)}^2}} \right] $ | (3) |
式中:σ是波高的均方根幅值;ω是地震波角频率;α是波的掠射角。由于掠射角与入射角互余,式(3)可写成包含射线参数的形式
| $ R(p, \omega ) = {R_0}\exp \left[ { - 2{{(\omega \sigma p)}^2}} \right] $ | (4) |
可见粗糙海面反射系数是地震波射线参数和角频率的函数。
由上述分析可知,多个单震源的虚震源在检波点的调谐组合子波可表示为
| $ {u^\prime }(t) = \sum\limits_i {\frac{R}{{r_i^\prime }}} {n_i}\left( {t - \frac{{r_i^\prime }}{c}} \right) $ | (5) |
式中:u′(t)表示位于检波点的虚震源信号的叠加信号;r′i表示检波点与单震源的虚震源之间的距离;R表示海面反射系数。
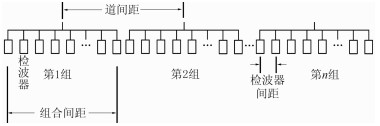
震源信号及其水面反射的地震波传播至接收电缆,以压力场变化的形式被检波器记录。为了压制噪声,每道由多个压力检波器以一定间隔平行连接,构成检波器组合阵列(图 1),组合后的地震波是各单独检波器记录地震波的简单叠加。根据检波器组合理论,地震道中记录的信号s(t)可表示为
|
图 1 电缆检波器组合示意图 |
| $ s(t) = \sum\limits_k {{h_k}} (t) $ | (6) |
式中hk(t)表示组合阵列中的第k个检波器记录的信号。
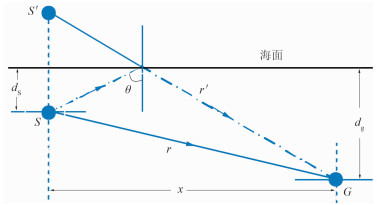
1.2 直达波与震源信号子波的关系方程直达波是指从震源出发沿介质直接传播到接收点的地震波。如果传播介质是常速的,其传播路径就是直线。在海洋地震勘探中,由于声波在水层中的传播速度近似常数,其直达波沿直线传播。如图 2所示,震源能量在海面的反射波被称为震源鬼波,可看作是从虚震源(S′,即震源点S关于水面的镜像点)发出的直达波。图中G为检波点,ds为震源沉放深度,dg为检波点沉放深度,x为炮检距,θ为海面反射的入射角,r表示震源到检波点的直达波传播距离,r′为虚震源到检波点的直达波传播距离。从该图可得如下关系式
|
图 2 直达波传播路径示意图 |
| $ r\mathit{'} = \sqrt {{{\left( {{d_{\rm{g}}} - {d_{\rm{s}}}} \right)}^2} + {x^2}} $ | (7) |
| $ r\mathit{'} = \sqrt {{{\left( {{d_{\rm{g}}} + {d_{\rm{s}}}} \right)}^2} + {x^2}} $ | (8) |
则震源直达波的时距曲线方程为
| $ t = \frac{r}{c} = \frac{1}{c}\sqrt {{{\left( {{d_{\rm{g}}} - {d_{\rm{s}}}} \right)}^2} + {x^2}} $ | (9) |
虚震源直达波的时距曲线方程为
| $ {t^\prime } = \frac{{{r^\prime }}}{c} = \frac{1}{c}\sqrt {{{\left( {{d_{\rm{g}}} + {d_{\rm{s}}}} \right)}^2} + {x^2}} $ | (10) |
从式(9)、式(10)可见:当震源深度与检波点相同时,震源直达波时距曲线是直线;否则,时距曲线为双曲线。虚震源直达波(水面反射波)的时距曲线是双曲线。射线参数可表示为
| $ p = \frac{{\sin \theta }}{c} = \frac{x}{{cr'}} = \frac{x}{{c\sqrt {{x^2} + {{\left( {{d_{\rm{s}}} + {d_{\rm{g}}}} \right)}^2}} }} $ | (11) |
海洋地震记录中的直达波h(t)是震源与虚震源直达波的叠合,即
| $ h(t)=u(t)+u^{\prime}(t) $ | (12) |
实际地震采集中,震源和接收点都是由组合阵列组成。对于检波器阵列中的每一个检波器,它记录的震源信号来自于震源阵列中的每一单个震源。设震源由m个互不相干的单震源组合而成,检波点由l个检波器并联组合而成,每炮地震数据有n道记录;用i表示震源阵列中单个震源序号、j表示接收道序号、k表示地震道组合中检波器序号;sj(t)表示第j道的直达波记录,hjk(t)表示第j道中第k个检波器的记录,ni(t)表示震源阵列中第i个单震源的震源信号。由式(1)、式(5)、式(12)推知,单检波器记录的直达波叠加信号为
| $ {h_{jk}}(t) = \sum\limits_i {\left[ {\frac{{{n_i}\left( {t - \frac{{{r_{ijk}}}}{c}} \right)}}{{{r_{ijk}}}} + \frac{{R{n_i}\left( {t - \frac{{r_{ijk}^\prime }}{c}} \right)}}{{r_{ijk}^\prime }}} \right]} $ | (13) |
代入式(6)可得
| $ {s_j}(t) = \sum\limits_k {\sum\limits_i {\left[ {\frac{{{n_i}\left( {t - \frac{{{r_{ijk}}}}{c}} \right)}}{{{r_{jj}}}} + \frac{{R{n_i}\left( {t - \frac{{r_{ijk}^\prime }}{c}} \right)}}{{r_{ijk}^\prime }}} \right]} } $ | (14) |
变换到频率域
| $ {s_j}(\omega ) = \sum\limits_i {\left\{ {{n_i}(\omega )[} \right.} \sum\limits_k {\left( {\frac{{{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{r_{ijk}}}}{c}}}}}{{{r_{ijk}}}}} \right.} + \left. {\frac{{R{{\rm{e}}^{ - {\rm{i}}{\omega ^\prime }\frac{{r_{ijk}^\prime }}{c}}}}}{{r_{ijk}^\prime }}} \right)]\} $ | (15) |
对于有n个地震记录道的单炮记录,直达波与震源信号子波之间的关系可记成矩阵方程
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{AX}} $ | (16) |
其中
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{S_1}(\omega )}\\ {{S_2}(\omega )}\\ \vdots \\ {{S_n}(\omega )} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{n_1}(\omega )}\\ {{n_2}(\omega )}\\ \vdots \\ {{n_m}(\omega )} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} {\sum\limits_k {\left( {\frac{1}{{{r_{11k}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^r11k}}{c}}}} \right.} \left. { + \frac{R}{{r_{11k}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^{r'}11k}}{c}}}} \right)}& \cdots &{\sum\limits_k {\left( {\frac{1}{{{r_{m1k}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^rm1k}}{c}}}} \right.} \left. { + \frac{R}{{r_{m1k}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^{r'}m1k}}{c}}}} \right)}\\ \vdots & \ddots & \vdots \\ {\sum\limits_k {\left( {\frac{1}{{{r_{1nk}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^r1nk}}{c}}}} \right.} \left. { + \frac{R}{{r_{1nk}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^{r'}1nk}}{c}}}} \right)}& \cdots &{\sum\limits_k {\left( {\frac{1}{{{r_{mnk}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^rmnk}}{c}}}} \right.} \left. { + \frac{R}{{r_{mnk}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{^{r'}mnk}}{c}}}} \right)} \end{array}} \right] $ |
阵列震源的远场是相对于近场而言,远场距离的定义及计算公式[32-33]为
| $ d>\frac{D^{2}}{\lambda}=\frac{D^{2} f}{c} $ | (17) |
式中:f为激发子波频率;λ为激发子波最小波长;D为震源阵列组合的空间尺寸。例如,对于组合尺寸等于30m的震源阵列,观测数据中保留不高于250Hz震源信号的远场距离约为150m。这一条件对于海洋多道反射地震勘探而言通常是满足的,即地震采集的最小炮检距大于震源阵列的远场距离,因此可认为地震记录接收到的震源信号子波是震源阵列的远场子波。
在远场条件下,震源阵列可被视为位于震源阵列中心的点震源,则震源信号相位谱与炮检距不相关,式(16)中向量X也就退化为描述远场子波的单变量,记为w,矩阵方程退化为
| $ {s_j}(\omega ) = \mathit{w}(\omega )\sum\limits_k {\left( {\frac{1}{{{r_{jk}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{r_{jk}}}}{c}}}} \right.} \left. { + \frac{R}{{r_{jk}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{{r'}_{jk}}}}{c}}}} \right) $ | (18) |
且有
| $ \mathit{w}(\omega ) = {s_j}(\omega ){\left[ {\sum\limits_k {\left( {\frac{{{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{r_{jk}}}}{c}}}}}{{{r_{jk}}}}\left. { + \frac{{R{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{{r'}_{jk}}}}{c}}}}}{{r_{jk}^\prime }}} \right)} \right.} } \right]^{ - 1}} $ | (19) |
此即为直达波计算震源远场子波解析解公式。
实际地震数据处理中可利用叠加方法增强远场子波解的抗干扰能力,即
| $ \begin{array}{l} w(\omega ) = \frac{1}{n}\sum\limits_{j = 1}^n {{s_j}} (\omega ) \times \\ {\left[ {\sum\limits_k {\left( {\frac{1}{{{r_{jk}}}}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{r_{jk}}}}{c}}}\left. { + \frac{R}{{r_{jk}^\prime }}{{\rm{e}}^{ - {\rm{i}}\omega \frac{{{{r'}_{jk}}}}{c}}}} \right)} \right.} } \right]^{ - 1}} \end{array} $ | (20) |
此次合成了共计36道记录的直达波数据作为输入进行测试。使用有52ms延迟、主频为75Hz的Ricker子波作为震源信号,接收道炮检距范围是225.0~662.5m,道间距为12.5m,每个接收道由16个检波器组合构成,道内检波器等距组合、间距为0.781m,水速为1540m/s,水面反射系数选用常数-1,震源深度为7m,电缆深度为15m。
分别测试了无干扰、加入10%随机干扰和加入10%相干干扰(20Hz正弦波)等三种情形。从输入及输出结果(图 3)中可见无干扰情况下计算结果与输入震源信号相一致。由于使用了叠加方法,加入随机干扰后所得计算结果也具较高信噪比,加入相干干扰的输入数据对解的影响也很小。

|
图 3 合成数据测试 (a)震源信号;(b)合成的36道直达波数据;(c)加入10%随机干扰的直达波数据;(d)加入10%相干干扰的直达波数据;(e)、(f)、(g)分别是针对(b)、(c)、(d)直达波数据用本文方法计算得到的震源信号 |
使用本文方法从南海M区二维深水反射实际地震数据中提取远场子波,并与近场记录拟合的远场子波进行对比。部署该测线的目的是获取地壳深部结构信息。现场采集选用6420in3的大容量震源,采用5排、间隔10m的枪阵构成气枪阵列,每排枪(序列号依次为G1R1~G1R5)由5对相干枪组成,共计25对相干枪,每对相干枪含两支单枪。相干枪可被看作是单震源,在其上方1m处布设近场检波器。表 1列出了枪阵组合参数,包括每个相干枪的容量、通道号及x、y坐标。坐标系统以枪阵中心为原点、以船首方向为x轴、船右方向为y轴。采用Sercel公司Sentinel型24位数字固体(接收)电缆,共有480个地震道,每道由8个检波器组成,表 2为检波器组合参数。
|
|
表 1 枪阵组合参数 |
|
|
表 2 检波器组合参数 |
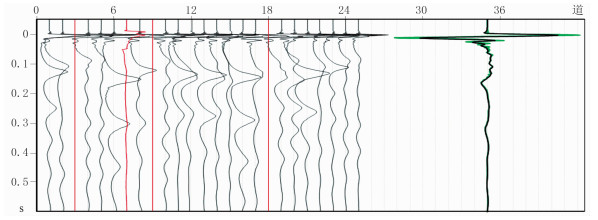
选取其中一炮的计算结果进行分析和说明。如图 4所示,1~25通道的地震信号分别对应25个近场检波器记录的震源激发所产生的近场信息,其中用红色线条显示的第3、9、18号相干枪未振动、第7号状态异常,其他21对相干枪工作正常。利用近场记录拟合的远场子波和利用本文方法提取的远场子波分别用绿色和黑色线条同时显示在35通道号位置,可见两条曲线几乎重合,所反映的气泡振荡周期完全相同,曲线正、负波峰峰值基本一致。二者的差异主要在高频部分。分析可能的原因:一方面与近场记录的高频干扰、拟合算法误差有关;另一方面,本文方法使用了叠加运算,当计算参数存在误差时,算法存在一定的高截滤波作用。
|
图 4 近场记录(1~25道)及利用其拟合的远场子波(35道,绿色)、采用本文方法提取的远场子波(35道,黑色) 红色线条表示该道对应的近场记录异常 |
为了测试从地震数据直达波提取震源信号远场子波方法的有效性和实用性,选取2015年5月采集于中国南海北部陆坡的S区二维地震测线的部分单炮数据进行实际资料计算。
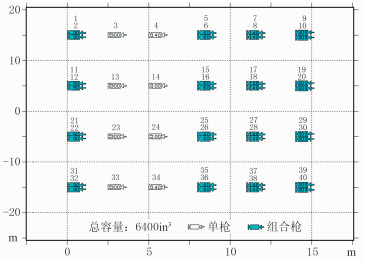
现场采集使用总容量6400in3的40枪组合阵列作为震源,枪阵由四排子阵构成,每排子阵阵列长度为15m,子阵间距为10m(图 5);枪阵沉放深度为8.5m,电缆沉放深度为16m;采用Sercel公司Sentinel型24位数字固体电缆;每个地震道由8个检波器组成,检波器灵敏度为19.7 μV/μbar(20℃),检波器组合参数参见表 2;地震接收道炮检距范围是225.0~6212.5m,道间距为12.5m,数据记录长度为8s,采样间隔为2ms,480道接收。在原始数据中,未记录近场信号。
|
图 5 枪阵组合结构图 |
地震数据预处理首先是根据导航信息定义精确的观测系统,明确地震数据炮点、检波点的水平和垂直位置,计算炮检距;然后进行一些必要的去噪处理,去除数据中的野值干扰、交流电噪声,消除直流漂移量,滤除低频涌浪干扰等,但不做任何改变信号子波或改变振幅强度等方面的处理;最后从地震数据中分离出直达波,该直达波数据长度从其初至时间开始计算,故应大于所求子波长度。基于直达波时距曲线,由式(9)和式(10)计算出不同炮检距的初至时间。
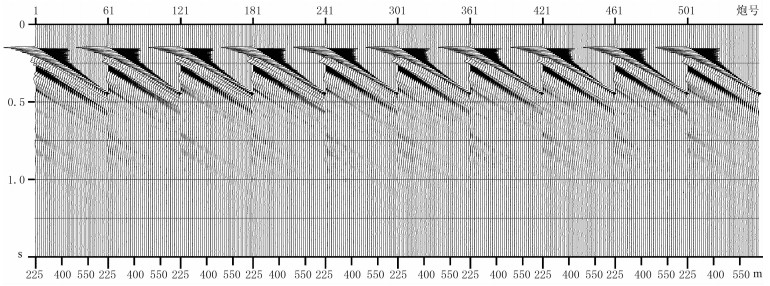
为使测试更具针对性,规避直达波与反射波混合的情形,选取数据的海底深度约为1600m,海底反射波出现在2s以后(图 6)。由枪阵组合尺寸、地震数据Nyquist频率及声波速度(1500m/s),利用式(17)可算出震源信号远场距离为150m,地震数据记录位置的最小炮检距满足远场接收条件。另外,从式(12)可见,震源直达波与虚震源直达波相位相反、二者时差随炮检距增大而减少,因此二者的叠加能量随炮检距的增大会快速减弱。虑及环境噪声的存在,远炮检距数据信噪比也会变得很低,因此所选数据炮检距不宜太大。选取近炮检距36个单炮作为测试输入数据,其炮检距范围约为225~663m(图 6矩形框)。图 7为其中10炮用于提取远场子波的直达波数据,截取1.5s数据长度以确保求取子波具有1s时长。

|
图 6 经过预处理的单炮记录 左上角白色矩形框圈出测试计算用数据范围 |
|
图 7 用于提取震源信号远场子波的直达波数据 |
有了直达波数据后首先预设一个声波速度,利用式(9)计算直达波的初至时间,调整声波速度直至所计算的初至时间与地震数据的初至时间基本一致。用该方法可确定测试数据的声波速度是1540m/s。从现场采集作业班报获知,本次测试数据采集时恰遇一定风浪,因此采用平均反射系数,但其值通过迭代计算确定,细述如下。
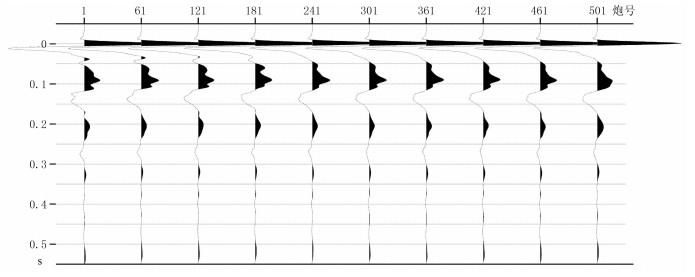
首先,依据式(20)在地震数据处理软件Omega系统上编制了在频率域用直达波提取震源信号远场子波的流程;预设R=-1,逐炮逐道计算;对于每一道数据,根据检波器组合参数算出每个检波器的位置,每一炮的子波是其36道数据计算的36个子波的叠加。然后,用计算出的子波预测直达波,逐步调整、加大反射系数R直至预测的直达波与实际地震数据的直达波基本一致。通过迭代,最后确定测试数据的平均反射系数R是-0.865。此时的子波计算结果就是本文方法最终结果,即利用直达波所提取的震源信号远场子波(图 8)。还可用检波器组的灵敏度将子波从电压单位V转换成通用的压力单位mbar。
|
图 8 从图 7炮记录直达波中提取的震源信号远场子波 |
利用震源信号子波预测直达波有两个主要目的:检验计算结果是否正确和确定平均反射系数。如前所述,当震源信号和声波速度确定后,直达波形态只与反射系数有关,通过对比预测直达波与地震记录即可判断反射系数的值是否合适。
选取测试数据第241炮记录中225.0、362.5、512.5、662.5m四个炮检距做对比显示(图 9),可见预测的直达波数据(红色曲线)与实际地震记录的直达波数据(蓝色曲线)基本吻合。

|
图 9 预测的直达波(红色)与实际地震记录(蓝色) |
提取的震源信号子波常用于气泡压制、子波一致性处理等,以改善地震数据质量。
在Omega系统中使用Debubble模块压制地震资料中的气泡,该模块要求输入每个单炮的震源信号及期望输出子波。考虑到鬼波效应,输入的震源信号是本文方法提取的子波加入了垂直方向的震源和检波点鬼波,期望输出子波是将作为输入的震源信号子波压制气泡脉冲后的子波。
在子波中压制气泡脉冲的方法是利用脉冲的周期性使用预测反褶积压缩子波,预测步长与脉冲周期基本一致,可通过子波自相关获得。经过预测反褶积处理后的子波,气泡脉冲被压制,只保留了主脉冲。
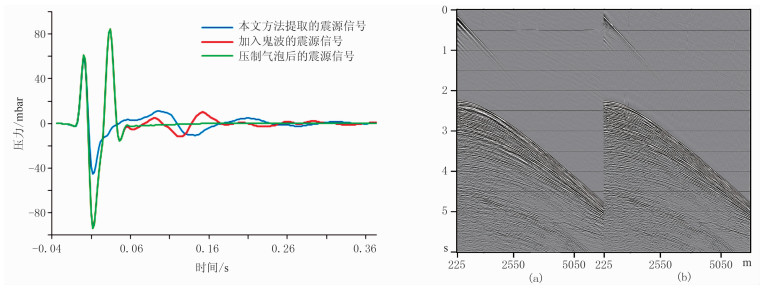
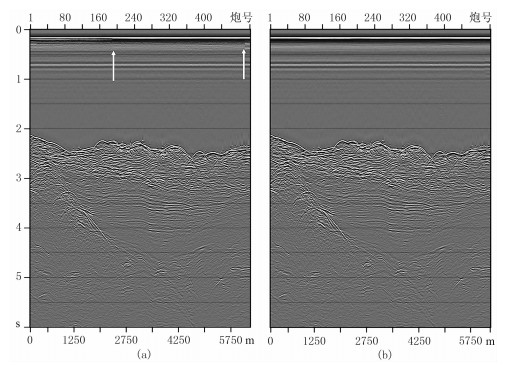
由于本文提取震源信号子波的处理流程是在Omega系统中实现的,因此易将提取的计算结果直接应用于Debubble模块以实现气泡压制功能(图 10)。Debubble模块的另一项功能是震源信号的一致性处理。尽管使用了相同的枪阵参数,气枪在激发过程中受其稳定性、环境因素等的影响,输出信号很难保证完全一致,这种不一致性导致地震剖面存在非地质因素的横向变化。Debubble模块使用匹配滤波法使其输出地震数据子波都与期望输出子波一致,从而消除了震源信号不一致对地震数据质量造成的影响(图 11)。
|
图 10 气泡压制即子波压缩过程 左图:蓝色线是本文方法提取的震源信号;红色线是加入鬼波后的震源信号;绿色线是经预测反褶积压制气泡脉冲后的震源信号 右图:(a)Debubble模块输入单炮记录;(b)Debubble模块输出单炮记录,从其直达波及反射波位置可清晰地看出气泡影响被削弱 |
|
图 11 对测试数据做子波一致性处理前(a)、后(b)的近道剖面 (a)炮号190和480附近红色箭头处存在气枪信号不一致导致的波形横向变化;(b)消除了子波变化引起的剖面横向变化 |
震源信号是地震数据处理的重要参数。从信号与系统的观点看,震源信号是主动源地震探测系统的输入函数,它不依赖于探测目标、只与震源系统有关,因此其提取方法应尽量消除地层信息的影响。在此基础上,本文提出一种地震子波提取的新思路,即从地震数据中分离出某类波场信息,且该波场传播的介质信息已知、并可建立地震子波与该波场之间的关系方程,然后通过解析方法计算得出地震子波。海洋地震探测由于其特殊的采集环境因素,地震数据中的直达波波场完全满足上述条件,通过推导直达波与震源信号之间的关系式,形成了利用海洋地震资料直达波提取震源子波的方法。
(1) 以气泡振荡理论、组合理论为基础,利用地震运动学方法建立了直达波与震源信号之间的矩阵方程,并在远场条件下将其简化且导出频率域利用直达波计算震源信号远场子波的解析式。
(2) 通过合成数据及实际地震数据测试,验证了方法的正确性,同时也证明该方法具有较高计算精度和较强抗干扰能力。
(3) 该方法适用于海洋地震资料的子波提取,无须近场记录和其他设备,不依赖于褶积模型、不需地层反射信息,对地震子波的相位特性不做任何假设,且支持超长序列地震子波提取。
(4) 震源信号子波在虚反射(鬼波)压制、全波形反演、多次波预测等地震数据处理领域具有广泛应用;文中实例说明该方法提取的震源子波可方便地应用于其他后续处理环节。
(5) 震源和检波器的空间位置、海面反射系数、组合参数等的准确与否直接影响计算结果的精度;准确的直达波场分离技术是提高子波提取效果的另一关键因素。
| [1] |
Chen J B. An average-derivative optimal scheme for frequency-domain scalar wave equation[J]. Geophy-sics, 2012, 77(6): T201-T210. |
| [2] |
Kim Y, Min D J, Shin C. Frequency-domain reverse-time migration with source estimation[J]. Geophy-sics, 2011, 76(2): S41-S49. |
| [3] |
Koo N H, Shin C, Min D J, et al. Source estimation and direct wave reconstruction in Laplace-domain waveform inversion for deep-sea seismic data[J]. Geophysical Journal International, 2011, 187(2): 861-870. |
| [4] |
Müller C, Bönnemann C, Neben S. AVO study of a gas-hydrate deposit, offshore Costa Rica[J]. Geophy-sical Prospecting, 2007, 55(5): 719-735. |
| [5] |
Liu Y T, Tinivella U, Liu X W. An inversion method for seafloor elastic parameters[J]. Geophysics, 2015, 80(3): N11-N21. DOI:10.1190/geo2014-0028.1 |
| [6] |
Verschuur D J, Berkhout A J, Wapenaar C P A.Wavelet estimation by prestack multiple elimination[C]. SEG Technical Program Expanded Abstracts, 1989, 8: 1129-1132.
|
| [7] |
Liu Y K, Jin D G, Chang X, et al. Multiple substraction using statistically estimated inverse wavlets[J]. Geophysics, 2010, 75(6): WB247-WB254. |
| [8] |
李福元, 韦成龙, 胡家赋, 等. 海洋二维双船拖缆与宽频带地震采集实验[J]. 石油地球物理勘探, 2018, 53(5): 887-895. LI Fuyuan, WEI Chenglong, HU Jiafu, et al. A dual-vessel broadband seismic acquisition experiment[J]. Oil Geophysical Prospecting, 2018, 53(5): 887-895. |
| [9] |
Berkhout A J. Seismic Migration, Imaging of Acoustic Energy by Wave Field Extrapolation, A:Theroretical Aspects[M]. Elsevier, 1982.
|
| [10] |
陈浩林, 全海燕, 刘军, 等. 基于近场测量的气枪阵列模拟远场子波[J]. 石油地球物理勘探, 2005, 40(6): 703-707. CHEN Haolin, QUAN Haiyan, LIU Jun, et al. Simulation of far-field wavelet based on near-field measuring gun-array[J]. Oil Geophysical Prospecting, 2005, 40(6): 703-707. DOI:10.3321/j.issn:1000-7210.2005.06.017 |
| [11] |
陈浩林, 倪成洲, 邢筱君, 等. 气枪阵列远场子波模拟与应用[J]. 石油地球物理勘探, 2008, 43(6): 623-625. CHEN Haolin, NI Chengzhou, XING Xiaojun, et al. Simulation and application of far-field wavelet for airgun array[J]. Oil Geophysical Prospecting, 2008, 43(6): 623-625. DOI:10.3321/j.issn:1000-7210.2008.06.002 |
| [12] |
Song J G, Deng Y, Tong X X. The simulation of far-field wavelets using frequency domain air-gun array nearfield wavelets[J]. Applied Geophysics, 2013, 10(4): 461-468. |
| [13] |
陈浩林, 於国平. 气枪震源单枪子波计算机模拟[J]. 物探装备, 2002, 12(4): 241-244. CHEN Haolin, YU Guoping. Computer simulation for single air gun signature[J]. Equipment for Geophysical Prospecting, 2002, 12(4): 241-244. DOI:10.3969/j.issn.1671-0657.2002.04.004 |
| [14] |
陈浩林, 宁舒年, 熊金良, 等. 气枪阵列子波数值模拟[J]. 石油地球物理勘探, 2003, 38(4): 363-368. CHEN Haolin, NING Shunian, XIONG Jinliang, et al. Numerical simulation of air-gun array wavelet[J]. Oil Geophysical Prospecting, 2003, 38(4): 363-368. DOI:10.3321/j.issn:1000-7210.2003.04.005 |
| [15] |
李绪宣, 温书亮, 顾汉明, 等. 海上气枪阵列震源子波数值模拟研究[J]. 中国海上油气, 2009, 21(4): 216-220. LI Xuxuan, WEN Shuliang, GU Hanming, et al. A simulation of wavelets from offshore air-gun array seismic source[J]. China Offshore Oil and Gas, 2009, 21(4): 216-220. |
| [16] |
Wang F F, Liu H S. Simulating the signature produced by a single airgun under real gas conditions[J]. Applied Geophysics, 2014, 11(1): 80-88. |
| [17] |
叶亚龙, 李艳青, 张阿漫. 平面气枪阵列远场子波模拟及优化[J]. 石油地球物理勘探, 2015, 50(1): 8-13. YE Yalong, LI Yanqing, ZHANG Aman. Simulation and optimization of far-field signature of planar air-gun arrays[J]. Oil Geophysical Prospecting, 2015, 50(1): 8-13. |
| [18] |
杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-128. YANG Peijie, YIN Xingyao. Summary of seismic wavelet pick-up[J]. Oil Geophysical Prospecting, 2008, 43(1): 123-128. DOI:10.3321/j.issn:1000-7210.2008.01.021 |
| [19] |
高少武, 赵波, 贺振华, 等. 地震子波提取方法研究进展[J]. 地球物理学进展, 2009, 24(4): 1384-1391. GAO Shaowu, ZHAO Bo, HE Zhenhua, et al. Research progress of seismic wavelet extraction[J]. Progress in Geophysics, 2009, 24(4): 1384-1391. DOI:10.3969/j.issn.1004-2903.2009.04.028 |
| [20] |
陈健, 戴永寿, 张亚南, 等. 基于高阶统计量的地震子波提取方法评价[J]. 石油地球物理勘探, 2013, 48(3): 497-503. CHEN Jian, DAI Yongshou, ZHANG Ya'nan, et al. Evaluation approaches for wavelet pickup based on high-order statistics[J]. Oil Geophysical Prospecting, 2013, 48(3): 497-503. |
| [21] |
Oliveira A S D. Seismic pulses obtained from the analysis of direct waves:A comparison to simulated pulses obtained with modeled notionals[J]. The Leading Edge, 2000, 19(1): 68-71. |
| [22] |
伍忠良, 曾宪军, 陆敬安. 海洋地震勘探直达波综合效应分析[J]. 海洋技术, 2006, 25(1): 111-114. WU Zhongliang, ZENG Xianjun, LU Jing'an. The synthetic analysis of the direct arrival in marine seismic survey[J]. Ocean Technology, 2006, 25(1): 111-114. DOI:10.3969/j.issn.1003-2029.2006.01.025 |
| [23] |
陈礼, 李列, 张治忠, 等. 深浅水变换带地震资料子波处理技术应用研究[J]. 工程地球物理学报, 2013, 10(4): 442-448. CHEN Li, LI Lie, ZHANG Zhizhong, et al. Application of seismic wavelet processing technology to deep and shallow water zones[J]. Chinese Journal of Engineering Geophysics, 2013, 10(4): 442-448. DOI:10.3969/j.issn.1672-7940.2013.04.003 |
| [24] |
郑江龙, 许江, 李海东, 等. 利用直达波提取地震子波进行相关滤波[J]. 地球物理学进展, 2015, 30(6): 2878-2884. ZHENG Jianglong, XU Jiang, LI Haidong, et al. Correlation filtering utilized the source wavelet extractingfrom the direct wave[J]. Progress in Geophysics, 2015, 30(6): 2878-2884. |
| [25] |
任婷, 彭海龙, 覃殿明, 等. 深水区直达波子波提取气泡效应压制技术[J]. 石油地球物理勘探, 2018, 53(2): 243-250. REN Ting, PENG Hailong, QIN Dianming, et al. De-bubble based on wavelet extraction from direct wave in deep water[J]. Oil Geophysical Prospecting, 2018, 53(2): 243-250. |
| [26] |
Keller J B, Kolodner I I. Damping of underwater explosion bubble oscillations[J]. Journal of Applied Physics, 1956, 27(10): 1152-1161. |
| [27] |
Ziolkowski A, Parkes G, Hatton L, et al. The signature of an air gun array:Computation from near-field measurements including interactions[J]. Geophysics, 1982, 47(10): 1413-1421. DOI:10.1190/1.1441289 |
| [28] |
Parkes G E, Ziolkowski A, Hatton L, et al. The signature of an air gun array:Computation from near-field measurements including interactions-Practical considerations[J]. Geophysics, 1984, 49(2): 105-111. |
| [29] |
郑晓东. 转换波和非转换波与射线参数p的关系[J]. 地球物理学报, 1991, 34(6): 781-787. ZHENG Xiaodong. Relationships between converted and non-converted waves and parameter p[J]. Acta Geophysica Sinica, 1991, 34(6): 781-787. DOI:10.3321/j.issn:0001-5733.1991.06.013 |
| [30] |
Aki K, Richards P G. Quantitative Seismology[M]. W H Freeman and Co, 1980: 144-151.
|
| [31] |
Jovanovich D B, Sumner R D, Akins-Easterlin S L. Ghosting and marine signature deconvolution:a prerequisite for detailed seismic interpretation[J]. Geophysics, 1983, 48(11): 1468-1485. |
| [32] |
Stoffa P L, Ziolkowski A. Seismic source decomposition[J]. Geophysics, 1983, 48(1): 1-11. |
| [33] |
陈浩林, 全海燕, 於国平, 等. 气枪震源理论与技术综述(上)[J]. 物探装备, 2008, 18(4): 211-217. CHEN Haolin, QUAN Haiyan, YU Guoping, et al. Summary of airgun source theory and technology (1)[J]. Equipment for Geophysical Prospecting, 2008, 18(4): 211-217. DOI:10.3969/j.issn.1671-0657.2008.04.001 |



 李福元, 广东省广州市广海路188号自然资源部中国地质调查局广州海洋地质调查局, 510760。Email:
李福元, 广东省广州市广海路188号自然资源部中国地质调查局广州海洋地质调查局, 510760。Email: