② 中国科学院渗流流体力学研究所, 河北廊坊 065007;
③ 中国石油勘探开发研究院, 河北廊坊 065007
② Institute of Porous Flow and Fluid Mechanics, Chinese Academy of Sciences, Langfang, Hebei 065007, China;
③ Research Institute of Petroleum Exploration & Development, PetroChina, Langfang, Hebei 065007, China
全球页岩气资源非常丰富,页岩气的规模开发促进了全球能源结构的调整和改变,影响着世界能源生产与消费格局的深刻变化。随着页岩气开采的快速发展,非常规天然气开采成本不断下降,2016年EIA(美国能源信息署)预测,到2040年全球页岩气产量占天然气产量的比例将提高到30%[1]。截止2017年底,中国累计探明页岩气地质储量近1.0×1012m3[2],可采储量达全球第一。从2009年第一口页岩气资源战略调查井到2017年底页岩气年产量超过90×108m3[2],中国的页岩气开发呈飞跃式发展,成为继美国、加拿大之后,第三个形成规模和产业的国家。中国《页岩气发展规划(2016~2020年)》的数据表明,中国力争在2020年实现页岩气产量300×108m3[3]。
页岩储层孔隙非常小,以纳米孔隙为主,一般有效孔隙度低于10%,渗透率也极低,一般低于1mD,具有典型的超低孔、超低渗特征[4]。页岩微裂缝发育,孔缝系统是页岩气储集的主要空间,也是页岩气渗流的主要通道[5]。页岩储层呈岩石类型多样性和独特性[3]。多样性表现为:北美德克萨斯州西部的Bossier页岩储层含有页岩、砂岩和粉砂岩等岩相;黑色页岩为主的美国福特沃斯盆地的Barnett页岩储层、阿巴拉契亚盆地的Ohio页岩储层;钙质含量高的中国渤海湾盆地、柴达木盆地的钙质页岩储层;富含有机质的页岩沉积系统,如广泛分布于北美密歇根盆地的Antrim页岩系统以及硅质页岩、砂质页岩、泥页岩等。独特性表现为页岩储层的非均质性极强,主要体现在页岩气储层的结构和构造方面。岩石的非均质性控制着储层孔隙空间中流体的分布和流动[4]。页岩的发育和分布以及组成主要受地质背景的影响,如北美含气页岩富集带,由于其特殊的构造背景和复杂的沉积环境,页岩具有多种成熟程度和天然气成因以及多种岩相。
Mayerhofer等[6]在研究美国福特沃斯盆地Barnett页岩的微地震裂缝映射结果与压裂裂缝变化时提出储层改造(SRV)的思路,现阶段页岩气开采增产的主要措施就是进行储层改造,而储层改造的主要技术手段是水力压裂。体积压裂和缝网压裂都是水力压裂发展的重要技术。体积压裂是指通过水力压裂对油气储集层实施的三维立体改造,尽可能采用较大液体用量和较高的施工排量在主裂缝侧向强制形成次生裂缝,并在次生裂缝上继续分支形成二级次生裂缝,最终使主裂缝与多级次生裂缝相互交织,形成人工裂缝立体网络[7],实现储层内压裂裂缝波及体积的最大化,从而极大地提高储层有效渗透率,提高油气井的产量。缝网压裂是利用储层两个水平主应力差值与裂缝延伸净压力的关系,一旦实现压裂延伸净压力大于两个水平主应力的差值,就会产生分支缝,分支缝沿着天然裂缝继续延伸,最终形成以主裂缝为主干的纵横交错的“网状缝”系统[7]。对于期望形成的人工裂缝和天然裂缝共同作用的形态,如果在直井实施称为缝网压裂,在水平井实施称为体积压裂。在一般情况下,体积压裂又称缝网压裂,二者并无明显区别,主要特征都是在岩层中形成复杂的裂缝网络。
实现页岩气的全井段储层缝网体积改造是获得理想产能的关键。然而,影响页岩压裂缝网形态的因素较多,缝网的扩展机理和空间展布尚不明确,如何合理表征复杂缝网是目前页岩气有效开采面临的问题和难点,国际上目前对压裂缝网扩展及形态没有统一认识,亟待深入研究。本文通过调研大量页岩压裂缝网研究的矿场试验、室内实验以及数值模拟方法及研究成果,尤其对比、分析了各种数值模拟方法的发展和现状,展望了数值模拟技术的发展方向,并系统归纳了影响缝网的主控因素及其影响机理,旨在为页岩储层压裂缝网模拟提供参考。
1 压裂缝网研究方法研究者广泛研究了水力裂缝起裂和裂缝网络扩展,包括矿场试验、室内实验、数值模拟等。图貌监测目前贯穿于各种试验或实验方法中,作为一种监测手段主要用于矿场试验和室内实验中,在数值模拟中主要用于模拟指导和结果对比、验证。
1.1 矿场试验进行矿场试验的必要性在于通过对现场工程结果的直观了解,指导和深化实验研究,以便更好地反馈现场工程工作。
Warpinski[8]开展的矿场试验研究表明,水力裂缝存在三种延伸模式:穿过天然裂缝、被张开破裂的天然裂缝阻止延伸、被剪切破裂的天然裂缝阻止延伸。任岚等[9]基于页岩气开发同步压裂基本原理率先开展超低渗砂岩储层同步压裂先导性矿场试验,通过分析影响裂缝延伸的地质适应性,优化设计同步压裂并在矿场实施及分析同步压裂。
储层压裂过程中微地震监测技术对于裂缝追踪、反演等具有独特的优势,已经广泛用于矿场试验和实际工程。目前在中国该项技术在直观描绘页岩压裂缝网形态方面还不够成熟。
杨瑞召等[10]在微地震监测技术的基础上发展了细化地震发射层析成像(TSET)方法。该方法经过一系列后处理技术能直观地显示人工水力压裂裂缝成像结果。成像分析表明,水力压裂能够激活天然裂缝并在远井诱发形成“诱发破裂裂缝”,同时验证了人工裂缝与天然裂缝的相互作用模式。
由于矿场试验的区域性强、代价高,因此大多应用于现场大规模试验,对于一般科研和工程工作具有局限性。
1.2 室内实验在岩体压裂研究中,室内实验的优点在于对一些简单的水力压裂过程进行实验研究,能够取得较满意的现场指导结果。
为了深刻了解裂缝扩展、延伸及缝网形态,很早以前有人进行了岩体压裂的室内实验。早在1963年,Lamont等[11]对6种岩体在不同的天然裂缝和人工裂缝逼近角下研究了天然裂缝和人工压裂裂缝的相互作用问题,进行了70次试验并取得成功。Warpinski等[12]采用真三轴实验系统研究了地质非连续体对水力裂缝的影响,给出了不同水平应力差和逼近角情况下水力裂缝和天然裂缝的相互作用扩展模式。Blanton[13]对三轴压应力下的天然裂缝岩块进行了水力压裂实验,实验结果与Warpinski等[12]的实验结果一致,并且指出在裂缝性地层的压裂中几乎不会产生单一平面且关于井眼对称的双翼垂直裂缝。Beugelsdijk等[14]、Pater等[15]也对包含天然裂缝的岩石块体利用三轴水力压裂实验研究了水力裂缝的扩展问题,研究结果表明,注入高排量和高黏度的压裂液易使水力裂缝穿透天然裂缝扩展。陈勉等[16]、周健等[17]也曾用大尺度真三轴实验系统进行岩样水力压裂实验,研究了影响压裂裂缝扩展的相关因素。付海峰等[18]基于声波监测技术进行了超大尺寸水力压裂裂缝扩展实验,认为实验与现场裂缝延伸净压力的受控因素不同,应适当降低岩样断裂韧性,以提高流体黏性。随后,付海峰[19]又选择具有不同天然裂缝、地应力分布的南方海相页岩岩样,利用大物模实验系统研究了水力裂缝形态及复杂程度,分析了岩性、水平地应力差、流体黏度对裂缝形态的影响。衡帅等[20]通过室内页岩水力压裂大型物模实验了解了页岩试样压裂后水力裂缝的延伸规律与空间形态,并在此基础上初步揭示了页岩水力压裂缝网的形成机理。张士诚等[21]对页岩露头样品开展了大尺寸真三轴压裂模拟实验,对压裂岩心进行高能物理CT扫描,研究了排量、地应力、天然裂缝和沉积层理、压裂液黏度等对页岩压裂缝网复杂度的影响。
室内物理模拟实验可在一定程度上分析储层物性、施工参数等对水力裂缝扩展路径和扩展规律的影响,但由于实验规模以及实验条件等与现场的差异性,并不能直观地反映真实复杂的压裂过程中地层的物理(力学)性质。此外,实验技术、参数的限制也很难顾及地层中的复杂非线性流动等问题。数值模拟具有低成本、高效率以及对复杂过程的仿真模拟和强大的数据系统化处理等优势,因此室内物理模拟实验可作为矿场试验和室内研究的有效补充手段。
1.3 数值模拟随着数值计算方法的不断创新和计算机硬件的飞速发展,数值模拟已发展为研究水力裂缝扩展、延伸的重要方法,被广泛用于工程实践。现场微地震监测表明,页岩压裂过程中水力裂缝能沟通井筒周围的天然裂缝、层理并相互作用形成复杂的非平面、非对称的网状裂缝[22]。目前的缝网数值模拟手段主要有:基于边界元法的位移不连续模型、基于有限元法的有限元和扩展有限元模型、基于离散元和解析法[23]的离散裂缝和非常规网络模型以及基于分形方法的分形裂缝网络模型等。
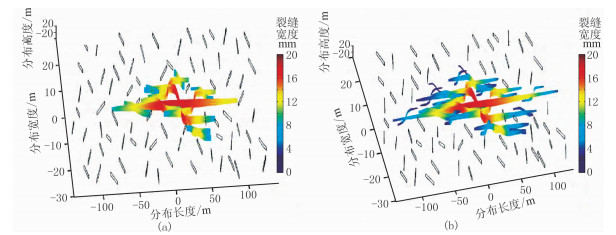
1.3.1 位移不连续数值模型(DDM)DDM基于边界元法。边界元法是一种较精确、有效的数值模拟方法,与有限元法在连续体域内划分单元的基本思想不同,边界元法只在定义域的边界上划分单元,以定义在边界上的边界积分方程为控制方程,通过对边界分元插值、离散,化为代数方程组求解。在求解裂缝延伸等位移不连续场问题时,将裂缝划分为一系列位移不连续的单元,并且通过在新产生的裂尖增加单元,将裂缝的破裂视为有限长度单元的不连续位移问题,通过建立控制方程逼近边界条件,从而体现裂缝参数控制,表征裂缝扩展状态。随机天然裂缝影响下缝网三维动态延伸模拟结果如图 1所示。
|
图 1 缝网三维动态延伸模拟结果[24] (a)60min效果图;(b)130min效果图 |
研究者通过位移不连续法描述了压裂裂缝网络,取得了一定的成果(表 1)。总体来说,目前建立的二维以及初步的三维DDM研究了水平井多段压裂时地层中人工裂缝和天然裂缝相交形成复杂缝网的问题、压裂缝间应力干扰效应对裂缝扩展形态的影响等,部分研究者从不同角度出发建立了扩展模型、应力场模型及断裂力学模型等。
|
|
表 1 位移不连续模型(DDM)研究进展 |
位移不连续方法对于处理二维不连续面问题十分实用,广泛用于岩体内断层、节理以及裂缝面等不连续面的处理。但是因为边界元法的应用以存在相应微分算子的基本解为前提,在遇到与非线性项对应的区域积分时,由于存在积分区域奇异点的奇异性,求解困难,因而难以处理材料非均匀性和各向异性等问题。
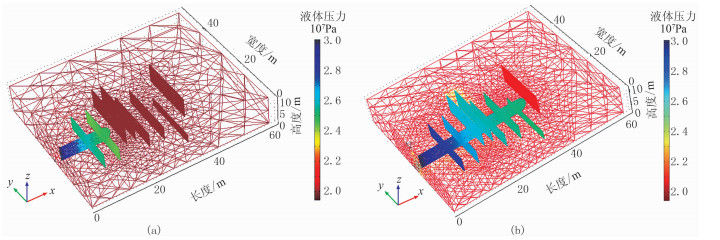
1.3.2 有限元模型(FEM)FEM通过网格描述裂缝几何形态。有限元法将待解区域通过单元分割,离散为一组单元的组合体,通过对有限个单元作分片插值,用这些单元场函数的集合近似代表整个连续体场函数。有限元法的形函数采用连续函数,处理裂缝不连续问题时将裂缝边设为单元边,裂尖设为单元节点。图 2为不同时间ALE (任意的拉格朗日—欧拉自适应网格)算法建立的复杂裂缝FEM扩展结果[31],表 2为FEM研究进展。
|
|
表 2 FEM研究进展 |
|
图 2 不同时间ALE算法建立的复杂裂缝FEM扩展结果[31] (a)时间步20步;(b)时间步50步 |
基于简单的二维水力压裂FEM,有人在FEM中引入了Cohesive黏聚力单元,在模拟过程中裂缝只沿着预置的Cohesive单元边界扩展,且扩展过程不需要网格重构。通过储层岩体介质假设、考虑岩石基质渗流、考虑裂缝流体流动耦合作用等分别建立了二维水力压裂FEM、非线性流—固耦合水力压裂FEM以及黏弹性储层性质的水力压裂三维FEM等。同时人们针对有限元模型计算复杂度进行了一系列算法优化,通过组集裂缝上、下面节点自由度进行流—固耦合迭代引入缩减算法,引入自适应网格以及在自适应网格基础上建立了时空间断伽辽金有限元法模拟了水力裂缝的起裂和扩展。
水力压裂FEM在简单缝网模拟过程中弥补了DDM难以处理材料非均匀和各向异性等问题的短板,模拟效果好,计算效率高,局限性在于在复杂缝网模拟过程中该模型需要使裂缝面与单元边界重合。由于自适应网格具有随机性,利用Cohesive黏聚力单元具有扩展路径预置性并且不考虑裂缝偏转,因此扩展有限元模型(XFEM)应运而生。
1.3.3 扩展有限元模型(XFEM)XFEM通过改进传统有限单元法的差值形函数,用扩充的带有不连续性质的差值形函数增加广义节点位移自由度描述裂缝域内的间断,通过求解扩展裂缝尖端不连续问题。上述过程完全独立于网格边界,不需要网格重划,可实现裂缝在规则网格中的任意扩展,反映了水力压裂裂缝的实际扩展规律。表 3为XFEM研究进展。目前人们考虑水力裂缝与天然裂缝相互作用、岩体变形和裂缝内流体流动、摩擦裂缝面剪切滑移效应等因素建立了二维流—固耦合水力压裂XFEM;考虑正交各向异性岩石中的裂缝扩展建立了二维正交各向异性岩石水力压裂XFEM;考虑储层变形多孔介质建立了基于内聚力裂缝模型的水力压裂XFEM。针对水力裂缝裂尖流体压力奇异性和裂尖流体延滞问题、流体压力和裂缝开度的近似、单元内裂缝扩展及流—固耦合迭代和摩擦裂缝接触迭代等问题,分别利用隐式水平集方法、特殊的XFEM裂尖增强函数、引入虚拟节点以及引入缩减算法增强单元自由度参与等优化模型算法。
|
|
表 3 XFEM研究进展 |
XFEM基于FEM,在继承其优点的同时又容易处理岩体非均质性和各向异性等问题,并且不需要通过网格重划描述裂缝几何形态,可实现裂缝在规则网格中的任意扩展,在大型水力压裂复杂缝网模拟中有独特优势。目前在很大程度上还停留在对水力压裂缝网的二维扩展模拟,并且模拟过程中对缝网影响因素的考虑缺乏系统化,有待于在综合考虑缝网扩展主控因素的情况下从二维向拟三维、真三维模型过渡、发展。
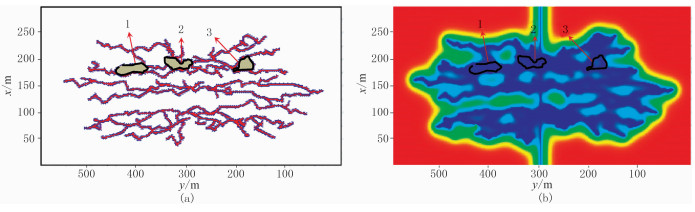
1.3.4 离散裂缝网络模型(DFN)DFN基于Warren等的双重介质模型[50],利用网格系统模拟裂缝在3个主平面的拟三维离散化扩展,通过连续性原理及网格计算方法获得压裂后缝网几何形态。模型包括三维线网模型、二维离散裂缝模型以及随机分布的多裂缝模型[51]。图 3为DFN模拟压裂缝网结果,表 4列出了DFN研究进展。
|
图 3 DFN模拟压裂缝网结果[52] (a)缝网展布简图;(b)缝网压力分布云图。图中编号1、2、3表示缝网完善程度分别为0.97、0.99、0.96 |
|
|
表 4 DFN研究进展 |
DFN从二维的线网模型到三维正交分布线网模型再到三维离散裂缝网络模型,考虑了压裂液、天然裂缝、基质渗透率及裂缝与流体作用等因素。发展的三维水力压裂DFN在模拟水力裂缝与大量天然裂缝相交形成复杂缝网的过程中发挥了重要作用。特别是二维、三维DFN模型考虑了缝间干扰和压裂液滤失问题后,可更准确地描述缝网几何形态及其内部压裂液流动规律,对缝网优化设计具有重要意义。但对于复杂裂缝的描述,由于人为设定因素突出、约束条件较差,需要利用大量的精细模型数据信息。根据地质资料、实验数据、测井数据、压裂数据等给出基础性参数的概率分布模型,引入裂缝边界识别算法,更精确地赋予裂缝扩展关系及边界条件。
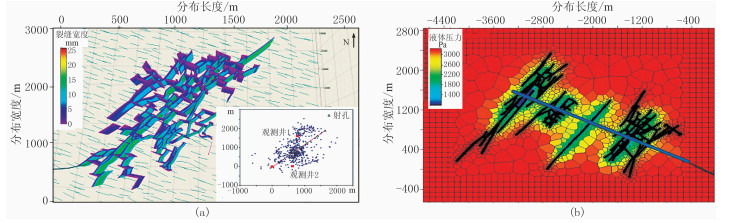
1.3.5 非常规裂缝网模型(UFM)UFM是在DFN基础上提出的,通过建立裂缝端部扩展准则,考虑了压裂液的一维流动、支撑剂的输送和裂缝宽度的弹性变形等因素,通过计算应力阴影考虑相邻人工裂缝间的相互作用。图 4为UFM模拟压裂缝网结果,表 5为UFM研究进展。
|
图 4 UFM模拟压裂缝网结果[63] (a)缝网空间展布简图;(b)缝网压力分布云图 |
|
|
表 5 UFM研究进展 |
部分研究者探讨了二维位移不连续方法在UFM中的应用,有人在后续研究中考虑了裂缝间应力阴影计算并基于微地震数据建立UFM扩展模型模拟地层缝网。
UFM充分考虑了储层岩石力学性质、不规则的裂缝形态以及水力裂缝间的干扰作用,利用三维裂缝高度方程和支撑剂沉降方程分别精确地预测裂缝分布、几何形态和支撑剂分布。为减少计算量和降低裂缝相关参数的高精度要求,在模拟时假设天然裂缝和水力裂缝均是垂直的,需要在拟三维模型中引入裂缝高度增长算法,结合裂缝起裂扩展力学特征优化裂缝网络几何形态。
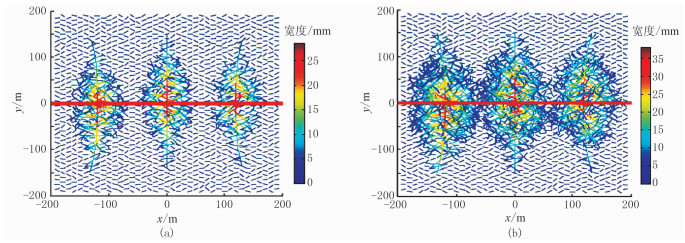
1.3.6 分形裂缝网模型(FFM)基于分形理论,可以认为分支缝是主裂缝的自相似性的分形,据此计算分支缝的分形维数建立FFM,描述裂缝网络延伸分布[68]。图 5为模拟的分形分叉裂缝网络形态[69],表 6为FFM研究进展[70-77]。
|
|
表 6 FFM研究进展 |
|
图 5 模拟的分形分叉裂缝网络形态[69] (a)流体压力为30MPa;(b)流体压力为40MPa |
结合裂缝起裂扩展的分形分析方法尚处于起步阶段,相关研究者基于分形方法尝试裂缝形貌表征方法,主要通过分形维数和分叉级数表征缝网,在考虑岩石脆性和天然薄弱面等情况下系统研究了分形缝网。
分形理论广泛用于自然科学研究的各个领域。裂缝的分形分析方法全面、定量地分析裂缝的分形分布结构,不仅反映裂缝的平均效果,而且反映裂缝分布的非均匀性[78]及其发育程度的差异。但对裂缝性储层的分形特征未形成系统认识,致使多级分形用于缝网扩展受到限制。目前分形维数法应用二维网络覆盖法预测缝网扩展已成为一条新途径,应结合裂缝多尺度空间效应,建立多级分形介质模型。
2 页岩压裂缝网扩展的主控因素 2.1 地质因素主要包括岩矿成分和岩石力学参数、天然裂缝产状和地应力、层理面强度以及缝内压力和内摩擦角等。
岩石的脆性由岩石的矿物成分控制,岩石中脆性矿物含量越高,岩石脆性越强,在压裂外力作用下越易形成缝网裂缝[79]。岩石力学参数对页岩储层岩石的可压性具有重要作用和影响,即弹性模量越高、泊松比越低,页岩的脆性越强[79]。Rickman等[80]认为,岩石脆性特征参数大于50的储层裂缝形态趋向形成缝网。在一定的逼近角和水平主应力差条件下,天然裂缝会改变水力裂缝的延伸形态和扩展模式。在中、高逼近角及高应力差的情况下,水力裂缝倾向于穿过天然裂缝而继续延伸;在低逼近角及低应力差的情况下,水力裂缝倾向于张开天然裂缝并改变压裂液流动方向而继续延伸;在高逼近角及低应力差的情况下,水力裂缝在与天然裂缝相交后常常伴随穿过、张开和分支三种模式混合延伸的情况[13]。天然裂缝逼近角越大,形成复杂缝网的概率也相对越大[62]。水平主应力差增大,体积裂缝的分布长度(水平最大主应力方向压裂裂缝的展布距离)增加、分布宽度(水平最小主应力方向压裂裂缝的展布距离)减小,即体积裂缝的长宽比增加[24]。页岩层理的发育和胶结强度严重影响压裂裂缝的复杂程度。沉积层理发育、胶结脆弱或微裂缝发育处易发生压裂缝的分叉、转向,伴随着与主裂缝相交的次生裂缝或沿层理面的贯穿裂缝产生大量开裂,形成网状裂缝[20-21]。层理面过弱或过强都不利于网状裂缝的形成;层理面胶结强度适中的地层,地应力对裂缝的延伸有较大影响。天然裂缝越发育、裂缝面摩擦系数越小、缝内净压力越高,水力裂缝越容易沿天然裂缝转向。随着缝内压力的升高新裂缝起裂角不断增大,在低逼近角的条件下适当提高缝内压力可以显著改变新裂缝起裂方向[81]。天然裂缝内摩擦角越小,天然裂缝连通面积越大,越易形成复杂网络裂缝[62]。
2.2 工程因素主要包括施工净压力和压裂施工排量、压裂液和支撑剂以及布孔间距等。
一般裂缝内净压力越大,对形成缝网越有利[29]。在一定的范围内排量影响裂缝复杂度,当排量特别低时,压裂液基本沿天然裂缝和层理缝滤失流动,且净压力较低,水力裂缝难以自由转向。当排量增加到一定程度后,水力裂缝更容易从最优裂缝面(最大主应力方向)自由偏转,从而沟通天然裂缝,增加裂缝体积。当排量继续增加,过高的净压力会导致水力裂缝更容易穿透闭合的天然裂缝,从而沿最优裂缝面扩展,在一定程度上降低了裂缝的复杂度[27]。压裂液与储层的润湿性越强、天然裂缝宽度越小、初始长度越长,越容易造成天然裂缝的起裂和扩展,形成的裂缝网络越复杂[82]。低黏度压裂液可以更好地传导压力,并能沟通更多的天然裂缝,且易使微裂缝产生错位和滑移,从而增加微裂缝的导流能力,此时小粒径支撑剂则更易进入细小的裂缝中起支撑作用,提高裂缝导流能力[83]。当裂缝间距较小时,裂缝偏离初始方向的角度越大,两侧裂缝越易向外扩展。随着布孔间距增大,裂缝扩展受“应力阴影”影响减小,裂缝弯曲扩展角度减小。此外,射孔间距越小,裂缝相互作用增强,总体缝网带宽减小;射孔间距越大,缝网带范围扩大,但相互作用减弱,缝网横向延伸不充分,致使缝网密度减小[9]。
综上所述,体积压裂缝网扩展的主控因素可以概括为地质和施工两大因素。前者是储层本身的地质特征和背景条件,即“甜点”区的选取是体积压裂形成复杂缝网的地质基础;后者是工程因素,合理的压裂施工参数能够引导水力裂缝充分扩展,形成复杂、有利的裂缝网络。目前建立的页岩水力压裂缝网扩展数值模型大多停留在仅考虑部分上述主控因素进行静态模拟,有待于进一步综合考虑各主控因素开展融合不同模型算法的动态缝网模拟。
3 认识与展望页岩储层压裂缝网表征作为现阶段页岩气开采的主要问题,因此在了解缝网扩展主控因素的基础上选择合理的具有优势的实验(试验)和模拟方法是有效推进页岩开采的重要环节。本文通过对页岩储层压裂缝网扩展各类方法的调研分析,重点评价了数值模拟方法特点并得到以下认识。
(1) 页岩储层压裂缝网数值模拟方法中基于FEM的XFEM、在DFN基础上发展的UFM以及从分形理论出发的FFM在页岩复杂缝网模拟中体现了优越性和可持续发展性。基于现阶段模拟水平,XFEM有待综合考虑缝网扩展主控因素从二维向拟三维、真三维模型过渡发展;DFN需要利用大量的精细模型数据信息,根据地质资料、实验数据、测井数据、压裂数据等给出基础性参数的概率分布模型,引入裂缝边界识别算法,以更精确地赋予裂缝扩展关系及边界条件;UFM可在拟三维模型中引入裂缝高度增长算法,结合裂缝起裂扩展力学特征优化裂缝网络几何形态;FFM可结合裂缝多尺度空间效应,建立多级分形介质模型。
(2) 从水力裂缝起裂、诱导和沟通天然裂缝的角度出发,裂缝扩展在真实地层中主要受控于缝内压力、岩石脆性、地应力、层理和天然裂缝。页岩储层岩石脆性较强,层理发育,天然裂缝广泛分布,极大地增加了缝网复杂程度,可以认为裂缝扩展整体上主要是以上因素共同作用的结果,为后续缝网扩展几何建模和扩展模拟提供了重要基础。
(3) 现阶段复杂裂缝网络模拟方法基于边界元、有限元、离散元、解析法,由于每种方法的特征和适用性不同,融合不同数值方法的建模、求解更有模拟潜力。基于目前认识的页岩压裂破裂、裂缝扩展机理及微地震监测等手段获取的数据建立规模化储层压裂缝网扩展模型,可以是等效分形分叉状、等效板砖缝网状或随机裂缝网络状等。模型求解进行离散化模块处理,对页岩岩体中断层、节理以及裂缝面等不连续面应用位移不连续法处理;对于主裂缝等可以跟踪的大型裂缝通过有限元划分网格描述;对于多级次生裂缝等利用扩展有限元法使其在规则网格中实现任意扩展或应用分形分析方法描述;对裂缝端部、缝内流体等用非常规裂缝方法处理。将各模型及算法特征梳理进行建模求解、交叉、融合,并用于水力压裂模拟。在综合考虑缝网扩展主控因素情况下,建立多尺度、多物理场耦合的三维动态混合介质复杂缝网模型,以期取得良好的页岩压裂缝网表征效果。由于分形理论具有描述不规则物体的优越性和精确性,为描述页岩储层裂缝网络扩展的不规则性和复杂性提供了有力工具,同时也需要不断地丰富和发展。
| [1] |
U.S.Energy Information Administration (EIA).Shale Gas Production Drives World Natural Gas Production Growth[R], 2016.
|
| [2] |
马永生, 蔡勋育, 赵培荣. 中国页岩气勘探开发理论认识与实践[J]. 石油勘探与开发, 2018, 45(4): 1-14. MA Yongsheng, CAI Xunyu, ZHAO Peirong. China's shale gas exploration and development:Understanding and practice[J]. Petroleum Exploration and Development, 2018, 45(4): 1-14. |
| [3] |
邹才能, 赵群, 董大忠, 等. 页岩气基本特征、主要挑战与未来前景[J]. 天然气地球科学, 2017, 28(12): 1781-1796. ZOU Caineng, ZHAO Qun, DONG Dazhong, et al. Geological characteristics, main challenges and future prospect of shale gas[J]. Natural Gas Geoscience, 2017, 28(12): 1781-1796. |
| [4] |
琚宜文, 卜红玲, 王国昌. 页岩气储层主要特征及其对储层改造的影响[J]. 地球科学进展, 2014, 29(4): 492-506. JU Yiwen, BU Hongling, WANG Guochang. Main characteristics of shale gas reservoir and its effect on the reservoir reconstruction[J]. Advances in Earth Science, 2014, 29(4): 492-506. |
| [5] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [6] |
Mayerhofer M, Lolon E, Youngblood J, et al. Integration of microseismic fracture mapping results with numerical fracture network production modeling in the Barnett Shale[C].SPE Annual Technical Conferance and Exhibition, 2006, SPE-102103-MS.
|
| [7] |
门晓溪.岩体渗流-损伤耦合及其水力压裂机理数值试验研究[D].辽宁沈阳: 东北大学, 2015. MEN Xiaoxi. Numerical Experimental Study on Hydraulic Fracturing Mechanism and Coupling of Seepage and Damage of Rockmass[D].Northeastern University, Shenyang, Liaoning, 2015. |
| [8] |
Warpinski N R. Hydraulic fracturing in tight, fissured media[J]. Journal of Petroleum Technology, 1991, 43(2): 146-151. DOI:10.2118/20154-PA |
| [9] |
任岚, 陶永富, 赵金洲. 超低渗透砂岩储层同步压裂先导性矿场试验[J]. 岩石力学与工程学报, 2015, 34(2): 330-339. REN Lan, TAO Yongfu, ZHAO Jinzhou. Simultaneous hydraulic fracturing field tests in ultra-low permeability sandstone reservoirs of Changqing Oilfield[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 330-339. |
| [10] |
杨瑞召, 李德伟, 庞海玲, 等. 页岩气压裂微地震监测中的裂缝成像方法[J]. 天然气工业, 2017, 37(5): 31-37. YANG Ruizhao, LI Dewei, PANG Hailing, et al. Fracture imaging of the surface based microseismic monitoring in shale gas fracking:Methods and application[J]. Natural Gas Industry, 2017, 37(5): 31-37. |
| [11] |
Lamont N, Jessen F W. The effects of existing fractures in rock on the extension of hydraulic fracture[J]. Journal of Petroleum Technology, 1963, 15(2): 203-209. DOI:10.2118/419-PA |
| [12] |
Warpinski N R, Teufel L W. Influence of geologic discontinuities on hydraulic fracture propagation[J]. Journal of Canadian Petroleum Technology, 1984, 39(2): 209-220. |
| [13] |
Blanton T L.Propagation of hydraulically and dynamically induced fractures in naturally fractured reservoirs[C].SPE Unconventional Gas Technology Symposium, 1986, SPE-15261-MS.
|
| [14] |
Beugelsdijk L J L, Pater C J D, Sato K.Experimental hydraulic fracture propagation in a multi-fractured medium[C].SPE Asia Pacific Conference on Integrated Modelling for Asset Management, 2000, SPE-59419-MS.
|
| [15] |
Pater C J D, Beugelsdijk L J L.Experiments and numerical simulation of hydraulic fracturing in naturally fractured rock[C].U.S.Rock Mechanics Symposium and, U.S.Canada Rock Mechanics Symposium, 2005, ARMA-05-780.
|
| [16] |
陈勉, 庞飞, 金衍. 大尺寸真三轴水力压裂模拟与分析[J]. 岩石力学与工程学报, 2000, 19(增刊): 868-872. CHEN Mian, PANG Fei, JIN Yan. Experiments and analysis on hydraulic fracturing by a large-size triaxial simulator[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(S): 868-872. |
| [17] |
周健, 陈勉, 金衍, 等. 裂缝性储层水力裂缝扩展机理试验研究[J]. 石油学报, 2007, 28(5): 109-113. ZHOU Jian, CHEN Mian, JIN Yan, et al. Experimental study on propagation mechanism of hydraulic fracture in naturally fractured reservoir[J]. Acta Petrolei Sinica, 2007, 28(5): 109-113. DOI:10.3321/j.issn:0253-2697.2007.05.020 |
| [18] |
付海峰, 崔明月, 邹憬, 等. 基于声波监测技术的长庆砂岩裂缝扩展实验[J]. 东北石油大学学报, 2013, 37(2): 96-101. FU Haifeng, CUI Yueming, ZOU Jing, et al. Experimental study of Changqing sandstone fracture propagation based on acoustic monitoring[J]. Journal of Northeast Petroleum University, 2013, 37(2): 96-101. DOI:10.3969/j.issn.2095-4107.2013.02.012 |
| [19] |
付海峰.中国南方海相页岩水力裂缝形态实验研究[C].第十二届全国流变学学术会议论文集, 2014. FU Haifeng. Experimental study on hydraulic fracture geometry of marine shales in South China[C].The 12nd China Rheology Conference Proceedings, 2014. |
| [20] |
衡帅, 杨春和, 曾义金, 等. 页岩水力压裂裂缝形态的试验研究[J]. 岩土工程学报, 2014, 36(7): 1243-1251. HENG Shuai, YANG Chunhe, ZENG Yijin, et al. Experimental study on hydraulic fracture geometry of shale[J]. Chinese Journal of Geotechnical Enginee-ring, 2014, 36(7): 1243-1251. |
| [21] |
张士诚, 郭天魁, 周彤, 等. 天然页岩压裂裂缝扩展机理试验[J]. 石油学报, 2014, 35(3): 496-503, 518. ZHANG Shicheng, GUO Tiankui, ZHOU Tong, et al. Fracture propagation mechanism experiment of hydraulic fracturing in natural shale[J]. Acta Petrolei Sinica, 2014, 35(3): 496-503, 518. |
| [22] |
李强, 尹成, 王俊力, 等. 基于天然裂缝破坏行为的页岩储层压裂微地震事件预测[J]. 石油物探, 2018, 57(6): 878-883, 891. LI Qiang, YIN Cheng, WANG Junli, et al. Prediction of microseismic events in a fractured shale reservoir based on natural fracture failure behavior[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 878-883, 891. DOI:10.3969/j.issn.1000-1441.2018.06.010 |
| [23] |
汪勇, 段焱文, 安一凡, 等. 扩展的近似解析离散化方法及弹性波方程数值模拟[J]. 石油地球物理勘探, 2017, 52(5): 928-940, 955. WANG Yong, DUAN Yanwen, AN Yifan, et al. Expanded approximate analytic discretization and elastic wave numerical simulation[J]. Oil Geophysical Prospecting, 2017, 52(5): 928-940, 955. |
| [24] |
赵金洲, 李勇明, 王松, 等. 天然裂缝影响下的复杂压裂裂缝网络模拟[J]. 天然气工业, 2014, 34(1): 68-73. ZHAO Jinzhou, LI Yongming, WANG Song, et al. Simulation of a complex fracture network influenced by natural fractures[J]. Natural Gas Industry, 2014, 34(1): 68-73. DOI:10.3787/j.issn.1000-0976.2014.01.010 |
| [25] |
Olson J E. Predicting fracture swarms:the influence of subcritical crack growth and the crack-tip process zone on joint spacing in rock[J]. Geological Society of London Special Publications, 2004, 231(1): 73-88. DOI:10.1144/GSL.SP.2004.231.01.05 |
| [26] |
Olson J E, Taleghani A D.Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures[C].SPE Hydraulic Fracturing Technology Conference, 2007, doi: 10.2118/119739-MS.
|
| [27] |
Wu K, Olson J E.Mechanics analysis of interaction between hydraulic and natural fractures in shale re-servoirs[C].Unconventional Resources Technology Conference, 2014, doi: 10.15530/urtec-2014-1922946.
|
| [28] |
Gordeliy E, Detournay E. A fixed grid algorithm for simulating the propagation of a shallow hydraulic fracture with a fluid lag[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2011, 35(5): 602-629. |
| [29] |
郭建春, 李根, 周鑫浩. 页岩气藏缝网压裂裂缝间距优化研究[J]. 岩土力学, 2016, 37(11): 3123-3129. GUO Jianchun, LI Gen, ZHOU Xinhao. Optimization of fracture spacing in fracture network of shale gas reservoir[J]. Rock & Soil Mechanics, 2016, 37(11): 3123-3129. |
| [30] |
仲冠宇, 王瑞和, 周卫东, 等. 人工裂缝逼近条件下天然裂缝破坏特征分析[J]. 岩土力学, 2016, 37(1): 247-255. ZHONG Guanyu, WANG Ruihe, ZHOU Weidong, et al. Failure characteristics of natural fracture in the vicinity of hydrofractures[J]. Rock & Soil Mecha-nics, 2016, 37(1): 247-255. |
| [31] |
Li Y, Wei C, Qin G, et al. Numerical simulation of hydraulically induced fracture network propagation in shale formation[C].International Petroleum Techno-logy Conference, 2013, IPTC-16981-MS.
|
| [32] |
Hunsweck M J, Shen Y, Lew A J. A finite element approach to the simulation of hydraulic fractures with lag[J]. International Journal for Numerical & Analy-tical Methods in Geomechanics, 2013, 37(9): 993-1015. |
| [33] |
Bao J Q, Fathi E, Ameri S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique[J]. Engineering Fracture Mechanics, 2014, 131(2): 269-281. |
| [34] |
Ouyang S, Carey G F, Yew C H. An adaptive finite element scheme for hydraulic fracturing with proppant transport[J]. International Journal for Numerical Methods in Fluids, 2015, 24(7): 645-670. |
| [35] |
Omidi O, Abedi R, Enayatpour S.An adaptive meshing approach to capture hydraulic fracturing[C].U.S.Rock Mechanics/Geomechanics Symposium, 2015, ARMA-2015-572.
|
| [36] |
Chen Z, Bunger A P, Zhang X, et al. Cohesive zone finite element-based modeling of hydraulic fractures[J]. Acta Mechanica Solida Sinica, 2009, 22(5): 443-452. DOI:10.1016/S0894-9166(09)60295-0 |
| [37] |
Carrier B, Granet S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model[J]. Engineering Fracture Mechanics, 2012, 79(8): 312-328. |
| [38] |
Wang H, Liu H, Zhou X, et al. A 3D finite element model for simulating hydraulic fracturing processes with viscoelastic reservoir properties[J]. Oil Gas European Magazine, 2012, 38(4): 210-212. |
| [39] |
Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620. DOI:10.1002/(ISSN)1097-0207 |
| [40] |
Dahi T A.Analysis of Hydraulic Fracture Propagation in Fractured Reservoirs: An Improved Model for the Interaction Between Induced and Natural Fractures[D].The University of Texas at Austin, 2009.
|
| [41] |
Gordeliy E, Peirce A. Implicit level set schemes for modeling hydraulic fractures using the XFEM[J]. Computer Methods in Applied Mechanics & Engineering, 2013, 266(11): 125-143. |
| [42] |
Lecampion B. An extended finite element method for hydraulic fracture problems[J]. International Journal for Numerical Methods in Biomedical Engineering, 2009, 25(2): 121-133. |
| [43] |
Wang X L, Shi F, Liu H, et al. Numerical simulation of hydraulic fracturing in orthotropic formation based on the extended finite element method[J]. Journal of Natural Gas Science & Engineering, 2016, 33(1): 56-69. |
| [44] |
Mohammadnejad T, Khoei A R. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model[J]. Finite Elements in Analysis & Design, 2013, 73(15): 77-95. |
| [45] |
Khoei A R, Hirmand M, Vahab M, et al. An enriched FEM technique for modeling hydraulically driven cohesive fracture propagation in impermeable media with frictional natural faults:Numerical and experimental investigations[J]. International Journal for Numerical Methods in Engineering, 2015, 104(6): 439-468. DOI:10.1002/nme.v104.6 |
| [46] |
王小龙.扩展有限元法应用于页岩气藏水力压裂数值模拟研究[D].安徽合肥: 中国科学技术大学, 2017. WANG Xiaolong. Numerical Simulation of Hydraulic Fracturing in Shale Gas Seservoirs Based on the Extended Finite Element Method[D].University of Science and Technology of China, Hefei, Anhui, 2017. |
| [47] |
王涛, 高岳, 柳占立, 等. 基于扩展有限元法的水力压裂大物模实验的数值模拟[J]. 清华大学学报(自然科学版), 2014, 54(10): 1304-1309. WANG Tao, GAO Yue, LIU Zhanli, et al. Numerical simulations of hydraulic fracturing in large objects using an extended finite element method[J]. Journal of Tsinghua University(Science and Technology), 2014, 54(10): 1304-1309. |
| [48] |
师访.岩石破裂过程的扩展有限元法研究[D].江苏徐州: 中国矿业大学, 2015. SHI Fang. Study on the Cracking Process of Rock Using the Extended Finite Element Method[D].China University of Mining and Technology, Xuzhou, Jiangsu, 2015. |
| [49] |
Shi F, Wang X L, Liu C, et al. An XFEM-based method with reduction technique for modeling hydraulic fracture propagation in formations containing frictional natural fractures[J]. Engineering Fracture Mecha-nics, 2017, 173(1): 64-90. |
| [50] |
程远方, 李友志, 时贤, 等. 页岩气体积压裂缝网模型分析及应用[J]. 天然气工业, 2013, 33(9): 53-59. CHENG Yuanfang, LI Youzhi, SHI Xian, et al. Ana-lysis and application of fracture network models of volume fracturing in shale gas reservoirs[J]. Natural Gas Industry, 2013, 33(9): 53-59. |
| [51] |
张士诚, 牟松茹, 崔勇. 页岩气压裂数值模型分析[J]. 天然气工业, 2011, 31(12): 81-84. ZHANG Shicheng, MOU Songru, CUI Yong. Numerical simulation models with hydraulic fracturing in shale gas reservoirs[J]. Natural Gas Industry, 2011, 31(12): 81-84. DOI:10.3787/j.issn.1000-0976.2011.12.014 |
| [52] |
刘玉章, 杨立峰, 王欣, 等. 页岩气水力压裂裂缝缝网完善程度概论[J]. 天然气工业, 2017, 37(7): 34-39. LIU Yuzhang, YANG Lifeng, WANG Xin, et al. Introduction to the completion degree of hydraulic fracture networks in shale gas reservoirs[J]. Natural Gas Industry, 2017, 37(7): 34-39. |
| [53] |
Xu W, Thiercelin M J, Walton I C.Characterization of hydraulically-induced shale fracture network using an analytical/semi-analytical model[C].SPE Annual Technical Conference and Exhibition, 2009, doi: 10.2118/124697-MS.
|
| [54] |
Meyer B R, Bazan L W.A discrete fracture network model for hydraulically induced fractures-theory, parametric and case studies[C].SPE Hydraulic Fracturing Technology Conference, 2011, doi: 10.2118/140514-MS.
|
| [55] |
Dershowitz W S, Cottrell M G, Lim D H, et al. A discrete fracture network approach for evaluation hydraulic fracture stimulation of naturally fractured reservoirs[C].44th U.S.Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, 2010, ARMA-10-475.
|
| [56] |
Cottrell M, Hosseinpour H, Dershowitz W.Rapid discrete fracture analysis of hydraulic fracture development in naturally fractured reservoirs[C].Unconventional Resources Technology Conference, 2013, 2341-2353.
|
| [57] |
Cipolla C L, Lolon E, Mayerhofer M J.Reservoir modeling and production evaluation in shale-gas reservoirs[C].International Petroleum Technology Conference, 2009, doi: 10.2523//PTC-13185-MS.
|
| [58] |
Mcclure M W, Babazadeh M, Shiozawa S, et al. Fully coupled hydromechanical simulation of hydraulic fracturing in 3D discrete-fracture networks[J]. SPE Journal, 2016, 21(4): 1302-1320. DOI:10.2118/173354-PA |
| [59] |
孙海成, 汤达祯, 蒋廷学. 页岩气储层裂缝系统影响产量的数值模拟研究[J]. 石油钻探技术, 2011, 39(5): 63-67. SUN Haicheng, TANG Dazhen, JIANG Tingxue. Numerical simulation of the impact of fracture system on well production in shale formation[J]. Petroleum Drilling Techniques, 2011, 39(5): 63-67. DOI:10.3969/j.issn.1001-0890.2011.05.014 |
| [60] |
程远方, 王光磊, 李友志, 等. 致密油体积压裂缝网扩展模型建立与应用[J]. 特种油气藏, 2014, 21(4): 138-141. CHENG Yuanfang, WANG Guanglei, LI Youzhi, et al. Establishment and application of fracture propagation model for volumetric fracturing in tight oil reservoir[J]. Special Oil & Gas Reservoirs, 2014, 21(4): 138-141. DOI:10.3969/j.issn.1006-6535.2014.04.034 |
| [61] |
Riahi A, Damjanac B.Numerical study of the interaction between injection and the discrete fracture network in enhanced geothermal reservoirs[C].47th U.S.Rock Mechanics/Geomechanics Symposium, 2013, ARMA-2013-333.
|
| [62] |
李玉梅, 吕炜, 宋杰, 等. 层理性页岩气储层复杂网络裂缝数值模拟研究[J]. 石油钻探技术, 2016, 44(4): 108-113. LI Yumei, LYU Wei, SONG Jie, et al. Numerical simulation study on the complex network fractures of stratified shale gas reservoirs[J]. Petroleum Drilling Techniques, 2016, 44(4): 108-113. |
| [63] |
Weng X, Kresse O, Cohen C E, et al. Modeling of hydraulic-fracture-network propagation in a naturally fractured formation[J]. SPE Production & Operations, 2011, 26(4): 368-380. |
| [64] |
Kresse O, Weng X, Gu H, et al. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations[J]. Rock Mechanics & Rock Engineering, 2013, 46(3): 555-568. |
| [65] |
Wu R, Kresse O, Weng X, et al. Modeling of interaction of hydraulic fractures in complex fracture networks[C].doi: 10.2118/152052-MS,2012.
|
| [66] |
Haege M, Maxwell S, Sonneland L, et al. Rock fabric characterization using 3D reflection seismic integrated with microseismic[C].Extended Abstracts of 75th EAGE Conference & Exhibition, doi: 10.3997/2214-4609.2013024,2013.
|
| [67] |
Cipolla C, Weng X, Mack M, et al. Integrating microseismic mapping and complex fracture modeling to characterize hydraulic fracture complexity[C].SPE Hydraulic Fracturing Technology Conference, 2011, doi: 10.2118/140185-MS.
|
| [68] |
董少群, 曾联波, Xu Chaoshui, 等. 储层裂缝随机建模方法研究进展[J]. 石油地球物理勘探, 2018, 53(3): 625-641. DONG Shaoqun, ZENG Lianbo, XU Chaoshui, et al. Some progress in reservoir fracture stochastic modeling research[J]. Oil Geophysical Prospecting, 2018, 53(3): 625-641. |
| [69] |
苏玉亮, 王文东, 盛广龙. 体积压裂水平井复合流动模型[J]. 石油学报, 2014, 35(03): 504-510. SU Yuliang, WANG Wendong, SHENG Guang-long. Compound flow model of volume fractured ho-rizontal well[J]. Acta Petrolei Sinica, 2014, 35(3): 504-510. |
| [70] |
Mandelbrot B B, Wheeler J A.The Fractal Geometry of Nature[M].W.H.Freeman and Company, 1982.
|
| [71] |
Falconer K J. Fractal geometry:mathematical foundations and applications[J]. Biometrics, 2014, 46(3): 499. |
| [72] |
侯贵廷. 裂缝的分形分析方法[J]. 应用基础与工程科学学报, 1994, 2(4): 299-305. HOU Guiting. Fractal analysis of fractures[J]. Journal of Basic Science and Engineering, 1994, 2(4): 299-305. |
| [73] |
李玮.基于分形理论的储层特征及压裂造缝机理研究[D].黑龙江大庆: 大庆石油学院, 2010. LI Wei. Research on Reservoir Characteristics and Fracture Initiation Mechanism Based on Fractal Theory[D].Daqing Petroleum Institute, Daqing, Heilongjiang, 2010. |
| [74] |
Riley P, Tikoff B, Murray A B. Quantification of fracture networks in non-layered, massive rock using synthetic and natural data sets[J]. Tectonophysics, 2011, 505(1): 44-56. |
| [75] |
郭天魁, 张士诚, 葛洪魁. 评价页岩压裂形成缝网能力的新方法[J]. 岩土力学, 2013, 34(4): 947-954. GUO Tiankui, ZHANG Shicheng, GE Hongkui. A new method for evaluating ability of forming fracture network in shale reservoir[J]. Rock & Soil Mechanics, 2013, 34(4): 947-954. |
| [76] |
胡超洋, 艾池, 王凤娇. 基于分形方法的水力压裂分支裂缝分布模拟[J]. 油气地质与采收率, 2016, 13(5): 1-5. HU Chaoyang, AI Chi, WANG Fengjiao. Distribution simulation of branched hydraulic fracture based on fractal theory[J]. Petroleum Geology and Recovery Efficiency, 2016, 13(5): 1-5. DOI:10.3969/j.issn.1009-9603.2016.05.001 |
| [77] |
尚校森, 丁云宏, 卢拥军, 等. 一种页岩体积压裂复杂裂缝的量化表征[J]. 石油与天然气地质, 2017, 38(1): 189-196. SHANG Xiaosen, DING Yunhong, LU Yongjun, et al. Quantitative characterization of complex fractures after volume fracturing in shale[J]. Oil & Gas Geology, 2017, 38(1): 189-196. |
| [78] |
潘新朋, 张广智, 印兴耀. 非均质HTI介质裂缝弱度参数地震散射反演[J]. 石油地球物理勘探, 2017, 52(6): 1226-1235. PAN Xinpeng, ZHANG Guangzhi, YIN Xingyao. Seismic scattering inversion for fracture weakness in heterogeneous HTI media[J]. Oil Geophysical Prospecting, 2017, 52(6): 1226-1235. |
| [79] |
赵金洲, 任岚, 胡永全. 页岩储层压裂缝成网延伸的受控因素分析[J]. 西南石油大学学报(自然科学版), 2013, 35(1): 1-9. ZHAO Jinzhou, REN Lan, HU Yongquan. Controlling factors of hydraulic fractures extending into network in shale formations[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2013, 35(1): 1-9. |
| [80] |
Rickman R, Mullen M J, Petre J E, et al. A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the Barnett Shale[C].SPE Technical Conference and Exhibition, 2008, SPE-115258-MS.
|
| [81] |
程远方, 常鑫, 孙元伟, 等. 基于断裂力学的页岩储层缝网延伸形态研究[J]. 天然气地球科学, 2014, 25(4): 603-611. CHENG Yuanfang, CHANG Xin, SUN Yuanwei, et al. Research on fracture network propagation pattern of shale reservoir based on fracture mechanics[J]. Natural Gas Geoscience, 2014, 25(4): 603-611. |
| [82] |
王迪, 金衍, 陈勉, 等. 毛细管力影响下页岩储层液化石油气压裂裂缝网络扩展形态研究[J]. 中国科技论文, 2016, 11(21): 2440-2444. WANG Di, JIN Yan, CHEN Mian, et al. Study on fracture network development of LPG fracturing in shale considering capillary effect[J]. China Sciencepaper, 2016, 11(21): 2440-2444. DOI:10.3969/j.issn.2095-2783.2016.21.008 |
| [83] |
刘立峰, 张士诚. 通过改变近井地应力场实现页岩储层缝网压裂[J]. 石油钻采工艺, 2011, 33(4): 71-74. LIU Lifeng, ZHANG Shicheng. Net fracturing by changing the surrounding in-situ stress in shale reservoirs[J]. Oil Drilling & Production Technology, 2011, 33(4): 71-74. DOI:10.3969/j.issn.1000-7393.2011.04.019 |



 胡志明 河北省廊坊市广阳区万庄镇中国石油勘探开发研究院渗流流体力学研究所, 065007。Email:
胡志明 河北省廊坊市广阳区万庄镇中国石油勘探开发研究院渗流流体力学研究所, 065007。Email: 