② 东北大学资源与土木工程学院, 辽宁沈阳 110819;
③ 兰州大学地质科学与矿产资源学院, 甘肃兰州 730000;
④ 浙江大学地球科学学院, 浙江杭州 310058
② School of Resources and Civil Engineering, Northeastern University, Shenyang, Liaoning 110819, China;
③ School of Earth Sciences, Lanzhou University, Lanzhou, Gansu 730000, China;
④ School of Earth Sciences, Zhejiang University, Hangzhou, Zhejiang 310058, China
重力勘探是重要的物探方法之一,观测数据可用于地下空间物性分布[1]和场源位置[2]的计算。欧拉反褶积(Euler Deconvolution, ED)[3]是一种重磁勘探数据处理方法,可以计算地质体的埋深、位置等参数,被广泛应用于各类资源勘查工作中。相比于传统重力异常数据,重力梯度数据精度较高,信噪比也更高,包含更多的地质信息,在对地质体的边界[4]、形状识别[5]上有较好的应用效果。Zhang等[6]提出利用重力全张量梯度数据进行欧拉反褶积,能够更充分利用梯度数据。针对传统欧拉反褶积中反演结果多解性强和空间分辨率较低等问题,一些学者进行方法改进,包括引入基于水平梯度率[7]、均衡边界检测滤波器[8]、梯度反褶积[9]、垂向一阶导数[10]和解析信号比值[11]等;联合不同高度观测面上数据的欧拉反褶积,也被应用于实际勘探中[12-13]。以上研究均一定程度上改善了欧拉反褶积的计算效果。
本文在传统方法基础上提出重力梯度数据联合的欧拉反褶积(Joint Euler Deconvolution of Gravity Gradiometry Data, JEDGG)法,通过计算垂向导数重新推导了反演方程,联合多个梯度分量建立了新的方程组,避免了构造指数的选择以及不同分量间的换算。模型试验验证了该方法的有效性,并将其应用于文顿盐丘地区的实测重力数据,在盖岩东部发现了一处小型构造,进一步探明了该区地下地质结构。
1 重力梯度联合欧拉反褶积原理根据欧拉齐次方程的定义[3],传统欧拉反褶积公式为
| $ \begin{array}{*{20}{c}} {\left( {x - {x_0}} \right)\frac{{\partial f}}{{\partial x}} + \left( {y - {y_0}} \right)\frac{{\partial f}}{{\partial y}} + \left( {z - {z_0}} \right)\frac{{\partial f}}{{\partial z}}}\\ { = N\left( {B - f} \right)} \end{array} $ | (1) |
式中:(x, y, z)和(x0, y0, z0)分别代表观测点和地质体中心坐标,其中z0表示异常体中心深度;f和B分别表示观测异常场和背景场;N为构造指数,如薄板的N取0.5,而球体取2.0。将上式转化为向量积的形式
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial x}}}&{\frac{{\partial f}}{{\partial y}}}&{\frac{{\partial f}}{{\partial z}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}}\\ {{z_0}} \end{array}} \right]\\ \;\;\; = x\frac{{\partial f}}{{\partial x}} + y\frac{{\partial f}}{{\partial y}} + z\frac{{\partial f}}{{\partial z}} - N\left( {B - f} \right) \end{array} $ | (2) |
用引力位V在x、y和z三个方向的一阶导数分别替代式(1)中的f,有
| $ \left\{ \begin{array}{l} \left( {x - {x_0}} \right){V_{xx}} + \left( {y - {y_0}} \right){V_{xy}} + \left( {z - {z_0}} \right){V_{xz}}\\ \;\;\;\;\;\; = N\left( {B - {V_x}} \right)\\ \left( {x - {x_0}} \right){V_{xy}} + \left( {y - {y_0}} \right){V_{yy}} + \left( {z - {z_0}} \right){V_{yz}}\\ \;\;\;\;\;\; = N\left( {B - {V_y}} \right)\\ \left( {x - {x_0}} \right){V_{xz}} + \left( {y - {y_0}} \right){V_{yz}} + \left( {z - {z_0}} \right){V_{zz}}\\ \;\;\;\;\;\; = N\left( {B - {V_z}} \right) \end{array} \right. $ | (3) |
由于实际数据中缺少Vx和Vy,只能通过分量转换得到,故式(3)不适于高精度重力梯度数据的计算。对式(3)两端分别计算z方向上的导数,可得
| $ \left\{ \begin{array}{l} \left( {x - {x_0}} \right){V_{xxz}} + \left( {y - {y_0}} \right){V_{xyz}} + {V_{xz}} + \left( {z - {z_0}} \right){V_{xzz}}\\ \;\;\;\;\;\; = - N{V_{xz}}\\ \left( {x - {x_0}} \right){V_{xyz}} + \left( {y - {y_0}} \right){V_{yyz}} + {V_{yz}} + \left( {z - {z_0}} \right){V_{yzz}}\\ \;\;\;\;\;\; = - N{V_{yz}}\\ \left( {x - {x_0}} \right){V_{xzz}} + \left( {y - {y_0}} \right){V_{yzz}} + {V_{zz}} + \left( {z - {z_0}} \right){V_{zzz}}\\ \;\;\;\;\;\; = - N{V_{zz}} \end{array} \right. $ | (4) |
整理式(4),合并同类项,将三阶导数转化为计算二阶导数的一阶偏导数
| $ \left\{ \begin{array}{l} \left( {x - {x_0}} \right)\frac{{\partial {V_{xz}}}}{{\partial x}} + \left( {y - {y_0}} \right)\frac{{\partial {V_{xz}}}}{{\partial y}} + \left( {z - {z_0}} \right)\frac{{\partial {V_{zz}}}}{{\partial x}}\\ \;\;\;\;\;\; = - \left( {N + 1} \right){V_{xz}}\\ \left( {x - {x_0}} \right)\frac{{\partial {V_{yz}}}}{{\partial x}} + \left( {y - {y_0}} \right)\frac{{\partial {V_{yz}}}}{{\partial y}} + \left( {z - {z_0}} \right)\frac{{\partial {V_{zz}}}}{{\partial y}}\\ \;\;\;\;\;\; = - \left( {N + 1} \right){V_{yz}}\\ \left( {x - {x_0}} \right)\frac{{\partial {V_{zz}}}}{{\partial x}} + \left( {y - {y_0}} \right)\frac{{\partial {V_{zz}}}}{{\partial y}} + \left( {z - {z_0}} \right)\frac{{\partial {V_{zz}}}}{{\partial z}}\\ \;\;\;\;\;\; = - \left( {N + 1} \right){V_{zz}} \end{array} \right. $ | (5) |
式中Vxz、Vyz和Vzz为重力梯度数据,计算其导数后利用式(5)可求解地质体坐标。需要注意的是,理论上计算z方向导数不会对结果造成影响,但计算实际数据时,求导数相当于滤波,将会放大噪声。因此,本文将二阶导数的一阶垂向偏导数转化为一阶导数的二阶偏导数。由于引力位满足拉普拉斯方程,将式(5)中引力位在z方向的三阶偏导数转化为
| $ \frac{{\partial {V_{zz}}}}{{\partial z}} = \frac{{{\partial ^2}{V_z}}}{{\partial {z^2}}} = - \frac{{{\partial ^2}{V_z}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{V_z}}}{{\partial {y^2}}} = - \frac{{\partial {V_{xz}}}}{{\partial x}} - \frac{{\partial {V_{yz}}}}{{\partial y}} $ | (6) |
将式(6)代入式(5),转化为矩阵形式
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {V_{xz}}}}{{\partial x}}}&{\frac{{\partial {V_{xz}}}}{{\partial y}}}&{\frac{{\partial {V_{zz}}}}{{\partial x}}}&{{V_{xz}}}\\ {\frac{{\partial {V_{yz}}}}{{\partial x}}}&{\frac{{\partial {V_{yz}}}}{{\partial y}}}&{\frac{{\partial {V_{zz}}}}{{\partial y}}}&{{V_{yz}}}\\ {\frac{{\partial {V_{zz}}}}{{\partial x}}}&{\frac{{\partial {V_{zz}}}}{{\partial y}}}&{ - \left( {\frac{{\partial {V_{xz}}}}{{\partial x}} + \frac{{\partial {V_{yz}}}}{{\partial y}}} \right)}&{{V_{zz}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}}\\ {{z_0}}\\ { - N} \end{array}} \right]}\\ { = \left[ {\begin{array}{*{20}{c}} {x\frac{{\partial {V_{xz}}}}{{\partial x}} + y\frac{{\partial {V_{xz}}}}{{\partial y}} + z\frac{{\partial {V_{zz}}}}{{\partial x}} + {V_{xz}}}\\ {x\frac{{\partial {V_{yz}}}}{{\partial x}} + y\frac{{\partial {V_{yz}}}}{{\partial y}} + z\frac{{\partial {V_{zz}}}}{{\partial y}} + {V_{yz}}}\\ {x\frac{{\partial {V_{zz}}}}{{\partial x}} + y\frac{{\partial {V_{zz}}}}{{\partial y}} - z\left( {\frac{{\partial {V_{xz}}}}{{\partial x}} + \frac{{\partial {V_{yz}}}}{{\partial y}}} \right) + {V_{zz}}} \end{array}} \right]} \end{array} $ | (7) |
由式(7)可知,本文方法避免了构造指数的选择以及计算垂向导数引起的误差,计算形式更简单。联合Vxz、Vyz和Vzz,减少了分量转换步骤。与传统方法一样,梯度联合欧拉反褶积也需要使用滑动窗口,窗口中所有测点的方程构成方程组。
2 模型测试为测试方法的有效性,在笛卡尔坐标系下建立理论模型并进行试验。试验包含不加噪声、加入5%高斯噪声两种情况,并对比传统ED方法的结果。试验中长方体密度均设为1.0g/cm3。根据式(2)和式(7),可分别计算ED和JEDGG的结果。
2.1 单长方体模型首先设地下一长方体的顶面埋深为100m,三维尺寸为800m×800m×200m,观测点距为20m,异常体水平位置及理论异常见图 1。滑动窗口的大小为19×19,即窗口内包含19×19个测点。试验结果见图 2~图 5。

|
图 1 单长方体模型产生的理论重力梯度异常场(上)及含5%高斯噪声的重力梯度异常场(下) Vxz;(b)Vyz;(c)Vzz。矩形框表示长方体边界 |
|
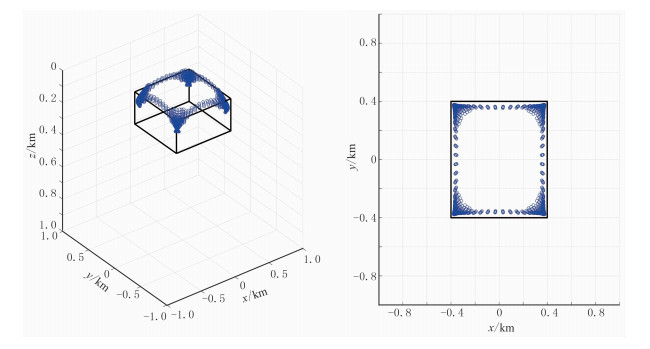
图 3 单长方体模型正演数据(无噪声)的ED结果 左:三维显示;右:z方向视图 |
|
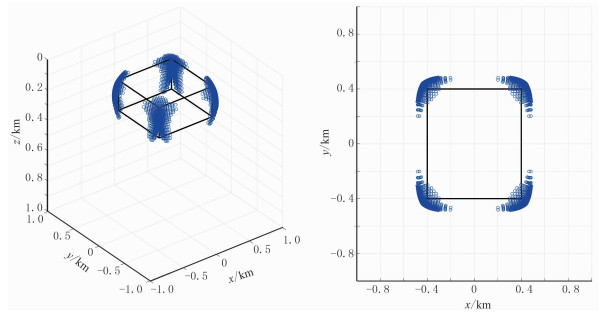
图 4 单长方体模型正演(含噪声)的JEDGG结果 左:三维显示;右:z方向视图 |

|
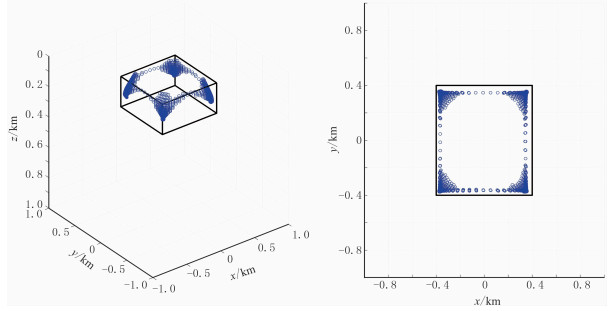
图 5 单长方体模型(含噪声)的ED结果 左:三维显示;右:z方向视图 |
从图 2、图 3可以看出,在无噪数据试验中,JEDGG结果与理论模型基本一致,长方体的水平边界被清晰地显示,三维结果可较准确地揭示长方体的埋深;相对地,ED结果的聚焦程度低于JEDGG,其反映的目标体的水平和深度方向上的范围均比真实值大,并且水平方向上边界不连续,仅能反映异常体顶点的位置。在含高斯噪声数据试验中,其结果(图 4、图 5)与无噪数据计算结果(图 2、图 3)相似,说明JEDGG适用于含噪声数据的反演。
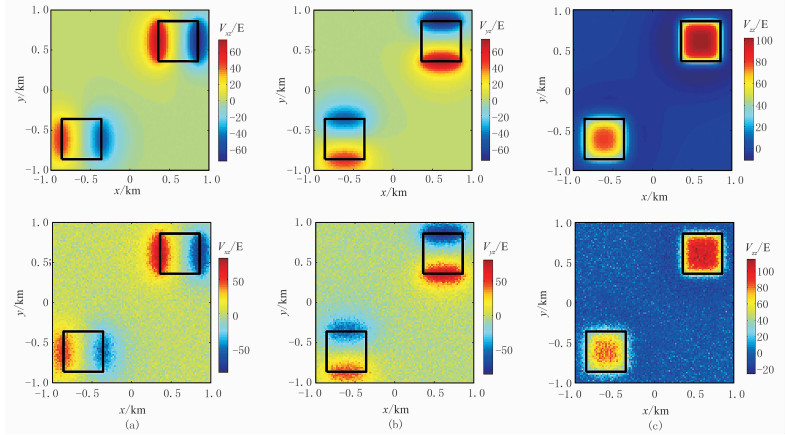
2.2 双长方体模型为了验证方法对不同埋深地质体模型的计算效果, 建立一个双异常体模型进行试验。设地下有两个完全相同的长方体,大小均为500m×500m×100m,顶面埋深分别为100m和200m,观测点距为20m,这两个异常体的平面位置及理论重力梯度异常场见图 6。如果JEDGG能够同时准确地反演出这两个长方体的空间位置,则验证了方法的有效性。计算中滑动窗口大小设为11×11,对该模型分别应用JEDGG和ED方法计算,结果见图 7~图 10。
|
图 6 双长方体模型产生的理论重力梯度异常场(上)及含5%高斯噪声的重力梯度异常场(下) (a)Vxz;(b)Vyz;(c)Vzz |
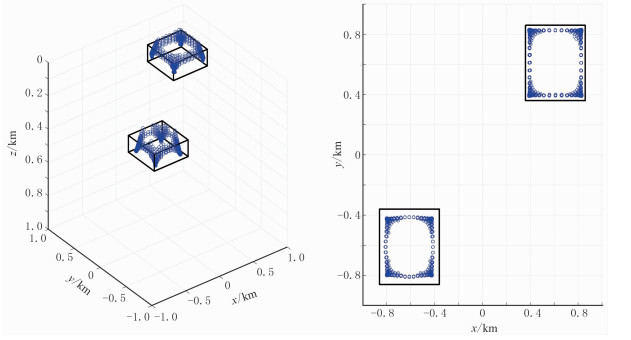
|
图 7 双长方体模型正演数据(无噪声)的JEDGG结果 左:三维显示;右:z方向视图 |
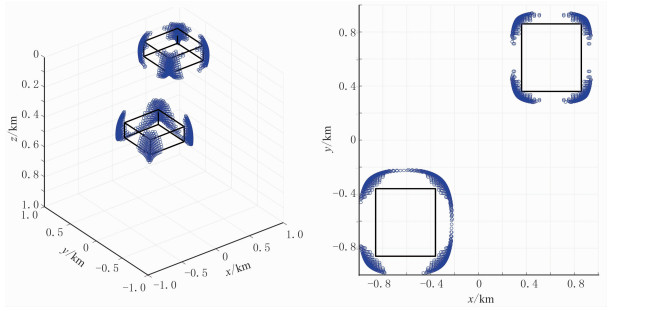
|
图 8 双长方体模型正演数据(无噪声)的ED结果 左:三维显示;右:z方向视图 |

|
图 9 双长方体模型正演数据(含噪声)的JEDGG结果 左:三维显示;右:z方向视图 |
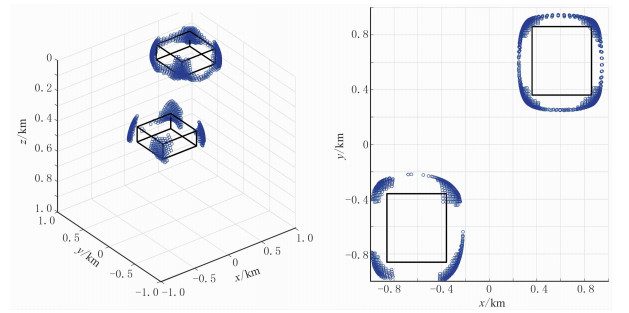
|
图 10 双长方体模型正演数据(含噪声)的ED结果 左:三维显示;右:z方向视图 |
从图 7和8可见,JEDGG法能够同时反演得到两个长方体的水平位置和埋深,其中深部长方体的范围比真实值略小。与ED法计算结果相比,JEDGG计算结果的空间分辨率更高,ED反演得到的异常体范围偏大、边界不连续。对于含噪声(图 9、图 10)情况,JEDGG法计算结果与理论值基本一致,仅在顶面顶点处出现了些许虚假解,即顶点的上方出现“发散状”的解,但不影响对长方体位置的判断;ED计算虽然没有这样的解,但是长方体范围仍偏大。这个试验也验证了JEDGG处理含噪数据的有效性。
理论数据和含噪数据试验结果都证明了JEDGG反演效果优于ED,结果更准确,且更适用于较复杂的地质情况。
3 应用实例基于上述对JEDGG方法的理论研究与模型试验,将其应用于文顿盐丘的实测重力全张量梯度数据。文顿盐丘位于美国路易斯安那州西南,由于富含油气资源而成为研究热点。文顿盐丘包含岩盐和上方的盖岩,实测异常主要来源于盖岩[14-16]。根据Ennen等[15]和Oliveria等[16]的研究,盖岩埋深约为160~650m。实测数据的x和y轴的正方向分别代表东、北。数据已经密度为2.2g/cm3的地形改正和低通滤波,选取Vxz、Vyz和Vzz三个分量进行JEDGG计算,结果见图 11。

|
图 11 文顿盐丘实测重力梯度数据JEDGG反演结果 (a)三维显示;(b)z方向视图;(c)y方向视图;(d)x方向视图 |
从图 11可以判断盖岩顶的水平范围,并与其他学者对该盖岩的研究结果[17-19]对比,发现基本吻合。还可以看出,盖岩的埋深在西部较小,约为125m,较深的位置出现在南部,约550m;顶部深度由东南分别向南部、东部增加,而盖岩两端的深度在减少,使盖岩形态在空间上呈弯曲的“W”形状。根据已有的密度分布资料[16-20]可知,盖岩的密度高值位于东南方向,即图 11c中东西方向442.5~443.0km、深度方向275~425m的区域,以及图 11d中南北向3334.0~3334.5km、深度250~550m的区域。结果表明JEDGG法对高密度区域反演效果较好。一般将剩余密度大于0.15g/cm3的区域解释为盖岩。从反演结果可见,JEDGG可以反演出剩余密度为0~0.15g/cm3的异常,即盖岩外围部分,盖岩呈“南高北低”、“东高西低”的形态。因此,JEDGG反演结果进一步完善了盖岩位置的解释结果。
另外,在图 11中可见,盖岩的东部可见一处小规模的、呈块状的解,常规密度反演[16-20]中没有该显示,初步认为这是一处低剩余密度、块状或脉状的异常体的顶端。另外,在埋深0~150m范围内还存在少量零星分布的解,分析认为是结果中的干扰成分,不具实际意义。
从图 11d可见,在南北方向3334km处、深度范围0~100m的区域为盖岩西部解的投影,不能解释为盖岩整体深度范围。
综上所述,利用JEDGG反演结果可以判断文顿盐丘地下盖岩的水平范围:东西方向441.7~442.9km,南北方向3333.8~3334.8km,深度125~550m。
盖岩东部还存在一小型构造,有待在以后的勘探工作中做进一步详查。
4 结束语本文提出了多分量重力梯度数据的欧拉反褶积方法,该方法避免了构造指数的选择和分量转换,充分利用了梯度数据的高精度特点,提高了地质体空间位置的反演精度。模型数据试验证明了该方法能够较准确地识别模型位置。将该方法应用于文顿盐丘的实际数据,圈定了盖岩的范围并发现盖岩东部还存在一小规模的地质体,丰富了该区域的地下构造信息。
感谢Bell Geospace Inc提供的实测重力全张量梯度数据。
| [1] |
耿美霞, 杨庆节. 应用RBF神经网络反演二维重力密度分布[J]. 石油地球物理勘探, 2013, 48(4): 651-657. GENG Meixia, YANG Qingjie. 2-D density inversion with the RBF neural network method[J]. Oil Geophysical Prospecting, 2013, 48(4): 651-657. |
| [2] |
林宝泽, 肖锋, 王明常. 二维重力数据径向反演及应用[J]. 石油地球物理勘探, 2018, 53(2): 403-409. LIN Baoze, XIAO Feng, WANG Mingchang. 2D gra-vity data radial inversion[J]. Oil Geophysical Prospecting, 2018, 53(2): 403-409. |
| [3] |
Thompson D T. EULDPH:A new technique for ma-king computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37. DOI:10.1190/1.1441278 |
| [4] |
周文纳, 杜晓娟, 李吉焱. 重力数据的平面全张量梯度角度边界识别方法[J]. 石油地球物理勘探, 2013, 48(6): 1009-1015. ZHOU Wenna, DU Xiaojuan, LI Jiyan. Gravity data edge identification using plane full tensor gradient angle[J]. Oil Geophysical Prospecting, 2013, 48(6): 1009-1015. |
| [5] |
王彦国, 吴姿颖, 邓居智, 等. 基于幂次平均的离散归一化总梯度法[J]. 石油地球物理勘探, 2018, 53(6): 1351-1364. WANG Yanguo, WU Ziying, DENG Juzhi, et al. Discretization of normalized total gradient method based on power mean[J]. Oil Geophysical Prospecting, 2018, 53(6): 1351-1364. |
| [6] |
Zhang C, Mushayandebvu M F, Reid A B, et al. Euler deconvolution of gravity tensor gradient data[J]. Geophysics, 2000, 65(2): 512-520. DOI:10.1190/1.1444745 |
| [7] |
Ma G. Combination of horizontal gradient ratio and Euler methods for the interpretation of potential field data[J]. Geophysics, 2013, 78(5): J53-J60. DOI:10.1190/geo2012-0490.1 |
| [8] |
Ma G, Huang D, Liu C. Application of balanced edge detection filters to estimate the location parameters of the causative sources using potential field data[J]. Journal of Applied Geophysics, 2013, 99: 18-23. DOI:10.1016/j.jappgeo.2013.09.009 |
| [9] |
马国庆, 杜晓娟, 李丽丽, 等. 梯度反褶积法及其在矿产勘探中的应用[J]. 吉林大学学报:地球科学版, 2013, 43(1): 259-266. MA Guoqing, DU Xiaojuan, LI Lili, et al. Gradient deconvolution method and its application in mineral exploration[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(1): 259-266. |
| [10] |
Guo C C, Xiong S Q, Xue D J, et al. Improved Euler method for the interpretation of potential data based on the ratio of the vertical first derivative to analytic signal[J]. Applied Geophysics, 2014, 11(3): 331-339. DOI:10.1007/s11770-014-0442-4 |
| [11] |
Ma G. The application of extended Euler deconvolution method in the interpretation of potential field data[J]. Journal of Applied Geophysics, 2014, 107: 188-194. DOI:10.1016/j.jappgeo.2014.06.002 |
| [12] |
Zhou W, Nan Z, Li J. Self-constrained Euler deconvolution using potential field data of different altitudes[J]. Pure & Applied Geophysics, 2016, 173(6): 2073-2085. |
| [13] |
周文月.重力及梯度数据联合欧拉反褶积方法研究[D].吉林长春: 吉林大学, 2016.
|
| [14] |
Coker M O, Bhattacharya J P, Marfurt K J.Fracture patterns within mudstones on the flanks of a salt dome: syneresis or slumping?[C].Gulf Coast Association of Geological Societies, 2007, 57: 125-137.
|
| [15] |
Ennen C, Hall S.Structural mapping of the Vinton salt dome, Louisiana, using gravity gradiometry data[C].SEG Technical Program Expanded Abstracts, 2011, 30: 830-835.
|
| [16] |
Oliveira Jr V C, Barbosa V C F. 3-D radial gravity gradient inversion[J]. Geophysical Journal International, 2013, 195(2): 883-902. DOI:10.1093/gji/ggt307 |
| [17] |
Hou Z, Huang D, Wei X. Fast inversion of probability tomography with gravity gradiometry data based on hybrid parallel programming[J]. Journal of Applied Geophysics, 2016, 124: 27-38. DOI:10.1016/j.jappgeo.2015.11.009 |
| [18] |
Hou Z, Wei X, Huang D. Fast density inversion solution for full tensor gravity gradiometry data[J]. Pure & Applied Geophysics, 2016, 173(2): 509-523. |
| [19] |
秦朋波, 黄大年. 重力和重力梯度数据联合聚焦反演方法[J]. 地球物理学报, 2016, 59(6): 2203-2224. QIN Pengbo, HUANG Danian. Integrated gravity and gravity gradient data focusing inversion[J]. Chinese Journal of Geophysics, 2016, 59(6): 2203-2224. |
| [20] |
王浩然, 陈超, 杜劲松. 重力梯度张量数据的三维反演方法与应用[J]. 石油地球物理勘探, 2013, 48(3): 474-481. WANG Haoran, CHEN Chao, DU Jinsong. 3-D inversion of gravity gradient tensor data and its applications[J]. Oil Geophysical Prospecting, 2013, 48(3): 474-481. |



 侯振隆 辽宁省沈阳市和平区文化路三巷11号东北大学, 110819。Email:
侯振隆 辽宁省沈阳市和平区文化路三巷11号东北大学, 110819。Email: