② 中国地质调查局西安地质调查中心, 陕西西安 710054;
③ 陕西省地质调查中心, 陕西西安 710068;
④ 长庆油田第十二采油厂, 甘肃庆阳 745400
② Xi'an Center, China Geological Survey, Xi'an, Shaanxi 710054, China;
③ Shaanxi Geological Survey Center, Xi'an, Shaanxi 710068, China;
④ The 12th Oil Production Plant, Changqing Oilfield Company, PetroChina, Qingyang, Gansu 745400, China
渭河盆地位于鄂尔多斯地块南缘渭北隆起与秦岭造山带的交接部位,是鄂尔多斯地块周缘新生代裂陷体系的重要组成部分[1-2],盆地新生界沉积巨厚,达4000~7000m[3]。渭河盆地油气成藏条件研究表明,盆地前新生界存在重要的潜在烃源岩,上古生界和下古生界已经具备油气成藏基本地质条件[3-4]。因此查明渭河盆地前新生界的地层分布及残余厚度对于盆地油气勘探具有重要意义,而盆地内前寒武系变质基底深度研究尤为重要。渭河盆地仅有渭4井和XR85井钻遇前寒武系,且均位于盆地边缘[1],因此目前对盆地内变质基底深度的认识仅限于少量地震剖面[5-6]、大地电磁剖面[4, 6]及重力—大地电磁联合解释剖面[7],缺少对整个区域的变质基底起伏变化特征的综合研究。
重力勘探方法因其数据横向分辨率高、成本低、可快速获得数据的优点而在盆地构造研究中发挥了重要作用[8-9]。由于盆地沉积层密度往往小于基底密度,故在沉积盆地之上可观测到明显的重力低异常,利用该异常可反演盆地基底起伏特征[10]。Bott[11]提出了根据剩余重力异常计算二维沉积盆地基底深度的方法,其原理是逐次逼近消除剩余异常,这一方法为后来的沉积盆地重力解释奠定了基础。该方法采用常密度差,即认为盆地的沉积层与基底的密度差为常数。然而受沉积作用、压实作用、胶结作用等影响,沉积岩石的密度随埋深而增加,并且在浅部增加较快而在深部增加较慢[12]。因此Cordell[13]利用指数函数拟合沉积岩石与基底的密度差随深度的变化,该密度—深度函数被广泛应用于沉积盆地基底的正、反演[10, 14-17]。
指数密度变化函数在空间域正、反演计算时无法得到解析表达式,此外指数密度函数图像在某些深度处接近线性特征,因此Murthy等[18]提出了线性密度变化函数。之后,Rao[19]提出了二次多项式密度函数,Garciá-Abdeslem[20]提出了三次多项式密度函数,并用于盆地基底重力反演。在解释盆地基底重力异常时,Rao等[21]认为双曲线密度函数[22]和抛物线密度函数[23]与沉积层真实密度差拟合最好,随后这两种变密度函数也被引入到沉积盆地基底反演之中[24-28]。
以上六种密度变化规律均为密度只随深度的一维变化,若地表密度差处处相同,则将其用于沉积盆地重力异常解释时,其实质相当于各沉积层为水平地层。针对一维密度变化的局限性,一些学者提出了密度同时沿水平和垂直两个方向变化的二维变密度函数,并将其引入沉积盆地或其他地质体的重力反演和解释[29-32]。然而受构造作用的影响,沉积盆地内部各地层形态变化较大,并且在盆地边缘以及内部,某些构造部位常发生地层缺失的现象。因此对绝大多数沉积盆地而言,现有的这种一维和二维的密度变化规律并不能准确表达沉积层的分布特征。针对沉积盆地密度变化特征,柴玉璞等[33]提出了基底控制型和沉积充填型密度变化函数,Zhou[34]定义了一种复杂的三维密度变化函数。但以上密度规律并不一定适合构造复杂的沉积盆地重力异常解释,例如多期构造叠合盆地。解释沉积盆地重力异常,需要考虑沉积作用和构造作用的影响。虽然地层并非水平等厚分布,但同一套地层的密度在横向上变化往往不大,而各地层在垂向上的变化可用密度仅沿垂向的变化因子控制。因此,在反演盆地重力异常时,可利用沿水平方向变化的地表密度差和不同垂向变化因子组合近似盆地内部沉积岩石密度变化,提高盆地基底深度反演的准确性。
准确建立沉积层密度模型是利用重力数据反演沉积盆地基底的关键。本文以渭河盆地变质基底起伏反演为目标,根据近年来少量的实测综合地球物理剖面及物性资料,重点研究建立盆地三维密度模型的方法,以此实现渭河盆地基底深度的准确反演,旨在为该盆地油气资源评价提供资料,也为解决类似地质—地球物理问题提供新的研究思路。
1 渭河盆地区域构造背景渭河盆地南侧为北秦岭造山带,北侧与鄂尔多斯地块相连,形成于晚中生代—新生代[35]。在两大构造体系作用下产生了一系列断裂、褶皱,控制了渭河盆地的构造格局,形成了南深北浅的箕状断陷[4]。依据断裂和新生界地层发育特征,渭河盆地内部划分为西部隆起、南部坳陷和北部斜坡三个一级构造单元。其中南部坳陷包括西安凹陷、固市凹陷及骊山凸起、咸渭凸起等4个二级构造单元;北部斜坡包括合阳—韩城凸起、蒲城—富平浅凹及乾县斜坡等3个二级构造单元[3, 36-37]。
渭河盆地基底以渭河断裂为界分为南北两区,北部基底为中—上元古界、下古生界的加里东构造层和残留的上古生界、中生界燕山构造层的沉积岩;南部基底主要是由太古界、元古界变质岩和加里东期—燕山期的花岗岩组成,以长安—临潼断裂为界南部基底可进一步划分为东部太古界变质岩区和西部元古界变质岩区[35, 38]。
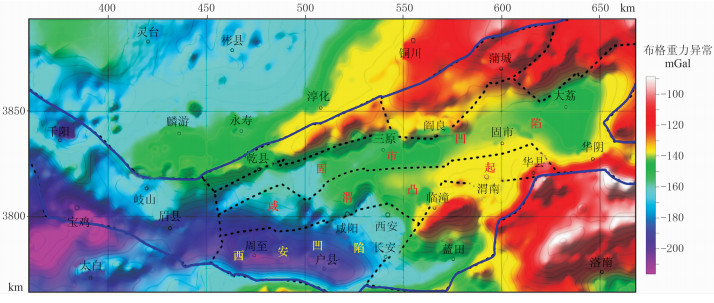
2 渭河盆地地球物理特征 2.1 重力场特征渭河盆地布格重力异常(图 1)在西安—宝鸡之间整体呈近EW向,西安以东呈NEE向。盆地内重力异常具有明显的分区性,北部由西向东大体由乾县—蒲城一线为NEE向展布的斜坡状重力高,异常值为-140~-100mGal;该斜坡状重力高之南为NEE走向的重力低值带,分别在三原、大荔形成重力低圈闭,异常值为-130~-160mGal,其与固市凹陷对应;盆地东南部为明显重力高值带,异常幅值大于30mGal,与骊山凸起对应,主要由太古界变质岩引起;盆地南部周至—西安一线为近EW向重力低值带,异常值为-140~-200mGal,与西安凹陷对应;盆地西部宝鸡—眉县为平缓重力低,异常值为-180~-200mGal。
|
图 1 渭河盆地及邻区布格重力异常图 |
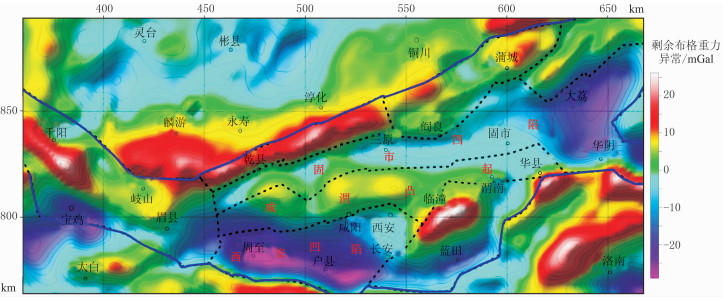
布格重力异常是地下所有密度不均匀体的综合反映,可分解为剩余重力异常和区域重力异常。一般而言,剩余重力异常反映浅层局部密度不均匀体(如盆地基底的隆坳)的特征,而区域重力异常反映较深层的构造特征(如莫霍面的起伏)。利用多次迭代滑动趋势分析方法[39]选用不同窗口大小和趋势面阶次进行计算,并与综合地球物理剖面等资料揭示的盆地构造进行对比,得到了能较好地反映渭河盆地构造的剩余布格重力异常(图 2)。
|
图 2 渭河盆地及邻区剩余布格重力异常图 |
由图 2可见,渭河盆地自南向北剩余布格重力高与异常低成带相间分布,呈两低一高的特征。重力高和重力低的平面形态为长条状,EW向长,NS向短。周至—西安一带的重力低呈近EW向,而三原—大荔一线的重力低大体呈NEE向。图 2清晰地反映了盆地构造单元形态,尤其两个明显的重力低值区揭示了西安凹陷和固市凹陷的范围,其中西安凹陷的重力最低值为-28mGal,而固市凹陷的重力值最小为-21mGal,二者之间以咸渭凸起分隔。
盆地沉积层的密度往往小于基底的密度,因此,重力异常的分布可反映基底起伏特征。仅从重力场特征来看,渭河盆地在南部周至—西安一带盖层厚度大,而三原—大荔一带盖层厚度稍小,即西安凹陷基底深度大,固市凹陷基底相对稍浅。然而综合地球物理剖面解释结果表明,西安凹陷基底深度接近8km[6],而固市凹陷基底深度最大超过9km[7]。显然这一特征与重力异常特征不符,其原因可能是同一套地层在两个凹陷内地层密度存在差异,也有可能是同一套地层厚度变化较大。
2.2 密度特征根据渭河盆地内地震波速—密度转换结果,结合前人研究成果[6-7],得到渭河盆地内西安凹陷和固市凹陷内各地层密度特征(表 1)。
|
|
表 1 渭河盆地不同凹陷内各地层密度统计表 |
从表 1可知,由于压实作用,研究区各时代地层自新到老密度逐渐增大。此外,西安凹陷和固市凹陷中同一套地层的密度存在差异。总体而言,西安凹陷各沉积层与基底的密度差大于固市凹陷沉积层与基底的密度差。这一密度变化特征可能会引起固市凹陷的重力异常小于西安凹陷的现象。渭河盆地各构造单元内地层密度存在较大差异,显然常密度重力反演不能准确刻画盆地前寒武系基底起伏特征,必须建立沉积层三维密度模型以较准确地反演盆地基底深度。
3 盆地基底三维变密度反演 3.1 密度差—深度函数仅考虑沉积层与基底的密度差随深度变化时,密度差—深度变化可归纳为以下四种函数表达式。
(1) 多项式密度差—深度函数
| $ \Delta \rho (z) = \Delta {\rho _0} + \sum\limits_{k = 1}^K {{a_k}} {z^k} $ | (1) |
式中:Δρ表示密度差;Δρ0为地表密度差;z为深度;k为多项式阶次;ak为多项式系数,即密度随深度变化因子。当k取1、2、3时,分别对应于线性(LDF)、二次(QDF)、三次(CDF)密度差—深度变化函数。
(2) 指数密度差—深度函数(EDF)
| $ \Delta \rho (z) = \Delta {\rho _0}{{\rm{e}}^{ - \lambda z}} $ | (2) |
(3) 双曲线密度差—深度函数(HDF)
| $ \Delta \rho (z) = \Delta {\rho _0}\frac{{{\beta ^2}}}{{{{(z + \beta )}^2}}} $ | (3) |
(4) 抛物线密度差—深度函数(PDF)
| $ \Delta \rho (z) = \frac{{\Delta \rho _0^3}}{{{{\left( {\Delta {\rho _0} - \alpha z} \right)}^2}}} $ | (4) |
式(2)~式(4)中,λ、β和α分别是相应函数中密度差随深度的变化因子。
利用以上密度差—深度函数时,需要确定密度差随深度变化因子。对于多项式密度差—深度变化函数(式1),可根据已知的深度—密度差数据,利用最小二乘方法拟合得到密度差随深度变化因子。对于式(2)的指数密度差—深度函数,该式两端分别取对数,可得
| $ \ln \Delta \rho (z) = \ln \Delta {\rho _0} - \lambda z $ | (5) |
上式为线性表达式,可利用最小二乘方法拟合得到λ。
对于HDF(式(3))和PDF(式(4)),可利用等效密度差[22]的方法分别得到密度随深度的变化因子β和α。Litinsky[22]给出了式(3)中β的表达式
| $ \beta = \frac{{\Delta \bar \rho H}}{{\Delta {\rho _0} - \Delta \bar \rho }} $ | (6) |
利用等效密度差方法推导出式(4)中α的表达式为
| $ \alpha = \frac{{\Delta \bar \rho \Delta {\rho _0} - \Delta \rho _0^2}}{{H\Delta \bar \rho }} $ | (7) |
式(6)和式(7)中:Δρ为根据盆地内各沉积层与基底的密度差Δρi和厚度hi计算的加权平均密度差,即沉积层等效密度差;H为沉积层总厚度。
若已知某处地下各地层的厚度及其密度差,则可利用以上各式拟合该处密度差随深度变化的函数。
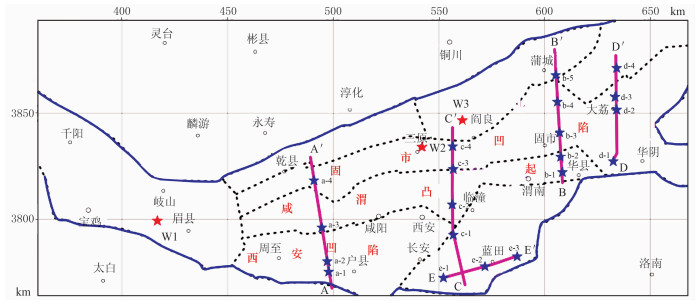
3.2 渭河盆地三维变密度模型研究密度变化规律时,钻井资料最有效,然而研究区仅有2口井钻遇了基底,且其均位于盆地边部,仅有3口井钻穿了新生界,因此主要根据2013年采集的2条重、磁、电、震综合剖面(位置见图 3中AA′和BB′)及2016年采集的3条重、电综合剖面(位置见图 3中CC′、DD′、EE′)并结合3口钻井建立盆地三维密度变化模型,2条重、磁、电、震剖面综合解释结果见图 4a和图 4b,3条重、电剖面综合解释结果见图 4c~图 4e。
|
图 3 渭河盆地地球物理剖面位置图 |

|
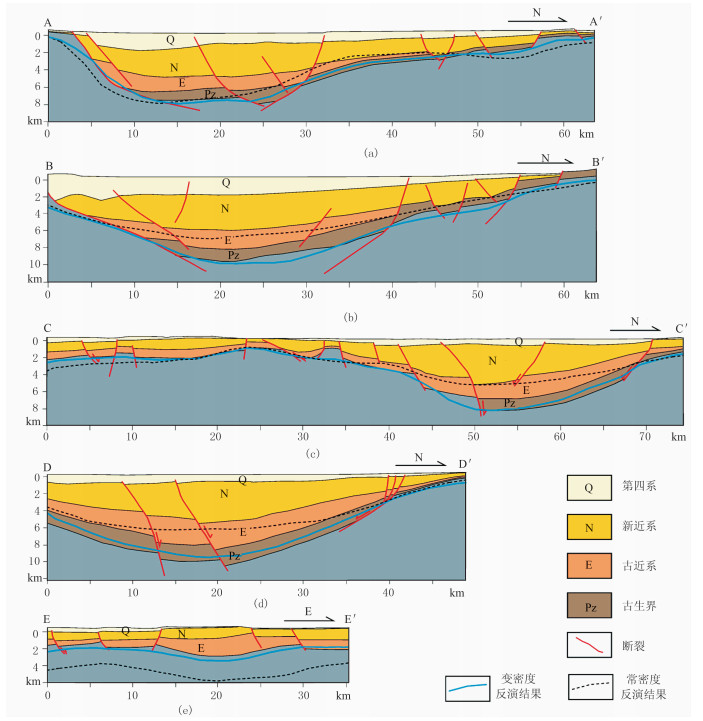
图 4 渭河盆地综合地球物理剖面解释结果 (a)AA′剖面;(b)BB′剖面;(c)CC′剖面;(d)DD′剖面;(e)EE′剖面 |
在这5条剖面上共选取了20个已知深度点(图 3中蓝色五角星所示)及3口钻井(图 3中红色五角星)共计23个已知深度点,利用综合剖面和钻井显示的深度点处各地层厚度和表 1中两个凹陷的各地层密度作为已知数据,利用式(1)~式(4)的密度差—深度函数分别在23个深度点处拟合6种密度差—深度函数,并统计其拟合误差(表 2)。三口钻井分层信息见表 3。
|
|
表 2 渭河盆地23个密度差—深度点不同变密度差函数拟合误差统计表 |
|
|
表 3 渭河盆地钻井分层底深统计表 |
表 2中拟合误差由沿深度选取若干个点并计算其实际密度与拟合密度的均方差而得。由表 2和表 3可见,当相邻各层密度差别不大且各层厚度差别不大时,拟合误差相对较小;反之,若相邻各层密度差别较大且厚度差较大时,拟合误差往往较大。这3口井所钻遇的地层厚度较小,并且缺失某些地层,造成上下相邻地层密度差较大,因此表 2中钻井处的拟合误差稍大。
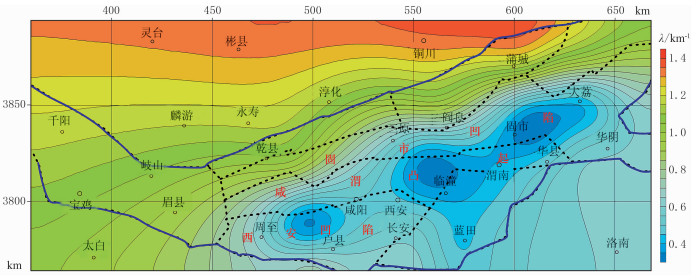
由表 2可以看出,不同点处的密度差—深度函数的拟合误差不尽相同,整体而言指数密度差—深度函数拟合误差最小。因此本文采用指数密度差—深度函数建立三维变密度差模型,提取此23个密度差—深度点处指数变密度差函数中的密度差随深度变化因子λ以及地表密度差Δρ0,再对数据网格化,得到了整个研究区的λ(图 5)和Δρ0(图 6)。利用各点的λ和Δρ0的组合,即得到了研究区的三维变密度差模型(图 7)。
|
图 5 渭河盆地及邻区网格化的密度差随深度的变化因子λ |
|
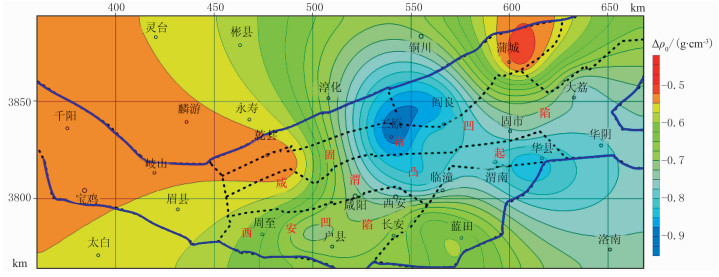
图 6 渭河盆地及邻区网格化的地表密度差Δρ0 |
利用重力异常反演沉积盆地基底时,Bott[11]提出的方法因其不涉及矩阵计算而效率较高[40]。变密度模式反演的迭代公式为

|
图 7 渭河盆地及邻区三维密度差模型 |
| $ \begin{array}{*{20}{l}} {{p^{(k)}}\left( {{x_i},{y_i}} \right) = {p^{(k - 1)}}\left( {{x_i},{y_i}} \right) + }&{}\\ {\frac{{{g^{{\rm{obs}}}}\left( {{x_i},{y_i}} \right) - {g^{{\rm{cal}}}}\left( {{x_i},{y_i}} \right)}}{{2\pi G\Delta \rho \left( {{x_i},{y_i},z} \right)}}}&{i = 1,2, \cdots ,N} \end{array} $ | (8) |
式中:G为万有引力常量;p(k)(xi, yi)和p(k-1)(xi, yi)分别为第i个计算点处第k次和第k-1次的反演结果;Δρ(xi, yi, z)为第i个计算点处的密度差,其值沿深度z变化,可用式(1)~式(4)的某一种形式表示;gobs(xi, yi)和gcal(xi, yi)分别为第i个点处实测的重力异常和第k次迭代时该点的正演重力异常。计算重力异常时将盆地基底之上的沉积层剖分为垂直并置的棱柱体,棱柱体位于重力计算点正下方,其个数与计算点数相同,水平尺寸与计算点间距一致,计算公式为
| $ {g^{{\rm{cal}}}}\left( {{x_i},{y_i}} \right) = \sum\limits_{j = 1}^N {{f_i}} \left( {{p_j}} \right) $ | (9) |
式中非线性函数fi(pj)表示第j个棱柱体在第i点处引起的重力异常,其表达式为
| $ \begin{array}{l} {f_i}\left( {{p_j}} \right) = G\int_{{\varepsilon _{{j_1}}}}^{{\xi _{{j_2}}}} {\int_{{\eta _{{j_1}}}}^{{\eta _{{j_2}}}} {\int_{{\zeta _1}}^{{\zeta _{{j_2}}}} \Delta } } \rho \left( {{x_i},{y_i},z} \right) \times \\ \frac{{{\zeta _j} - {z_i}}}{{{{\left[ {{{\left( {{\xi _j} - {x_i}} \right)}^2} + {{\left( {{\eta _j} - {y_i}} \right)}^2} + {{\left( {{\zeta _j} - {z_i}} \right)}^2}} \right]}^{\frac{3}{2}}}}}{\rm{d}}{\xi _j}{\rm{d}}{\eta _j}{\rm{d}}{\zeta _j} \end{array} $ | (10) |
式中:(ξj, ηj, ζj)为剖分的棱柱体内任一点的坐标;ξj1~ξj2、ηj1~ηj2、ζj1~ζj2分别为第j个棱柱体在x、y、z方向的坐标范围。
式(8)通过令p (0)=0开始迭代过程,并设定当gobs(xi, yi)与gcal(xi, yi)的均方差小于重力数据的噪声时终止迭代。
根据建立的密度模型及渭河盆地及邻区剩余布格重力异常数据,利用式(8)反演得到渭河盆地前寒武系基底深度(图 8),重力异常拟合误差如图 9所示。最大误差小于6.000mGal,均方差为0.871mGal,大部分区域拟合误差接近0。渭河盆地北部为隆起区,南部为坳陷区,反演结果清晰地显示了西安凹陷与固市凹陷的特征。西安凹陷基底深度主体为3.0~8.0km,深度最大处位于周至附近,约为8.5km。从基底形态来看,凹陷的沉积中心偏南,呈南深北浅的特征。固市凹陷基底深度主体为3.0~10.5km,基底自西向东深度增大,凹陷西部仅3.0~4.0km,而中部的三原—固市一带深度为4.0~8.0km,最深处在东部的大荔附近,基底深度超过10.0km。

|
图 8 渭河盆地前寒武系基底顶面三维变密度反演结果 |
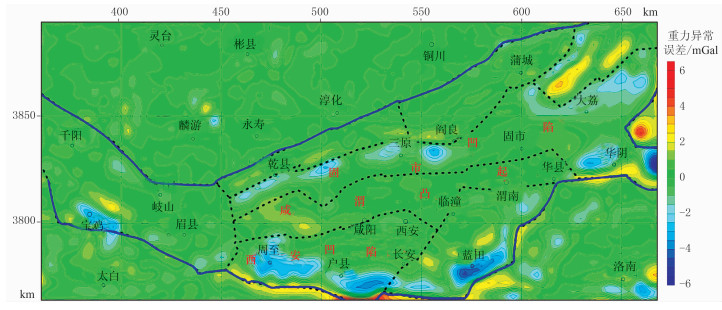
|
图 9 渭河盆地前寒武系基底变密度反演拟合重力异常误差 |
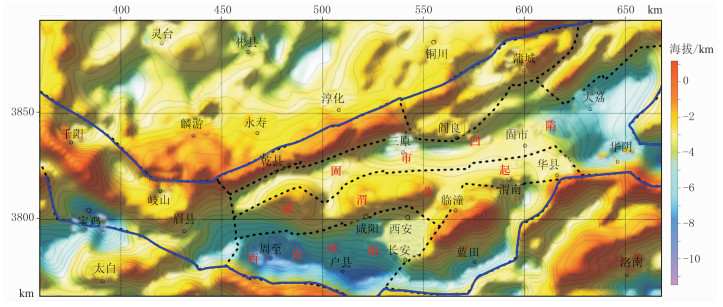
为了验证三维密度变化模型的合理性及有效性,本文亦对渭河盆地进行了常密度反演。反演之前首先计算沉积层与基底的等效密度差,同一套地层的密度值取两个凹陷的平均值,得到整个沉积层与基底的等效密度差为-0.304g/cm3,反演得到基底深度如图 10所示,正演拟合重力异常与观测数据(文中未展示)吻合较好。常密度反演结果中,西安凹陷基底深度主体为3.0~8.0km,深度最大处位于周至附近,这与图 8中的深度特征基本一致。固市凹陷基底深度为3.0~6.3km,其西部与中部深度几乎相同,均小于4.5km,而最深的大荔附近基底深度仅有6.3km。显然,常密度反演的固市凹陷基底浅于西安凹陷基底,这与目前基本的地质、地球物理认识不一致,而三维变密度反演结果更符合实际特征。
|
图 10 渭河盆地前寒武系基底顶面常密度反演结果 |
图 10的常密度反演结果中,蓝田附近的基底深度与变密度反演结果差别较大。常密度反演的基底最大深度接近6.0km,而综合剖面解释结果(图 4e)显示这一区域基底最大深度约为3.0km,变密度反演结果为3.0~3.6km,显然更符合实际特征。另外,从基底起伏形态来看,变密度反演结果中西安凹陷的东部边界在临潼至长安一带,而其东侧的临潼、蓝田一带为凸起区。然而常密度反演结果中西安凹陷与其东侧的蓝田一带并无明显界限,这与目前对于构造单元的认识不符[1-3]。
为进一步对比变密度反演效果,沿图 4中的5条剖面分别提取了三维变密度和等效常密度的反演结果(图 11)。结果显示变密度反演的基底起伏形态与综合剖面基本一致,仅在局部位置(如断裂附近)差别稍大,其原因是Bott提出的反演方法仅利用重力异常反演,结果为光滑的密度界面,而断裂附近的基底呈现非光滑形态。若利用非光滑形态密度界面反演方法[26-27],结果可能会更好一些,但本文主要针对密度变化规律进行研究,故没有进一步对此进行讨论。总体而言,若能建立合理的密度变化函数,则三维变密度反演结果明显优于常密度反演。
|
图 11 渭河盆地前寒武系基底三维变密度与等效常密度反演结果剖面对比 (a)AA′剖面;(b)BB′剖面;(c)CC′剖面;(d)DD′剖面;(e)EE′剖面 |
本文根据渭河盆地少量钻井、实测综合地球物理剖面及收集的物性资料建立了三维变密度模型,反演了渭河盆地变质基底深度。该方法考虑了盆地沉积层密度横向和纵向的变化,与常密度模式相比,反演结果更为准确。然而,用于建立变密度模型的不同先验资料的精度和准确度不同,会在一定程度上影响反演结果。
一般而言,钻井数据准确度最高,其次为综合解释剖面以及地震资料。因此,在建立变密度模型时或可考虑不同资料的权重。然而实际中很难衡量不同资料的精度(尤其是综合解释的成果),故很难根据资料的精度分配不同来源数据的权重。本文在不同深度点处利用6种密度差—深度函数进行拟合,选择全区拟合误差较小的函数,分别提取不同点处拟合的密度差—深度函数中的地表密度差和密度差随深度的变化因子,然后插值得到全区的地表密度差和密度差随深度的变化因子,即利用沿水平变化的地表密度差和不同点处变化的因子组合得到三维密度变化。即使能给定不同资料的权重,但权重大小很难融合于插值过程,当然若能研究出带权重的插值方法,这一问题或可解决。
5 结论利用重力资料开展了渭河盆地前寒武系基底深度反演,得到了渭河盆地变质基底起伏形态。由于渭河盆地不同构造单元内同一套地层密度存在差异,并且各地层厚度变化也较大,因此采用统一的密度差不能较准确地反演盆地基底。以渭河盆地内2条重、磁、电、震综合剖面和3条重、电剖面的综合解释结果为主,结合不同构造单元内各地层密度,建立了渭河盆地及邻区三维变密度模型,进而反演得到了盆地前寒武系变质基底深度。反演结果显示本文建立的三维密度变化模型是合理的,可应用于渭河盆地基底深度反演,其结果能为盆地油气勘探提供基础数据支撑。
| [1] |
王建强, 刘池洋, 高飞, 等. 陕西渭河盆地前新生界地质特征及其油气地质意义[J]. 地质通报, 2015, 34(10): 1981-1991. WANG Jianqiang, LIU Chiyang, GAO Fei, et al. Pre-Cenozoic geological characteristics and oil-gas significance in Weihe basin, Shaanxi Province[J]. Geological Bulletin of China, 2015, 34(10): 1981-1991. DOI:10.3969/j.issn.1671-2552.2015.10.024 |
| [2] |
李智超, 李文厚, 李永项, 等. 渭河盆地新生代沉积相研究[J]. 古地理学报, 2015, 17(4): 529-540. LI Zhichao, LI Wenhou, LI Yongxiang, et al. Sedimentary facies of the Cenozoic in Weihe Basin[J]. Journal of Palaeogeography, 2015, 17(4): 529-540. |
| [3] |
刘志武, 白勇, 周立发. 渭河盆地结构及其油气成藏地质条件[J]. 石油实验地质, 2016, 38(5): 584-591. LIU Zhiwu, BAI Yong, ZHOU Lifa. Basin structure and hydrocarbon accumulation conditions of the Weihe Basin[J]. Petroleum Geology & Experiment, 2016, 38(5): 584-591. |
| [4] |
王宏伟, 刘宝宪, 马占荣, 等. 渭河盆地前新生界分布的物探特征及油气成藏条件分析[J]. 地球物理学进展, 2010, 25(4): 1280-1287. WANG Hongwei, LIU Baoxian, MA Zhanrong, et al. Analysis of distribution of geophysical characteristics and reservoir-forming conditions in the pre-Cenozoic strata in the Weihe basin[J]. Progress in Geophysics, 2010, 25(4): 1280-1287. DOI:10.3969/j.issn.1004-2903.2010.04.016 |
| [5] |
任隽, 冯希杰, 王夫运, 等. 深反射地震剖面揭示的渭河盆地西安坳陷的地壳精细结构[J]. 地球物理学报, 2013, 56(2): 513-521. REN Juan, FENG Xijie, WANG Fuyun, et al. Fine crust structures of Xi'an sag in the Weihe basin revealed by a deep seismic reflection profile[J]. Chinese Journal of Geophysics, 2013, 56(2): 513-521. |
| [6] |
周少伟, 江桂, 谷开拓, 等. 大地电磁测深在西安凹陷基底探测中的应用[J]. 地球物理学进展, 2017, 32(5): 2274-2280. ZHOU Shaowei, JIANG Gui, GU Kaituo, et al. Application in the detection of basement of magnetotelluric sounding in Xi'an sag[J]. Progress in Geophysics, 2017, 32(5): 2274-2280. |
| [7] |
Shi Y, Hu Z, Huang W, et al. The distribution of deep source rocks in the GS sag:Joint MT-gravity modeling and constrained inversion[J]. Applied Geophy-sics, 2016, 13(3): 469-479. DOI:10.1007/s11770-016-0574-9 |
| [8] |
熊盛青, 丁燕云, 李占奎. 西藏羌塘盆地的重磁场特征及地质意义[J]. 石油地球物理勘探, 2013, 48(6): 999-1008. XIONG Shengqing, DING Yanyun, LI Zhankui. Gravity and magnetic field characteristics and their geolo-gical significance in the Qiangtang Basin, China[J]. Oil Geophysical Prospecting, 2013, 48(6): 999-1008. |
| [9] |
郭伟, 姚长利, 王亚民, 等. 重磁综合约束反演在大杨树盆地油气勘探中的应用[J]. 石油地球物理勘探, 2014, 49(增刊1): 233-242. GUO Wei, YAO Changli, WANG Yamin, et al. Comprehensive constrained inversion of gravity and magnetic in reservoir exploration in Dayangshu Basin[J]. Oil Geophysical Prospecting, 2014, 49(S1): 233-242. |
| [10] |
Chakravarthi V, Sastry S R, Ramamma B. MODTOHAFSD-A GUI based JAVA code for gravity analysis of strike limited sedimentary basins by means of growing bodies with exponential density contrast-depth variation:A space domain approach[J]. Computers & Geosciences, 2013, 56(56): 131-141. |
| [11] |
Bott M P H. The use of rapid digital computing me-thods for direct gravity interpretation of sedimentary basins[J]. Geophysical Journal of the Royal Astronomical Society, 1960, 3(1): 63-67. DOI:10.1111/gji.1960.3.issue-1 |
| [12] |
Athy L F. Density, porosity, and compaction of sedimentary rocks[J]. AAPG Bulletin, 1930, 14(1): 1-24. |
| [13] |
Cordell L. Gravity anomalies using an exponential density-depth function-San Jacinto graben, California[J]. Geophysics, 1973, 38(4): 684-690. DOI:10.1190/1.1440367 |
| [14] |
Granser H. Three-dimensional interpretation of gravity data from sedimentary basins using an exponential density-depth function[J]. Geophysical Prospecting, 1987, 35(9): 1030-1041. DOI:10.1111/gpr.1987.35.issue-9 |
| [15] |
Chai Y, Hinze W J. Gravity inversion of an interface above density contrast varies exponentially with depth[J]. Geophysics, 1988, 53(6): 837-845. DOI:10.1190/1.1442518 |
| [16] |
Cai H, Zhdanov M. Application of Cauchy-type inte-grals in developing effective methods for depth-to-basement inversion of gravity and gravity gradiometry data[J]. Geophysics, 2015, 80(2): G81-G94. DOI:10.1190/geo2014-0332.1 |
| [17] |
Chakravarthi V, Kumar M P, Ramamma B, et al. Automatic gravity modeling of sedimentary basins by means of polygonal source geometry and exponential density contrast variation:Two space domain based algorithms[J]. Journal of Applied Geophysics, 2016, 124: 54-61. DOI:10.1016/j.jappgeo.2015.11.007 |
| [18] |
Murthy I V R, Rao D B. Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth[J]. Geophysics, 1979, 44(9): 1525-1530. DOI:10.1190/1.1441023 |
| [19] |
Rao D B. Modelling of sedimentary basins from gravity anomalies with variable density contrast[J]. Geophysical Journal of the Royal Astronomical Society, 1986, 29(1): 207-212. |
| [20] |
Garciá-Abdeslem J. 2D modeling and inversion of gravity data using density contrast varying with depth and source-basement geometry described by the Fourier series[J]. Geophysics, 2003, 68(6): 1909-1916. DOI:10.1190/1.1635044 |
| [21] |
Rao C V, Chakravarthi V, Raju M L. Forward modeling:Gravity anomalies of two-dimensional bodies of arbitrary shape with hyperbolic and parabolic density functions[J]. Computers & Geosciences, 1994, 20(5): 873-880. |
| [22] |
Litinsky V A. Concept of effective density:Key to gravity depth determinations for sedimentary basins[J]. Geophysics, 1989, 54(11): 1474-1482. DOI:10.1190/1.1442611 |
| [23] |
Rao C V, Chakravarthi V, Raju M L. Parabolic density function in sedimentary basin modelling[J]. Pure & Applied Geophysics, 1993, 140(3): 493-501. |
| [24] |
Sari C, Salk M. Analysis of gravity anomalies with hyperbolic density contrast:An application to the gravity data of Western Anatolia[J]. Journal of the Balkan Geophysical Society, 2002, 5(3): 87-96. |
| [25] |
Silva J B C, Costa D C L, Barbosa V C F. Gravity inversion of basement relief and estimation of density contrast variation with depth[J]. Geophysics, 2006, 71(5): J51-J58. DOI:10.1190/1.2236383 |
| [26] |
Martins C M, Lima W A, Barbosa V C F, et al. Total variation regularization for depth-to-basement estimate:Part 1:Mathematical details and applications[J]. Geophysics, 2011, 76(1): I1-I12. |
| [27] |
冯旭亮, 王万银, 刘富强, 等. 裂陷盆地基底双界面模式二维重力反演[J]. 地球物理学报, 2014, 57(6): 1934-1945. FENG Xuliang, WANG Wanyin, LIU Fuqiang, et al. 2D gravity inversion of basement relief of rift basin based on a dual interface model[J]. Chinese Journal of Geophysics, 2014, 57(6): 1934-1945. |
| [28] |
商宇航, 邰振华, 秦涛. 基于双曲线密度模型的频率域界面反演[J]. 石油地球物理勘探, 2018, 53(4): 858-864. SHANG Yuhang, TAI Zhenhua, QIN Tao. Interface inversion in the frequency domain based on the hyperbolic density model[J]. Oil Geophysical Prospecting, 2018, 53(4): 858-864. |
| [29] |
Zhou X. General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast[J]. Geophysics, 2009, 74(2): I1-I7. DOI:10.1190/1.3073761 |
| [30] |
Zhou X. Analytic solution of the gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function[J]. Geophysics, 2010, 75(2): I11-I19. DOI:10.1190/1.3294699 |
| [31] |
Zhou X. Gravity inversion of 2D bedrock topography for heterogeneous sedimentary basins based on line integral and maximum difference reduction methods[J]. Geophysical Prospecting, 2013, 61(1): 220-234. DOI:10.1111/gpr.2013.61.issue-1 |
| [32] |
D'Urso M G. The gravity anomaly of a 2D polygonal body having density contrast given by polynomial functions[J]. Surveys in Geophysics, 2015, 36(3): 391-425. DOI:10.1007/s10712-015-9317-3 |
| [33] |
柴玉璞, 贾继军. Parker公式的一系列推广及其在石油重力勘探中的应用前景[J]. 石油地球物理勘探, 1990, 25(3): 321-332. CHAI Yupu, JIA Jijun. Parker's formulas in different forms and their applications to oil gravity survey[J]. Oil Geophysical Prospecting, 1990, 25(3): 321-332. |
| [34] |
Zhou X. 3D vector gravity potential and line integrals for the gravity anomaly of a rectangular prism with 3D variable density contrast[J]. Geophysics, 2009, 74(6): I43-I53. DOI:10.1190/1.3239518 |
| [35] |
张朝锋.渭河地堑的形成演化及其动力学机制[D].陕西西安: 西北大学, 2011. ZHANG Chaofeng. Evolution and Dynamics Mechanism of Weihe Graben[D].Northwest University, Xi'an, Shaanxi, 2011. |
| [36] |
权新昌. 渭河盆地断裂构造研究[J]. 中国煤田地质, 2005, 17(3): 1-4. QUAN Xinchang. Weihe basin faulted structure study[J]. Coal Geology of China, 2005, 17(3): 1-4. DOI:10.3969/j.issn.1674-1803.2005.03.001 |
| [37] |
许炳如. 渭河盆地区域和剩余重力图的初步解释[J]. 西安石油学院学报, 1990, 5(4): 9-15. XU Bingru. A preliminary interpretation on the regional and residual gravity maps of the Weihe basin[J]. Journal of Xi'an Petroleum Institute, 1990, 5(4): 9-15. |
| [38] |
王建强.鄂尔多斯盆地南部中新生代演化-改造及盆山耦合关系[D].陕西西安: 西北大学, 2010. WANG Jianqiang. Mesozoic-Cenozoic Basin Evolution-reforming and Basin-mountain Coupling in Sou-thern Ordos Basin[D].Northwest University, Xi'an, Shaanxi, 2010. |
| [39] |
刘申叔, 李上卿. 东海油气地球物理勘探[M]. 北京: 地质出版社, 2001.
|
| [40] |
Silva J B C, Santos D F, Gomes K P. Fast gravity inversion of basement relief[J]. Geophysics, 2014, 79(5): G79-G91. DOI:10.1190/geo2014-0024.1 |



 冯旭亮 陕西省西安市雁塔区电子二路东段18号西安石油大学地球科学与工程学院, 710065。Email:
冯旭亮 陕西省西安市雁塔区电子二路东段18号西安石油大学地球科学与工程学院, 710065。Email: 