饱和多孔介质(例如土壤、岩石)的电输运性质受孔隙空间的非导电固体基质和孔隙间充填的流体影响很大,相关研究成果在油藏工程与岩石物理学领域已经得到广泛应用[1]。沉积岩的电导率与孔隙形状、分布以及地层水电导率有很大关系,测量结果的解释有赖于对岩石导电机制的认识。常规理论模型假设仅存在一种导电组分(例如孔隙水),进而研究孔隙流体电导率、孔隙度、饱和度以及孔隙结构对岩石整体电导率的影响。以往的大部分研究多侧重于经验层面,或者是理论研究与经验公式的组合。其中最广泛应用于电阻率测井解释以及储层评价的岩石物理关系是Archie公式[2],它反映了骨架不含导电矿物成分情况下岩石电导率与孔隙度以及孔隙微观几何结构之间的关系。岩石的导电性不仅与泥质的附加导电性有关,还受到孔隙形状、尺寸以及分布的影响。Wyllie等[3]使用弯曲毛细管模型解释电流在复杂孔隙空间中的流动路径,将单位体积岩石的孔隙空间等效为一个相等直径的曲折毛细管,其体积等于孔隙空间,毛细管电导率等于岩石电导率。这种方法的缺点是没有考虑岩石孔隙直径大小的变化以及孔隙呈现复杂网络状的特征。Winsauer[4]提出地层因素可以表示为曲折度、导电电解质的表观横截面积与岩石所含电解质总横截面积之比的函数。该方法通过测量一定电位梯度下通过水相介质的离子传输时间确定完全盐水饱和砂岩的曲折度。在此基础上,Perkins等[5]通过实验研究了含有水和油的砂岩样品的水相的曲折度、饱和度、电导率与岩石整体电导率之间的关系。
Mandelbrot[6]首次提出分形概念并建立分形几何理论,用以解释自然界中不规则且具有高度复杂结构的现象。分形是具有非整数Hausdorff维数的集合,这些具有严格的或统计自相似性的附加属性的集合已被广泛用于模拟各种物理现象[7]。分形的维数称为分数维,是对分形几何复杂程度的定量表征,也是分形理论的基本参数。在分子尺度大小和微观范围内,包括天然岩石在内的大多数材料的表面都显示出不规则性和缺陷,在分辨率变化时,表现出自相似性。规则物体的测量结果与测量所选用的尺度无关,但用不同尺度测量具有分形特征的物体时,结果会有所不同。现有资料表明,天然多孔介质和部分人工制造的多孔介质的微观结构具有分形特征。目前,分形理论已在石油天然气行业取得了许多应用成果,例如识别沉积旋回[8]、表征油藏储层的孔隙结构[9]、渗透率[10]、岩性划分[11]、地震记录的分形结构[12]、裂缝形态分布[13-15]等。分形模型与传统模型的不同之处在于可以直接描述或通过实验验证岩石的微观结构。Katz等[16]和Krohn等[17]以岩心扫描电镜二维图像为基础,分析了砂岩、页岩和碳酸盐岩的孔隙结构。除此之外,还有其他实验方法可以进行岩石分形特征的研究,例如中子散射和X射线散射。Roy等[18]利用粒子扩散理论,推导出电导率与孔隙度之间存在一种指数关系。Nigmatullin[19]利用分形理论与毛细管束模型,推导出岩石电导率与孔隙度的关系。类似地,Wei等[20]通过研究得到了岩石整体电导率的分形表达式。
岩石的孔隙结构十分复杂,即使通过实验也无法准确描述岩石的微观结构及流体分布。学者们从不同方面对岩石电导率进行研究,取得了对岩石微观孔隙结构与电导率之间关系的认识与理解。本文从分形理论出发,建立了一种适用于研究区储层含水饱和度评价的导电模型,以提高该地区储层含水饱和度的解释准确度。
1 方法原理点、曲线、曲面和立方体的分形维数可用欧几里得几何方法描述,其分形维数分别为0、1、2和3。与每个维度相关联的是对相应物体的度量,例如线的长度、曲面的面积和立方体的体积。然而,自然界中的许多物体并不符合欧几里得描述特征,因为它们的长度、面积或体积与度量的尺度有关。分形物体的度量M(L)与测量尺度L满足标度关系[21]
| $ M\left( L \right) \sim {L^{{D_{\rm{f}}}}} $ | (1) |
式中Df是与分形过程相关的常数。对天然多孔介质的研究表明,孔隙系统具有分形性质。对于这样的复合系统,很明显,“微观”长度的尺度远小于宏观物体的尺寸,但远大于其组成分子的尺寸。
在完全破碎的分形多孔介质中,粒度确定了分形尺度的上限与下限,Rieu等[22]提出孔隙度Φ可以根据粒度定义为
| $ \mathit{\Phi } = 1 - {\left( {\frac{{{R_{\max }}}}{{{R_{\min }}}}} \right)^{3 - {D_{\rm{f}}}}} $ | (2) |
进而,孔隙分形维数Df可表示为
| $ {D_{\rm{f}}} = 3 - \frac{{\ln \left( {1 - \mathit{\Phi }} \right)}}{{\ln \frac{{{R_{\max }}}}{{{R_{\min }}}}}} $ | (3) |
式中Rmax和Rmin分别表示最大和最小粒径。将多孔介质简化为一簇变截面毛细管组成的毛细管束,则毛细管的直径λ与多孔介质的测量长度L0满足[23]
| $ L\left( \lambda \right) = {\lambda ^{1 - {D_T}}}L_0^{{D_T}} $ | (4) |
式中:L(λ)是弯曲毛细管的长度;DT是毛细管曲折度T的分形维数,对于二维和三维空间,其取值范围分别是1≤DT<2和1≤DT<3。当DT=1时,对应于直毛细管;1<DT<3表示曲折毛细管部分填充于欧几里得空间;DT=3则表示完全填充三维空间[20]。式(4)清楚地表明弯曲程度随着毛细管曲折度分形维数的增加而增加。
曲折度可以用电流必须经由的路径长度Le定义。因为电流的流动取决于岩石的孔隙结构与分布、润湿性和含水饱和度,所以相同含水饱和度时的曲折度并不是唯一的,它还与介质的分形特征有关。实际上,考虑分形特征的岩石导电性质的数学推导并不易实现。为了解决这个问题,可以采用一种简化方法,即含水饱和度Sw为1.0时的曲折度表示为
| $ T = \frac{{{L_{\rm{e}}}}}{{{L_0}}} $ | (5) |
Wyllie等[3, 24]将毛细管截面积Ae在不同的情况下分别表示为ΦA或Φ2A(其中A是样品的截面积);Cornell等[25]认为Ae=ΦAL0/Le;Abdassah等[26]考虑不同润湿性的影响,提出
| $ {A_{\rm{e}}} = A\mathit{\Phi }{S_{\rm{w}}}P/T $ | (6) |
式中P为导电连通的概率,其大小取决于岩石的润湿性。岩石的总电导率可表示为[26]
| $ \sigma = \frac{{{A_{\rm{e}}}{L_0}}}{{{R_{\rm{w}}}A{L_{\rm{e}}}}} $ | (7) |
联立式(5)~式(7),电阻率表达式为
| $ {R_{\rm{t}}} = \frac{{{R_{\rm{w}}}{T^2}}}{{\mathit{\Phi }{S_{\rm{w}}}P}} $ | (8) |
式中Rw是地层水电阻率。Wei等[20]认为使用等效曲折度Te代替式(8)中的T更为恰当。Te的表达 式为
| $ {T_{\rm{e}}} = \frac{{{D_{\rm{f}}}}}{{{D_{\rm{f}}} + {D_T} - 1}}{\mathit{\Phi }^{\left( {1 - {D_T}} \right)/\left( {3 - {D_{\rm{f}}}} \right)}} $ | (9) |
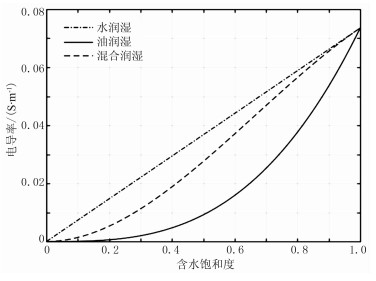
岩石的润湿性会影响流体在孔隙中的微观分布,从而引起岩石电导率的变化。润湿性差异会导致岩石电性的变化,这是影响电阻率测井识别油层与水层准确度的一个重要因素。当岩石为水润湿时,P=1;岩石为油润湿时,P=(Sw)2;对于混合润湿的情况,含油饱和度为1-Sw,电绝缘的概率为(1-Sw)2, 此时P=1-(1-Sw)2, 即P=2Sw-Sw2 [26]。由图 1所示模拟结果可见,即使岩石孔隙内充填相同的流体,在不同的表面润湿情况下,电导率也会呈现出较大的差异,这给饱和度的计算和识别储层所含流体类型带来较大困难,故在建立实际工区饱和度模型时必须考虑润湿性对导电性的影响。
|
图 1 不同润湿性时电导率与含水饱和度的关系曲线 Rw=0.3 Ω=·m,Φ=0.2 |
研究区储层孔隙度和渗透率较低,储层岩性复杂、物性差、非均质性较强。对储层特征研究的深度不够,导致对储层性质纵横向的变化认识不足,使得油水层识别困难,限制了油气勘探的步伐。因此,急需开展储层电性及油水层识别方法的研究,为下一步开发和增储增产提供技术支持。
确定含水饱和度的最准确和最可靠的方法是实验测量,但缺点是样品数量有限和测量成本较高。在测井解释中,含水饱和度的计算仍然是一个难题,尤其对于富含有机质或导电矿物且具有低孔隙度和低渗透率的储层。复杂储层中岩石电性往往表现出Archie公式不能描述的现象,即非Archie特性。为了适应这类储层饱和度评价的需要,以Archie公式为基础的经验性扩展模型已经得到了广泛的应用[27-29]。无论哪种饱和度模型都有其优势,但同时也存在一定的局限性。Archie公式只适用于孔隙结构比较简单的纯砂岩地层,参数涉及物性、岩性以及裂缝展布方向等,这些参数常由岩电实验确定。
研究区储层岩石呈油润湿,即P=(Sw)2,由式(8)和式(9)可得
| $ {S_{\rm{w}}} = \sqrt[3]{{\frac{{{R_{\rm{w}}}T_{\rm{e}}^2}}{{{R_{\rm{t}}}\mathit{\Phi }}}}} $ | (10) |
然而,使用上式计算得到的含水饱和度较岩心分析结果偏小,这种差异主要归因于泥质导致电阻率降低。对上式乘以一个因子
| $ c = {\left( {\frac{{\Delta {t_{{\rm{sh}}}}}}{{100}}} \right)^m} $ | (11) |
可修正这种影响。这样,含水饱和度的分形计算公式为
| $ {S_{\rm{w}}} = {\left( {\frac{{\Delta {t_{{\rm{sh}}}}}}{{100}}} \right)^m}\sqrt[3]{{\frac{{{R_{\rm{w}}}T_{\rm{e}}^2}}{{{R_{\rm{t}}}\mathit{\Phi }}}}} $ | (12) |
式中:Δtsh表示泥岩声波时差,其值应从整个井段选取;胶结指数m的计算方法参照文献[20]。根据式(12)就可以计算得到较为合理的储层含水饱和度Sw。
在含水饱和度解释中,将分形模型应用于研究区A井的实际资料处理,Rw取0.08~0.10 Ω·m,结果见图 2a。由图可见,基于分形模型的计算结果与实测含水饱和度的变化趋势大致相同。

|
图 2 A井(a)和B井(b)基于分形模型计算的Sw曲线及岩心分析数据 |
为了验证估计参数的合理性,选择邻近B井同一层段、具有岩心分析资料的井段进行处理,结果见图 2b。由图可见,基于分形模型计算得到的含水饱和度与岩心分析数据结果基本一致。
该区两口井的应用结果表明,利用本文方法计算得到的含水饱和度可靠性高。
3 结论与认识储层岩石孔隙的分形维数反映孔隙结构的复杂程度,孔隙结构的分形维数越大,则孔隙结构越复杂,非均质性也越强。本文在岩石孔隙具有分形特征基础上,基于分形理论建立了导电模型,并对实际数据进行了处理。通过测井资料,可以直接求取孔隙度,据此可得到模型计算所需的参数。对研究区两口井的含水饱和度解释结果与实际岩心测试资料进行比较,二者的一致性较高,证明本文方法可计算得到较为准确可靠的含水饱和度数据,为有效储层评价和生产开发提供了可靠依据。
| [1] |
Cai J, Wei W, Hu X, et al. Electrical conductivity mo-dels in saturated porous media:A review[J]. Earth-Science Reviews, 2017, 171: 419-433. DOI:10.1016/j.earscirev.2017.06.013 |
| [2] |
Archie G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Tran-sactions of the AIME, 1942, 146(1): 54-62. DOI:10.2118/942054-G |
| [3] |
Wyllie M R J, Rose W D. Some theoretical considerations related to the quantitative evaluation of the physical characteristics of reservoir rock from electrical log data[J]. Journal of Petroleum Technology, 1950, 2(4): 105-118. DOI:10.2118/950105-G |
| [4] |
Winsauer W O. Resistivity of brine-saturated sands in relation to pore geometry[J]. AAPG Bulletin, 1952, 36(2): 230-252. |
| [5] |
Perkins Jr F M, Osoba J S, Ribe K H. Resistivity of sandstones as related to the geometry of their interstitial water[J]. Geophysics, 1956, 21(4): 1071-1084. DOI:10.1190/1.1438302 |
| [6] |
Mandelbrot B B. The fractal geometry of nature[M]. W H Freeman: New York, 1982.
|
| [7] |
Hutchinson J E. Fractals and self similarity[J]. Indiana University Mathematics Journal, 1981, 30(5): 713-747. DOI:10.1512/iumj.1981.30.30055 |
| [8] |
毛宁波, 戴塔根, 常德双, 等. 沉积旋回的地震时频特征、地震分形特征和地震灰色特征研究[J]. 石油地球物理勘探, 2003, 38(增刊1): 134-137. MAO Ningbo, DAI Tagen, CHANG Deshuang, et al. Seismic time-frequency characteristics of sedimentary cycles, seismic fractal features and seismic grey features[J]. Oil Geophysical Prospecting, 2003, 38(S1): 134-137. |
| [9] |
吴国铭, 李熙喆, 高树生, 等. 基于分形理论探究碳酸盐岩CT图像二值化最佳阈值[J]. 石油地球物理勘探, 2017, 52(5): 1025-1032. WU Guoming, LI Xizhe, GAO Shusheng, et al. Optimal thresholding in carbonate reservoir CT image binarization based on fractal theory[J]. Oil Geophysical Prospecting, 2017, 52(5): 1025-1032. |
| [10] |
Li K. More general capillary pressure and relative permeability models from fractal geometry[J]. Journal of Contaminant Hydrology, 2010, 111(1-4): 13-24. DOI:10.1016/j.jconhyd.2009.10.005 |
| [11] |
Cámara J, Gómez-Miguel V, Martín M Á. Identification of bedrock lithology using fractal dimensions of drainage networks extracted from medium resolution LiDAR digital terrain models[J]. Pure & Applied Geophysics, 2015, 173(3): 1-17. |
| [12] |
Boadu F K. Use of multifractal seismic waveform parameters to characterize the hydraulic properties of fractured media:numerical experiments[J]. Geophysical Journal International, 2003, 155(2): 557-566. DOI:10.1046/j.1365-246X.2003.02066.x |
| [13] |
饶华, 李建民, 孙夕平. 利用分形理论预测潜山储层裂缝的分布[J]. 石油地球物理勘探, 2009, 44(1): 98-103. RAO Hua, LI Jianmin, SUN Xiping. Using fractal theory to predict distribution of fracture in buried-hill reservoir[J]. Oil Geophysical Prospecting, 2009, 44(1): 98-103. DOI:10.3321/j.issn:1000-7210.2009.01.019 |
| [14] |
Sarkheil H, Hassani H, Alinia F. Fractures distribution modeling using fractal and multi-fractal-neural network analysis in Tabnak hydrocarbon field, Fars, Iran[J]. Arabian Journal of Geosciences, 2013, 6(3): 945-956. DOI:10.1007/s12517-011-0400-x |
| [15] |
董少群, 曾联波, Xu Chaoshui, 等. 储层裂缝随机建模方法研究进展[J]. 石油地球物理勘探, 2018, 53(3): 625-641. DONG Shaoqun, ZENG Lianbo, XU Chaoshui, et al. Some progress in reservoir fracture stochastic modeling research[J]. Oil Geophysical Prospecting, 2018, 53(3): 625-641. |
| [16] |
Katz A J, Thompson A H. Fractal sandstone pores:implications for conductivity and pore formation[J]. Physical Review Letters, 1985, 54(12): 1325. DOI:10.1103/PhysRevLett.54.1325 |
| [17] |
Krohn C E, Thompson A H. Fractal sandstone pores:Automated measurements using scanning-electron-microscope images[J]. Physical Review B, 1986, 33(9): 6366-6374. DOI:10.1103/PhysRevB.33.6366 |
| [18] |
Roy S, Tarafdar S. Archie's law from a fractal model for porous rocks[J]. Physical Review B, 1997, 55(13): 8038-8041. DOI:10.1103/PhysRevB.55.8038 |
| [19] |
Nigmatullin R R. The generalized fractals and statistical properties of the pore space of the sedimentary rocks[J]. Physica Status Solidi (b), 1989, 153(1): 49-57. |
| [20] |
Wei W, Cai J, Hu X, et al. An electrical conductivity model for fractal porous media[J]. Geophysical Research Letters, 2015, 42(12): 4833-4840. DOI:10.1002/2015GL064460 |
| [21] |
Pitchumani R, Ramakrishnan B. A fractal geometry model for evaluating permeabilities of porous performs used in liquid composite molding[J]. International Journal of Heat and Mass Transfer, 1999, 42(12): 2219-2232. DOI:10.1016/S0017-9310(98)00261-0 |
| [22] |
Rieu M, Sposito G. Fractal fragmentation, soil porosity, and soil water properties Ⅰ:Theory[J]. Soil Science Society of America Journal, 1991, 55(5): 1231-1238. DOI:10.2136/sssaj1991.03615995005500050006x |
| [23] |
Yu B, Cheng P. A fractal permeability model for bi-dispersed porous media[J]. International Journal of Heat and Mass Transfer, 2002, 45(14): 2983-2993. DOI:10.1016/S0017-9310(02)00014-5 |
| [24] |
Wyllie M R J, Gardner G H F. Permeability and the size distribution of pores[J]. Nature, 1958, 181(4607): 477. |
| [25] |
Cornell D, Katz D L. Flow of gases through consolidated porous media[J]. Industrial & Engineering Chemistry, 1953, 45(10): 2145-2152. |
| [26] |
Abdassah D, Permadi P, Sumantri Y, et al. Saturation exponent at various wetting condition:fractal modeling of thin-sections[J]. Journal of Petroleum Science and Engineering, 1998, 20(3-4): 147-154. DOI:10.1016/S0920-4105(98)00014-X |
| [27] |
Waxman M H, Smits L J M. Electrical conductivities in oil-bearing shaly sands[J]. Society of Petroleum Engineers Journal, 1968, 8(2): 107-122. DOI:10.2118/1863-A |
| [28] |
Clavier C, Coates G, Dumanoir J. Theoretical and ex-perimental bases for the dual-water model for inter-pretation of shaly sands[J]. Society of Petroleum Engineers Journal, 1984, 24(2): 153-168. DOI:10.2118/6859-PA |
| [29] |
Budebes S, Hamdy T, Al-Farisi O, et al. Carbonate archie exponants correction model and variable determination[C].SPE Reservoir Characterization and Simulation Conference and Exhibition, Society of Petro-leum Engineers, 2011.
|



 王京悉 上海市四平路1239号同济大学海洋地质国家重点实验室, 200092。Email:
王京悉 上海市四平路1239号同济大学海洋地质国家重点实验室, 200092。Email: 