② 地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074
② Hubei Subsurface Multi-scale Imaging Key Laboratory, Wuhan, Hubei 430074, China
致密砂岩气储层作为一种非常规气藏,在油气勘探开发中受到了越来越多的关注[1],准确识别和评价致密砂岩气储层是成功开采气藏的前提。测井作为重要的油气勘探手段,信息量大且数据连续,能有效地识别各类储层。但是,在致密气藏的测井解释中,通常面临着低信噪比、低分辨率和非均质、非线性等难点。常规的测井解释[2-4]往往需要通过专业知识与地区经验,尽量挖掘测井资料中的隐藏信息,计算孔隙度、渗透率等地质参数,人工判定不同的测井解释结论。这些工作往往效率极低且易出错,因此,寻求新的致密砂岩气储层测井解释技术成为当今致密砂岩气藏勘探中急需解决的重点问题[5]。
近年来,机器学习作为一种高效的数据挖掘方法,越来越多地应用于测井解释之中:Rogers等[6]、Baldwin等[7]基于人工神经网络(ANNs),使用测井数据进行岩性识别与测井评价;张向君等[8]、Anazi等[9]、Sebtosheikh等[10]使用支持向量机算法(SVM)进行储层预测;Shi等[11]、Li等[12]通过决策树(DT)算法进行气层识别与测井解释。实际测井数据特征往往具有不均衡性,数据集中某些类的样本远多于其他类,单一模型的算法对于测井解释具有一定的局限性,集成学习(Ensemble Learning)方法则可以很好地解决这一问题[13-14]。李诒靖等[14]将集成学习方法中的提升(boosting)算法应用于储层含油性识别;宋建国等[15]、Cracknell等[16]、周雪晴等[17]分别将随机森林(RF)分类与回归方法用于储层预测与岩相分类之中。极端梯度提升(XGBoost, eXtreme Gradient Boosting)算法是对提升算法的优化[18],具有更高的模型精度与泛化能力,并加入了防止过拟合的正则项,且支持并行计算,在金融、图像识别、医学等领域得到了广泛应用[19-20],但在地球物理领域中应用较少。
致密砂岩气储层的测井数据属于典型的不均衡数据,非储层的样本数量远远大于储层。基于A工区测井资料,通过XGBoost算法预测该区孔隙度与渗透率参数,进一步对该区储层进行预测分类,并与同为集成学习方法的随机森林方法和单一模型的支持向量机算法进行比较,以最终分类结果的混淆矩阵和准确率作为评价标准,研究XGBoost算法在致密砂岩气储层测井解释方面的应用。
1 XGBoost算法理论集成学习方法是指将多个学习模型组合,以获得更好的效果。提升算法属于集成学习方法,其基本思想是将数以百计的低精度简单树模型结合起来,在每次迭代后都会为模型生成一棵新树,以建立更精确的模型。目前最有效的建立树模型方法是由Friedman[21]提出的梯度提升树,它利用梯度下降法生成基于所有先前树的新树,从而将目标函数推向最小方向。
极端梯度提升算法是对梯度提升树算法的优化,可以应用于回归问题与分类问题,相较于梯度提升算法,该方法对目标误差函数以二阶泰勒公式展开,并加入了正则项。
使用XGBoost算法建立测井解释模型时,首先基于分类回归树(CART)作为基分类器定义目标函数,它包含损失函数与正则项)
| $ {\rm{obj}} = \sum\limits_{i = 1}^n l \left( {{y_i}, {{\hat y}_i}} \right) + \sum\limits_{k = 1}^K \mathit{\Omega} \left( {{f_k}} \right) $ | (1) |
| $ \mathit{\Omega} \left( {{f_k}} \right) = \alpha T + \frac{1}{2}\lambda \sum\limits_{j = 1}^T {\omega _j^2} $ | (2) |
式中:$l\left(y_{i}, \hat{y}_{i}\right)$为样本xi的训练误差,${{{\hat y}_i}}$、yi分别表示样本xi预测和实际的分类标签或具体数值;Ω(fk)为第k棵分类回归树的正则项;T表示分类回归树叶节点个数;ωj表示对应叶节点的权重;α、λ为常数,表示惩罚系数。
之后输入测井数据进行累加训练,对于第t轮迭代,模型目标函数可表示为
| $ {\rm{ob}}{{\rm{j}}^{(c)}} = \sum\limits_{i = 1}^n l \left[ {{y_i},\hat y_i^{(t - 1)} + {f_t}\left( {{x_i}} \right)} \right] + \sum\limits_{k = 1}^K \mathit{\Omega} \left( {{f_k}} \right) + C $ | (3) |
式中:ft(xi)表示加入的第t棵分类回归树;常数C表示前t-1棵树的复杂程度。
通过泰勒公式近似目标函数,对式(3)以二阶泰勒公式展开
| $ \begin{array}{l} {\rm{ob}}{{\rm{j}}^{(t)}} \simeq \sum\limits_{i = 1}^n {\left[ {l\left( {{y_i},\hat y_i^{(t - 1)}} \right) + {g_i}{f_t}\left( {{x_i}} \right) + \frac{1}{2}{h_i}f_t^2\left( {{x_i}} \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^K \mathit{\Omega} \left( {{f_k}} \right) + C \end{array} $ | (4) |
式中:gi表示$l\left({{y_i}, \hat y_i^{(t - 1)}} \right)$对${\hat y_i^{(t - 1)}}$的一阶导数;hi表示$l\left({{y_i}, \hat y_i^{(t - 1)}} \right)$对${\hat y_i^{(t - 1)}}$的二阶导数。化简后可得到最终的目标函数
| $ {\rm{ob}}{{\rm{j}}^{(t)}} \simeq \sum\limits_{j = 1}^T {\left[ {\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right){\omega _j} + \frac{1}{2}\left( {\sum\limits_{i \in {I_j}} {{h_i}} + \lambda } \right)\omega _j^2} \right]} + \alpha T $ | (5) |
目标函数obj(t)对ωj求偏导,并令其等于0,可得到使该目标函数值最小的最优权重
| $ \omega _j^* = - \frac{{\sum\limits_{i \in {I_j}} {{g_i}} }}{{\sum\limits_{i \in {I_j}} {{h_i}} + \lambda }} $ | (6) |
将式(6)代入式(5),得到目标函数的最优值
| $ {\rm{ob}}{{\rm{j}}^{(t)}} = - \frac{1}{2}\frac{{{{\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right)}^2}}}{{\sum\limits_{i \in {I_j}} {{h_i}} + \lambda }} + \alpha T $ | (7) |
XGBoost算法在训练过程中借鉴了随机森林[15]的思想,在迭代过程中没有用到所有样本特征,而是采用了随机子空间方法。若输入的特征变量由I种不同的测井参数Li组成,则每一个节点从中随机选择部分特征,并比较其中的最优分割进行节点分裂,可有效提高模型的泛化能力。为此,在选择子树分裂点时,定义增益
| $ {\mathop{\rm Gain}\nolimits} = \frac{1}{2}\left[ {\frac{{{{\left( {\sum\limits_{i \in {I_{\rm{L}}}} {{g_i}} } \right)}^2}}}{{\sum\limits_{i \in {I_{\rm{L}}}} {{h_i}} + \lambda }} + \frac{{{{\left( {\sum\limits_{i \in {I_{\rm{R}}}} {{g_i}} } \right)}^2}}}{{\sum\limits_{i \in {I_{\rm{R}}}} {{h_i}} + \lambda }} - \frac{{{{\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right)}^2}}}{{\sum\limits_{i \in {I_j}} {{h_i}} + \lambda }}} \right] - \alpha $ | (8) |
式中:$\sum\limits_{i \in {I_{\rm{L}}}} {{g_i}}、\sum\limits_{i \in {I_{\rm{L}}}} {{h_i}} $为分裂点左侧子树的梯度值, IL为左侧子树分裂点总集合;$\sum\limits_{i \in {I_{\rm{R}}}} {{g_i}}、\sum\limits_{i \in {I_{\rm{R}}}} {{h_i}} $为分裂点右侧子树的梯度值,IR为右侧子树分裂点总集合。
将输入的测井参数特征Li排列后使用式(8)遍历每一维特征的每一个分裂点,通过使增益Gain的值最大来判别最佳分裂点。
2 应用实例将XGBoost算法应用于A工区致密气藏的储层类型识别。该区发育南北向展布的三角洲前缘砂体,储集物性较好,有利于岩性圈闭气藏的形成。该区油气藏属于典型的致密砂岩气藏。样本数据为A工区已完成测井解释的31口井的测井资料,首先通过建立XGBoost回归模型进行孔隙度与渗透率参数的预测。然后将预测结果作为新的特征加入输入变量,用于该工区致密砂岩气储层的识别。
在样本数据中随机抽取24口井(共计3414个样本数据)作为训练集,其中7口井(共计921个样本数据)作为测试集,以评估模型的预测效果。
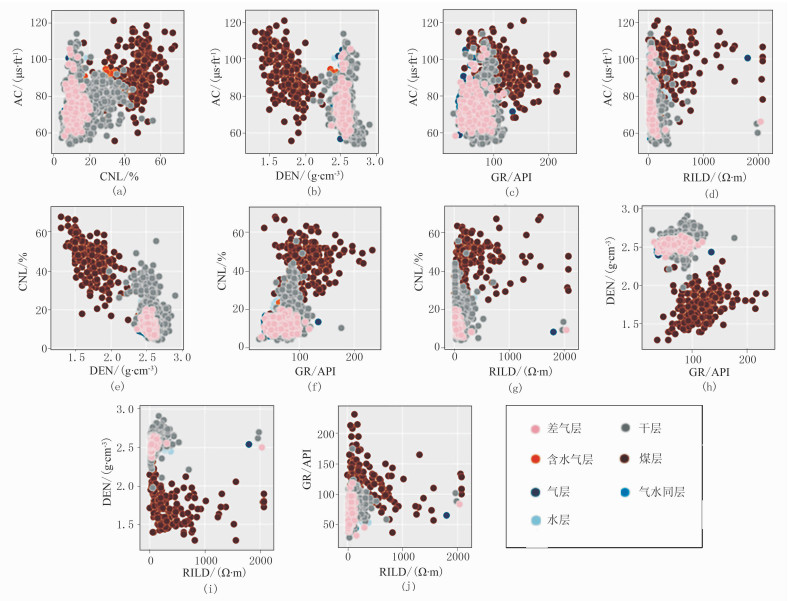
2.1 测井响应参数交会分析经统计,该区主要的测井解释结论有差气层、干层、含水气层、煤层、气层、气水同层、水层7种。通过对测井曲线资料进行分析,提取适合A工区判定储层类型的测井响应参数,其中选取声波时差(AC)、体积密度(DEN)、补偿中子(CNL)、自然伽马(GR)与深感应电阻率(RILD)等5类,根据人工实测测井解释资料统计结果,对该区块各类测井响应参数做交会分析,分析各类测井响应参数对于储层的敏感性,结果如图 1所示。
|
图 1 测井曲线响应特征与测井解释交会图 (a)AC与CNL;(b)AC与DEN;(c)AC与GR;(d)AC与RILD;(e)CNL与DEN;(f)CNL与GR;(g)CNL与RILD;(h)DEN与GR;(i)DEN与RILD;(j)GR与RILD |
图 1中各个窗格分别显示了不同储层与对应横、纵坐标轴上两个响应参数之间的关系,从图中可以看出,各类测井响应参数对于大部分储层的判别均比较敏感。
2.2 孔隙度与渗透率预测孔隙度与渗透率是评价储层性质的重要物性参数,通常是依据各类测井曲线,通过一定的数学公式及经验公式、交会图法等进行计算[22],或者利用一些地球物理反演方法[23-25]进行预测。文中采用XGBoost算法,将测井响应参数作为训练模型的输入参数,分别建立预测该区域孔隙度与渗透率的XGBoost回归预测模型。由于XGBoost算法基分类器采用树模型,对参数特征的敏感度较低,因此无需对输入数据归一化。提取训练集24口井的AC、DEN、CNL、GR与RILD等5类测井响应参数作为特征变量,孔隙度与渗透率数据作为预测结果,形成了3414组样本数据。该区实测孔隙度的极大值为16.4%,极小值为0,均值为6.5%。实测渗透率极大值为8.95mD,极小值为0.01mD,均值为0.318mD。训练集部分样本数据如表 1所示。
|
|
表 1 训练集部分样本数据 |
通过XGBoost算法建立该区孔隙度与渗透率的回归预测模型,按照孔隙度、渗透率预测值与实测值的均方根误差公式计算训练误差或测试误差
| $ {\mathop{\rm RMSE}\nolimits} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{n}} $ | (9) |
式中:${{{\hat y}_i}}$为第i个样本的孔隙度或渗透率预测值;yi为相应实测值;n为样本数。
通过XGBoost算法建立回归预测模型,需要设置的参数主要有:迭代次数,即加入的分类回归树个数t;用于控制模型复杂度的分类回归树的最大深度(Dmax)和子节点中最小样本权重和(Wmin);正则项中的惩罚系数α、λ;在使用随机子空间时用于增加模型随机性的参数随机采样训练样本(Ss)、列采样(Cs);以及判断节点是否分裂的阈值,即所需的最小损失函数下降值γ。
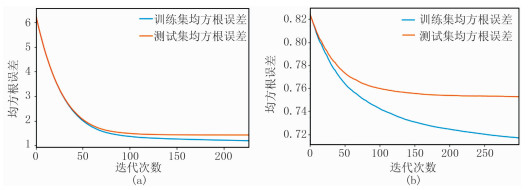
在大致确定其他参数的情况下,统计回归预测模型迭代次数从1~300时每次相应的训练集和测试集的均方根误差(RMSE)。迭代统计结果如图 2所示。统计结果表明,随着迭代次数增加,XGBoost回归预测模型的训练误差和测试误差均逐渐下降。当迭代到一定次数时,均方根误差值基本趋于稳定。在孔隙度预测中,训练集的均方根误差值最终在1.6左右轻微浮动,测试集误差在1.8左右浮动;渗透率预测中,训练集的均方根误差值最终在0.72左右浮动,测试集的误差在0.75左右浮动。说明XGBoost回归预测模型对于不同的训练样本具有一定的稳定性。但在进行渗透率预测时,测试集最终的均方根误差要明显高于训练集,可见XGBoost回归预测模型对于该区渗透率预测的泛化能力较弱,之后可以通过降低模型复杂程度与增加模型随机性避免渗透率预测中的过拟合现象。迭代次数以精度不再发生明显变化为原则,本区孔隙度预测一般可设置为200次迭代,渗透率预测一般可设置250次迭代。
|
图 2 孔隙度(a)与渗透率(b)预测结果均根方误差随迭代次数变化 |
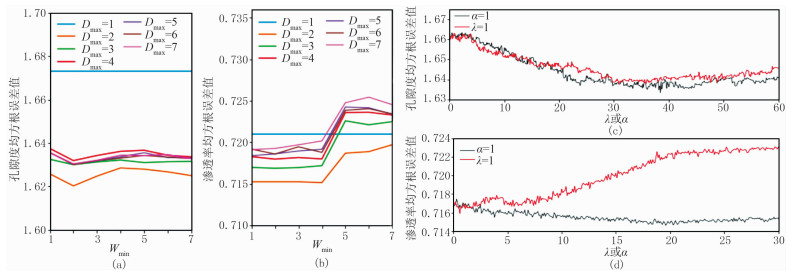
在选定孔隙度、渗透率预测迭代次数分别为200与250次后,首先调节Dmax与Wmin。可以通过适当降低Dmax及增大Wmin控制模型复杂度,避免模型过拟合。在训练集中,令Dmax与Wmin分别从1变化到7,并统计不同组合下的误差结果。孔隙度与渗透率预测中的误差结果分别如图 3a、图 3b所示。误差值总体变化不大,且在Dmax=2、Wmin=2时孔隙度预测误差最小;Dmax=2、Wmin=4时渗透率预测误差最小。之后调节正则项中的惩罚系数α、λ,在训练集中,λ=1时α在不同取值情况下的误差统计如图 3c、图 3d中的红线所示,α=1时λ在不同取值下的误差统计如图 3c、图 3d中的黑线所示。统计结果表明,在孔隙度预测中,α=35、λ=39时误差最小;在渗透率预测中,α=0.9、λ=19时误差最小。
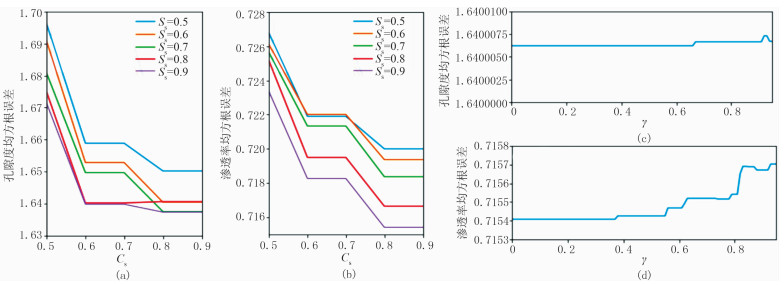
确定以上参数后,调节Ss和Cs。Ss决定用于训练模型的子样本占整个样本集合的比例;Cs表示创建分类回归树时对特征(即测井参数的种类)采样的比例。两者可用于增加采样随机性,防止模型过拟合,但取值过小时容易导致欠拟合,取值范围一般为0.5~1.0。在训练集中,令Ss与Cs分别从0.5变化到1.0,并统计不同组合下的均方根误差值。孔隙度与渗透率预测误差分别如图 4a、图 4b所示,孔隙度、渗透率预测均方根误差均在Ss =0.9、Cs=0.8时最小。之后调节参数γ,γ设置为损失函数减小的最低阈值,如果分裂使损失函数减小的值大于γ值,则这个节点才分裂,孔隙度与渗透率预测中的误差结果分别如图 4c、图 4d所示。根据统计结果,γ对于该区孔隙度与渗透率预测结果精度影响较小,最优参数均取0.3即可。
|
图 3 部分参数对于均根方误差影响统计图 (a)孔隙度预测误差随Dmax、Wmin变化;(b)渗透率预测误差随Dmax、Wmin变化;(c)孔隙度预测误差随λ、α变化;(d)渗透率预测误差随λ、α变化 |
|
图 4 部分参数对于均根方误差影响统计图 (a)孔隙度预测误差随Ss和Cs变化;(b)渗透率预测误差随Ss和Cs变化;(c)孔隙度预测误差随γ变化;(d)渗透率预测误差随γ变化 |
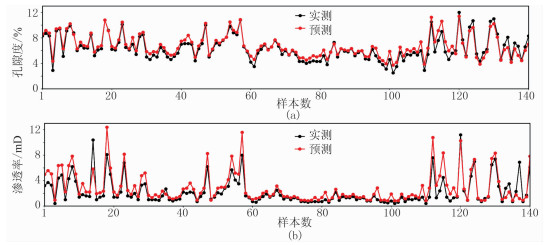
从统计结果可以看出,虽然XGBoost算法参数较多,但相较于迭代次数,其他参数对于回归预测精度影响较小。因此,利用XGBoost算法对孔隙度、渗透率预测,只需要保证迭代次数足够大即可。根据均方根误差统计结果优化参数,最终建立适用于该区的孔隙度、渗透率回归预测模型,并用于测试集7口井的预测。测试集中的KT-a井孔隙度、渗透率预测结果散点图如图 5所示。
|
图 5 KT-a井孔隙度(a)与渗透率(b)预测结果统计图 |
计算测试集数据中样本预测值相对于实测值的平均相对误差
| $ \delta = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{{y_i}}}} \times 100\% $ | (10) |
在测试集中,孔隙度预测结果平均相对误差为17.45%;渗透率预测结果平均相对误差为33.90%,计算结果表明,通过XGBoost算法建立的回归模型在该工区总体预测效果较好。
2.3 储层分类预测为研究XGBoost算法分类预测在该区储层识别中的应用,本文利用XGBoost算法建立分类模型对该区储层类型进行预测。将回归预测计算出的孔隙度、渗透率参数融入特征变量,与AC、DEN、CNL、GR、RILD等5类测井响应参数组成新的特征变量加入训练,并优化模型参数,使分类预测模型达到最佳效果(训练样本分类准确率最高)。对测试集的7口井的储层类型进行分类预测,以研究模型预测效果。将输出的分类结果以混淆矩阵的方式统计,如表 2所示。
|
|
表 2 XGBoost识别结果混淆矩阵 |
表 2中每列代表样本储层类型的预测类别,每行代表样本储层的真实归属,对角线上数据为各个储层类型正确分类的数量。储层预测模型的准确率表示模型正确预测的样本个数与测试集中该类储层样本总和的比值(即对角线上数值与每行总和的比值),精确率表示每类储层被正确预测的个数与该储层被预测出的总数比值(即对角线上数值与每列总和的比值)。
从表 2中可以看出,XGBoost算法对于该区测井解释的分类效果较好,准确率为0.846。对于煤层、气层的识别较为准确,识别出了100%的煤层、65%的气层和64%的含水气层。
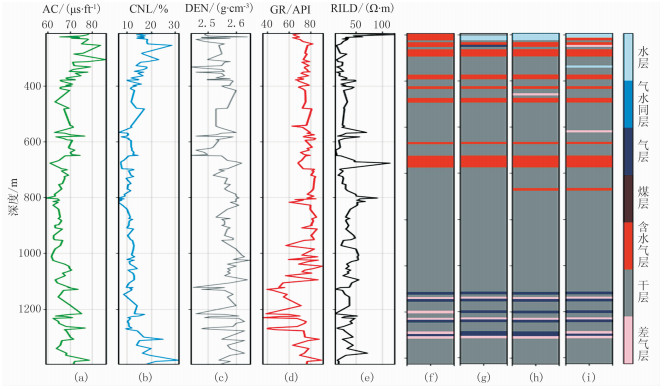
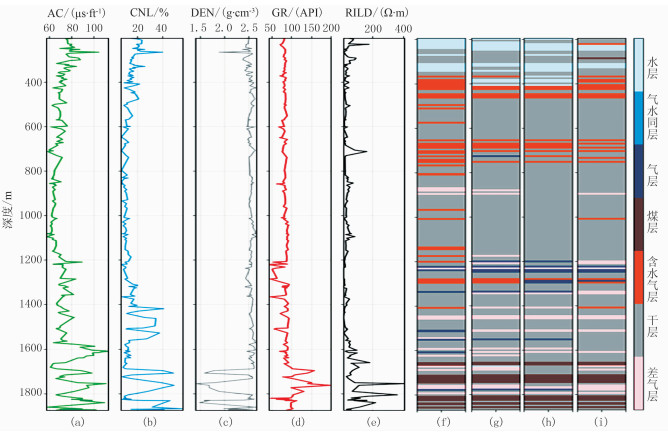
之后分别使用随机森林模型和支持向量机模型对该区储层类型进行预测,分类结果统计如表 3、表 4所示。对比三种机器学习模型的预测效果,其中:XGBoost模型预测准确率为0.846;随机森林模型预测准确率为0.824;支持向量机模型预测准确率为0.810。从表中可以看出,XGBoost模型针对该区储层类型的预测效果要优于其他两类机器学习模型,而随机森林模型预测准确率虽然低于XGBoost模型,但依旧高于支持向量机模型,这进一步证明了集成学习方法在处理致密砂岩气储层测井数据中的优势。在测试集中选取KT-a、KT-b两口井柱状图进行比较,如图 6、图 7所示。
|
图 6 不同机器学习模型关于KT-a井储层预测结果对比 (a)AC测井曲线;(b)CNL测井曲线;(c)DEN测井曲线;(d)GR测井曲线;(e)RILD测井曲线;(f)实际测井解释;(g)XGBoost预测结果;(h)随机森林预测结果;(i)支持向量机预测结果 |
|
图 7 不同机器学习模型关于KT-b井储层预测结果对比 (a)AC测井曲线;(b)CNL测井曲线;(c)DEN测井曲线;(d)GR测井曲线;(e)RILD测井曲线;(f)实际测井解释;(g)XGBoost预测结果;(h)随机森林预测结果;(i)支持向量机预测结果 |
|
|
表 3 随机森林识别结果混淆矩阵 |
|
|
表 4 支持向量机识别结果混淆矩阵 |
从图 6、图 7中可以进一步看出,XGBoost模型对于各段储层的识别准确率高于随机森林与支持向量机模型,尤其对于气层的识别较为准确,能识别出绝大部分的气层。但对于部分差气层与气层的区分效果较差。总体而言XGBoost模型有着良好的泛化能力,在处理致密砂岩气储层测井数据时具有一定的优势。
3 结束语针对致密砂岩气储层测井数据在应用于测井解释时存在的种种难点,文中基于A工区测井解释资料,通过XGBoost算法建立回归模型与分类模型,分别用于该区孔隙度、渗透率预测与储层分类预测,讨论不同参数对于模型预测精度的影响,并将分类预测模型与随机森林模型、支持向量机模型进行对比,得出以下结论。
(1) 基于XGBoost算法建立的回归预测模型在A工区致密砂岩气储层的孔隙度与渗透率预测中具有较高的准确性。虽然XGBoost算法需要优化的参数较多,但在迭代次数(即加入的分类回归树个数)达到一定数量后,训练与测试样本误差便趋于稳定。相较于孔隙度预测,回归模型在该工区渗透率预测中泛化能力较弱,可以适当降低模型复杂度或增加基分类器采样随机性避免过拟合现象。
(2) XGBoost分类预测模型在该工区致密砂岩气藏的储层预测中也收到了良好的效果,优于传统单一模型的支持向量机算法与集成方法中的随机森林方法,可有效地应用于致密砂岩气储层的储层识别中。
| [1] |
罗瑞兰, 雷群, 范继武, 等. 低渗透致密气藏压裂气井动态储量预测新方法--以苏里格气田为例[J]. 天然气工业, 2010, 30(7): 28-31. LUO Ruilan, LEI Qun, FAN Jiwu, et al. A new approach to the dynamic reserve estimation of fractured gas wells in low-permeability tight gas reservoirs:The Sulige Gas Field as a case study[J]. Natural Gas Industry, 2010, 30(7): 28-31. DOI:10.3787/j.issn.1000-0976.2010.07.007 |
| [2] |
赵彦超, 吴春萍, 吴东平. 致密砂岩气层的测井评价--以鄂尔多斯盆地大牛地山西组一段气田为例[J]. 地质科技情报, 2003, 22(4): 65-70. ZHAO Yanchao, WU Chunping, WU Dongping. Logging evaluation to tight gas sandstone:a case study from the first member of Shanxi formation in Daniudi gas pool, Ordos basin, China[J]. Geological Science and Technology Information, 2003, 22(4): 65-70. |
| [3] |
杨双定. 鄂尔多斯盆地致密砂岩气层测井评价新技术[J]. 天然气工业, 2005, 25(9): 45-47. YANG Shuangding. New methods of Log Evaluation of the Tight Sandstone Gas Reservoirs in E'erduosi Basin[J]. Natural Gas Industry, 2005, 25(9): 45-47. DOI:10.3321/j.issn:1000-0976.2005.09.015 |
| [4] |
魏钦廉, 肖玲, 李康悌. 常规测井识别致密地层含气性[J]. 特种油气藏, 2007, 14(4): 22-25. WEI Qinlian, XIAO Ling, LI Kangti. Identify gas potential in tight reservoir by conventional logging[J]. Special Oil and Gas Reservoirs, 2007, 14(4): 22-25. DOI:10.3969/j.issn.1006-6535.2007.04.005 |
| [5] |
章雄, 潘和平, 骆淼, 等. 致密砂岩气层测井解释方法综述[J]. 工程地球物理学报, 2005, 2(6): 431-436. ZHANG Xiong, PAN Heping, LUO Miao, et al. Summary of logging interpretation for gas-bearing tight sandstone[J]. Chinese Journal of Engineering Geophysics, 2005, 2(6): 431-436. DOI:10.3969/j.issn.1672-7940.2005.06.006 |
| [6] |
Rogers S J, Fang J H, Karr C L, et al. Determination of lithology from well logs using a neural network[J]. AAPG Bulletin, 1992, 76(5): 731-739. |
| [7] |
Baldwin J L, Bateman R M, Wheatley C L. Application of a neural network to the problem of mineral identification from well logs[J]. Log Analyst, 1990, 3(5): 279-293. |
| [8] |
张向君, 张晔. 基于支持向量机的交互检验储层预测[J]. 石油物探, 2018, 57(4): 597-600. ZHANG Xiangjun, ZHANG Ye. Reservoir prediction through cross-validation based on support vector machine[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 597-600. DOI:10.3969/j.issn.1000-1441.2018.04.014 |
| [9] |
Anazi A, Gates I D. On the capability of support vector machines to classify lithology from well logs[J]. Natural Resources Research, 2010, 19(2): 125-139. DOI:10.1007/s11053-010-9118-9 |
| [10] |
Sebtosheikh M A, Motafakkerfard R, Riahi M A, et al. Support vector machine method, a new technique for lithology prediction in an Iranian heterogeneous carbonate reservoir using petrophysical well logs[J]. Carbonates Evaporites, 2015, 30(1): 59-68. DOI:10.1007/s13146-014-0199-0 |
| [11] |
Shi N, Li H, Luo W. Data mining and well logging interpretation:application to a conglomerate reservoir[J]. Applied Geophysics, 2015, 12(2): 263-272. DOI:10.1007/s11770-015-0490-4 |
| [12] |
Li H, Tan F, Xu C, et al. Lithology identification of conglomerate reservoir based on decision tree method[J]. Well Logging Technology, 2010, 34(1): 16-21. |
| [13] |
柴明锐, 程丹, 张昌民, 等. 机器学习方法对砂砾岩岩屑成分的预测--以西北缘X723井百口泉组为例[J]. 西安石油大学学报(自然科学版), 2017, 32(5): 22-28. CHAI Mingrui, CHENG Dan, ZHANG Changmin, et al. Prediction of debris composition in glutenite by machine learning method:a case study in Baikouquan formation of well X723 in the NW Margin of Junggar Basin[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2017, 32(5): 22-28. DOI:10.3969/j.issn.1673-064X.2017.05.004 |
| [14] |
李诒靖, 郭海湘, 李亚楠, 等. 一种基于Boosting的集成学习算法在不均衡数据中的分类[J]. 系统工程理论与实践, 2016, 36(1): 189-199. LI Yijing, GUO Haixiang, LI Ya'nan, et al. A boosting based ensemble learning algorithm in imbalanced data classification[J]. Systems Engingeering Theory & Practice, 2016, 36(1): 189-199. |
| [15] |
宋建国, 杨璐, 高强山, 等. 强容噪性随机森林算法在地震储层预测中的应用[J]. 石油地球物理勘探, 2018, 53(5): 954-960. SONG Jianguo, YANG Lu, GAO Qiangshan, et al. Strong tolerance random forest algorithm in seismic reservoir prediction[J]. Oil Geophysical Prospecting, 2018, 53(5): 954-960. |
| [16] |
Cracknell M J, Reading A M. The upside of uncertainty:Identification of lithology contact zones from airborne geophysics and satellite data using random forest and support vector machines[J]. Geophysics, 2013, 78(3): WB113-WB126. DOI:10.1190/geo2012-0411.1 |
| [17] |
周雪晴, 张占松, 张超谟, 等. 基于粗糙集--随机森林算法的复杂岩性识别[J]. 大庆石油地质与开发, 2017, 36(6): 127-133. ZHOU Xueqing, ZHANG Zhansong, ZHANG Chaomo, et al. Complex lithologic identification based on rough set-random forest algorithm[J]. Petroleum Geology and Oilfield Development in Daqing, 2017, 36(6): 127-133. |
| [18] |
Chen T, Guestrin C.XGBoost: A scalable tree boos-ting system[C].ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, 785-794.
|
| [19] |
Torlay L, Perrone-Bertolotti M, Thomas E, et al. Machine learning-XGBoost analysis of language networks to classify patients with epilepsy[J]. Brain Informa-tics, 2017, 4(3): 159-169. DOI:10.1007/s40708-017-0065-7 |
| [20] |
贾文慧, 孙林子, 景英川. 基于XGBoost模型的股骨颈骨折手术预后质量评分预测[J]. 太原理工大学学报, 2018, 49(1): 174-178. JIA Wenhui, SUN Linzi, JING Yingchuan. Surgical prognosis quality score of femoral neck fracture base on XGBoost model[J]. Journal of Taiyuan University of Technology, 2018, 49(1): 174-178. |
| [21] |
Friedman J H. Greedy function approximation:A gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. |
| [22] |
范铭涛, 沈全意, 吴辉, 等. 复杂岩性裂缝-孔隙型储层孔隙度计算方法研究[J]. 天然气工业, 2005, 25(5): 29-30. FAN Mingtao, SHEN Quanyi, WU Hui, et al. Porosity calculation method of complex lithological fractured-porous reservoir[J]. Natural Gas Industry, 2005, 25(5): 29-30. DOI:10.3321/j.issn:1000-0976.2005.05.008 |
| [23] |
牛聪, 张益明, 王迪, 等. LA地区盒8段优质储层的特征与分布预测[J]. 石油地球物理勘探, 2017, 52(3): 591-598. NIU Cong, ZHANG Yiming, WANG Di, et al. Prediction of high-quality reservoir characteristics and distribution in the area LA[J]. Oil Geophysical Prospecting, 2017, 52(3): 591-598. |
| [24] |
方兴, 孙夕平, 张明, 等. 基于AVO流体反演的储层孔隙度预测技术[J]. 石油地球物理勘探, 2012, 47(3): 469-472. FANG Xing, SUN Xiping, ZHANG Ming, et al. Re-servoir porosity prediction based on AVO fluid inver-sion[J]. Oil Geophysical Prospecting, 2012, 47(3): 469-472. |
| [25] |
潘豪杰, 张研, 李红兵, 等. 基于贝叶斯理论的天然气水合物储层弹性-电性数据联合反演[J]. 石油地球物理勘探, 2018, 53(3): 568-577, 586. PAN Haojie, ZHANG Yan, LI Hongbing, et al. Joint inversion of elastic-electrical data for gas hydrate re-servoirs based on Bayesian theory[J]. Oil Geophysical Prospecting, 2018, 53(3): 568-577, 586. |



 顾汉明 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
顾汉明 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: 