② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580
② Laboratory for Marine Mineral Resource Evaluation and Detection, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China
反射系数公式定量描述了地震反射波振幅与介质弹性参数随炮检距、方位角的变化特征,是研究地震波正演与反演的理论基础。在均匀各向同性地层中,地震振幅具有随炮检距变化的特征,当地震波传播到弹性分界面处时,会产生纵横波反射与透射现象。Zoeppritz等[1]对各向同性弹性分界面处的纵横波反射、透射系数进行了定量表征;Aki等[2]基于Zoeppritz方程推导了基于纵横波速度、密度的纵波反射系数近似公式,更为直观地描述了弹性分界面处的介质参数差异与地震反射波振幅的关系。
随着油气勘探领域的不断发展,非常规油气藏的勘探与开发在油气勘探领域具有重要意义。裂缝具有储存与运移油气的作用,裂缝型储层成为非常规油气勘探的研究重点。裂缝型储层不同于均匀各向同性地层,由于定向排列近似垂直的裂缝,因此可等效为HTI介质,因而各向同性反射系数公式不适用于裂缝型储层。
基于Thomsen[3]的弱各向异性介质理论与各向异性参数,Rüger[4]研究了HTI介质反射系数近似公式,以纵横波速度、密度与各向异性参数对弹性分界面处的反射系数进行描述。Vavryuk等[5]基于纵波速度、慢横波速度、密度与各向异性参数构建了另一种HTI介质的线性化反射系数近似公式。朱兆林等[6]对比分析了这两种近似公式在中、大入射角下的精度。基于吴国忱[7]对TTI介质相速度、偏振方向的研究,梁锴等[8]推导了TTI介质qP波反射透射系数精确公式与反射系数近似公式。司芗等[9]推导了TTI介质三维反射透射系数精确公式;李春鹏[10]构建了HTI介质反射透射系数精确公式。张广智等[11]研究了Rüger近似公式在小角度近似条件下的简化形式,推导了基于纵横波阻抗反射系数与各向异性梯度反射系数的各向异性近似公式。杜炳毅等[12]基于Rüger近似公式,推导了杨氏模量、泊松比与各向异性梯度表征的反射系数近似公式。根据地震散射理论,潘新朋等[13]构建了非均质HTI介质纵波散射系数公式。结合介质分解理论与扰动思想,吴国忱等[14]构建了TI介质岩石弹性模量一阶扰动近似公式。
基于反射系数近似公式,可建立地震数据与介质弹性参数之间的联系,Rüger反射系数近似公式的提出奠定了各向异性介质方位AVO正演和反演的理论基础。基于对裂缝物性参数与AVO方位特征的研究,刘洋等[15]认为裂缝倾角的变化影响方位AVO特征;毛宁波等[16]基于Rüger反射系数近似公式对四类含气裂缝型储层的AVO特征进行了研究;刘百红等[17]研究了裂缝密度、裂缝方位和裂缝填充物对地震波方位AVO的影响。近年来,为了提高各向异性储层油气勘探精度,宽方位高密度地震勘探的应用趋于普遍,获得的叠前地震道集同时具有炮检距和方位信息,基于“五维”(三维坐标+炮检距+方位角)叠前地震道集的地震资料处理技术也得到了发展。众多学者以Rüger近似公式作为各向异性理论基础展开了研究:刘依谋等[18]、印兴耀等[19]从地震采集、处理和解释各方面对宽方位地震勘探进行了系统的描述与讨论;基于Vermeer[20]与Cary[21]提出的OVT(Offset Vector Tile,炮检距向量片)概念,詹仕凡等[22]建立了方位角—炮检距叠加模板,采用多尺度、多方位各向异性分析对基于五维地震道集的地震属性分析技术进行了研究;党青宁等[23]、古发明等[24]、林娟等[25]将OVT域处理技术应用于实际地震数据。但是前人研究表明,Rüger近似公式仅在小炮检距范围内具有较高精度,基于Rüger近似公式的“五维”地震正演模拟与分析不能充分发挥“五维”地震数据丰富的炮检距信息。
本文根据散射矩阵与介质分解理论,以HTI介质精确的反射透射系数公式为基础,推导了HTI介质PP波反射系数一阶扰动近似公式,提高了中远炮检距反射系数的精度,从而提高“五维”叠前地震数据中远炮检距信息的利用率,为利用中远炮检距信息进行弹性参数反演提供了理论基础。
1 HTI介质反射系数一阶扰动近似定量表征根据介质等效理论,地下发育有高角度近垂直裂缝的储层可等效为具有水平对称轴的横向各向同性介质(HTI介质)。基于弱各向异性假设,Rüger引入类似Thomsen各向异性参数,利用五个弹性参数对HTI介质刚度矩阵
| $ {\mathit{\boldsymbol{C}}}= \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{13}}}&{{c_{13}}}&{}&{}&{}\\ {{c_{13}}}&{{c_{33}}}&{{c_{23}}}&{}&{}&{}\\ {{c_{13}}}&{{c_{23}}}&{{c_{33}}}&{}&{}&{}\\ {}&{}&{}&{{c_{44}}}&{}&{}\\ {}&{}&{}&{}&{{c_{55}}}&{}\\ {}&{}&{}&{}&{}&{{c_{66}}} \end{array}} \right] $ | (1) |
进行表征,即
| $ \left\{ \begin{array}{l} {c_{11}} = \rho V_{{\rm{P0}}}^2\left[ {1 + 2{\varepsilon ^{\left( {\rm{V}} \right)}}} \right]\\ {c_{66}} = \rho V_{{\rm{S0}}}^2\left[ {1 + 2{\gamma ^{\left( {\rm{V}} \right)}}} \right]\\ {c_{33}} = \rho V_{{\rm{P0}}}^2\\ {c_{44}} = \rho V_{{\rm{S0}}}^2\\ {c_{23}} = {c_{33}} - 2{c_{44}}\\ {c_{13}} = \sqrt {\left[ {1 + 2{\delta ^{\left( {\rm{V}} \right)}}} \right]{{\left( {{c_{33}} - {c_{66}}} \right)}^2} + 2{\delta ^{\left( {\rm{V}} \right)}}{c_{66}}\left( {{c_{33}} - 2{c_{66}}} \right)} - \\ \;\;\;\;\;\;\;{c_{66}} \end{array} \right. $ | (2) |
式中:δ(V)、ε(V)、γ(V)为Thomsen各向异性参数;ρ为介质密度;VP0为P波垂直入射到介质中的速度,VS0为SH波垂直入射到介质中的速度。
李春鹏[10]基于HTI介质刚度矩阵,在位移连续与应力连续的条件下得到的HTI介质反射透射系数精确公式为
| $ \left[ {\begin{array}{*{20}{c}} {{M_{11}}}&{{M_{12}}}&{{M_{13}}}&{{M_{14}}}&{{M_{15}}}&{{M_{16}}}\\ {{M_{21}}}&{{M_{22}}}&{{M_{23}}}&{{M_{24}}}&{{M_{25}}}&{{M_{26}}}\\ {{M_{13}}}&{{M_{32}}}&{{M_{33}}}&{{M_{34}}}&{{M_{35}}}&{{M_{36}}}\\ {{M_{41}}}&{{M_{42}}}&{{M_{43}}}&{{M_{44}}}&{{M_{45}}}&{{M_{46}}}\\ {{M_{51}}}&{{M_{52}}}&{{M_{53}}}&{{M_{54}}}&{{M_{55}}}&{{M_{56}}}\\ {{M_{61}}}&{{M_{62}}}&{{M_{63}}}&{{M_{64}}}&{{M_{65}}}&{{M_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PSV}}}}}\\ {{R_{{\rm{PSH}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PSV}}}}}\\ {{T_{{\rm{PSH}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{N_1}}\\ {{N_2}}\\ {{N_3}}\\ {{N_4}}\\ {{N_5}}\\ {{N_6}} \end{array}} \right] $ | (3) |
可以表示为
| $ \mathit{\boldsymbol{MR}} = \mathit{\boldsymbol{N}} $ | (4) |
式中:M和N为系数矩阵,与入射波、散射波相关;R为仅考虑P波入射的散射矩阵。
考虑双层介质,假设介质为弱各向异性介质,且弹性界面两侧参数变化较小,基于散射理论与介质分解理论,可将M、R、N分解为背景项与扰动项的形式
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{M}}\\ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{R}}\\ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{N}} \end{array} \right. $ | (5) |
式中:Mu、Ru、Nu为背景项,弹性参数不发生变化,不具有方位特征;ΔM、ΔR、ΔN为一阶扰动项,与弹性参数的一阶扰动变化和各向异性参数有关,具有方位特征。
由于介质各向异性程度较弱,可忽略各向异性参数高阶项,HTI介质qP波、qSV波和SH波相速度可近似为
| $ \left\{ \begin{array}{l} {V_{\rm{P}}} \approx {V_{{\rm{P0}}}}\left\{ {1 + {\delta ^{\left( {\rm{V}} \right)}}{{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\left( {\varphi - {\varphi _0}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left[ {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right]{{\sin }^4}{\theta _{\rm{P}}}{{\cos }^4}\left( {\varphi - {\varphi _0}} \right)} \right\}\\ {V_{\rm{S}}} \approx {V_{{\rm{S0}}}}\left\{ {1 + {\gamma ^{\left( {\rm{V}} \right)}} + \frac{{V_{{\rm{P0}}}^2}}{{V_{{\rm{SV0}}}^2}}\left[ {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right] \times } \right.\\ \;\;\;\;\;\;\;\left[ {{{\cos }^2}{\theta _{{\rm{SV}}}} + {{\sin }^2}{\theta _{{\rm{SV}}}}{{\cos }^2}\left( {\varphi - {\varphi _0}} \right)} \right] \times \\ \;\;\;\;\;\;\;\left. {{{\sin }^2}{\theta _{{\rm{SV}}}}{{\cos }^2}\left( {\varphi - {\varphi _0}} \right)} \right\}\\ {V_{{\rm{SH}}}} \approx {V_{{\rm{S0}}}}\left[ {1 + {\gamma ^{\left( {\rm{V}} \right)}}{{\sin }^2}{\theta _{{\rm{SH}}}}{{\cos }^2}\left( {\varphi - {\varphi _0}} \right)} \right] \end{array} \right. $ | (6) |
式中:θP为纵波入射角、反射角或透射角;θSV为SV波反射角或透射角;θSH为SH波反射角或透射角;φ为观测方位角;φ0为测线与介质对称轴的夹角。由式(5)可看出,相速度与该层介质弹性参数有关。在弹性界面两侧参数变化较小的条件下,界面两侧弹性参数也可以扰动形式定义为
| $ \left\{ \begin{array}{l} \Delta {V_{{\rm{P01}}}} = {{\bar V}_{{\rm{P0}}}} - \frac{{\Delta {V_{{\rm{P0}}}}}}{2}\\ \Delta {V_{{\rm{P02}}}} = {{\bar V}_{{\rm{P0}}}} + \frac{{\Delta {V_{{\rm{P0}}}}}}{2} \end{array} \right. $ | (7) |
| $ \left\{ \begin{array}{l} \Delta {V_{{\rm{S01}}}} = {{\bar V}_{{\rm{S0}}}} - \frac{{\Delta {V_{{\rm{S0}}}}}}{2}\\ \Delta {V_{{\rm{S02}}}} = {{\bar V}_{{\rm{S0}}}} + \frac{{\Delta {V_{{\rm{S0}}}}}}{2} \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} {\rho _1} = \bar \rho - \frac{{\Delta \rho }}{2}\\ {\rho _2} = \bar \rho + \frac{{\Delta \rho }}{2} \end{array} \right. $ | (9) |
| $ \left\{ \begin{array}{l} {\theta _{{\rm{P1}}}} = {{\bar \theta }_{\rm{P}}} - \frac{{\Delta {\theta _{\rm{P}}}}}{2}\\ {\theta _{{\rm{P2}}}} = {{\bar \theta }_{\rm{P}}} + \frac{{\Delta {\theta _{\rm{P}}}}}{2} \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} {\theta _{{\rm{SV1}}}} = {{\bar \theta }_{{\rm{SV}}}} - \frac{{\Delta {\theta _{{\rm{SV}}}}}}{2}\\ {\theta _{{\rm{SV2}}}} = {{\bar \theta }_{{\rm{SV}}}} + \frac{{\Delta {\theta _{{\rm{SV}}}}}}{2} \end{array} \right. $ | (11) |
| $ \left\{ \begin{array}{l} {\theta _{{\rm{SH1}}}} = {{\bar \theta }_{{\rm{SH}}}} - \frac{{\Delta {\theta _{{\rm{SH}}}}}}{2}\\ {\theta _{{\rm{SH2}}}} = {{\bar \theta }_{{\rm{SH}}}} + \frac{{\Delta {\theta _{{\rm{SH}}}}}}{2} \end{array} \right. $ | (12) |
式中:VP01、VS01为垂直入射到上覆介质中的纵横波速度,ρ1为上覆介质的密度;VP02、VS02为垂直入射到下伏介质的纵横波速度,ρ2为下伏介质的密度;θP1、θSV1、θSH1为上覆介质纵波入射角或反射角、SV波反射角与SH波反射角;θP2、θSV2、θSH2为下伏介质纵波透射角、SV波透射角与SH波透射角;上划线表示界面两侧参数的均值;“Δ”表示界面两侧参数的差值。
将式(5)代入式(4),有
| $ \left( {{\mathit{\boldsymbol{M}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{M}}} \right)\left( {{\mathit{\boldsymbol{R}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{R}}} \right) = \left( {{\mathit{\boldsymbol{N}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{N}}} \right) $ | (13) |
假设背景介质弹性参数不变,即仅考虑均匀各向同性情况,则有
| $ {\mathit{\boldsymbol{M}}^{\rm{u}}}{\mathit{\boldsymbol{R}}^{\rm{u}}} = {\mathit{\boldsymbol{N}}^{\rm{u}}} $ | (14) |
在背景介质为均匀各向同性介质情况下,P波入射时介质中不存在反射P波,且不产生转换波,因此在式(15)中,Ru中仅有P波透射系数为1,矩阵中的其余系数为0,即
| $ {\mathit{\boldsymbol{R}}^{\rm{u}}} = {\left( {\begin{array}{*{20}{c}} 0&0&0&1&0&0 \end{array}} \right)^{\rm{T}}} $ | (15) |
由于弹性界面两侧参数变化较小,且介质各向异性程度较弱,可忽略ΔM、ΔN二阶及高阶项,整理可得
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + {\left( {{\mathit{\boldsymbol{M}}^{\rm{u}}}} \right)^{ - 1}}\left( {\Delta \mathit{\boldsymbol{N}} - \Delta \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{R}}^{\rm{u}}}} \right) $ | (16) |
将式(15)代入式(16),整理可得
| $ \mathit{\boldsymbol{R}} = {\left( {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{R}}_{{\rm{PP}}}}}&{\Delta {\mathit{\boldsymbol{R}}_{{\rm{PSV}}}}}&{\Delta {\mathit{\boldsymbol{R}}_{{\rm{PSH}}}}}&{\Delta {\mathit{\boldsymbol{T}}_{{\rm{PP}}}} + 1}&{\Delta {\mathit{\boldsymbol{T}}_{{\rm{PSV}}}}}&{\Delta {\mathit{\boldsymbol{T}}_{{\rm{SH}}}}} \end{array}} \right)^{\rm{T}}} $ | (17) |
上式即为P波入射时弹性界面上的纵横波反射透射系数近似公式。忽略弹性参数高阶项与各向异性参数高阶项,对式(17)进行化简整理可得(详细推导见附录A)
| $ \begin{array}{l} {R_{{\rm{PP}}}}\left( {\theta ,\varphi } \right)\\ = \frac{1}{2}\left( {1 + {{\tan }^2}{{\bar \theta }_{\rm{P}}}} \right)\frac{{\Delta {V_{{\rm{P0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}} - 4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}\frac{{\Delta {V_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{S0}}}}}} + \\ \;\;\;\frac{1}{2}\left[ {1 - 4{{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)}^2}{{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right]\frac{{\Delta \rho }}{{\bar \rho }} + \\ \;\;\;\frac{1}{2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\left( {\varphi - {\varphi _0}} \right)\left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right) \times \\ \;\;\;\left[ {1 - {{\sin }^2}{{\bar \theta }_{\rm{P}}}{{\cos }^2}\left( {\varphi - {\varphi _0}} \right)} \right]\Delta {\delta ^{\left( {\rm{V}} \right)}} + \\ \;\;\;\frac{1}{2}{\sin ^4}{{\bar \theta }_{\rm{P}}}{\cos ^4}\left( {\varphi - {\varphi _0}} \right)\left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right)\Delta {\varepsilon ^{\left( {\rm{V}} \right)}} - \\ \;\;\;4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\left( {\varphi - {\varphi _0}} \right)\Delta {\gamma ^{\left( {\rm{V}} \right)}} \end{array} $ | (18) |
上式即为基于方位观测系统的HTI介质P波入射情况下P波反射系数一阶扰动近似公式。若定义的测线方向与介质对称轴方向平行,则式(18)可简化为
| $ \begin{array}{l} {R_{{\rm{PP}}}}\left( {\theta ,\varphi } \right)\\ = \frac{1}{2}\left( {1 + {{\tan }^2}{{\bar \theta }_{\rm{P}}}} \right)\frac{{\Delta {V_{{\rm{P0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}} - 4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}\frac{{\Delta {V_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{S0}}}}}} + \\ \;\;\;\frac{1}{2}\left[ {1 - 4{{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)}^2}{{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right]\frac{{\Delta \rho }}{{\bar \rho }} + \\ \;\;\;\frac{1}{2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\varphi \left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right) \times \\ \;\;\;\left( {1 - {{\sin }^2}{{\bar \theta }_{\rm{P}}}{{\cos }^2}\varphi } \right)\Delta {\delta ^{\left( {\rm{V}} \right)}} + \\ \;\;\;\frac{1}{2}{\sin ^4}{{\bar \theta }_{\rm{P}}}{\cos ^4}\varphi \left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right)\Delta {\varepsilon ^{\left( {\rm{V}} \right)}} - \\ \;\;\;4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\varphi \Delta {\gamma ^{\left( {\rm{V}} \right)}} \end{array} $ | (19) |
若弹性界面上覆介质为各向同性介质,忽略式(19)中的各向异性参数项,可得
| $ \begin{array}{l} {R_{{\rm{PP}}}}\left( {\overline {{\theta _{\rm{P}}}} } \right) = \frac{1}{2}\left( {1 + {{\tan }^2}{{\bar \theta }_{\rm{P}}}} \right)\frac{{\Delta {V_{{\rm{P0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}} - \\ \;\;\;4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}\frac{{\Delta {V_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{S0}}}}}} + \frac{1}{2}\left[ {1 - 4{{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)}^2}{{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right]\frac{{\Delta \rho }}{{\bar \rho }} \end{array} $ | (20) |
上式即为Aki-Richards近似公式。由此可知,当地震波入射HTI介质时,所产生的响应特征可看作各向同性背景下地震波的响应特征与各向异性扰动的响应特征之和,且仅考虑一阶扰动近似时,HTI介质方位信息受控于各向异性参数,仅有各向异性参数扰动项具有方位特征。因此,基于散射矩阵的HTI介质一阶扰动近似公式推导具有合理性。
2 HTI介质PP波反射系数一阶扰动近似公式精度分析为了验证上述推导公式精度,设计三层模型进行正演模拟:模型Ⅰ第一层为各向同性介质,第二层为HTI介质,第三层为各向同性介质;模型Ⅱ三层均为HTI介质(图 1)。以第一层介质表面为xoy平面,z轴垂直xoy面向下表示地层深度,建立三维观测坐标系。
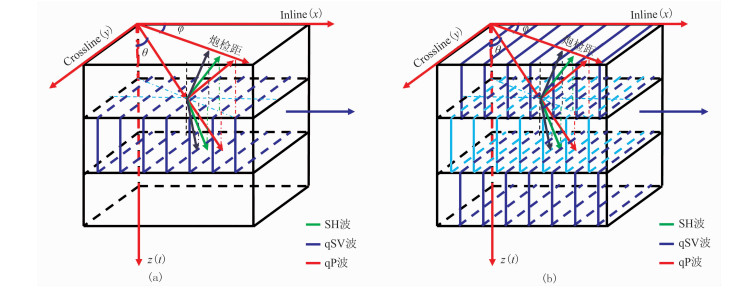
|
图 1 三层模型方位观测系统示意图 (a)模型Ⅰ;(b)模型Ⅱ |
模型Ⅰ的三层介质弹性参数如表 1所示。
|
|
表 1 模型Ⅰ弹性参数 |
图 2为模型Ⅰ利用本文所推导的公式与HTI介质反射系数精确公式、Rüger近似公式、各向同性Wang二阶近似公式[26]所计算的纵波反射系数曲线。三个近似公式的纵波反射系数曲线在小入射角时都有较高的精度,然而由于忽略了弹性参数高阶项信息,随着入射角的增大,近似公式与精确公式的误差逐渐增大。由图 2a的各向同性/HTI界面的纵波反射系数特征曲线可知,本文所推导的一阶扰动近似公式与反射系数精确公式的误差较小,与Rüger近似公式相比具有更高的精度。图 2b为HTI/各向同性界面的纵波反射系数曲线,随着炮检距的增大,Rüger近似公式与一阶扰动近似公式出现差异,在一定入射角范围内,Rüger近似公式精度较高,但一阶扰动近似公式与精确公式特征曲线变化趋势一致,说明了弹性参数高阶项对近似公式精度的影响。
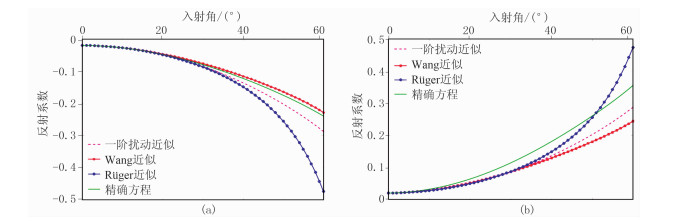
|
图 2 模型Ⅰ纵波反射系数RPP曲线对比(方位角为0°) (a)各向同性/HTI界面;(b)HTI/各向同性界面 |
当上覆介质为各向同性介质、下伏介质为HTI介质时,各向同性二阶近似公式精度远高于两类线性近似公式。由于不考虑各向异性参数项,图 2a仅反映了纵横波速度、密度高阶项对近似公式精度的影响。当上覆介质为HTI介质,下伏介质为各向同性介质时,一阶扰动近似公式精度高于各向同性二阶近似公式(图 2b)。
本文所推导一阶扰动近似公式与Rüger近似公式的误差主要是由于对各向异性参数项的表征不同。基于上述介质分解理论,纵波反射系数近似公式可分解为各向同性反射系数项与各向异性反射系数项,本文所推导的一阶扰动近似公式与Rüger近似公式具有相似的各向同性反射系数项,因此两个公式的误差主要受控于各向异性反射系数项的定量表征。同时也说明了研究高阶扰动近似公式对提高大入射角反射系数精度具有重要意义。
基于表 1中模型参数,利用式(19)计算弹性界面处的方位纵波反射系数RPP,得到纵波反射系数RPP随入射角和方位角变化的曲面(图 3)。
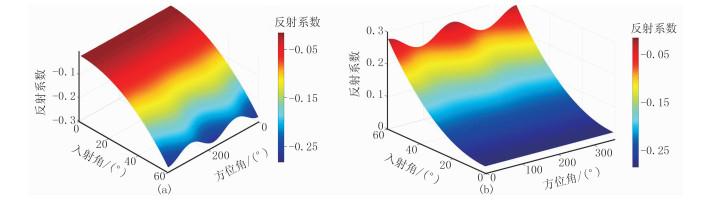
|
图 3 模型Ⅰ纵波反射系数RPP曲面 (a)各向同性/HTI界面;(b)HTI/各向同性界面 |
对于各向同性/HTI界面,在入射角较小时,反射系数方位特征不明显,随着入射角的增大,反射系数随方位角的变化特征逐渐明显,变化特征可表示为一条周期为π的余弦曲线(图 3a)。HTI介质具有水平对称轴,平行于对称轴方向的各向异性特征最为明显,垂直于对称轴方向不具有各向异性特征,因此,基于测线方向与HTI介质对称轴方向相同的假设,受各向异性参数项的影响,平行于测线方向(方位角为0°)的纵波反射系数曲线随入射角变化的幅度最大,垂直于测线方向(方位角为90°)的纵波反射系数曲线随入射角变化的幅度最小。对于HTI/各向同性界面,纵波反射系数也具有相似的方位变化特征(图 3b)。因此,可利用HTI介质的方位AVO特征进行弹性参数反演。
2.2 模型Ⅱ正演分析模型Ⅱ中三层介质均为HTI介质,弹性参数如表 2所示,假设HTI介质对称轴与测线方向平行。
|
|
表 2 模型Ⅱ弹性参数 |
图 4为利用一阶扰动近似公式、Rüger近似公式与HTI介质反射系数精确公式计算的模型Ⅱ不同方位角的纵波反射系数曲线。与模型Ⅰ结果相似,小入射角时,利用三个公式所计算的纵波反射系数特征曲线拟合度较高,具有较高的精度;由于忽略了弹性参数高阶近似项,在中、大入射角时,近似公式与精确公式的误差逐渐增大。上界面的纵波反射系数特征曲线(图 4a),一阶扰动近似公式比Rüger近似公式具有更高的精度。下界面的纵波反射系数特征曲线(图 4b),与模型Ⅰ结果相似,在中入射角时,Rüger近似公式与一阶扰动近似公式出现误差,但基于一阶扰动近似公式所算得的反射系数曲线与精确公式的曲线具有相似的变化趋势。可见,本文所推导的一阶扰动近似公式与Rüger近似公式的误差随着方位角的变化而变化,随着方位角的增大,各向异性参数项对于纵波反射系数的影响逐渐减小,当方位角为90°时,各向异性参数为0,此时弹性分界面两侧均为各向同性介质,反射系数近似公式仅受控于纵横波速度项与密度项。

|
图 4 模型Ⅱ方位角为0°(左)、45°(中)、90°(右)纵波反射系数RPP曲线对比 (a)上界面;(b)下界面 |
图 5为模型Ⅱ纵波反射系数曲面,相比于模型Ⅰ纵波反射系数曲面,当纵波传播至HTI1/HTI2界面时,在小角度范围内,反射系数随方位角变化特征与模型Ⅰ相同,随着入射角的增大,反射系数随方位角变化的特征趋于明显。
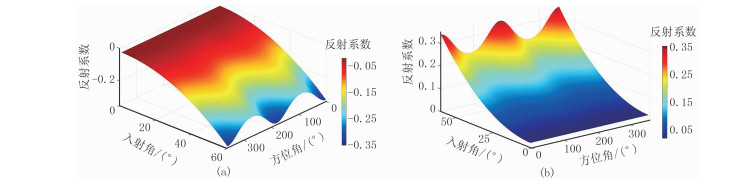
|
图 5 模型Ⅱ纵波反射系数RPP曲面 (a)HTI1/HTI2界面;(b)HTI2/HTI1界面 |
由于模型Ⅱ界面两侧介质均为HTI介质,各向异性对界面处纵波反射系数的传播特征影响更为剧烈,因此相较于模型Ⅰ,在中远炮检距范围内,模型Ⅱ纵波反射系数随方位角的变化特征更为明显,当界面两侧介质为HTI2/HTI1时,纵波反射系数方位变化特征相似。
综合分析图 3与图 5,本文所推导的扰动近似方程不仅适用于描述各向同性/HTI界面处的纵波反射系数特征,当界面两侧均为HTI介质时,该方程同样能够对界面纵波反射系数变化特征进行表述,证明了该方程具有较高的精度和一定适用性。
综上所述,纵波反射系数变化特征随炮检距的增大而增大,当测线方向与介质对称轴方向呈一定差值时,纵波反射系数特征也随之变化。基于在中远炮检距范围内纵波反射系数的变化特征,可进行介质弹性参数反演;基于纵波反射系数在中远炮检距的方位变化特征,可进行裂缝预测。本文所推导的方位观测系统下纵波反射系数一阶扰动近似方程提高了中远炮检距纵波反射系数的精度,进而可更为明显地对HTI介质的方位AVO特征进行表征,达到提高参数反演与裂缝预测精度的目的。
3 结论与认识本文以HTI介质精确反射透射系数公式为基础,根据散射矩阵与介质分解理论推导了HTI介质一阶扰动近似公式,在方位观测系统下计算两个三层模型的反射系数。
对于三层模型的上界面,本文所推导的HTI介质一阶反射系数近似公式比Rüger近似公式明显具有更高的精度,使中远炮检距信息的利用率得以提升。对于三层模型的下界面,本文所推导的近似公式精度低于Rüger近似公式,但曲线变化趋势与精确公式更加吻合。该公式可作为五维地震反演方法的理论基础,应用五维叠前地震数据中丰富的炮检距与方位角信息,能提高反演精度。
由于忽略弹性参数高阶项,该公式仅针对各向异性参数项反演精度有一定提升,若想进一步提高弹性参数反演精度,则需利用弹性参数高阶项,构建高阶近似公式。
附录A HTI介质方位观测PP波反射系数一阶扰动近似推导基于弱各向异性假设,若测线方向与介质对称轴方向平行,忽略弹性参数高阶项,对相速度与波的偏振方向进行近似表征
| $ \left\{ \begin{array}{l} {V_{\rm{P}}} \approx {V_{{\rm{P0}}}}\left\{ {1 + {\delta ^{\left( {\rm{V}} \right)}}{{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi + } \right.\\ \;\;\;\;\;\;\left. {\left[ {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right]{{\sin }^4}{\theta _{\rm{P}}}{{\cos }^4}\varphi } \right\}\\ {V_{{\rm{SV}}}} \approx {V_{{\rm{S0}}}}\left\{ {1 + {\gamma ^{\left( {\rm{V}} \right)}} + \frac{{V_{{\rm{P0}}}^2}}{{V_{{\rm{SV0}}}^2}}\left[ {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right] \times } \right.\\ \;\;\;\;\;\left. {\left( {{{\cos }^2}{\theta _{{\rm{SV}}}} + {{\sin }^2}{\theta _{{\rm{SV}}}}{{\cos }^2}\varphi } \right){{\sin }^2}{\theta _{{\rm{SV}}}}{{\cos }^2}\varphi } \right\}\\ {V_{{\rm{SH}}}} \approx {V_{{\rm{S0}}}}\left[ {1 + {\gamma ^{\left( {\rm{V}} \right)}}{{\sin }^2}{\theta _{{\rm{SH}}}}{{\cos }^2}\varphi } \right] \end{array} \right. $ | (A-1) |
| $ {\mathit{\boldsymbol{P}}_{{\rm{qP}}}} \approx \left[ \begin{array}{l} \sin {\theta _{\rm{P}}}\cos \varphi \left\{ {1 + \left( {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right) \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left[ {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right]{{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\}\\ \sin {\theta _{\rm{P}}}\sin \varphi \left\{ {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left( {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right){{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\}\\ \cos {\theta _{\rm{P}}}\left\{ {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left( {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right){{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\} \end{array} \right] $ | (A-2) |
| $ {\mathit{\boldsymbol{P}}_{{\rm{qSV}}}} \approx \left[ \begin{array}{l} \left( {{{\cos }^2}{\theta _{\rm{P}}} + {{\sin }^2}{\theta _{\rm{P}}}\sin \varphi } \right)\left\{ {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left( {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right){{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\}\\ - \sin {\theta _{\rm{P}}}\cos {\theta _{\rm{P}}}\cos \varphi \left\{ {1 + \left( {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right) \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left( {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right){{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\}\\ - \sin {\theta _{\rm{P}}}\cos {\theta _{\rm{P}}}\cos \varphi \left\{ {1 + \left( {1 - {{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right) \times } \right.\\ \;\;\;\;\left. {f\left[ {{\delta ^{\left( {\rm{V}} \right)}} - 2\left( {{\varepsilon ^{\left( {\rm{V}} \right)}} - {\delta ^{\left( {\rm{V}} \right)}}} \right){{\sin }^2}{\theta _{\rm{P}}}{{\cos }^2}\varphi } \right]} \right\} \end{array} \right] $ | (A-3) |
| $ {\mathit{\boldsymbol{P}}_{{\rm{SH}}}} \approx \left( {\begin{array}{*{20}{c}} 0\\ { - \cos {\theta _{{\rm{SH}}}}}\\ {\sin {\theta _{{\rm{SH}}}}\sin \varphi } \end{array}} \right) $ | (A-4) |
式中
| $ f = \frac{{V_{{\rm{P0}}}^2}}{{V_{{\rm{P0}}}^2 - V_{{\rm{S0}}}^2}} = {\left( {1 - \frac{{V_{{\rm{S0}}}^2}}{{V_{{\rm{P0}}}^2}}} \right)^{ - 1}} $ | (A-5) |
将上述近似表征代入系数矩阵,基于扰动思想与介质分解理论,可将矩阵分解为背景矩阵(Mu,Nu,Ru)与一阶扰动矩阵(ΔM,ΔN,ΔR),其中背景矩阵元素为
| $ \left\{ \begin{array}{l} M_{11}^{\rm{u}} = - M_{14}^{\rm{u}} = - N_1^{\rm{u}} = \sin {{\bar \theta }_{\rm{P}}}\cos \varphi \\ M_{12}^{\rm{u}} = - M_{15}^{\rm{u}} = 1 - {\sin ^2}{{\bar \theta }_{{\rm{SV}}}}{\cos ^2}\varphi \\ M_{13}^{\rm{u}} = M_{16}^{\rm{u}} = 0 \end{array} \right. $ | (A-6) |
| $ \left\{ \begin{array}{l} M_{21}^{\rm{u}} = - M_{24}^{\rm{u}} = - N_2^{\rm{u}} = \sin {{\bar \theta }_{\rm{P}}}\sin \varphi \\ M_{22}^{\rm{u}} = - M_{25}^{\rm{u}} = - {\sin ^2}{{\bar \theta }_{{\rm{SV}}}}\sin \varphi \cos \varphi \\ M_{23}^{\rm{u}} = M_{26}^{\rm{u}} = \cos {{\bar \theta }_{{\rm{SH}}}}\\ M_{31}^{\rm{u}} = M_{34}^{\rm{u}} = N_3^{\rm{u}} = - \cos {{\bar \theta }_{\rm{P}}}\\ M_{32}^{\rm{u}} = M_{35}^{\rm{u}} = \sin {{\bar \theta }_{{\rm{SV}}}}\cos {{\bar \theta }_{{\rm{SV}}}}\cos \varphi \\ M_{33}^{\rm{u}} = - M_{36}^{\rm{u}} = \sin {{\bar \theta }_{{\rm{SH}}}}\sin \varphi \\ M_{41}^{\rm{u}} = M_{44}^{\rm{u}} = N_4^{\rm{u}} = - 2\bar \rho \bar V_{{\rm{S0}}}^2p\cos {{\bar \theta }_{\rm{P}}}\sin \varphi \\ M_{42}^{\rm{u}} = M_{45}^{\rm{u}} = - \bar \rho {{\bar V}_{{\rm{S0}}}}\cos {{\bar V}_{{\rm{SV}}}}\left( {1 - {{\sin }^2}{{\bar \theta }_{{\rm{SV}}}}{{\cos }^2}\varphi } \right)\\ M_{43}^{\rm{u}} = - M_{16}^{\rm{u}} = \bar \rho \bar V_{{\rm{S0}}}^2p\sin {{\bar \theta }_{{\rm{SH}}}}\sin \varphi \cos \varphi \end{array} \right. $ | (A-7) |
| $ \left\{ \begin{array}{l} M_{51}^{\rm{u}} = M_{54}^{\rm{u}} = N_5^{\rm{u}} = - 2\bar \rho \bar V_{{\rm{S0}}}^2p\cos {{\bar \theta }_{\rm{P}}}\sin \varphi \\ M_{52}^{\rm{u}} = M_{55}^{\rm{u}} = 2\bar \rho \bar V_{{\rm{S0}}}^2p\sin {{\bar \theta }_{{\rm{SV}}}}\cos {{\bar \theta }_{{\rm{SV}}}}\sin \varphi \cos \varphi \\ M_{53}^{\rm{u}} = - M_{56}^{\rm{u}} = - \bar \rho \bar V_{{\rm{S0}}}^2\left( {\frac{1}{{{{\bar V}_{{\rm{S0}}}}}} - p\sin {{\bar \theta }_{{\rm{SH}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {p\sin {{\bar \theta }_{{\rm{SH}}}}{{\sin }^2}\varphi } \right)\\ M_{61}^{\rm{u}} = - M_{64}^{\rm{u}} = - N_6^{\rm{u}} = \bar \rho {{\bar V}_{{\rm{P0}}}} - 2\bar \rho \bar V_{{\rm{S0}}}^2p\sin {{\bar \theta }_{\rm{P}}}\\ M_{62}^{\rm{u}} = - M_{65}^{\rm{u}} = - 2\bar \rho \bar V_{{\rm{S0}}}^2p{\cos ^2}{{\bar \theta }_{{\rm{SV}}}}\cos \varphi \\ M_{63}^{\rm{u}} = M_{66}^{\rm{u}} = - 2\bar \rho \bar V_{{\rm{S0}}}^2p\cos {{\bar \theta }_{{\rm{SH}}}}\sin\varphi \end{array} \right. $ | (A-8) |
式中
| $ p \approx \frac{{\sin {{\bar \theta }_{\rm{P}}}}}{{{{\bar V}_{{\rm{P0}}}}}} = \frac{{\sin {{\bar \theta }_{\rm{S}}}}}{{{{\bar V}_{{\rm{S0}}}}}} $ | (A-9) |
当仅背景介质为均匀各向同性介质时,反射系数背景矩阵可表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}^{\rm{u}}} = {\left[ {\begin{array}{*{20}{c}} {R_{{\rm{PP}}}^{\rm{u}}}&{R_{{\rm{PSV}}}^{\rm{u}}}&{R_{{\rm{PSH}}}^{\rm{u}}}&{T_{{\rm{PP}}}^{\rm{u}}}&{T_{{\rm{PSV}}}^{\rm{u}}}&{T_{{\rm{PSH}}}^{\rm{u}}} \end{array}} \right]^{\rm{T}}}\\ \;\;\;\;\; = {\left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0 \end{array}} \right]^{\rm{T}}} \end{array} $ | (A-10) |
对矩阵各参数取一阶扰动项,将背景项与一阶扰动项代入表达式
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{R}} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{u}}}} \right)^{ - 1}}\left( {\Delta \mathit{\boldsymbol{N}} - \Delta \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{R}}^{\rm{u}}}} \right) $ | (A-11) |
通过计算整理,可得到HTI介质方位观测五维一阶扰动近似公式
| $ \begin{array}{l} {R_{{\rm{PP}}}}\left( {\theta ,\varphi } \right)\\ = \frac{1}{2}\left( {1 + {{\tan }^2}{{\bar \theta }_{\rm{P}}}} \right)\frac{{\Delta {V_{{\rm{P0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}} - 4\frac{{\bar V_{{\rm{S0}}}^2}}{{\bar V_{{\rm{P0}}}^2}}{\sin ^2}{{\bar \theta }_{\rm{P}}}\frac{{\Delta {V_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{S0}}}}}} + \\ \;\;\;\frac{1}{2}\left[ {1 - 4{{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)}^2}{{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right]\frac{{\Delta \rho }}{{\bar \rho }} + \\ \;\;\;\frac{1}{2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\varphi \left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right) \times \\ \;\;\;\left( {1 - {{\sin }^2}{{\bar \theta }_{\rm{P}}}{{\cos }^2}\varphi } \right)\Delta {\delta ^{\left( {\rm{V}} \right)}} + \\ \;\;\;\frac{1}{2}{\sin ^4}{{\bar \theta }_{\rm{P}}}{\cos ^4}\varphi \left( {1 + {{\sin }^2}{{\bar \theta }_{\rm{P}}}} \right)\Delta {\varepsilon ^{\left( {\rm{V}} \right)}} - \\ \;\;\;4{\left( {\frac{{{{\bar V}_{{\rm{S0}}}}}}{{{{\bar V}_{{\rm{P0}}}}}}} \right)^2}{\sin ^2}{{\bar \theta }_{\rm{P}}}{\cos ^2}\varphi \Delta {\gamma ^{\left( {\rm{V}} \right)}} \end{array} $ | (A-12) |
| [1] |
Zoeppritz K, Erdbebnenwellen V. On the reflection and penetration of seismic waves through unstable layers[J]. Göettinger Nachrichten, 1919, 1(1): 66-84. |
| [2] |
Aki K, Richards P G. Quantitative Seismology:Theory and Methods[M]. W H Freeman and Co Cambridge, 1980.
|
| [3] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [4] |
Rüger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [5] |
Vavryuk V, PšEník I. PP-wave reflection coeffi-cients in weakly anisotropic elastic media[J]. Geophysics, 1998, 63(6): 2129-2141. DOI:10.1190/1.1444506 |
| [6] |
朱兆林, 赵爱国. 裂缝介质的纵波方位AVO反演研究[J]. 石油物探, 2005, 44(5): 499-503. ZHU Zhaolin, ZHAO Aiguo. Azimuthal AVO inversion of P-wave in fractured medium[J]. Geophysical Prospecting for Petroleum, 2005, 44(5): 499-503. DOI:10.3969/j.issn.1000-1441.2005.05.019 |
| [7] |
吴国忱. 各向异性介质地震波传播与成像[M]. 山东东营: 石油大学出版社, 2006. WU Guochen. Seismic Wave Propagation and Imaging in Anisotropic Media[M]. Dongying, Shandong: Petroleum University Press, 2006. |
| [8] |
梁锴, 印兴耀, 吴国忱. TTI介质qP波入射精确和近似反射透射系数[J]. 地球物理学报, 2011, 54(1): 208-217. LIANG Kai, YIN Xingyao, WU Guochen. Exact and approximate reflection and transmission coefficient for incident qP wave in TTI media[J]. Chinese Journal of Geophysics, 2011, 54(1): 208-217. DOI:10.3969/j.issn.0001-5733.2011.01.022 |
| [9] |
司芗, 吴国忱. 裂隙等效TTI介质qP波反射特征研究[J]. 地球物理学进展, 2012, 27(5): 2091-2099. SI Xiang, WU Guochen. Study on qP-wave reflectivity in fracture equivalent TTI media[J]. Progress in Geophysics, 2012, 27(5): 2091-2099. |
| [10] |
李春鹏.基于方位地震道集的裂缝型储层预测方法研究[D].山东青岛: 中国石油大学(华东), 2013. LI Chunpeng. Research on Fractured Reservoir Prediction with Azimuthal Seismic Data[D].China University of Petroleum(East China), Qingdao, Shandong, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10425-1015024755.htm |
| [11] |
张广智, 陈怀震, 印兴耀, 等. 基于各向异性AVO的裂缝弹性参数叠前反演方法[J]. 吉林大学学报(地球科学版), 2012, 42(3): 845-851. ZHANG Guangzhi, CHEN Huaizhen, YIN Xingyao, et al. Method of fracture elastic parameter inversion based on anisotropic AVO[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(3): 845-851. |
| [12] |
杜炳毅, 杨午阳, 王恩利, 等. 基于杨氏模量、泊松比和各向异性梯度的裂缝介质AVAZ反演方法[J]. 石油物探, 2015, 54(2): 218-225. DU Bingyi, YANG Wuyang, Wang Enli, et al. AVAZ inversion based on Young's modulus, Poisson's ratio and anisotropy gradient in fractured media[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 218-225. DOI:10.3969/j.issn.1000-1441.2015.02.014 |
| [13] |
潘新朋, 张广智, 印兴耀. 非均质HTI介质裂缝弱度参数地震散射反演[J]. 石油地球物理勘探, 2017, 52(6): 1226-1235. PAN Xinpeng, ZHANG Guangzhi, YIN Xingyao. Seismic scattering inversion for fracture weakness in heterogeneous HTI media[J]. Oil Geophysical Prospecting, 2017, 52(6): 1226-1235. |
| [14] |
吴国忱, 赵小龙, 唐杰, 等. 横观各向同性(TI)岩石弹性模量一阶扰动近似[J]. 中国科学:地球科学, 2017, 47(8): 916-926. WU Guochen, ZHAO Xiaolong, TANG Jie, et al. First-order perturbation approximation for rock elastic moduli in transversely isotropic media[J]. Science China:Earth Sciences, 2017, 47(8): 916-926. |
| [15] |
刘洋, 董敏煜. 各向异性介质中的方位AVO[J]. 石油地球物理勘探, 1999, 34(3): 260-268. LIU Yang, DONG Minyu. Azimuth AVO in anisotropic media[J]. Oil Geophysical Prospecting, 1999, 34(3): 260-268. |
| [16] |
毛宁波, 谢涛, 杨凯, 等. 裂缝储层地震方位AVO正演模拟研究及应用[J]. 石油天然气学报, 2008, 30(5): 59-63. MAO Ningbo, XIE Tao, Yang Kai, et al. Study and application on AVO forward modeling of seismic orientation for fractured reservoirs[J]. Journal of Oil and Gas Technology, 2008, 30(5): 59-63. DOI:10.3969/j.issn.1000-9752.2008.05.014 |
| [17] |
刘百红, 杨强, 石展, 等. HTI介质的方位AVO正演研究[J]. 石油物探, 2010, 49(3): 232-239. LIU Baihong, YANG Qiang, SHI Zhan, et al. Azimuthal AVO simulation for HTI media[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 232-239. DOI:10.3969/j.issn.1000-1441.2010.03.004 |
| [18] |
刘依谋, 印兴耀, 张三元, 等. 宽方位地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 596-610. LIU Yimou, YIN Xingyao, ZHANG Sanyuan, et al. Recent advances in wide-azimuth seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 596-610. |
| [19] |
印兴耀, 张洪学, 宗兆云. OVT数据域五维地震资料解释技术研究现状与进展[J]. 石油物探, 2018, 57(2): 155-178. YIN Xingyao, ZHANG Hongxue, ZONG Zhaoyun. Research status and progress of 5D seismic data interpretation in OVT domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 155-178. DOI:10.3969/j.issn.1000-1441.2018.02.001 |
| [20] |
Vermeer G J O. Creating image gathers in the absence of proper common-offset gathers[J]. Exploration Geophysics, 1998, 29(4): 636-642. |
| [21] |
Cary P W.Common-offset-vector gathers: An alternative to cross-spreads for wide-azimuth 3-D surveys[C].SEG Technical Program Expanded Abstracts, 1999, 18: 1496-1499.
|
| [22] |
詹仕凡, 陈茂山, 李磊, 等. OVT域宽方位叠前地震属性分析方法[J]. 石油地球物理勘探, 2015, 50(5): 956-966. ZHAN Shifan, CHEN Maoshan, LI Lei, et al. OVT-domain wide-azimuth prestack seismic attribute analysis[J]. Oil Geophysical Prospecting, 2015, 50(5): 956-966. |
| [23] |
党青宁, 崔永福, 陈猛, 等. OVT域叠前裂缝预测技术--以塔里木盆地塔中ZG地区奥陶系碳酸盐岩为例[J]. 物探与化探, 2016, 40(2): 398-404. DANG Qingning, CUI Yongfu, CHEN Meng, et al. Fracture detection with prestack seismic data in OVT domain:A case study of the Ordovician carbonate re-servoir in ZG area of Tazhong district in Tarim Basin[J]. Geophysical and Geochemical Exploration, 2016, 40(2): 398-404. |
| [24] |
古发明, 李进步, 邹新宁, 等. 炮检距向量片技术在苏里格致密砂岩储层预测中的应用[J]. 地球物理学进展, 2017, 32(2): 610-617. GU Faming, LI Jinbu, ZOU Xinning, et al. Application of the offset vector tile technique in the Sulige tight sandstone reservoir prediction[J]. Progress in Geophysics, 2017, 32(2): 610-617. |
| [25] |
林娟, 娄兵, 张淑萍, 等. 准噶尔盆地玛湖1井区高密度三维OVT域裂缝预测的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 146-152. LIN Juan, LOU Bing, ZHANG Shuping, et al. Fracture prediction with the high-density 3D OVT domain in the Well Mahu 1 area, Junggar Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 146-152. |
| [26] |
Wang Y H. Approximations to Zoeppritz equations and their use in AVO analysis[J]. Geophysics, 1999, 64(6): 1920-1927. DOI:10.1190/1.1444698 |



 吴国忱 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
吴国忱 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: