② 中国石化胜利油田分公司勘探开发研究院, 山东东营 257015
② Research Institute of Exploration & Production, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257015, China
断层的精细识别与描述对于断块型油气藏的勘探开发具有重要意义。断块型油气藏断层复杂,人工解释断层的工作量与难度都较大,需借助相干、边缘检测、曲率等[1]地震属性技术或者不同手段结合的综合解释方法[2]进行断层的追踪与识别。断层解释精度与地震资料信噪比有关,一般的地震数据受到地质条件、采集条件和资料处理等多个因素的影响,信噪比通常较低,特别是中深层资料。为了提高地震资料的信噪比,同时保护断层等地质体边缘信息,需要对地震数据做具有保边作用的去噪处理。
使用双边滤波、Radon变换、F-X滤波等[3-5]传统滤波方法去噪,并不能有效保护断层等地质体的边界及方向信息。近年来,考虑地质体构造和裂缝发育方向的保边滤波技术得到了很大的发展。赵明章等[6]利用构造导向滤波技术提高地震资料信噪比,落实复杂断块圈闭;尹川等[7]利用基于倾角控制的构造导向滤波技术在断层识别中取得了很好的效果;徐红霞等[8]基于构造导向滤波技术将多属性分析技术应用在断溶体预测中,提高了预测精度和实际钻井吻合率;问雪等[9]利用构造导向平滑方法进行了断层解释工作,提高了解释效率及精度;Fehmers等[10]首次将各向异性扩散滤波技术应用于地震数据去噪,在保护断层等有用的构造信息的同时,提高了数据的信噪比;Weickert[11]和Lavialle等[12]对一致性增强滤波进行了改进,能更好地兼顾去噪与保护断层等构造边界信息;杨培杰等[13]提出了一种方向性边界保护滤波方法,在提高信噪比同时,较好地保持了断层信息;孙夕平等[14]讨论了如何选取各向异性扩散滤波的参数,提出了具有旋转不变特性的改进方法;王旭松等[15]结合倾角信息对各向异性扩散滤波构造张量矩阵进行了简化,提高了效率;张尔华等[16]将各向异性扩散滤波方法拓展到三维,在三维实际数据去噪中取得了较好的效果;严哲等[17]在各向异性扩散滤波算法中将相干值作为一个参数引入具体算法中,提高了对横向不连续点的保护性能;杨千里等[18]和姚振岸等[19-20]应用各向异性扩散滤波进行去噪,断层形态更清晰、准确。
本文在前人研究基础之上,结合图像处理中熵的概念及特征[21-24],提出了一种基于熵的各向异性扩散保边滤波方法。在地震数据连续性较好的区域,熵值较大;而在包含断点等特殊地质构造区域,其熵值较小。根据熵的特征,其大小只与数据的总体结构有关,与具体的振幅值无关。在计算数据的各向异性扩散幅度时,本文方法能在剔除噪声异常点影响情况下,定量控制保护特殊地质边界的二阶导数所占比例,从而更准确地保持断层等边界信息。
1 方法原理 1.1 各向异性扩散滤波各向异性扩散滤波的扩散过程等价于物理学热传导过程,类似于热传导方程,可以将扩散过程统一表示为[24-25]
| $ \frac{{\partial U}}{{\partial t}} = {\rm{div}}\left( {c\nabla U} \right) $ | (1) |
式中:U表示地震数据的振幅信息;c为扩散系数;t为扩散时间。
(1) 当系数c为常数时,扩散方程是线性各向同性方程,等同于对数据做高斯滤波,能够提高信噪比,但不能保护好断层等地质体的边界及方向信息;
(2) 当系数c使用图像递减函数[26]等改进系数来代替,扩散方程就是非线性各向同性方程,这种情况下去噪易造成阶梯效应和针孔效应,且对强噪区域无效;
(3) 使用扩散张量矩阵D替代扩散系数,则是真正意义上的各向异性扩散,各向异性信息隐藏在张量D中,在一些方向允许扩散,在其他方向如断层等地质体边界区域减少或者不允许扩散,既提高了信噪比,又保护了边界信息。
因此,三维各向异性扩散滤波方程最终可以表示为
| $ \left\{ \begin{array}{l} \frac{{\partial U\left( {x,y,z,t} \right)}}{{\partial t}} = {\rm{div}}\left[ {\mathit{\boldsymbol{D}} \cdot \nabla U\left( {x,y,z,t} \right)} \right]\\ U\left( {x,y,z,0} \right) = {U_0}\left( {x,y,z} \right) \end{array} \right. $ | (2) |
熵的概念由Clausius首先给出,用来评价能量在空间中的分布均匀程度,熵值越大说明能量分布越均匀[24]。当整个空间的能量完全均匀时,熵值达到最大。“图像熵”是对图像特征的一种统计表示,能够评价图像的平均信息量。相比于方差、均值等统计量,熵只与图像的总体结构有关,与具体的像素灰度值大小无关,可以避免噪声变化对图像梯度值的影响,从而可以更好地反映图像的变化。图像熵定义为
| $ H = \sum\limits_{i = 0}^{255} {{p_i}\lg {p_i}} $ | (3) |
式中pi表示图像中灰度值为i的像素所占比例。
类似于图像纹理,地震数据具有同样的纹理结构。引入熵的概念,在不受噪声干扰的情况下评价区域内振幅的隐含信息:当熵值较大时,说明该区域为常规地层;当熵值较小时,说明该区域振幅变化大,应包含着断层等特殊地质体的结构信息。计算地震数据熵的步骤如下。
(1)将地震数据灰度值化。
(2) 以目标点为中心,选择3×3×3大小的窗口构建一个灰度值数据子体,而后利用熵的概念,计算该子体的熵值作为该目标点的熵值,然后依次对每个点逐次扫描计算其熵值
| $ {H_{i,j,k}} = \sum\limits_{t \in {\mathit{\boldsymbol{\eta }}_{\rm{s}}}} {{p_{i,j,k,t}}\lg {p_{i,j,k,t}}} $ | (4) |
式中:(i,j,k)表示目标点的坐标信息;pi,j,k,t表示灰度数据子体中灰度值为t的像素所占比例;ηs表示以目标点为中心构建的窗口内灰度值级数大小。
(3) 对计算得到的所有数据点的熵值大小进行无量纲[0, 1]区间的归一化处理,得到归一化后的熵值数据H1。
(4) 计算地震数据的熵信息阈值
| $ {H_0} = \frac{{\sum {{H_1}} }}{{{N_\mathit{\boldsymbol{x}}} \times {N_y} \times {N_t}}} $ | (5) |
式中:Nx为Inline方向的道数;Ny为Crossline方向的道数;Nt为时间方向的采样点数。
一般在断层等特殊地质体边界处,其振幅二阶导数具有局部极大值,其他平坦区域,二阶导数值很小,与熵值呈负相关的关系。因此,在计算具有区域方向信息的结构张量矩阵并添加二阶导数辅助保护断层等特殊地质体边界信息时,可将改造后的熵值作为二阶导数添加量的比例系数
| $ {a_{i,j,k}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {H_0} - {H_{i,j,k}}\\ 0 \end{array}&\begin{array}{l} {H_{i,j,k}} < {H_0}\\ {H_{i,j,k}} \ge {H_0} \end{array} \end{array}} \right. $ | (6) |
当计算点的熵值大于阈值时,认为该区域近似平层,不需要添加二阶导数信息。为了后续各向异性扩散滤波迭代的稳定性,阈值设置不宜较大。
1.3 扩散张量的构建各向异性扩散滤波的关键就是构建扩散张量D。这就需要计算局部方向信息,然后依此作为特征向量构建扩散张量D。一般使用具有对称半正定的结构张量计算方向信息,即
| $ {\mathit{\boldsymbol{S}}_a} = {K_a} * \left( {\nabla {U_\sigma } \otimes \nabla {U_\sigma }} \right) $ | (7) |
式中:Uσ=Kσ*U,其中Kσ为高斯核函数,“*”为褶积运算符,σ为噪声尺度;“⊗”表示矩阵转置与矩阵相乘;Kα为高斯核函数,其中α为整合尺度,一般应大于噪声尺度;▽Uσ为数据的梯度信息,即
| $ \nabla {U_\sigma } = \left( {\frac{{\partial {U_\sigma }}}{{\partial x}},\frac{{\partial {U_\sigma }}}{{\partial y}},\frac{{\partial {U_\sigma }}}{{\partial z}}} \right) $ | (8) |
添加二阶导数信息后,结构张量重新写为
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_a} = {K_a} * \left[ {\nabla {U_\sigma } \otimes \nabla {U_\sigma } + } \right.\\ \;\;\;\;\left. {{a_{i,j,k}}{{\left( {\frac{{{\partial ^2}{U_\sigma }}}{{\partial {x^2}}},\frac{{{\partial ^2}{U_\sigma }}}{{\partial {y^2}}},\frac{{{\partial ^2}{U_\sigma }}}{{\partial {z^2}}}} \right)}^{\rm{T}}}{{\left( {\frac{{{\partial ^2}{U_\sigma }}}{{\partial {x^2}}},\frac{{{\partial ^2}{U_\sigma }}}{{\partial {y^2}}},\frac{{{\partial ^2}{U_\sigma }}}{{\partial {z^2}}}} \right)}^{\rm{T}}}} \right] \end{array} $ | (9) |
式中:ai,j,k为根地震数据的“熵”信息计算得到的系数;
| $ \mathit{\boldsymbol{D}} = \varepsilon \left( {{\xi _1},{\xi _2},{\xi _3}} \right)\left[ {\begin{array}{*{20}{c}} {{\beta _1}}&0&0\\ 0&{{\beta _2}}&0\\ 0&0&{{\beta _3}} \end{array}} \right]{\left( {{\xi _1},{\xi _2},{\xi _3}} \right)^{\rm{T}}} $ | (10) |
式中:ε代表横向不连续因子,对于连续地层ε→1,在断层位置ε→0,本文选取归一化相干值作为连续因子;β1、β2、β3为D的特征值,可以写为
| $ \left\{ \begin{array}{l} {\beta _1} = b\\ {\beta _2} = {\beta _3} = \left\{ \begin{array}{l} b\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0\\ b + \left( {1 - b} \right)\exp \left( { - \frac{C}{k}} \right)\;\;\;\;\;其他 \end{array} \right. \end{array} \right. $ | (11) |
式中:b为一个接近于0的正数,代表扩散强度;C通常设置为1;k为一致性参数,有
| $ k = {\left( {{\beta _1} - {\beta _2}} \right)^2} + {\left( {{\beta _1} - {\beta _3}} \right)^2} + {\left( {{\beta _2} - {\beta _3}} \right)^2} $ | (12) |
在一致性较高区域k远大于C,β2=β3≈1,扩散模型沿ξ2、ξ3方向扩散;在各向同性区域(k近似于0),三个方向扩散强度都很小。
得到扩散张量D后,就可以通过迭代法求解式(2),最终得到扩散后的数据
| $ \begin{array}{l} {U^{n + 1}} = {U^n} + \Delta t \cdot {\rm{div}}\left( {\mathit{\boldsymbol{D}} \cdot \nabla {U^n}} \right)\\ \;\;\;\;\;\;\; = {U^n}\left( {\frac{{\partial {U^n}}}{{\partial x}},\frac{{\partial {U^n}}}{{\partial y}},\frac{{\partial {U^n}}}{{\partial z}}} \right) \cdot \mathit{\boldsymbol{D}} \cdot {\left( {\frac{{\partial {U^n}}}{{\partial x}},\frac{{\partial {U^n}}}{{\partial y}},\frac{{\partial {U^n}}}{{\partial z}}} \right)^{\rm{T}}} \end{array} $ | (13) |
式中:Un和Un+1分别为第n次和第n+1次迭代得到的数据;Δt为迭代步长。
1.4 方法的实现基于熵的三维各向异性扩散滤波的具体实现过程为:
(1) 定义迭代次数为n=0,并设置最大迭代次数为N,此时,原始数据U0(x,y,z)为迭代初始值;
(2) 使用噪声尺度为σ的高斯核函数对数据进行预处理;
(3) 计算熵值,重构结构张量矩阵,求取矩阵的特征值及对应的特征向量;
(4) 计算扩散张量的特征值,确定横向连续性因子ε;
(5) 构建扩散张量矩阵D,根据式(13)计算第1次迭代结果,更新迭代次数n;
(6) 如果n < N,重复步骤(2)~步骤(5),否则输出结果。
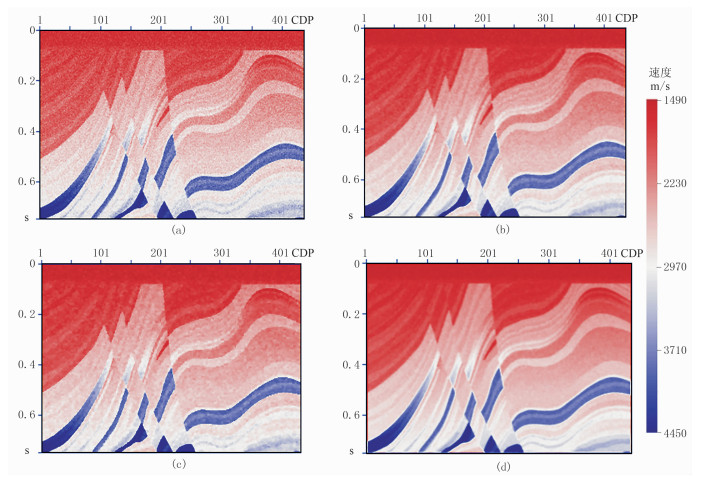
2 理论模型测试Marmousi模型是一个包含复杂构造特征的经典地质模型,本文截取其中包含断层构造的部分数据并添加了一些随机噪声后的模型(图 1a,信噪比为4)进行测试。
|
图 1 含噪Marmousi模型及不同方法去噪结果对比 (a)Marmousi模型(信噪比为4);(b)双边滤波;(c)Kuwaharab滤波;(d)本文方法 |
为了对比分析不同方法去噪保边的效果,分别采用双边滤波、Kuwaharab滤波与本文方法对模型进行处理,结果如图 1b~图 1d所示。可以看出:双边滤波方法虽在一定程度上消除了噪声,但平滑作用较强,边缘保持不理想;Kuwaharab滤波虽然能保持边缘信息,但去噪效果比双边滤波差;而本文方法消除噪声效果良好,同时较好保护了边缘特征,滤波后地质边界清晰,同相轴连续性也得到了强化,说明了本文方法保边去噪的有效性。
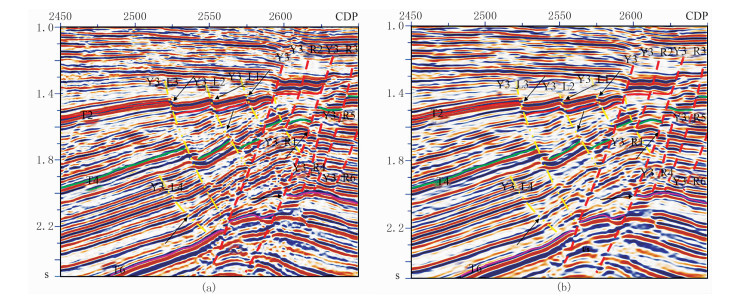
3 实际资料应用选取断裂众多、结构复杂、勘探难度较大的胜利油田M断块油藏实际资料验证本文方法的应用效果。图 2为应用基于图像熵的各向异性扩散保边滤波对地震数据进行去噪处理前、后Inline4080剖面,可见:滤波后同相轴更连续,断点更清晰(黑色箭头所示),断层更易识别,说明本文方法在提高资料信噪比的同时也保护了断层等地质体的边缘信息。
|
图 2 本文方法滤波前(a)、后(b)Inline4080剖面对比 |
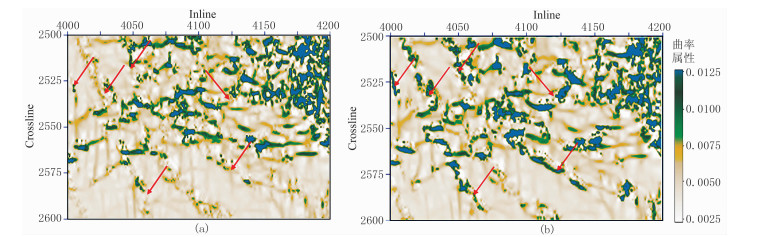
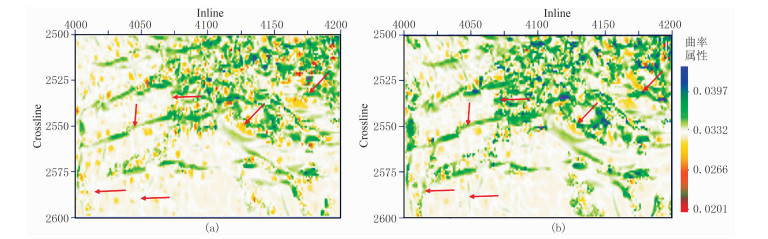
对应用本文滤波方法前、后的地震数据体分别计算最大正曲率属性。图 3为1.55s时间切片,图 4为沿T4的层位属性切片。可见,无论是时间切片还是沿层切片,滤波后都提高了分辨率,断层的形态及展布更符合地质规律,滤波前一些不易识别的断层(红色箭头所示)在滤波后其形态及展布更清晰,对后续的油藏开发具有重要意义。
|
图 3 滤波前(a)、后(b)曲率属性1.55s时间切片对比 |
|
图 4 滤波前(a)、后(b)沿T4层曲率属性切片对比 |
提高地震数据信噪比的同时保持断层等地质体的边界信息,对于后续的地震精细解释具有非常重要的意义。根据数据的熵信息,在构建携带方向信息的结构张量矩阵时,添加合适比例的二阶导数信息,在各向异性扩散滤波过程中,能更好地保护边界信息。模型测试及实际地震资料的应用结果表明,滤波后的地震资料信噪比明显提高,在连续地层区域,地震同相轴连续性增强,断层等地质体边界得到有效保护,断点更清晰。但由于需要计算地震数据熵信息,导致计算量增大,耗时较多,且对一些能量较弱区域去噪会造成细节丢失。因此,如何提高计算效率且不造成细节丢失是需要重点改进的方向。
| [1] |
张军华. 断块、裂缝型油气藏地震精细描述技术[M]. 山东青岛: 中国石油大学出版社, 2012.
|
| [2] |
李飞跃, 张功成, 杨海长, 等. 复杂断裂综合解释方法在长昌凹陷的应用[J]. 石油物探, 2017, 56(4): 543-550. LI Feiyue, ZHANG Gongcheng, YANG Haizhang, et al. Application of comprehensive interpretation me-thod for complicated fractures in Changchang Sag[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 543-550. DOI:10.3969/j.issn.1000-1441.2017.04.010 |
| [3] |
孙抗, 汪渤, 周志强, 等. 基于双边滤波的实时图像去雾技术研究[J]. 北京理工大学学报, 2011, 31(7): 810-813, 822. SUN Kang, WANG Bo, ZHOU Zhiqiang, et al. Real time image haze removal using bilateral filter[J]. Transactions of Beijing Institute of Technology, 2011, 31(7): 810-813, 822. |
| [4] |
薛昭, 董良国, 单联瑜. Radon变换去噪方法的保幅性理论分析[J]. 石油地球物理勘探, 2012, 47(6): 858-867. XUE Zhao, DONG Liangguo, SHAN Lianyu. Amplitude preservation theoretical analysis of Radon transforms de-noising method[J]. Oil Geophysical Prospecting, 2012, 47(6): 858-867. |
| [5] |
国九英, 周兴元. 用f-x域预测技术消除随机噪音[J]. 石油地球物理勘探, 1992, 27(5): 655-661. GUO Jiuying, ZHOU Xingyuan. Random nosie elimination using f-x domain prediction[J]. Oil Geophysical Prospecting, 1992, 27(5): 655-661. |
| [6] |
赵明章, 范雪辉, 刘春芳, 等. 利用构造导向滤波技术识别复杂断块圈闭[J]. 石油地球物理勘探, 2011, 46(增刊1): 128-133. ZHAO Mingzhang, FAN Xuehui, LIU Chunfang, et al. Complex fault-block traps identification with structure-oriented filter[J]. Oil Geophysical Prospecting, 2011, 46(S1): 128-133. |
| [7] |
尹川, 杜向东, 赵汝敏, 等. 基于倾角控制的构造导向滤波及其应用[J]. 地球物理学进展, 2014, 29(6): 2818-2822. YIN Chuan, DU Xiangdong, ZHAO Rumin, et al. Dip steered structure oriented filter and its application[J]. Progress in Geophysics, 2014, 29(6): 2818-2822. |
| [8] |
徐红霞, 沈春光, 李斌, 等. 多属性分析技术在碳酸盐岩断溶体预测中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 158-163. XU Hongxia, SHEN Chunguang, LI Bin, et al. Fault-karst carbonate reservoir prediction with comprehensive multi-attribute analysis[J]. Oil Geophysical Prospecting, 2017, 52(S2): 158-163. |
| [9] |
问雪, 陈雪芳, 陈胜红, 等. 利用结构导向平滑方法解释断层[J]. 石油地球物理勘探, 2017, 52(1): 146-151. WEN Xue, CHEN Xuefang, CHEN Shenghong, et al. Fault interpretation based on structure-oriented smoothing method[J]. Oil Geophysical Prospecting, 2017, 52(1): 146-151. |
| [10] |
Fehmers G C, Hocker C F W. Fast structural interpretation with structure-oriented filtering[J]. Geophysics, 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [11] |
Weickert J. Coherence-enhancing diffusion filtering[J]. International Journal of Computer Vision, 1999, 31(2/3): 111-127. DOI:10.1023/A:1008009714131 |
| [12] |
Lavialle O, Pop S, Germain C, et al. Seismic fault preserving diffusion[J]. Journal of Applied Geophysics, 2007, 61(2): 132-141. DOI:10.1016/j.jappgeo.2006.06.002 |
| [13] |
杨培杰, 穆星, 张景涛. 方向性边界保持断层增强技术[J]. 地球物理学报, 2010, 53(12): 2992-2997. YANG Peijie, MU Xing, ZHANG Jingtao. Orientational edge preserving fault enhance[J]. Chinese Journal of Geophysics, 2010, 53(12): 2992-2997. DOI:10.3969/j.issn.0001-5733.2010.12.023 |
| [14] |
孙夕平, 杜世通, 汤磊. 相干增强各向异性扩散滤波技术[J]. 石油地球物理勘探, 2004, 39(6): 651-655, 665. SUN Xiping, DU Shitong, TANG Lei. Coherent-enhancing anisotropic diffusion filtering technique[J]. Oil Geophysical Prospecting, 2004, 39(6): 651-655, 665. DOI:10.3321/j.issn:1000-7210.2004.06.006 |
| [15] |
王旭松, 杨长春. 对地震图像进行保护边缘滤波的非线性各向异性扩散算法[J]. 地球物理学进展, 2006, 21(2): 452-457. WANG Xusong, YANG Changchun. An edge preserving smoothing algorithm of seismic image using nonlinear anisotropic diffusion equation[J]. Progress in Geophysics, 2006, 21(2): 452-457. DOI:10.3969/j.issn.1004-2903.2006.02.017 |
| [16] |
张尔华, 王伟, 高静怀, 等. 非线性各向异性扩散滤波器用于三维地震资料噪声衰减与结构特征增强[J]. 地球物理学进展, 2010, 25(3): 866-870. ZHANG Erhua, WANG Wei, GAO Jinghuai. Non-li-near anisotropic diffusion filtering for 3D seismic noise removal and structure enhancement[J]. Progress in Geophysics, 2010, 25(3): 866-870. DOI:10.3969/j.issn.1004-2903.2010.03.019 |
| [17] |
严哲, 顾汉明, 蔡成国. 基于各向异性扩散滤波的地震图像增强处理[J]. 石油地球物理勘探, 2013, 48(3): 390-394. YAN Zhe, GU Hanming, CAI Chengguo. Seismic image enhancement based on anisotropic diffusion[J]. Oil Geophysical Prospecting, 2013, 48(3): 390-394. |
| [18] |
杨千里, 吴国忱, 赵小龙. 三维各向异性扩散滤波在地震数据处理中的应用[J]. 地球物理学进展, 2015, 30(5): 2287-2292. YANG Qianli, WU Guochen, ZHAO Xiaolong. Application of 3D anisotropic diffusion filter in seismic data processing[J]. Progress in Geophysics, 2015, 30(5): 2287-2292. |
| [19] |
姚振岸, 孙成禹, 石小磊, 等. 基于曲波变化和各向异性扩散滤波的联合去噪技术[J]. 石油学报, 2016, 37(4): 490-498, 507. YAO Zhen'an, SUN Chengyu, SHI Xiaolei, et al. A combined denoising method on Curvelet transform and anisotropic diffusion filtering[J]. Acta Petrolei Sinica, 2016, 37(4): 490-498, 507. |
| [20] |
姚振岸, 孙成禹, 唐杰.面向地质体边界保持的随机噪音压制方法研究[C].SPG/SEG北京2016国际地球物理会议, 2016, 203-206. YAO Zhen'an, SUN Chengyu, TANG Jie. Geologic-target amplitude and edge preserving oriented random noise elimination[C].SPG/SEG Beijing 2016 International Geophysical Conference, 2016, 203-206. |
| [21] |
Entropy Wikipedia.http://en.wikipedia.org/wiki/Entropy, 2012.
|
| [22] |
曹雪虹, 张宗橙. 信息论与编码[M]. 北京: 清华大学出版社, 2009.
|
| [23] |
李金才, 马自辉, 彭宇行, 等. 基于图像熵的各向异性扩散相干斑噪声抑制[J]. 物理学报, 2013, 62(9): 099501. LI Jincai, MA Zihui, PENG Yuxing, et al. Speckle reduction by image entropy anisotropic diffusion[J]. Acta Physica Sinica, 2013, 62(9): 099501. |
| [24] |
Koenderink J. The structure of images[J]. Biological Cybernetics, 1984, 50(5): 363-370. DOI:10.1007/BF00336961 |
| [25] |
乔刚.基于各向异性扩散的图像处理技术及其应用[D].四川成都: 电子科技大学, 2012, 24-30. QIAO Gang. Image Processing Technology Based on Anisotropic Diffusion and Its Application[D].Uni-versity of Electronic and Technology of China, Chengdu, Sichuan, 2012, 24-30. http://cdmd.cnki.com.cn/Article/CDMD-10614-1012472711.htm |
| [26] |
Perona P, Malik J. Scale space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639. DOI:10.1109/34.56205 |



 张军华 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张军华 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: