② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
③ 海底科学与探测技术教育部重点实验室, 山东青岛 266100
② Laboratory of Marine Mineral Resource Evaluation and Detection, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China;
③ Key Laboratory of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Qingdao, Shandong 266100, China
速度是地震波在地下传播过程中的重要物性参数之一,速度建模是高精度地震成像和资料解释的重要基础。全波形反演综合利用了地震波场中的运动学和动力学信息,可进行高精度、多参数建模,满足复杂构造的精度要求,是勘探地球物理领域的研究热点[1-4]。
全波形反演方法具有完备的理论基础[5-7],该方法基于最小二乘最佳拟合原理,利用正传波场与伴随震源的反传波场的互相关构造梯度,以此作为速度模型的更新方向。由于反演是一个非线性过程,常规全波形反演容易陷入局部极小值[8],为解决这个问题,Bunks等[9]提出了时间域多尺度分频处理的理念,通过对资料做分频处理,从低频信息开始反演,把反演更新的速度模型作为初始模型逐步向高频反演。Pica等[10]和Pratt[11-12]提出了频率域全波形反演的思想,相比时间域反演,其计算速度更快。Brossier等[13]在频率域实现了弹性波全波形反演,随着模型的增大,频率域正演需要海量内存[14],在很大程度上限制了频率域反演在实际三维地震勘探中的应用。结合时间域正演和频率域反演的优势,Sirgue等[15]提出了时间域正演及频率域反演的混合反演策略,避免了时间域波场反传的计算,提高了计算效率。
对于实际资料,全波形反演的建模精度受震源子波的影响。在野外采集环节很难获得准确的震源子波信息,且反演过程中震源子波的微小误差即可能造成反演结果和实际模型不匹配。目前子波求取方法大致包括三类。第一类方法主要基于地震反褶积模型,分为确定性和统计性两种方法[16-17]。提取确定性子波需要利用测井资料求解反射系数,因此在没有测井资料时该方法很难实现;统计性子波方法仅使用实测地震记录就可以提取地震子波,但如果没有明确的地层反射系数信息,精度很难保证[18]。第二类方法为反演子波法,Song等[19]提出在反演过程中统一计算子波,子波随模型的更新而更新。此种方法对初始模型的依赖性大,在没有精确初始模型的情况下很难取得理想效果。胡勇等[20]利用直达波信息构造反演目标震源函数,用全波形反演方法反演子波,取得了较好效果。第三类方法为不依赖子波法,即在反演过程中去除子波的影响。Choi等[21]在频率域提出利用褶积法和反褶积法消除子波对反演结果的影响,将观测数据与模拟数据的振幅与各自参考道的振幅先相除后计算差值,构建目标函数,此方法称为反褶积法;之后Choi等[22]提出了时间域去除子波影响的全波形反演,其实质是把波场和特征道在时间域做卷积处理,取得了较好的效果。敖瑞德等[23]把该方法应用到基于包络的全波形反演。王毓伟等[24]把地震道包络的全波形反演推广到弹性波,并结合时间域正演、频率域反演实现了对弹性参数的高精度重建。
以上去除子波影响的方法都是基于声波方程实现的,为了更接近地震波在地下介质传播的真实情况,满足全波形反演在内存和计算效率上的需求,本文提出不依赖子波的弹性波混合域全波形反演。文中给出了不依赖子波的弹性波混合域全波形的目标函数,并推导了反传震源的公式。相比于常规的全波形反演,在震源子波不准确的情况下,该方法依然能取得较好的反演结果。
1 方法理论 1.1 常规弹性波混合域全波形反演正演模拟采用二阶弹性波应力—位移方程
| $ \left\{ \begin{array}{l} \rho \frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}\\ \rho \frac{{{\partial ^2}{u_z}}}{{\partial {t^2}}} = \frac{{\partial {\tau _{zz}}}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}}\\ {\tau _{xx}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {u_x}}}{{\partial x}} + \lambda \frac{{\partial {u_z}}}{{\partial z}}\\ {\tau _{zz}} = \lambda \frac{{\partial {u_x}}}{{\partial x}} + \left( {\lambda + 2\mu } \right)\frac{{\partial {u_z}}}{{\partial z}}\\ {\tau _{xz}} = \mu \left( {\frac{{\partial {u_z}}}{{\partial x}} + \frac{{\partial {u_x}}}{{\partial z}}} \right) \end{array} \right. $ | (1) |
式中:ux、uz分别表示x、z分量的位移;τxx、τzz表示正应力;τxz表示剪应力;ρ为密度;λ、μ为拉梅常数。
全波形反演的目标函数有多种求法,本文使用最常用的L2范数下的目标函数
| $ E\left( \mathit{\boldsymbol{v}} \right) = \frac{1}{2}\sum\limits_{i = 1}^{{n_{\rm{s}}}} {{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^ * }} $ | (2) |
式中:v表示模型参数;ui表示第i炮频率域模拟记录;di表示第i炮频率域观测记录;上标“*”表示复共轭。频率域梯度可表示为
| $ \begin{array}{*{20}{c}} {\frac{{\partial E\left( \mathit{\boldsymbol{v}} \right)}}{{\partial \mathit{\boldsymbol{v}}}} = {\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\frac{{{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^{\rm{T}}}}}{{\partial \mathit{\boldsymbol{v}}}}{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^ * }} } \right]}\\ { = {\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {{{\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{v}}}}} \right)}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^ * }} } \right]} \end{array} $ | (3) |
式中:Re(·)表示取实部;ns为总炮数。频率域波动方程可以表示为S(ω)u(ω)=f(ω),这里S是阻抗矩阵,u为频率域波场列向量,f为震源矢量。等式两边对v求导并代入式(3),可得[6, 25-27]
| $ \frac{{\partial E}}{{\partial \mathit{\boldsymbol{v}}}} = {\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\mathit{\boldsymbol{u}}_i^{\rm{T}}{{\left( {\frac{{\partial \mathit{\boldsymbol{S}}}}{{\partial \mathit{\boldsymbol{v}}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{S}}^{ - 1}}{{\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{d}}_i}} \right)}^ * }} } \right] $ | (4) |
在弹性波混合域反演中,一般先计算目标函数关于λ、μ的导数,然后通过链式法则得到关于纵波速度vP、横波速度vS的导数。由式(5)~式(8)可推导弹性波频率域梯度
| $ \frac{{\partial E}}{{\partial \lambda }} = - {\mathop{\rm Re}\nolimits} \left[ {\left( {\frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_z}}}{{\partial z}}} \right)\left( {\frac{{\partial {{\tilde u}_x}}}{{\partial x}} + \frac{{\partial {{\tilde u}_z}}}{{\partial z}}} \right)} \right] $ | (5) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial E}}{{\partial \mu }} = - {\mathop{\rm Re}\nolimits} \left[ {\left( {\frac{{\partial {u_x}}}{{\partial z}} + \frac{{\partial {u_z}}}{{\partial x}}} \right)\left( {\frac{{\partial {{\tilde u}_z}}}{{\partial x}} + \frac{{\partial {{\tilde u}_x}}}{{\partial z}}} \right) + } \right.}\\ {\left. {2\left( {\frac{{\partial {u_x}}}{{\partial x}}\frac{{\partial {{\tilde u}_x}}}{{\partial x}} + \frac{{\partial {u_z}}}{{\partial z}}\frac{{\partial {{\tilde u}_z}}}{{\partial z}}} \right)} \right]} \end{array} $ | (6) |
| $ \frac{{\partial E}}{{\partial {v_{\rm{P}}}}} = 2\rho {v_{\rm{P}}}\frac{{\partial E}}{{\partial \lambda }} $ | (7) |
| $ \frac{{\partial E}}{{\partial {v_{\rm{S}}}}} = 2\rho {v_{\rm{S}}}\left( {\frac{{\partial E}}{{\partial \mu }} - 2\frac{{\partial E}}{{\partial \lambda }}} \right) $ | (8) |
式中ũx、ũz表示频率域反传波场。
1.2 不依赖子波的全波形反演地震波场记录d(t)可以用震源子波s(t)与脉冲响应I(t)的卷积表示
| $ d\left( t \right) = s\left( t \right) \otimes I\left( t \right) $ | (9) |
将式(9)变换到频率域, 可得
| $ d\left( \omega \right) = s\left( \omega \right)I\left( \omega \right) $ | (10) |
选第k个检波点作为特征道,在频率域将实测波场数乘以模拟波场的特征道,模拟波场数乘以实测波场的特征道[18],两个乘积的差值为
| $ D_{i,j}^x = u_{i,k}^xd_{i,j}^x - d_{i,k}^xu_{i,j}^x $ | (11) |
| $ D_{i,j}^z = u_{i,k}^zd_{i,j}^z - d_{i,k}^zu_{i,j}^z $ | (12) |
式中j表示检波点号。把式(11)、式(12)代入式(10)可得x、z分量的残差统一表达式
| $ \begin{array}{l} {D_{i,j}} = {u_{i,k}}{d_{i,j}} - {d_{i,k}}{u_{i,j}} = s_i^uI_{i,k}^us_i^dI_{i,k}^d - \\ \;\;\;\;\;\;\;\;s_i^dI_{i,k}^ds_i^uI_{i,j}^u \end{array} $ | (13) |
可以看出求取残差的两项都含有siusid,把这两项看成一个整体,即相当于实测波场与模拟波场拥有相同的震源子波,从而达到消除震源子波对反演结果影响的目的。
依据以上理论,构造弹性波的L2范数的目标函数
| $ E\left( \mathit{\boldsymbol{v}} \right) = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {{{\left[ {\begin{array}{*{20}{c}} {D_{i,j}^x}\\ {D_{i,j}^z} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {D_{i,j}^{x * }}\\ {D_{i,j}^{z * }} \end{array}} \right]} } } \right\} $ | (14) |
式中:nr表示检波点总数。用目标函数对模型参数v的偏导数作为模型更新的梯度方向,可得
| $ \begin{array}{*{20}{c}} {\frac{{\partial E}}{{\partial \mathit{\boldsymbol{v}}}} = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {{{\left[ {\begin{array}{*{20}{c}} {\frac{{\partial u_{i,k}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ {\frac{{\partial u_{i,k}^z}}{{\partial \mathit{\boldsymbol{v}}}}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {d_{i,j}^xD_{i,j}^{x * }}\\ {d_{i,j}^zD_{i,j}^{z * }} \end{array}} \right]} } } \right\} - }\\ {{\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {{{\left[ {\begin{array}{*{20}{c}} {\frac{{\partial u_{i,j}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ {\frac{{\partial u_{i,j}^z}}{{\partial \mathit{\boldsymbol{v}}}}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {d_{i,k}^xD_{i,j}^{x * }}\\ {d_{i,k}^zD_{i,j}^{z * }} \end{array}} \right]} } } \right\}} \end{array} $ | (15) |
将式(15)展开,可得
| $ \begin{array}{*{20}{c}} {\frac{{\partial E}}{{\partial \mathit{\boldsymbol{v}}}} = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {{{\left[ {\begin{array}{*{20}{c}} {\frac{{\partial u_{i,1}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,j}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,{n_{\rm{r}}}}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ {\frac{{\partial u_{i,1}^z}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,j}^z}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,{n_{\rm{r}}}}^z}}{{\partial \mathit{\boldsymbol{v}}}}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} 0\\ \vdots \\ {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {d_{i,j}^xD_{i,j}^{x * }} }\\ \vdots \\ 0\\ 0\\ \vdots \\ {\sum\limits_{j = 1}^{{n_{\rm{r}}}} {d_{i,j}^zD_{i,j}^{z * }} }\\ \vdots \\ 0 \end{array}} \right]} } \right\} - }\\ {{\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {{{\left[ {\begin{array}{*{20}{c}} {\frac{{\partial u_{i,1}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,j}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,{n_{\rm{r}}}}^x}}{{\partial \mathit{\boldsymbol{v}}}}}\\ {\frac{{\partial u_{i,1}^z}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,j}^z}}{{\partial \mathit{\boldsymbol{v}}}}}\\ \vdots \\ {\frac{{\partial u_{i,{n_{\rm{r}}}}^z}}{{\partial \mathit{\boldsymbol{v}}}}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {d_{i,k}^xD_{i,1}^{x * }}\\ \vdots \\ {d_{i,k}^xD_{i,j}^{x * }}\\ \vdots \\ {d_{i,k}^xD_{i,{n_r}}^{x * }}\\ {d_{i,k}^zD_{i,1}^{z * }}\\ \vdots \\ {d_{i,k}^zD_{i,j}^{z * }}\\ \vdots \\ {d_{i,k}^zD_{i,{n_{\rm{r}}}}^{z * }} \end{array}} \right]} } \right\}} \end{array} $ | (16) |
方程S(ω)u(ω)=f(ω)两边同时对模型参数v求导并代入式(16),可以得到
| $ \frac{{\partial E}}{{\partial \mathit{\boldsymbol{v}}}} = {\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{i = 1}^{{n_{\rm{s}}}} {\mathit{\boldsymbol{u}}_i^{\rm{T}}{{\left( {\frac{{\partial \mathit{\boldsymbol{S}}}}{{\partial \mathit{\boldsymbol{v}}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{S}}^{ - 1}}{{\left( {\mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{\beta }}} \right)}^ * }} } \right] $ | (17) |
式中
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\alpha }} = \left[ {d_{i,k}^{x * }D_{i,1}^x \cdots d_{i,k}^{x * }D_{i,j}^x \cdots d_{i,k}^{x * }D_{i,{n_{\rm{r}}}}^x \cdots } \right.\\ \;\;\;\;\;\;{\left. {d_{i,k}^{z * }D_{i,1}^z \cdots d_{i,k}^{z * }D_{i,j}^z \cdots d_{i,k}^{x * }D_{i,{n_{\rm{r}}}}^z} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{\beta }} = {\left[ {\begin{array}{*{20}{c}} {0 \cdots \sum\limits_{j = 1}^{{n_{\rm{r}}}} {d_{i,j}^{x * }D_{i,j}^x} \cdots 0}&{0 \cdots \sum\limits_{j = 1}^{{n_{\rm{r}}}} {d_{i,j}^{z * }D_{i,j}^z} \cdots 0} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (18) |
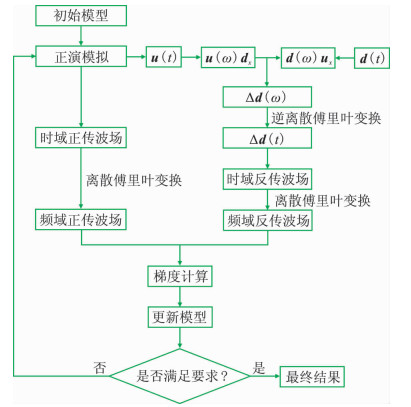
式(17)即为不依赖子波的弹性波频率域梯度表达式,其形式与式(4)基本相同,唯一不同之处在于伴随震源的求取方式,其中β的非零项所在的行为第k行。还可以看出,在频率域以(α-β)*为震源正演模拟得到的波场,或在时间域将(α-β)反传波场与正演波场做互相关就可以求出单炮梯度,最终梯度为所有炮梯度的累加。从图 1可以看出,不依赖子波的弹性波混合域全波形反演的计算过程相比于时间域每一炮的计算都减少了一次波场反传的过程,提高了计算效率,额外增加的离散傅里叶变换计算过程对整个计算效率的影响可以忽略不计。
|
图 1 不依赖子波的弹性波混合域全波形反演流程 |
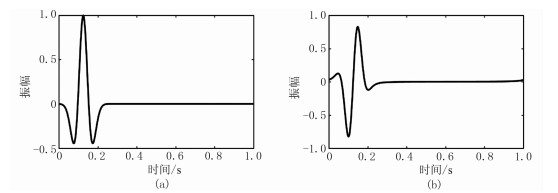
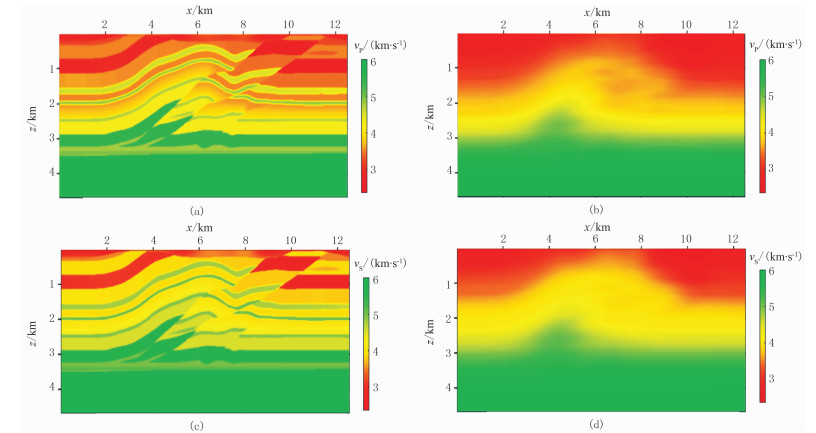
对Overthrust模型进行基于弹性波混合域全波形反演四种方案的试算:错误子波的常规全波形反演、正确子波的常规全波形反演和分别采用正确子波、错误子波的不依赖子波全波形反演。试算范围为12.5km(x)×4.675km(y),剖分网格距为25m。观测数据所用子波为雷克子波,主频为8.0Hz(图 2a),模拟数据所用子波为原始子波经过Hilbert变换后的子波(图 2b),即错误的子波。从子波波形图可以看出模拟子波与实际子波在振幅和相位上均有很大区别。图 3分别为真实纵(图 3a)、横(图 3c)波速度模型和经过高斯平滑后的反演初始纵(图 3b)、横(图 3d)波模型。本文采用全排列接收,采样间隔为2ms,共500个检波器,间隔为25m,炮间距为250m,共49炮。使用二阶应力—位移方程的交错网格高阶有限差分方法进行弹性波正演模拟,反演频率从低频3.0Hz到高频16.5Hz,频率间隔为1.5Hz,反演特征道选择最小炮检距道[23],每个频率点迭代20次,共200次。
|
图 2 模型试算采用的两种子波 (a)雷克子波;(b)Hilbert变换后的子波 |
|
图 3 Overthrust纵、横波速度模型 (a)实际纵波模型;(b)初始纵波模型;(c)实际横波模型;(d)初始横波模型 |
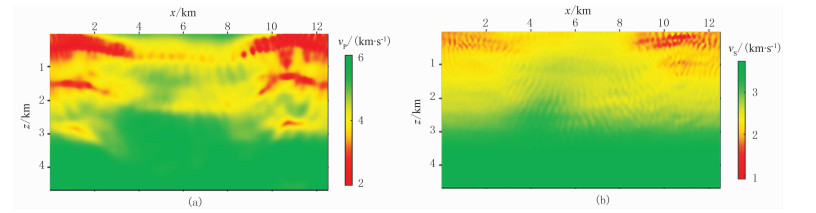
为验证本文方法的有效性,分别用经过Hilbert变换后的错误子波进行常规的全波形反演和本文不依赖子波的全波形反演。由于使用的子波与真实子波差别太大,常规反演方法合成的地震记录不仅受模型影响,还受子波影响,结果与实际记录相差太大,无法获得正确更新方向,致使计算误差越来越大,最终在第68次迭代时程序终止。因此,选取第67次迭代更新得到的速度模型反演结果(图 4), 可以看出,用错误的子波进行常规反演更新得到的模型与实际速度模型相差很大,说明用错误子波求取的速度更新方向本身是错误的。图 5为用本文方法得到的第67次迭代结果,与实际模型对比来看,不依赖子波的方法已经对模型的正确更新初见成效,反演出了模型的大致构造形态。
|
图 4 错误子波常规方法第67次迭代纵波(a)、横波(b)速度更新结果 |

|
图 5 错误子波本文方法第67次迭代纵波(a)、横波(b)速度更新结果 |
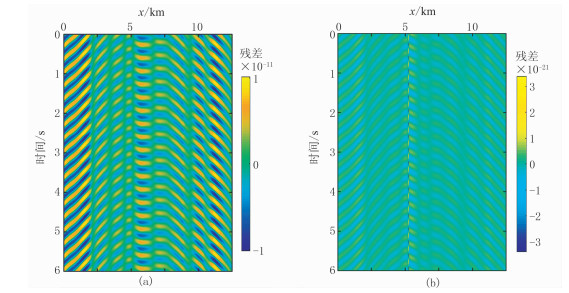
为对比本文方法与常规方法反传震源的区别,选取了频率为3Hz第15次迭代第21炮x分量的记录残差(图 6),从记录残差上可以看到,用不依赖子波的全波形反演得到的记录残差与用常规方法得到的记录残差的能量不在同一个数量级上,这主要是由于不依赖子波的反传震源求取中使用了记录与特征道相乘的方法。从图 6b可以看出,本文方法的第21炮记录残差的最小炮检距道出现异常,其原因是式(18)中β的特征道是非零项。由此可见,用本文方法得到的反传震源与式(18)是吻合的。
|
图 6 第21炮x分量3Hz记录残差 (a)常规反演;(b)本文方法 |
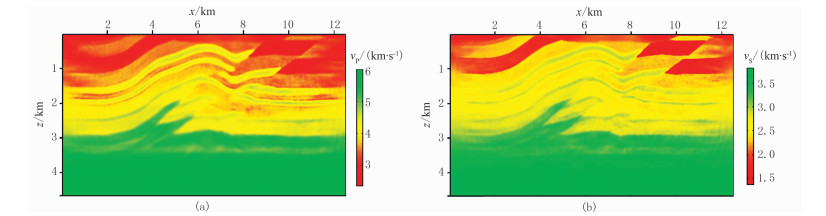
为进一步说明本文方法对子波的不依赖性,分别采用正确的子波和错误的子波进行不依赖子波的全波形反演,得到图 7和图 8所示最终反演结果,图 9是x=8.75km处的速度对比曲线。可以看出,用错误子波得到的结果与用正确子波得到的结果基本一致,证明了本文方法不依赖于子波。
|
图 7 正确子波本文方法的纵波(a)、横波(b)速度反演结果 |

|
图 8 错误子波本文方法的纵波(a)、横波(b)速度反演结果 |

|
图 9 不依赖子波反演x=8.75km处纵波(a)、横波(b)速度曲线对比 |
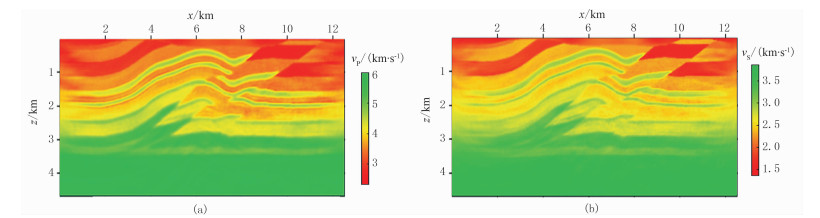
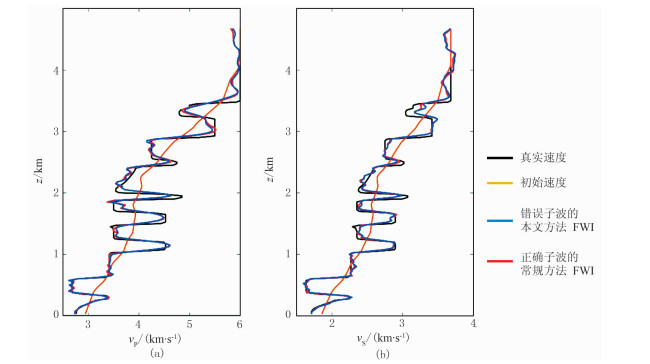
图 10是模拟子波与实际子波一致的情况下常规正演波形反演得到的弹性波反演结果。在实际应用中,很难得到准确的震源子波。从图 8可见,在模型参数全部一致的情况下,不依赖子波的反演结果与常规正演波形反演结果基本一致。这说明即使使用错误的子波,利用不依赖子波的正演波形反演依然能够得到正确速度模型。为了对比两种方法的模型速度变化,抽取模型x=8.75km处的速度值进行对比(图 11),可以看出两种方法的速度误差极小,速度曲线基本重合。
|
图 10 正确子波常规方法的纵波(a)、横波(b)速度反演结果 |
|
图 11 x=8.75km处纵波(a)、横波(b)速度不同方法反演结果对比 |
混合域全波形反演结合了时间域和频率域的优势,不仅提高了计算效率,还解决了频率域正演需要海量内存的困难。相比声波全波形反演,弹性波全波形反演具有更丰富的物性参数,更趋近地下真实情况,也更有利于复杂构造的多参数精确建模。用不准确的子波进行常规全波形反演得到的结果与真实模型相差很大,而用不依赖子波的全波形反演在子波不准确的情况下依然能够得到较好的反演效果,且不增加额外的正演运算过程。将此方法沿用到弹性波混合域,对三维实际资料的全波形反演具有重要意义。
| [1] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 77-83. YANG Qinyong, HU Guanghui, WANG Lixin. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. DOI:10.3969/j.issn.1000-1441.2014.01.011 |
| [2] |
苗永康. 基于L-BFGS算法的时间域全波形反演[J]. 石油地球物理勘探, 2015, 50(3): 469-474. MIAO Yongkang. Full waveform inversion in time domain based on limited-memory BFGS algorithm[J]. Oil Geophysical Prospecting, 2015, 50(3): 469-474. |
| [3] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |
| [4] |
李海山, 杨午阳, 雍学善. 三维一阶速度-应力声波方程全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 730-736. LI Haishan, YANG Wuyang, YONG Xueshan. Three-dimensional full waveform inversion based on the first-order velocity-stress acoustic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(4): 730-736. |
| [5] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [6] |
Tarantola A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Society for Industrial & Applied Mathematics, Philadelphia Pa, 2005: 342.
|
| [7] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 5(5): 1893-1903. |
| [8] |
梁展源, 吴国忱, 王玉梅. 基于波动方程重建震源子波的三维全波形反演[J]. 石油地球物理勘探, 2017, 52(6): 1200-1207. LIANG Zhanyuan, WU Guochen, WANG Yumei. A 3D full waveform inversion method based on reconstructed source wavelet with wave equation[J]. Oil Geophysical Prospecting, 2017, 52(6): 1200-1207. |
| [9] |
Bunks C, Saleck F, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [10] |
Pica A J, Diet P, Tarantola A. Nonlinear inversion of seismic reflection data in laterally invariant medium[J]. Geophysics, 1990, 55(1): 284-292. |
| [11] |
Pratt R G. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [12] |
Pratt R G. Inverse theory applied to multi-source cross-hole tomography, part 2:Elastic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 311-329. DOI:10.1111/gpr.1990.38.issue-3 |
| [13] |
Brossier R, Operto S, Virieux J. Seismic imaging of complex onshore structure by 2D elastic frequency-domain full waveform inversion[J]. Geophysics, 2009, 74(6): WCC105-WCC118. DOI:10.1190/1.3215771 |
| [14] |
Operto S, Virieux J, Amestoy P, et al. 3D finite-diffe-rence frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:a feasibility study[J]. Geophysics, 2007, 72(5): SM195-SM211. DOI:10.1190/1.2759835 |
| [15] |
Sirgue L, Etgen J T, Albertin U.3D frequency domain waveform inversion using time domain finite diffe-rence methods[C].Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, F022.
|
| [16] |
Fu L Y. Joint inversions of seismic data for acoustic impedance[J]. Geophysics, 2004, 69(6): 994-1004. |
| [17] |
杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-128. YANG Peijie, YIN Xingyao. Summary of seismic wavelet pick-up[J]. Oil Geophysical Prospecting, 2008, 43(1): 123-128. DOI:10.3321/j.issn:1000-7210.2008.01.021 |
| [18] |
陈健, 戴永寿, 张亚南, 等. 基于高阶统计量的地震子波提取方法评价[J]. 石油地球物理勘探, 2013, 48(3): 497-503. CHEN Jian, DAI Yongshou, ZHANG Yanan, et al. Evaluation approaches for wavelet pickup based on high-order statistics[J]. Oil Geophysical Prospecting, 2013, 48(3): 497-503. |
| [19] |
Song Z M, Williamson P R, Pratt R G. Frequency-domain acoustic-wave modeling and inversion of crosshole data, PartⅡ:Inversion method, synthetic experiments and real-data results[J]. Geophysics, 1995, 60(3): 796-809. DOI:10.1190/1.1443818 |
| [20] |
胡勇, 韩立国, 许卓, 等. 基于精确震源函数的解调包络多尺度全波形反演[J]. 地球物理学报, 2017, 60(3): 1088-1105. HU Yong, HAN Liguo, XU Zhuo, et al. Demodulation envelope multi-scale full waveform inversion based on precise seismic source function[J]. Chinese Journal of Geophysics, 2017, 60(3): 1088-1105. |
| [21] |
Choi Y, Shin C, Min D J, et al. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion:An amplitude approach[J]. Journal of Computational Physics, 2005, 208(2): 455-468. DOI:10.1016/j.jcp.2004.09.019 |
| [22] |
Choi Y, Alkhalifah T. Source-independent time-domain waveform inversion using convolved wavefields:Application to the Encoded Multisource Waveform Inversion[J]. Geophysics, 2011, 76(5): R125-R134. DOI:10.1190/geo2010-0210.1 |
| [23] |
敖瑞德, 董良国, 迟本鑫. 不依赖子波、基于包络的FWI初始模型建立方法研究[J]. 地球物理学报, 2015, 58(6): 1998-2010. AO Ruide, DONG Liangguo, CHI Benxin. Source-independent envelope-based FWI to build an initial model[J]. Chinese Journal of Geophysics, 2015, 58(6): 1998-2010. |
| [24] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. A multi-step strategy for mitigating severe nonli-nearity in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294. |
| [25] |
Crase E C, Wideman M Noble, Tarantola A. Nonlinear elastic inversion of land seismic reflection data[J]. Journal of Geophysical Research, 1992, 97(B4): 4685-4705. DOI:10.1029/90JB00832 |
| [26] |
Köhn D.Time domain 2D elastic full waveform tomography[D].Christian-Albrechts-Universität zu Kiel, 2011.
|
| [27] |
Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysical Journal International, 1987, 201(3): 1324-1334. |



 张会星 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
张会星 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: