早在20世纪80年代,Whitmore[1]就提出了叠前逆时偏移方法,但是其发展受到当时计算及存储能力的制约。近年来,随着计算机软、硬件水平的提升,逆时偏移逐渐成为高精度复杂构造成像的关键技术[2-8]。
为了避免逆时偏移计算过程的海量存储问题,Robert[9]采用随机边界的思想减小了存储量,在逆时延拓过程中利用最大时刻波场作为初始条件,通过逆时反传得到震源逆时传播波场。针对逆时偏移成像中伴随的强振幅低频噪声,Zhang等[10]提出了利用拉普拉斯滤波算子进行低频噪声压制的方法,刘红伟等[11]实现了该方法的GPU加速;陈康等[12]在此基础上提出了高阶拉普拉斯滤波算子;唐永杰等[13]提出一种基于波长平滑算子的回转波假象去除方法。
地震各向异性在真实介质中是普遍存在的,常规各向同性逆时偏移方法在处理各向异性问题时会导致层位成像不准确、同相轴能量不聚焦等问题,而弹性波逆时偏移成像需要考虑波场分离和串扰噪声等问题而使成像难度大大增加。徐文才等[14]在频率波数域求解Christoffel矩阵计算P波和S波在波数域的极化方向,得到空间域的波场分离算子; 杜启振等[15]从二维弹性波速度—应力方程出发,实现了VTI介质中二维弹性波叠前多分量逆时深度偏移。Alkhalifah[16-17]基于声波近似推导了VTI介质四阶拟声波方程,克服了弹性波各向异性数值模拟的缺陷。各向异性的声波近似能准确模拟qP波的运动学特征,但会受到qSV伪横波的干扰,Duveneck等[18]通过在激发点设定各向同性或椭圆各向异性震源环压制伪横波在成像中的干扰,杨富森等[19]采用旋转坐标系将VTI介质推广到TTI介质。Yoon等[20]和Costa等[21]通过计算震源和检波点波场的坡印廷矢量高效地提取各向同性介质的角度域共成像点道集(ADCIGs);李海强等[22]采取局部平面波分解法将震源波场和检波点波场分解为局部角度分量进行互相关成像得到角道集。
本文的VTI介质角度叠加逆时偏移方法,突破了各向同性方法不能准确模拟波场在实际介质中的传播规律而导致成像不准确或产生成像假象的瓶颈。首先,应用声波近似方程模拟qP波在VTI介质中的波场传播,在震源激发位置设定平滑的各向同性或椭圆各向异性震源环以压制qSV波的影响;在此基础上,提出了VTI介质逆时偏移的角度叠加实现策略,目的在于利用角度域共成像点道集中不同角度成像结果的叠加压制低频噪声,提高成像精度;最后,利用VTI逆冲断层模型以及A探区实际资料对本文方法进行算法测试与应用。
1 基本原理 1.1 VTI介质拟声波方程实际介质中,地震波沿不同方向的传播速度不同,基于各向同性介质假设的波动方程无法准确描述与模拟实际波场的传播,产生成像假象。Thom-sen[23]将这种速度差异参数化为Thomsen参数和背景速度,Alkhalifah[17]对VTI介质参数进行了声学近似,令横波速度为零,得到用Thomsen参数表示的VTI介质声波近似胡克定律
| $ \left[ {\begin{array}{*{20}{c}} {{\sigma _{xx}}}\\ {{\sigma _{yy}}}\\ {{\sigma _{zz}}}\\ {{\sigma _{yz}}}\\ {{\sigma _{xz}}}\\ {{\sigma _{xy}}} \end{array}} \right] = V_0^2\left[ {\begin{array}{*{20}{c}} {1 + 2\varepsilon }&{1 + 2\varepsilon }&{\sqrt {1 + 2\delta } }&0&0&0\\ {1 + 2\varepsilon }&{1 + 2\varepsilon }&{\sqrt {1 + 2\delta } }&0&0&0\\ {\sqrt {1 + 2\delta } }&{\sqrt {1 + 2\delta } }&1&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\tau _{xx}}}\\ {{\tau _{yy}}}\\ {{\tau _{zz}}}\\ {{\tau _{yz}}}\\ {{\tau _{xz}}}\\ {{\tau _{xy}}} \end{array}} \right] $ | (1) |
式中:σij和τij(i, j=x, y, z)分别代表不同方向的应力张量和应变张量;V0、ε、δ分别表示纵波背景速度和Thomsen参数。对式(1)两端求时间偏导数,并根据运动学方程
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = \frac{{\partial p}}{{\partial x}}\\ \frac{{\partial v}}{{\partial t}} = \frac{{\partial p}}{{\partial y}}\\ \frac{{\partial w}}{{\partial t}} = \frac{{\partial q}}{{\partial z}}\\ \frac{{\partial p}}{{\partial t}} = V_x^2\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) + {V_0}{V_{\rm{n}}}\frac{{\partial w}}{{\partial z}}\\ \frac{{\partial q}}{{\partial t}} = {V_0}{V_{\rm{n}}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) + V_0^2\frac{{\partial w}}{{\partial z}} \end{array} \right. $ | (2) |
式中:p=σxx=σyy, q=σzz分别代表水平应力分量和垂直应力分量;Vx为垂直于对称轴方向的qP波速度,且Vx2=V02(1+2ε);Vn为正常时差速度,且Vn2=V02(1+2δ)。基于同样的声波近似关系,Du等[24]推导了二阶VTI介质拟声波方程
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}p}}{{\partial {t^2}}} = V_x^2\left( {\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {y^2}}}} \right) + V_0^2\frac{{{\partial ^2}q}}{{\partial {z^2}}}\\ \frac{{{\partial ^2}q}}{{\partial {t^2}}} = V_{\rm{n}}^2\left( {\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {y^2}}}} \right) + V_0^2\frac{{{\partial ^2}q}}{{\partial {z^2}}} \end{array} \right. $ | (3) |
此外,Hestholm[25]在式(3)的基础上推导了含中间变量的拟声波一阶偏微分方程。VTI介质拟声波方程的形式多样,式(2)和式(3)可以较准确地还原qP波的运动学特征,但在波场传播过程中伴随一种菱形的人为干扰波——qSV伪横波。逆时偏移成像中qSV波会在浅表层成像,导致表层能量过强而掩盖有效信息,但可通过在震源激发位置设定平滑的各向同性或椭圆各向异性震源环压制qSV波。
1.2 qSV波产生机理与压制VTI介质拟声波方程是以沿垂向(对称轴方向)的剪切波相速度等于零的假设为前提条件,但qSV波在非垂向的相速度和群速度均不为零。将拟声波方程的平面波解代入式(3)后得到两组复数解
| $ \left\{ \begin{array}{l} {F_1}\left( {x,z,t} \right) = \exp \left[ { \pm \sqrt {\frac{{{a_1}t}}{2}} + {\rm{i}}\left( {{k_x}x + {k_z}z} \right)} \right]\\ {F_2}\left( {x,z,t} \right) = \exp \left[ { \pm \sqrt {\frac{{{a_2}t}}{2}} + {\rm{i}}\left( {{k_x}x + {k_z}z} \right)} \right] \end{array} \right. $ | (4) |
式中
| $ \left\{ \begin{array}{l} {a_1} = - V_x^2k_x^2 - V_0^2k_z^2 - b\\ {a_2} = - V_x^2k_x^2 - V_0^2k_z^2 + b\\ b = \sqrt { - 8\eta V_{\rm{n}}^2k_x^2v_0^2k_z^2 + {{\left( {V_{\rm{n}}^2k_x^2 + 2\eta V_{\rm{n}}^2k_x^2 + V_{\rm{0}}^2k_z^2} \right)}^2}} \\ \eta = \frac{{\varepsilon - \delta }}{{1 + 2\delta }} \end{array} \right. $ | (5) |
其中:kx、kz分别为x、z方向的波数;F1(x, z, t)代表qP波解;F2(x, z, t)代表qSV波解,其速度小于qP波速度。在VTI介质中a1恒为负;a2与η异号,当a2>0, η<0时,F2(x, z, t)数值解不稳定,这也解释了一般情况下ε>δ的原因;当a2<0, η>0时,F2(x, z, t)即为qSV波数值解。qSV波在实际波场中并不存在,当η=0即ε=δ时对应的qSV波速度为零,介质为椭圆各向异性介质或各向同性介质。可见,可以在震源位置设定各向同性(ε=δ=0)或椭圆各向异性(ε=δ≠0)震源环压制qSV波,但震源环必须是光滑的,以消除本身产生的反射层。
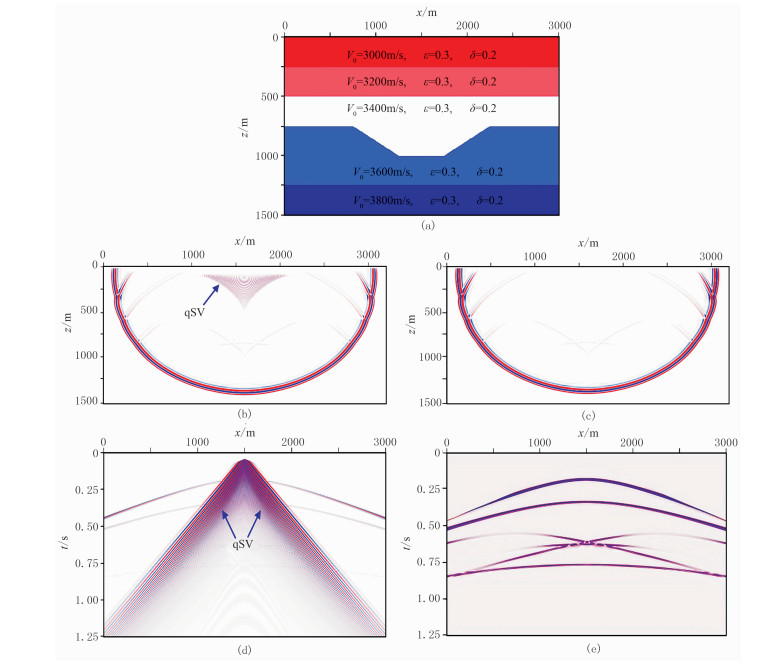
利用VTI洼陷模型测试qSV波压制效果,速度及各向异性参数设置如图 1a所示。正演参数为:纵横向网格数为301×601,纵横向采样间隔均为5m,时间采样间隔为0.5ms,雷克子波主频为40Hz,炮点位于1500m处,震源同时加载在qP波的p、q分量上。图 1b和图 1c为压制qSV波前、后的波场快照,图 1d和图 1e为压制qSV波前、后的炮记录(直达波已切除),通过对比可以发现,qSV波能量大于qP反射波能量,并且容易产生频散淹没有效信息,本文采用的方法能够有效地压制qSV波。
|
图 1 qSV波压制效果 (a)VTI洼陷模型;(b)压制前波场快照;(c)压制后波场快照;(d)压制前单炮记录;(e)压制后单炮记录 |
逆时偏移利用双程波动方程进行时间外推,能精准还原沿不同方向传播的波场从而使成像不受地层倾角限制,但成像结果常伴随强振幅低频噪声。利用不同方向的波场进行成像可以有效地压制低频噪声,这体现了角度域成像的重要性。本文利用坡印廷矢量法在逆时延拓过程中计算震源波场和检波点波场的传播方向及入射角来获取角道集,通过叠加不同角度成像结果达到压制低频噪声提高成像质量的目的。
波场P的坡印廷矢量S定义为
| $ \mathit{\boldsymbol{S}} = - \nabla P\frac{{\partial P}}{{\partial t}} $ | (6) |
qP波坡印廷矢量的求解需要考虑p、q分量。结合式(2),二维情况下的震源波场坡印廷矢量SS与检波点波场坡印廷矢量SR可以写为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{S}}_{\rm{S}}} = - \left( {\frac{{\partial {u_{\rm{S}}}}}{{\partial t}}\frac{{\partial {p_{\rm{S}}}}}{{\partial t}},\frac{{\partial {w_{\rm{S}}}}}{{\partial t}}\frac{{\partial {q_{\rm{S}}}}}{{\partial t}}} \right)\\ {\mathit{\boldsymbol{S}}_{\rm{R}}} = - \left( {\frac{{\partial {u_{\rm{R}}}}}{{\partial t}}\frac{{\partial {p_{\rm{R}}}}}{{\partial t}},\frac{{\partial {w_{\rm{R}}}}}{{\partial t}}\frac{{\partial {q_{\rm{R}}}}}{{\partial t}}} \right) \end{array} \right. $ | (7) |
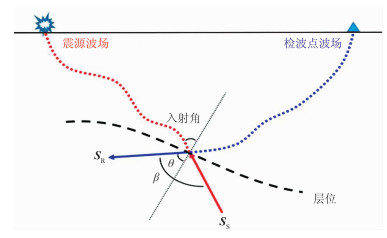
式中下标“S、R”分别表示震源波场和检波点波场。角道集是在逆时延拓过程中提取的,图 2所示为逆时反传过程中的SS和SR,但是按照SS、SR方向计算出的角度为入射角的余角,所以需要取-SS和SR计算入射角。
|
图 2 坡印廷矢量计算入射角 |
利用-SS与SR之间的夹角β计算入射角的公式为
| $ \theta = \frac{1}{2}\beta = \frac{1}{2}\arccos \frac{{ - {\mathit{\boldsymbol{S}}_{\rm{S}}} \cdot {\mathit{\boldsymbol{S}}_{\rm{R}}}}}{{\left| { - {\mathit{\boldsymbol{S}}_{\rm{S}}}} \right|\left| {{\mathit{\boldsymbol{S}}_{\rm{R}}}} \right|}} $ | (8) |
qP波成像不同于声波,需要考虑qP波的p和q分量,这一点在式(7)中得以体现。大量试算证明拟声波p分量的成像结果无异于q分量,因此本文不再做qP波p和q分量成像差异的讨论,采用p分量进行偏移成像。基于波场分离原理,利用不同方向的波场进行成像可以有效压制低频噪声改善单炮成像结果,同样,利用不同角度的成像结果进行叠加成像也可以有效地压制低频噪声。常规逆时偏移不对成像角度进行控制,成像范围相当于0°~180°,此时大角度折射波叠加成像导致大量的低频噪声,在成像剖面的浅层尤其明显。角度叠加逆时偏移,在成像之前对速度模型进行倾角扫描,将最大倾角设置为最大成像角度,在保证大角度构造成像不受损害的前提下,有效地压制了浅层低频噪声。
2 模型试算与应用实例 2.1 VTI逆冲断层模型试算首先利用VTI逆冲断层模型(图 3a)验证本文方法的正确性。模型的网格点数为300×711,纵横向采样间隔均为5m,仅逆冲断层为VTI介质(Thomsen参数ε、δ为非零值);各向同性和VTI正演参数相同:时间采样间隔为0.5ms,地震子波主频40Hz,地表全孔径接收,共200炮。需要注意的是,各向同性成像结果是利用各向同性逆时偏移处理各向同性数据得到的(并非采用各向同性偏移处理各向异性数据),VTI成像结果是利用VTI逆时偏移处理各向异性数据得到的。
|
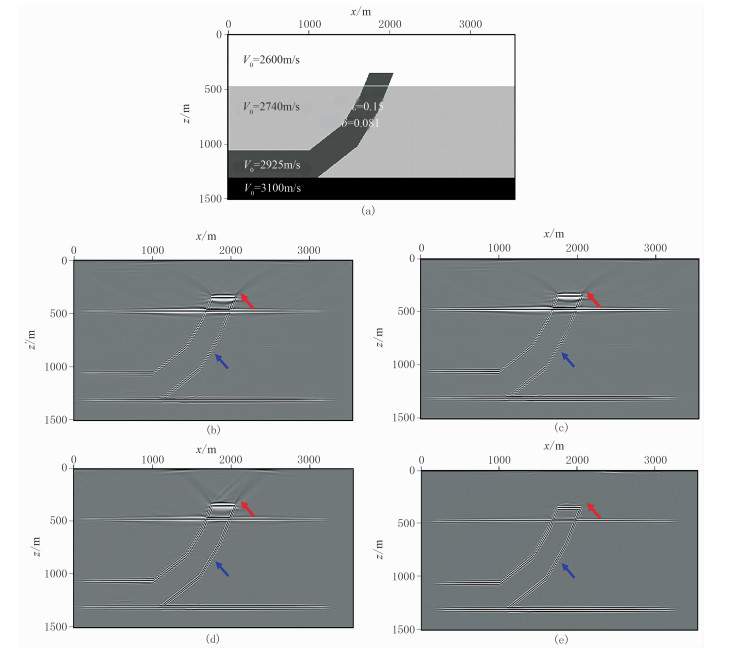
图 3 逆冲断层各向同性与各向异性逆时偏移成像结果对比 (a)VTI逆冲断层模型;(b)各向同性常规逆时偏移;(c)各向同性角度叠加逆时偏移;(d)VTI常规逆时偏移;(e)VTI角度叠加逆时偏移 |
对比图 3b~图 3e(蓝色箭头位置处)可以发现:各向同性逆时偏移与VTI逆时偏移对于平层的成像差异不大,但是各向同性偏移在陡倾位置处的成像结果能量弱、质量差,随着地层倾角的加大能量差异加剧,甚至出现同相轴消失的现象,而VTI偏移较好地解决了这一问题。此外,对比图 3b~图 3e中红色箭头位置处的成像结果可以看出,与常规逆时偏移成像结果相比,角度叠加逆时偏移的成像结果有效压制了逆冲断层顶端的低频成像噪声。逆冲断层模型的试算结果表明:VTI偏移算法能够解决各向同性偏移在陡倾地层中成像能量弱的问题,角度叠加偏移算法能够压制常规逆时偏移的低频噪声问题,验证了本文方法的正确性和成像优势。
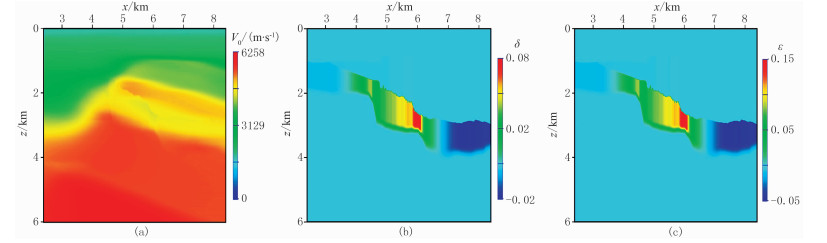
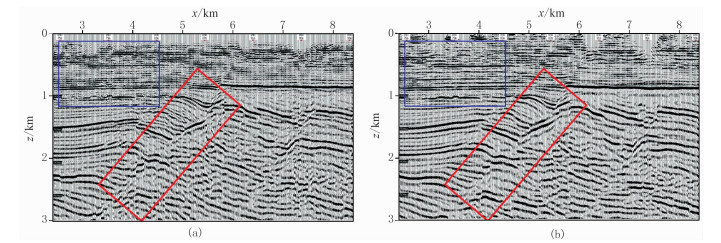
2.2 A探区应用实例利用中国东部A探区实际资料检验本文的VTI介质角度叠加逆时偏移。该探区断层发育,速度横向变化大,各向异性特征较为明显。图 4为利用各向异性偏移与参数反演得到的纵波速度场以及Thomsen各向异性参数场,纵横向采样点数为1201×481,纵横向采样间隔分别为5m和12.5m。利用图 4所示参数场进行各向同性偏移和VTI偏移(图 5)。对比图 5a与图 5b可见:同常规各向同性逆时偏移成像结果相比,本文的VTI角度叠加逆时偏移成像结果,无论在高陡断面(红框所示)的成像方面,还是在平层界面(蓝框所示)的成像方面,均具有较大优势,地层的接触关系更加合理,低频噪声较少,同相轴的能量更为均衡,进一步验证了本文方法的正确性和有效性。
|
图 4 A探区实际资料速度场和Thomsen参数场 (a)V0;(b)δ;(c)ε |
|
图 5 A探区实际资料各向同性(a)与VTI(b)逆时偏移成像结果对比 |
本文在利用声波近似方程模拟VTI介质中qP波传播规律的基础上,发展了一种VTI介质角度叠加逆时偏移方法,得出几点结论:
(1) 通过在震源位置设置震源环以压制qSV波的影响,能够提高逆时偏移中地震波场延拓的准确性,减少成像结果中与qSV波有关的成像噪声;
(2) 逆时偏移的角度叠加实现策略,能够利用角道集中不同角度成像结果的叠加压制低频噪声,提高成像精度;
(3) 模型试算结果证明了本文方法能够对大倾角复杂构造准确成像,且能量均衡、低频噪声压制效果较好,应用实例进一步验证了本文方法的有效性和实用性。
| [1] |
Whitmore N D.Iterative depth migration by backward time propagation[C].SEG Technical Program Expanded Abstracts, 1983, 2: 827-830.
|
| [2] |
张慧, 蔡其新, 秦广胜, 等. 基于GPU并行加速的逆时偏移成像方法[J]. 石油地球物理勘探, 2013, 48(5): 707-710. ZHANG Hui, CAI Qixin, QIN Guangsheng, et al. GPU-accelerated reverse time migration and its application[J]. Oil Geophysical Prospecting, 2013, 48(5): 707-710. |
| [3] |
刘文卿, 王宇超, 雍学善, 等. 基于GPU/CPU叠前逆时偏移研究及应用[J]. 石油地球物理勘探, 2012, 47(5): 712-716. LIU Wenqing, WANG Yuchao, YONG Xueshan, et al. Prestack reverse time migration on GPU/CPU co-parallel computation[J]. Oil Geophysical Prospecting, 2012, 47(5): 712-716. |
| [4] |
唐祥功, 匡斌, 杜继修, 等. 多GPU协同三维叠前逆时偏移方法研究与应用[J]. 石油地球物理勘探, 2013, 48(6): 910-914. TANG Xianggong, KUANG Bin, DU Jixiu, et al. 3D prestack reverse time migration based on multiple-GPU collaboration[J]. Oil Geophysical Prospecting, 2013, 48(6): 910-914. |
| [5] |
杨午阳, 张厚柱, 撒利明, 等. 逆时偏移关键问题探讨[J]. 石油地球物理勘探, 2016, 51(6): 1251-1262. YANG Wuyang, ZHANG Houzhu, SA Liming, et al. Some issues about reverse time migration[J]. Oil Geo-physical Prospecting, 2016, 51(6): 1251-1262. |
| [6] |
魏石磊, 张大洲, 李明智, 等. VTI介质中波场分离算子特征研究[J]. 石油地球物理勘探, 2016, 51(3): 506-512. WEI Shilei, ZHANG Dazhou, LI Mingzhi, et al. Wave field separation operator characteristics in the VTI media[J]. Oil Geophysical Prospecting, 2016, 51(3): 506-512. |
| [7] |
杨富森, 李振春, 王小丹. TTI介质一阶qP波稳定方程波场数值模拟及逆时偏移[J]. 石油地球物理勘探, 2016, 51(3): 497-505. YANG Fusen, LI Zhenchun, WANG Xiaodan. Wave-field numerical simulation and reverse-time migration based on the stable TTI first-order qP-wave equations[J]. Oil Geophysical Prospecting, 2016, 51(3): 497-505. |
| [8] |
王鹏飞, 何兵寿. 基于行波分离的三维弹性波矢量场点积互相关成像条件[J]. 石油地球物理勘探, 2017, 52(3): 477-483. WANG Pengfei, HE Bingshou. Vector field dot pro-duct cross-correlation imaging based on 3D elastic wave separation[J]. Oil Geophysical Prospecting, 2017, 52(3): 477-483. |
| [9] |
Robert G C.Reverse time migration with random boundary[C].SEG Technical Program Expanded Abstracts, 2009, 28: 2809-2813.
|
| [10] |
Zhang Y, Sun J. Practical issues in reverse time migration:true amplitude gathers, noise removal and harmonic source encoding[J]. First Break, 2009, 26(1): 29-35. |
| [11] |
刘红伟, 刘洪, 邹振. 地震叠前逆时偏移中的去噪与存储[J]. 地球物理学报, 2010, 53(9): 2171-2180. LIU Hongwei, LIU Hong, ZOU Zhen. The problems of denoise and storage in seismic reverse time migration[J]. Chinese Journal of Geophysics, 2010, 53(9): 2171-2180. DOI:10.3969/j.issn.0001-5733.2010.09.017 |
| [12] |
陈康, 吴国忱. 逆时偏移拉普拉斯算子滤波改进算法[J]. 石油地球物理勘探, 2012, 47(2): 249-255. CHEN Kang, WU Guochen. An improved filter algorithm based on Laplace operator in reverse-time migration[J]. Oil Geophysical Prospecting, 2012, 47(2): 249-255. |
| [13] |
唐永杰, 宋桂桥, 刘少勇, 等. 基于波长平滑算子的逆时偏移回转波假象去除方法[J]. 石油地球物理勘探, 2018, 53(1): 80-86. TANG Yongjie, SONG Guiqiao, LIU Shaoyong, et al. Turning wave false image removal based on wavelength-dependent smoothing operator in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(1): 80-86. |
| [14] |
徐文才, 李振春.各向异性介质弹性波逆时偏移[C].2014年中国地球科学联合学术年会, 2014, P1162. XU Wencai, LI Zhenchun. Reverse time migration of elastic waves in anisotropic media[C].2014 China Geosciences Joint Academic Annual Meeting, 2014, P1162. |
| [15] |
杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移[J]. 地球物理学报, 2009, 52(3): 801-807. DU Qizhen, QIN Tong. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J]. Chinese Journal of Geophysics, 2009, 52(3): 801-807. |
| [16] |
Alkhalifah T. Acoustics approximations for process-ing in transversely isotropic media[J]. Geophysics, 1998, 63(3): 623-631. |
| [17] |
Alkhalifah T. An acoustic wave equation for aniso-tropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [18] |
Duveneck E, Milcik P, Bakker P M.Acoustic VTI wave equations and their application for anisotropic reverse time migration[C].SEG Technical Program Expanded Abstracts, 2008, 27: 2186-2190.
|
| [19] |
杨富森, 李振春, 王小丹, 等. 等价各向异性介质一阶拟声波方程正演模拟及其效率分析[J]. 地震学报, 2015, 37(4): 648-660. YANG Fusen, LI Zhenchun, WANG Xiaodan, et al. Equivalent anisotropic first-order pseudo-acoustic wave equations modeling and its efficiency analysis[J]. Acta Seismologica Sinica, 2015, 37(4): 648-660. |
| [20] |
Yoon K, Marfurt K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 59(1): 102-107. |
| [21] |
Costa J C, Silva Neto F A, Alcabtara M R, et al. Obliquity-correction imaging condition for reverse time migration[J]. Geophysics, 2009, 74(3): S57-S66. DOI:10.1190/1.3110589 |
| [22] |
李海强, 杨国权, 李振春, 等. 基于局部平面波分解的逆时偏移角道集提取方法[J]. 石油地球物理勘探, 2017, 52(6): 1177-1183. LI Haiqiang, YANG Guoquan, LI Zhenchun, et al. A method for extracting angle-domain common-image gathers based on local plane wave decomposition[J]. Oil Geophysical Prospecting, 2017, 52(6): 1177-1183. |
| [23] |
Thomsen L. Weak elastic anisotropics[J]. Geophy-sics, 1986, 51(10): 1954-1966. |
| [24] |
Du X, Fletcher R, Fowler P J.A new pseudo-acoustic wave equation for VTI media[C].Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, 1024-1028.
|
| [25] |
Hestholm S. Acoustic VTI modeling using high-order finite differences[J]. Geophysics, 2009, 74(5): T67-T73. DOI:10.1190/1.3157242 |



 秦宁 山东省东营市东营区北一路210号中国石化胜利油田物探研究院处理二室, 257022。Email:
秦宁 山东省东营市东营区北一路210号中国石化胜利油田物探研究院处理二室, 257022。Email: