② 长安大学地质工程与测绘学院, 陕西西安 710054
② School of Geological Engineering and Geomatics, Chang'an University, Xi'an, Shaanxi 710054, China
地球介质一般具有各向异性特征,其中VTI介质(具有垂直对称轴的横向各向同性介质)是一种常见的各向异性介质。在地震勘探中一般将各向异性视为速度各向异性,在研究区域构造时是可行的。随着勘探目标体尺度的缩小,忽略地层各向异性影响的地震偏移成像导致目标区空间反射波归位不准确,绕射波不能完全收敛,甚至产生构造扭曲或构造假象,严重降低了地震成像精度[1-3]。近年来,人们研究了VTI介质的偏移方法。例如:Alkhalifah[4]实现了VTI介质的相移偏移方法,但该方法无法适应介质速度的横向变化;吴国忱等[5]实现了VTI介质广义屏叠前深度偏移方法,但其中对各向异性频散关系的近似使该方法仅局限于弱各向异性介质;韩建光等[6-7]提出了VTI介质高斯束叠前深度偏移方法,数值实验表明,该方法不受各向异性程度的限制,能适应强各向异性介质。虽然高斯束偏移方法具有高效、灵活的优点,但成像效果明显受速度横向变化剧烈的影响,因此人们利用波动方程叠前深度偏移对复杂区精确成像。刘礼农等[8-9]发展了VTI介质波动方程最优分裂傅里叶偏移方法;程玖兵等[10-11]研究了qP波在各向异性介质中的传播模式;Sun等[12]等发展了VTI介质逆时偏移方法;Zhang等[13]提出了一种三维TTI介质纯P波方程求解方法;Hua等[14]、黄建平等[15]、朱峰等[16]发展了VTI介质和黏声VTI介质的有限差分叠前深度偏移方法。但以上波动方程类偏移方法大多是在炮域实现叠前偏移,研究表明,在横向变速剧烈情况下,共炮偏移生成的炮域共成像点道集在运动学和动力学上存在假象。为此,Hoop等[17]、Xu等[18]研究了角度域共成像点道集对射线多路径问题的适应性,提出通过角道集的叠加成像可以避免构造假象,有效提高偏移剖面的成像效果。Stork等[19]进一步证明,基于波动方程偏移提取的角度域共成像点道集(ADCIG)不存在假象。Xie等[20]通过Gabor-Daubechies框架小波束域波场分解进行叠前角度域偏移;James等[21]通过波动方程偏移提取炮检距域共成像点道集和ADCIG;Save等[22]提出一种采用波动方程偏移提取ADCIG的方法,将偏移过程和ADCIG计算过程分离,即在成像空间通过傅里叶域的径向道变换计算出以入射角为参数的角道集,并对众多提取ADCIG的方法进行了分类和总结。Biondi[23]讨论了各向异性偏移的ADCIG;李振春等[24]、张敏等[25]对比、分析了单平方根和双平方根偏移提取ADCIG的方法,并发展了保幅的角度域偏移成像方法。Tang等[26]发展了角度域平面波逆时偏移方法。由于ADCIG是目前唯一不存在假象的道集,因此在地震数据处理中具有优势[27]。
本文研究了VTI介质角度域偏移方法,以各向同性双平方根方程的角度域偏移方法为基础,从VTI介质qP波频散关系出发,推导出VTI介质角度域偏移的波场延拓算子,在频率-波数域处理以横向均匀速度传播的波场,在空间域处理具有速度扰动特征的波场以提高波场延拓精度。断层模型和Hess VTI模型测试结果表明:该方法不受介质各向异性程度的影响,可使地震波场准确归位、绕射波收敛,从而对VTI介质精确成像;与各向同性偏移方法相比,该方法消除了各向异性效应对波场传播的影响,明显提高了成像精度;偏移生成的ADCIG避免了各向同性偏移方法使成像道集无法校平的缺陷,且具有更丰富的角度信息。实际资料的应用效果证实了本文方法的实用性。
1 VTI介质qP波频散方程VTI介质描述了由周期性的薄互层和平行排列的微裂隙引起的各向异性特征。在各向同性介质中,纵、横波以各自的射线速度(群速度)独立传播。在VTI介质中,纵、横波相互耦合,并且在一般情况下波的极化方向与传播方向既不垂直也不平行,因此VTI介质中的纵、横波又被称为qP波、qSV波和qSH波,相互耦合的纵、横波传播波动方程为[28]
| $ \rho \frac{\partial }{{\partial {t^2}}}\mathit{\boldsymbol{U}} = \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{U}}} \right) + \rho \mathit{\boldsymbol{F}} $ | (1) |
式中: U=(ux, uy, uz)T为波场位移,ux、uy、uz分别为U在空间坐标x、y、z的分量;ρ为介质密度;F=(fx, fy, fz)T为单位质量元素的体力,fx, fy, fz分别为F在x、y、z的分量;t为时间;C为VTI介质刚度矩阵;L为偏导数算子矩阵。
式(1)描述了VTI介质中各质点在不同时刻的位移情况和弹性波传播规律。虽然式(1)的每一项都有明确的物理意义,但并没有体现波在VTI介质中的传播特性,如相速度、群速度或频散,因此有必要推导体现波在VTI介质中传播的特性方程。去掉式(1)的体力项,其平面波的解为
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{A}}\exp \left[ {{\rm{i}}k\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{x}} - vt} \right)} \right] $ | (2) |
式中:x=(x, y, z)T为位置矢量;n=(nx, ny, nz)T为波的传播方向矢量,nx、ny、nz分别为n在x、y、z的分量;v为平面波的相速度;
| $ \left| {\begin{array}{*{20}{c}} {{\mathit{\Gamma }_{11}} - \rho {\omega ^2}}&{{\mathit{\Gamma }_{12}}}&{{\mathit{\Gamma }_{13}}}\\ {{\mathit{\Gamma }_{12}}}&{{\mathit{\Gamma }_{22}} - \rho {\omega ^2}}&{{\mathit{\Gamma }_{23}}}\\ {{\mathit{\Gamma }_{13}}}&{{\mathit{\Gamma }_{23}}}&{{\mathit{\Gamma }_{33}} - \rho {\omega ^2}} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{A_x}}\\ {{A_y}}\\ {{A_z}} \end{array}} \right| = 0 $ | (3) |
其中
| $ \left\{ \begin{array}{l} {\mathit{\Gamma }_{11}} = {c_{11}}k_x^2 + {c_{66}}k_y^2 + {c_{44}}k_z^2\\ {\mathit{\Gamma }_{12}} = \left( {{c_{12}} + {c_{66}}} \right){k_x}{k_y}\\ {\mathit{\Gamma }_{13}} = \left( {{c_{13}} + {c_{66}}} \right){k_x}{k_z}\\ {\mathit{\Gamma }_{22}} = {c_{66}}k_x^2 + {c_{11}}k_y^2 + {c_{44}}k_z^2\\ {\mathit{\Gamma }_{23}} = \left( {{c_{13}} + {c_{44}}} \right){k_z}{k_y}\\ {\mathit{\Gamma }_{33}} = {c_{44}}k_x^2 + {c_{44}}k_y^2 + {c_{33}}k_z^2 \end{array} \right. $ | (4) |
式(3)、式(4)中:Ax、Ay、Az分别为A在x、y、z的分量;kx、ky、kz分别为k在x、y、z的分量;c11、c66、c44、c12、c13、c33分别为C中不同位置的元素。
式(3)即为Kelvin-Christoffel方程,在数学上描述了本征值问题,是关于ρω2的一元三次方程。在VTI介质中,给定波场传播方向,由式(3)得到3个相速度解,分别对应qP波、qSV波、qSH波。地震波在各向异性介质中传播时纵、横波是相互耦合的,在计算qP波垂直波数时,qSV波速度影响较小,可以忽略。为了从式(3)中分离qP波,令横波速度为零,进行拟声波近似[4]。将Thomsen各向异性参数VP0、ε、δ[29]代入式(4),有
| $ \left\{ \begin{array}{l} {\mathit{\Gamma }_{11}} = \rho \left( {1 + 2\varepsilon } \right)V_{{\rm{P0}}}^2k_x^2\\ {\mathit{\Gamma }_{12}} = \rho \left( {1 + 2\varepsilon } \right)V_{{\rm{P0}}}^2{k_x}{k_y}\\ {\mathit{\Gamma }_{13}} = \rho V_{{\rm{P0}}}^2\sqrt {1 + 2\delta } {k_x}{k_z}\\ {\mathit{\Gamma }_{22}} = \rho V_{{\rm{P0}}}^2\left( {1 + 2\varepsilon } \right)k_y^2\\ {\mathit{\Gamma }_{23}} = \rho V_{{\rm{P0}}}^2\sqrt {1 + 2\delta } {k_y}{k_z}\\ {\mathit{\Gamma }_{33}} = \rho V_{{\rm{P0}}}^2k_z^2 \end{array} \right. $ | (5) |
将式(5)代入式(3)求解,可得VTI介质qP波频散方程,即
| $ \begin{array}{*{20}{c}} {{\omega ^4} = {\omega ^2}V_{{\rm{P0}}}^2\left[ {\left( {1 + 2\varepsilon } \right)\left( {k_x^2 + k_y^2} \right) + k_z^2} \right] - }\\ {2\left( {\varepsilon - \delta } \right)V_{{\rm{P0}}}^4\left( {k_x^2 + k_y^2} \right)k_z^2} \end{array} $ | (6) |
如果仅考虑xoz平面内的情况,求解式(6)可得二维VTI介质qP波垂直波数表达式
| $ {k_z} = \pm \frac{\omega }{{{V_{{\rm{P0}}}}}}\sqrt {\frac{{{\omega ^2} - \left( {1 + 2\varepsilon } \right)V_{{\rm{P0}}}^2k_x^2}}{{{\omega ^2} - 2\left( {\varepsilon - \delta } \right)V_{{\rm{P0}}}^2k_x^2}}} $ | (7) |
当ε=δ=0时,对应各向同性介质;当ε=δ≠0时,对应椭圆各向异性介质;当ε≠0, δ≠0且ε≠δ时,对应一般各向异性介质。
2 VTI介质角度域偏移成像 2.1 VTI介质中角度域偏移的波场延拓本文的角度域偏移采用双平方根(DSR)方程定义波场U的传播特征,在频率-波数域可表示为
| $ \frac{\partial }{{\partial z}}\mathit{\boldsymbol{U}}\left( {{k_m},{k_h},z,\omega } \right) = {\rm{i}}{k_z}\mathit{\boldsymbol{U}}\left( {{k_m},{k_h},z,\omega } \right) $ | (8) |
式中: km、kh分别为中点、半炮检距分量的波数;kz为同时包含炮点和检波点的垂直波数,即
| $ {k_z} = {k_{z{\rm{s}}}} + {k_{z{\rm{g}}}} $ | (9) |
由VTI介质的频散方程得
| $ {k_z} = \frac{\omega }{v}\sqrt {\frac{{{\omega ^2} - {v^2}\left( {1 + 2\varepsilon } \right)k_{mh}^2}}{{{\omega ^2} - 2\left( {\varepsilon - \delta } \right){v^2}k_{mh}^2}}} $ | (10) |
式中kmh=(km
| $ \begin{array}{l} U\left( {{k_m},{k_h},z + \Delta z,\omega ,\varepsilon ,\delta } \right) = U\left( {{k_m},{k_h},z,\omega ,\varepsilon ,\delta } \right) \times \\ \;\;\;\;\;\;\exp \left[ {{\rm{i}}\Delta z\left( {{k_{z{\rm{s}}0}} + {k_{z{\rm{g}}0}}} \right)} \right] \end{array} $ | (11) |
式中kzs0、kzg0为v=v0、ε=ε0、δ=δ0时的背景波数,可表示为
| $ {k_{z0}} = {k_{z{\rm{s}}0}} + {k_{z{\rm{g}}0}} = \frac{\omega }{{{v_0}}}\sqrt {\frac{{{\omega ^2} - v_0^2\left( {1 + 2{\varepsilon _0}} \right)k_{mh}^2}}{{{\omega ^2} - 2\left( {{\varepsilon _0} - {\delta _0}} \right){v^2}k_{mh}^2}}} $ | (12) |
相移法适用于横向均匀层状介质。为了解决复杂构造的成像问题,本文借用双域法的研究思路处理横向非均匀VTI介质。将横向非均匀VTI介质分解为横向均匀的速度、各向异性参数及其扰动量,在频率-波数域处理横向均匀的速度及各向异性参数背景场,然后在空间域基于速度及各向异性扰动对波数域计算结果进行时移校正。
将速度及各向异性参数分解为背景场(·)和扰动场Δ(·),其中背景参数由模型平滑而得,各参数的扰动量同样包括炮点和检波点两部分。为方便推导,统一讨论各参数炮点和检波点分量,在实际计算过程中将其分开。各参数分量表示为
| $ \left\{ \begin{array}{l} v\left( {x,z} \right) = {v_0}\left( {x,z} \right) + \Delta v\left( {x,z} \right)\\ \varepsilon \left( {x,z} \right) = {\varepsilon _0}\left( {x,z} \right) + \Delta \varepsilon \left( {x,z} \right)\\ \delta \left( {x,z} \right) = {\delta _0}\left( {x,z} \right) + \Delta \delta \left( {x,z} \right) \end{array} \right. $ | (13) |
则VTI介质的垂直波数kz可分解为各向异性背景介质垂直波数kz0和扰动介质散射波场垂直波数kr
| $ {k_z}\left( {x,z,{k_m},{k_h}} \right) = {k_{z0}}\left( {z,{k_m},{k_h}} \right) + {k_r}\left( {x,z,{k_m},{k_h}} \right) $ | (14) |
则
| $ \begin{array}{l} {k_r}\left( {x,z,{k_m},{k_h}} \right) = {k_z}\left( {x,z,{k_m},{k_h}} \right) - {k_{z0}}\left( {z,{k_m},{k_h}} \right)\\ \;\;\;\;\;\;\; = \frac{\omega }{v}\sqrt {\frac{{{\omega ^2} - {v^2}\left( {1 + 2\varepsilon } \right)k_{mh}^2}}{{{\omega ^2} - 2\left( {\varepsilon - \delta } \right){v^2}k_{mh}^2}}} - \\ \;\;\;\;\;\;\;\;\;\;\frac{\omega }{{{v_0}}}\sqrt {\frac{{{\omega ^2} - v_0^2\left( {1 + 2{\varepsilon _0}} \right)k_{mh}^2}}{{{\omega ^2} - 2\left( {{\varepsilon _0} - {\delta _0}} \right)v_0^2k_{mh}^2}}} \end{array} $ | (15) |
将kz、kz0在各向异性背景参数处展开,在小扰动假设下,忽略各向异性参数扰动的二阶及以上项,整理后可得
| $ \begin{array}{l} {k_r}\left( {x,z,{k_m},{k_h}} \right) = {a_s}\left( {z,{k_{mh}}} \right)\Delta s\left( {x,z} \right) + \\ {a_\varepsilon }\left( {z,{k_{mh}}} \right) = \Delta \varepsilon \left( {x,z} \right) + {a_\delta }\left( {z,{k_{mh}}} \right)\Delta \delta \left( {x,z} \right) \end{array} $ | (16) |
其中
| $ \begin{array}{l} {a_s}\left( {z,{k_{mh}}} \right)\\ \;\;\;\; = \frac{{{k_0}\left[ {1 - 4\left( {{\varepsilon _0} - {\delta _0}} \right){\gamma ^2} + 2\left( {1 + 2{\varepsilon _0}} \right)\left( {{\varepsilon _0} - {\delta _0}} \right){\gamma ^4}} \right]}}{{{k_{z0}}{{\left[ {1 - 2\left( {{\varepsilon _0} - {\delta _0}} \right){\gamma ^2}} \right]}^2}}} \end{array} $ |
| $ {a_\varepsilon }\left( {z,{k_{mh}}} \right) = - \frac{{k_0^2\left( {1 + 2{\delta _0}} \right){\gamma ^4}}}{{{k_{z0}}{{\left[ {1 - 2\left( {{\varepsilon _0} - {\delta _0}} \right){\gamma ^2}} \right]}^2}}} $ |
| $ {a_\delta }\left( {z,{k_{mh}}} \right) = - \frac{{k_0^2{\gamma ^2}\left[ {1 - \left( {1 + 2{\varepsilon _0}} \right){\gamma ^2}} \right]}}{{{k_{z0}}{{\left[ {1 - 2\left( {{\varepsilon _0} - {\delta _0}} \right){\gamma ^2}} \right]}^2}}} $ |
| $ {k_0} = \frac{\omega }{{{v_0}}} $ |
而
| $ \gamma = \frac{{{k_0}}}{{{k_{mh}}}} $ |
根据各向异性相关理论可知:在各向异性介质波数展开式中,慢度扰动项Δs(x, z)主要影响低阶次项,表现为对小角度传播波场的影响,各向异性参数扰动项主要影响高阶次项,表现为对高角度传播波场的影响[5]。因此总的扰动介质垂直波数kr可由三部分组成
| $ \begin{array}{l} {k_r}\left( {x,z,{k_m},{k_h}} \right) = {k_{\Delta s}}\left( {x,z,{k_m},{k_h}} \right) + \\ \;\;\;\;\;\;{k_{\Delta \varepsilon }}\left( {x,z,{k_m},{k_h}} \right) + {k_{\Delta \delta }}\left( {x,z,{k_m},{k_h}} \right) \end{array} $ | (17) |
结合式(13),可将VTI介质波场传播算子P分解为背景波场的相移传播算子PPS、慢度扰动传播算子PΔs、ε扰动传播算子PΔε和δ扰动传播算子PΔδ。即
| $ P = {P_{{\rm{PS}}}} + {P_{\Delta s}} + {P_{\Delta \varepsilon }} + {P_{\Delta \delta }} $ | (18) |
其中
| $ {P_{{\rm{PS}}}} = \exp \left( {{\rm{i}}{k_{z0}}\Delta z} \right)\exp \left( {{\rm{i}}\omega \Delta s\Delta z} \right) $ |
| $ \begin{array}{l} {P_{\Delta s}} = {\rm{i}}\left[ {{a_s}\left( {z,{k_{mh}}} \right) - {a_s}\left( {z,0} \right)} \right]\Delta s\Delta z \times \\ \;\;\;\;\;\;\;\;\exp \left( {{\rm{i}}{k_{z0}}\Delta z} \right)\exp \left( {{\rm{i}}\omega \Delta s\Delta z} \right) \end{array} $ |
| $ {P_{\Delta \varepsilon }} = {\rm{i}}{a_\varepsilon }\Delta s\Delta z\exp \left( {{\rm{i}}{k_{z0}}\Delta z} \right)\exp \left( {{\rm{i}}\omega \Delta s\Delta z} \right) $ |
| $ {P_{\Delta \delta }} = {\rm{i}}{a_\delta }\Delta \delta \Delta z\exp \left( {{\rm{i}}{k_{z0}}\Delta z} \right)\exp \left( {{\rm{i}}\omega \Delta s\Delta z} \right) $ |
可以看出P为双域传播算子。首先基于速度扰动校正相移背景波场,还考虑了各向异性参数扰动对高角度入射波场传播的影响,并对相移结果进行进一步补偿,较好地提高了非均匀各向异性介质中波场延拓精度。
综上所述,将VTI介质角度域偏移的波场延拓过程分述如下。
(1) 频率-波数域相移。
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_1}\left( {{k_m},{k_h},z + \Delta z,\omega ,\varepsilon ,\delta } \right)\\ \;\;\;\;\;\;\;\; = \mathit{\boldsymbol{U}}\left( {{k_m},{k_h},z,\omega ,\varepsilon ,\delta } \right)\exp \left( {{\rm{i}}\Delta z{k_{z0}}} \right) \end{array} $ | (19) |
其中
| $ {k_{z0}} = \frac{\omega }{{{v_0}}}\sqrt {\frac{{{\omega ^2} - v_0^2\left( {1 + 2{\varepsilon _0}} \right)k_{mh}^2}}{{{\omega ^2} - 2\left( {{\varepsilon _0} - {\delta _0}} \right){v^2}k_{mh}^2}}} $ |
相移处理实现了背景波场在VTI介质中的传播。
(2) 频率-空间域时移。
| $ {\mathit{\boldsymbol{U}}_2}\left( {{k_m},{k_h},z + \Delta z,\omega ,\varepsilon ,\delta } \right) = {\mathit{\boldsymbol{U}}_1}\exp \left[ {{\rm{i}}\Delta z\omega \Delta s} \right] $ | (20) |
式中
(3) 频率-空间域各向异性参数校正。
| $ \begin{array}{l} \mathit{\boldsymbol{U}}\left( {{k_m},{k_h},z + \Delta z,\omega ,\varepsilon ,\delta } \right)\\ \;\;\;\;\; = {\mathit{\boldsymbol{U}}_2}\exp \left\{ {{\rm{i}}\Delta z\left[ {{a_s}\left( {z,{k_{mh}}} \right) - {a_s}\left( {z,0} \right)} \right]\Delta s + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{a_\varepsilon }\Delta \varepsilon + {a_\delta }\Delta \delta } \right\}\\ \;\;\;\;\; \approx {\mathit{\boldsymbol{U}}_2}\left\{ {1 + {\rm{i}}\Delta z\left[ {\left( {{a_s}\left( {z,{k_{mh}}} \right) - {a_s}\left( {z,0} \right)} \right)\Delta s + } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {{a_\varepsilon }\Delta \varepsilon + {a_\delta }\Delta \delta } \right]} \right\} \end{array} $ | (21) |
校正由各向异性参数扰动引起的大角度入射波场传播误差。
2.2 成像空间的角度映射关系波场延拓后,对成像空间的地震波场进行数据映射获得角度域共成像点道集[22-25, 30]。对于常速介质,反射波旅行时t为炮点、检波点位置和成像深度的函数(图 1),即t=t(z, s, g)。t对z求导,得
| $ \frac{{\partial t}}{{\partial z}} = \frac{{\cos \left( {\alpha - \beta } \right) + \cos \left( {\alpha + \beta } \right)}}{v} = - \frac{{2\cos \alpha \cos \beta }}{v} $ | (22) |
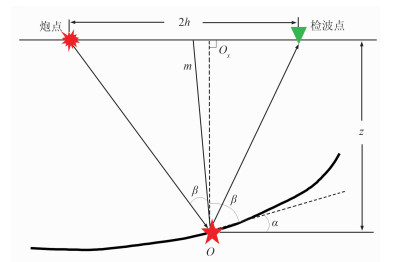
|
图 1 常速介质中的射线传播路径示意图 α为地层倾角,β为局部入射角,v为地层速度,2h为炮检距,z为反射点的深度 |
成像点局部半炮检距射线参数可表示为
| $ \begin{array}{l} {p_h} = \frac{{\partial t}}{{\partial h}} = \frac{{\partial t}}{{\partial g}} - \frac{{\partial t}}{{\partial s}} = \frac{{\sin \left( {\alpha + \beta } \right)}}{v} - \frac{{\sin \left( {\alpha - \beta } \right)}}{v}\\ \;\;\;\; = \frac{{2\cos \alpha \sin \beta }}{v} \end{array} $ | (23) |
由以上两式得
| $ \frac{{\partial t}}{{\partial h}}/\frac{{\partial t}}{{\partial z}} = - \tan \beta $ | (24) |
在频率-波数域,有
| $ \tan \beta = - \frac{{{k_h}}}{{{k_z}}} $ | (25) |
式中kh和kz分别为局部半炮检距波数和局部深度波数。式(25)即为成像空间炮检距域向角度域的映射公式,将波场由kh-kz域变换到β-kz域。
2.3 角度域成像在完成每步波场延拓后,首先提取零时间非零炮检距成像值,得到炮检距域共成像点道集(ODCIG),局部成像公式为
| $ I\left( {m,h,{z_{i + 1}}} \right) = {\rm{FT}}_{{k_m}}^{ - 1}\left[ {\frac{1}{{{N_\omega }}}\sum\limits_\omega {\mathit{\boldsymbol{\bar U}}\left( {{k_m},{k_h},z + \Delta z,\omega } \right)} } \right] $ | (26) |
式中
| $ I\left( {m,h,z} \right) \Rightarrow I\left( {m,\beta ,z} \right) $ | (27) |
式中:“
图 2展示了水平层状模型ADCIG提取过程。首先使用局部成像条件获得波动方程ODCIG(图 2b),ODCIG在成像点深度聚焦为一个点;然后在频率-波数域利用局部炮检距和入射角的映射关系,将局部炮检距转化为角度信息,最终获得ADCIG(图 2c),ADCIG在成像点深度为拉平的直线,同时包含了丰富的角度信息,具有更高的信噪比和分辨率。
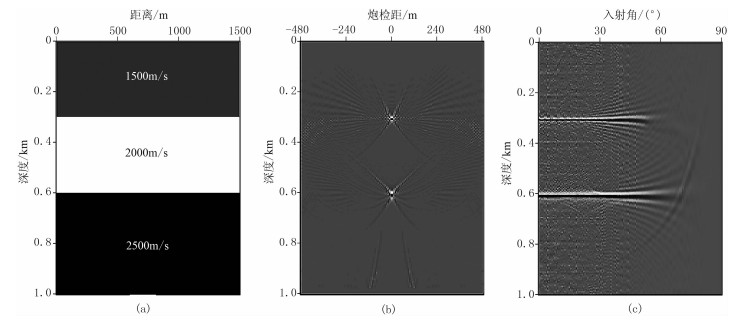
|
图 2 水平层状模型ADCIG (a)模型速度场;(b)ODCIG;(c)ADCIG |
为了验证VTI介质角度域偏移方法,设计了VTI介质模型(图 3)进行正演,图 4为正演记录。由图可见,炮集覆盖范围分别对应高速异常体和各向异性异常体位置,反射波较明显,较好地反映了地下构造,但由于存在异常体及断层,炮集记录中同时存在严重的绕射波干扰。
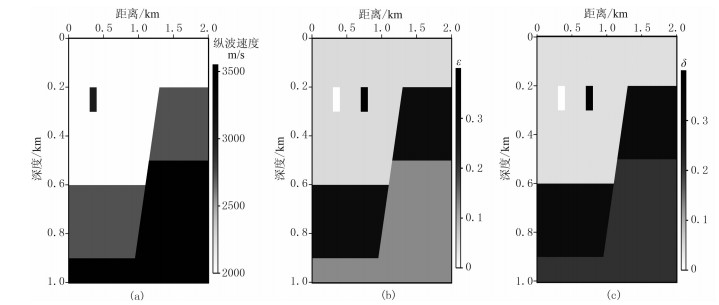
|
图 3 VTI介质模型
(a)纵波速度;(b)ε;(c)δ 模型速度由浅到深逐渐增大,在浅层从左至右存在一个高速异常体(呈弱各向异性)、一个ε、δ各向异性异常体(呈强各向异性)、一条正断层 |

|
图 4 正演记录 |
以此数据为基础,分别进行常规角度域偏移和考虑各向异性影响的VTI介质角度域偏移。图 5为各向同性、各向异性角度域叠前深度偏移剖面。由图可见:①由于未考虑各向异性参数的影响,各向同性偏移成像效果相对较差,浅层高速异常体边界成像模糊,分辨率较低;反映各向异性异常体的反射同相轴能量很弱,几乎没有反映下边界;对于右侧的断层成像,断点绕射波没有完全收敛(图 5a)。②各向异性偏移提高了高速异常体的成像分辨率,边界刻画清晰;各向异性异常体成像能量增强,且明显反映了下边界;提高了断层区域成像信噪比,断点绕射波收敛较好,构造特征更清晰;深层反射波能量增强,提高了信噪比、分辨率,明显改善了总体成像效果(图 5b)。

|
图 5 各向同性(a)、各向异性(b)角度域叠前深度偏移剖面 |
为了更直观地展示各向异性偏移的优势,分别提取具有典型构造特征位置处的ADCIG进行对比。图 6为由各向同性、各向异性偏移方法提取的ADCIG。由图可见:①在两个异常体位置处,各向同性偏移ADCIG同相轴无法校平,存在不同程度的向上弯曲(图 6a左、图 6a中);各向异性偏移ADCIG同相轴较为平直,而且可观测到更宽的角度范围(图 6b左、图 6b中)。②在断层处各向同性偏移ADCIG同相轴短小、弯曲、连续性较差,在局部区域还产生多组同相轴,出现构造假象(图 6a右);各向异性偏移ADCIG同相轴平直,消除了同相轴假象,剖面信噪比大大提高,较准确地反映了真实的构造特征(图 6b右)。
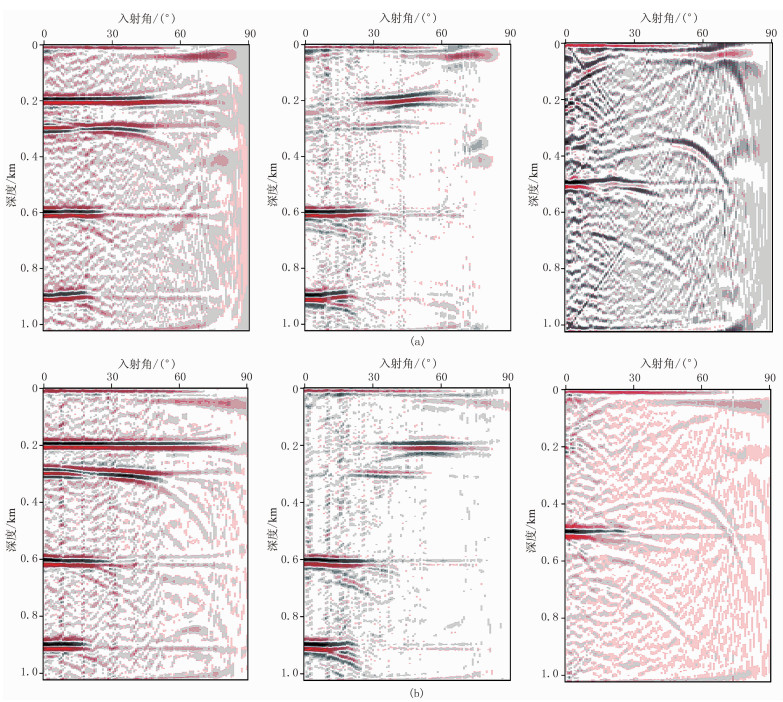
|
图 6 由各向同性(a)、各向异性(b)偏移方法提取的ADCIG 从左至右依次为CMP70、CMP150和CMP240处的ADCIG |
简单模型的成像测试证明了本文的VTI介质角度域偏移方法的可行性,可以处理VTI介质成像问题。
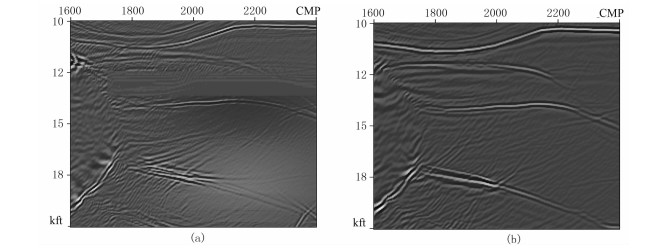
3.2 Hess VTI模型为了进一步验证本文的VTI介质角度域叠前深度偏移方法的成像效果,选取SEG 2D Hess VTI模型(图 7)进行偏移测试。图 8为各向同性偏移和VTI介质偏移剖面对比。由图可见:①各向同性偏移虽然可以对模型进行构造成像,并可以刻画各个界面,但成像分辨率较低,部分绕射波没有完全收敛,深层同相轴能量较弱,特别是高速盐丘体边界成像模糊,并在盐丘上部出现构造异常;无法对上部透镜体正确成像,中、下部的透镜体成像杂乱,分辨率较低;大断层处存在断面绕射波,成像位置出现偏差,整体成像效果较差(图 8a)。②VTI介质角度域偏移对各个层位的成像更清晰,清晰地刻画了盐丘底界面、三个透镜体,大断层的断点清晰,断点绕射波收敛较好,断层位置更精确,明显提高了剖面信噪比(图 8b)。图 9为透镜体区域各向同性和各向异性偏移结果对比。由图可见,各向异性偏移消除了构造假象,绕射波完全收敛,成像精度更高(图 9b)。
|
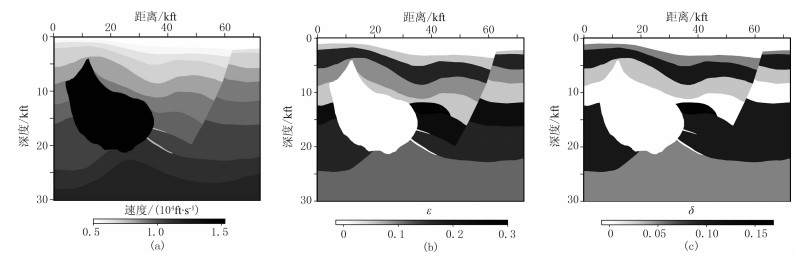
图 7 SEG 2D Hess VTI模型
(a)速度场;(b)ε;(c)δ 从左至右存在一个高速盐丘(速度约为围岩速度的1.5~2倍,盐丘边界的倾角达70°以上)、三个透镜体(各向异性异常体)、一条陡倾断层,其中上部透镜体成块状,中、下部的透镜体成条带状,规模较小 |

|
图 8 各向同性偏移(a)和VTI介质偏移(b)剖面对比 |
|
图 9 透镜体区域各向同性(a)和各向异性(b)偏移结果对比 |
Hess VTI模型测试结果表明,本文的VTI介质角度域偏移方法可以较好地处理复杂地质构造的成像问题。
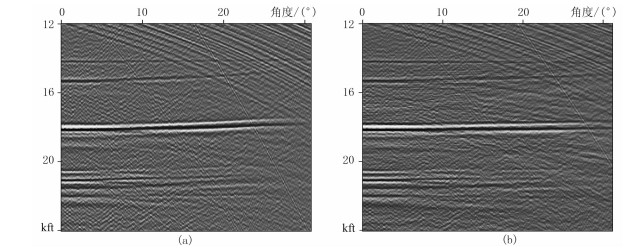
图 10为各向同性和各向异性偏移提取的ADCIG。由图可见:各向同性偏移的ADCIG同相轴无法完全校平,还残留部分绕射波,信噪比和分辨率较低(图 10a);VTI介质偏移的ADCIG同相轴较为平直,信噪比和分辨率较高,进一步说明VTI介质角度域偏移的可行性(图 10b)。
|
图 10 各向同性(a)和各向异性(b)偏移提取的ADCIG |
受各向异性参数建模技术的制约,VTI介质偏移方法在实际数据处理中存在困难。为了验证本文方法对实际数据处理的适应性,将偏移速度分析获得的速度模型作为各向异性偏移中的qP波速度,通过
| $ \left\{ \begin{array}{l} \varepsilon \left( {x,z} \right) = \frac{{0.606\left[ {v\left( {x,z} \right) - {v_{\min }}} \right]}}{{{v_{\max }}}}\\ \delta \left( {x,z} \right) = \frac{{0.485\left[ {v\left( {x,z} \right) - {v_{\min }}} \right]}}{{{v_{\max }}}} \end{array} \right. $ | (28) |
求取各向异性参数ε、δ[15]。计算获得的ε、δ最大值分别为0.45和0.36,在地球介质各向异性参数取值范围内。将以上参数用于实际数据的VTI介质角度域偏移。图 11为各向同性偏移和VTI介质偏移剖面。由图可见,各向同性偏移与各向异性偏移结果的构造形态基本一致,但后者在成像细节方面有所改进(图 11b),表现为:剖面左侧断点绕射波进一步收敛,断层下盘反射波能量增强,断面刻画更清晰;剖面右侧向斜区域成像清晰,中深层反射波能量得到增强,主要层位的反射同相轴连续性更好,提高了剖面分辨率。图 12为CDP560处提取的ADCIG。由图可见,VTI介质偏移的角道集同相轴更平直,连续性更好,可观测到更宽的角度范围(图 12b)。

|
图 11 实际数据各向同性偏移(a)和VTI介质偏移(b)剖面 |

|
图 12 CDP560处提取的ADCIG (a)各向同性偏移;(b)VTI介质偏移 |
将VTI介质qP波的频散关系引入双平方根方程,以各向同性偏移的波场延拓为基础,推导了VTI介质双平方根偏移的波场延拓算子,考虑了各向异性因素对波场传播引起的扰动,在波场延拓过程中进行频率-空间域误差校正。通过对延拓波场进行局部炮检距成像和角度转化,最终实现VTI介质角度域叠前深度偏移。
模型试算和实际资料处理结果表明:各向同性偏移方法由于未考虑各向异性参数的影响,绕射波不能完全收敛,波场聚焦效果差,降低了成像剖面的分辨率和信噪比,不能对地质构造精确成像;VTI介质角度域偏移可对断层、盐丘、小尺度地质体精确成像。对于角度域偏移产生的ADCIG而言,各向同性偏移的ADCIG同相轴无法校平,残留断点绕射波,波场无法正确聚焦,不能正确反映局部地质特征;VTI介质偏移的ADCIG同相轴较平直,角度范围更宽,波场归位准确,精度较高。因此,利用VTI介质角度域偏移方法可对复杂构造精确成像。
| [1] |
Pommier A, Leinenweber K, Kohlstedt D L, et al. Experimental constraints on the electrical anisotropy of the lithosphere asthenosphere system[J]. Nature, 2015, 522(3): 202-206. |
| [2] |
王赟, 杨顶辉, 殷长春, 等. 各向异性地球物理与矢量场[J]. 科学通报, 2017, 62(23): 2595-2605. WANG Yun, YANG Dinghui, YIN Changchun, et al. Anisotropic geophysics and vector field[J]. Chinese Science Bulletin, 2017, 62(23): 2595-2605. |
| [3] |
王咸彬. TTI各向异性逆时偏移技术[J]. 石油物探, 2017, 56(4): 534-542. WANG Xianbin. Anisotropic reverse time migration technique in TTI media and its application[J]. Geophysical Prospecting for Petroleun, 2017, 56(4): 534-542. DOI:10.3969/j.issn.1000-1441.2017.04.009 |
| [4] |
Alkhalifah T. An acoustic wave equation for aniso-tropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [5] |
吴国忱, 梁锴, 王华忠. VTI介质qP波广义高阶屏单程传播算子[J]. 石油地球物理勘探, 2007, 42(6): 640-650. WU Guochen, LIANG Kai, WANG Huazhong. High order one way generalized screen propagation operator of qP wave in VTI medium[J]. Oil Geophysical Prospecting, 2007, 42(6): 640-650. DOI:10.3321/j.issn:1000-7210.2007.06.007 |
| [6] |
韩建光, 王赟, 张晓波, 等. VTI介质高斯束叠前深度偏移[J]. 石油地球物理勘探, 2015, 50(2): 267-273. HAN Jianguang, WANG Yun, ZHANG Xiaobo, et al. Gaussian beam prestack depth migration in VTI media[J]. Oil Geophysical Prospecting, 2015, 50(2): 267-273. |
| [7] |
韩建光, 王赟, 陈传绪, 等. 二维各向异性多波高斯束叠前深度偏移[J]. 地球物理学进展, 2017, 32(3): 1130-1139. HAN Jianguang, WANG Yun, CHEN Chuanxu, et al. Multiwave Gaussian beam prestack depth migration for 2D anisotropic media[J]. Progress in Geophysics, 2017, 32(3): 1130-1139. |
| [8] |
刘礼农, 高红伟, 刘洪, 等. 三维VTI介质中波动方程深度偏移的最优分裂Fourier方法[J]. 地球物理学报, 2005, 48(2): 406-414. LIU Linong, GAO Hongwei, LIU Hong, et al. Wave equation depth migration with optimum split step Fourier method in 3D VTI media[J]. Chinese Journal of Geophysics, 2005, 48(2): 406-414. DOI:10.3321/j.issn:0001-5733.2005.02.025 |
| [9] |
刘礼农, 张剑锋. 三维各向异性介质中的波动方程叠前深度偏移方法[J]. 地球物理学报, 2011, 54(11): 2906-2915. LIU Linong, ZHANG Jianfeng. Wave equation prestack depth migration method in 3D VTI media[J]. Chinese Journal of Geophysics, 2011, 54(11): 2906-2915. DOI:10.3969/j.issn.0001-5733.2011.11.020 |
| [10] |
程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10): 3474-3486. CHENG Jiubing, KANG Wei, WANG Tengfei. Description of qP wave propagation in anisotropic media, Part Ⅰ:Pseudo-pure-mode wave equation[J]. ChineseJournal of Geophysics, 2013, 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
| [11] |
程玖兵, 陈茂根, 王腾飞, 等. 各向异性介质qP波传播描述Ⅱ:分离纯模式标量波[J]. 地球物理学报, 2014, 57(10): 3389-3401. CHENG Jiubing, CHEN Maogen, WANG Tenfei, et al. Description of qP wave propagation in anisotropic media, Part Ⅱ:Separation of pure-mode scalar wave[J]. Chinese Journal of Geophysics, 2014, 57(10): 3389-3401. DOI:10.6038/cjg20141025 |
| [12] |
Sun X D, Ge Z H, Li Z C, et al. The stability problem of reverse time migration for viscoacoustic VTI media[J]. Applied Geophysics, 2016, 13(4): 608-613. DOI:10.1007/s11770-016-0590-9 |
| [13] |
Zhang J M, He B S, Tang H G. Pure quasi P wave equation and numerical solution in 3D TTI media[J]. Applied Geophysics, 2017, 14(1): 125-132. DOI:10.1007/s11770-017-0613-1 |
| [14] |
Hua B, Lencrerot R, Williamson P, et al. High-order and high-accuracy 3D Fourier finite difference depth migration with an optimally reduced coefficient table for the tilted transversely isotropic media[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3794-3798.
|
| [15] |
黄建平, 朱峰, 李振春, 等. VTI介质FFD叠前深度偏移成像方法[J]. 石油地球物理勘探, 2017, 52(3): 491-501. HUANG Jianping, ZHU Feng, LI Zhenchun, et al. FFD prestack depth migration imaging method for VTI medium[J]. Oil Geophysical Prospecting, 2017, 52(3): 491-501. |
| [16] |
朱峰, 黄建平, 李振春. 黏声VTI介质傅里叶有限差分叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(5): 956-966. ZHU Feng, HUANG Jianping, LI Zhenchun. FFD prestack depth migration for visco-acoustic VTI me-dium[J]. Oil Geophysical Prospecting, 2017, 52(5): 956-966. |
| [17] |
Hoop D E, Le Rousseau J H, Wu R S. Generalization of the phase approximation for the scattering of acoustic waves[J]. Wave Motion, 2000, 31(1): 43-70. DOI:10.1016/S0165-2125(99)00026-8 |
| [18] |
Xu S, Chauris H, Lambare G, et al. Common angle migration:A strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [19] |
Stork C, Symes W. Kinematic artifacts in prestack depth migration[J]. Geophysics, 2004, 69(2): 562-575. DOI:10.1190/1.1707076 |
| [20] |
Xie X, Wu R.Extracting angle domain information from migration wave field[C].SEG Technical Program Expanded Abstracts, 2002, 21: 1360-1363.
|
| [21] |
James E, Rickett J E, Save P C. Offset and angle domain common image point gather for shot profile migration[J]. Geophysics, 2002, 67(3): 883-889. DOI:10.1190/1.1484531 |
| [22] |
Save P, Fomel S. Angle domain common image gathers by wavefield continuation[J]. Geophysics, 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [23] |
Biondi B. Angle domain common image gathers from anisotropic migration[J]. Geophysics, 2007, 72(2): S81-91. DOI:10.1190/1.2430561 |
| [24] |
李振春, 朱莉, 叶月明, 等. 角度域共成像点道集的提取与叠加成像[J]. 石油物探, 2008, 47(6): 567-572. LI Zhenchun, ZHU Li, YE Yueming, et al. Extraction and stack imaging of angle domain common image gathers[J]. Geophysical Prospecting for Petroleum, 2008, 47(6): 567-572. DOI:10.3969/j.issn.1000-1441.2008.06.004 |
| [25] |
张敏, 李振春, 叶月明, 等. 基于双平方根算子的保幅角度域成像[J]. 中国石油大学学报, 2011, 35(2): 45-50. ZHANG Min, LI Zhenchun, YE Yueming, et al. Amplitude preserved imaging based on double sqraretoor wave equation in angle domain[J]. Journal of China University of Petroleum, 2011, 35(2): 45-50. DOI:10.3969/j.issn.1673-5005.2011.02.008 |
| [26] |
Tang B, Xu S, Zhang Y. 3D angle gathers from plane-wave reverse time migration[J]. Geophysics, 2013, 78(2): 117-123. DOI:10.1190/geo2012-0313.1 |
| [27] |
张广智, 常德宽, 王一惠, 等. 波动方程叠前深度偏移角度道集求取方法[J]. 石油地球物理勘探, 2016, 51(3): 529-536. ZHANG Guangzhi, CHANG Dekuan, WANG Yihui, et al. Angle domain common image gather calculation based on wave equation prestack depth migration[J]. Oil Geophysical Prospecting, 2016, 51(3): 529-536. |
| [28] |
方伍宝, 刘定进. 深度域地震成像新技术理论与实践[M]. 北京: 中国石化出版社, 2014.
|
| [29] |
Thomesen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(6): 1954-1966. |
| [30] |
Zhang K, Li Z C, Zeng T S, et al. Residual curvature migration velocity analysis for angle domain common imaging gathers[J]. Applied Geophysics, 2010, 7(1): 49-56. DOI:10.1007/s11770-010-0006-1 |



 李庆春 陕西省西安市雁塔区雁塔路南段126号长安大学地质工程与测绘学院, 710054。Email:
李庆春 陕西省西安市雁塔区雁塔路南段126号长安大学地质工程与测绘学院, 710054。Email: