为了简便起见,在地震勘探中通常把地下介质视为各向同性介质。但研究结果表明,介质的各向异性性质广泛存在。人们根据介质性质,又将各向异性介质细分为不同类型,常见的有横向各向同性介质(Transversely Isotropic Media, TI)。具有垂直对称轴的TI介质称为VTI介质,如果对称轴是倾斜的,则称为TTI介质。正演模拟是认识地震波传播规律的有效手段,也是实现逆时偏移(Reverse Time Migration、RTM)、波动方程层析成像以及全波形反演(Full Waveform Inversion,FWI)的核心内容。各向异性全弹性波动方程可准确、全面地描述地震波在地层中的传播情况,但是全弹性波正演、成像与反演还面临诸多困难,目前TI介质正演模拟、RTM以及参数反演主要采用简化的qP波方程[1]。
与各向同性介质相比,TI介质是有5个独立的弹性系数,波动方程形式更复杂。在垂直传播面内,平行对称轴和垂直对称轴两个方向的纵波(P波)和横波(SV波)是解耦的,其他传播方向的P波和SV波是耦合的。另外,TI介质的P波极化方向和传播方向不一致,SV波极化方向不垂直于传播方向,因此又分别称为准纵波(qP波)和准横波(qSV波)。由于qP波和qSV波耦合,在TI介质波动方程数值模拟中分离P、S波存在困难。为了得到独立传播的qP波和qSV波方程,一般需要对介质做近似处理,如小倾角近似、椭圆近似、弱各向异性近似、声学近似等[2]。
声学近似简单、方便,计算量小,在RTM成像中发挥着重要作用。Alkhalifah[3-4]提出了声学近似,将沿着对称轴方向的S波速度设置为零,从Thomsen参数表示的频散关系出发,推导了四阶qP-qSV波耦合波动方程,方程中的四阶混合偏导数增加了数值模拟的复杂度。Zhou等[5]基于相同的频散关系,通过引入辅助函数,导出了qP-qSV波耦合的二阶波动方程,数值模拟也更易实现。随后Zhou等[6]把qP-qSV波耦合的二阶波动方程推广到TTI介质。Zhang等[7]基于声学近似假设,推导了TTI介质的四阶P波波动方程。Zhang等[8]、Zhang等[9]实现了三维TTI介质RTM。Fletcher等[10]把VTI介质的伪声波波动方程扩展到TTI介质。梁锴等[11]导出了三维TTI介质声学近似qP波波动方程。虽然基于声学近似的伪P波波动方程可以精确地保留P波运动学特征,但其P、S波并非完全解耦,容易产生两个问题,一是伪横波噪声干扰,二是复杂介质条件下方程的解不稳定。在各向异性介质中,地震波的传播速度是传播方向的函数,仅把对称轴方向的S波速度人为设置为零,以这种方式推导出的伪声波方程并不能真正地消除S波的影响,所以严格意义上不应称为声波波动方程。当震源位于VTI或TTI介质中时,在数值模拟时会出现S波,另外在界面处也会产生转换S波。在椭圆型各向异性介质中不会激发S波,实际介质中椭圆型各向异性介质很少见。各向异性参数匹配法是压制伪横波噪声的一种有效手段,在声学假设条件下,通过在震源附近设置各向同性层或者椭圆各向异性层消除伪横波噪声的影响,但在各向异性参数变化剧烈的区域仍然会产生S波干扰。Yoon等[12]在陡倾区域设置椭圆各向异性层减少S波干扰,将剧烈变化的模型各向异性参数简化为连续变化,也能改善模拟效果,但在改变模型局部特征的同时,也改变了波场的运动学特征。张岩等[13]借助于辅助场,给出了一种空间域的简单、高效的压制伪横波噪声的方法。Fowler等[14]推导了对称轴方向S波速度不为零的VTI介质二阶耦合波动方程。Fletcher等[15]通过把对称轴方向的S波速度设置为非零值,在一定程度上解决了不稳定性问题,但会增强伪横波噪声干扰强度,随着递推时间增加,数值频散也变得更严重。
一般通过直接推导qP-qSV波完全解耦的纯P波方程解决由声学近似带来的数值不稳定问题。Du等[16-17]基于弱各向异性近似和平方根近似,推导了TTI介质时间—波数域纯qP波解耦方程。Liu等[18]推导了VTI介质时间—空间域纯qP波波动方程。Pestana等[19-20]基于快速展开法(Rapid Expansion Method,REM)实现了VTI介质时间—波数域纯qP波RTM成像。Chu等[21]利用泰勒展开公式,推导了TTI介质解耦纯qP波波动方程。Zhan等[22]利用REM的混合有限差分与伪谱法实现了TTI介质纯qP波RTM。王伟国等[23]实现了TTI介质qP波伪谱法RTM。黄建平等[24]基于伪谱法实现了TTI介质一阶qP波方程正演模拟。黄金强等[1]借助Low-rank分解,实现了一种间接的纯qP波波场外推方案。郭成锋等[25]利用伪谱法和有限差分法联合实现了纯qP波波场延拓,提高了计算效率。
本文从Tsvankin[26]的VTI介质qP波精确相速度表达式出发,引入单位向量,利用坐标变换的方法把qP波的精确相速度扩展到三维TTI介质。基于弱各向异性近似和平方根近似,推导了三维TTI介质纯qP波近似相速度和频散关系。根据频散关系构建了纯qP波时间—波数域的波场递推格式,并进行了相应的稳定性分析。最后利用伪谱法对不同的TI模型进行了qP波数值模拟。
1 方法原理 1.1 TTI介质的相速度对于VTI介质,Tsvankin[26]给出了qP波精确相速度表达式
| $ \begin{array}{l} \frac{{V_{\rm{P}}^2\left( \theta \right)}}{{V_{{\rm{P}}z}^2}} = 1 + \varepsilon {\sin ^2}\theta - \frac{f}{2} + \\ \frac{f}{2}\sqrt {1 + \frac{{4{{\sin }^2}\theta }}{f}\left( {2\delta {{\cos }^2}\theta - \varepsilon \cos 2\theta } \right) + \frac{{4{\varepsilon ^2}{{\sin }^4}\theta }}{{{f^2}}}} \end{array} $ | (1) |
式中:VP(θ)为相速度,θ为传播方向与对称轴(z轴)方向的夹角,表示平面波的相角;VPz为z方向的P波速度;ε和δ为Thomsen各向异性参数[27];f≡1-VSz2/VPz2,VSz为z方向的S波速度。
当介质的ε和δ远小于1时,称为弱各向异性介质,实际介质大多为弱各向异性介质。因为式(1)较复杂,将式中的根式进行泰勒展开,根据弱各向异性假设,舍去ε和δ的二次及以上高次项,得到线性近似的相速度表达式[26]
| $ \frac{{V_{\rm{P}}^2\left( \theta \right)}}{{V_{{\rm{P}}z}^2}} = 1 + 2\delta {\sin ^2}\theta {\cos ^2}\theta + 2\varepsilon {\sin ^4}\theta $ | (2) |
式(2)为纯qP波相速度表达式,无S波项。
对于TTI介质,将式(1)、式(2)进行坐标旋转可得到相应的qP波相速度。郝重涛等[28]基于坐标变换的方法给出了TI介质qP、qSV和qSH波精确相速度表达式。姚振岸等[29]利用Bond变换导出了TI介质弹性波速度解析式,但精确相速度表达式较复杂。本文基于弱各向异性近似,导出相应的线性近似相速度公式。由于目前的TI介质RTM主要基于qP波,故本文主要讨论qP波相速度。
设TI介质对称轴与z轴的夹角为θ0, 当θ0=0°时为VTI介质,当θ0≠0°时则为TTI介质。利用旋转坐标法,将TTI介质的qP波相速度表示为
| $ \begin{array}{l} \frac{{V_{\rm{P}}^2\left( \gamma \right)}}{{V_{{\rm{P}}z}^2}} = 1 + \varepsilon {\sin ^2}\gamma - \frac{f}{2} + \\ \;\;\;\;\frac{f}{2}\sqrt {1 + \frac{{4{{\sin }^2}\gamma }}{f}\left( {2\delta {{\cos }^2}\gamma - \varepsilon {{\cos }2}\gamma } \right) + \frac{{4{\varepsilon ^2}{{\sin }^4}\theta }}{{{f^2}}}} \end{array} $ | (3) |
同理,可近似简化为
| $ \frac{{V_{\rm{P}}^2\left( \gamma \right)}}{{V_{{\rm{P}}z}^2}} = 1 + 2\delta {\sin ^2}\gamma {\cos ^2}\gamma + 2\varepsilon {\sin ^4}\gamma $ | (4) |
式中γ为qP波传播方向与对称轴的夹角,式(3)、式(4)中其他参数的含义同式(1)、式(2)。可以看到,除了θ换成γ外,式(3)、式(4)和式(1)、式(2)在形式上完全一样。本文用θ表示地震波传播方向与z轴的夹角,γ表示地震波传播方向与对称轴的夹角。很显然,VTI介质的对称轴与z轴重合,即γ=θ;TTI介质的对称轴与z轴的夹角为θ0,即γ=θ+θ0。
郝重涛等[28]的研究结果表明,TI介质中体波速度随传播方向变化的速度图案取决于对称轴方向,并与TI介质的Thomsen参数相关。速度特征只依赖于传播矢量与对称轴的夹角,具有一定的对称性、渐变性和重复性。在各向异性参数确定的条件下,式(3)和式(4)只与γ相关,这与文献[28]的研究结果一致。通过合理的简化,将对称轴的方位角设置为0,即对称轴位于垂直面xoz内,这样只需考虑θ0、θ以及传播方向的方位角φ等三个变量。
为了计算的方便,引入单位向量,其中s为TI介质对称轴方向的单位向量,r为地震波传播方向的单位向量,i为x轴方向的单位向量,j为y轴方向的单位向量,k为z轴方向的单位向量。根据地震波传播方向和坐标轴的关系(图 1),单位向量表示为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{s}} = \sin {\theta _0}\mathit{\boldsymbol{i}} + \cos {\theta _0}\mathit{\boldsymbol{k}}\\ \mathit{\boldsymbol{r}} = \sin \theta \cos \varphi \mathit{\boldsymbol{i}} + \sin \theta \sin \varphi \mathit{\boldsymbol{j}} + \cos \theta \mathit{\boldsymbol{k}} \end{array} \right. $ | (5) |

|
图 1 地震波传播方向与坐标轴的关系 |
s和r的夹角为γ,通过s与r的矢量积及数量积得到
| $ \cos \gamma = \sin \theta \cos \varphi \sin {\theta _0} + \cos \theta \cos {\theta _0} $ | (6) |
| $ \begin{array}{l} {\sin ^2}\gamma = {\sin ^2}\theta {\sin ^2}\varphi + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {\sin \theta \cos \varphi \cos {\theta _0} - \cos \theta \sin {\theta _0}} \right)^2} \end{array} $ | (7) |
将式(6)、式(7)代入式(3)和式(4)即可求出相速度。虽然计算涉及到θ、θ0和φ三个变量,但最终都归结到γ一个变量。
表 1为TI介质各向异性参数,根据对称轴方向的变化,对比、分析TTI介质的qP波线性近似相速度与精确相速度的逼近程度。
|
|
表 1 TI介质各向异性参数 |
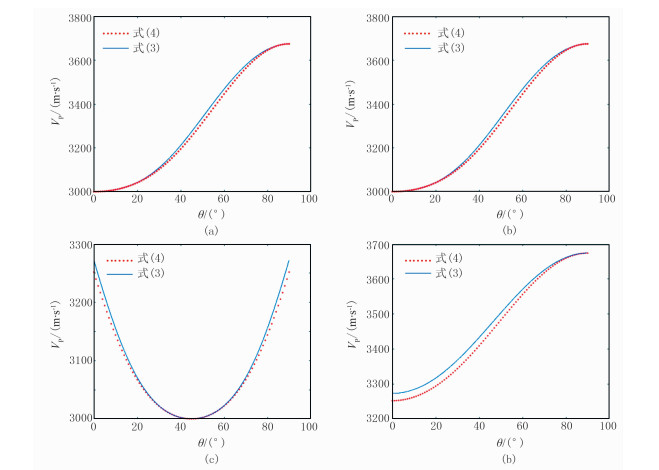
图 2为由式(3)、式(4)得到的相速度。由图可见:①近似式(式(4))的均方差ΔVRMS较小,表明由式(4)能较好地逼近精确公式(式(3));②在VTI介质中,当θ0=0°、φ=0°(图 2a)与θ0=0°、φ=90°(图 2b)时得到的曲线完全一样,说明VTI介质的速度特征与传播方位角无关;③在TTI介质中速度特征具有方位性(图 2c、图 2d)。
|
图 2 由式(3)、式(4)得到的相速度 (a)VTI介质,θ0=0°,φ=0°,ΔVRMS=13.4154m/s; (b)VTI介质,θ0=0°,φ=90°,ΔVRMS=13.4154m/s; (c)TTI介质,θ0=45°,φ=0°,ΔVRMS=13.4605m/s; (d)TTI介质,θ0=45°,φ=90°,ΔVRMS=18.5240m/s |
伪谱法的基本思想是在波数域计算空间导数,采用有限差分法计算时间导数[24]。在三维(x, y, z)空间内传播的平面波有下列相角关系
| $ \left\{ \begin{array}{l} \sin \theta \cos \varphi = \frac{{{V_{\rm{P}}}\left( {\theta ,\varphi } \right){k_x}}}{\omega }\\ \sin \theta \sin \varphi = \frac{{{V_{\rm{P}}}\left( {\theta ,\varphi } \right){k_y}}}{\omega }\\ \cos \theta = \frac{{{V_{\rm{P}}}\left( {\theta ,\varphi } \right){k_z}}}{\omega } \end{array} \right. $ | (8) |
式中:VP为相速度;kx、ky、kz为波数;ω为角频率。
将式(8)代入式(1),得到VTI介质的qP-qSV波频散关系。Fletcher等[15]利用旋转波数导出了TTI介质的频散关系
| $ \begin{array}{l} {\omega ^4} = \left[ {\left( {V_{{\rm{P}}x}^2 + V_{{\rm{S}}z}^2} \right)\left( {\hat k_x^2 + \hat k_y^2} \right) + \left( {V_{{\rm{P}}z}^2 + V_{{\rm{S}}z}^2} \right)\hat k_z^2} \right]{\omega ^2} - \\ \;\;\;\;\;\;\;\;V_{{\rm{P}}x}^2V_{{\rm{S}}z}^2{\left( {\hat k_x^2 + \hat k_z^2} \right)^2} - V_{{\rm{P}}z}^2V_{{\rm{S}}z}^2\hat k_z^4 + \\ \;\;\;\;\;\;\;\;\left[ {V_{{\rm{P}}z}^2\left( {V_{{\rm{P}}n}^2 - V_{{\rm{P}}x}^2} \right) - V_{{\rm{S}}z}^2\left( {V_{{\rm{P}}n}^2 - V_{{\rm{P}}z}^2} \right)} \right] \times \\ \;\;\;\;\;\;\;\;\left( {\hat k_x^2 + \hat k_y^2} \right)\hat k_z^2 \end{array} $ | (9) |
式中:VPn2=VPz2(1+2δ); VPx2=VPz2(1+2ε);
| $ \left\{ \begin{array}{l} {{\hat k}_x} = {k_x}\cos {\theta _0}\cos {\varphi _0} + {k_y}\cos {\theta _0}\sin {\varphi _0} - {k_z}\sin {\theta _0}\\ {{\hat k}_y} = - {k_x}\sin {\varphi _0} + {k_y}\cos {\varphi _0}\\ {{\hat k}_z} = {k_x}\sin {\theta _0}\cos {\varphi _0} + {k_y}\sin {\theta _0}\sin {\varphi _0} + {k_z}\cos {\theta _0}\\ \hat k_x^2 + \hat k_y^2 + \hat k_z^2 = k_x^2 + k_y^2 + k_z^2 \end{array} \right. $ | (10) |
式中φ0为对称轴的方位角。令VSz=0,式(9)变为TTI介质的声学近似qP波频散关系[4]
| $ \begin{array}{l} {\omega ^4} = \left[ {V_{{\rm{P}}x}^2\left( {\hat k_x^2 + \hat k_y^2} \right) + V_{{\rm{P}}z}^2\hat k_z^2} \right]{\omega ^2} + \\ \;\;\;\;\;\;\;V_{{\rm{P}}z}^2\left( {V_{{\rm{P}}n}^2 - V_{{\rm{P}}x}^2} \right)\left( {\hat k_x^2 + \hat k_y^2} \right)\hat k_z^2 \end{array} $ | (11) |
令f=1,将式(6)、式(7)代入式(3)也可导出式(11)。对式(11)进行傅里叶逆变换,得到时间—空间域的4阶偏微分方程,方程的解较为复杂。通过引入辅助函数
| $ \begin{array}{l} q\left( {{k_x},{k_y},{k_z},\omega } \right) = \frac{{{\omega ^2} + \left( {V_{{\rm{P}}n}^2 - V_{{\rm{P}}x}^2} \right)\left( {\hat k_x^2 + \hat k_y^2} \right)}}{{{\omega ^2}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\left( {{k_x},{k_y},{k_z},\omega } \right) \end{array} $ | (12) |
Fletcher等[15]将四阶偏微分方程转换为等价的2阶耦合方程。式(11)两边乘以p(kx, ky, kz, ω),化简后有
| $ \begin{array}{l} {\omega ^2}p\left( {{k_x},{k_y},{k_z},\omega } \right) = V_{{\rm{P}}x}^2\left( {\hat k_x^2 + \hat k_y^2} \right)p\left( {{k_x},{k_y},{k_z},\omega } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;V_{{\rm{P}}z}^2\hat k_z^2q\left( {{k_x},{k_y},{k_z},\omega } \right) \end{array} $ | (13) |
| $ \begin{array}{l} {\omega ^2}q\left( {{k_x},{k_y},{k_z},\omega } \right) = V_{{\rm{P}}n}^2\left( {\hat k_x^2 + \hat k_y^2} \right)p\left( {{k_x},{k_y},{k_z},\omega } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;V_{{\rm{P}}z}^2\hat k_z^2q\left( {{k_x},{k_y},{k_z},\omega } \right) \end{array} $ | (14) |
对式(13)、式(14)进行傅里叶逆变换,得到声学近似二阶耦合波动方程
| $ \frac{{{\partial ^2}p}}{{\partial {t^2}}} = V_{{\rm{P}}x}^2\left( {\frac{{{\partial ^2}p}}{{\partial {{\hat x}^2}}} + \frac{{{\partial ^2}p}}{{\partial {{\hat y}^2}}}} \right) + V_{{\rm{P}}z}^2\frac{{{\partial ^2}q}}{{\partial {{\hat z}^2}}} $ | (15) |
| $ \frac{{{\partial ^2}q}}{{\partial {t^2}}} = V_{{\rm{P}}n}^2\left( {\frac{{{\partial ^2}p}}{{\partial {{\hat x}^2}}} + \frac{{{\partial ^2}p}}{{\partial {{\hat y}^2}}}} \right) + V_{{\rm{P}}z}^2\frac{{{\partial ^2}q}}{{\partial {{\hat z}^2}}} $ | (16) |
式中p为压力波场。式中的偏微分算子为
| $ \begin{array}{l} \frac{{{\partial ^2}}}{{\partial {{\hat x}^2}}} = {\cos ^2}{\theta _0}{\cos ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {\cos ^2}{\theta _0}{\sin ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {y^2}}} + \\ \;\;\;\;\;\;{\sin ^2}{\theta _0}\frac{{{\partial ^2}}}{{\partial {z^2}}} + {\cos ^2}{\theta _0}\sin 2{\varphi _0}\frac{{{\partial ^2}}}{{\partial x\partial y}} - \\ \;\;\;\;\;\;\sin 2{\theta _0}\cos {\varphi _0}\frac{{{\partial ^2}}}{{\partial x\partial z}} - \sin 2{\theta _0}\sin {\varphi _0}\frac{{{\partial ^2}}}{{\partial y\partial z}} \end{array} $ | (17) |
| $ \frac{{{\partial ^2}}}{{\partial {{\hat y}^2}}} = {\sin ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {\cos ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {y^2}}} - \sin 2{\varphi _0}\frac{{{\partial ^2}}}{{\partial x\partial y}} $ | (18) |
| $ \begin{array}{l} \frac{{{\partial ^2}}}{{\partial {{\hat z}^2}}} = {\sin ^2}{\theta _0}{\cos ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {\sin ^2}{\theta _0}{\sin ^2}{\varphi _0}\frac{{{\partial ^2}}}{{\partial {y^2}}} + \\ \;\;\;\;\;{\cos ^2}{\theta _0}\frac{{{\partial ^2}}}{{\partial {z^2}}} + {\sin ^2}{\theta _0}\sin 2{\varphi _0}\frac{{{\partial ^2}}}{{\partial x\partial y}} + \\ \;\;\;\;\;\sin 2{\theta _0}\cos {\varphi _0}\frac{{{\partial ^2}}}{{\partial x\partial z}} + \sin 2{\theta _0}\sin {\varphi _0}\frac{{{\partial ^2}}}{{\partial y\partial z}} \end{array} $ | (19) |
从式(4)出发,导出纯qP波时间—波数域波动方程。将式(6)和式(7)代入式(4),等式两边同乘以时间—波数域的波场U(kx, ky, kz, t);再利用式(8),同时仅在频域应用傅里叶逆变换,便可得到TTI介质纯qP波时间—波数域波动方程
| $ \begin{array}{l} \frac{{{\partial ^2}{U_P}\left( {{k_x},{k_y},{k_z},t} \right)}}{{\partial {t^2}}} = - V_{{\rm{P}}z}^2\left[ {k_x^2 + k_y^2 + k_z^2 + } \right.\\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\cos }^4}{\theta _0}} \right)\frac{{k_x^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {\delta \sin 4{\theta _0} - 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_x^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}2{\theta _0} - \sigma {{\sin }^2}2{\theta _0} + 3\varepsilon {{\sin }^2}2{\theta _0}} \right)\frac{{k_x^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} - \\ \;\;\;\left( {\delta \sin 4{\theta _0} + 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_z^3{k_x}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\sin }^4}{\theta _0}} \right)\frac{{k_z^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0} + 4\varepsilon {{\cos }^2}{\theta _0}} \right)\frac{{k_x^2k_y^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta \sin 2{\theta _0} - 4\varepsilon \sin 2{\theta _0}} \right)\frac{{{k_x}k_y^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}{\theta _0} + 4\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_y^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left. {2\varepsilon \frac{{k_y^4}}{{k_x^2 + k_y^2 + k_z^2}}} \right]{U_{\rm{P}}}\left( {{k_x},{k_y},{k_z},t} \right) \end{array} $ | (20) |
式(20)等号左边的二阶时间偏导数可写成有限差分的形式,等号右边则用简单的波数计算替代复杂的空间导数计算。
波动方程数值模拟的吸收边界条件大致分为两种:一类是傍轴近似的吸收边界条件;另一类是阻尼层吸收边界条件。当前通用的吸收边界条件是最佳匹配层(PML)吸收边界条件,属于第二种吸收边界条件。PML吸收边界条件是由一阶波动方程得到的,无论是分裂算法还是非分裂算法,推广到二阶系统时算法较为复杂,对内存需求也较大,故本文采用Cerjan等[30]提出的阻尼吸收边界条件。
在数值模拟计算时,首先必须考虑方程解的稳定性条件,此处给出θ0=0°时(VTI介质)的稳定性条件(详细推导过程见附录A)
| $ \frac{{{V_{{\rm{P}}z}}\Delta t}}{{\Delta d}} < \frac{2}{{{\rm{ \mathsf{ π} }}\sqrt {4\alpha + 3} }} $ | (21) |
式中:Δt为时间步长;Δd为网格空间步长;α=min[abs(ε), abs(δ)]。
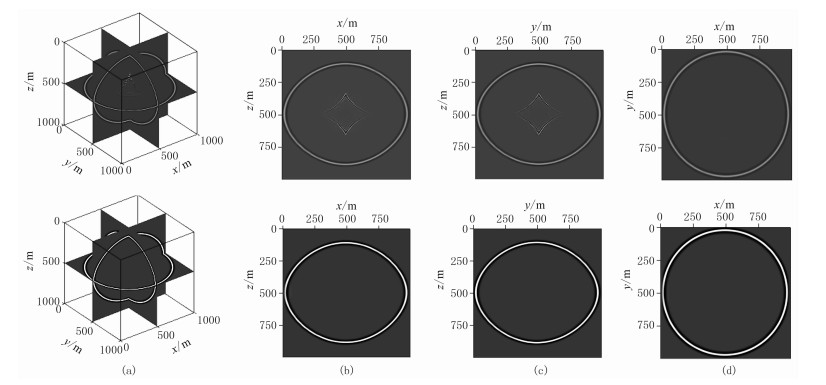
2 数值计算 2.1 均匀模型首先设计一个VTI均匀介质模型,图 3为由式(15)、式(16)及式(20)模拟得到的VTI均匀介质模型在139ms的波场快照。由图可见:由声学近似二阶耦合方程(式(15)、式(16))、纯qP波方程(式(20))得到的波场快照的波场传播特征十分吻合,但前者存在明显的qSV波干扰(图 3a上~图 3c上),后者没有qSV波干扰(图 3a下~图 3c下);由于VTI介质对称轴垂直,在任意方向的垂直切片的地震波场特征一致,故垂直切片的波前形态一致(图 3b、图 3c),而水平切片反映了各向同性层,波前呈圆形(图 3d)。
|
图 3 由式(15)、式(16)(上)及式(20)(下)得到的VTI均匀介质模型在139ms的波场快照
(a)三维正交切片;(b)xoz切片;(c)yoz切片;(d)xoy切片 模型网格数为201×201×201,网格间距为dx=dy=dz=5m,各向异性参数:VPz=3000m/s;ε=0.25;δ=0.1,VTI介质对称轴倾斜角θ0=0°。震源函数采用雷克子波,主频为100Hz,震源坐标为(x, y, z)=(500m, 500m, 500m)。数值计算的时间步长为0.1ms,总采样时长为150ms |
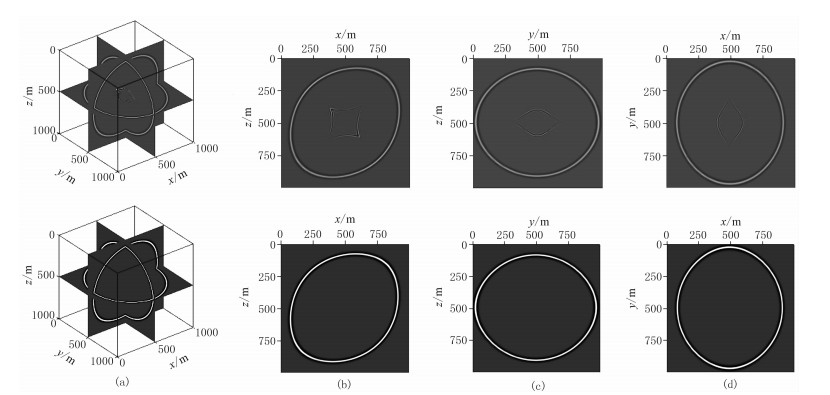
图 4为由式(15)、式(16)及式(20)得到的TTI均匀介质模型在139ms的波场快照。由图可见:由纯qP波方程(式(20))得到的波场快照只有纯qP传播,没有伪横波噪声干扰(图 4a下~图 4d下);由于TTI介质对称轴在xoz面内倾斜,故相对于VTI介质xoz垂直切片的波场发生旋转(图 4b);由于对称轴位于yoz面外,在yoz面内地震波传播方向与对称轴方向的夹角缺少0°~45°范围内的值,故在xoz面(图 4b)与yoz面的垂直切片(图 4c)的波场特征不同;由于xoz面外的任意水平或垂直平面都与对称轴相交,这些平面内的地震波传播方向与对称轴方向的夹角缺少0°~β(小于对称轴倾角的角度)范围内的值,故不同方位的垂直波场切片形态也不同,因此xoy面内的波场切片(图 4d)表征了TTI介质的方位各向异性。
|
图 4 由式(15)、式(16)(上)及式(20)(下)得到的TTI均匀介质模型在139ms的波场快照
(a)三维正交切片;(b)xoz切片;(c)yoz切片;(d)xoy切片 模型对称轴倾角θ0= 45°,其他参数同图 3 |
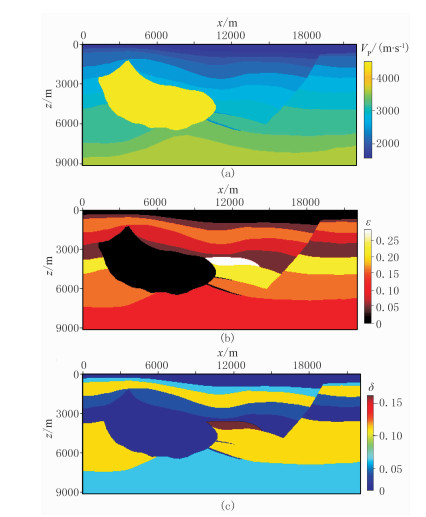
图 5为Hess VTI模型。考虑到计算稳定性条件,选取网格间距dx=dz=6.096m,时间采样间隔为0.5ms,采样时长为1.5s,震源坐标为(x, z)=(11009m, 3645m),震源函数采用雷克子波,主频为20Hz。图 6为Hess VTI模型在1.5s的波场快照。由图可见,由式(15)、式(16)(图 6a)和式(20) (图 6b)得到的波场快照的波场特征基本一致,说明声学近似方程与纯qP波方程的等价性,但前者存在伪横波,在震源附近出现频散,后者没有伪横波干扰。
|
图 5 Hess VTI模型 (a)VPz;(b)ε;(c)δ |

|
图 6 Hess VTI模型在1.5s的波场快照 (a)式(15)、式(16);(b)式(20) |
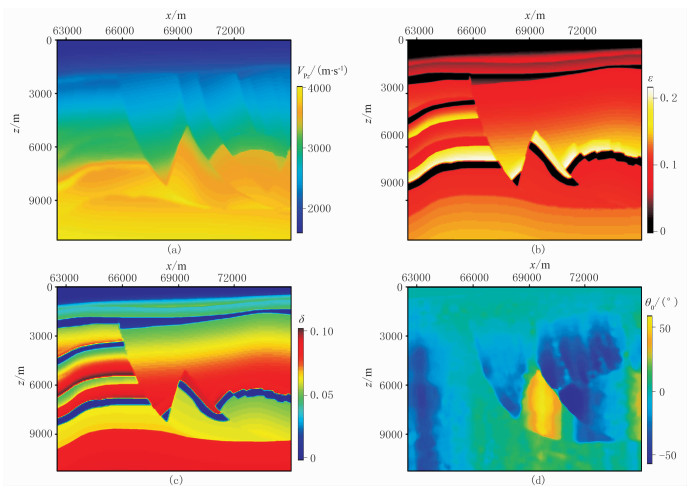
图 7为BP 2007 TTI模型。由图可见,存在强各向异性地层,局部区域发生对称轴倾斜,呈TTI介质特征。由于原始模型较大,本文选择部分典型区域进行正演计算。图 8为BP 2007 TTI模型在1.5s的波场快照。由图可见,由声学近似方程(图 8a)和纯qP波方程(图 8b)得到的波场快照的波场特征基本一致,但后者的波场稳定,未出现频散现象,说明本文方法对复杂TTI模型具有较好的适应性。
|
图 7 BP 2007 TTI模型 (a)VPz;(b)ε;(c)δ;(d)对称轴倾角θ0 |

|
图 8 BP 2007 TTI模型在1.5s的波场快照
(a)式(15)、式(16);(b)式(20) 网格间距为dx=dz=12.5m, 震源坐标为(x, z)=(68750m, 2625m), 其他参数同图 6 |
伪谱法涉及到傅里叶变换,计算效率低于有限差分法,但在同样精度条件下,伪谱法可选取更大的空间网格间距和时间采样间隔[24]。进行大区域或三维模型数值模拟时,伪谱法的计算时间较长。如果计算机硬件条件有限,可以采用混合法计算,即用有限差分法计算简单的空间偏导数项,用伪谱法计算复杂的空间偏导数项,减少了傅里叶变换次数,提高了计算效率,可在一定程度上减少计算耗时。
3 结束语本文利用坐标变换的方法,把Tsvankin[26]的VTI介质qP波精确相速度扩展到三维空间,基于弱各向异性近似推导了三维线性近似qP波相速度表达式,构建了时间—波数域的纯qP波波动方程,并给出了稳定性条件。通过对比、分析数值计算结果,得到以下认识。
(1) 在各向异性参数确定的条件下,任意对称轴取向的TI介质中qP波的传播速度取决于传播方向与TI对称轴的夹角。
(2) 把TTI介质对称轴的方位角取为0°,简化了计算,文中的各向异性模型为2.5维,但不同方向的切片仍然可以表征TTI介质的方位各向异性。
(3) 本文的纯qP波波动方程可以较好地应用于TTI介质正演模拟,得到的波场快照没有伪横波干扰,对复杂TTI模型仍然保持较好的波场稳定性。伪谱法计算量较大,可以和有限差分法联合使用以减少计算时间。
感谢Hess公司提供了VTI模型,感谢BP公司提供了BP 2007 TTI模型。
附录A TTI介质纯qP波时间—波数域波场递推格式| $ \begin{array}{l} {U_\text{P}}\left( {{k_x},{k_y},{k_z},t + \Delta t} \right) - 2{U_\text{P}}\left( {{k_x},{k_y},{k_z},t} \right) + \\ \;\;\;{U_P}\left( {{k_x},{k_y},{k_z},t - \Delta t} \right) = - \Delta {t^2}V_{{\rm{P}}z}^2\left[ {k_x^2 + k_y^2 + k_z^2 + } \right.\\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\cos }^4}{\theta _0}} \right)\frac{{k_x^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {\delta \sin 4{\theta _0} - 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_x^3{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}2{\theta _0} - \delta {{\sin }^2}2{\theta _0} + 3\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_x^2{k_z^2}}}{{k_x^2 + k_y^2 + k_z^2}} - \\ \;\;\;\left( {\delta \sin 4{\theta _0} + 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_z^3{k_x}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\sin }^4}{\theta _0}} \right)\frac{{k_z^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0} + 4\varepsilon {{\cos }^2}{\theta _0}} \right)\frac{{k_x^2k_y^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta \sin 2{\theta _0} - 4\varepsilon \sin 2{\theta _0}} \right)\frac{{{k_x}k_y^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}{\theta _0} + 4\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_y^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left. {2\varepsilon \frac{{k_y^4}}{{k_x^2 + k_y^2 + k_z^2}}} \right]{U_{\rm{P}}}\left( {{k_x},{k_y},{k_z},t} \right) \end{array} $ | (A-1) |
把试验解ei(kxx+kyy+kzz-ωt)代入式(A-1),得
| $ \begin{array}{l} {{\rm{e}}^{ - {\rm{i}}\omega \Delta t}} - 2 + {{\rm{e}}^{{\rm{i}}\omega \Delta t}} = - \Delta {t^2}V_{{\rm{P}}z}^2\left[ {k_x^2 + k_y^2 + k_z^2 + } \right.\\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\cos }^4}{\theta _0}} \right)\frac{{k_x^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {\delta \sin 4{\theta _0} - 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_x^3{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}2{\theta _0} - \delta {{\sin }^2}2{\theta _0} + 3\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_x^2{k_z^2}}}{{k_x^2 + k_y^2 + k_z^2}} - \\ \;\;\;\left( {\delta \sin 4{\theta _0} + 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_z^3{k_x}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\sin }^4}{\theta _0}} \right)\frac{{k_z^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0} + 4\varepsilon {{\cos }^2}{\theta _0}} \right)\frac{{k_x^2k_y^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta \sin 2{\theta _0} - 4\varepsilon \sin 2{\theta _0}} \right)\frac{{{k_x}k_y^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}{\theta _0} + 4\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_y^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left. {2\varepsilon \frac{{k_y^4}}{{k_x^2 + k_y^2 + k_z^2}}} \right] \end{array} $ | (A-2) |
利用倍角公式
| $ \begin{array}{l} 4{\sin ^2}\frac{{\omega \Delta t}}{2} = \Delta {t^2}V_{{\rm{P}}z}^2\left[ {k_x^2 + k_y^2 + k_z^2 + } \right.\\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\cos }^4}{\theta _0}} \right)\frac{{k_x^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {\delta \sin 4{\theta _0} - 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_x^3{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}2{\theta _0} - \delta {{\sin }^2}2{\theta _0} + 3\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_x^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} - \\ \;\;\;\left( {\delta \sin 4{\theta _0} + 8\varepsilon \sin {\theta _0}{{\cos }^3}{\theta _0}} \right)\frac{{k_z^3{k_x}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0}{{\cos }^2}{\theta _0} + 2\varepsilon {{\sin }^4}{\theta _0}} \right)\frac{{k_z^4}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\sin }^2}{\theta _0} + 4\varepsilon {{\cos }^2}{\theta _0}} \right)\frac{{k_x^2k_y^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta \sin 2{\theta _0} - 4\varepsilon \sin 2{\theta _0}} \right)\frac{{{k_x}k_y^2{k_z}}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left( {2\delta {{\cos }^2}{\theta _0} + 4\varepsilon {{\sin }^2}{\theta _0}} \right)\frac{{k_y^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + \\ \;\;\;\left. {2\varepsilon \frac{{k_y^4}}{{k_x^2 + k_y^2 + k_z^2}}} \right] \end{array} $ | (A-3) |
式(A-3)形式仍然很复杂,将式(A-3)等号两边开平方,并且取θ0=0°,得到VTI介质的稳定性条件
| $ \begin{array}{l} 2 > \Delta t{V_{{\rm{P}}z}} \times \\ \;\;\;\sqrt {k_x^2 + k_y^2 + k_z^2 + 2\varepsilon \frac{{k_x^4}}{{k_x^2 + k_y^2 + k_z^2}} + 2\delta \frac{{k_x^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + 4\varepsilon \frac{{k_x^2k_y^2}}{{k_x^2 + k_y^2 + k_z^2}} + 2\delta \frac{{k_y^2k_z^2}}{{k_x^2 + k_y^2 + k_z^2}} + 2\varepsilon \frac{{k_y^4}}{{k_x^2 + k_y^2 + k_z^2}}} \end{array} $ | (A-4) |
令α=min[abs(ε), abs(δ)],则式(A-4)简化为
| $ 2 > \Delta t{V_{{\rm{P}}z}}\sqrt {k_x^2 + k_y^2 + k_z^2 + 2\alpha \left( {k_x^2 + k_y^2} \right)} $ | (A-5) |
根据采样定理,信号带宽应小于奈奎斯特频率(采样频率的二分之一),即有
| $ {k_x},{k_y},{k_z} < \frac{1}{2}\frac{{2{\rm{ \mathsf{ π} }}}}{{\Delta d}} = \frac{{\rm{ \mathsf{ π} }}}{{\Delta d}} $ |
式中Δd为网格尺寸(空间步长)。整理上式,得
| $ \frac{{{V_{{\rm{P}}z}}\Delta t}}{{\Delta d}} < \frac{2}{{{\rm{ \mathsf{ π} }}\sqrt {4\alpha + 3} }} $ | (A-6) |
| [1] |
黄金强, 李振春. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [2] |
王娟, 李振春, 孙小东, 等. TTI介质逆时偏移成像[J]. 石油地球物理勘探, 2012, 47(4): 573-577. WANG Juan, LI Zhenchun, SUN Xiaodong, et al. Reverse time migration in tilt transversely isotropic(TTI) media[J]. Oil Geophysical Prospecting, 2012, 47(4): 573-577. |
| [3] |
Alkhalifah T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631. |
| [4] |
Alkhalifah T. An acoustic wave equation for aniso-tropic media[J]. Geophysics, 2000, 65(4): 1239-1250. |
| [5] |
Zhou H, Zhang G, Bloor R.An anisotropic acoustic wave equation for VTI media[C]. Extended Abstracts of 68th EAGE Conference & Exhibition, 2006, H033.
|
| [6] |
Zhou H, Zhang G, Bloor R.An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 194-198.
|
| [7] |
Zhang L, Rector J W, Hoversten G M. Finite-differ-ence modelling of wave propagation in acoustic tilted TI media[J]. Geophysical Prospecting, 2005, 53(6): 843-852. DOI:10.1111/gpr.2005.53.issue-6 |
| [8] |
Zhang H, Zhang Y.Reverse time migration in 3D heterogeneous TTI media[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2196-2200. https://www.researchgate.net/publication/240736933_Reverse_time_migration_in_3D_heterogeneous_TTI_media
|
| [9] |
Zhang Y, Zhang H.A stable TTI reverse time migration and its implementation[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2794-2798. https://www.researchgate.net/publication/301434048_A_Stable_TTI_Reverse_Time_Migration?ev=auth_pub
|
| [10] |
Fletcher R P, Du X, Fowler P J.A new pseudo-acoustic wave equation for TI media[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2082-2086. https://www.researchgate.net/publication/249862440_A_New_Pseudo-acoustic_Wave_Equation_for_VTI_Media
|
| [11] |
梁锴, 吴国忱, 印兴耀, 等. 三维TTI介质波动方程分解[J]. 石油地球物理勘探, 2009, 44(1): 19-27. LIANG Kai, WU Guochen, YING Xinyao, et al. Wave equation decomposition in 3-D TTI medium[J]. Oil Geophysical Prospecting, 2009, 44(1): 19-27. DOI:10.3321/j.issn:1000-7210.2009.01.005 |
| [12] |
Yoon K, Suh S, Ji J, et al. Stability and speedup issues in TTI RTM implementation[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3221-3225. https://www.researchgate.net/publication/269069126_Stability_and_speedup_issues_in_TTI_RTM_implementation?ev=auth_pub
|
| [13] |
张岩, 吴国忱. TTI介质qP波逆时偏移中伪横波噪声压制方法[J]. 地球物理学报, 2013, 56(6): 2065-2076. ZHANG Yan, WU Guochen. Methods of removing pseudo SV-wave artifacts in TTI media qP-wave reverse-time migration[J]. Chinese Journal of Geophysics, 2013, 56(6): 2065-2076. |
| [14] |
Fowler P J, Du X, Fletcher R P. Coupled equations for reverse time migration in transversely isotropic media[J]. Geophysics, 2010, 75(1): S11-S22. |
| [15] |
Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [16] |
Du X, Bancroft J C, Lines L R.Reverse-time migration for tilted TI media[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1930-1934.
|
| [17] |
Du X, Bancroft J C, Lines L R. Anisotropic reverse-time migration for tilted TI media[J]. Geophysical Prospecting, 2007, 55(6): 853-869. DOI:10.1111/gpr.2007.55.issue-6 |
| [18] |
Liu F Q, Morton S A, Jiang S S, et al. Decoupled wave equations for P and SV waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844-2848.
|
| [19] |
Pestana R C, Stoffa P L. Time evolution of the wave equation using rapid expansion method[J]. Geophy-sics, 2010, 75(4): 121-131. |
| [20] |
Pestana R C, Ursin B, Stoffa P L.Separate P-and SV-wave equations for VTI media[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 163-167.
|
| [21] |
Chu C, Macy B K, Anno P D. Approximation of pure acoustic seismic wave propagation in TTI media[J]. Geophysics, 2011, 76(5): WB97-WB107. DOI:10.1190/geo2011-0092.1 |
| [22] |
Zhan G, Pestana R C, Stoffa P L. Decoupled equations for reverse time migration in tilted transversely isotropic media[J]. Geophysics, 2012, 77(2): 37-45. DOI:10.1190/geo2011-0175.1 |
| [23] |
王伟国, 熊水金, 徐华宁, 等. TTI介质各向异性伪谱法逆时偏移[J]. 石油地球物理勘探, 2012, 47(4): 566-572. WANG Weiguo, XIONG Shuijin, XU Huaning, et al. Reverse-time migration using pseudo-spectral method for tilted TI media[J]. Oil Geophysical Prospecting, 2012, 47(4): 566-572. |
| [24] |
黄建平, 黄金强, 李振春, 等. TTI介质一阶qP波方程交错网格伪谱法正演模拟[J]. 石油地球物理勘探, 2016, 51(3): 487-496. HUANG Jianping, HUANG Jinqiang, LI Zhenchun, et al. Staggered grid pseudo-spectral numerical simulation of first-order quasi P-wave equation for TTI media[J]. Oil Geophysical Prospecting, 2016, 51(3): 487-496. |
| [25] |
郭成锋, 杜启振, 张明强, 等. 改进的TTI介质纯P波方程正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(1): 258-270. GUO Chengfeng, DU Qizhen, ZHANG Mingqiang, et al. Numerical simulation and reverse time migration using an improved pure P-wave equation in tilted transversely isotropic media[J]. Chinese Journal of Geophysics, 2017, 60(1): 258-270. |
| [26] |
Tsvankin I. P-wave signatures and notation for tranversely isotropic media:An overview[J]. Geophysics, 1996, 61(2): 467-483. DOI:10.1190/1.1443974 |
| [27] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [28] |
郝重涛, 姚陈. 任意空间取向TI介质中体波速度特征[J]. 地球物理学报, 2007, 50(2): 546-555. HAO Chongtao, YAO Chen. Analysis of body-wave velocity characteristic for TI medium with arbitrary spatial orientation[J]. Chinese Journal of Geophysics, 2007, 50(2): 546-555. DOI:10.3321/j.issn:0001-5733.2007.02.028 |
| [29] |
姚振岸, 孙成禹, 邓小凡, 等. 任意空间取向TI介质弹性波速度特征分析[J]. 石油地球物理勘探, 2017, 52(4): 715-733. YAO Zhen'an, SUN Chengyu, DENG Xiaofan, et al. Velocity characteristic analysis of elastic wave for TI media with arbitrary spatial orientation[J]. Oil Geophysical Prospecting, 2017, 52(4): 715-733. |
| [30] |
Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equation[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |



 朱国维 北京市海淀区学院路丁11号中国矿业大学(北京)地球科学与测绘工程学院, 100083。Email:
朱国维 北京市海淀区学院路丁11号中国矿业大学(北京)地球科学与测绘工程学院, 100083。Email: