② 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
③ 南方科技大学地球与空间科学系, 广东深圳 518055;
④ 中煤科工集团西安研究院有限公司, 陕西西安 710077
② CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Beijing 102249, China;
③ Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China;
④ Xi'an Research Institute, China Coal Technology & Engineering Group, Xi'an, Shaanxi 710077, China
噪声一直是影响地震资料品质的重要因素之一,地震资料处理的最基本目标就是消除地震记录中的各种噪声,最大程度地提高地震资料信噪比。对随机噪声的压制许多学者已提出了大量的方法并取得了很多研究成果,这些方法主要有中值滤波方法[1]、f-x反褶积方法[2]、离散余弦变换方法[3]、小波变换方法[4-6]、独立分量分析方法[7]、经验模态分解[8]、f-x预测滤波方法[9-10]、字典学习方法[11]以及奇异值分解(SVD)[12-15]方法等。
刘财等[1]将二维多级中值滤波应用到地震勘探中的噪声压制,研究了噪声强度与滤波因子的关系。陆文凯[3]在离散余弦变换域中利用预测滤波器压制噪声。Cao等[5]给出了一种柔性的基于提升法的小波构造方法,适用线性、非线性或空间变化的预测和更新算子,并能确保变换的可逆性。刘洋等[6]采用高阶seislet变换的提升算法对地震信号去噪,重点考虑了去噪阈值选取。Bekara等[8]在f-x域采用经验模态分解降噪;以此为基础,Chen等[9]在f-x域中先使用倾角滤波器,再利用经验模态分解压制了复杂地层结构中的噪声。Liu等[10]在f-x域中采用整形正则化约束预测倾角压制噪声,滤波器长度和整形算子是该方法中二个重要参数。陆文凯等[12-13]采用SVD方法实现地震资料的降噪,之后在纹理方向检测倾角的基础上再用SVD方法压制噪声。徐彦凯等[15]采用奇异值选择的自适应方法压制地震资料中的噪声。
上述方法均探讨了如何将信号与噪声有效分离。当然,信噪分离效果的好坏与压制噪声的阈值、滤波器算子长度的大小有很大关系。阈值较小或滤波器算子较短,信噪分离的程度相对较小,即去噪后的地震资料中还存在较多噪声;反之,若将噪声完全从地震资料中去除,地震信号可能会受到部分损伤,即去除的噪声中尚存部分有效信号。为了提高地震资料信噪比,本文充分利用了信号和随机噪声的不相关性,依据信号与噪声满足的局部正交化准则,从分离后的噪声中再提取地震信息。
1 基本原理地震数据d可看成由理想地震信号s和随机噪声n两部分组成,即
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} \approx {\mathit{\boldsymbol{s}}_0} + {\mathit{\boldsymbol{n}}_0} $ | (1) |
式中s0和n0分别为采用传统方法处理得到的信号与噪声,即第一次分离出的信号与噪声。
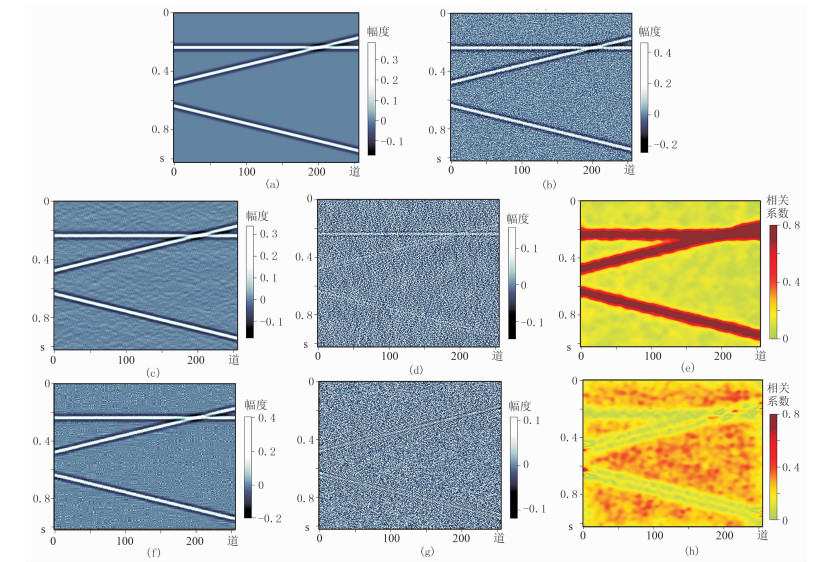
大多数情况下,第一次分离噪声n0不等于n和n0中含有的残留信号s1。从图 1a~图 1d、图 1f、图 1g可见:两种方法分离的噪声中都含有一些信号的影子。对分离后的信号与噪声做相关分析,得到相关系数剖面(图 1e、图 1h),可见分离出的噪声与信号有很强相关性。依据其相关特性估计噪声中的残留信号。残留信号s1由分离出的信号s0加权[16]表示为
| $ {\mathit{\boldsymbol{s}}_1} = \mathit{\boldsymbol{w}} \circ {\mathit{\boldsymbol{s}}_0} = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{s}}_0} = {\mathit{\boldsymbol{S}}_0}\mathit{\boldsymbol{w}} $ | (2) |
|
图 1 常规处理后信号与噪声及相关性 (a)理想信号;(b)信噪比为-2.25dB加噪信号;(c)、(d)分别为f-x滤波后的信号和噪声;(e)图c与图d的相关系数;(f)、(g)分别为采用秩是2的SVD滤波后信号和噪声;(h)图f与图g的相关系数 |
式中:w表示通过s0估计s1的权重因子;“○”表示hadamard积;W=diag(w);S0=diag(s0)。
1.1 局部正交准则设
| $ \mathit{\boldsymbol{\hat s}} = {\mathit{\boldsymbol{s}}_0} + w{\mathit{\boldsymbol{s}}_0} $ | (3) |
同理,
| $ \mathit{\boldsymbol{\hat n}} = {\mathit{\boldsymbol{n}}_0} - w{\mathit{\boldsymbol{s}}_0} $ | (4) |
式(3)和式(4)中w表示全局权重系数。
由于信号s与随机噪声n不相关,则
| $ {{\mathit{\boldsymbol{\hat s}}}^{\rm{T}}}\mathit{\boldsymbol{\hat n}} = 0 $ | (5) |
将式(3)和式(4)代入式(5),可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat s}}}^{\rm{T}}}\mathit{\boldsymbol{\hat n}} = {\left( {{\mathit{\boldsymbol{s}}_0} + w{\mathit{\boldsymbol{s}}_0}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{n}}_0} - w{\mathit{\boldsymbol{s}}_0}} \right)\\ \;\;\;\;\;\; = \mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0} + w\mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0} - w\mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{s}}_0} - {w^2}\mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{s}}_0} = 0 \end{array} $ | (6) |
由此得到全局权重系数
| $ w = \frac{{\mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0}}}{{\mathit{\boldsymbol{s}}_0^{\rm{T}}{\mathit{\boldsymbol{s}}_0}}} $ | (7) |
加窗后式(7)改写为[16]
| $ w\left( t \right) = \frac{{\sum\limits_{i = t - 0.5m}^{t + 0.5m} {{s_0}\left( i \right){n_0}\left( i \right)} }}{{\sum\limits_{i = t - 0.5m}^{t + 0.5m} {s_0^2\left( i \right)} }} $ | (8) |
w(t)是t点处窗长m区域内满足局部正交准则的权重系数。式(8)的矩阵形式为
| $ \mathit{\boldsymbol{S}}_0^{\rm{T}}{\mathit{\boldsymbol{S}}_0}\mathit{\boldsymbol{w}} = \mathit{\boldsymbol{S}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0} $ | (9) |
与全局正交相比,采用局部正交准则能根据有效信号缺失程度自适应地优化权重因子w。
从式(9)可见:当已知S0和n0时,计算权重因子w是不适定问题。对此,可采用整形正则化求解。
1.2 整形正则化正则化目的是对估计的模型解强加限制,以使不适定问题得以求解,其中Tikhonov正则化为一种经典方法。在此基础上,Fomel[17]考虑整形算子的平滑作用,提出了整形正则化理论。
式(9)可转化为最小平方意义下目标函数优化
| $ \mathit{\boldsymbol{w}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{w}} \left\| {{\mathit{\boldsymbol{n}}_0} - {\mathit{\boldsymbol{S}}_0}\mathit{\boldsymbol{w}}} \right\|_2^2 $ | (10) |
对目标函数加约束,式(10)改写为
| $ \mathit{\boldsymbol{w}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{w}} \left\| {{\mathit{\boldsymbol{n}}_0} - {\mathit{\boldsymbol{S}}_0}\mathit{\boldsymbol{w}}} \right\|_2^2 + \varepsilon \left\| {\mathit{\boldsymbol{Dw}}} \right\|_2^2 $ | (11) |
式中:D为对权重因子w加以光滑约束的Tikhonov正则化项;ε为正则化系数。采用最小二乘法得到其解为
| $ \mathit{\boldsymbol{\tilde w}} = {\left( {\mathit{\boldsymbol{S}}_0^{\rm{T}}{\mathit{\boldsymbol{S}}_0} + {\varepsilon ^2}{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}}} \right)^{ - 1}}\mathit{\boldsymbol{S}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0} $ | (12) |
求解式(11)的优化问题时,考虑解的平滑性和收敛速度,引入约束模型在可接受空间映射的整形算子[18]
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = {\left( {\mathit{\boldsymbol{I}} + {\varepsilon ^2}{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}}} \right)^{ - 1}} $ | (13) |
式(12)可改写为
| $ \mathit{\boldsymbol{\tilde w}} = {\left[ {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {\mathit{\boldsymbol{S}}_0^{\rm{T}}{\mathit{\boldsymbol{S}}_0} - \mathit{\boldsymbol{I}}} \right)} \right]^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} S}}_0^{\rm{T}}{\mathit{\boldsymbol{n}}_0} $ | (14) |
将式(14)代入式(3),得到信号s的估计
估计
设地震道记录中每道有N个采样点。该记录可用矩阵
| $ {\mathit{\boldsymbol{A}}_{N \times M}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1M}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2M}}}\\ \cdots & \cdots & \cdots & \cdots \\ {{a_{N1}}}&{{a_{N2}}}& \cdots &{{a_{NM}}} \end{array}} \right] $ | (15) |
表示,其元素为aij(i为道号,j为时间样点号)。
设矩阵AN×M(N≤M)的秩为r,则存在两正交矩阵U、V和对角矩阵Λ,且满足
| $ {\mathit{\boldsymbol{A}}_{N \times M}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (16) |
其中
| $ \begin{array}{*{20}{c}} \begin{array}{l} \mathit{\boldsymbol{U}} = \left[ {{\mathit{\boldsymbol{u}}_1},{\mathit{\boldsymbol{u}}_2}, \cdots ,{\mathit{\boldsymbol{u}}_N}} \right]\\ \mathit{\boldsymbol{V}} = \left[ {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}, \cdots ,{\mathit{\boldsymbol{v}}_M}} \right] \end{array}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}&{\bf{0}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right]} \end{array} $ |
式中:Δ=diag[σ1, σ2, …, σr], σ1≥σ2…≥σr>0;σi是矩阵A的奇异值;ui、vi分别是矩阵A的左、右奇异向量。
地震信号经过奇异值分解后,奇异值仅集中在前几个。这样,信号奇异值分布有一个陡降,而随机噪声奇异值由大到小的递减幅度统计近似相同,因此采用相邻奇异值增量分离地震资料中的随机噪声。相邻奇异值增量定义为
| $ \Delta {\sigma _i} = {\sigma _i} - {\sigma _{i + 1}} $ | (17) |
ASVD是将数据做SVD得到奇异值后,计算奇异值增量的幅度和序号以及阈值,在序号内确定最大奇异值增量,由阈值确定保留奇异值的个数,从而实现信号和噪声分离。
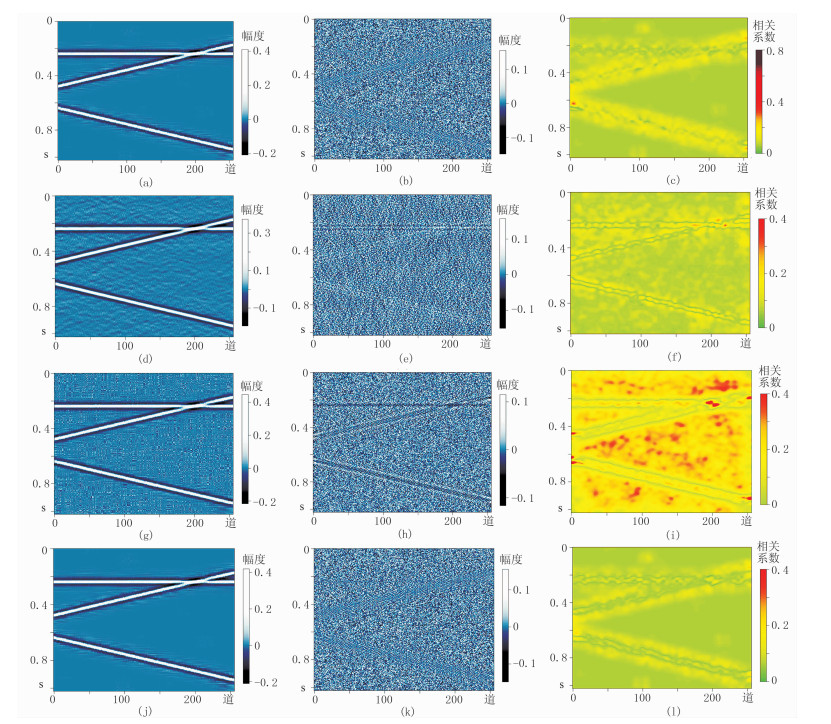
2 模型与实际资料处理 2.1 模型试验为了检验本文算法的有效性,首先对图 1b做ASVD,图 2a与2b分别为分离得到的信号与噪声,可见图 2a中噪声很少;计算二者的相关性(图 2c)后与图 1e和图 1h比较,可见由ASVD得到的信号与噪声的相关性更小。
|
图 2 局部正交法压噪效果 (a)ASVD分离后信号;(b)ASVD分离出的噪声;(c)图a与图b的相关;(d)、(g)、(j)分别为采用f-x、常规SVD和ASVD三种方法+局部正交法分离的总信号;(e)、(h)、(k)分别为对应噪声;(f)、(i)、(l)分别为对应的相关系数 |
在此基础上,采用整形正则化的局部正交法从分离出的噪声中提取残留信号并进行处理,然后与分离前的相关系数(图 1e、图 1h)及采用f-x[16]、常规SVD方法的结果进行对比(图 2)。可见分离后信号(图 2d、图 2g、图 2j)与噪声(图 2e、图 2h、图 2k)的相关系数(图 2f、图 2i、图 2l)都有不同程度的减小;本文方法得到的有效信号剖面更干净清晰,相关系数明显小于文献方法的结果[16]。
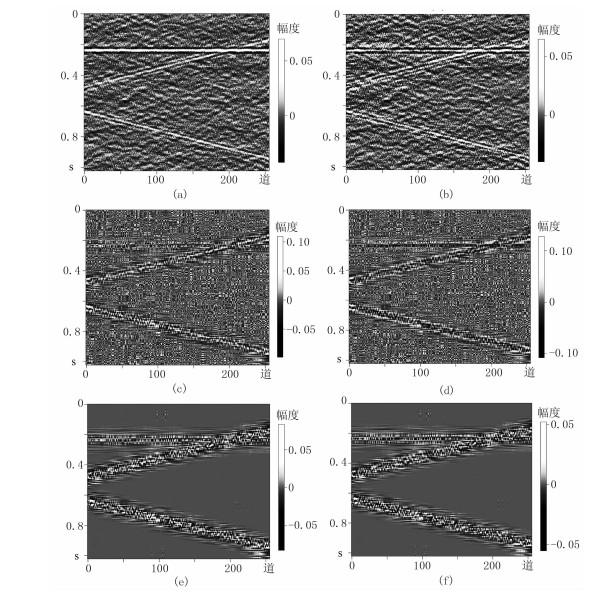
图 3a、图 3c、图 3e分别为理想信号与用f-x、常规SVD和ASVD三种方法压制噪声后信号的误差剖面;图 3b、图 3d、图 3f为分别为f-x、常规SVD和ASVD三种方法基础上采用局部正交法分离得到的误差剖面。对比这两组剖面可见:f-x和ASVD两种方法采用局部正交法处理后的误差小于未采用的;采用局部正交法分离将f-x方法的误差剖面(图 3a)上水平同相轴信息得到了充分提取(图 3b);由于ASVD方法中倾斜同相轴不能全部集中在前几个奇异值上,所以图 3e中倾斜同相轴误差较大,采用局部正交法分离将ASVD方法的误差剖面(图 3e)中倾斜同相轴信息实现了较好地提取,得到误差剖面图 3f。
|
图 3 图 2对应的误差剖面 (a)、(c)、(e)分别为理想信号与用f-x、常规SVD和ASVD三种方法压制噪声后信号的误差剖面;(b)、(d)、(f)为对应的利用局部正交法得到的误差剖面 |
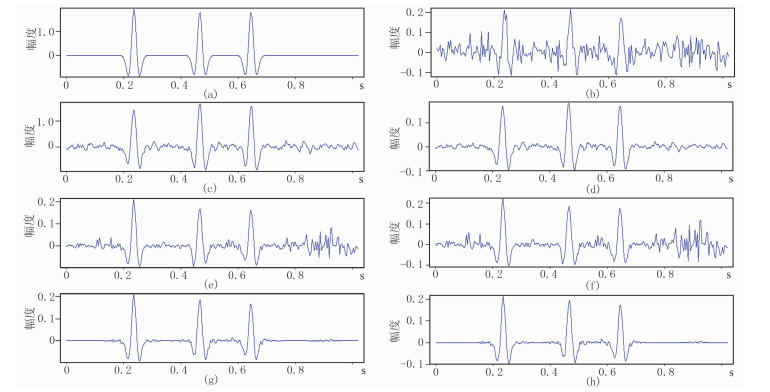
抽取图 1中第10道的理想信号(图 4a)和加噪信号(图 4b),以及f-x、常规SVD和ASVD三种方法处理结果(图 4c、图 4e、图 4g)、对应的局部正交法处理后结果的第10道(图 4d、图 4f、图 4h),可见用ASVD方法+局部正交法(图 4h)压制噪声效果最好。为了便于量化对比几种方法的压噪效果,计算了局部正交法分离前、后的信噪比(表 1)。
|
图 4 图 2中第10道压噪效果 (a)理想信号;(b)加噪信号;(c)、(e)、(g)分别为f-x、常规SVD和ASVD三种方法处理结果;(d)、(f)、(h)为对应的局部正交法处理结果 |
|
|
表 1 局部正交法分离前、后信噪比 |
表 1中f-x和ASVD分离信噪比较高,信号中含随机噪声较少,通过局部正交法分离的噪声中能有效提取残留信号,从而提高分离后的信噪比。SVD方法分离的信号中噪声较多,采用局部正交法从分离的噪声提取的残留信号中噪声较多,因此分离后的信噪比反而减小。由上可知,采用局部正交分离要求分离前的信号含噪少。
为了进一步验证局部正交法信噪分离效果,对水平地层模型做ASVD降噪处理[15]后,又采用局部正交法提取分离噪声中的残留信息。设炮点到各层的最小时间t01~t05分别为0.1、0.4、0.6、0.8、0.95s,对应速度v1~v5分别为950、1000、1100、1200、1500m/s;采样间隔为4ms;采样点数为300;道间距为10m;道数为81;雷克子波峰值频率为35Hz。在合成的CDP道集(图 5a)上,加入一定噪声后得到信噪比为-1dB的记录(图 5b),并对其进行无拉伸动校处理(图 5c);应用ASVD进行信噪分离,得到一次分离后的信号(图 5d)、噪声(图 5e)及其二者的相关系数(图 5f);采用局部正交法从一次分离的噪声中提取残留信号,得到最终的信号(图 5g)、噪声(图 5h)及其二者的相关系数(图 5i);对图 5d和图 5g分别做反无拉伸动校处理,得到对应地震记录(图 5j、图 5k,其信噪比分别为6.4、7.5dB)、一次分离后(图 5l)及最终(图 5m)噪声。从二次分离前后的信号、噪声及其相关性可见:局部正交法可有效提取噪声中的残留信号,大大降低信号与噪声的相关性,从而最大限度地保留有效信号并压制噪声,进而提高地震记录信噪比。

|
图 5 合成地震记录ASVD及局部正交法去噪效果 (a)合成CDP道集;(b)信噪比为-1dB的含噪记录;(c)无拉伸动校后记录;(d)、(e)、(f)分别为ASVD第一次分离后信号、噪声及二者相关系数;(g)、(h)、(i)局部正交法处理后的信号、噪声及二者相关系数;(j)、(k)分别是图d、图g的反无拉伸动校后记录;(l)一次分离后噪声;(m)最终噪声 |
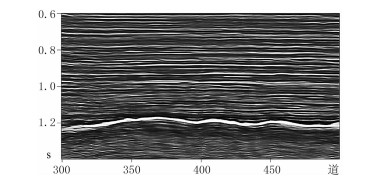
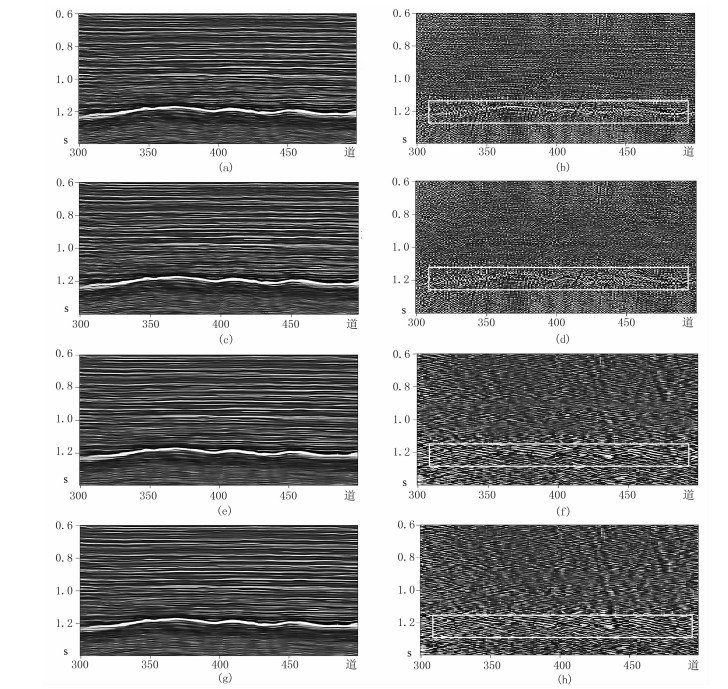
选取实际二维叠加数据(图 6)的第300~500道,其采样间隔为2ms,每道400个采样点。进行f-x处理(图 7a)和局部正交处理(图 7c),得到相应的差剖面(图 7b、图 7d);再做ASVD处理(图 7e)和局部正交处理(图 7g),得到对应的差剖面(图 7f、图 7h)。从上述差剖面中方框部分可见:局部正交处理前的差剖面(图 7b、图 7f)都含有明显的同相轴信息,而局部正交处理后的差剖面(图 7d、图 7h)中同相轴信息较好地被提取;对比局部正交处理后的f-x方法(图 7d)与ASVD方法(图 7h)差剖面,可见后者处理效果更好;同时,其对应的叠加剖面图 7g的信噪比高于图 7c。
|
图 6 实际二维叠加地震数据 |
|
图 7 实际地震数据的不同处理方法剖面对比 (a)、(c)分别为f-x和f-x+局部正交处理的叠加剖面;(b)、(d)分别为f-x和f-x+局部正交处理的差剖面;(e)、(g)分别为ASVD和ASVD+局部正交处理的叠加剖面;(f)、(h)分别为ASVD和ASVD+局部正交处理的差剖面 |
地震数据处理中,常规方法压制随机噪声后,滤除噪声中尚存一定量有效信号。本文提出的基于整形正则化的局部正交方法可从常规分离的噪声中有效提取残留信号。该方法要求常规分离的信号中噪声较少。与f-x、SVD方法相比,ASVD方法压噪性能更强。模型和实际资料处理结果均表明,在ASVD降噪基础上采用局部正交法可有效压制地震数据中随机噪声,显著提高地震资料信噪比。
| [1] |
刘财, 王典, 刘洋, 等. 二维多级中值滤波技术在随机噪声消除中的应用初探[J]. 石油地球物理勘探, 2005, 40(2): 163-167. LIU Cai, WANG Dian, LIU Yang, et al. Preliminary study of using 2D multi-level median filtering technique to eliminate random noises[J]. Oil Geophysical Prospecting, 2005, 40(2): 163-167. DOI:10.3321/j.issn:1000-7210.2005.02.015 |
| [2] |
Canales L L.Random noise reduction[C]. SEG Technical Program Expanded Abstracts, 1984, 3: 525-527. https://www.researchgate.net/publication/249858508_Random_noise_reduction
|
| [3] |
陆文凯. 基于离散余弦变换的地震随机噪声压制技术[J]. 石油地球物理勘探, 2011, 46(2): 202-206. LU Wenkai. Seismic random noise suppression based on the discrete cosine transform[J]. Oil Geophysical Prospecting, 2011, 46(2): 202-206. |
| [4] |
吴爱弟, 曹思远. 用正交多小波压制地震信号的随机噪声[J]. 石油地球物理勘探, 2002, 37(5): 473-476. WU Aidi, CAO Siyuan. Random noise suppression of seismic signal using orthogonal multi-wavelets[J]. Oil Geophysical Prospecting, 2002, 37(5): 473-476. DOI:10.3321/j.issn:1000-7210.2002.05.008 |
| [5] |
Cao S Y, Chen X P. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2005, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
| [6] |
刘洋, Fomel Sergey, 刘财, 等. 高阶Seislet变换及其在随机噪声消除中的应用[J]. 地球物理学报, 2009, 52(8): 2142-2151. LIU Yang, Fomel S, LIU Cai, et al. High order Seislet transform and its application of random noise attenua-tion[J]. Chinese Journal of Geophysics, 2009, 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 |
| [7] |
张念, 刘天佑, 李杰, 等. Fast ICA算法及其在地震信号去噪中的应用[J]. 计算机应用研究, 2009, 26(4): 1432-1434. ZHANG Nian, LIU Tianyou, LI Jie, et al. Fast ICA algorithm and its application in seismic signal noise elimination[J]. Application Research of Computer, 2009, 26(4): 1432-1434. DOI:10.3969/j.issn.1001-3695.2009.04.068 |
| [8] |
Bekara M, Baan M V D. Random and coherent noise attenuation by empirical mode decomposition[J]. Geophysics, 2011, 74(5): V89-V98. |
| [9] |
Chen Y K, Ma J T. Random noise attenuation by f-x empirical mode decomposition predictive filtering[J]. Geophysics, 2014, 79(3): V81-V91. DOI:10.1190/geo2013-0080.1 |
| [10] |
Liu G C, Chen X H, Du J, et al. Random noise attenuation using f-x regularized non-stationary auto regression[J]. Geophysics, 2012, 77(2): V61-V69. DOI:10.1190/geo2011-0117.1 |
| [11] |
张岩, 任伟建, 唐国维. 利用多道相似组稀疏表示方压制随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 442-450. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression based on sparse representation of multi-trace similarity group[J]. Oil Geophysical Prospecting, 2017, 52(3): 442-450. |
| [12] |
陆文凯, 李衍达. SVD分解提高地震资料的信噪比和分辨率[J]. 石油地球物理勘探, 1998, 33(增刊1): 145-149. LU Wenkai, LI Yanda. A SVD method to improve SNR and resolution[J]. Oil Geophysical Prospecting, 1998, 33(S1): 145-149. |
| [13] |
Lu W K. Adaptive noise attenuation of seismic images based on singular value decomposition and texture direction detection[J]. Journal of Geophysics and Engineering, 2006, 3(3): 28-34. |
| [14] |
刘志鹏, 赵伟, 陈小宏, 等. 局部频率域SVD压制随机噪声方法[J]. 石油地球物理勘探, 2012, 47(2): 202-206. LIU Zhipeng, ZHAO Wei, CHEN Xiaohong, et al. Local SVD for random noise suppression of seismic data in frequency domain[J]. Oil Geophysical Prospecting, 2012, 47(2): 202-206. |
| [15] |
徐彦凯, 曹思远, 何元. 双曲Radon-ASVD方法压制叠前地震数据随机噪声研究[J]. 石油地球物理勘探, 2017, 52(3): 451-457. XU Yankai, CAO Siyuan, HE Yuan. Prestack seismic random noise attenuation with a hyperbolic Radon-ASVD[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457. |
| [16] |
ChenY K, Fomel S. Random noise attenuation using local signal-and-noise orthogonalization[J]. Geophy-sics, 2015, 80(6): WD1-WD9. |
| [17] |
Fomel S. Shaping regularization in geophysical-estimation problems[J]. Geophysics, 2007, 72(2): R29-R36. |
| [18] |
Fomel S. Local seismic attributes[J]. Geophysics, 2007, 72(3): A29-A33. DOI:10.1190/1.2437573 |



 曹思远 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email:
曹思远 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email: