为了避免交叉干扰,传统地震采集邻炮之间都设置了足够长的等待时间,现场采集作业时间长,效率很低。常规的可控震源交替扫描采集日效在200~500炮,井炮激发则更低,造成勘探成本过高,限制了覆盖次数的增加,也严重制约了地震资料品质的提高。为了满足高精度地震勘探的需求,尤其是受到低油价带来巨大成本压力的影响,近几年高密度高效地震数据采集技术得到了迅猛的发展。国内外油公司不断探索提高地震勘探采集效率的方式,先后提出了滑动扫描(日效1500~2000炮)、同步激发滑动扫描(DS3,日效10000炮以上)等技术,并在中东和北非得到广泛应用[1-2]。2006年BP公司提出独立同步激发(ISS,日效20000炮以上)技术,2008年在利比亚利用该技术成功完成了13000km2三维项目采集[3-4]。阿曼国家石油公司(PDO)提出了超高效混叠采集方法(Ultra High Productivity,UHP),2015~2017年先后成功完成了四次现场采集试验[5],并于2017年9月正式投入应用。UHP采集的基本原理是,多组可控震源在满足一定时距规则的条件下独立自主激发,日效比ISS更高,可达到3~5万炮。ISS与UHP等混叠采集技术缩短了采集时间,极大地提高了地震采集效率,降低了成本。但是由于震源激发时间间隔较短,导致来自不同震源点的地震波发生混叠,严重降低了地震数据信噪比和成像质量。因此,信噪分离是高效混叠采集数据处理的必要环节。
混叠采集数据分离方法可分为两类:基于去噪的分离方法和基于稀疏反演的分离方法。由于高效混叠采集方法大多采用随机时间延迟, 因此在共检波点域、共中心点域或共炮检距域中,有效信号是连续的,混叠噪声是随机离散的。基于去噪的分离方法就是利用邻炮干扰在非炮集上的随机特征压制混叠噪声。Hoover等[6]使用随机噪声衰减(RNA)压制ISS数据邻炮干扰;Zhang等[7]采用加权τ-p变换压制邻炮干扰;Huo等[8]在共中心点域使用矢量中值滤波压制混叠噪声;王文闯等[9]提出用α-trimmed矢量中值滤波方法去噪,在压制邻炮干扰的同时能更好地保留主炮能量。但是,当地震数据混叠度较高时,上述直接去噪法会损伤有效信号,导致信噪分离效果不理想。为此,一些学者利用相干信号与混叠噪声之间的可预测性特征,提出用迭代方法分离信号与噪声。Doulgeris等[10]和Mahdad等[11]相继提出了共检波点道集上利用f-k滤波消除混叠噪声的迭代算法;周丽等[12]提出利用自适应迭代多级中值滤波法分离海上多震源混合波场,通过减小中值滤波窗口逐步提取波场细节。
如果将混叠采集视为正演过程,那么混叠数据的分离就是一个反演问题。基于稀疏反演的分离方法主要是利用信号在变换域中的稀疏性特征,在迭代过程中不断收缩阈值,逐步提取有效信号,并消除由信号预测的混叠噪声,改善信噪分离结果。国内外学者在反演法混采分离方面做了大量富有成效的研究工作。Akerberg等[13]利用稀疏Radon变换分离混采数据;Abma等[14]在傅里叶变换域利用POCS算法获得了高质量的分离结果;Lin等[15]提出了基于curvelet域L1约束的分离方法;Qu等[16]比较了curvelet变换结合不同正则化约束的混采分离算法;Zu等[17]提出周期震源编码海上混采方式,改善了curvelet域反演结果;Chen等[18]利用seislet域整形正则化方法取得了不错的数据分离结果。这些方法的主要区别在于选择的稀疏变换或正则化约束存在差异。相对于基于去噪的分离方法,稀疏反演方法混采数据分离效果更好,但计算成本较高,难以推广到实际应用。尤其对于高效混采数据,由于混叠度高、信噪比低、数据量大,对分离方法提出了更加严峻的挑战。
本文提出一种适应三维高效混采数据的信噪分离方法,它属于稀疏反演法的范畴。该方法在三维共检波点道集上采用FKK域L0范数约束,迭代分离信号和噪声,由于各检波点相互独立,因此算法易于并行。此外,本方法采用快速傅里叶变换提高计算效率,利用指数阈值加快迭代收敛速度,以期精确、稳定、快速地分离高混叠度的地震数据。
1 方法原理在高效混叠采集中,每个检波点接收到的多震源混合记录可表示为[19]
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} m}} $ | (1) |
式中:d为混叠采集数据;m为未混叠的有效信号;Γ为混叠算子,包含了震源的激发时间和位置信息。由于混叠采集时多个激发源同步激发,但检波点仅接收一套数据,即混采数据样点数远少于有效信号样点数,这就造成混采数据的反演分离成为欠定性问题。因此,虽然已知混采数据和混叠算子,但难以通过式(1)直接求解。为了获得唯一解,需要对未知的信号模型施加额外约束。
有效信号和混叠噪声在时空域共检波点道集上存在相干性差异,这种差异可以通过两者在FKK域的稀疏度进行表征。因此,提出在FKK域对信号模型施加L0范数稀疏约束,建立目标函数
| $ J\left( \mathit{\boldsymbol{m}} \right) = \left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{ \boldsymbol{\varGamma} m}}} \right\|_2^2 + \lambda {\left\| {\mathit{\boldsymbol{Fm}}} \right\|_0} $ | (2) |
式中:F为三维快速傅里叶变换算子;λ为正则化参数,控制误差项和约束项权重。式(2)可以写成标准的带约束目标泛函
| $ \left\{ \begin{array}{l} J\left( \mathit{\boldsymbol{x}} \right) = \left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Lx}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_0}\\ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{Fm}}\\ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{F}}^{ - 1}} \end{array} \right. $ | (3) |
式中F-1为三维快速傅里叶反变换。
上述目标函数最小化问题可通过迭代收缩阈值法[20]求解
| $ {\mathit{\boldsymbol{x}}_{i + 1}} = {\mathit{\boldsymbol{T}}_\tau }[{\mathit{\boldsymbol{x}}_i} + {\mathit{\boldsymbol{L}}^{\rm{H}}}(\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{x}}_i})] $ | (4) |
将式(3)中L和x的表达式代入式(4), 整理得到
| $ {\mathit{\boldsymbol{m}}_{i + 1}} = {\mathit{\boldsymbol{F}}^{ - 1}}{\mathit{\boldsymbol{T}}_\tau }\mathit{\boldsymbol{F}}[{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{H}}}\mathit{\boldsymbol{d}} - ({\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} - \mathit{\boldsymbol{I}}){\mathit{\boldsymbol{m}}_i}] $ | (5) |
式中:ΓH为混叠算子的共轭;ΓHd为伪分离的共检波点道集,包含有效信号和混叠噪声;(ΓHΓ-I)mi表示由信号模型mi预测的混叠噪声,有效信号初始模型一般设置为零;Tτ为变换域的阈值算子;I为单位矩阵。本文采用硬阈值函数,对振幅小于给定阈值τ的数据置零,即
| $ {\mathit{\boldsymbol{T}}_\tau }\left[ {f\left( \mathit{\boldsymbol{m}} \right)} \right] = \left\{ {\begin{array}{*{20}{c}} {f\left( \mathit{\boldsymbol{m}} \right)}&{\left| {f\left( \mathit{\boldsymbol{m}} \right)} \right| \ge \tau }\\ 0&{\left| {f\left( \mathit{\boldsymbol{m}} \right)} \right| < \tau } \end{array}} \right. $ | (6) |
式中f(m)为FKK域数据。
为了加快收敛速度,利用指数阈值函数
| $ {\tau _k} = {\tau _0}{a^k}\;\;\;\;\;\;\;\;k = 1, 2, \ldots , N $ | (7) |
式中:τk为第k次迭代的阈值,N为总的迭代次数;a为阈值衰减系数;τ0为伪分离数据在FKK域的最大振幅。
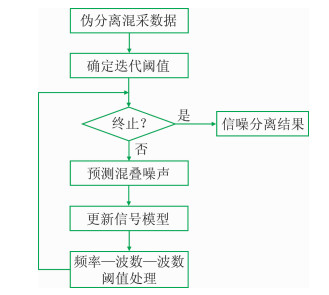
图 1为本文反演分离算法流程图,具体实现步骤叙述如下。
|
图 1 FKK域反演分离算法 |
(1) 伪分离混采数据,获得包含有效信号和混叠噪声的共检波点道集ΓHd;
(2) 将伪分离道集变换到FKK域统计最大振幅,确定阈值收缩函数;
(3) 由信号模型预测混叠噪声(ΓHΓ-I)mi;
(4) 从伪分离道集中减去混叠噪声,得到信噪比逐步改善的信号模型ΓHd-(ΓHΓ-I)mi;
(5) 对信号模型进行FKK域阈值处理,得到F-1TτF[ΓHd-(ΓHΓ-I)mi];
(6) 重复步骤(3)~步骤(5),直至达到最大迭代次数,完成共检波点道集信噪分离。
2 应用实例分别在高混叠度的三维模拟混采数据和实际混采数据上,测试FKK域反演分离方法的有效性。
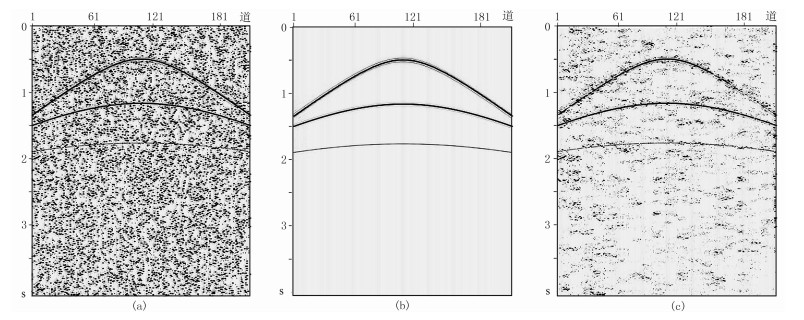
2.1 模拟数据图 2a展示了混叠度(即同步激发的震源数目)为24的三维共检波点道集。混叠过程如下:首先正演模拟得到常规的地震数据;然后根据炮点的分布情况,按照混叠度分组(本例分24组);再以道距为间隔设计每组炮点的激发时间,并加上随机延迟时间;最后根据每个炮点的激发时间将对应的地震道进行时移。由于各炮激发时间存在随机延迟,在共检波点道集上邻炮干扰噪声呈现伪随机特征,而有效反射是连续的。采用本文提出的FKK域稀疏反演方法分离的有效信号如图 2b所示,混叠噪声完全消除,深层的弱信号得到了较好的恢复。图 2c是中值滤波去噪法的分离结果,有效信号和混叠噪声都有明显泄漏。
|
图 2 模拟共检波点道集分离结果 (a)混叠的共检波点道集; (b)本文反演法分离结果; (c)中值滤波去噪法分离结果 |
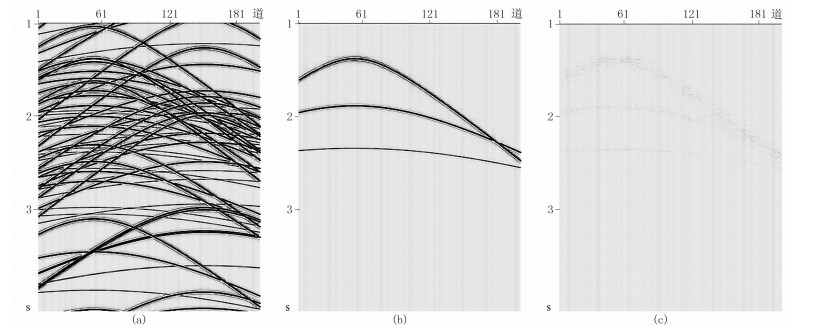
图 3展示了炮集分离结果。混叠炮集(图 3a)上存在大量邻炮干扰,用本文方法准确地分离出了主炮信号(图 3b)。由于真实的未混叠数据与分离结果基本一致,这里不另做展示。为了验证本方法对有效信号的保护能力,图 3c展示了分离结果与未混叠数据的差值剖面,可以发现两者之间仅存在微弱的差异,而良好的保幅性对于高混叠度数据分离尤为重要。模拟数据应用结果表明,本文方法在消除混叠噪声的同时也能很好地保护有效信号。
|
图 3 本文方法对模拟炮集的分离结果 (a)混叠炮集; (b)本文方法分离的主炮信号; (c)分离结果与未混叠数据之差 |
利用实际混采地震数据进一步验证本文方法的有效性。实际数据来自中东某地区的高效混采先导性现场采集试验,采用18线798道固定排列接收(共14364道),检波点距离25m,检波线距离250m;12组震源同步施工,每台震源使用1.5~96Hz、9s长度扫描信号,采样率为4ms;炮点网格尺寸为25m×25m,共81条炮线, 每条炮线398个炮点, 共32238炮。
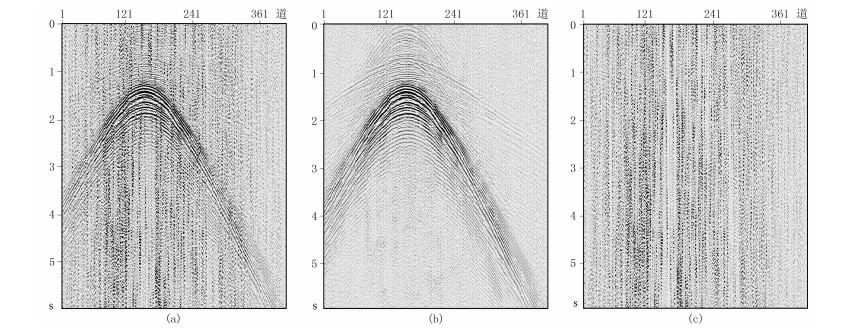
图 4a为混叠的共检波点道集,混叠噪声散布在整个道集中;图 4b为本文方法迭代分离的有效信号,可以看到,剖面信噪比显著提高,弱反射能量凸显出来;图 4c为分离的混叠噪声。信号和噪声得到了完全分离,说明本文方法具有很强的信噪识别能力。
|
图 4 实际共检波点道集分离结果 (a)混叠共检波点道集; (b)分离的有效信号; (c)分离的混叠噪声 |
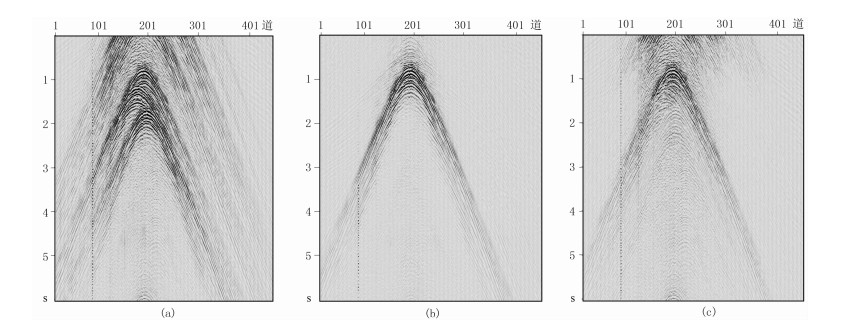
图 5展示了实际数据炮集分离结果。伪分离炮集上(图 5a)至少包含6炮的反射能量,各炮反射顶点位置接近,干涉严重,说明施工时各同步激发震源在纵测线方向的空间距离接近,这加大了混采分离难度。分离的主炮信号(图 5b)上,没有发现明显的邻炮干扰残余,反射同相轴连续性加强,主体反射前的弱信号得到了有效保护。对于这种混叠程度高、干涉严重的高效混采数据,去噪类方法一般会失效。图 5c展示了利用去噪法得到的分离结果,可以看到,邻炮干扰残余严重,而且主炮能量受到了损伤。图 6在叠加剖面上展示了反演法的分离结果,分离前的叠加剖面上(图 6a)大量的混叠噪声淹没了有效反射。经过本文方法分离后,剖面的信噪比显著提高,反射同相轴的连续性增强(图 6b)。更重要的是,压制的噪声中没有发现信号的损伤(图 6c),验证了本文方法在高效混采数据分离上的有效性。
|
图 5 实际炮集数据分离结果 (a)伪分离炮集; (b)反演法分离结果; (c)去噪法分离结果 |

|
图 6 实际数据反演法分离结果的叠加剖面显示 (a)分离前叠加剖面; (b)分离的信号; (c)分离的噪声 |
本文提出了一种精确、稳定、快速的基于反演的混采数据分离方法,针对三维共检波点道集,采用FKK域基于L0范数约束的稀疏反演,通过不断收缩阈值提取有效信号,逐步迭代分离有效信号和混叠噪声。模拟与实际高效混采数据测试结果表明,本文方法能够较好地分离主炮信号与混叠炮干扰,且收敛速度快、计算效率高,具有实际应用价值。应该指出的是,由于本方法需要使用FKK变换,对炮点的空间分布密度与规则性有一定的要求,大炮线距的采集方式可能降低该方法的应用效果。
| [1] |
Rozemond H J.Slip-sweep acquisition[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 64-67. http://en.cnki.com.cn/Article_en/CJFDTotal-WTZB199901003.htm
|
| [2] |
Bouska J.Distance separated simultaneous sweeping: The world's fastest vibroseis technique[C]. Extended Abstracts of 70th EAGE Conference & Exhibition, 2008.
|
| [3] |
Howe D, Foster M, Allen T, et al. Independent simultaneous sweeping: a method to increase the productivity of land seismic crews[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2826-2830. https://www.researchgate.net/publication/240736954_Independent_Simultaneous_Sweeping_-_a_method_to_increase_the_productivity_of_land_seismic_crews
|
| [4] |
Howe D, Foster M, Allen T, et al. Independent simultaneous sweeping in Libya: Full scale implementation and new developments[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 109-111.
|
| [5] |
Zhao J, Jin H, Zhu Y, et al. Vibroseis ultra high productivity blended acquisiton: Field trial and full scale implementation in Oman[C]. CPS/SEG 2018 Beijing International Geophysical Conference & Exposition, 2018, 150-153.
|
| [6] |
Hoover G, Sublett V, Carter C, et al. Infield processing of an ISS dataset south-east Algeria[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 468-472. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SEGEAB000029000001000468000001&idtype=cvips&gifs=Yes
|
| [7] |
Zhang C, Olofsson B.Separating simultaneous source data using weighted tau-p transform[C]. Extended Abstracts of 74th EAGE Conference & Exhibition, 2012.
|
| [8] |
Huo S, Luo Y, Kelamis P.Simultaneous sources separation via multi-directional vector-median filter[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 31-35. https://www.researchgate.net/publication/258647078_Simultaneous_sources_separation_via_multi-directional_vector-median_filter
|
| [9] |
王文闯, 李合群, 赵波, 等. 基于α-trimmed矢量中值滤波压制同步激发邻炮干扰[J]. 石油地球物理勘探, 2014, 49(6): 1061-1067. WANG Wenchuang, LI Hequn, ZHAO Bo, et al. Cross interference noise attenuation using alpha-trimmed vector median filtering[J]. Oil Geophysical Prospecting, 2014, 49(6): 1061-1067. |
| [10] |
Doulgeris P, Mahdad A, Blacquiere G.Iterative separation of blended marine data: discussion on the coherency-pass filter[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 26-31. https://www.researchgate.net/publication/254890360_Iterative_separation_of_blended_marine_data_Discussion_on_the_coherence-pass_filter
|
| [11] |
Mahdad A, Doulgeris P, Blacquiere G. Separation of blended data by iterative estimation and subtraction of blending interference noise[J]. Geophysics, 2011, 76(3): Q9-Q17. DOI:10.1190/1.3556597 |
| [12] |
周丽, 庄众, 成景旺, 等. 利用自适应迭代多级中值滤波法分离海上多震源混合波场[J]. 石油地球物理勘探, 2016, 51(3): 434-443. ZHOU Li, ZHUANG Zhong, CHENG Jingwang, et al. Multi-source blended wavefield separation for marine seismic based on an adaptive iterative multi-level median filtering[J]. Oil Geophysical Prospecting, 2016, 51(3): 434-443. |
| [13] |
Akerberg P, Hampson G, Martin H, et al. Simultaneous sources separation by sparse Radon transform[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2801-2805. https://www.researchgate.net/publication/269065288_Simultaneous_source_separation_by_sparse_Radon_transform
|
| [14] |
Abma R, Manning T, Tanis M, et al. High quality separation of simultaneous sources by sparse inversion[C]. Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, B003.
|
| [15] |
Lin T, Herrmann F.Designing simultaneous acquisi-tion with compressive sensing[C]. Extended Abstracts of 71st EAGE Conference & Exhibition, 2009.
|
| [16] |
Qu S, Zhou H, Liu R, et al. Deblending of simultaneous source seismic data using fast iterative shrinkage thresholding algorithm with firm thresholding[J]. Acta Geophysica, 2016, 64(4): 1064-1092. DOI:10.1515/acgeo-2016-0043 |
| [17] |
Zu S, Zhou H, Chen Y, et al. A periodically varying code for improving deblending of simultaneous sources in marine acquisition[J]. Geophysics, 2016, 81(3): V213-V225. DOI:10.1190/geo2015-0447.1 |
| [18] |
Chen Y, Fomel S, Hu J. Iterative deblending of simultaneous source seismic data using seislet-domain shaping regularization[J]. Geophysics, 2014, 79(5): V179-V189. DOI:10.1190/geo2013-0449.1 |
| [19] |
Berkhout A J. Changing the mindset in seismic data acquisition[J]. The Leading Edge, 2008, 27(7): 924-938. DOI:10.1190/1.2954035 |
| [20] |
Daubechies I, Defrise M, Mol C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/(ISSN)1097-0312 |



 宋家文 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072750。Email:
宋家文 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072750。Email: