地震勘探由于激发和接收均在地表,因此需要消除地表起伏及近地表速度横向变化对反射信号的影响[1],其主要处理方式有两种:①通过静校正技术将炮点、检波点校正到统一基准面上[2-3],在消除近地表对反射波影响的同时也可使一些基于水平地表假设的方法(如水平叠加等)可行;②直接进行基于起伏地表的处理,在算法内部考虑近地表的影响(如起伏地表条件下的速度建模、偏移成像等)[4-5]。不管采用哪种方式,都需要进行近地表建模,因此近地表建模方法的研究对油气地震勘探具有重要意义。
近地表建模主要利用地震记录中的初至波,可分为基于波动理论和射线理论的层析,也可分为波形层析和旅行时层析[6]。由于观测误差、噪声等因素的影响,很难直接进行波形匹配,因此目前以旅行时层析为主[7]。由于计算能力的限制,旅行时层析以基于射线理论的方法为主,而基于波动理论的旅行时层析还未得到大规模应用[8]。
常规的基于射线理论的旅行时层析方法(常规射线层析)[9]是基于射线追踪方程或程函方程、通过迭代求解正演旅行时与观测旅行时的最优拟合,可获取较高精度的近地表模型。但由于需要大量的正演及反演计算,计算量较大,特别是对于目前的高密度、宽方位地震数据,限制了方法的大规模应用。除了常规射线层析反演,还有一类方法是通过对速度分布做进一步假设构建快速近地表建模方法,该类方法在天然地震研究中广泛应用,通常用来构建一维参考模型[10]。Diebold等[11]采用截断时间求和方法利用折射波与反射波旅行时构建一维速度模型;Rühl等[12]利用最大深度方法构建近地表模型并将其应用于静校正,实际数据测试验证了由该方法计算的长波长静校正量的准确性;Nowack[13]、Novotný等[14]、胡自多等[15]、徐涛等[16]利用Herglotz-Wiechert方法构建近地表模型;Shi等[17]在线性速度分布假设下采用层剥离的方法进行快速近地表建模。
本文通过假设速度随深度线性变化发展了一种快速的回转波近地表建模方法。通过在算法内部采用多基准面校正降低地表起伏对反演结果的影响,提高反演精度;应用基于局部加权的稳定射线参数估计方法降低初至拾取误差对反演结果的影响,增强反演的稳定性。理论模型数据与实际数据测试验证了方法的有效性及高效性。
1 方法原理 1.1 基本原理假设在最大炮检距范围内近地表速度横向不变但随深度线性变化,此时近地表的速度变化趋势可表述为
| $ v\left( z \right) = {v_0} + gz $ | (1) |
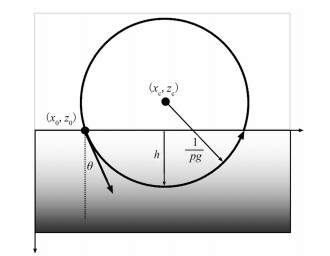
式中:v0为地表速度;z为深度;g为速度梯度。在该介质中传播的地震波称为回转波。给定射线入射角度θ、起始坐标(x0,z0)可导出其射线路径、炮检距、初至时间的理论表达式(图 1)。具体来说,其射线路径为一圆弧,圆心位于点[18]
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{c}}} = {x_0} + \frac{{\sqrt {1 - v_0^2{p^2}} }}{{pg}}}\\ {{z_{\rm{c}}} = {z_0} - \frac{{{v_0}}}{g}} \end{array}} \right. $ | (2) |
|
图 1 地震波在速度随深度线性变换介质中的传播路径 |
半径为
| $ r = \frac{1}{{pg}} $ | (3) |
式中p=sinθ/v为射线参数。相应地可求得对应的炮检距H及初至时间t
| $ \left\{ {\begin{array}{*{20}{l}} {H = \frac{2}{{pg}}\sqrt {1 - {p^2}v_0^2} }\\ {t = \frac{2}{g}{\rm{ln}}\left( {\frac{{1 + \sqrt {1 - {p^2}v_0^2} }}{{p{v_0}}}} \right)} \end{array}} \right. $ | (4) |
对于速度反演,已知炮检距、初至时间,求取地下不同位置处的速度参数。假设速度水平横向不变,地震波的传播射线参数保持不变,可据此求得回转点处的速度为
| $ {v_{\rm{T}}} = \frac{1}{p} $ | (5) |
由式(2)和式(3)可求得回转点的深度为
| $ h = \frac{1}{{pg}} - \frac{{{v_0}}}{g} $ | (6) |
射线参数p可由初至时间估算;地表速度v0由近炮检距数据计算或由先验信息给定。速度随深度变化的梯度通过求解目标函数
| $\begin{array}{l} O\left( g \right) = {\left( {Hg - \frac{2}{p}\sqrt {1 - {p^2}v_0^2} } \right)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;{W^2}\left[ {tg - 2{\rm{ln}}{{\left( {\frac{{1 + \sqrt {1 - {p^2}v_0^2} }}{{p{v_0}}}} \right)}^2}} \right] \end{array} $ | (7) |
获得。式中W为加权因子,调整炮检距项(第一项)与时间项(第二项)的权重。当炮检距单位为m、时间单位为s时,加权因子W设为1000,以均衡由于不同测量单位固有的加权效应。
利用式(5)~式(7)可获取一个炮检距—初至时间对所对应回转点的速度及其深度。通过在由近及远的炮检距范围内进行初至反演,可获取由浅到深的速度参数;通过对不同空间位置点进行相同的处理,可获取整个三维空间的速度参数。给定离散的空间网格,将相应的速度参数投影到对应的网格点上,然后进行对应的速度内插、平滑等处理,可得到规则网格点上最终的速度参数。
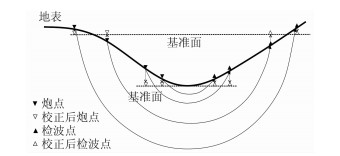
1.2 多基准面初至时间校正由于上述方法基于水平地表假设,起伏地表情况下需要将其校正到水平基准面上。如图 2所示,本文通过两方面的策略保持校正精度:①将数据抽至CMP道集后再进行后续的处理,保证炮检点的空间局部性;②根据地表起伏的情况,针对不同的炮检距范围利用不同的基准面进行高程校正,尽量缩小校正时间以减少高程校正带来的误差。一般情况下,近炮检距范围采用CMP点处的高程作为反演的基准面,远炮检距范围内采用炮检点的平均高程作为反演基准面。
|
图 2 多基准面校正示意图 |
射线参数又称为视慢度,可通过估算炮检距—初至时间曲线不同点的斜率获取。射线参数估计的精度及稳定性直接影响最终的反演结果。本文提出了一种基于局部加权的稳定射线参数估计方法,可有效降低初至拾取误差、异常值的影响,实现相对稳定的射线参数估计。
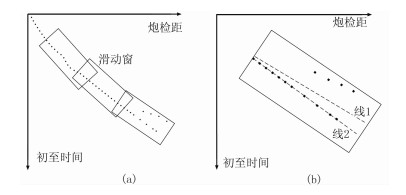
对于一个CMP道集,利用一个固定宽度的窗口沿炮检距—初至时间进行滑动,对平滑窗内的数据进行直线拟合[19],所拟合直线的斜率即为该平滑窗中心位置对应的射线参数,如图 3a所示。利用这种直线拟合的方式可消除小的拾取误差对射线参数估计的影响,但是对于大的拾取误差容错能力较弱。借鉴Cleveland[20]局部加权平滑的相关思想,本文在直线拟合的过程中引入局部加权减少大的拾取误差对射线参数估计的影响。
|
图 3 射线参数估计示意图 (a)射线参数整体估计方法示意图;(b)基于局部加权的拟合方法(线2)与常规拟合方法(线1)的对比 |
基于局部加权的直线拟合,可以表述为求解目标函数[20]
| $ {O_{{\rm{lin}}}}({t_0}, p) = \sum\limits_{k = 1}^N {{{\left| {{w_k}({t_k} - {t_0} - p{H_k})} \right|}_2}} $ | (8) |
式中:N为平滑窗内的点数;tk、Hk为第k个点处的初至时间与炮检距;t0、p分别为所拟合直线的截距时间与斜率(即射线参数);wk为第k个点处的加权系数。
稳定的参数估计方法主要分为两步:①将所有点处的加权系数wk设为1,首先进行常规线性拟合;②计算所有点与拟合直线的距离,根据给定的可容许的最大时间差Δtmax,重新设置其加权系数为
| $ {w_k} = \left\{ {\begin{array}{*{20}{c}} 0&{\left| {{t_k} - {t_0} - p{x_k}} \right| > \Delta {t_{{\rm{max}}}}}\\ 1&{其他} \end{array}} \right. $ | (9) |
利用新的加权系数再进行一次线性拟合,消除异常初至对射线参数估计的影响,如图 3b所示。
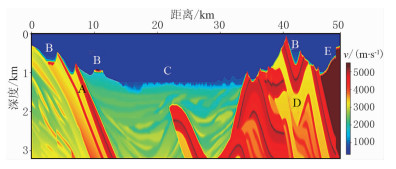
2 理论数据测试为了说明本文方法的有效性,选用Amoco静校正基准测试模型[21](图 4)进行理论数据的测试。该模型包含了大部分常见的近地表地质构造,如高速层出露(区域A)、局部高速、低速异常体(区域B)、浅层低速层(区域C)、近地表复杂构造(区域D)及极浅层低速体(区域E)等,可在一定程度上说明该方法对不同近地表地质构造的适应性。
|
图 4 Amoco静校正基准测试模型 |
原有模型横向范围为50km,纵向深6km,由于本文只进行近地表模型的建立,因此只截取了浅部3.2km的部分模型进行测试。模型纵、横向采样间隔均为5m,横向共10001个采样点,纵向共647个采样点,最大速度为5760 m/s,最小速度约为800m/s。观测数据共1998炮,炮点以25m的间隔均匀分布于地表以下10m处,第一个炮点位于横向位置10m处。按照陆上采集方式布设观测系统,最大炮检距为7.5km,检波点间距为10m。为了避免初至拾取巨大的工作量以及拾取误差对分析的影响,利用有限差分求解程函方程计算得到各个检波点处的初至时间作为反演的输入。
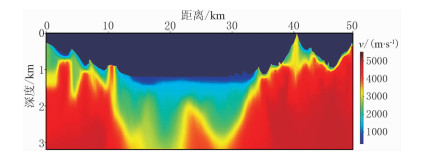
本文方法反演的速度模型如图 5所示。对比图 4与图 5可知,本文方法除了在复杂构造区域(图 4中D标识区域)反演效果较差外,其余部分反演结果与真实模型形态均相似。对于高速层出露区域(图 4中A标识区域)反演结果具有与真实相似的构造形态。高速、低速体标识区域(图 4中B标识区域),近地表低速异常均得到有效的反演,部分高速层的构造形态较为清晰。由于该方法基于速度线性递增假设,在反演之后对沿深度出现速度反转的部分进行人为处理。B标识区域中近地表高速异常构造形态上的差异均是由该处理引起的。浅层低速层区域(图 4中C标识区域)是最常见的地质构造,反演结果与真实模型结果较为接近,反演精度较高。近地表复杂构造区域(图 4中D标识区域),利用简单的线性速度假设已不能对其进行很好的近似,因此反演结果与真实模型差距较大,但极浅层的速度变化还是得到了一定的反映。极浅层低速体区域(图 4中E标识区域)类似常规山地地质情况,地表存在一极浅低速层,下面紧邻致密高速岩石。通过对比图 4与图 5中E标识区域可知,在这种地质条件下该反演方法的反演结果同样是可接受的。
|
图 5 原始数据回转波层析结果 |
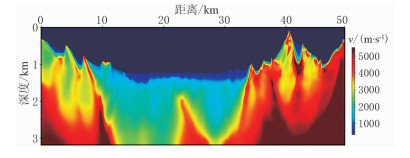
将图 5所示反演结果作为初始模型,然后利用射线层析做进一步的反演优化,得到最终的射线层析反演结果(图 6)。对比图 6与图 4可知,反演结果与真实模型非常接近,说明本文方法得到的模型可作为射线类初至旅行时层析的初始模型。相对于常规的梯度类初始模型,本文方法具有如下优势:①结果与真实模型更为接近,将其作为初至旅行时层析的初始模型可减少迭代次数,对于此次试验,相对于梯度类初始模型,可节省约5次迭代;②计算效率极高,该理论数据处理仅耗时25s,但反演结果却反应了近地表速度变化的大体结构,可对进一步初至旅行时层析反演的参数设定起到参考作用。
|
图 6 将图 5所示结果作为初始模型的常规射线层析结果 |
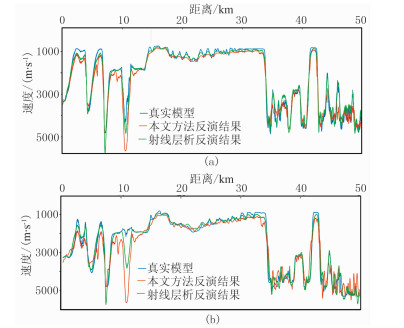
对比图 5与图 6可知,除了A、D标识区域因为构造过于复杂不满足假设条件而引起较大差别外,其余部分反演结果均可接受。对于近地表复杂构造区域,由于反演分辨率的限制,即使采用常规射线层析方法也很难获取较高精度的反演模型。分别抽取真实模型、本文方法反演模型、初至旅行时层析反演模型地表以下50和100m处的速度曲线,如图 7所示。对比分析图 5~图 7可知:①本文方法以极小的计算成本快速获取了一个精度较高近地表模型;②该近地表模型在未出现速度反转区域反演精度较高,在存在速度反转区域可靠性变差;③该速度模型可用作初至旅行时层析反演的初始模型以提高其收敛速率,在构造相对简单区域,该模型可直接用于层析静校正等处理。
|
图 7 地表以下不同深度处速度曲线对比 (a)地表以下50m;(b)地表以下100m |
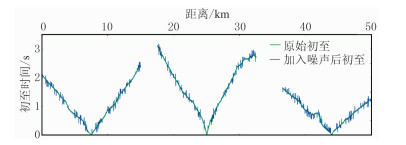
为了验证拾取误差对反演结果的影响,在初至中加入噪声进行相应的数值测试。加入的噪声主要分为两类,一类加在所有数据上,为幅值在[-12ms,12ms]范围内的随机噪声,模拟小的拾取误差;第二类为在随机选取50%炮上加入幅值在[-0.3s,0.3s]范围内的随机噪声,模拟大的异常初至。图 8为其中三炮加噪前、后的初至对比。
|
图 8 原始初至与加入随机噪声后的初至对比 |
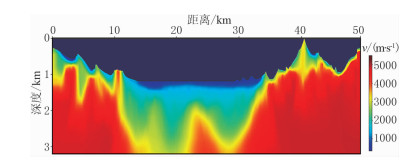
图 9为利用加入噪声之后的初至得到的反演结果。对比图 9与图 5可知,加入随机噪声对反演结果基本没有影响,验证了基于局部加权的稳定射线参数估计方法的抗噪性和有效性。
|
图 9 利用加入噪声初至进行回转波层析的结果 |
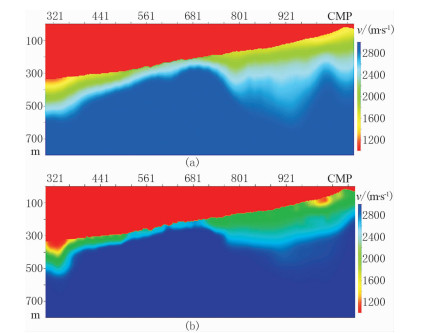
为了验证本文所述方法在实际资料上的应用效果,选取中国西部M工区三维实际资料中的两束线进行测试。该工区地表最大高差约为400m,地表相对较为平缓。由数据分析可知,近地表存在较为明显的低速异常体以及低速层厚度变化。试验所用数据共867炮、8352个检波点,道间距为30m。定义观测系统后,共68条CMP线,CMP线间距为30m;每条CMP线共800个CMP,CMP间距为15m。采用自动拾取与人工修正相结合的方法进行初至拾取,利用拾取后的初至分别进行本文方法以及常规射线类层析的近地表速度反演(图 10)。
|
图 10 实际数据本文方法(a)和常规射线层析(b)反演结果 |
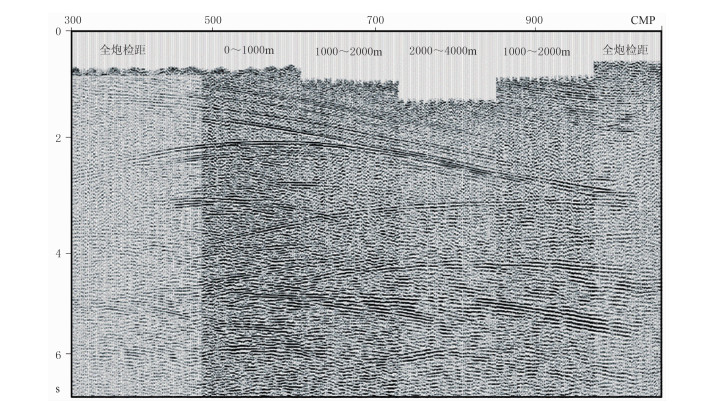
对比图 10a与图 10b可知,不管是地表附近的低速异常还是高速层的基本形态,本文方法与常规射线层析方法反演得到的速度模型基本一致。分炮检距叠加是验证是否解决长波长静校正的一种常用质控手段,若不同炮检距段叠加剖面横向连续性好,没有因为叠加所用炮检距范围的变化而出现叠加剖面上同相轴的错动,则说明长波长静校正量得到了有效解决。图 11为利用本文方法进行层析静校正之后的分炮检距叠加结果,可以看出,同相轴连续性好,从另一个侧面说明了本文所述方法反演得到的模型能够满足层析静校正的需求。
|
图 11 本文方法层析静校正后分炮检距叠加结果 |
由表 1的效率对比可见,本文方法比常规的射线类层析方法快了两个数量级,大大降低了近地表建模对大规模计算资源的要求,可用于大数据量处理,实现快速近地表速度建模。
|
|
表 1 计算效率对比 |
本文方法之所以能够进行快速的近地表建模,主要依赖于对近地表速度分布局部横向不变及线性递增假设或者对射线路径的圆弧状假设。可从以下几个方面讨论这种假设的合理性。
(1) 关于速度局部横向均匀假设。地质构造的尺度通常要比地震观测最大炮检距的尺度大得多,在最大炮检距范围内将其假设为横向均匀是可接受的,也是地震资料处理过程中常用的一种假设条件。本文方法与常规射线类层析方法的关系可类比于叠前时间偏移与叠前深度偏移的关系。
(2) 关于速度纵向线性递增假设。由于压实的作用,地层的速度通常是随深度逐渐增加的,特别是对于距地表几百米以内的速度分布(近地表建模主要关注的区域)这种现象更为明显[22]。近地表速度分布的线性递增假设符合大部分地区地质规律。
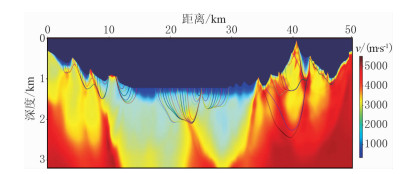
(3) 本文方法基于射线路径圆弧状假设,换一个角度来说,等价于利用圆弧状射线路径去拟合实际观测旅行时。由于射线类层析分辨率的限制(不小于第一菲涅耳带)[23],这种假设与常规射线类层析反演方法同样是非常接近的。图 12为利用图 6所示的反演结果对不同位置的三炮进行射线追踪的结果,由射线路径分布可见,除了速度结构特别复杂的区域外,大部分射线路径与圆弧较为接近。
|
图 12 利用图 6所示反演模型计算的三炮的射线路径 |
对于大部分地区,以上假设是成立的,也就是说本文所述方法可取得较为理想的效果。对于复杂地区,本文所述方法反演的精度受到一定限制,但由于其极高的计算效率,仍然具有较强实际应用意义:①本文方法的反演结果可以作为常规射线层析方法的初始模型,相对于简单的梯度模型,使用精度更高的初始模型可减少迭代次数;②以极少的计算成本获取了近地表速度分布的基本规律、不同地区的复杂程度,可对随后的常规射线层析类方法等处理起到参考作用。
鉴于本文所述方法主要利用回转波,因此在满足回转波假设的地区将获得更佳的效果。可通过两条途径来判定是否满足假设:①基于对该探区的地质认识,比如黄土塬等探区由于压实作用,近地表速度横向变化不大、随深度逐渐增加[24];②基于炮集上初至随炮检距的变化形态,若在消除地表高程的影响之后,初至波视速度随炮检距线性增加[25],则可判定该地区适用于本文方法。
5 结束语本文发展了一种利用回转波进行快速近地表建模的方法,通过采用多基准面高程校正方法增强了对起伏地表的适应性,通过采用基于局部加权的稳定射线参数估计方法提高了抗噪性。相对于常规的射线类层析反演方法,在大部分情况下,该方法能够以极小的计算成本提供了一个与之相当的近地表模型,具有极大的实际应用价值。
与常规的射线类层析反演方法类似,本文所述方法存在无法对速度反转进行反演、复杂构造区域反演效果较差的问题。一种解决策略是将本文所述方法作为初始模型采用精度更高的反演方法(如波动方程旅行时反演、波形反演等)进行近地表建模;另一种可能的解决策略是采用新的反演思路,如利用深度神经网络等机器学习算法,这也是下一步研究方向。
| [1] |
Cox M.Static Corrections for Seismic Reflection Surveys[M]. SEG, Tulsa, 1999.
|
| [2] |
Zhu X H, Sixta D P, Angstman B G. Tomostatics:Turning-ray tomography + static corrections[J]. The Leading Edge, 1992, 11(12): 15-23. DOI:10.1190/1.1436864 |
| [3] |
曾庆才, 曾同生, 欧阳永林, 等. 复杂山地层析反演静校正新方法及应用[J]. 石油地球物理勘探, 2017, 52(3): 418-425, 441. ZENG Qingcai, ZENG Tongsheng, OUYANG Yonglin, et al. A new tomographic inversion for static corrections in complex mountain areas[J]. Oil Geophysical Prospecting, 2017, 52(3): 418-425, 441. |
| [4] |
Sun C W, Jing P G, and Pu Y.Seismic imaging in the mountainous area of Southern China: Statics correction compared with migration from topography[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2965-2969.
|
| [5] |
王东, 李文卉, 熊登, 等. 静校正对波动方程叠前深度偏移成像效果的影响[J]. 石油地球物理勘探, 2017, 52(增刊2): 76-80. WANG Dong, LI Wenhui, XIONG Deng, et al. Static corrections influence on wave equation prestack depth migration[J]. Oil Geophysical Prospecting, 2017, 52(S2): 76-80. |
| [6] |
Schuster G T.Seismic Inversion[M]. SEG, Tulsa, 2017.
|
| [7] |
Luo Y, Ma Y, Wu Y, et al. Full-traveltime inversion[J]. Geophysics, 2016, 81(5): R261-R274. DOI:10.1190/geo2015-0353.1 |
| [8] |
Fu L, Hanafi S M. Ray-tracing traveltime tomography vs wave-equation traveltime inversion for near-surface seismic land data[J]. Interpretation, 2017, 5(3): 1-35. |
| [9] |
Guust N.A Breviary of Seismic Tomography: Imaging the Interior of the Earth and Sun[M]. Cambridge University Press, 2008.
|
| [10] |
Kennett B L N. On seismological reference models and the perceived nature of heterogeneity[J]. Physics of the Earth & Planetary Interiors, 2006, 159(3): 129-139. |
| [11] |
Diebold J B, Stoffa P L. The traveltime equation, tau-p mapping and inversion of common midpoint data[J]. Geophysics, 1981, 46(3): 238-254. DOI:10.1190/1.1441196 |
| [12] |
Rühl T, Lüschen E. Inversion of first-break traveltime data of deep seismic reflection profiles[J]. Geophysical Prospecting, 2010, 38(3): 247-266. |
| [13] |
Nowack R L. Tomography and the Herglotz-Wiechert inverse formulation[J]. Pure & Applied Geophysics, 1990, 133(2): 305-315. |
| [14] |
Novotný O, Janský J, Málek J. Some aspects of the application of the Wiechert-Herglotz method to refraction data from Western Bohemia[J]. Acta Geodynamica Et Geomaterialia, 2004, 1(2): 157-164. |
| [15] |
胡自多, 贺振华, 王西文, 等. 无射线追踪层析静校正技术在黄土塬区的应用[J]. 石油地球物理勘探, 2010, 45(增刊1): 94-100. HU Ziduo, HE Zhenhua, WANG Xiwen, et al. Application of non ray-tracing tomography static correction technique in Loess Plateau[J]. Oil Geophysical Prospecting, 2010, 45(S1): 94-100. |
| [16] |
徐涛, 徐果明, 张忠杰, 等.利用地震初至波反演浅层地壳速度结构的快速Wiechert-Herglotz方法[C].中国地球科学联合学术年会, 2014. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW201410072016.htm
|
| [17] |
Shi T K, Zhang J Z, Huang Z, et al. A layer-stripping method for 3d near-surface velocity model building using seismic first-arrival times[J]. Journal of Earth Science, 2015, 26(4): 502-507. DOI:10.1007/s12583-015-0569-0 |
| [18] |
Cerveny V.Seismic Ray Theory[M]. Cambridge University Press, 2001.
|
| [19] |
William H.Numerical Recipes[M]. Cambridge Uni-versity Press, 1986.
|
| [20] |
Cleveland W S. Robust locally weighted regression and smoothing scatterplots[J]. Journal of the American Statistical Association, 1979, 74(368): 829-836. DOI:10.1080/01621459.1979.10481038 |
| [21] |
Taillandier C, Noble M, Chauris H, et al. First-arrival traveltime tomography based on the adjoint-state method[J]. Geophysics, 2009, 74(6): WCB1-WCB10. DOI:10.1190/1.3250266 |
| [22] |
郑鸿明, 吕焕通, 娄兵, 等. 地震勘探近地表异常校正[M]. 北京: 石油工业出版, 2009.
|
| [23] |
Williamson P R, Worthington M H. Resolution limits in ray tomography due to wave behavior:Numerical experiments[J]. Geophysics, 1993, 58(5): 727-735. DOI:10.1190/1.1443457 |
| [24] |
夏竹, 张少华, 王学军. 中国西部复杂地区近地表特征与表层结构探讨[J]. 石油地球物理勘探, 2003, 38(4): 414-424. XIA Zhu, ZHANG Shaohua, WANG Xuejun. Discussion on near-surface characters and structures in complex area of western China[J]. Oil Geophysical Prospecting, 2003, 38(4): 414-424. DOI:10.3321/j.issn:1000-7210.2003.04.015 |
| [25] |
陆基孟. 地震勘探原理[M]. 山东东营: 石油大学出版社, 1993.
|



 郭振波 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email:
郭振波 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email: