基于双程波动方程,逆时偏移(RTM)能够避免对波动方程的近似,不受速度模型的横向变化和反射界面倾角限制[1-4],可以对复杂结构的地质体实现高保真度成像[5-6]。由于计算机能力的提升和GPU技术的推广,RTM已广泛应用于复杂构造的实际数据成像[7-8]。
基于双程波动方程实现大型三维RTM,计算成本非常昂贵[6]。复杂地质结构成像精度要求高,采用精细化网格实现成像,会导致高速区域出现空间和时间过采样。针对此问题,一些学者进行了研究和探索。Kreiss等[9]应用伪谱法实现RTM,该方法利用傅里叶变换计算空间导数[10],具有实现简单、稳定性强等优点,但受限于速度模型地表形状,难以选择合适的映射函数;Jastram等[11]提出了垂向不连续网格自适应有限差分法,提升了计算效率,但需要耗费大量的存储空间;黄建平等[12]实现了TTI介质一阶qP波方程交错网格伪谱法正演模拟;Fomel等[13]借助空间波数矩阵的低秩(Low-rank)近似构造一个波场传播算子,并应用于RTM地震成像中,其优点是能够用可分离的矩阵表示直接近似混合域波场外推算子,使每个时间步的快速傅里叶变换(FFT)的运算量最小化;刘红伟等[14]用GPU实现了高阶有限差分法RTM,将RTM算法的速度提升了30倍;Nunes等[15]利用运算放大原理与RTM相结合,产生捕获精细尺度信息的波动方程的粗尺度解,从而实现理想加速而不增加存储。另外,改进差分算子[16]、不规则网格[17]、可变网格[18-19]、自适应网格细化[20]、空变时变网格[21]等方法也能够不同程度降低RTM的计算成本,但网格精细化差分导致的内存和磁盘空间占用过大问题仍未能有效解决。Alkhalifah等[22]引入速度加权的思路,提出了曲线坐标系,降低高速区域的过采样,特别对速度剧烈变化区域以及深部高速区域效果更加明显。李庆洋等[23]研究了基于Alkhalifah曲坐标系下的伪深度域正演模拟。Plessix等[24]和Li等[25]将曲坐标系方法分别扩展到全波形反演和最小二乘逆时偏移,减少了传统方法的垂直网格点数并降低了存储需求。
考虑到RTM的成像需要同时进行正向和反向波场外推,通常需要至少存储其中一个波场,因此存储问题也是制约RTM成像应用的瓶颈[4, 26]。使用已保存的边界波场(如果采用吸收边界条件)和最后时刻的波场[27-28]进行波场重建是RTM的常规策略,即有效边界存储策略;杨仁虎等[29]将有效边界存储策略应用于逆时偏移成像,模型试验证明了该方法的有效性;Symes[30]提出了只在检查点(Checkpoint)处存储波场的方法,从而减少RTM的存储量;宋立伟等[31]联合有效内边界存储和检查点方法降低存储需求,实现了TTI介质震源波场的精确重建和逆时偏移,与波场全存储、有效边界存储方法及其改进方法相比,检查点方法的存储要求较低,但增加了一定的计算量[28];Clapp[32]提出了在计算区域周围增加随机边界的方法,并利用源波场的最后两个时间片重建源波场,该方法不需要在正向传播过程中存储冗余波场信息,但需要通过多炮叠加消除由随机边界产生的漫反射(随机边界的主要缺点);王保利等[33]使用Checkpoint技术改进了有效边界存储策略;Feng等[34]则提出一种近似重构源波场的方法,能够显著减少数据存储总量,但以在边界附近丧失空间精度为代价;Sun等[35]讨论了基于奈奎斯特采样定理和基于无损压缩算法减少数据存储量;Nguyen等[36]讨论了五种在二维叠前RTM中减少源波场存储的方法;Liu等[37]提出了一种基于线性组合的波场重构方法,能够有效降低存储量,同时保证成像精度;Vasmel等[38]实现了交错网格的多点震源法,能够保证差分精度不变而减少存储量。
本文引入Alkhalifah提出的曲线坐标系,将笛卡尔坐标系下的深度域速度场转换为曲线坐标系下的垂直时域速度场,并在垂直时域推导了一阶速度—应力波动方程。曲线坐标系变换是一种速度加权映射关系的转换,能够显著降低垂直时域的高速层采样点数,这对于中深部高速区影响更为明显。从近似源波场的思路出发,推导了优化算子近似源波场的差分公式,通过存储每一时间片在计算区域周围各点的优化算子,利用优化算子重构计算区域内部N层波场(2N为差分阶数),改进了垂直时域下的RTM算法。与有效边界存储方法需要存储层边界波场相比,本文方法相当于仅存储一层边界波场,能够大幅减少存储量与边界计算量。通过上述改进,实现了一种基于优化算子边界存储策略的高效垂直时域RTM算法。
1 方法原理 1.1 垂直时域的逆时偏移方法二维深度域一阶应力—速度方程为
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = \frac{1}{{{\rho _{\rm{d}}}}}\frac{{\partial p}}{{\partial x}}\\ \frac{{\partial w}}{{\partial t}} = \frac{1}{{{\rho _{\rm{d}}}}}\frac{{\partial p}}{{\partial z}}\\ \frac{{\partial p}}{{\partial t}} = {\rho _{\rm{d}}}v_{\rm{d}}^2\left( {\frac{{\partial u}}{{\partial t}} + \frac{{\partial w}}{{\partial z}}} \right) \end{array} \right. $ | (1) |
式中:u、w为质点振动速度的x、z方向分量;p为压力;ρd为深度域介质密度;vd为深度域介质速度。基于Alkhalifah等[22]提出的曲线坐标系,将笛卡尔坐标系下的深度域微分dz除以当前点的平滑速度vsm(x,z)变换为曲线坐标系下的垂直时域微分dτ(x,z),即
| $ {\rm{d}}\tau \left( {x,z} \right) = \frac{{{\rm{d}}z}}{{{v_{{\rm{sm}}}}\left( {x,z} \right)}} $ | (2) |
其反变换可表示为
| $ {\rm{d}}z\left( {x,z} \right) = {v_{{\rm{sm}}}}\left( {x,\tau } \right){\rm{d}}\tau $ | (3) |
式中vsm(x,τ)为垂直时域的介质平滑速度。通过式(2)将深度坐标转换为单程垂向旅行时坐标,相应的坐标系变量为
| $ \left\{ \begin{array}{l} \xi = x\\ \eta = \tau \end{array} \right. $ | (4) |
引入微分算子
| $ {f_x} \equiv \frac{{\partial f}}{{\partial x}} $ | (5) |
定义垂向时间域算子α=-ηx,两个坐标系导数关系为
| $ \left\{ \begin{array}{l} {x_\xi } = 1\\ {z_\xi } = - \alpha {v_{{\rm{sm}}}}\\ {x_\eta } = 0\\ {z_\eta } = {v_{{\rm{sm}}}} \end{array} \right. $ | (6) |
假定笛卡尔坐标系x、z方向的单位矢量为i、k,曲线坐标系ξ、η的单位矢量为e1、e3,则两组单位矢量的关系为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{e}}_1} = {x_\xi }\mathit{\boldsymbol{i}} + {z_\xi }\mathit{\boldsymbol{k}} = \mathit{\boldsymbol{i}} - {v_{{\rm{sm}}}}\alpha \mathit{\boldsymbol{k}}\\ {\mathit{\boldsymbol{e}}_3} = {x_\eta }\mathit{\boldsymbol{i}} + {z_\eta }\mathit{\boldsymbol{k}} = {v_{{\rm{sm}}}}\mathit{\boldsymbol{k}} \end{array} \right. $ | (7) |
由散度定理可得,任意矢量场M在曲线坐标系下的散度和梯度的表达式分别为
| $ \nabla \cdot \mathit{\boldsymbol{M}} = \frac{1}{{{v_{{\rm{sm}}}}}}\left[ {{{\left( {{v_{{\rm{sm}}}}{M_1}} \right)}_\xi } + {{\left( {{v_{{\rm{sm}}}}{M_3}} \right)}_\xi }} \right] $ | (8) |
| $ \nabla \mathit{\boldsymbol{M}} = \left( {{M_\xi } + \alpha {M_\eta }} \right){\mathit{\boldsymbol{e}}_1} + \left( {{\alpha ^2}{M_\eta } + \frac{1}{{v_{{\rm{sm}}}^2}}{M_\xi }} \right){\mathit{\boldsymbol{e}}_3} $ | (9) |
将式(8)、式(9)代入式(1),可得到垂直时域的二维一阶速度—压力波动方程
| $ \left\{ \begin{array}{l} \frac{{\partial U}}{{\partial t}} = \frac{1}{{{\rho _\tau }}}\left( {\frac{{\partial P}}{{\partial \xi }} + \alpha \frac{{\partial P}}{{\partial \eta }}} \right)\\ \frac{{\partial W}}{{\partial t}} = \frac{1}{{{\rho _\tau }}}\left( {\alpha \frac{{\partial P}}{{\partial \xi }} + \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{{\partial P}}{{\partial \eta }}} \right)\\ \frac{{\partial P}}{{\partial t}} = \frac{{{\rho _\tau }V_\tau ^2}}{{{v_{{\rm{sm}}}}}}\left[ {\frac{{\partial \left( {{v_{{\rm{sm}}}}U} \right)}}{{\partial \xi }} + \frac{{\partial \left( {{v_{{\rm{sm}}}}W} \right)}}{{\partial \eta }}} \right] \end{array} \right. $ | (10) |
式中:U、W为垂直时域沿ξ、η方向的速度分量;P为垂直时域的压力波场;ρτ为垂直时域的介质密度;Vτ为垂直时域的速度。上述垂直时域的模型参数均由深度域模型参数经式(2)变换获得;垂直时域算子α表示垂直时域的纵坐标η沿x方向的一阶偏导数。
通过式(10)可实现垂直时域的正演模拟和RTM。
1.2 优化算子边界存储策略为降低震源波场重构的存储需求,提出一种优化算子边界存储策略。此处,假定波场延拓中采用的有限差分阶数为2N,通过引入优化算子A代替有效边界存储策略所需存储的N层边界波场,其中优化算子A是边界域Ω中波场值Ss (ξ, η; t)的线性加权。采用式(10)作为控制方程,在垂直时域进行震源波场重构,以优化算子A作为震源波场重构所需的边界条件,相应的震源波场重构方程为
| $ \left\{ \begin{array}{l} \frac{{\partial {U_{\rm{s}}}}}{{\partial t}} = \frac{1}{{{\rho _\tau }}}\left( {\frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }} + \alpha \frac{{\partial {P_{\rm{s}}}}}{{\partial \eta }}} \right)\\ \frac{{\partial {W_{\rm{s}}}}}{{\partial t}} = \frac{1}{{{\rho _\tau }}}\left( {\alpha \frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }} + \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{{\partial {P_{\rm{s}}}}}{{\partial \eta }}} \right)\\ \frac{{\partial {P_{\rm{s}}}}}{{\partial t}} = \frac{{{\rho _\tau }V_\tau ^2}}{{{v_{{\rm{sm}}}}}}\left[ {\frac{{\partial \left( {{v_{{\rm{sm}}}}{U_{\rm{s}}}} \right)}}{{\partial \xi }} + \frac{{\partial \left( {{v_{{\rm{sm}}}}{W_{\rm{s}}}} \right)}}{{\partial \eta }}} \right]\\ {P_{\rm{s}}}\left( {\xi ,\eta } \right) = {S_{\rm{s}}}\left( {\xi ,\eta ;t} \right) \end{array} \right. $ | (11) |
式中下标“s”表示重建的震源波场。
借鉴有限差分的思想,采用有限差分法近似式(11)中的空间偏导。以
| $ \frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }}\left| {_{\frac{1}{2},j}} \right. \approx \frac{1}{h}\sum\limits_{k = 1}^N {{a_k}\left( {{P_{{\rm{s}},k,j}} - {P_{{\rm{s}}, - k + 1,j}}} \right)} $ | (12) |
式中:Ps, i, j表示压力波场Ps在(ξ=i-h/2,η=j)处的值;ak为震源波场重构方程的第一组近似空间差分系数,k=1,2,…,N。用优化算子A替换式(12)中最右端的差分项,则有
| $ \frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }}\left| {_{\frac{1}{2},j}} \right. \approx \frac{1}{h}\left( {\sum\limits_{k = 1}^N {{a_i}{P_{{\rm{s}},i,j}} - {A_j}} } \right) $ | (13) |
同理,一阶偏导项
| $ \left\{ \begin{array}{l} {\frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }}_{\frac{3}{2},j}} \approx \frac{1}{h}\left[ {{b_{1,1}}\left( {{P_{{\rm{s}},2,j}} - {P_{{\rm{s}},1,j}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{b_{1,2}}\left( {\sum\limits_{i = 1}^N {{a_i}{P_{{\rm{s}},i + 1,j}} - {A_j}} } \right)} \right]\\ {\frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }}_{\frac{5}{2},j}} \approx \frac{1}{h}\left[ {\sum\limits_{i = 1}^2 {{b_{2,i}}\left( {{P_{{\rm{s}},i + 2,j}} - {P_{{\rm{s}},3 - i,j}}} \right)} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{b_{2,3}}\left( {\sum\limits_{i = 1}^N {{a_i}{P_{{\rm{s}},i + 4,j}} - {A_j}} } \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\frac{{\partial {P_{\rm{s}}}}}{{\partial \xi }}_{N - \frac{1}{2},j}} \approx \frac{1}{h}\left[ {\sum\limits_{i = 1}^{N - 1} {{b_{1,i}}\left( {{P_{{\rm{s}},i + N - 1,j}} - {P_{{\rm{s}},N - i,j}}} \right)} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{b_{N,N - 1}}\left( {\sum\limits_{i = 1}^N {{a_i}{P_{{\rm{s}},i + 2\left( {N - 1} \right),j}} - {A_j}} } \right)} \right] \end{array} \right. $ | (14) |
式中:bi, k为震源波场重构方程的第二组近似空间差分系数,i=1,2,…,N,k=1,2,…,N。由此可知,优化算子A仅与优化算子系数ai、bi, k和波场值有关。为了寻求优化系数ai与bi, k的隐含关系,将式(13)和式(14)变换至傅里叶域,有
| $ \left\{ \begin{array}{l} \left( {{k_x}h} \right) \approx 2\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i - \frac{1}{2}} \right)h{k_x}} \right]} \\ \left( {{k_x}h} \right) \approx 2{b_{1,1}}\sin \left( {\frac{1}{2}h{k_x}} \right) + \\ \;\;\;\;\;\;\;\;\;\;2{b_{1,2}}\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i + \frac{1}{2}} \right)h{k_x}} \right]} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \end{array} \right. $ | (15a) |
| $ \left\{ \begin{array}{l} \left( {{k_x}h} \right) \approx 2\sum\limits_{i = 1}^{N - 1} {{b_{N - 1,i}}\sin \left[ {\left( {i - \frac{1}{2}} \right)h{k_x}} \right]} + \\ \;\;\;\;\;\;2{b_{N,N - 1}}\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i + N - \frac{3}{2}} \right)h{k_x}} \right]} \end{array} \right. $ | (15b) |
为了寻找能满足差分精度和稳定性条件的最优系数,利用最小误差原理构建最优化函数
| $ \left\{ \begin{array}{l} {F_1} = \int\limits_0^{{{\max }_1}} {\left\{ {1 - \frac{2}{\lambda }\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i - \frac{1}{2}} \right)\lambda } \right]} } \right\}{\rm{d}}\lambda } \\ {F_2} = \int\limits_0^{{{\max }_2}} {\left\{ {1 - \frac{2}{\lambda }\sin \left( {\frac{1}{2}\lambda } \right) - } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\frac{2}{\lambda }{b_{1,2}}\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i + \frac{1}{2}} \right)\frac{2}{\lambda }} \right]} } \right\}{\rm{d}}\lambda \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {F_N} = \int\limits_0^{{{\max }_N}} {\left\{ {\frac{2}{\lambda }{b_{N - 1,i}}\sin \left[ {\left( {i - \frac{1}{2}} \right)\lambda } \right] + \frac{2}{\lambda }{b_{N,N - 1}} \times } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\sum\limits_{i = 1}^N {{a_i}\sin \left[ {\left( {i + N - \frac{3}{2}} \right)\lambda } \right]} } \right\}{\rm{d}}\lambda \end{array} \right. $ | (16) |
式中:λ=hkξ;maxi为压力场Pi的最大波数,i=1,2,…,N。由误差函数Fi(i=1,2,…,N)的性质可知,误差上限maxi表示傅里叶域中的最大波数,该取值将会影响到误差函数的稳定性。经过严谨的数学实验,认为误差上限maxi的取值在1.0~2.0范围内为最佳,此时波场存在极小值且收敛于有效范围内。在优化函数式(16)中加入约束条件使优化函数值降到误差阈值之下,即优化函数达到极小,则有
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{a_i}{i^2}} = 1\\ {b_{1,1}} + {b_{1,2}}\sum\limits_{i = 1}^N {{a_i}{{\left( {i + 1} \right)}^2}} = 1\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \sum\limits_{i = 1}^N {{b_{N - 1,i}}{i^2}} + {b_{N,N - 1}}\sum\limits_{i = 1}^N {{a_i}{{\left( {i + N - 1} \right)}^2}} = 1 \end{array} \right. $ | (17) |
联立式(16)和式(17)进行求解,即可获得不同差分阶数对应的优化系数ai和bi, k。
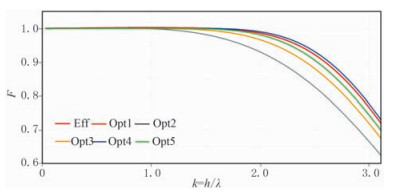
表 1为差分阶数为8、10、12时的优化算子A在边界内层N个点的优化系数ai和bi, k。图 1为当差分阶数为10时,优化算子边界存储策略(Opt)与有效边界存储策略(Eff)在边界内5点处的精度对比,其中精度曲线Opt1~Opt5表示边界层内1~5个点,这些点均由优化算子边界存储策略在波数域构建的目标泛函而得,精度曲线Eff由有效边界存储策略根据交错网格差分系数构建的目标泛函而得。边界层内第一个点Opt1和第三个点Opt3的精度高于有效边界存储策略,其他三点精度略低,但其误差阈值严格控制在0.0015范围内。由图 1可知,优化算子边界存储策略通过构建的波场重构近似差分公式,获得满足精度要求的优化算子,从而避免保存多层边界波场。由图 2可知,在差分阶数为2N的情况下,有效边界策略需要存储N层边界重构震源波场,而优化算子边界存储策略只需存储优化算子A,相当于仅存储一层边界。优化算子边界存储策略通过微小牺牲部分差分权重较低点的精度,提升权重较大点的精度,极大地降低存储需求与I/O压力。
|
|
表 1 差分阶次为8、10、12时的边界优化算子系数表 |
|
图 1 10阶有效边界及优化算子边界存储精度对比 |
|
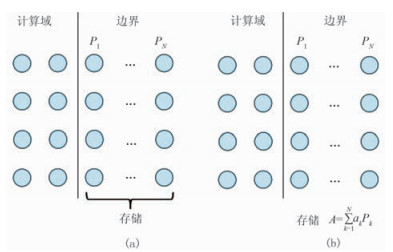
图 2 有效边界(a)与优化算子边界(b)存储策略示意图 |
以二维模型为例,假定模型大小为Nξ×Nη,时间域采样点数为Nt,差分阶数为2N,有效边界存储策略需要存储2N×(Nξ+Nη)×Nt个边界波场用于重构(图 2a),而优化算子边界存储策略仅需要存储2(Nξ+Nη)×Nt个边界波场(图 2b),减少了2(N-1)×(Nξ+Nη)×Nt个。通过理论分析可知,本文方法整体精度略低于有效边界存储策略,但在不影响精度的基础上,能够降低RTM在波场重构时消耗的大量存储空间与I/O数据量,对于三维RTM存储问题效果尤为明显。
2 模型试算本文在模型正演模拟与逆时偏移中差分阶数均为10。
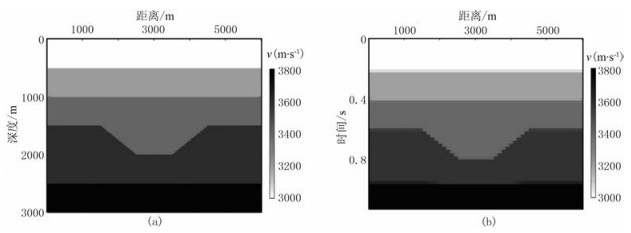
2.1 凹陷模型首先,为了验证本文方法的效果,设计了凹陷模型(图 3a)进行实验。模型参数为:网格数为601×301,纵、横向网格间距均为10m,震源是主频为30Hz的Ricker子波,共31炮。图 3b为垂直时域下的凹陷模型,由图 3a变换得到,网格数为601×134,相比于深度域模型纵向网格减少了167个点,对应的纵向采样间隔为6ms。
|
图 3 深度域(a)和垂直时域(b)凹陷模型 |
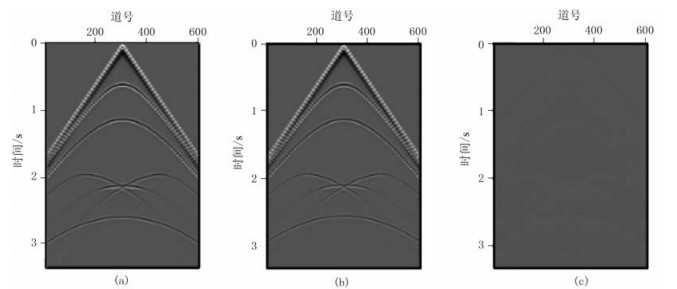
图 4a和图 4b分别为深度域与垂直时域凹陷模型t=850ms波场快照。深度域单炮正演计算时间为188.40ms,垂直时域计算时间为102.89ms,约为深度域耗时的54%。图 4c为t=850ms垂直时域的波场快照反变换至深度域的结果,图 4d为图 4c与图 4a的差。由图 4d可以看出:振幅残差低于0.01%,基本没有走时误差,对后续的成像精度的影响可以忽略。因此垂直时域正演模拟能够在保证成像精度的前提下,大幅提升计算效率。对比深度域与垂直时域的单炮记录(图 5a和图 5b)可见,二者走时信息基本一致,残差(图 5c)数量级为深度域单炮记录(图 5a)的0.01%,因此变换到垂直时域进行正演模拟对后续成像影响可以忽略。

|
图 4 凹陷模型850 ms波场快照 (a)深度域波场快照;(b)垂直时域波场快照;(c)图b反变换到深度域波场快照;(d)图a与图c波场快照的残差 |
|
图 5 深度域(a)与垂直时域(b)单炮记录及其差值记录(c) |
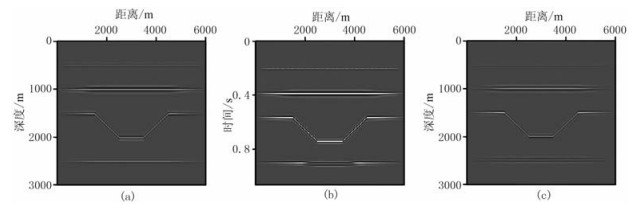
图 6a和图 6b分别为深度域与垂直时域凹陷模型的成像结果对比,深度域计算时间为328s,占用21MB存储空间;垂直时域计算时间为173s,占用3.2MB存储空间,时间节省了约48%,仅需传统RTM存储空间的15%。由图 6b可见,垂直时域凹陷模型第一、第二界面成像结果与深度域结果一致,第三界面成像中部发生小部分畸变,这是由于垂直时域的坐标系是曲线坐标系。图 6b反变换至深度域结果如图 6c所示,可以看出:对于垂直时域的偏移成像结果而言,由于非等间距变换导致的畸变能够在反变换至深度域时得到修正,且对简单凹陷模型具有良好的适应性,而仅需54%的计算量和15%的存储量。
|
图 6 深度域偏移结果(a)、垂直时域偏移结果(b)及其变换到深度域结果(c) |
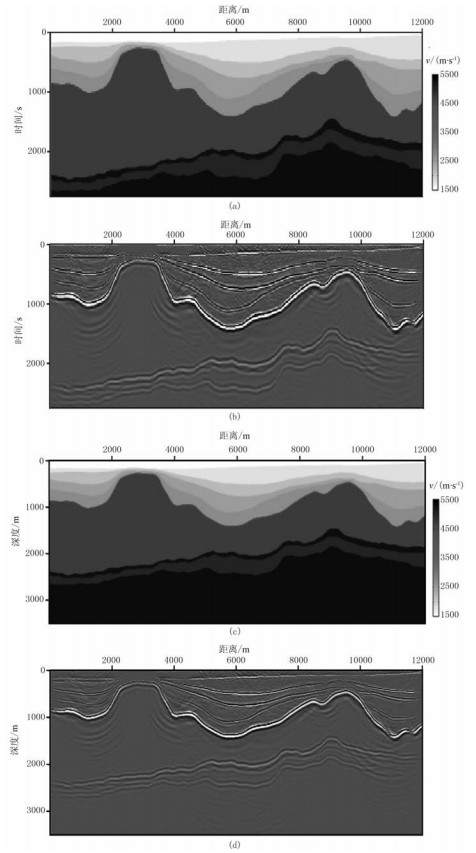
用盐丘模型(图 7a)验证本文方法对复杂模型的适应性,速度范围为1500~5500 m/s。正演参数:网格数为1201×267,横向网格间距为10m,纵向网格间距为5ms,震源为主频30Hz的Ricker子波,总炮数为80,炮点间隔为150m,记录时间为4s,时间间隔为1ms。
|
图 7 垂直时域的盐丘模型(a)和偏移结果(b)及变换至深度域的速度模型(c)和偏移结果(d) |
在垂直时域对盐丘模型(图 7a)进行地震模拟,得到相应的优化算子、最后时刻的波场快照与80炮的地震记录,以此为基础在垂直时域进行RTM,得到成像结果(图 7b)。利用式(2)将垂直时域的模型与偏移结果变换到深度域(图 7c与图 7d)。对比成像结果图 7b和图 7d可知,在垂直时域下进行RTM能够对复杂构造的起伏界面成像,并且不会产生由于样点数降低而导致的精度下降问题,变换至深度域后界面归位准确,且没有产生噪声。由此可知,本文将优化算子边界存储策略与垂直时域RTM相结合的方法能够针对盐丘构造等界面起伏较大的区域成像,与传统RTM成像结果一致。与传统RTM方法相比,本文方法可以减少68.4%存储需求和节省约35%的计算时间。
3 结论在前人研究的基础上,本文首先从曲线坐标系的概念出发,推导了垂直时域一阶速度—应力方程,构建了垂直时域下的RTM方案;然后利用波场重构近似差分方法,提出了优化算子边界存储策略,实现了波场重构的存储量最小化,其精度等效于有效边界存储策略,且存储成本低于绝大多数波场重构方法;最终形成了一套基于优化算子边界存储策略的垂直时域高效RTM流程。通过典型模型试算,得出以下结论。
(1) 垂直时域下的RTM弥补了传统RTM计算效率低的不足,通过引入曲线坐标系,避免了复杂构造的纵向过采样带来的巨大计算量,减少了计算时间。
(2) 优化算子边界存储策略解决了传统RTM存储量大的问题,利用近似波场重构差分公式,提出借助优化算子对源波场进行波场重构。本文方法克服了有效边界存储策略需要存储差分阶数层边界的缺陷,其波场重构效果能满足RTM的精度要求。
(3) 本文提出的两种策略结合的RTM流程对于凹陷模型和复杂构造模型都能获得很好的正演及偏移结果,其适用于含高速层的复杂介质,能够解决三维RTM中存储量大与计算效率低等一系列问题。同时可以推广到弹性波各向异性介质,也可以用于最小二乘RTM与全波形反演。
综上所述,本文提出的一种基于优化算子边界存储策略的高效RTM方法能够对复杂结构进行精确成像,可减少RTM的存储需求和计算时间。但尚未应用于实际数据,垂直时域变换是否适用于各类复杂模型有待后续深入研究。
| [1] |
Baysal E, Kosloff D D, Sherwood W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [2] |
McMechan G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [3] |
Whitmore N D.Iterative depth migration by backward time propagation[C]. SEG Technical Program Expanded Abstracts, 1983, 2: 382-385. https://www.onepetro.org/conference-paper/SEG-1983-0382
|
| [4] |
Biondi B and Shan G.Prestack imaging of overturned reflections by reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1284-1287. http://www.mendeley.com/catalog/prestack-imaging-overturned-reflections-reverse-time-migration/
|
| [5] |
Yoon K, Marfurt K J, Starr W.Challenges in reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2004: 23: 1057-1060. https://www.onepetro.org/conference-paper/SEG-2004-1057
|
| [6] |
杨午阳, 张厚柱, 撒利明, 等. RTM有关问题探讨[J]. 石油地球物理勘探, 2016, 51(6): 1251-1262. YANG Wuyang, ZHANG Houzhu, SA Liming, et al. Some issues about reverse time migration[J]. Oil Geo-physical Prospecting, 2016, 51(6): 1251-1262. |
| [7] |
姜国博, 曾庆芹, 李虹, 等. RTM技术在土库曼斯坦地区的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 81-83, 103. JIANG Guobo, ZENG Qingqin, LI Hong, et al. Reverse time migration for the Block X in Turkmenistan[J]. Oil Geophysical Prospecting, 2017, 52(S2): 81-85, 103. |
| [8] |
李海强, 杨国权, 李振春, 等. 基于局部平面波分解的逆时偏移角道集提取方法[J]. 石油地球物理勘探, 2017, 52(6): 1177-1183. LI Haiqiang, YANG Guoquan, LI Zhenchun, et al. A method for extracting angle-domain common image gathers based on local plane wave decomposition[J]. Oil Geophysical Prospecting, 2017, 52(6): 1177-1183. |
| [9] |
Kreiss H O, Oliger J. Comparison of accurate methods for the integration of hyperbolic equations[J]. Tellus, 1972, 24(3): 199-215. DOI:10.3402/tellusa.v24i3.10634 |
| [10] |
王伟国, 熊水金, 徐华宁, 等. TTI介质各向异性伪谱法RTM[J]. 石油地球物理勘探, 2012, 47(4): 566-572. WANG Weiguo, XIONG Shuijin, XU Huaning, et al. Reverse time migration using pseudo-spectral method for tilted TI media[J]. Oil Geophysical Prospecting, 2012, 47(4): 566-572. |
| [11] |
Jastram C, Tessmer E. Elastic modelling on a grid with vertically varying spacing[J]. Geophysical Prospecting, 1994, 42(4): 357-370. DOI:10.1111/gpr.1994.42.issue-4 |
| [12] |
黄建平, 黄金强, 李振春, 等. TTI介质一阶qP波方程交错网格伪谱法正演模拟[J]. 石油地球物理勘探, 2016, 51(3): 487-496. HUANG Jianping, HUANG Jinqiang, LI Zhenchun, et al. Staggered grid pseudo-spectral numerical simulation of first-order quasi P-wave equation for TTI media[J]. Oil Geophysical Prospecting, 2016, 51(3): 487-496. |
| [13] |
Fomel S, Ying L, Song X. Seismic wave extrapolation using low rank symbol approximation[J]. Geophysical Prospecting, 2013, 61(3): 526-536. DOI:10.1111/gpr.2013.61.issue-3 |
| [14] |
刘红伟, 李博, 刘洪, 等. 地震叠前RTM高阶有限差分算法及GPU实现[J]. 地球物理学报, 2010, 53(7): 1725-1733. LIU Hongwei, LI Bo, LIU Hong, et al. The reverse time algorithm of high order finite difference pre-stack migration and GPU implementation[J]. Chinese Journal of Geophysics, 2010, 53(7): 1725-1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 |
| [15] |
Nunes V, Minkoff S E.Imaging via subgrid upscaling and reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 4008-4013.
|
| [16] |
Liu Y, Sen M K. A new time-space domain high-order finite-difference method for the acoustic wave equa-tion[J]. Journal of Computational Physics, 2009, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
| [17] |
张剑锋. 弹性波数值模拟的非规则网格差分法[J]. 地球物理学报, 1998, 41(增刊1): 357-366. ZHANG Jianfeng. Non-orthogonal grid finite difference method for numerical simulation of elastic wave propagation[J]. Chinese Journal of Geophysics, 1998, 41(S1): 357-366. |
| [18] |
Moczo P. Finite-difference technique for SH-waves in 2-D media using irregular grids:application to the seismic response problem[J]. Geophysical Journal International, 1989, 99(2): 321-329. DOI:10.1111/gji.1989.99.issue-2 |
| [19] |
黄超, 董良国. 可变网格与局部时间步长的交错网格高阶差分弹性波模拟[J]. 地球物理学报, 2009, 52(11): 2870-2878. HUANG Chao, DONG Liangguo. Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time-steps[J]. Chinese Journal of Geophysics, 2009, 52(11): 2870-2878. |
| [20] |
宓铁良, 孙兵兵, 杨慧珠. 基于第二代小波自适应网格的二维声波方程波传模拟[J]. 地球物理学报, 2009, 52(11): 2862-2869. MI Tieliang, SUN Bingbing, YANG Huizhu. Adaptive mesh based on second generation wavelet simulation wave propagation for 2D acoustic wave equation[J]. Chinese Journal of Geophysics, 2009, 52(11): 2862-2869. |
| [21] |
Tessmer E. Seismic finite-difference modeling with spatially varying time steps[J]. Geophysics, 2000, 65(4): 1290-1293. DOI:10.1190/1.1444820 |
| [22] |
Alkhalifah T, Fomel S, Biondi B. The space-time domain:Theory and modelling for anisotropic media[J]. Geophysical Journal International, 2001, 144(1): 105-113. DOI:10.1046/j.1365-246x.2001.00300.x |
| [23] |
李庆洋, 黄建平, 李振春, 等. 伪深度域声波数值模拟方法及应用[J]. 石油地球物理勘探, 2015, 50(2): 283-289. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Acoustic wave numerical simulation in pseudo-depth domain[J]. Oil Geophysical Prospecting, 2015, 50(2): 283-289. |
| [24] |
Plessix R E, Milcik P, Corcoran C, et al.Full wave-form inversion with a pseudo-time approach[C]. Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, W012.
|
| [25] |
Li Q Y, Li Z C, Huang J P, et al.Least-squares reverse time migration in pseudo-time domain[C]. Extended Abstracts of 78th EAGE Conference & Exhibition, 2016, P105.
|
| [26] |
Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [27] |
Gauthier O, Virieux J, Tarantola A. Two-dimensional nonlinear inversion of seismic waveforms:Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [28] |
Dussaud E, Symes W W, Williamson P, et al.Computational strategies for reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2267-2271. https://www.mendeley.com/catalogue/computational-strategies-reversetime-migration/
|
| [29] |
杨仁虎, 凌云, 瞿立建, 等. 基于边界存储的地震波场重构及RTM成像应用研究[J]. 地球物理学进展, 2017, 32(3): 1286-1289. YANG Renhu, LING Yun, QU Lijian, et al. Seismic wavefield reconstruction based on boundary storage and application of reverse time migration[J]. Progress in Geophysics, 2017, 32(3): 1286-1289. |
| [30] |
Symes W W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [31] |
宋利伟, 石颖, 柯璇, 等. 基于检查点方法的各向异性介质逆时偏移[J]. 石油物探, 2018, 57(2): 274-282. SONG Liwei, SHI Ying, KE Xuan, et al. Reverse time migration of anisotropic media using the checkpoint method[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 274-282. DOI:10.3969/j.issn.1000-1441.2018.02.013 |
| [32] |
Clapp R.Reverse time migration with random bound-aries[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2809-2813. https://www.onepetro.org/conference-paper/SEG-2009-2809
|
| [33] |
王保利, 高静怀, 陈文超, 等. 地震叠前RTM的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 2412-2421. WANG Baoli, GAO Jinghuai, CHEN Wenchao, et al. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese Journal of Geophy-sics, 2012, 55(7): 2412-2421. |
| [34] |
Feng B, Wang H Z. Reverse time migration with source wavefield reconstruction strategy[J]. Journal of Geophysics and Engineering, 2012, 9(1): 69-74. DOI:10.1088/1742-2132/9/1/008 |
| [35] |
Sun W, Fu L Y. Two effective approaches to reduce data storage in reverse time migration[J]. Computers & Geosciences, 2013, 56: 69-75. |
| [36] |
Nguyen B D, McMechan G A. Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration[J]. Geophysics, 2015, 80(1): S1-S18. |
| [37] |
Liu S, Li X, Wang W, et al. Source wavefield reconstruction using a linear combination of the boundary wavefield in reverse time migration[J]. Geophysics, 2015, 80(6): S203-S212. DOI:10.1190/geo2015-0109.1 |
| [38] |
Vasmel M, Robertsson J O A. Exact wavefield reconstruction on finite-difference grids with minimal me-mory requirements[J]. Geophysics, 2016, 81(6): T303-T309. DOI:10.1190/geo2016-0060.1 |



 段沛然, 山东省青岛市黄岛区长江中路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
段沛然, 山东省青岛市黄岛区长江中路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: