② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
③ 东方地球物理公司装备服务处测量服务中心, 河北涿州 072751;
④ 东方地球物理公司信息技术中心, 北京 100043
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China;
③ Surveying Service Center, Equipment Service Department, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China;
④ Information Technology Center, BGP Inc., CNPC, Beijing 100043, China
近年来,OBC(Ocean Bottom Cable)技术在浅海石油勘探中得到广泛应用,取得了显著经济效益[1]。在OBC地震数据采集中,通常需安置和定位大量海底地震检波器和采集站点。检波器可利用初至波进行定位,但需确定地震波速度场和较高精度的震源船位置[2]。声学二次定位利用低成本、体积小且重量轻的海底应答器与海底检波器进行捆绑定位,可满足浅海石油勘探的需求。
声学二次定位系统一般包括主控机、换能器和声学应答器以及相关的辅助设备。定位船通常搭载可在全球范围内提供服务的星站差分定位系统,其定位精度目前优于20cm,可满足高精度的实时导航定位需求。目前的海底应答器可将声学测距的时延误差以及声波信号的脉冲测量控制在较高的精度,但走航船持续走航作业导致发射声波位置和收到反馈信号位置并非严格相同,存在一定的时间测量误差[3]。浅海声速剖面可通过温盐压传感器或声速剖面测量仪(CTD)测得,但声速剖面误差也是影响声学测距误差的重要因素。声波在海水中传播时,会在介质常数不同的两个界面上产生反射、折射和某种程度的反向散射,从而导致波束声线弯曲和传播速度发生改变,入射角越大,声速变化越大,弯曲越显著[4-6]。在浅海海底应答器的定位过程中,大量声学观测数据的入射角超过65°,声学弯曲误差成为影响高精度声学定位的重要因素。为了降低声速误差的影响,得到高精度的定位结果,很多学者利用实时的声速剖面数据研究声学弯曲对浅海目标的影响[7-8]。但在实际的海上石油勘探过程中,实时准确的声速剖面很难获得。
因此本文研究如何消除浅海声线弯曲对海底应答器定位精度的影响。针对存在较大量级的声线弯曲误差的情况,依据浅海海底局部范围内地势平坦的特性,本文基于无声速定位模式设计了序贯最小二乘解算方案,并提出了将声线弯曲误差按入射角分组、多应答器序贯估计的浅海多应答器快速定位方法。结合仿真和实测实验,将新算法与传统几何法、入射角截止法及走航式历元间差分算法的结果进行比较。
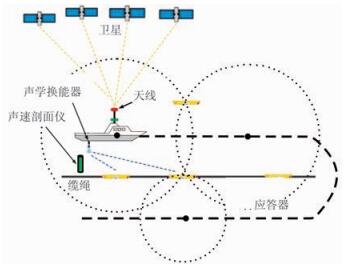
1 浅海声学定位算法和声速改正参数估计 1.1 浅海声学定位算法浅海声学二次定位系统包括主控机、换能器和声学应答器及相关辅助设备(图 1)[9]。声学定位实际是一种前方交会测量,假设ti时刻由GPS得到测量船位置为Xik,海底应答器(k为其序号)的坐标为XTk,测得的测量船至应答器的距离(传播时间乘以声速)为ρik。若不考虑姿态测量误差(最多为厘米级别)影响,仅考虑与声速有关的误差和测量随机误差,则观测方程[10, 12-13]可写为
|
图 1 浅海声学二次定位示意图 |
| $ \rho _i^k = f\left( {\mathit{\boldsymbol{X}}_i^k - \mathit{\boldsymbol{X}}_{\rm{T}}^k} \right) + {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k + \varepsilon _i^k $ | (1) |
| $ \begin{array}{l} f\left( {\mathit{\boldsymbol{X}}_{\rm{T}}^k,\mathit{\boldsymbol{X}}_i^k} \right)\\ \;\;\;\;\;\; = \sqrt {{{\left( {x_{\rm{T}}^k - x_i^k} \right)}^2} + {{\left( {y_{\rm{T}}^k - y_i^k} \right)}^2} + {{\left( {z_{\rm{T}}^k - z_i^k} \right)}^2}} \end{array} $ | (2) |
式中:f(XTk, Xik)为测量船到海底应答器的真实距离,i表示观测时刻;δρυik为声线弯曲误差及与入射角有关的误差;εik为其他测距随机误差。
如果声速剖面已知,则可得到Harmonic平均声速,那么式(1)可线性化为
| $ \rho _{{i_o}}^k - f\left( {\mathit{\boldsymbol{X}}_i^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right) = a_{{i_o}}^k{\rm{d}}x + {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k + \varepsilon _i^k + b_{{i_o}}^k\varepsilon _{pi}^k $ | (3) |
式中:ρiok=Ce·tik,Ce为平均声速,o表示近似坐标,tik是单程传播时间;
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{A}}{\rm{d}}x + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (4) |
式中Δ为真误差。对于浅海多目标的声学二次定位,一般很难获得准确的声速剖面。当代入的声速值与实际情况不符时,应答器的坐标精度会降低。可以通过设置初始声速值并估计其声速的改正数。此时的观测方程[16]可表示为
| $ \tilde \rho _{{i_o}}^k - f\left( {\mathit{\boldsymbol{X}}_i^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right) = a_{{i_o}}^k{\rm{d}}x + t_i^k{\rm{d}}c + {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k + \varepsilon _i^k + b_{{i_o}}^k\varepsilon _{pi}^k $ | (5) |
式中
由于放缆作业区域一般较小,单次作业时间通常较短(如1小时),若不考虑短周期内波和负荷潮等因素的影响,在较稳定的海洋观测环境下,可认为观测期间声速改正数是近似的,利用所有应答器观测数据通过序贯最小二乘估计声速改正数。式(5)可改写为
| $ {\mathit{\boldsymbol{C}}_1}{\rm{d}}x + {\mathit{\boldsymbol{C}}_2}{\rm{d}}c = \mathit{\boldsymbol{L}} $ | (6) |
式中:C1为雅可比矩阵;C2为声速改正数系数阵。式(6)可简化为
| $ {\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{C}}1}}{\mathit{\boldsymbol{C}}_2}{\rm{d}}c = {\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{C}}1}}\mathit{\boldsymbol{L}} $ | (7) |
式中RC1=I-C1(C1TC1)-1C1T。此时可应用序贯最小二乘算法求解声速改正数
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_1} = \mathit{\boldsymbol{P}}_{{{\hat X}_1}}^{ - 1}\mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{L}}_1}\\ {{\mathit{\boldsymbol{\hat X}}}_2} = \mathit{\boldsymbol{P}}_{{{\hat X}_2}}^{ - 1}\left( {\mathit{\boldsymbol{A}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{L}}_2} + \mathit{\boldsymbol{P}}_{{{\hat X}_1}}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_1}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {{\mathit{\boldsymbol{\hat X}}}_k} = \mathit{\boldsymbol{P}}_{{{\hat X}_k}}^{ - 1}\left( {\mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_k}{\mathit{\boldsymbol{L}}_k} + \mathit{\boldsymbol{P}}_{{{\hat X}_{k - 1}}}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k - 1}}} \right) \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_{{{\hat X}_1}}} = \mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{A}}_1}\\ {\mathit{\boldsymbol{P}}_{{{\hat X}_2}}} = {\mathit{\boldsymbol{P}}_{{{\hat X}_1}}} + \mathit{\boldsymbol{A}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{A}}_2}\\ \;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{P}}_{{{\hat X}_k}}} = {\mathit{\boldsymbol{P}}_{{{\hat X}_{k - 1}}}} + \mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_k}{\mathit{\boldsymbol{A}}_k} \end{array} \right. $ | (9) |
式中:Ai=(RC1C2)i;
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{{\hat X}_k}}} = \mathit{\boldsymbol{P}}_{{{\hat X}_k}}^{ - 1}\mathit{\boldsymbol{\hat \sigma }}_{{0_k}}^2 $ | (10) |
| $ \mathit{\boldsymbol{\hat \sigma }}_{{0_k}}^2 = \frac{{\mathit{\boldsymbol{V}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_k}{\mathit{\boldsymbol{V}}_k} + {{\left( {{{\mathit{\boldsymbol{\hat X}}}_k} - {{\mathit{\boldsymbol{\hat X}}}_{k - 1}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{{{\hat X}_{k - 1}}}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k} - {{\mathit{\boldsymbol{\hat X}}}_{k - 1}}} \right)}}{{{n_k}}} $ | (11) |
虽然定位一个应答器仅有数十个观测数据,但是几十个应答器可测得数千个声学观测数据。在小区域且地形平坦的情况下,可认为其声学环境相同,使用序贯最小二乘求解声速改正数,可避免同时解算所有数据造成的计算负担,有利于后续算法的开展。
2 顾及声线弯曲误差的多目标定位新算法 2.1 声线弯曲参数化求解方法在小范围、短时间内的多应答器定位过程中,可以假设相同的入射角具有近似的声线弯曲误差。基于这个原理,可以基于将声线弯曲改正数按入射角分成不同组,并进行统一估计。假设将声线按入射角不同分为M类,待求参数包括坐标参数和声线弯曲改正数,待求参数可写为XTk=[xTk, yTk, zTk, C1, C2, …, Cm]。观测方程可写为
| $ {\mathit{\boldsymbol{L}}_a} = {\mathit{\boldsymbol{B}}_a}{\rm{d}}x_{\rm{T}}^k + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (12) |
式中Ba=[B1, B2],且满足p1+p2+…+pm=n,其中
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{B}}_1} = {\left[ {\begin{array}{*{20}{c}} {a_{{1_o}}^k}\\ {a_{{2_o}}^k}\\ \vdots \\ {a_{{n_o}}^k} \end{array}} \right]_{n \times 3}}\\ {\mathit{\boldsymbol{B}}_2} = {\left[ {\begin{array}{*{20}{c}} {{\rm{ones}}\left( {{p_1}} \right)}&0&0&0\\ 0&{{\rm{ones}}\left( {{p_1}} \right)}&0&0\\ 0&0& \ddots &0\\ 0&0&0&{{\rm{ones}}\left( {{p_m}} \right)} \end{array}} \right]_{n \times m}} \end{array} \right. $ | (13) |
| $ {\mathit{\boldsymbol{L}}_a} = \left[ {\begin{array}{*{20}{c}} {\tilde \rho _{{1_o}}^k - f\left( {\mathit{\boldsymbol{X}}_1^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)}\\ {\tilde \rho _{{2_o}}^k - f\left( {\mathit{\boldsymbol{X}}_2^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)}\\ \vdots \\ {\tilde \rho _{{n_o}}^k - f\left( {\mathit{\boldsymbol{X}}_n^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)} \end{array}} \right] $ | (14) |
对于第一个应答器,采用最小二乘法求解坐标和声线弯曲改正数及协方差矩阵。在浅海声学二次定位中,对于不同的应答器,如果声学数据入射角相近,由于其采集时间相近,距离相近,水深几乎不变,可认为声学环境类似,声线弯曲误差相同。因此可利用所有应答器的观测数据,采用序贯最小二乘法求解各个阈值范围内的声线弯曲误差改正量
| $ {\mathit{\boldsymbol{L}}_c} = {\mathit{\boldsymbol{B}}_c}{\rm{d}}x_{\rm{T}}^k + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (15) |
此时观测方程的系数阵和观测值扩展为
| $ {\mathit{\boldsymbol{B}}_c} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_a}}&{{\rm{eye}}\left( m \right)} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{L}}_c} = \left[ {{\mathit{\boldsymbol{L}}_a};\hat C_1^{k - 1}; \cdots ;\hat C_m^{k - 1}} \right] $ |
采用序贯最小二次算法可避免所有观测数据同时解声线弯曲改正数造成的巨大计算负担,同时充分利用了声学环境下的所有观测数据。当解算完最后一个应答器的数据时,再用最终的声线弯曲误差改正数修正所有观测数据。尽管解算的声线弯曲改正数和实际声学数据存在的声线弯曲误差有所差异,但该方法通过按入射角进行分组估计,尽可能减弱该影响。
2.2 声线弯曲模型化求解方法对于声线弯曲误差还可以通过建立数学模型进行处理,按照不同的定位方式以及观测时间存在不同形式的模型化[15-20]。例如Fujita等[19]提出将声线弯曲误差按观测时间进行一阶或二阶线性回归,可表示为
| $ \left\{ \begin{array}{l} {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k = {a_0} + {a_1}\left( {{t_i} - {t_0}} \right)\;\;\;\;\;或\\ {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k = {a_0} + {a_1}\left( {{t_i} - {t_0}} \right) + {a_2}{\left( {{t_i} - {t_0}} \right)^2} \end{array} \right. $ | (16) |
该模型通常用于声线弯曲误差与时间成明显线性关系的情况。例如采用浮标对深海应答器进行长时间观测过程中,由于浮标移动速度缓慢,入射角变化短期内一般不大,声学弯曲误差多和观测时间有一定的关系。
对于短时间入射角变化较大的观测情况,例如定位船采用走航式定位浅海应答器,可通过按入射角建模进行估计,常用经验公式为
| $ {\rm{ \mathsf{ δ} }}\rho _{{v_i}}^k = a{\left( {{t_r} - t_i^k\cos {\theta _i}} \right)^2} $ | (17) |
式中:tr为最小入射角对应的传播时间;a可作为参数进行估计。虽然对于声学弯曲有所考虑,但由于模型过于简单,模型化误差会随着入射角的增大而增大。
本文基于走航式定位模式的特点,通过设置不同的入射角阈值,对观测数据中的声线弯曲误差进行分段模型化求解。假设将声线按入射角不同分为M类,将求解的参数表示为dxTk=[xTk, yTk, zTk, Ce, a1, …, am],新观测方程可写为
| $ {\mathit{\boldsymbol{L}}_b} = {\mathit{\boldsymbol{B}}_b}{\rm{d}}x_{\rm{T}}^k + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} $ | (18) |
式中Bb=[B1, B2],且p1+p2+…+pm=n。系数阵的组成如下
| $ {\mathit{\boldsymbol{B}}_1} = {\left[ {\begin{array}{*{20}{c}} {a_{{1_o}}^k}\\ {a_{{2_o}}^k}\\ \vdots \\ {a_{{n_o}}^k} \end{array}} \right]_{n \times 3}},{\mathit{\boldsymbol{B}}_2} =\\ {\left[ {\begin{array}{*{20}{c}} {{\rm{ones}}\left( n \right)}&{\begin{array}{*{20}{c}} {{{\left( {{t_{{r_1}}} - t_i^k\cos {\theta _i}} \right)}^2}}&0&0&0\\ 0&{{{\left( {{t_{{r_2}}} - t_i^k\cos {\theta _i}} \right)}^2}}& \ddots &0\\ 0&0&0&0\\ 0&0&0&{{{\left( {{t_{{r_m}}} - t_i^k\cos {\theta _i}} \right)}^2}} \end{array}} \end{array}} \right]_{n \times m}} $ | (19) |
Lb表示n×1阶列向量,观测值向量为
| $ {\mathit{\boldsymbol{L}}_b} = \left[ {\begin{array}{*{20}{c}} {\tilde \rho _{{1_o}}^k - f\left( {\mathit{\boldsymbol{X}}_1^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)}\\ {\tilde \rho _{{2_o}}^k - f\left( {\mathit{\boldsymbol{X}}_2^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)}\\ \vdots \\ {\tilde \rho _{{n_o}}^k - f\left( {\mathit{\boldsymbol{X}}_n^k - \mathit{\boldsymbol{X}}_{{{\rm{T}}_o}}^k} \right)} \end{array}} \right] $ | (20) |
该方案同样采用序贯最小二乘法求解水下多个应答器在各个阈值范围内的声线弯曲误差模型参数。
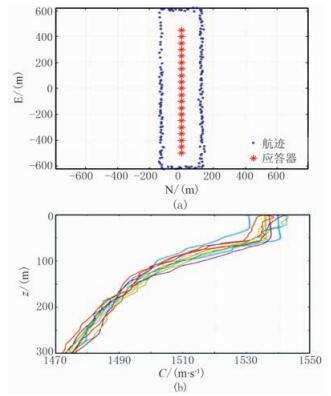
3 实验验证 3.1 仿真实验本文采用仿真实验验证新算法的有效性(图 2a)。在水深100m处分别布设20个应答器,相邻应答器的间距为50m,勘探船绕应答器进行走航式观测。
|
图 2 测量船和应答器位置(a)及300m水深声速剖面(b)示意图 |
由于整个测量过程时间较短,可认为观测期间声学环境未发生变化,结合图 2b声速剖面数据,采用射线声学跟踪方法正演观测时间。分别给应答器的定位坐标添加3cm的随机误差,声学测距的观测时间添加10ms的随机误差。入射角变化范围是40°~ 80°。
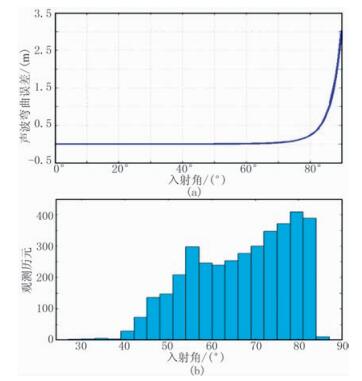
为严格论证本文提出模型的可靠性,研究了固定水深100m情况下的声线弯曲误差与入射角的直接关系,并统计了不同入射角的观测数据的分布直方图(图 3)。由图 3a中声线弯曲误差与入射角的关系知,当入射角大于65°时,声线弯曲误差会随着入射角的增大迅速增大,入射角为80°时,声线弯曲误差大约为0.2m。
|
图 3 声线弯曲误差与入射角的关系(a)及不同入射角对应的观测历元数直方图(b) |
采用以下六种方法解算20个应答器的坐标,并与坐标真值求差。六种方法分别是:最小二乘法,简写为LS(A);截止入射角为65°的最小二乘法,简写为LS(B);历元间单差法,简写为SD;设置截止入射角的无声速最小二乘方法,简写为US(A);基于声线弯曲参数化和模型化的两种新算法,分别简写为US(B)和US(M)。统计20个应答器N、E、U三方向的坐标均方根误差(RMS,表 1)。
|
|
表 1 六种方法解算应答器的定位精度 |
从表 1可看出,采用对称观测解算得到的应答器平面位置的定位精度优于垂直方向的精度。仅考虑声线弯曲情况下,六种方法都可得到厘米级的定位精度。LS(A)方法虽然采用了入射角大于65°的数据,但由于对称观测结构及最小二乘的均摊效应,声线弯曲误差得到一定的减弱。
LS(B)是处理声线弯曲误差相对简单的方法,实验中可看出该方法定位效果与未设截止入射角的LS(A)方法相近,主要原因是该方法将入射角大于65°的观测数据剔除掉,可用观测数减少了一半以上,此时观测值中虽然声线弯曲误差影响很小,但定位和测距的随机误差成为影响该方法定位精度的主要因素。因此在浅海声学二次定位中,往往需要利用这些大入射角数据。SD法解算结果较前两种方法有一定提高,该算法利用所有历元观测数据,并采用历元间差分的方式进行解算,可一定程度上削弱声线弯曲误差的影响。但是由于水深较浅,差分后观测方程的结构会变得不稳定,容易受随机误差的影响。
US(A)、US(B)和US(M)三种方法都不需要非常准确的声速剖面数据。从表 1可看出US(A)方法可得到与LS(B)相当的水平精度,但垂直方向上的精度受声速估计误差的影响,精度要低一些。US(B)方法和US(M)方法解算的结果明显优于其他四种方法,垂直方向上的定位精度甚至优于2cm,说明基于声线弯曲参数化和模型化的两种新算法都可以有效地减弱声线弯曲误差。
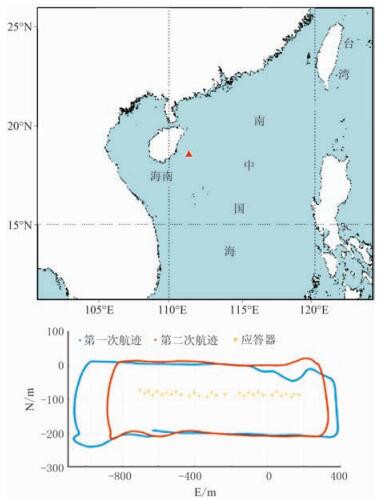
3.2 海上测试为研究浅海多目标定位算法的可靠性,笔者于2016年10月24日~11月7日在中国南海海域进行了海上实验测试(图 4)。本次实验搭乘东方地球物理公司勘探2号勘探船,船上搭载了电罗经、星站差分定位系统、测深仪、声速剖面仪及Sonardyne公司的OBC声学定位系统等。
|
图 4 实验区域以及勘探船轨迹和应答器位置 |
缆绳上间隔50m钩挂检波器和应答器,共30个。由于测量船离陆地较远,无法采用岸基网络RTK技术和RT-PPP技术导航定位,本次实验采用星站差分定位系统和电罗经对测量船进行导航。采用声速剖面仪测量测区声速,与时间相乘求得换能器与应答器之间距离。沉入海底的缆绳通常短时间内位置不变,实验中对该条缆绳上的应答器进行两次重复实验,采用不同解算方法下的坐标偏差验证定位精度。
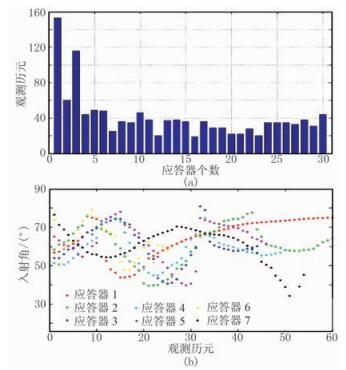
勘探船采用星站差分技术可得到优于20cm的平面定位精度。应答器的观测历元被统计记下来,如图 5a,每个应答器对应的观测历元平均约为40个。统计了7个应答器入射角随历元变化的情况。入射角约为60°,且其中相当多的观测数据的入射角大于65°。由于每个应答器对应的观测数据数目较少,因此仍然需要这部分大入射角数据。
|
图 5 应答器对应的观测历元数(a)及应答器入射角随历元的变化(b) |
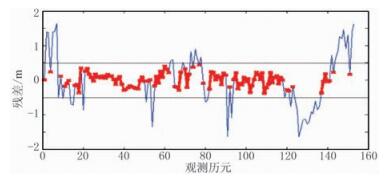
数据预处理阶段,初始坐标位置可用放缆船坐标近似代替,或采用观测方程历元间做差解算初始坐标,然后采用抗差估计的IGG3方案迭代解算应答器的坐标位置作为拟准应答器位置。一号应答器观测值残差如图 6所示,统计残差绝对值大于1的观测数据约占总观测数据的13%。
|
图 6 一号应答器抗差估计后残差分布情况 |
分别采用设置截止入射角的抗差估计(IGG3方案)、无声速模式设置截止入射角算法、无声速模式截止入射角序贯解、非序贯和序贯模式声线弯曲参数化等方法,解算上述30个应答器的坐标,并通过下式
| $ {E_{{\rm{MPB}}}} = \sum\limits_{i = 1}^n {{\rm{norm}}\left[ {\frac{{{{\left( {{x_1},{y_1},{z_1}} \right)}_i} - {{\left( {{x_2},{y_2},{z_2}} \right)}_i}}}{n}} \right]} $ | (21) |
统计其精度。式中:norm(·)表示向量求模运算;(x1, y1, z1)i和(x2, y2, z2)i为两次观测解算的第i个应答器坐标,可理解为单个应答器的平均定位精度。
如表 2,随着截止入射角增加,IGG3方案解算的平均定位精度提高,入射角在75°时定位精度最高到0.50m。由于单个应答器观测历元较少,采用无声速法解单个应答器定位精度要低于IGG3方案,定位精度最高为0.64m。声线弯曲参数法解算单应答器,受粗差以及偶然误差的影响非常明显,该方法定位效果并不理想。特别需要说明的是本文采用的无声速序贯模式优于有声速的方法,原因可能是测量时声速剖面仪数据与实际声速数据有差异导致。但序贯无声速法和序贯声线弯曲参数法解的定位效果优于非序贯解,各应答器所有历元的观测数据可参与计算平均声速以及声学弯曲参数,定位精度有明显的提高。声学弯曲参数法还考虑了大入射角声线弯曲的情况,定位精度高于无声速模型的序贯法。
|
|
表 2 五种方法解算应答器的平均定位精度(单位:m) |
声线弯曲是影响浅海多目标定位精度的重要因素。本文针对浅海石油勘探声学二次定位过程中声线弯曲误差对声学定位的影响进行研究。假设声线弯曲误差在短时间内仅与入射角有明显关系,设计了序贯式解法,采用所有观测历元解算声线弯曲参数,通过模型化和参数化解算声线弯曲误差的改正数,提高了水下应答器的解算精度。针对石油勘探过程中通常需投放大量声学应答器,声线弯曲是影响浅海多目标定位精度的重要因素。本文针对浅海石油勘探中声学二次定位过程中声线弯曲误差对声学定位影响进行了研究。基于声线弯曲误差在短时间内与入射角的关系进行建模和参数化,并采用序贯最小二乘求解模型参数,提高了水下应答器的解算精度。仿真和实测实验验证了新算法可有效提高水下多目标定位精度,由于缺乏长期稳定的声学观测资料(一天以上),声速随时间和入射角的变化对定位的影响还有待后续深入探究。
| [1] |
刘振武, 撒利明, 董世泰, 等. 中国石油物探技术现状与发展方向[J]. 石油科技论坛, 2015, 28(3): 21-29. LIU Zhenwu, SA Liming, DONG Shitai, et al. Present situation and development direction of petroleum exploration technology in China[J]. Oil Forum, 2015, 28(3): 21-29. |
| [2] |
金翔龙. 海洋地球物理研究与海底探测声学技术的发展[J]. 地球物理学进展, 2007, 22(4): 1243-1249. JIN Xianglong. The development of research in marine geophysies and acoustic technology for submarine exploration[J]. Progress in Geophysics, 2007, 22(4): 1243-1249. DOI:10.3969/j.issn.1004-2903.2007.04.034 |
| [3] |
程元方, 李素闪, 张文栋, 等. 海底电缆资料处理关键技术及其应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 26-31. CHENG Yuanfang, LI Sushan, ZHANG Wendong, et al. Key techniques for OBC data processing[J]. Oil Geophysical Prospecting, 2017, 52(S2): 26-31. |
| [4] |
方守川, 秦学彬, 任文静, 等. 基于多换能器的声学短基线海底电缆定位方法[J]. 石油地球物理勘探, 2014, 49(5): 825-828. FANG Shouchuan, QIN Xuebin, REN Wenjing, et al. Ocean buttom cable positioning based on multi-transducer short baseline acoustic method[J]. Oil Geophysical Prospecting, 2014, 49(5): 825-828. |
| [5] |
易昌华, 韩华, 方守川, 等. 海上地震勘探罗经鸟数据对拖缆空间位置的影响[J]. 石油地球物理勘探, 2015, 50(5): 809-814. YI Changhua, HAN Hua, FANG Shouchuan, et al. Compass data influence on towed streamer positioning in marine seismic[J]. Oil Geophysical Prospecting, 2015, 50(5): 809-814. |
| [6] |
易昌华, 任文静, 王钗. 二次水声定位系统误差分析[J]. 石油地球物理勘探, 2009, 44(2): 136-139. YI Changhua, REN Wenjing, WANG Chai. Analysis on error of secondary acoustic positioning system[J]. Oil Geophysical Prospecting, 2009, 44(2): 136-139. DOI:10.3321/j.issn:1000-7210.2009.02.003 |
| [7] |
赵爽, 王振杰, 吴绍玉, 等. 基于选权迭代的走航式水声差分定位方法[J]. 石油地球物理勘探, 2017, 52(6): 1137-1145. ZHAO Shuang, WANG Zhenjie, WU Shaoyu, et al. A ship-board acoustic difference positioning method based on selection weight iteration[J]. Oil Geophysical Prospecting, 2017, 52(6): 1137-1145. |
| [8] |
Zhao Shuang, Wang Zhenjie, He Kaifei, et al. Investi-gation on underwater positioning stochastic model based on acoustic ray incidence angle[J]. Applied Ocean Research, 2018, 77(8): 69-77. |
| [9] |
赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 湖北武汉: 武汉大学出版社, 2008.
|
| [10] |
Kido M, Osada Y, Fujimoto H. Temporal variation of sound speed in ocean:a comparison between GPS/acoustic and in situ measurements[J]. Earth, Planets and Space, 2008, 60(3): 229-234. DOI:10.1186/BF03352785 |
| [11] |
苏林, 马力, 宋文华, 等. 声速剖面对不同深度声源定位的影响[J]. 物理学报, 2015, 64(2): 24302-024302. SU Lin, MA Li, SONG Wenhua, et al. Influences of sound speed profile on the source localization of dif-ferent depths[J]. Acta Physica Sinica, 2015, 64(2): 24302-024302. |
| [12] |
王毅.石油勘探中水下高精度定位算法研究[D].山东青岛: 中国石油大学(华东), 2014. WANG Yi.Research on Algorithms of High-Precision Underwater Positioning in Petroleum Exploration[D].China University of Petroleum (East China), Qingdao, Shandong, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016750431.htm |
| [13] |
方守川.海底电缆地震勘探导航定位关键技术研究及系统研制[D].湖北武汉: 武汉大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015550338.htm
|
| [14] |
Xu P, Ando M, Tadokoro K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795-808. DOI:10.1186/BF03351859 |
| [15] |
Chen H H. Travel-time approximation of acoustic ranging in GPS/Acoustic seafloor geodesy[J]. Ocean Engineering, 2014, 84: 133-144. DOI:10.1016/j.oceaneng.2014.04.015 |
| [16] |
Yang F, Lu X, Li J, et al. Precise positioning of underwater static objects without sound speed profile[J]. Marine Geodesy, 2011, 34(2): 138-151. DOI:10.1080/01490419.2010.518501 |
| [17] |
Kido M. Detecting horizontal gradient of sound speed in ocean[J]. Earth, Planets and Space, 2007, 59(8): e33-e36. DOI:10.1186/BF03352027 |
| [18] |
Spiess F N, Chadwell C D, Hildebrand J A, et al. Precise GPS/Acoustic positioning of seafloor reference points for tectonic studies[J]. Physics of the Earth and Planetary Interiors, 1998, 108(2): 101-112. DOI:10.1016/S0031-9201(98)00089-2 |
| [19] |
Fujita M, Ishikawa T, Mochizuki M, et al. GPS/Acoustic seafloor geodetic observation:method of data analysis and its application[J]. Earth, Planets and Space, 2006, 58(3): 265-275. DOI:10.1186/BF03351923 |
| [20] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 湖北武汉: 武汉大学出版社, 2003.
|



 王振杰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
王振杰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: