地下介质的黏滞特性会导致地震波能量耗散、相位畸变、地震剖面分辨率降低。基于品质因子Q与频率无关或随频率变化弱的假设[1-2],一般采用反Q滤波[3-5]或黏声波方程叠前深度偏移[6-7]两种方法进行衰减补偿。对叠后剖面应用反Q滤波时,没有考虑地震波真实的传播路径,补偿精度不能得到保证;叠前深度偏移在波场延拓中利用黏声波动方程模拟地震波的传播,精度高但层Q模型求取十分困难。
关于Q值的求取,前人已做了大量研究[8-12]。常用谱比法和频移法基于VSP数据求取地层的Q值,但对于地面地震而言,受薄互层调谐效应及资料信噪比影响,Q值求取精度仍需进一步提高。在利用地震数据与井数据联合求取Q上,业界也有不少尝试,但在两种数据生成的Q值标定融合方面没有形成统一的认识与标准。
对于横向速度变化不是很剧烈的复杂构造,叠前时间偏移是一种有效的成像方法。成像过程中偏移孔径直接影响叠前时间偏移的信噪比,偏移孔径过小,成像信噪比较高,但大倾角构造面临成像不足的风险;过大的偏移孔径可以保证陡倾构造成像但是增加了偏移噪声和计算量。
通常偏移孔径是根据地层倾角估算的,但在成像前获取准确的地层倾角十分困难。基于地层倾角与偏移孔径的关系,很多学者利用地层倾角约束偏移孔径,进而达到改善成像质量的目的。一般采用倾角扫描的方式获取地下地层倾角,如果扫描时窗内有多个同相轴,且每个同相轴对应的倾角不同,则扫描结果会出现不稳定的现象。此外倾角扫描对数据的信噪比也有一定要求,信噪比较低扫描结果误差较大。有的学者利用地震波的传播路径计算地震反射倾角,但通过计算方式直接获取地层倾角的研究目前较少[13-17]。
为了提高叠前时间偏移成像的计算效率,很多学者将目光转向了GPU技术。李博等[18]将非对称旅行时叠前时间偏移方法移植到了GPU平台,取得了较好的加速效果;李肯立等[19]利用GPU对叠前时间偏移进行了移植和效率测试;马召贵等[20]利用GPU技术对Kirchhoff叠前时间偏移进行了优化,计算效率明显提升。与常规叠前时间偏移不同,衰减补偿的叠前时间偏移需要在频率域完成每个频率点的补偿,计算量巨大,因此GPU加速对衰减补偿叠前时间偏移尤为重要。
本文通过引入等效Q参数实现衰减补偿叠前时间偏移,并针对现有技术求取Q场存在的弊端、偏移孔径难以确定及偏移方法效率低的难题,给出了针对性的解决方案。在Q场建模方面,通过VSP资料与地面反射地震资料联合应用求取Q值,并基于衰减合成地震记录与井旁地震道的匹配情况判断Q值是否合理;在压制偏移噪声方面,通过孔径自适应改变,有效压制偏移噪声;在提高计算效率方面,采用GPU加速,有效解决了频率域吸收补偿叠前时间偏移计算效率低的问题。
1 方法原理 1.1 井震联合求取Q场由于在实际生产中不可能通过岩心样本得到所有地层的真实Q值,对Q值的合理性判断也就缺乏客观标准,因此根据Q值的应用目的选取判断标准更具有现实意义。如果Q是用于黏滞介质叠前时间偏移补偿地震波衰减,那么Q值的选取应由井上的衰减合成地震记录与井旁原始地震道是否匹配来决定。也有学者基于“衰减补偿”模式,即通过不同Q值的补偿结果与无衰减合成地震记录是否匹配判断Q值的合理性,但对于中深层低信噪比地震数据,为了压制高频补偿噪声而经常使用的增益控制因子对频带与振幅增益都做了限制,导致中深层补偿效果较差,与合成地震记录匹配效果差,直接影响了中深层Q值的选取[12]。本文利用井上衰减合成地震记录与井旁原始地震道匹配效果,选择合理的Q值,运算过程没有用到增益控制因子,从根本上避免了上述问题的出现。
为了方便研究,引入了等效Q值的概念[21-22],并假定地下某点的吸收只与该点的等效Q值有关,而不受上覆地层吸收的影响。等效Q值的定义为
| $ \frac{1}{{{Q_{{\rm{eff}}}}}} = \frac{1}{T}\sum\limits_{i = 1}^n {\frac{{\Delta {T_i}}}{{{Q_i}}}} $ | (1) |
式中:T代表地震波垂直单程旅行时;ΔTi为地震波在第i层内垂直单程旅行时;Qi为第i层的Q值;n为地层层数。
利用VSP数据与地面地震数据联合求取Q值的思路是:首先利用VSP数据求取Q值,然后以该Q值作为初始值,生成衰减合成地震记录,并根据该合成地震记录与井旁道原始地震数据匹配情况调整优化Q值,然后采用对数谱比求导算法求取地震数据的Q值,最后将两种Q值标定融合得到整个工区的Q值。
通过分析VSP数据直达波的频率与振幅属性,采用质心频移法[21]计算Q值
| $ {Q_{{\rm{well}}}} = \frac{{{\rm{ \mathsf{ π} }}\tau {\sigma ^2}}}{{{f_{{\rm{shot}}}} - {f_{{\rm{geo}}}}}} $ | (2) |
式中:τ为地震波在地层内的传播时间;σ2是震源子波方差;fshot和fgeo分别是炮、检点地震波主频。
衰减合成记录的生成分为两步:首先利用雷克子波生成不考虑衰减的常规合成记录,在确定子波主频时,可以根据浅层地震数据的主频及目的层对分辨率的需求联合确定;然后基于VSP数据生成的Q值,利用正Q滤波算法对该合成记录进行处理,得到了考虑衰减的合成记录,其中VSP生成的Q值在纵向上是连续变化的,不是一个常数。上述合成记录生成方法的特点是雷克子波主频在时间方向不发生变化,而通过Q值的变化描述地震波的衰减。另外还可以通过主频时变的雷克子波直接生成吸收衰减合成记录,但面临着主频不易准确求取的巨大困难,因此不建议使用该方法。
根据衰减合成记录与井旁道原始地震数据的相关性开展局部Q值优化与调整,并迭代更新吸收衰减合成记录,再次进行相关性计算,直至衰减合成记录与井旁道原始地震数据达到最佳相关时停止迭代计算。
在利用地面地震数据求取Q值时,采用了对数谱比求导的计算方法[22],与常规对数谱比法相比,该方法克服了地震数据的薄层调谐效应的不利影响。首先采用Q扫描方法对参考点(假设没有衰减)的地震记录进行衰减,每个Q对应的时域波形短时傅里叶变换模为FQ(ω),地下样本点对应的时域波形短时傅里叶变换模为F(ω),则谱比频率导数指标为
| $ \delta = \sum\limits_\omega {\frac{{\rm{d}}}{{{\rm{d}}\omega }}\left[ {\ln F\left( \omega \right) - \ln {F_{\rm{Q}}}\left( \omega \right)} \right]} $ | (3) |
当δ绝对值为零或最小时,表明FQ(ω)与F(ω)最接近,便认为对应的Q是最合理的。这种Q值求取方法与以往相比有一定改进与不同[11]。前人是对地下样本点进行“Q扫描+衰减补偿”处理,需要对叠前数据进行多轮次成像,计算量大,又由于增益控制因子的作用,低信噪比数据Q值求取稳定性差,另外在求取Q值过程中没有用到井信息,只利用了单一的叠前地震数据。而本文方法只对参考点进行“Q扫描+衰减”处理,对于叠后地震剖面而言,参考点选取若干即可,计算量大大降低。虽然该方法是在叠后开展的,但基于地震资料求取的Q值在空间上的趋势是有保证的,最后利用VSP数据计算的Q值对地面地震数据生成的Q场进行标定融合,从而又保证了Q值的数值精度。
1.2 衰减补偿叠前时间偏移与常规Kirchhoff积分法叠前时间偏移不同,衰减补偿叠前时间偏移不仅考虑了波场走时和球面扩散效应,还考虑了地震波传播时的吸收效应。
本文假设Q值与频率无关或随频率缓慢变化。单道地震数据在频率域可用f(ω)表示,基于深度偏移的相移法,检波点波场的深度延拓可表示为
| $ \begin{array}{l} P\left( {{k_x},\omega ,z + \Delta z} \right) = P\left( {{k_x},\omega ,z} \right)\exp \left( { - {\rm{i}}{k_z}\Delta z} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f\left( \omega \right)\exp \left( { - {\rm{i}}{k_z}\Delta z} \right) \end{array} $ | (4) |
将频散关系
| $ {k_z} = \sqrt {{{\left[ {\frac{\omega }{{c\left( \omega \right)}}} \right]}^2} - k_x^2} $ | (5) |
代入式(4),有
| $ \begin{array}{l} P\left( {{k_x},\omega ,z + \Delta z} \right)\\ \;\;\;\;\;\;\; = f\left( \omega \right)\exp \left\{ { - {\rm{i}}\Delta z\sqrt {{{\left[ {\frac{\omega }{{c\left( \omega \right)}}} \right]}^2} - k_x^2} } \right\} \end{array} $ | (6) |
式中c(ω)为复速度,与实速度v(ω)关系为
| $ \left\{ \begin{array}{l} \frac{1}{{c\left( \omega \right)}} = \frac{1}{{v\left( \omega \right)}}\left( {1 - \frac{{\rm{i}}}{{2Q}}} \right)\\ v\left( \omega \right) = v\left( {{\omega _{\rm{c}}}} \right)\left( {1 + \frac{1}{{{\rm{ \mathsf{ π} }}Q}}\ln \frac{\omega }{{{\omega _{\rm{c}}}}}} \right) \end{array} \right. $ | (7) |
其中ωc为高截频。当频率趋向于ωc时,实速度v(ω)将趋近于常值,本文用主频ω0代替高截频ωc,因为主频对应的实速度更容易获得。经过变换消去ωc项,并代入式(7),可得
| $ \frac{1}{{c\left( \omega \right)}} = \frac{1}{v}\left( {1 - \frac{{\rm{i}}}{{2Q}}} \right)\left( {1 - \frac{1}{{{\rm{ \mathsf{ π} }}Q}}\ln \frac{\omega }{{{\omega _{\rm{c}}}}}} \right) $ | (8) |
将式(8)代入式(6),简化可得
| $ \begin{array}{l} P\left( {{k_x},\omega ,z + \Delta z} \right)\\ \approx f\left( \omega \right)\exp \left[ { - \frac{{{\rm{i}}\omega \Delta z}}{v}\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}Q}}\ln \frac{\omega }{{{\omega _0}}} - {{\left( {\frac{v}{\omega }} \right)}^2}k_x^2 - \frac{{\rm{i}}}{Q}} } \right] \end{array} $ | (9) |
式中舍去了Q的高阶项。用ΔTi替换Δz,将波场从地表(z=0)处向下延拓至
| $ \begin{array}{l} P\left( {{k_x},\omega ,T} \right) \approx f\left( \omega \right) \times \\ \;\;\exp \left[ { - {\rm{i}}\omega \sum\limits_{i = 1}^n {\Delta {T_i}\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_i}}}\ln \frac{\omega }{{{\omega _0}}} - {{\left( {\frac{{{v_i}}}{\omega }} \right)}^2}k_x^2 - \frac{{\rm{i}}}{{{Q_i}}}} } } \right] \end{array} $ | (10) |
式中:vi为第i层主频对应的实速度;ΔTi=Δzi/vi。定义等效速度为
| $ {v_{{\rm{rms}}}} = \sqrt {\frac{1}{T}\sum\limits_{i = 1}^n {v_i^2\Delta {T_i}} } $ | (11) |
根据式(1)和式(11),有
| $ \begin{array}{l} \sum\limits_{i = 1}^n {\Delta {T_i}\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_i}}}\ln \frac{\omega }{{{\omega _0}}} - {{\left( {\frac{{{v_i}}}{\omega }} \right)}^2}k_x^2 - \frac{{\rm{i}}}{{{Q_i}}}} } \\ \;\;\; \approx T\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}} - {{\left( {\frac{{{v_{{\rm{rms}}}}}}{\omega }} \right)}^2}k_x^2 - \frac{{\rm{i}}}{{{Q_{{\rm{eff}}}}}}} - \\ \;\;\;\;\;\;\frac{{{\rm{i}}T}}{{2{Q_{{\rm{eff}}}}\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}} - {{\left( {\frac{{{v_{{\rm{rms}}}}}}{\omega }} \right)}^2}k_x^2} }} \end{array} $ | (12) |
将式(12)代入式(10),做空间逆傅里叶变换,可得
| $ \begin{array}{l} P\left( {x,\omega ,T} \right) \approx \frac{\omega }{{2{\rm{ \mathsf{ π} }}}}\int {f\left( \omega \right)} \times \\ \;\;\;\exp \left[ {{\rm{i}}\omega \left( {T\sqrt {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}} - v_{{\rm{rms}}}^2p_x^2} + {p_x}x} \right)} \right] \times \\ \;\;\;\exp \left[ {\frac{{\omega t}}{{2{Q_{{\rm{eff}}}}}}{{\left( {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}} - v_{{\rm{rms}}}^2p_x^2} \right)}^{ - \frac{1}{2}}}} \right]{\rm{d}}{p_x} \end{array} $ | (13) |
式中px=kx/ω为x方向的射线参数。应用稳相点原理求得上式渐近解[23]
| $ \begin{array}{*{20}{c}} {P\left( {x,\omega ,T} \right) = f\left( \omega \right)\sqrt \omega \exp \left( { - \frac{{{\rm{i \mathsf{ π} }}}}{4}} \right)\frac{T}{{\tau _g^2v_{{\rm{rms}}}^2}} \times }\\ {\exp \left[ {{\rm{i}}\omega {\tau _g}\left( {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}}} \right)} \right]\exp \left( {\frac{{\omega {\tau _{\rm{g}}}}}{{2{Q_{{\rm{eff}}}}}}} \right)} \end{array} $ | (14) |
上式为检波点到成像深度的反向传播表达式。同样可得炮点到成像深度点的正向传播波场
| $ \begin{array}{l} {P^{\rm{D}}}\left( {x,\omega ,T} \right) = S\left( \omega \right)\sqrt \omega \exp \left( {\frac{{{\rm{i \mathsf{ π} }}}}{4}} \right)\frac{T}{{\tau _g^2v_{{\rm{rms}}}^2}} \times \\ \;\;\;\;\exp \left[ { - {\rm{i}}\omega {\tau _g}\left( {1 - \frac{2}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}}} \right)} \right]\exp \left( { - \frac{{\omega {\tau _{\rm{s}}}}}{{2{Q_{{\rm{eff}}}}}}} \right) \end{array} $ | (15) |
式中:S(ω)是震源子波的傅里叶变换;τg、τs分别为地震波从成像深度到检波点的旅行时和炮点到成像深度的旅行时。因为反褶积可以消除子波的影响,因此忽略上式中的S(ω)
| $ \begin{array}{l} I\left( {x,T} \right) = \frac{{{\tau _{\rm{s}}}}}{{{\tau _{\rm{g}}}}}\int {f\left( \omega \right)\sqrt \omega \exp \left( { - \frac{{{\rm{i \mathsf{ π} }}}}{4}} \right)} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {{\rm{i}}\omega \left( {{\tau _{\rm{s}}} + {\tau _{\rm{g}}}} \right)\left( {1 - \frac{1}{{{\rm{ \mathsf{ π} }}{Q_{{\rm{eff}}}}}}\ln \frac{\omega }{{{\omega _0}}}} \right)} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ {\frac{{\omega \left( {{\tau _{\rm{s}}} + {\tau _{\rm{g}}}} \right)}}{{2{Q_{{\rm{eff}}}}}}} \right]{\rm{d}}\omega \end{array} $ | (16) |
将成像点所有的成像结果进行累加便可得到黏滞介质中衰减补偿叠前时间偏移的成像结果[24]。
1.3 倾角域自适应偏移孔径偏移孔径是影响叠前时间偏移成像信噪比的重要因素,但实际应用中,受限于偏移算法,通常采用统一的偏移孔径。由于地层倾角是空变的,对某一成像点适合的孔径,对另一成像点就可能过大或过小。为了解决这个难题,本文采用倾角自适应的偏移孔径。
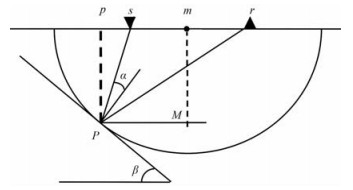
本文采用输入道的方式实现衰减补偿叠前时间偏移,可以根据地层倾角确定偏移脉冲响应在任一成像深度偏移孔径的范围,这种成像方式使偏移孔径时变与空变成为可能。根据图 1,以下关系成立
| $ \tan \left( {\beta + \alpha } \right) = \frac{{L + h}}{{{v_{{\rm{rms}}}}t}} $ | (17) |
| $ \tan \left( {\beta - \alpha } \right) = \frac{{L - h}}{{{v_{{\rm{rms}}}}t}} $ | (18) |
|
图 1 偏移孔径与地层倾角的关系 m为炮点s与接收点r的中点,设定输入地震数据的半炮检距为h,β为深度t处的地层倾角,P为深度t处最远成像道对应的成像点,p为成像点P在地面的投影,M为过点m的垂线与过P点的水平线的交点,α是地震波在成像点处的最大入射角 |
式中:t是成像点对应的时间深度,为单程旅行时;L为点M与点P之间的水平距离,也是时间深度t处地层倾角β对应的偏移孔径。联立式(17)与式(18),求解可得
| $ L = \frac{{{v_{{\rm{rms}}}}t\left( {{{\tan }^2}\beta - 1} \right) + \sqrt {v_{{\rm{rms}}}^2{t^2}\left( {1 + {{\tan }^2}\beta } \right) + 4{h^2}{{\tan }^2}\beta } }}{{2\tan \beta }} $ | (19) |
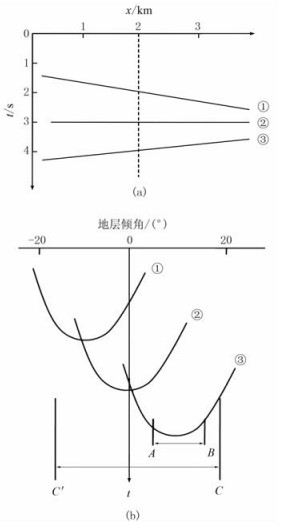
由上式可以看出,当vrms、t、h三个参数固定时,偏移孔径L随着地层倾角的增大而增大。图 2a是一个四层地质模型[13],其中①和③表示两个倾斜界面,②为一个水平界面;图 2b为该地质模型数据对应的倾角成像道集,其中①、②与③分别代表三个同相轴,与图 2a中的界面编号一一对应。在倾角成像道集上,界面③的拟双曲线顶点对应的角度便是真实地层倾角,可以确定倾角成像区为[A,B],而常规方法为了实现构造的正确成像,偏移孔径[C,C′]过大而不够精确,引入了额外的偏移噪声,降低了地震数据的成像品质。
|
图 2 地质模型(a)及其对应的倾角成像道集(b) |
吸收衰减补偿的叠前时间偏移计算步骤如下:
(1) 常规预处理;
(2) 在炮检距初叠剖面上选取若干CDP样本;
(3) 生成样本CDP对应的倾角成像道集,并确定样本CDP对应的倾角成像区;
(4) 利用样本CDP对应的倾角成像区插值出所有CDP对应的倾角成像区;
(5) 在CDP对应的倾角成像区内,对叠前数据进行衰减补偿成像处理;
(6) 重复步骤(5),得到所有CDP最终的成像结果。
与常规叠前时间偏移事先将不同炮检距组对应的偏移孔径计算出来不同,文中给出的叠前时间偏移方法无需事先计算孔径,只需对倾角成像区内的地震数据进行补偿成像即可,在保证构造正确成像的同时,最大限度地压制了偏移噪声。另外实际成像计算区域与常规孔径对应区域相比有明显减少,计算效率也得到了一定提高。
与常规叠前时间偏移相比,衰减补偿叠前时间偏移最大的不同在于成像时根据Q值及地震走时逐频率点进行衰减补偿,计算量巨大,计算效率低。
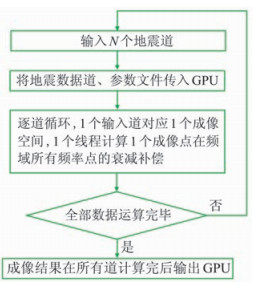
1.4.2 GPU加速实现业界对利用GPU进行加速的研究已经十分成熟,GPU的加速性能体现在单个GPU设备有很多计算核心,并且可以同时发起多个计算线程,而单个CPU设备则不具备。对于叠前衰减补偿时间偏移而言,实现GPU加速,需要在计算热点、计算粒度与存储等方面重点考虑。
GPU设备适合并行非逻辑性运算,比如常规的加减乘除,而选择、判断等逻辑运算更适合用CPU设备去处理,因此利用GPU设备实现程序加速,不是简单的将程序加载到GPU设备上运算,而是将程序中计算量最大、耗时最长的部分,在这里称之为计算热点,放到GPU设备上进行加速,因此计算热点的选取直接决定了整体的加速效果。本文将频率点的衰减补偿运算作为计算热点,这是因为每个成像点都要在有效频带内逐频点做衰减补偿运算,计算量与耗时在整个程序中是最大的,并且各频率点的运算互不影响,没有先后顺序,更适合并行运算。计算粒度是用来描述计算单元大小的指标,一个线程可以计算一个频率点的衰减补偿,也可以计算整个成像空间所有频率点的衰减补偿,本文将前者称之为细粒度计算,后者称之为粗粒度计算。在细粒度计算中,线程并发量很大,每个线程的计算量却很小,线程的数据读取与交换用时比有效计算时间要大得多,总体加速效果不理想。在粗粒度计算中,线程的并发量太小,GPU中处于计算激活状态的单元少,设备中很多计算单元没有充分利用起来,负载率低,最终的加速效果也不好。借鉴这两种计算粒度的不足,本文对成像空间进行区块划分,每个线程只负责单个成像点的衰减补偿运算,既兼顾了线程计算量,又考虑了GPU的线程并发量,可以获得最佳的加速效果。
衰减补偿的叠前时间偏移在成像过程中需要叠加速度场、地层倾角及Qeff场等参数文件,对存储空间需求较大,每一个成像点计算时都需要读取这些信息,访问量大,访问频率高。虽然GPU上存储器种类多,但存储能力相差较大,本文将这些参数文件放于存储速度较慢但空间较大的全局存储器上。一般情况下,稳定性增益控制函数是采用表驱动的方式进行运算的,事先将补偿值计算出来存于表中,在频率点补偿运算时,直接从表中读取相应的补偿值,避免了大量重复运算,这种存储换计算的策略应用在CPU上时,对计算效率提高贡献很大,但在GPU上时,会出现存储读取问题。该补偿表占用内存空间较大,运算时所有并发线程会同时从补偿表中读取补偿值,进而出现多个线程排队读取同一位置数值的情况,给计算效率带来了不利影响。针对该问题,稳定性增益函数不再采用表驱动的方式,而是以补偿因子的形式实时参与运算,这种策略表面上增大了线程计算量,但避免了多线程排队读取内存的问题,整体计算效率仍有大幅提高。
基于上述计算策略,实现了基于GPU计算架构的叠前衰减补偿时间偏移(图 3),与只采用CPU相比,计算效率提高了40倍左右,加速效果十分明显。
|
图 3 GPU计算架构 |
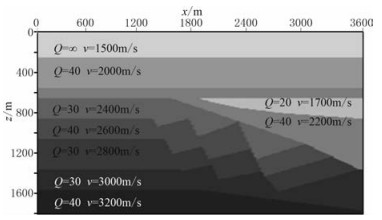
图 4为二维黏弹模型。基于双程黏性声波方程利用频率域有限差分方法模拟地震数据,共51炮,炮点位置从447.75m移动到3147.75m,炮点距为54m。每炮有200道,道间距为18m。
|
图 4 二维模型 |
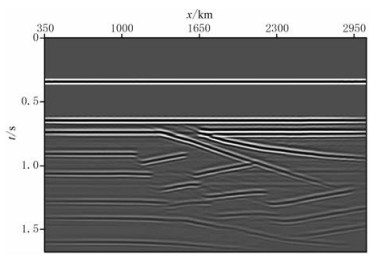
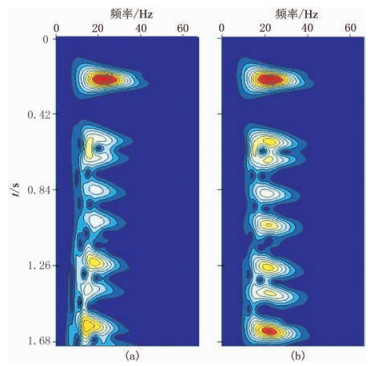
图 5为模拟数据常规叠前时间偏移剖面,应用了增益显示。图 6为衰减补偿叠前时间偏移剖面。对比图 5、图 6可知,二者都可以得到正确的成像结果,但图 6的成像结果分辨率更高。图 7为x=690m处单道偏移结果的时频谱对比,可以看出,衰减补偿偏移剖面频带宽度从浅到深一致,然而常规偏移剖面的频带却随着深度的增加逐渐变窄。

|
图 5 常规叠前时间偏移剖面 |
|
图 6 衰减补偿叠前时间偏移剖面 |
|
图 7 x=690m处常规(a)和衰减补偿(b)叠前时间偏移单道时频谱对比 |
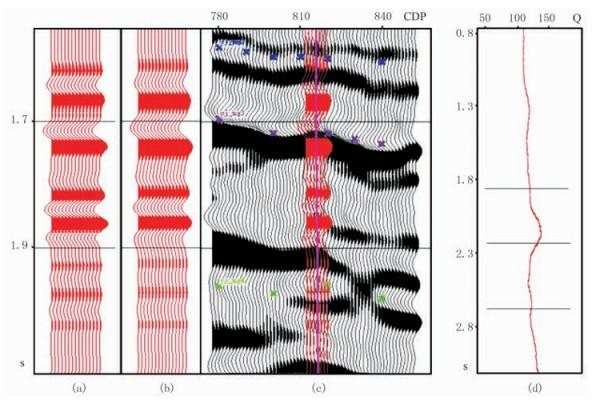
南堡凹陷老爷庙火成岩分布广泛,导致中深层地震信号能量衰减严重[25]。首先利用雷克子波生成了不考虑衰减效应的常规合成记录(图 8a);然后基于VSP数据求取的Q值,利用正Q滤波算法对该合成记录进行处理,得到考虑衰减效应的合成记录(图 8b),将该衰减合成记录与井旁道原始地震数据叠合显示(图 8c),根据二者的匹配结果对VSP生成的Q值进行局部优化与调整(图 8d),并迭代更新衰减合成记录,直至吸收衰减合成记录与井旁道原始地震数据达到最佳匹配。
|
图 8 Q值求取过程 (a)常规合成记录;(b)衰减合成记录;(c)衰减合成记录与地震剖面的标定结果;(d)优化调整后的Q值曲线 |
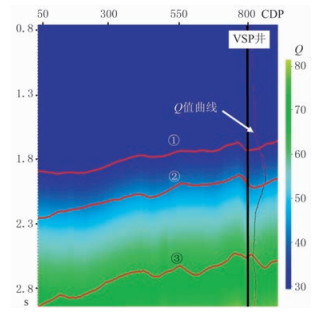
对工区内其他VSP数据重复该过程,最后利用所有优化调整后的Q值去标定地震数据求取的Q场,得到全工区的Q场(图 9)。根据地层分布与Q值的数值结构,将Q值曲线划分为三层(图 8d上①、②、③标识的横线),可以对地震数据求取的Q场起到层控约束作用(图 9上①、②、③标识的层控约束线)。
|
图 9 地震资料求取的Q场VSP标定结果 |
基于井震联合方法求取的Q场,应用衰减补偿叠前时间偏移方法对老爷庙实际数据进行成像,并与常规叠前时间偏移及其反Q滤波结果进行对比(图 10)。反Q滤波没有考虑地震波实际的传播路径,对中高频信号成分的补偿力度要明显高于低频信号,这就会造成低频信号的相对丢失。另外有效信息的恢复完全取决于输入的叠后数据,并没有在补偿过程中引入新的信息。本文方法在成像过程中对不同传播路径的地震信号进行了相应补偿,有效恢复了地震信号的高频能量信息,拓宽了有效频带,改善了地震数据整体的频谱形态,因此在偏移剖面上地质信息变得更加真实丰富。另外衰减补偿叠前时间偏移剖面的信噪比较高,偏移噪声与补偿噪声均被控制在一个较低水平。

|
图 10 常规叠前时间偏移剖面(a)及其反Q滤波结果(b)与衰减补偿叠前时间偏移剖面(c)对比 |
图 11是图 10中矩形框局部放大,可以看出衰减补偿叠前时间偏移剖面在成像效果上改善较大,细节信息明显增多。图 12是三者的频谱对比,衰减补偿叠前时间偏移剖面的频谱信息更加丰富,低频与高频信息均得到了有效拓展,而反Q滤波后虽然高频信息得到一定恢复,但低频信息有所损失,有效频带拓宽能力不如本文方法。
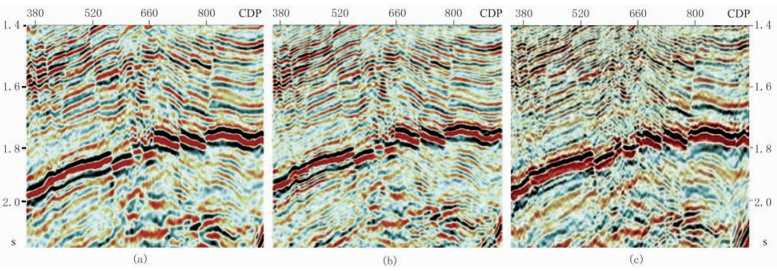
|
图 11 常规叠前时间偏移剖面(a)及其反Q滤波结果(b)与衰减补偿叠前时间偏移剖面(c)局部细节对比 |

|
图 12 常规叠前时间偏移剖面(蓝色)及其反Q滤波结果(绿色)与衰减补偿叠前时间偏移剖面(红色)的频谱对比 |
本文提出的衰减补偿叠前时间偏移方法,可以在叠前偏移中沿波场传播路径补偿黏性介质的吸收效应,提高地震分辨率,且偏移前道集预处理与常规偏移方法一致,可以方便地融入现有处理技术流程。在Q场建模、压制偏移噪声和提高计算效率方面,均采用了针对性的技术策略。通过模型数据验证了方法的有效性与可行性。对于实际数据应用本文方法得到了分辨率更高、成像更清晰的剖面,与常规叠前时间偏移剖面及其反Q滤波结果相比,波组特征更好、地质信息更加丰富,因此本文方法在中深层信号衰减强烈且信噪比较低的地区有着广阔的应用前景。对于Q场的求取,虽然文中给出了一套切实可行的解决方案,但Q的精度依然有较大提升空间,这将是下一步研究的重点。
| [1] |
Futterman W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [2] |
Kjartansson E. Constant Q wave propagation and attenuation[J]. Journal of Geophysics Research, 1979, 84(1): 4737-4748. |
| [3] |
Hargreaves N D, Calvert A J. Inverse Q filtering by fourier transform[J]. Geophysics, 1991, 56(1): 519-527. |
| [4] |
Wang Y. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(1): 657-663. |
| [5] |
陈增保, 陈小宏, 李景叶, 等. 一种带限稳定的反Q滤波算法[J]. 石油地球物理勘探, 2014, 49(1): 68-74. CHEN Zengbao, CHEN Xiaohong, LI Jingye, et al. A band-limited and robust inverse Q filtering algorithm[J]. Oil Geophysical Prospecting, 2014, 49(1): 68-74. |
| [6] |
Mittet R, Sollie R, Hokstak K. Prestack depth migration with compensation for absorption and dispersion[J]. Geophysics, 1995, 60(1): 1485-1494. |
| [7] |
Zhang J, Wapenaar K. Wavefield extrapolation and prestack depth migration in anelastic inhomogeneous media[J]. Geophysics Prospecting, 2002, 50(1): 629-643. |
| [8] |
Tonn R. The determination of the seismic quality factor Q from VSP data:A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/gpr.1991.39.issue-1 |
| [9] |
Quan Y, Harris J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(1): 895-905. |
| [10] |
Xin K, Hung B.3-D tomographic Q inversion for compensation frequency dependent attenuation and dispersion[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 4014-4017. http://library.seg.org/doi/abs/10.1190/1.3255707
|
| [11] |
Zhang C, Ulrych T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(1): 1542-1547. |
| [12] |
Zhang J F, Wu J Z, and Li X Y. Compensation for absorption and dispersion in prestack migration:An effective Q approach[J]. Geophysics, 2013, 78(1): 1-14. |
| [13] |
吴吉忠, 刘成权, 张建坤, 等. 倾角域自适应孔径叠前时间偏移[J]. 石油地球物理勘探, 2017, 52(3): 502-508. WU Jizhong, LIU Chengquan, ZHANG Jiankun, et al. Adaptive aperture prestack time migration in the dip angle domain[J]. Oil Geophysical Prospecting, 2017, 52(3): 502-508. |
| [14] |
Klokov A, Fomel S.Optimal migration aperture for conflicting dips[C]. SEG Technical Program Expan-ded Abstracts, 2012, 31: 504-507.
|
| [15] |
陈志德, 初海红. 黏滞介质吸收补偿叠前时间偏移的倾角道集孔径优选[J]. 石油地球物理勘探, 2016, 51(3): 444-451. CHEN Zhide, CHU Haihong. Optimization of vari-able migration aperture in dip angle gathers for pre-stack time migration with absorption compensation in viscous elastic media[J]. Oil Geophysical Prospecting, 2016, 51(3): 444-451. |
| [16] |
Audebert F, Froidevaux P, Racotoarisoa H, et al.Insights into migration in the angle domain[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1188-1191. https://www.onepetro.org/conference-paper/SEG-2002-1188
|
| [17] |
刘和年, 王建立, 吴蕾, 等. 地层倾角约束自适应孔径叠前时间偏移[J]. 石油地球物理勘探, 2014, 49(5): 899-903. LIU Henian, WANG Jianli, WU Lei, et al. Adaptive aperture prestack time migration with dip constrain[J]. Oil Geophysical Prospecting, 2014, 49(5): 899-903. |
| [18] |
李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法[J]. 地球物理学报, 2009, 52(1): 245-252. LI Bo, LIU Guofeng, LIU Hong. A method of using GPU to accelerate seismic pre-stack time migration[J]. Chinese Journal of Geophysics, 2009, 52(1): 245-252. |
| [19] |
李肯立, 彭俊杰, 周仕勇. 基于CUDA的Kirchhoff叠前时间偏移算法设计与实现[J]. 计算机应用研究, 2009, 26(12): 4474-4477. LI Kenli, PENG Junjie, ZHOU Shiyong. Implement Kirchhoff prestack time migration algorithm on CUDA architecture[J]. Application Research of Compu-ters, 2009, 26(12): 4474-4477. DOI:10.3969/j.issn.1001-3695.2009.12.020 |
| [20] |
马召贵, 赵改善, 武港山, 等. Kirchhoff叠前时间偏移的GPU移植与性能优化技术[J]. 石油学报, 2014, 35(4): 700-705. MA Zhaogui, ZHAO Gaishan, WU Gangshan, et al. GPU-based porting and optimization of Kirchhoff pre-stack time migration[J]. Acta Petrolei Sinica, 2014, 35(4): 700-705. |
| [21] |
陈志德, 赵忠华, 王成. 黏滞声学介质地震波吸收补偿叠前时间偏移方法[J]. 石油地球物理勘探, 2016, 51(2): 325-333. CHEN Zhide, ZHAO Zhonghua, WANG Cheng. Prestack time migration with compensation for absorption of viscous-elastic media[J]. Oil Geophysical Prospecting, 2016, 51(2): 325-333. |
| [22] |
吴吉忠, 杨晓利, 龙洋. 一种稳定高效的等效Q值反Q滤波算法及应用[J]. 石油地球物理勘探, 2016, 51(1): 63-70. WU Jizhong, YANG Xiaoli, LONG Yang. A roubust approach of inverse Q filtering with equivalent Q[J]. Oil Geophysical Prospecting, 2016, 51(1): 63-70. |
| [23] |
Bleistein N, Cohen J K, Stockwell J W. Mathematics of Multidimensional Seismic Inversion[M]. Springer, 2001.
|
| [24] |
卢宝坤, 张剑锋, 蒲泊伶. 角度域叠前时间偏移:非均匀介质中的单程波方法[J]. 地球物理学报, 2012, 55(11): 3795-3804. LU Baokun, ZHANG Jianfeng, PU Boling. Pre-stack time migration in angle domain:a one-way propagator approach in inhomogeneous media[J]. Chinese Journal of Geophysics, 2012, 55(11): 3795-3804. DOI:10.6038/j.issn.0001-5733.2012.11.026 |
| [25] |
吴吉忠, 李君, 石文武. 南堡1号构造火成岩发育区稳健保幅处理技术[J]. 石油地球物理勘探, 2017, 52(增刊1): 1-9. WU Jizhong, LI Jun, SHI Wenwu. Robust amplitude-preserving processing strategy for well-developed igneous rocks in the structure Nanpu 1[J]. Oil Geophysical Prospecting, 2017, 52(S1): 1-9. |



 吴吉忠, 河北省唐山市新华西道101号冀东油田勘探开发研究院物探一室, 063004。Email:
吴吉忠, 河北省唐山市新华西道101号冀东油田勘探开发研究院物探一室, 063004。Email: