② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
③ 北京大学地球与空间科学学院石油与天然气研究中心, 北京 100871
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ Institute of Oil & Gas, School of Earth and Space Sciences, Peking University, Beijing 100871, China
储层孔隙中含有油气水等流体,会引起地震波传播过程中的强振幅衰减和相位畸变[1],从而导致传统的声波或者弹性波偏移方法分辨率降低或者失效。关于地震波在黏弹性介质中的传播机理,主要有Maxwell模型、Kelvin-Vogit模型、标准线性固体、广义标准线性体、分数阶常Q模型等[2-6]。早期的地震资料衰减补偿主要是使用反Q滤波在数据域实现[7-10],如Blanch等[11-12]提出用τ方法模拟常Q,并基于伴随状态法在τ-p域中用线性反演方法恢复黏声介质的短波长分量。考虑到地震波衰减是在传播过程中发生的,融合衰减补偿的偏移方法越来越受到重视。Xin等[13]和Xie等[14]利用射线追踪的方法在叠前深度偏移过程中进行衰减补偿;白敏等[15]和代福材等[16]在高斯束叠前深度偏移过程中补偿振幅衰减和校正相位畸变;Dai等[17]、Yu等[18]、Wang[19]和Valenciano等[20]在频率域用单程波动方程偏移进行衰减补偿;陈志德等[21]引入等效Q值实现频率域波场延拓,基于单程波方程和稳定相点原理实现黏声叠前时间偏移,并提高了补偿算法的稳定性。朱峰等[22]推导了黏声VTI介质高阶傅里叶有限差分波场延拓算子,实现了适应高角度入射波场的黏声叠前深度偏移方法。
不同学者提出了多种黏声波动方程,在逆时偏移过程中分别对振幅损失和相位畸变进行补偿和校正[23-27]。李振春等[28]基于广义标准线性体模型对黏声介质波动方程进行线性化,并借助伴随状态法实现了黏声介质最小二乘逆时偏移(Q-LSRTM)的迭代算法,获得了较高的成像分辨率。Dutta等[29]、Dai等[30]基于一阶松弛机制时间域黏声波动方程,用迭代的Q-LSRTM有效补偿和校正了强衰减层导致的振幅损失和相位畸变。徐凯等[31]在反演框架下,构建了Q-LSRTM多约束正则化目标函数,并采用变分方法求解,消除了震源波场与接收点波场互相关引起的噪声,提高了复杂地质体成像的精度、增强了保幅性。相比于传统声波LSRTM,Q-LSRTM能实现反射体的精确归位且振幅更均衡,收敛速率更快[32]。但Q-LSRTM也存在一定问题:其一,由于在传统Q-LSRTM中用于反传数据残差的伴随Q传播算子也是衰减的,导致成像结果分辨率降低;其二,基于时间域黏声波动的LSRTM计算成本较高,尤其是需要很多次迭代才能达到预期成像效果。在完全弹性情况下,为了提高传统LSRTM的收敛速度,李闯等[33]发展了一种预条件偏移算法,提高了盐下构造成像的分辨率和保幅性。
在实际野外地震勘探中,由于稀疏的震源和检波器,记录偏移孔径有限、速度变化快及构造复杂,以及不均匀的地震照明等原因,偏移剖面当中往往存在多种假象[34]。为了消除偏移假象、提升成像分辨率,偏移反褶积被广泛采用[35]。偏移成像本质上就是真实反射率的一种模糊,模糊算子即为Hessian算子,而偏移反褶积处理就等效于一种近似的Hessian逆处理。Hu等[34-35]在空间—波数域设计了一个偏移反褶积算子压制叠后偏移假象;Yu等[36]将偏移反褶积从叠后偏移拓展到叠前深度偏移。Guitton[37]直接在空间域构建了一系列匹配滤波器近似Hessian矩阵的逆实现偏移反褶积,后来这些匹配滤波器被Aoki等[38]作为预条件化因子用于传统的LSRTM,获得了良好的成像效果,这些匹配滤波器也被称为去模糊滤波器。针对多震源LSRTM,Dai等[39-40]用去模糊滤波器减少串扰噪声并且加速多震源LSRTM的收敛。但目前偏移反褶积的原理和实施都是基于无耗散介质假设,而地下储层往往具有衰减性质。
为了克服Q-LSRTM的缺陷,本文将匹配滤波偏移反褶积与Q-LSRTM相结合。首先基于点扩散函数(PSF)构建黏声去模糊滤波器,然后将其作为Q-LSRTM迭代过程中的预条件化因子,最终实现高分辨的衰减补偿偏移。相比于Q-LSRTM,预条件Q-LSRTM成像结果分辨率更高,反射体振幅更均衡,收敛速度更快。就计算成本来说,尽管预条件Q-LSRTM需要预先计算黏声去模糊滤波器,但其达到预期成像效果需要的迭代次数远比Q-LSRTM少。
1 理论方法 1.1 点扩散函数与去模糊滤波器在声学介质中,基于Born近似,观测地震记录d的形成过程可以表示为
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_0} $ | (1) |
式中:L表示线性模拟算子,与观测系统、震源子波和地下介质模型参数有关;m0是地下反射率模型。对应L,可以获得其伴随偏移算子LT,则偏移结果mmig可表示为
| $ {\mathit{\boldsymbol{m}}_{{\rm{mig}}}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{d}} = \overbrace {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}}^{模糊算子}{\mathit{\boldsymbol{m}}_0} $ | (2) |
mmig其实是真实反射率模型m0的模糊版本,LTL就是一个模糊算子,即偏移格林函数[41],也被称为点扩散函数(PSF)。由于震源子波、观测系统等多种因素的影响,偏移成像中往往存在较多的假象。为了获得更清晰的成像结果,可以取LTL的逆并作用于成像结果
| $ {\mathit{\boldsymbol{m}}_0} = \overbrace {{{\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)}^{ - 1}}}^{去模糊算子}{\mathit{\boldsymbol{m}}_{{\rm{mig}}}} $ | (3) |
但在地震成像时,直接计算(LTL)-1是不现实的,为此采用迭代LSRTM方法予以求解,但其计算量往往比标准偏移成像大一个数量级。为了加速收敛,设计去模糊算子的近似逆算子(LTL)-1,并在LSRTM中作为预条件化算子[35-39]。
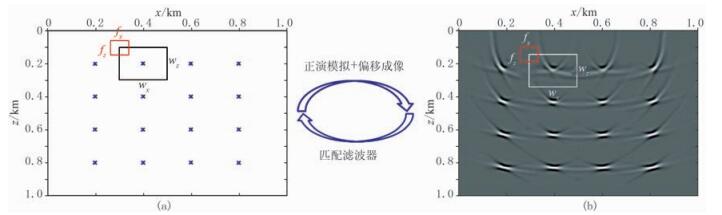
实际应用中,去模糊滤波器基于背景模型即偏移速度场和参考反射率模型获得,以均匀介质速度背景场和均匀分布点散射体反射率模型为例阐述去模糊滤波器的获取过程。图 1a为均匀分布点散射体模型,图 1b为对应的叠前深度偏移成像结果,其中震源和检波器均匀分布于模型上方。单个散射体的PSF响应即为其偏移结果。记参考反射率模型为mref,则在Bron近似下利用式(1)可获得正演模拟数据dref,继而可以获得标准的参考偏移结果
|
图 1 点散射模型及其偏移成像转换示意图 (a)点散射体模型;(b)偏移结果。图中fx×fz为滤波器的空间尺寸;wx×wz为窗口尺寸 |
| $ {\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{m}}_{{\rm{ref}}}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{ref}}}} $ | (4) |
将点散射体模型分解成多个子区域(如图 1a中黑色矩形框),使点散射体位于矩形窗口的中央,窗口大小为wx×wz,足以覆盖其PSF响应的有效能量(图 1b中矩形框)。在这个局部窗口内,假设PSF保持不变。在wx×wz局部窗口区域内,去模糊滤波器将参考偏移成像结果和参考反射率模型联系起来[38, 40],即
| $ \begin{array}{l} {\mathit{\boldsymbol{m}}_{{\rm{ref}}}}{\left( {x,z} \right)_i} = \int_{{V_i}} {{F_i}\left( {x - {x_0},z - {z_0}} \right) \times } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}{\left( {{x_0},{z_0}} \right)_i}{\rm{d}}V \end{array} $ | (5) |
式中:i为局部窗口序号;积分限Vi为整个局部窗口区域。式(5)写成矩阵形式为
| $ {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{ref}}}}} \right]_i} = {\mathit{\boldsymbol{F}}_i} \otimes {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i} $ | (6) |
式中:“⊗”表示空间卷积;[mref]i和[mmig-ref]i分别为第i个局部窗口内参考反射率模型和参考偏移成像结果。与PSF相同,在每个局部窗口内去模糊滤波器保持不变,定义滤波器的空间尺寸为fx×fz。
由卷积的交换律可得
| $ {\mathit{\boldsymbol{F}}_i} \otimes {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i} = {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i} \otimes {\mathit{\boldsymbol{F}}_i} $ | (7) |
将上述卷积运算写成矩阵运算形式,参考偏移结果[mmin-ref]i变成一个(N+M-1)×N阶卷积矩阵,去模糊滤波器Fi变为N×1阶向量f,其中N=fx×fz且M=wx×wz,即为
| $ {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i}{\mathit{\boldsymbol{f}}_i} = {\left[ {{\mathit{\boldsymbol{m}}_{{\rm{ref}}}}} \right]_i} $ | (8) |
上式为超定方程,可以采用最小二乘方法求解,在其两端乘以[mmig-ref]iT变成标准方程形式
| $ \left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i^{\rm{T}}{\left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i}{\mathit{\boldsymbol{f}}_i} = \left[ {{\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}}} \right]_i^{\rm{T}}{\left[ {{\mathit{\boldsymbol{m}}_{{\rm{ref}}}}} \right]_i} $ | (9) |
继而采用三角(LU)分解方法求解式(9)即可获得去模糊滤波器,在第i个局部窗口内近似等于(LTL)-1。在实际应用中,为了保证计算效果,建议局部窗口长度不超过1.5倍地震波长。
1.2 黏声介质中的去模糊滤波器将去模糊滤波器应用到偏移成像的过程就是一种偏移反褶积处理。前人对偏移反褶积的研究都集中在无耗散介质当中,但强吸收会对地震波振幅和相位产生明显的衰减和畸变[1]。为了补偿衰减效应,Dutta等[29]发展了时间域Q-LSRTM技术,成像结果归位更精确,振幅更均衡。在传统Q-LSRTM中,用于反传数据残差的伴随Q传播算子也是衰减的,因此成像分辨率有一定的损失。
这种分辨率的损失能通过黏声介质中的PSF即偏移格林函数予以解释。给定速度为v0的均匀介质和位于xs处角频率为ω的简谐点源,声学格林函数可以表示为
| $ G\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_s}} \right) = \frac{{\exp \left( {\frac{{{\rm{i}}\omega \left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right|}}{{{v_0}}}} \right)}}{{\left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right|}} $ | (10) |
如果介质是耗散的,则将完全弹性介质中的实速度v0替换成复速度[1]
| $ v\left( \omega \right) = {v_0}\left( {1 + \frac{1}{{\mathit{\pi }Q}}\ln \frac{\omega }{{{\omega _0}}}} \right)\left( {1 - \frac{{\rm{i}}}{{2Q}}} \right) $ | (11) |
从而得到黏声介质格林函数
| $ \begin{array}{l} G\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_s}} \right) = \frac{1}{{\left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right|}} \times \\ \;\;\;\;\;\;\;\overbrace {\exp \left( {{\rm{i}}\omega \frac{{\left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right|}}{{{v_0}\xi }}} \right)}^{相位畸变}\overbrace {\exp \left( { - \frac{{\omega \left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right|}}{{2Q{v_0}\xi }}} \right)}^{振幅/频率衰减} \end{array} $ | (12) |
式中:Q是品质因子;ω0是参考角频率;
| $ \begin{array}{l} {\mathit{\Gamma }_{\rm{A}}} = \int_\omega {{\rm{d}}\omega \sum\limits_s {\sum\limits_r \times } } \\ \;\;\;\;\frac{{\exp \left( {\frac{{{\rm{i}}\omega R}}{{{v_0}\xi }}} \right)\exp \left( { - \frac{{\omega R}}{{2Q{v_0}\xi }}} \right)\exp \left( { - \frac{{{\rm{i}}\omega {R_0}}}{{{v_0}}}} \right)}}{{\left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right| \times \left| {{\mathit{\boldsymbol{x}}_r} - \mathit{\boldsymbol{x}}} \right| \times \left| {{\mathit{\boldsymbol{x}}_s} - {\mathit{\boldsymbol{x}}_0}} \right| \times \left| {{\mathit{\boldsymbol{x}}_r} - {\mathit{\boldsymbol{x}}_0}} \right|}} \end{array} $ | (13) |
| $ \begin{array}{l} {\mathit{\Gamma }_{\rm{Q}}} = \int_\omega {{\rm{d}}\omega \sum\limits_s {\sum\limits_r \times } } \\ \;\;\;\;\frac{{\exp \left( {\frac{{{\rm{i}}\omega \left( {R - {R_0}} \right)}}{{{v_0}\xi }}} \right)\exp \left( { - \frac{{\omega \left( {R + {R_0}} \right)}}{{2Q{v_0}\xi }}} \right)}}{{\left| {{\mathit{\boldsymbol{x}}_s} - \mathit{\boldsymbol{x}}} \right| \times \left| {{\mathit{\boldsymbol{x}}_r} - \mathit{\boldsymbol{x}}} \right| \times \left| {{\mathit{\boldsymbol{x}}_s} - {\mathit{\boldsymbol{x}}_0}} \right| \times \left| {{\mathit{\boldsymbol{x}}_r} - {\mathit{\boldsymbol{x}}_0}} \right|}} \end{array} $ | (14) |
式中:R=|xs-x|+|xr-x|;R0=|xs-x0|+|xr-x0|,xr为检波点坐标。从式(13)可以看出,当采用声波偏移(声学伴随算子)对黏声数据进行成像时,反射能量将聚焦在R/ξ=R0的位置,而不是R0所对应的位置x0。而当采用黏声偏移的时候,反射体会成像在正确的位置x0。但是在黏声逆时偏移的过程当中,由于
为了提高Q-LSRTM成像的分辨率并加速最小二乘迭代的收敛,类似于声学去模糊滤波器的构建方法,本文采用局部黏声去模糊滤波器。首先选定一个均匀分布的点散射体模型作为参考反射率模型,然后结合背景速度模型和Q模型合成参考黏声数据drefQ,最后对黏声数据进行Q逆时偏移(Q-RTM)
| $ \mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}^{\rm{Q}} = \mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}{\mathit{\boldsymbol{L}}_{\rm{Q}}}{\mathit{\boldsymbol{m}}_{{\rm{ref}}}} = \mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}\mathit{\boldsymbol{d}}_{\rm{Q}}^{{\rm{ref}}} $ | (15) |
如1.1所述,在偏移成像的不同子区域内,通过匹配参考成像数据和参考反射率模型,得到局部去模糊滤波器,即
| $ \left[ {{\mathit{\boldsymbol{m}}_{{\rm{ref}}}}} \right] = {\left[ {{\mathit{\boldsymbol{F}}_{\rm{Q}}}} \right]_i} \otimes {\left( {\mathit{\boldsymbol{m}}_{{\rm{mig - ref}}}^{\rm{Q}}} \right)_i} $ | (16) |
在实际操作当中,背景速度场选定为偏移速度场和偏移Q值模型,并在与实际相同的观测系统和地震子波情况下估计黏声去模糊滤波器,因此,这些黏声滤波器可以近似视为Hessian算子(LQTLQ)-1的一种估计。
1.3 黏声最小二乘逆时偏移基于标准线性固体(SLS)黏弹性模型一阶松弛机制,二维黏声介质波动程可写为[11, 42]
| $ \left\{ \begin{array}{l} \frac{{\partial P}}{{\partial t}} + K\left( {\tau + 1} \right)\nabla \cdot \mathit{\boldsymbol{v}} + {\gamma _p} = S\left( {{\mathit{\boldsymbol{x}}_s},t} \right)\\ \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial t}} + \frac{1}{\rho }\nabla P = 0\\ \frac{{\partial {\mathit{\boldsymbol{\gamma }}_p}}}{{\partial t}} + \frac{1}{{{\tau _\sigma }}}\left( {{\gamma _p} + \tau K\nabla \cdot \mathit{\boldsymbol{v}}} \right) = 0 \end{array} \right. $ | (17) |
式中:ρ为密度;P为压力;K为体积模量;S为震源子波;γp为记忆变量;v为质点速度向量;τ与品质因子Q有关,可表示为
| $ \tau = \frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}} - 1 = \frac{2}{Q}\left( {\frac{1}{Q} + \sqrt {1 + \frac{1}{{{Q^2}}}} } \right) $ | (18) |
其中τσ和τε分别表示应力和应变松弛时间。在Born近似的框架下,对体积模量K做一定扰动δK,则扰动场可以写为
| $ \left\{ \begin{array}{l} \frac{{\partial \delta P}}{{\partial t}} + K\left( {\tau + 1} \right)\left( {\nabla \cdot \delta \mathit{\boldsymbol{v}}} \right) + \delta {\gamma _p}\\ \;\;\;\;\;\;\; = - \delta K\left( {\tau + 1} \right)\nabla \cdot \mathit{\boldsymbol{v}}\\ \frac{{\partial \delta \mathit{\boldsymbol{v}}}}{{\partial t}} + \frac{1}{\rho }\nabla \delta P = 0\\ \frac{{\partial \delta {\mathit{\boldsymbol{\gamma }}_p}}}{{\partial t}} + \frac{1}{{{\tau _\sigma }}}\left( {\delta {\gamma _p} + \tau K\nabla \cdot \delta \mathit{\boldsymbol{v}}} \right)\\ \;\;\;\;\;\;\;\; = - \frac{\tau }{{{\tau _\sigma }}}\delta K\nabla \cdot \mathit{\boldsymbol{v}} \end{array} \right. $ | (19) |
式中忽略了二阶扰动变量。若用压力和记忆变量格林函数GP(xr, t; x0, 0)和Gγp(xr, t; x0, 0),式(19)也可表示为
| $ \begin{array}{l} \delta P\left( {{\mathit{\boldsymbol{x}}_r},t;{\mathit{\boldsymbol{x}}_s}} \right)\\ \;\;\;\; = \int_{V0} { - \delta K\left( {{\mathit{\boldsymbol{x}}_0}} \right)\left\{ {\left[ {\tau \left( {{\mathit{\boldsymbol{x}}_0}} \right) + 1} \right]{G_P}\left( {{\mathit{\boldsymbol{x}}_r},t;{\mathit{\boldsymbol{x}}_0},0} \right) * } \right.} \\ \;\;\;\;\;\;\nabla \cdot \mathit{\boldsymbol{v}}\left( {{\mathit{\boldsymbol{x}}_0},t;{\mathit{\boldsymbol{x}}_s}} \right) + \frac{{\tau \left( {{\mathit{\boldsymbol{x}}_0}} \right)}}{{{\tau _\sigma }\left( {{\mathit{\boldsymbol{x}}_0}} \right)}}{G_{{\tau _p}}}\left( {{\mathit{\boldsymbol{x}}_r},t;{\mathit{\boldsymbol{x}}_0},0} \right) * \\ \;\;\;\;\;\;\left. {\nabla \cdot \mathit{\boldsymbol{v}}\left( {{\mathit{\boldsymbol{x}}_0},t;{\mathit{\boldsymbol{x}}_s}} \right)} \right\}{\rm{d}}V \end{array} $ | (20) |
式中“*”表示时间方向的褶积运算。
在Q-LSRTM的框架下,式(20)的解等效于矩阵—向量运算
| $ {\mathit{\boldsymbol{d}}_{\rm{Q}}} = {\mathit{\boldsymbol{L}}_{\rm{Q}}}{\mathit{\boldsymbol{m}}_0} $ | (21) |
式中:dQ为Born模拟的黏声地震数据;LQ为线性黏声模拟算子;m0为地下介质反射率。用伴随状态法可推导式(19)的伴随方程[11, 12, 43]为
| $ \left\{ \begin{array}{l} \frac{{\partial q}}{{\partial t}} + \nabla \cdot \left( {\frac{\mathit{\boldsymbol{u}}}{\rho }} \right) = - \Delta d\left( {{\mathit{\boldsymbol{x}}_g},t;{\mathit{\boldsymbol{x}}_s}} \right)\\ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \left[ {K\left( {1 + \tau } \right)q} \right] + \nabla \left( {\frac{1}{{{\tau _\sigma }}}K\tau s} \right) = 0\\ \frac{{\partial s}}{{\partial t}} - \frac{s}{{{\tau _\sigma }}} - q = 0 \end{array} \right. $ | (22) |
式中:(q,u,s)为(P,v,γp)的伴随状态变量;Δd表示每次迭代中实际观测数据和正演数据之间的残差。
成像扰动δm与体积模量扰动δK近似线性相关,而δK可由背景场(通过式(19)计算)和伴随场(通过式(22)计算)之间的零时间延迟互相关得到,即
| $ \delta m \approx \delta K = \int_0^T {\left( {1 + \tau } \right)\left( {\nabla \cdot \mathit{\boldsymbol{v}}} \right)q} + \frac{\tau }{{{\tau _\sigma }}}\left( {\nabla \cdot \mathit{\boldsymbol{v}}} \right)s{\rm{d}}t $ | (23) |
上式可用格林函数表示为
| $ \begin{array}{l} \delta m \approx \delta K = \sum\limits_r {\sum\limits_s {\int_0^T {{\rm{d}}t\left\{ {\left[ {\tau \left( \mathit{\boldsymbol{x}} \right) + 1} \right]\nabla \cdot \mathit{\boldsymbol{v}}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right) \times } \right.} } } \\ \;\;\;\;\;\;\;\left[ {{G_P}\left( {{\mathit{\boldsymbol{x}}_r}, - t;\mathit{\boldsymbol{x}},0} \right) * \Delta P\left( {{\mathit{\boldsymbol{x}}_r},t;{\mathit{\boldsymbol{x}}_s}} \right)} \right] + \\ \;\;\;\;\;\;\;\frac{{\tau \left( \mathit{\boldsymbol{x}} \right)}}{{{\tau _\sigma }\left( \mathit{\boldsymbol{x}} \right)}}\nabla \cdot \mathit{\boldsymbol{v}}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right) \times \\ \;\;\;\;\;\;\;\left. {\left[ {{G_{{\tau _P}}}\left( {{\mathit{\boldsymbol{x}}_r}, - t;\mathit{\boldsymbol{x}},0} \right) * \Delta P\left( {{\mathit{\boldsymbol{x}}_r},t;{\mathit{\boldsymbol{x}}_s}} \right)} \right]} \right\}\\ \;\;\;\;\;\;\; = \sum\limits_s {\int {{\rm{d}}t\left\{ {\left[ {\tau \left( \mathit{\boldsymbol{x}} \right) + 1} \right]\nabla \cdot \mathit{\boldsymbol{v}}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right)q\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right) + } \right.} } \\ \;\;\;\;\;\;\;\left. {\left[ {\frac{{\tau \left( \mathit{\boldsymbol{x}} \right)}}{{{\tau _\sigma }\left( \mathit{\boldsymbol{x}} \right)}}\nabla \cdot \mathit{\boldsymbol{v}}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right)sq\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_s}} \right)} \right]} \right\} \end{array} $ | (24) |
用矩阵可以表示为
| $ {\mathit{\boldsymbol{m}}_{{\rm{mig}}}} = \mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{Q}}} $ | (25) |
Q-LSRTM的误差泛函[29]为
| $ \varepsilon = \frac{1}{2}{\left\| {{\mathit{\boldsymbol{L}}_{\rm{Q}}}{\mathit{\boldsymbol{m}}^{\left( k \right)}} - \mathit{\boldsymbol{d}}_{\rm{Q}}^{{\rm{obs}}}} \right\|^2} $ | (26) |
式中:dQobs表示包含衰减损失的观测数据;m(k)表示第k次迭代的偏移成像。在高斯牛顿框架下,误差泛函梯度为
| $ {\mathit{\boldsymbol{g}}^{\left( k \right)}} = \left( {\mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}{\mathit{\boldsymbol{L}}_{\rm{Q}}}} \right)\Delta {\mathit{\boldsymbol{m}}^{\left( k \right)}} = \mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}\left[ {{\mathit{\boldsymbol{L}}_{\rm{Q}}}{\mathit{\boldsymbol{m}}^{\left( k \right)}} - \mathit{\boldsymbol{d}}_{\rm{Q}}^{{\rm{obs}}}} \right] $ | (27) |
从上式可以看出,每次迭代梯度g(k)是期望模型更新Δm(k)的模糊版本,模糊算子为黏声偏移格林函数LQTLQ。于是,模型梯度可通过黏声去模糊滤波器近似[LQTLQ]-1≈FQ得到,从而预条件化梯度被用于迭代更新方程
| $ {\mathit{\boldsymbol{m}}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{m}}^{\left( k \right)}} - \alpha {\mathit{\boldsymbol{F}}_{\rm{Q}}} * \left[ {\mathit{\boldsymbol{L}}_{\rm{Q}}^{\rm{T}}\left( {{\mathit{\boldsymbol{L}}_{\rm{Q}}}{\mathit{\boldsymbol{m}}^{\left( k \right)}} - \mathit{\boldsymbol{d}}_{\rm{Q}}^{{\rm{obs}}}} \right)} \right] $ | (28) |
式中α是更新步长。
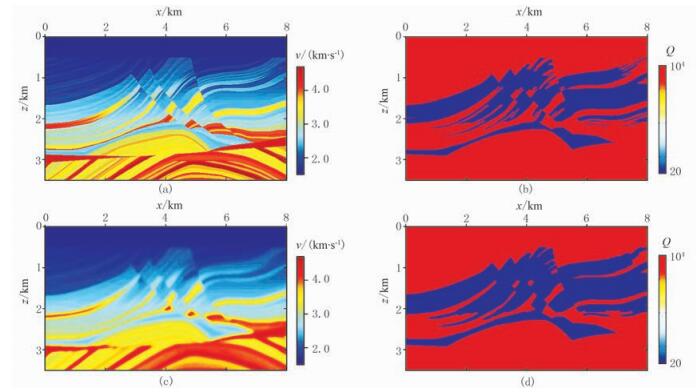
2 Marmousi Ⅱ模型测试为了说明本文提出的预条件Q-LSRTM的有效性,应用Marmousi Ⅱ模型进行测试。图 2a和图 2b分别为正演速度模型和Q值模型,其中Q只取两个值,Q=20表示衰减层,Q=10000可视为弹性介质。整个模型的网格点数为801×351,模型纵横向采样间隔均为10m。在合成黏声地震记录时,炮间隔为50m,共计150炮均匀分布在模型表面,道间距为10m,震源采用主频为15Hz的Ricker子波。采集系统位于地表,且排列长度固定为整个模型的长度。计算中采用时间二阶精度、空间八阶精度的时间域交错网格有限差分法及C-PML边界条件。本文共用到两套数据,一套是基于声波方程的正演结果,另一套是基于一阶松弛机制黏声波动方程的正演结果。对真实速度模型和Q值模型进行二维平滑,得到偏移速度模型(图 2c)和偏移Q值模型(图 2d)。分别执行声波LSRTM、Q-LSRTM、预条件Q-LSRTM三种最小二乘逆时偏移,迭代次数均为20次,其中第1次迭代结果即为声波逆时偏移(RTM)、Q-RTM和预条件Q-RTM的成像结果。
|
图 2 Marmousi Ⅱ速度及Q模型 (a)正演速度模型;(b)正演Q值模型;(c)偏移速度模型;(d)偏移Q值模型 |
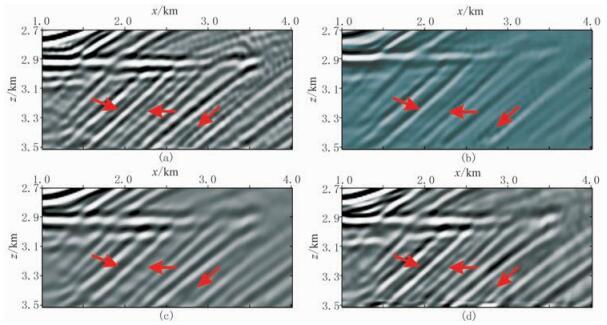
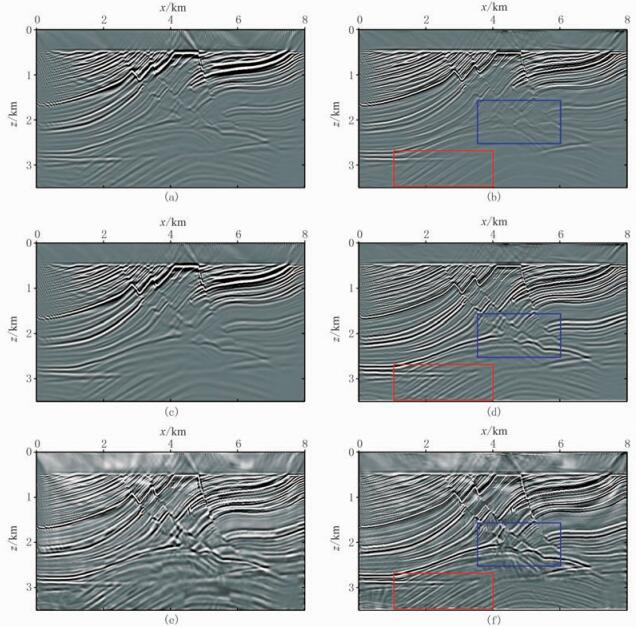
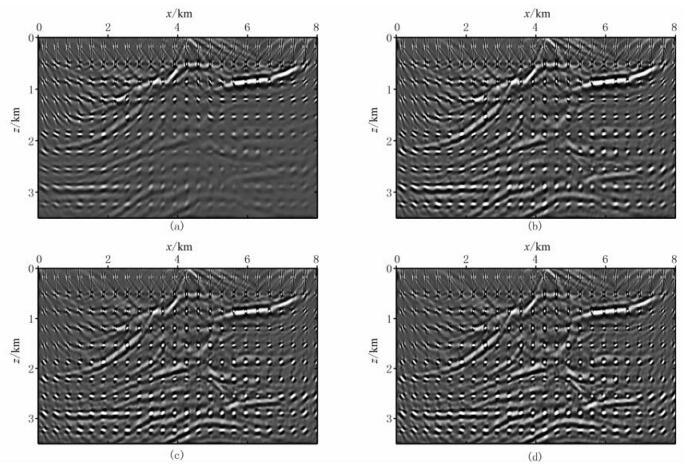
图 3为声波数据声波RTM和LSRTM成像结果,并以此作为基准对比数据。图 4为黏声数据不同方法的偏移结果,可以看出:①利用传统RTM(图 4a)和LSRTM(图 4b)对黏声数据处理获得的成像结果都不能有效恢复衰减层及其下方的反射体振幅,只能粗略体现地下构造形态;②Q-RTM成像结果(图 4c)分辨率比传统RTM(图 4a)还要低,这是由于伴随算子LQT的衰减性质决定的;③与传统LSRTM成像结果相比(图 4b),Q-LSRTM(图 4d)明显提高了分辨率,但与基准声波LSRTM成像结果(图 3b)相比,分辨率还是相对较低,其原因还是由于伴随算子LQT具有衰减性质;④预条件Q-RTM成像结果(图 4e)增强了衰减层及其下方反射体振幅,但整体噪声有所增强,且最下方背斜同相轴归位不准,这与参考点散射体模型的选取有关;⑤预条件Q-LSRTM成像结果(图 4f)与基准声波LSRTM成像结果(图 3b)较为接近,具有较高的分辨率,与Q-LSRTM成像结果(图 4d)相比,其深层反射体的振幅更加均衡。
|
图 3 声波数据声波RTM(a)和LSRTM(b)成像结果 |
|
图 4 黏声数据不同方法成像结果对比 (a)RTM;(b)LSRTM;(c)Q-RTM;(d)Q-LSRTM;(e)预条件Q-RTM;(f)预条件Q-LSRTM |
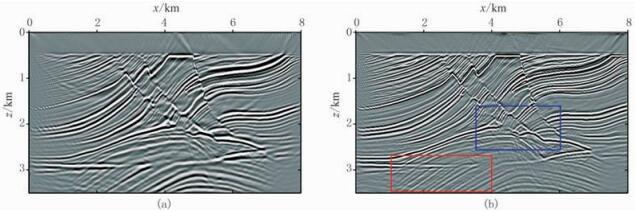
图 5、图 6分别为声波数据LSRTM(图 3b)、黏声数据LSRTM(图 4b)、Q-LSRTM(图 4d)、预条件Q-LSRTM(图 4f)成像结果蓝色、红色矩形框局部放大显示,可以看出:预条件Q-LSRTM提高了黏声数据的成像精度和分辨率(蓝色箭头所指);采用LSRTM对黏声数据进行成像时,不仅存在成像分辨率低的问题,而且由于介质黏弹性导致地震波振幅和相位的畸变,还会导致深层反射体归位出现错乱(图 6b红色箭头所指)。相对而言,尽管Q-LSRTM能有效归位主要反射界面,但分辨率较低,且不能呈现构造细节,预条件Q-LSRTM成像与基准声波LSRTM结果比较接近,分辨率较高。
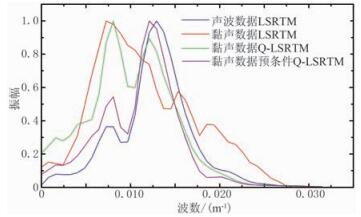
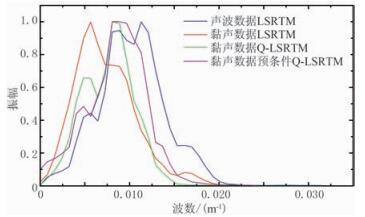
图 7为声波数据LSRTM(图 5a)、黏声数据LSRTM(图 5b)、Q-LSRTM(图 5c)、预条件Q-LSRTM(图 5d)在x=5.0km处成像结果的中深层归一化波数谱对比,可以看出,传统LSRTM和Q-LSRTM的主波数都相对偏低,只有预条件Q-LSRTM的波数谱与基准声波LSRTM接近,也说明预条件Q-LSRTM提高了黏声数据的成像分辨率。图 8为声波数据LSRTM(图 6a)、黏声数据LSRTM(图 6b)、Q-LSRTM(图 6c)、预条件Q-LSRTM(图 6d)在x=2.6km处成像结果的深层归一化波数谱对比,可以看出,黏声数据的声波LSRTM波数谱严重偏离基准数据谱,Q-LSRTM有所改善,预条件Q-LSRTM能恢复出高波数细节信息,最接近于基准数据。
|
图 7 x=5.0km处不同方法成像结果的中深层波数谱对比 |
|
图 8 x=2.6km处不同方法成像结果的深层波数谱对比 |
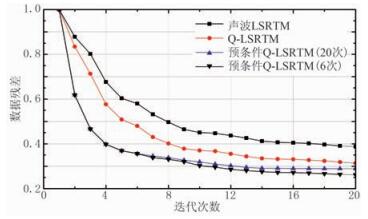
图 9为黏声数据声波LSRTM、Q-LSRTM、预条件Q-LSRTM(预条件20次)、预条件Q-LSRTM(预条件6次)四种情况下数据残差随着迭代次数的变化曲线,可以看出,四种偏移成像结果的精度是逐渐升高的。就收敛速率来看,预条件Q-LSRTM第4次迭代和第8次迭代时的数据残差接近于Q-LSRTM第8次和第20次迭代的数据残差,因此预条件Q-LSRTM能减少约50%的计算量,尤其在早期的几次迭代当中体现的更为明显。预条件Q-LSRTM收敛速率提升的原因在于黏声去模糊滤波器是Hessian算子逆的一种有效近似估计,尽管需要预先计算去模糊滤波器,但计算成本还是要比Q-LSRTM低得多。兼顾到计算精度和计算效率,参考反射率模型中点散射体的布置应该相对稀疏,由此会引入一些全局噪声,如果预条件在第6次迭代后终止,数据残差会进一步减小,相应地成像精度也有所提高。
|
图 9 数据残差随着迭代次数的变化曲线 |
为了测试预条件Q-LSRTM对Q值的敏感性,分别应用Q=20、40、80、100四种模型进行偏移成像,结果如图 4f、图 10所示,图 11为对应的参考反射率模型的黏声PSF,可以看出:随着Q值的增大,衰减层及其下部的反射体的成像振幅逐渐减弱,成像分辨率逐渐降低;相反地,当Q值越大时,衰减越弱,参考反射率模型中的点散射体偏移响应即PSF越强,从而用其构建黏声去模糊滤波器时,考虑到的衰减效应越弱、成像精度越低。因此,一个相对精确的偏移Q值模型是预条件Q-LSRTM取得良好成像效果的前提。

|
图 10 不同Q值偏移模型的预条件Q-LSRTM偏移结果 (a)Q=40;(b)Q=80;(c)Q=100 |
|
图 11 不同Q值偏移模型的参考反射率模型的黏声PSF (a)Q=20;(b)Q=40;(c)Q=80;(d)Q=100 |
(1) 在传统Q-LSRTM成像当中,数据残差的反传过程也是衰减的,会导致成像分辨率降低;而基于PSF的预条件Q-LSRTM方法采用黏声去模糊滤波器补偿由于地下强衰减导致的振幅和分辨率降低,能得到较高的成像精度和更均衡的成像振幅。
(2) 由于地下模型是未知的,构建黏声去模糊滤波器时一般选用均匀分布的点散射体模型。基于偏移速度场和Q值模型,采用和实际一致的观测系统和地震子波,通过正演模拟和偏移成像获得黏声PSF,最终采用匹配滤波的思想构建黏声去模糊滤波器。兼顾到计算精度和计算效率,参考反射率模型中点散射体密度和局部窗口长度需根据构造复杂度确定。
(3) 与Q-LSRTM相比,预条件Q-LSRTM的收敛效率得到大幅度提升,在前几次迭代中更为明显。为了获得更高的成像精度和计算效率,预条件Q-LSRTM只在前几次迭代中使用为宜。就计算成本而言,尽管预条件Q-LSRTM需要预先计算黏声去模糊滤波器,但计算耗时仍然比Q-LSRTM小得多。
(4) 与Q-LSRTM类似,为了获得较好的成像效果,预条件Q-LSRTM也需要一个相对精确的Q值模型估计,同时也必须有一个相对精确的偏移速度模型。
(5) 本文的方法可拓展到黏弹各向异性等更复杂介质的偏移成像当中,考虑到计算量,建议采用并行加速计算。
| [1] |
Aki K, Richards P G.Quantitative Seismology: Theory and Methods[M].W H Freeman, 1980.
|
| [2] |
Carcione J M.Wave Fields in Real Media[M].Elsevier, 2007.
|
| [3] |
孙成禹, 印兴耀. 三参数常Q黏弹性模型构造方法研究[J]. 地震学报, 2007, 29(4): 348-357. SUN Chengyu, YIN Xingyao. Construction of constant-Q viscoelastic model with three parameters[J]. Acta Seismologica Sinica, 2007, 29(4): 348-357. DOI:10.3321/j.issn:0253-3782.2007.04.002 |
| [4] |
孙成禹, 乔志浩, 伍敦仕, 等. 常Q衰减介质分数阶波动方程优化有限差分模拟[J]. 地震学报, 2017, 39(3): 343-355. SUN Chengyu, QIAO Zhihao, WU Dunshi, et al. Modeling of wave equation with fractional derivative using optimal finite-difference method in constant-Q attenuation media[J]. Acta Seismologica Sinica, 2017, 39(3): 343-355. |
| [5] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN Hongyong, LIU Yang. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [6] |
姚振岸, 孙成禹, 唐杰, 等. 基于不同震源机制的黏弹各向异性微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(1): 63-70. YAO Zhen'an, SUN Chengyu, TANG Jie, et al. Micro-seismic forward modeling in viscoelastic anisotropic media based on different focal mechanisms[J]. Oil Geophysical Prospecting, 2017, 52(1): 63-70. |
| [7] |
Bickel S, Natarajan R. Plane wave Q deconvolution[J]. Geophysics, 1985, 50(9): 1426-1439. DOI:10.1190/1.1442011 |
| [8] |
Hargreaves N, Calvert A. Inverse Q filtering by Fourier transform[J]. Geophysics, 1991, 56(4): 519-527. DOI:10.1190/1.1443067 |
| [9] |
Wang Y H.Seismic Inverse Q Filtering[M].Black-well Publishing, 2007.
|
| [10] |
张立彬, 王华忠. 稳定的反Q偏移方法研究[J]. 石油物探, 2010, 49(2): 115-120. ZHANG Libin, WANG Huazhong. A stable inverse Q migration method[J]. Geophysical Prospecting for Petroleum, 2010, 49(2): 115-120. DOI:10.3969/j.issn.1000-1441.2010.02.002 |
| [11] |
Blanch J O, Symes W W.Linear inversion in layered viscoacoustic media using a time-domain method[C].SEG Technical Program Expanded Abstracts, 1994, 13: 1053-1056.
|
| [12] |
Blanch J O, Robertsson J O, Symes W W. Modeling of a constant Q:Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique[J]. Geophysics, 1995, 60(1): 176-184. DOI:10.1190/1.1443744 |
| [13] |
Xin K, Hung B, Birdus S, et al.3D tomographic amplitude inversion for compensating amplitude attenuation in the overburden[C].SEG Technical Program Expanded Abstracts, 2008, 27: 3239-3243. https://www.researchgate.net/publication/301386841_3-D_Tomographic_Amplitude_Inversion_for_Compensating_Transmission_Losses_in_the_Overburden
|
| [14] |
Xie Y, Xin K, Sun J, et al.3D prestack depth migration with compensation for frequency dependent absorption and dispersion[C].SEG Technical Program Expanded Abstracts, 2009, 28: 2919-2923.
|
| [15] |
白敏, 陈小宏, 吴娟, 等. 基于吸收衰减补偿的多分量高斯束逆时偏移[J]. 地球物理学报, 2016, 59(9): 3379-3393. BAI Min, CHEN Xiaohong, WU Juan, et al. Multiple-component Gaussian beam reverse-time migration based on attenuation compensation[J]. Chinese Journal of Geophysics, 2016, 59(9): 3379-3393. |
| [16] |
代福材, 黄建平, 李振春, 等. 角度域黏声介质高斯束叠前深度偏移方法[J]. 石油地球物理勘探, 2017, 52(2): 283-293. DAI Fucai, HUANG Jianping, LI Zhenchun, et al. Angle domain prestack Gaussian beam migration for visco-acoustic media[J]. Oil Geophysical Prospecting, 2017, 52(2): 283-293. |
| [17] |
Dai N, West G F.Inverse Q migration[C].SEG Technical Program Expanded Abstracts, 1994, 13: 1418-1421.
|
| [18] |
Yu Y, Lu R S, Deal M M.Compensation for the effects of shallow gas attenuation with viscoacoustic wave-equation migration[C].SEG Technical Program Expanded Abstracts, 2002, 21: 2062-2065. https://www.researchgate.net/publication/249858218_Compensation_for_the_effects_of_shallow_gas_attenuation_with_viscoacoustic_wave-equation_migration
|
| [19] |
Wang Y H. Inverse-Q filtered migration[J]. Geophy-sics, 2007, 73(1): S1-S6. |
| [20] |
Valenciano A A, Chemingui N, Whitmore D, et al.Wave equation migration with attenuation and anisotropy compensation[C].SEG Technical Program Expanded Abstracts, 2011, 30: 232-236.
|
| [21] |
陈志德, 赵忠华, 王成. 黏滞声学介质地震波吸收补偿叠前时间偏移方法[J]. 石油地球物理勘探, 2016, 51(2): 325-333. CHEN Zhide, ZHAO Zhonghua, WANG Cheng. Prestack time migration with compensation for absorption of viscous-elastic media[J]. Oil Geophysical Prospecting, 2016, 51(2): 325-333. |
| [22] |
朱峰, 黄建平, 李振春. 黏声VTI介质傅里叶有限差分叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(5): 956-966. ZHU Feng, HUANG Jianping, LI Zhenchun. FFD prestack depth migration for visco-acoustic VTI me-dium[J]. Oil Geophysical Prospecting, 2017, 52(5): 956-966. |
| [23] |
Zhang Y, Zhang P, Zhang H.Compensating for visco-acoustic effects in reverse time migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3160-3164. https://www.researchgate.net/publication/269069109_Compensating_for_visco-acoustic_effects_in_reverse-time_migration
|
| [24] |
Suh S, Yoon K, Cai J, et al.Compensating visco-acoustic effects in anisotropic resverse-time migration[C].SEG Technical Program Expanded Abstracts, 2012, 31.
|
| [25] |
Fletcher R, Nichols D, Cavalca M.Wavepath-consis-tent effective Q estimation for Q-compensated reverse-time migration[C].Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, A020.
|
| [26] |
Zhu T, Harris J M, Biondi B. Q-compensated reverse-time migration[J]. Geophysics, 2014, 79(3): S77-S87. DOI:10.1190/geo2013-0344.1 |
| [27] |
Zhu T, Harris J M. Improved seismic image by Q-compensated reverse time migration:Application to crosswell field data, West Texas[J]. Geophysics, 2015, 80(2): B61-B67. DOI:10.1190/geo2014-0463.1 |
| [28] |
李振春, 郭振波, 田坤. 黏声介质最小平方逆时偏移[J]. 地球物理学报, 2014, 57(1): 214-228. LI Zhenchun, GUO Zhenbo, TIAN Kun. Least-squares reverse time migration in visco-acoustic medium[J]. Chinese Journal of Geophysics, 2014, 57(1): 214-228. |
| [29] |
Dutta G, Schuster G T. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation[J]. Geophysics, 2014, 79(6): S251-S262. DOI:10.1190/geo2013-0414.1 |
| [30] |
Dai W, Xu Z, Coates R.Least-squares reverse-time migration for visco-acoustic media[C].SEG Technical Program Expanded Abstracts, 2015, 34: 3387-3391.
|
| [31] |
徐凯, 孙赞东. 基于粘声衰减补偿的最小二乘逆时偏移[J]. 石油物探, 2018, 57(3): 419-427. XU Kai, SUN Zandong. Least-squares reverse time migration based on visco-acoustic attenuation compensation[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 419-427. DOI:10.3969/j.issn.1000-1441.2018.03.011 |
| [32] |
Sun J, Fomel S, Zhu T, et al. Q-compensated least-squares reverse time migration using low-rank one-step wave extrapolation[J]. Geophysics, 2016, 81(4): S271-S279. DOI:10.1190/geo2015-0520.1 |
| [33] |
李闯, 黄建平, 李振春, 等. 预条件最小二乘逆时偏移方法[J]. 石油地球物理勘探, 2016, 51(3): 513-520. LI Chuang, HUANG Jianping, LI Zhenchun, et al. Preconditioned least-squares reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(3): 513-520. |
| [34] |
Hu J, Schuster G T.Migration deconvolution[C].SPIE's International Symposium on Optical Science, 1998, 118-124.
|
| [35] |
Hu J, Schuster G T, Valasek P. Poststack migration deconvolution[J]. Geophysics, 2001, 66(3): 939-952. DOI:10.1190/1.1444984 |
| [36] |
Yu J, Hu J, Schuster G T, et al. Prestack migration deconvolution[J]. Geophysics, 2006, 71(2): S53-S62. DOI:10.1190/1.2187783 |
| [37] |
Guitton A. Amplitude and kinematic corrections of migrated images for nonunitary imaging operators[J]. Geophysics, 2004, 69(10): 1017-1024. |
| [38] |
Aoki N, Schuster G T. Fast least-squares migration with a deblurring filter[J]. Geophysics, 2009, 74(6): WCA83-WCA93. DOI:10.1190/1.3155162 |
| [39] |
Dai W, Schuster G T.Least-squares migration of si-multaneous sources data with a deblurring filter[C].SEG Technical Program Expanded Abstracts, 2009, 28: 2990-2994.
|
| [40] |
Dai W, Wang X, Schuster G T. Least-squares migration of multisource data with a deblurring filter[J]. Geophysics, 2011, 76(5): R135-R146. DOI:10.1190/geo2010-0159.1 |
| [41] |
Schuster G T, Hu J. Green's function for migration:Continuous recording geometry[J]. Geophysics, 2000, 65(1): 167-175. DOI:10.1190/1.1444707 |
| [42] |
Carcione J M, Kosloff D, Kosloff R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401. DOI:10.1111/j.1365-246X.1988.tb02010.x |
| [43] |
Lailly P.The seismic inverse problem as a sequence of before stack migrations[C].Conference on Inverse Scattering: Theory and Application, 1983, 467-481.
|



 姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: