② 中国地质大学(北京)能源学院, 北京 100083
② School of Energy Resources, China University of Geosciences(Beijing), Beijing 100083, China
传统地震勘探利用纵波信息解决构造问题,但随着剩余油气藏勘探难度的增加,仅使用纵波信息已不能满足现代油气勘探的需求。多分量地震勘探技术可以充分利用纵波和转换波信息[1-2]。
随着各向异性理论的发展,多分量地震数据的各向异性叠前时间偏移(Pre-stack time migration,PSTM)已成为地震勘探的前沿技术,各向异性参数也被证明是提高地震偏移成像精度的关键因素[3]。Kirchhoff叠前时间偏移算法是经典偏移算法,该算法计算量庞大,也是整个常规数据处理周期中最为费时的环节[4-5]。随着勘探目标数据体越来越大,地震数据处理周期也越来越长,难以满足地震资料高效解释的需求,亟待尝试并行计算缩短处理时间,提高计算效率[6-7]。
前人已经进行了一些关于叠前时间偏移算法的并行化研究,包括基于多节点CPU的MPI(Message passing interface,消息传递接口)技术和基于GPU(Graphics processing unit,图形处理器)的CUDA(Compute unified device architecture,计算同一设备架构)并行架构。其中,马召贵等[8]提出了一种基于CPU的多级并行优化方案,并应用于起伏地表的叠前时间偏移中。该方案消除了成像域并行的通讯耗费,降低了系统I/O对计算性能的影响。Alves等[9]提出一种针对CPU指令集的手动向量化算法优化方法,在不使用协处理的情况下,算法加速比达到了4倍。但是CPU限于其自身的硬件结构特点,计算密集型算法仍不适宜在CPU结构上展开。李肯立等[10]利用CUDA将GPU协同CPU计算应用到纵波Kirchhoff叠前时间偏移,使用单个8800GT型号GPU协同CPU并行,较CPU串行算法获得了6倍的加速效果,但其使用测试数据的规模及计算效果很难满足实际应用的需求。喻勤等[11]提出基于CUDA和MPI的多节点并行Kirchhoff叠前时间偏移算法,使用两个M2070型号GPU节点并行,加速比达到了300。使用多个节点必然会增加服务器成本,并且导致通信开销增大[12],如果通过增加GPU个数增强单个服务器的计算能力,那么在节省部分成本的同时,还可达到与多节点类似的加速效果,并具有较低能耗[13]。
本文使用纵波、转换波数据进行叠前时间偏移,全面地反映地下复杂构造,并且加入各向异性参数提高成像精度;同时将OpenMP和CUDA结合在一起,实现单节点上CPU与多个GPU协同并行的叠前时间偏移算法,使用内存映射的方法进行地震数据的I/O优化以及多主测线(Inline)输入输出的方法读写数据,在降低计算成本的同时,使大规模地震数据资料可以在小内存服务器上并行计算,达到了较高加速比。
1 多分量各向异性PSTM方法本文算法是基于Kirchhoff积分各向异性叠前时间偏移算法,其流程如图 1所示,即将特定位置的输入地震数据(PP波为CMP道集,PS波为ACP道集)叠加映射到成像空间(CIP道集)中。其中,数据位置由计算地震波上、下行旅行时得出。相比常规叠前时间偏移,各向异性叠前时间偏移在每个网格点上加入了反映当前工区点地下特征的各向异性参数η,以提高成像精度,因此计算量会有常量级的增加。具体旅行时计算方法由杨震等[14]根据文献[15]改进得到。即有VTI介质精确时差公式

|
图 1 叠前时间偏移串行算法流程 |
| $ \begin{array}{l} {t_{{\rm{PS}}}} = \sqrt {t_{0{\rm{PS}}}^2 + \frac{{x_{\rm{P}}^2}}{{V_{\rm{P}}^2(1 + 2{\eta _{\rm{P}}}{{\sin }^2}{\theta _{\rm{P}}})}}} + \\ \;\;\;\;\;\;\sqrt {\;t_{{\rm{0PS}}}^2 + \frac{{x_{\rm{S}}^2}}{{V_{\rm{S}}^2(1 + 2{\eta _{\rm{S}}}{{\sin }^2}{\theta _{\rm{S}}})}}} \end{array} $ | (1) |
| $ \begin{array}{l} {t_{{\rm{PP}}}} = \sqrt {t_{{\rm{0P}}}^2 + \frac{{x_{{\rm{P1}}}^2}}{{V_{\rm{P}}^2(1 + 2{\eta _{\rm{P}}}{{\sin }^2}{\theta _{{\rm{P1}}}})}}} + \\ \;\;\;\;\;\;\;\sqrt {\;t_{{\rm{0P}}}^2 + \frac{{x_{{\rm{P2}}}^2}}{{V_{\rm{P}}^2(1 + 2{\eta _{\rm{P}}}{{\sin }^2}{\theta _{{\rm{P2}}}})}}} \end{array} $ | (2) |
式中:tPS是PS波旅行时;tPP是PP波旅行时;xP和xP1分别是PS波和PP波的下行P波的炮点到成像点水平距离;xS和xP2分别是PS波上行S波和PP波上行P波的检波点到成像点水平距离;t0PP和t0PS分别是PP波与PS波自激自收时间;VP是PP波NMO速度;VS是S波NMO速度;θP和θP1分别是PS波和PP波入射角;θS和θP2分别是PS、PP波的出射角;ηP和ηS分别是P波和S波速度的各向异性参数。
如图 1所示,串行算法采用面向成像域的实现策略,即先读取工区属性和偏移参数,根据读到的成像主测线、联络线范围及测线间隔建立成像网格。在成像网格中按顺序选定一道成像道(一道成像道即一个成像网格点),根据成像道位置读取一道速度数据,根据成像道位置及偏移参数中的扩展线数读取一道输入地震数据,其中,扩展线数x作用是当偏移第A(数字)号线时,输入A-x到A+x号线地震数据共同对第A号线进行偏移,以提高偏移成像效果及分辨率。同时,算法的整体计算量相比无扩展线数算法成倍增加。从成像道内按顺序选定一个采样点,将该点位置、偏移参数及读取的速度数据等代入式(1)或式(2)后,计算该道输入地震数据相对该采样点的地震波旅行时。然后提取该道输入地震数据中,计算所得旅行时对应位置的地震数据,并叠加到该采样点上,第一轮判断成像道内每个采样点计算是否完毕:“否”则选取成像道内下一个采样点进行偏移计算。“是”则第二轮判断是否将扩展线内全部输入地震数据读取完毕:“否”则读取扩展线内下一道输入地震数据,“是”则第三轮判断是否全部成像道计算完毕:“否”则选取成像网格中下一道成像道,“是”则输出成像空间,算法结束。
从图 1可知,算法的计算核心是计算地震波旅行时及输入数据叠加采样点部分,叠前时间偏移算法整体的计算量取决于成像网格点数k、扩展线中包含的输入地震道数m及每道数据的采样点数n,算法时间复杂度为O(kmn)。如果对由上百万(106)地震道组成、每道采样点数为103的小规模数据以扩展线数为2(扩展线包含的输入地震道数约为104)、成像网格点数为104的成像参数进行偏移,算法的时间复杂度约为1011,需在服务器上运行数十小时。需要对其进行并行化运算,而算法并行化的必要条件是计算过程中不存在数据依赖,即成像网格内任一成像点的偏移不依赖于其他成像点。从图 1中可以看出,本算法中的各个成像点之间相互独立,不存在数据依赖,具备并行化条件。
除计算量巨大外,运算过程内存消耗也很大。实际地震数据处理时,无法将地震数据及速度数据整体存放于内存中,因此必须调整计算思路。
2 CPU与GPU协同并行偏移算法 2.1 CPU与GPU并行并行指在同一时间内由多个处理器同时处理同一个任务的不同部分,从而达到加速处理的效果[16-17]。
CPU和GPU都可以通过成熟的编程框架进行并行编程,但CPU的结构设计偏向于计算机逻辑指令的编译和执行,而GPU的结构设计更偏向于大规模的数据计算,其浮点数运算速度可达到CPU的数十倍[18-20],因此合理使用并行框架,发挥各自擅长的能力处理问题成为并行化的关键。OpenMP和CUDA分别是常用基于CPU和GPU的并行框架。
OpenMP是一种用于共享内存系统的CPU多线程并行方案,提供了很多库函数来解决常见的多线程程序设计问题[21-22]。在本文中,其作用是在CPU上开启多个线程与多个GPU一一对应,将读取到的数据分发给不同的GPU并控制对应的GPU进行数据计算,以及计算完成后接收多个GPU的计算结果,按顺序写入结果文件。
CUDA是NVIDIA(英伟达)公司发布的应用于GPU的并行编程模型。在CUDA中,GPU及其内存称为设备(Device),CPU以及系统的内存称为主机(Host)。由于主机内存与设备内存相互独立,所以,在实际使用CUDA时,必须将GPU计算所需数据从主机内存传输到设备内存,以便GPU读取数据进行计算,且在计算完成后,必须将计算结果从设备内存传输到主机内存,以便CPU输出计算结果。使用CUDA提供的类C语言函数就可实现分配设备空间、主机和设备间的数据传输以及释放设备空间等必要操作。
设备内存包括几种不同特点的存储结构,根据不同数据的读取方式,使用与之适应的存储方法,以提高并行算法性能。全局内存(Global memory)是可读写的设备内存,容量最大,但是读取速度慢,用来存储从主机传输到设备上的数据。纹理内存(Texture memory)和常量内存(Constant memory)是在核函数执行期间只读的设备内存,分别缓存在纹理缓存(Texture cache)和常量缓存(Constant cache)上,容量小但是读取速度快。此外,纹理内存的特点是当多个线程在读取数据的位置非常邻近时,可以加快数据的读取速度。
核(Kernel)函数是每个GPU线程在GPU设备上执行的函数,一般对应串行算法中计算最密集、计算量最大的部分。CUDA通过控制GPU中的流处理器(Stream processor,SP),同时启动大量GPU线程,执行同一个核函数对数据进行操作,达到并行计算的目的。在启动CUDA核函数进行计算时,会伴随着分配设备存储空间、主机与设备间相互传输数据以及回收设备上的存储空间等一系列必要操作以配合计算,这些操作存在一定的时间开销,所以在设计并行算法时,应该尽量减少核函数启动次数,降低花费在分配空间、传输数据以及回收空间操作上的时间[23-24]。
2.2 CPU与GPU协同并行偏移算法实现本文提出的CPU与多个GPU协同并行算法的流程图如图 2所示。

|
图 2 并行算法流程 |
本算法将全部偏移任务分成多个计算周期完成,点线框包含的步骤为一个计算周期,由CPU进行算法中的逻辑处理、数据读写及分发,由各GPU进行旅行时计算,并根据得到的旅行时偏移输入地震数据。具体方案是由每个GPU负责一条主测线的成像,因此一个计算周期内可以偏移计算GPU个数条成像主测线。在GPU内部,每个GPU线程与读取的扩展线内每道输入地震数据一一对应,以控制各道输入地震数据的偏移。各GPU线程并行计算各道输入地震数据相对各成像道(一个成像网格点)内每个采样点的地震波旅行时,再根据计算所得旅行时,从输入地震数据中提取数据,叠加到相应的成像采样点上。本文采用在扩展线内包含的输入地震数据道数粒度(104)并行的原因,主要是该粒度数量级与GPU中可同时并发线程数量级一致,每个GPU线程的计算量比较均衡,能充分利用GPU多线程并发的特点及GPU的浮点计算能力。
本文以包含N条主测线(线号为1~N)的地震数据,使用4个GPU协同CPU并行成像计算为例,解释算法流程;同时,考虑到计算效率和成像效果,将扩展线数设置为2。
算法的第一个计算周期在GPU上的并行计算方法如图 3所示,首先将计算所需的地震数据与速度数据由硬盘读入CPU内存,在第一个计算周期,即对1到4号测线进行偏移计算时,由于成像空间位于工区边界,根据扩展线数为2,需读取1到6号共6条主测线数据及速度模型数据。由于地震数据及速度数据量较大,本文在CPU端使用内存映射方法进行读取,即把地震数据文件映射进CPU内存,得到一个指向整体数据起始位置的指针,通过给指针附加偏移量读取指定位置的数据。并建立一个地址索引数组来记录各地震道相对起始位置的偏移量,以帮助算法快速而准确地切换数据读取位置。速度模型数据使用相同的内存映射方法进行读取。
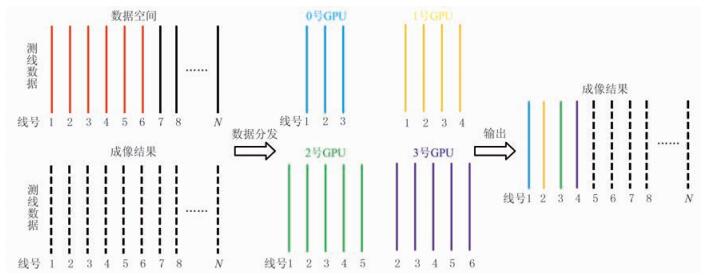
|
图 3 并行算法第一个计算周期示意图 |
CPU读取相关数据后,利用OpenMP开启多个CPU线程,每个CPU线程控制一个GPU设备,各个CPU线程将读取到的数据分块传输到各个GPU上,过程如图 3的中部所示。由于第一个周期的测线处在成像空间左边界且扩展线数为2,因此只有1到3号主测线数据传输到0号GPU上偏移计算1号成像域主测线,1到4号主测线数据传输到1号GPU上偏移计算2号成像域主测线。其他非工区边界情况如图 3中2号GPU与3号GPU部分所示。因扩展线数为2,故使用5条输入主测线数据偏移计算1条成像主测线。对于量大的地震数据,将其传输到空间较大但读取相对较慢的GPU全局内存上,对于频繁读取且读取位置邻近的速度数据,本文将其绑定在读取较快但空间相对较小的GPU纹理内存上。
各GPU接收到数据后,如前所述每个GPU负责一条成像域主测线的偏移成像计算,如图 3所示,0号GPU偏移计算1号成像域主测线的成像空间,1号GPU偏移计算2号成像域主测线的成像空间,以此类推。然后以一个GPU线程对应一道地震道数据的原则,开启各GPU线程并启动GPU上的核函数并行偏移计算。通过每个线程专属的线程号控制核函数,依次计算各地震道在不同炮检距的地震波的旅行时,然后各GPU线程将旅行时对应的输入地震数据叠加到成像采样点上。各GPU内成像主测线并行偏移计算完毕后,各GPU分别传输各自所得成像空间数据到CPU,并且释放GPU上所有分配的内存空间。所得成像空间数据由CPU按顺序写入到偏移结果文件中,本计算周期计算结束。
第二个计算周期与第一个计算周期过程相似,不同点在于第二个计算周期将针对5~8号成像空间进行并行偏移计算,由于不涉及工区边界,所以需读取3~10号共8条输入测线数据和速度数据,分发数据时也按照各GPU偏移计算所需数据范围进行分发,依次循环,直至全部成像空间计算完毕。
当运算到工区右边界时,若剩余成像空间主测线数小于当前开启GPU个数,则自动修正参与计算的GPU个数为剩余成像空间主测线数,以保证一个GPU偏移计算一条成像域主测线。
3 实际数据应用与性能分析测试数据来自新场工区的X分量和Z分量数据,主测线范围是1380~1595,联络线范围是1002~1779,每个地震道采样点数为3500,采样点间隔为2ms,每个分量数据量约为29GB。成像网格主测线范围是1380~1595,联络线范围是1002~1779,成像的时间长度为6998。硬件环境方面,CPU为2路Intel Xeon E5-2695v2,核心频率为2.4GHz,设计功耗为115W。每个GPU为NVIDIA Tesla K40M计算卡,该型号有2880个CUDA计算核心,存储空间约为12GB,存储带宽为288GB/s,单精度浮点数计算峰值为4.29Tflops(每秒万亿次浮点运算),双精度浮点数计算峰值为1.43Tflops,设计功耗为235W。
首先对比CPU串行算法与本并行算法结果,以转换波叠前时间偏移算法为例,随机提取某一相同位置剖面(图 4),左侧为CPU串行计算结果,右侧为并行算法计算结果,可见反映的地下构造几乎相同,证明了并行算法的正确性。

|
图 4 CPU串行(a)、并行(b)算法偏移处理结果对比 |
图 5分别是纵波与转换波使用本文并行PSTM算法偏移结果的同一测线剖面,从波组特征可见纵波2.5~3.1s层位(红箭头)对应转换波3.5~4.5s时段,纵波3.6~3.9s层位(蓝箭头)对应转换波5.0~5.5s时段。
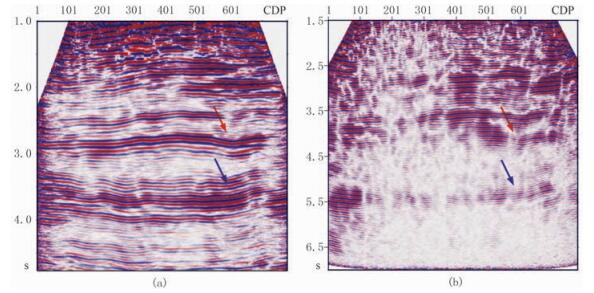
|
图 5 纵波(a)与转换波(b)偏移处理结果对比 |
表 1是PSTM串行算法与不同GPU个数协同CPU算法并行的运行时耗统计,从加速比可看出并行算法的性能指标明显较高。图 6是纵波PSTM算法的并行效果与理想加速效果的折线图对比,其中,理想加速比用来判断CPU的并行效果,是指在使用OpenMP开启多CPU线程控制多GPU协同CPU计算时,各CPU线程之间无线程同步等损耗的线性加速比,即实际加速比曲线越接近线性理想加速比,算法的并行度越高,并行效果越好。可见通过使用OpenMP技术,同时使用多个GPU偏移计算,具有较好加速效果,未达到线性加速比的原因主要是由于随着CPU开启线程数的增加,在线程同步上花费的时间也随之增加。由于转换波PSTM相比纵波PSTM计算量稍多,所以实际加速效果也稍好。
|
|
表 1 纵波与转换波PSTM串、并行性能对比 |
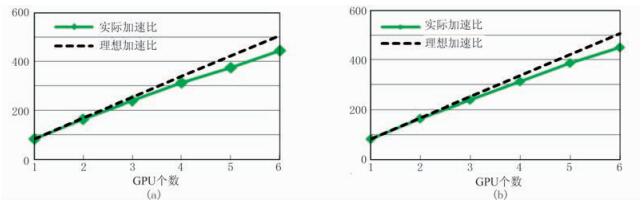
|
图 6 纵波(a)及转换波(b)PSTM并行方式实际加速比与理想加速比对比 |
内存使用方面,由于本算法分割了成像空间,所以在每个计算周期,系统的内存只存放该计算周期所需数据,在原始地震数据成倍增长的情况下,也不会导致内存溢出、无法计算的情形。
此外,现在业界普遍使用CPU集群加速计算,而CPU并行试算的理想加速比是并行使用的核心总数,但由于并行模型的通信等问题,实际加速比往往低于理论加速比,并且本文提出的6个GPU协同CPU的并行算法加速比已能达到444和449,若想通过CPU集群计算达到类似加速比,则至少需要450个CPU核心的计算资源,相当于一个数+计算节点的CPU集群规模。所以从系统造价及能耗角度看,GPU并行明显优于CPU并行。
4 结束语本文提出了基于CPU与GPU协同并行的多分量地震数据各向异性叠前时间偏移算法,优化了传统偏移方法的I/O方式,使用多次读取、每次读取多主测线、每次计算GPU个数条成像主测线的方法分解计算任务,兼顾了算法占用的内存空间和计算效率。在一台服务器上对实际工区约29G的纵波及转换波数据使用6个GPU协同CPU进行PSTM算法并行时,纵波PSTM算法的加速比可以达到444,转换波PSTM算法的加速比可以达到449,加速比相比传统的通过增加CPU集群数量的并行方式有大幅度提高,且充分利用了单个服务器上的设备接口数量,相比多个单GPU计算节点,避免了节点间的通信开销同时降低了计算成本。
| [1] |
赵波, 王赟, 芦俊. 多分量地震勘探技术新进展及关键问题探讨[J]. 石油地球物理勘探, 2012, 47(3): 506-516. ZHAO Bo, WANG Yun, LU Jun. Recent advances of multi-component seismic and some of its key issues[J]. Oil Geophysical Prospecting, 2012, 47(3): 506-516. |
| [2] |
周丽, 顾汉明, 成景旺, 等. 基于MPI的OBC三维多波多分量地震观测正演模拟并行算法实现[J]. 石油物探, 2014, 53(6): 665-674. ZHOU Li, GU Hanming, CHENG Jingwang, et al. Algorithm realization of parallel forward modeling of 3D multi-wave and multicomponent seismic survey for OBC observation based on MPI[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 665-674. DOI:10.3969/j.issn.1000-1441.2014.06.006 |
| [3] |
荣骏召, 芦俊, 李建峰, 等. 矢量Kirchhoff叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(6): 1170-1176. RONG Junzhao, LU Jun, LI Jianfeng, et al. Vector prestack depth migration based on Kirchhoff integral equation[J]. Oil Geophysical Prospecting, 2017, 52(6): 1170-1176. |
| [4] |
赵长海, 罗国安, 张旭东, 等. 大规模异构集群上Kirchhoff叠前时间偏移并行算法[J]. 石油地球物理勘探, 2016, 51(5): 1040-1048. ZHAO Changhai, LUO Guoan, ZHANG Xudong, et al. Kirchhoff prestack time migration on large heterogeneous computing systems[J]. Oil Geophysical Prospecting, 2016, 51(5): 1040-1048. |
| [5] |
马召贵, 赵改善, 武港山, 等. 基于CPU+GPU联合计算真地表叠前时间偏移实用化研究[J]. 石油地球物理勘探, 2014, 49(3): 530-537. MA Zhaogui, ZHAO Gaishan, WU Gangshan, et al. Kirchhoff pre-stack time migration of complex surface data on CPU+GPU[J]. Oil Geophysical Prospecting, 2014, 49(3): 530-537. |
| [6] |
熊敏, 王勇献. 面向CPU+MIC混合易购平台的地震波叠前时间偏移算法并行与优化策略[J]. 计算机工程与科学, 2015, 37(1): 13-22. XIONG Min, WANG Yongxian. Parallel optimization of the seismic wave PKTM algorithm on CPU+MIC heterogeneous platform[J]. Computer Engineering & Science, 2015, 37(1): 13-22. |
| [7] |
蔡志成, 顾汉明, 成景旺, 等. 大规模变网格三维地震正演MPI并行策略与实现[J]. 石油地球物理勘探, 2017, 52(3): 468-476. CAI Zhicheng, GU Hanming, CHENG Jingwang, et al. Parallel large-scale variable grid 3D seismic wave modeling[J]. Oil Geophysical Prospecting, 2017, 52(3): 468-476. |
| [8] |
马召贵, 赵改善, 武港山, 等. 起伏地表叠前时间偏移的多级并行优化技术[J]. 石油物探, 2013, 52(3): 280-287. MA Zhaogui, ZHAO Gaishan, WU Gangshan, et al. Multi-level parallel optimization technique for pre-stack time migration from rugged topography[J]. Geophysical Prospecting for Petroleum, 2013, 52(3): 280-287. DOI:10.3969/j.issn.1000-1441.2013.03.009 |
| [9] |
Alves M M, Pestana R D C, Silva R A P D, et al. Accelerating pre-stack Kirchhoff time migration by manual vectorization[J]. Concurrency & Computation Practice & Experience, 2016. |
| [10] |
李肯立, 彭俊杰, 周仕勇. 基于CUDA的Kirchhoff叠前时间偏移算法设计与实现[J]. 计算机应用研究, 2009, 26(12): 4474-4477. LI Kenli, PENG Junjie, ZHOU Shiyong. Implement Kirchhoff prestack time migration algorithm on CUDA architecture[J]. Application Research of Computers, 2009, 26(12): 4474-4477. DOI:10.3969/j.issn.1001-3695.2009.12.020 |
| [11] |
喻勤, 张少华, 孔选林. 基于MPI和CUDA的转换波Kirchhoff叠前时间偏移并行计算[J]. 石油物探, 2013, 52(1): 60-64. YU Qin, ZHANG Shaohua, KONG Xuanlin. Converted-wave Kirchhoff prestack time migration parallel computation based on MPI+CUDA[J]. Geophy-sical Prospecting for Petroleum, 2013, 52(1): 60-64. DOI:10.3969/j.issn.1000-1441.2013.01.010 |
| [12] |
亢永敢, 赵改善, 魏嘉, 等. 基于Hadoop的Kirchhoff叠前时间偏移并行算法[J]. 石油地球物理勘探, 2015, 50(6): 1213-1218. KANG Yonggan, ZHAO Gaishan, WEI Jia, et al. Para-llel algorithms of Kirchhoff prestack time migration based on Hadoop[J]. Oil Geophysical Prospecting, 2015, 50(6): 1213-1218. |
| [13] |
刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现[J]. 地球物理学报, 2009, 52(12): 3101-3108. LIU Guofeng, LIU Hong, LI Bo, et al. Method of prestack time migration of seismic data of moutainous regions and its GPU implementation[J]. Chinese Journal of Geophysics, 2009, 52(21): 3101-3108. |
| [14] |
杨震, 芦俊, 王赟, 等.转换波时距曲线精度对比[C].中国地球科学联合学术年会, 北京, 2015.
|
| [15] |
Alkhalifah T, Tsvankin I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [16] |
Dai H. Parallel processing of prestack Kirchhoff time migration on a PC cluster[J]. Computers & Geosciences, 2005, 31(7): 891-899. |
| [17] |
Yao L, Ji X, Liu S, et al.Parallel implementation and performance comparison of BICGStab for massive sparse linear system of equations on GPU libraries[C].The 12th Annual International Conference on Advanced and Trusted Computing(UIC-ATC-ScalCom-CBDCom-IoP), Beijing, China, 2015, 603-608. https://www.researchgate.net/publication/307786008_Parallel_Implementation_and_Performance_Comparison_of_BiCGStab_for_Massive_Sparse_Linear_System_of_Equations_on_GPU_Libraries
|
| [18] |
Panetta J, Teixeira T, de Souza Filho P R P, et al. Accelerating time and depth seismic migration by CPU and GPU cooperation[J]. International Journal of Parallel Programming, 2012, 40(3): 290-312. DOI:10.1007/s10766-011-0185-2 |
| [19] |
Shi X, Li C, Wang S. Computing prestack Kirchhoff time migration on general purpose[J]. Computers & Geosciences, 2011, 37(10): 1702-1710. |
| [20] |
Rahmad M H, Meng S S, Karuppiah Ek, et al.Comparision of CPU and GPU implementation of computing absolute difference[C].International Conference on Control System, Computing and Engineering(ICCSCE), IEEE, Penang, Malaysia, 2011, 132-137. https://www.researchgate.net/publication/254029620_Comparison_of_CPU_and_GPU_implementation_of_computing_absolute_difference
|
| [21] |
白洪涛, 范翠松, 李昂, 等. 基于OpenMP+MPI的2.5维电磁场正演并行化方法[J]. 石油地球物理勘探, 2015, 50(1): 170-176. BAI Hongtao, FAN Cuisong, LI Ang, et al. 2.5 dimension eletromagnetic forward parallel computing based on MPI+OpenMP[J]. Oil Geophysical Prospecting, 2015, 50(1): 170-176. |
| [22] |
Tian Xinmin, Bik Aart, Girkai Milind, et al. Intel OpenMP C++/Fortran compiler for hyper-threading technology:Implementation and Performance[J]. Intel Technology Journal, 2002, 6(1): 1-11. |
| [23] |
王玉凤.三维多波地震资料逆时偏移成像技术及GPU并行实现[D].山东青岛: 中国海洋大学, 2014. WANG Yufeng.Reverse-time Migration Imaging and GPU Parallel Implementation of 3D Multi-wave Seismic Data[D].Ocean University of China, Qingdao, Shandong, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D547982 |
| [24] |
喻勤, 程冰洁, 孔选林. 基于CUDA的转换波Kirchhoff叠前时间偏移算法研究与实现[J]. 石油地球物理勘探, 2013, 48(1): 58-63. YU Qin, CHENG Bingjie, KONG Xuanlin. Converted-wave Kirchhoff prestack time migration based on CUDA[J]. Oil Geophysical Prospecting, 2013, 48(1): 58-63. |



 季晓慧, 北京市海淀区学院路29号中国地质大学(北京)信息工程学院, 100083。Email:
季晓慧, 北京市海淀区学院路29号中国地质大学(北京)信息工程学院, 100083。Email: