② 中国地质大学(北京)地球物理与信息技术学院, 北京 100089;
③ 中石化石油工程地球物理有限公司, 北京 100020;
④ 东方地球物理公司培训中心, 河北涿州 072750
② School of Geophysics and Information Technology, China University of Geosciences(Beijing), Beijing, 100089 China;
③ SINOPEC Geophysical Corporation, Beijing 100020, China;
④ BGP Training Center, CNPC, Zhuozhou, Hebei 072750, China
从微地震数据中提取微地震事件,可实时监测裂缝的空间位置与尺度,为后续压裂参数的调整与控制提供数据支撑,微地震监测对油气开发具有重要的指导意义[1]。
当前微地震监测面临的主要问题是资料信噪比较低[2-4],甚至有效信号被噪声完全掩盖。这对以初至拾取为基础的震源定位、压裂预测、机制分析等后续工作造成了严重影响。因此,针对低信噪比或超低信噪比的微地震资料,选择合理有效的初至拾取方法是微地震资料处理的关键。
通常,初至拾取以信号与噪声在振幅、频率、偏振等方面的差异为基础。常采用长短时窗平均能量比(STA/LTA)法[5-7]、基于自回归模型的Aksike信息准则(AIC)法[8]、相关法[9-12]、偏振分析法[13]、二分法[14]、分维相关法、时频分析法、神经网络法[15]、独立分量法[16]、基于高阶统计量的PAI-S/K法[17]以及基于小波分解的高阶统计初至拾取方法[18]。Coppens[19]对不同时窗内不同炮检距道集的能量进行统计相关分析,提出一种自动定位初至点的方法,有效提高了拾取精度;邹红星[20]提出一种基于自回归模型的判读法,该方法具有一定自适应能力,可对不同噪声影响程度的接受信息进行初至拾取。贾瑞生等[21]、蔡剑华等[22]基于经验模态分解(EMD)和本征模态函数(IMF)重构对低信噪比信号去噪,然后应用正交性指标与能量保存度指标对传统EMD中的端点效应进行压制,从而实现震相初至的拾取,其应用效果优于常规基于AIC准则的拾取方法。谭玉阳等[23]提出了基于信号信噪比构造不同检测函数的初至拾取算法(SLPEA),通过综合考虑有效信号与环境噪声间的多种特征差异,提高拾取过程的抗噪能力,但时窗的选择依据并不明确,需依赖经验或反复调试。
在前人的基础上,本文基于三分量间有效成分的特征相似性,采用CEEMDAN算法对各分量信号进行分解,然后用各阶IMF构建三分量IMF矩阵,再进行主成分分析(PCA),提取主成分特征,达到对低信噪比微地震资料有效波初至拾取的目的。通过对不同信噪比合成信号与实测信号的处理,证实该方法具有很强的抗噪能力,适用于有效信号被噪声掩盖的低信噪比微地震资料。
1 方法原理 1.1 CEEMDAN算法原理EMD可将信号x(t)分解为一系列IMF,但信号需要满足两个条件:①极值点数与过零点数相等或相差不超过一个;②上、下包络线的均值在各处均为0。
对于实际非平稳时变信号,常规EMD会受到模态混叠的影响。通过引入正态分布的白噪声,形成噪声辅助信号处理方法(NADA),即为常用的EEMD[24]。而本文采用基于改进EEMD方法——CEEMDAN算法,通过在原始信号上加入有限方差约束的多组独立同分布自适应白噪声,得到含噪信号的集合。该改进方法可进一步降低迭代次数,压缩频率混叠区域,提高收敛性能,对于非平稳信号不同频率成分具有更高的分辨能力。
对信号x(n)的CEEMDAN的实现步骤如下。
(1) 生成含噪信号集
| $ {x^i}\left( n \right) = x\left( n \right) + {w^i}\left( n \right) $ | (1) |
式中wi(n)(i=1,2,…,I)为满足高斯分布的噪声,I为集合样本数;
(2) 对xi(n)进行EMD,得到各样本的一阶IMF F1i,再计算其均值作为x(n)的一阶IMF
| $ {{\tilde F}_1}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {F_1^i} $ | (2) |
(3) 计算一阶残差量
| $ {r_1}\left( n \right) = x\left( n \right) - {{\tilde F}_1}\left( n \right) $ | (3) |
(4) 计算二阶IMF
| $ {{\tilde F}_2}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}\left\{ {{r_1}\left( n \right) + {\varepsilon _1}{E_1}\left[ {{w^i}\left( n \right)} \right]} \right\}} $ | (4) |
式中:Ej(·)表示信号的j阶IMF;εj为控制白噪能量的参数,Wu等[24]认为对于主频较高的信号,取值应较小,反之较大,本文采用较小常量进行试算。
(5) 对于k(k=2,3,…,K,K为设置的最高IMF阶次)阶分量,计算k阶残差
| $ {r_k}\left( n \right) = {r_{k - 1}}\left( n \right) - {{\tilde F}_k}\left( n \right) $ | (5) |
(6) 计算k+1阶分量
| $ {{\tilde F}_{k + 1}}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}\left\{ {{r_k}\left( n \right) + {\varepsilon _k}{E_k}\left[ {{w^i}\left( n \right)} \right]} \right\}} $ | (6) |
(7) 重复步骤(5)、步骤(6)直到残差不可再分解或达到最高IMF阶次。
最终残差满足
| $ R\left( n \right) = x\left( n \right) - \sum\limits_{k = 1}^K {{{\tilde F}_k}\left( n \right)} $ | (7) |
信号可表示为
| $ x\left( n \right) = \sum\limits_{k = 1}^K {{{\tilde F}_k}\left( n \right)} + R\left( n \right) $ | (8) |
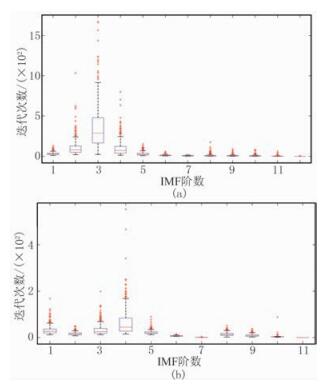
与传统EEMD方法相比,CEEMDAN算法最终得到的各阶IMF分量对原始信号频率成分的表征不同。如图 1所示,对3~6阶IMF分量进行频谱对比,可见传统EEMD各分量间能量差异较大,频率混置区较大。而CEEMDAN方法得到的各IMF分量间能量均衡,频率混叠区较窄,对于非平稳信号,不同频率成分具有更高的分辨能力。通过对心电图信号(图 1a)的测试考察其计算性能,该信号具有非平衡性、非线性与随机性,具有丰富的频率成分,适合用于时频分析方法测试。该测试信号的各阶分量的迭代次数箱形图如图 2所示,可见CEEMDAN各阶分量的迭代次数均显著降低。对于主要承载有效信息的3阶至6阶IMF分量,CEEMDAN方法的计算量约为EEMD方法的1/3。

|
图 1 原始信号(a)及其EEMD(b)和CEEMDAN(c)方法分解的3~7阶IMF频谱对比 |
|
图 2 不同分解方法各阶IMF迭代次数统计结果(a)EEMD;(b)CEEMDAN 蓝色方框为四分位区间;红色横线为中位数;蓝色虚线范围为上下限区间;红色十字点为分布外的异常值 |
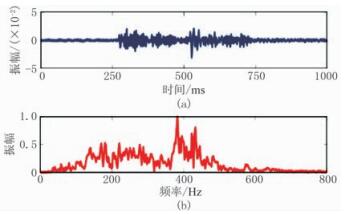
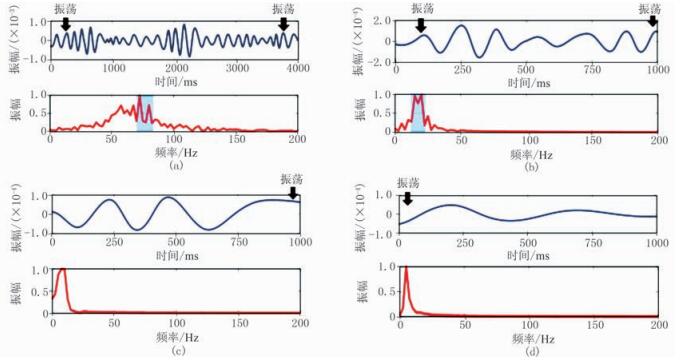
图 3为实测微地震信号及其频谱,信号采样间隔为0.25ms。图 4为实际微地震数据传统EMD方法分解的6~9阶IMF及其频谱。各阶IMF在靠近端点处产生较大幅度的振荡,并且在6阶和7阶IMF对应的频谱上均显示了两个明显峰值(图 4a、图 4b中的蓝色区域),明显包含两组频率成分,表明存在明显的模态混叠现象[25-26]。
|
图 3 实际微地震信号(上)及其频谱(下) |
|
图 4 实际微地震信号传统EMD方法6~9阶IMF分解结果(上)及其频谱(下) (a)6阶;(b)7阶;(c)8阶;(d)9阶 |
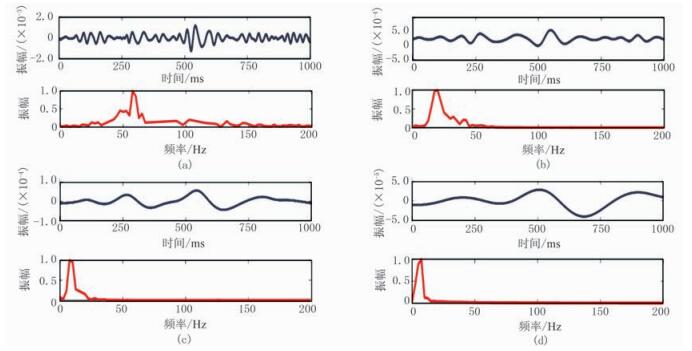
图 5为实际微地震数据CEEMDAN方法分解的6~9阶IMF分量及其频谱,端点附近的异常振荡得到有效压制,且各阶IMF对应的频谱均无明显的多峰现象,模态混叠现象得到有效消除。这是因为CEEMDAN方法利用高斯白噪声频率均匀分布的统计特征,向原始信号中加入不同的白噪声,使信号在不同尺度上具有连续性,并通过在分解时的每一阶段添加特定白噪声,并计算一个唯一残差以得到每个IMF分量,使原始信号的模态频谱分离效果更好,端点效果的影响显著降低。
|
图 5 实际微地震信号CEEMDAN方法6~9阶IMF分解结果(上)及其频谱(下) (a)6阶;(b)7阶;(c)8阶;(d)9阶 |
通常采用三分量检波器采集微地震数据,有效信号在各分量上能量不同,但初至点一致、有效成分波形高度相似,故可通过对三分量信号先进行PCA,再进行特征提取。微地震信号中常出现的噪声为近似满足独立高斯分布的自然噪声与低频震荡。通过CEEMDAN分解,不同阶次的IMF承载原始信号中的不同信息。由于原信号中噪声能量强于有效成分,故在各阶IMF中,仍存在噪声能量,可采用PCA对三分量IMF矩阵提取主成分。三分量数据的k阶IMF矩阵可表示为
| $ \mathit{\boldsymbol{M}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}_x^k}\\ {\mathit{\boldsymbol{D}}_y^k}\\ {\mathit{\boldsymbol{D}}_z^k} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {D_x^k\left( 1 \right)}&{D_x^k\left( 2 \right)}& \cdots &{D_x^k\left( N \right)}\\ {D_y^k\left( 1 \right)}&{D_y^k\left( 2 \right)}& \cdots &{D_y^k\left( N \right)}\\ {D_z^k\left( 1 \right)}&{D_z^k\left( 2 \right)}& \cdots &{D_z^k\left( N \right)} \end{array}} \right] $ | (9) |
式中:Dxk、Dyk、Dzk分别为x、y、z分量的k阶IMF;N为各阶IMF样点数。计算构建的三分量IMF矩阵M(k)的特征向量W,可测得矩阵在各特征向量上的能量分配
| $ {E^k} = \mathit{\boldsymbol{M}}\left( k \right) \cdot \mathit{\boldsymbol{W}} $ | (10) |
其中第一主成分对应的特征向量,应该满足
| $ {\mathit{\boldsymbol{W}}_1} = \arg {\max _{\left\| \mathit{\boldsymbol{W}} \right\| = 1}}\left\{ {\sum\limits_k {\left[ {\mathit{\boldsymbol{M}}\left( k \right) \cdot \mathit{\boldsymbol{W}}} \right]} } \right\} $ | (11) |
写成矩阵形式
| $ {\mathit{\boldsymbol{W}}_1} = \arg {\max _{\left\| \mathit{\boldsymbol{W}} \right\| = 1}}\left[ {{{\left( {{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}}} \right)}^{ - 1}}{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{M}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{M}}\left( k \right)\mathit{\boldsymbol{W}}} \right] $ | (12) |
W1使第一主成分具有最高能量,第一主成分能量可表示为
| $ E_1^k = \mathit{\boldsymbol{M}}\left( k \right) \cdot {\mathit{\boldsymbol{W}}_1} $ | (13) |
将求取的主成分从原矩阵M(k)中剔除,得到剩余矩阵
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over M} }} = \mathit{\boldsymbol{M}}\left( k \right) - \mathit{\boldsymbol{M}}\left( k \right){\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{W}}_1^{\rm{T}} $ | (14) |
令M(k)=
| $ E_S^k = \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over M} }} \cdot {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} }}}_i} $ | (15) |
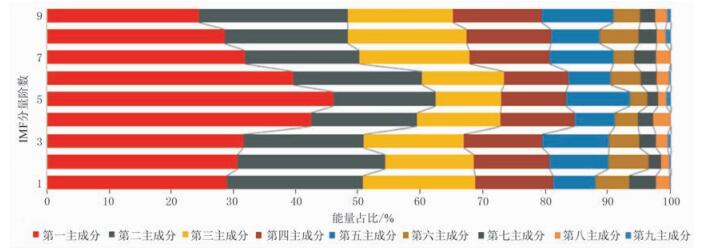
通过对相邻三道三分量微地震记录的各阶IMF进行PCA,统计各主成分所占的能量百分比(图 6),可见4、5、6阶IMF的第一主成分具有明显的能量优势。其原因在于有效成分能量主要落于这三阶IMF的第一主成分中,而其他各阶IMF中,前三项主成分能量差异不大,主要由高能量的噪声构成。通过将高能量噪声等特征较弱的成分分配到各阶IMF中,而特征明显的有效成分能量则集中分配于前几项主成分中,剔除后几项主成分,可对有效成分进行提取。
|
图 6 各阶IMF主成分能量统计 |
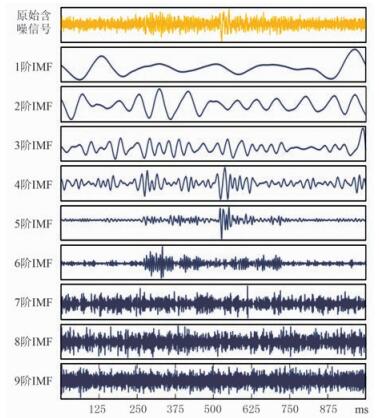
对三分量数据进行CEEMD后,对各阶IMF进行PCA,选取目标主成分,最后加权重构。通过CEEMD分解得到的各阶IMF,反映出信号的不同成分。以图 7含噪信号为例,可以看出,1、2阶IMF主要反映信号的大体趋势,7~9阶IMF则主要承载高频信息。在低信噪比情况下,高频信息主要为噪声,那么有效信号的时域特征则主要由中间的3~6阶IMF反映。因此,重构时,可将1、2阶和7~9阶IMF的权重减少,将3~6阶IMF的权重加大,以便更加突出有效信号的特征。
|
图 7 实测含噪信号及其各阶IMF |
对于重构时各级主成分权重系数的选取,本文的思路如下。
(1) 归一化处理:将各阶IMF主成分单独重构回时域波形,对时域波形进行振幅归一化处理;
(2) 计算各阶时域波形与原始信号所提取的子波间的相关系数;
(3) 以相关系数绝对值作为各阶IMF主成分的重构权值。
1.4 处理流程针对低信噪比条件下的微地震信号,首先对原始信号进行CEEMDAN;然后基于同一检波器中三个分量间的有效成分相关性,在IMF域内从高能量噪声中提取出有效成分特征,并剔除其余成分;最后将剩余的IMF主成分加权重构,得到体现有效信号特征的时域波形。具体处理流程如下:
(1) 对三分量微地震资料进行CEEMDAN;
(2) 对三分量中各阶IMF分量进行PCA,以75%为门槛值,剔除次要成分;
(3) 按不同权值进行IMF主成分重构,得到主成分在时域内波形。
2 模型测试与实际应用采用两组模型对本文方法进行可行性测试与适应性测试。模型Ⅰ采用合成信号与白噪声,测试该方法对噪声掩盖下的具有内在固有特征成分检测能力。模型Ⅱ采用实际有效信号,叠加白噪声,通过调整噪声能量,测试该方法适用的信噪比下限。通过对2000组信号测试,对比基于本文方法与常规基于AIC信息准则的长短视时窗(STA/LTA-AIC)方法的拾取误差。最后对具有不同品质的低信噪比实测资料进行了处理。
2.1 模型Ⅰ设计模型Ⅰ合成信号为
| $ x\left( t \right) = \lambda y\left( t \right) \otimes \left[ {\exp \left( { - 4.5t} \right)\sin \left( {100{\rm{ \mathsf{ π} }}t} \right)} \right] + w\left( t \right) $ | (16) |
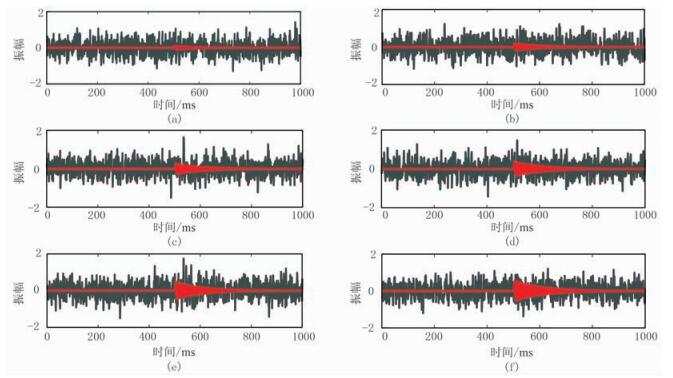
式中:y(t)为标准Ricker子波;“⊗”为褶积运算符;w(t)为白噪声;λ为振幅因子,控制合成信号的信噪比。初至时间设置为500ms,采样间隔为0.25ms,用式(16)生成能量随时间呈指数衰减的正弦信号与标准Ricker子波的褶积作为有效信号(图 8中红线),调整λ得到一系列不同信噪比(SNR)的测试信号(图 8中黑线)。
|
图 8 模型Ⅰ不同SNR的合成信号(红线代表有效信号、黑线代表加噪信号) (a)-19.6268;(b)-13.5986; (c)-10.1930;(d)-8.1059;(e)-6.0972;(f)-4.5360 |
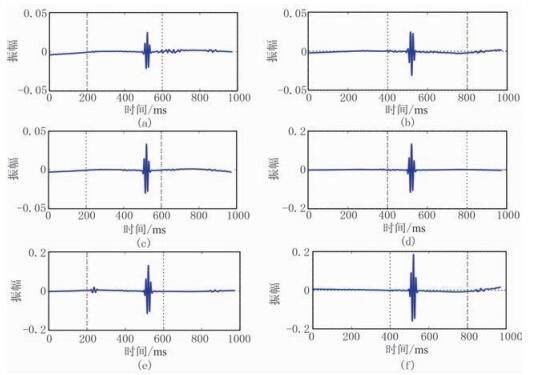
应用本文方法对测试信号进行处理,结果如图 9所示。图 9a中由于信噪比过低,在500~650ms可以看到持续的低能量伪响应,随着SNR的提高,该伪响应的相对能量降低。经过本文方法处理后,初至事件的响应清晰度与分辨率都有显著提升,应用常规方法在该结果上均能得到高精度的初至拾取结果。需要指明,有效事件的检测响应,需要一致地出现在三分量信号中的至少两个分量上,否则不应被视为微地震事件的有效响应。如图 9e中所示,在约210ms处出现单一响应,而在其他分量上则并没有同时出现同步响应,因此将其作为伪响应剔除。该模型测试结果表明,本文方法最低可适用于SNR=-20dB的信号。当SNR低于-20dB,有效信号因能量过低而无法识别。
|
图 9 模型Ⅰ不同SNR数据本文方法处理结果 (a)-19.6268;(b)-13.5986; (c)-10.1930;(d)-8.1059;(e)-6.0972;(f)-4.5360 |
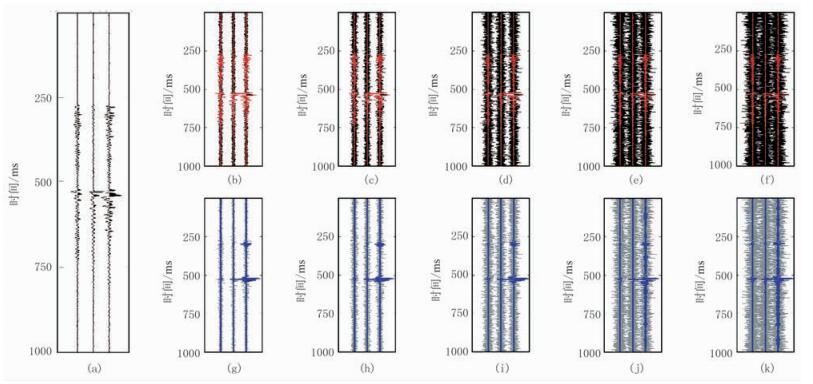
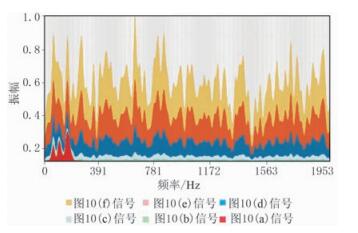
江汉油田水力压裂实验中采集到高信噪比微地震信号(图 10a),采样频率为4000Hz,有效频带为50~220Hz。利用常规方法(如STA/LTA-AIC等)拾取的P波初至为287.50ms,S波初至为527.25ms。加入不同能量的白噪声,获得模型Ⅱ不同SNR的合成数据(图 10b~图 10f),当SNR降至-6.9787dB时(图 10c),STA/LTA方法无法有效拾取初至。不同SNR的测试信号频谱如图 11所示,随着噪声能量的加强,有效频段的能量优势逐渐消失。本文方法对不同SNR的合成数据(图 10b~图 10f)的处理结果如图 10g~图 10k所示,可以看出,即使SNR降到-19.0199dB,处理后仍可对微地震事件进行有效检测。
|
图 10 模型Ⅱ合成信号及本文方法处理结果 (a)原始微地震信号;(b)SNR为-0.9581dB的合成信号;(c)SNR为-6.9787dB的合成信号;(d)SNR为-12.9993dB的合成信号;(e)SNR为-16.5211dB的合成信号;(f)SNR为-19.0199dB的合成信号;(g)图 10b合成信号的检测响应;(h)图 10c合成信号的检测响应;(i)图 10d合成信号的检测响应;(j)图 10e合成信号的检测响应;(k)图 10f合成信号的检测响应 |
|
图 11 模型Ⅱ不同噪声能量下的合成信号频谱 |
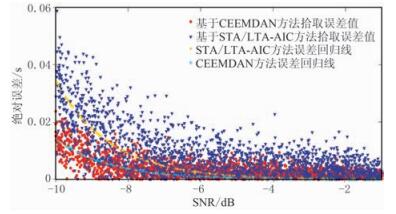
通过对2000组不同信噪比信号的测试,本文方法与常规STA/LTA-AIC法的拾取精度误差统计结果如图 12所示。可见本文方法的拾取精度在SNR为-2~-20dB时,远优于常规STA/LTA-AIC方法。
|
图 12 模型Ⅱ不同方法初至拾取误差统计 |
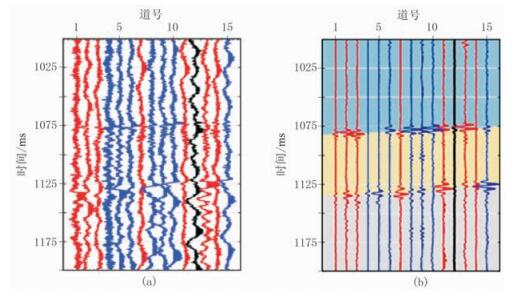
实测井下压裂微地震数据(图 13a)采样频率为4000Hz,部分记录数据品质较差,常规方法拾取效果不理想。图 13a中蓝色显示的记录上可肉眼观测到疑似P波与S波初至波峰,约在1080ms与1130ms处(激发时刻不为0),在红色显示的纪录上仅在1230ms附近可见单一疑似初至波峰,而在黑色显示的纪录上,无任何突变波形体现。本文方法处理结果如图 13b所示,蓝、红色记录均可见明确的检测响应。而对于黑色记录,本文方法没有得到有效的处理结果,原因在于有效成分能量过低,处理后仍被噪声残留成分所淹没。在蓝、红色记录的检测结果基础上,采用常规STA/LTA-AIC方法拾取初至,以图 13b中不同底色(蓝—黄、黄—灰)的分界线标识P波、S波初始时刻。
|
图 13 实际井下微地震数据(a)及本文方法处理结果(b) |
本文针对噪声能量较大、有效信号被淹没的初至拾取难题,提出在CEEMDAN的基础上,利用微地震记录中三分量信号有效成分具有高度相似性,对三分量信号的各阶IMF进行主成分分析,保留有效成分的特征,剔除干扰成分,有效实现了低信噪比资料中的初至特征检测。实际资料的处理结果表明该方法对于在有效信号被噪声掩盖的情况下仍能有效、精确地拾取初至。
| [1] |
杨升宇, 张金川, 黄卫东, 等. 吐哈盆地柯柯亚地区致密砂岩气储层"甜点"类型及成因[J]. 石油学报, 2013, 34(2): 272-282. YANG Shengyu, ZHANG Jinchuan, HUANG Weidong, et al. "Sweet spot" types of reservoirs and genesis of tight sandstone gas in Kekeya area, Turpan-Hami Basin[J]. Acta Petrolei Sinica, 2013, 34(2): 272-282. |
| [2] |
张东晓, 杨婷云. 页岩气开发综述[J]. 石油学报, 2013, 34(4): 792-801. ZHANG Dongxiao, YANG Tingyun. An overview of shale-gas production[J]. Acta Petrolei Sinica, 2013, 34(4): 792-801. |
| [3] |
刘翰林, 吴庆举. 地震自动识别及震相自动拾取方法研究进展[J]. 地球物理学进展, 2017, 32(3): 1000-1007. LIU Hanlin, WU Qingju. Developments of research on earthquake detection and seismic phase picking[J]. Progress in Geophysics, 2017, 32(3): 1000-1007. |
| [4] |
唐杰, 方兵, 蓝阳, 等. 压裂诱发的微地震震源机制及信号传播特性[J]. 石油地球物理勘探, 2015, 50(4): 643-649. TANG Jie, FANG Bing, LAN Yang, et al. Focal mechanism of micro-seismic induced by hydrofracture and its signal propagation characteristics[J]. Oil Geophysical Prospecting, 2015, 50(4): 643-649. |
| [5] |
Allen R. Automatic earthquake recognition and timing from single traces[J]. Bulletin of the Seismological Society of America, 1978, 68(1): 1521-1532. |
| [6] |
刘晗, 张建中. 微地震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展, 2014, 29(4): 1708-1714. LIU Han, ZHANG Jianzhong. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J]. Progress in Geophysics, 2014, 29(4): 1708-1714. |
| [7] |
程仲平, 陈鹰鹏, 何超群. 空变时窗约束地震波初至的拾取方法[J]. 地球物理学进展, 2011, 26(5): 1626-1631. CHENG Zhongping, CHEN Yingpeng, HE Chaoqun. A method of first break picking in seismic data constrained by space-varied time window[J]. Progress in Geophysics, 2011, 26(5): 1626-1631. DOI:10.3969/j.issn.1004-2903.2011.05.015 |
| [8] |
Maeda N. A method for reading and checking phase times in auto-processing system of seismic wave data[J]. Journal of the Seismic Society of Japan, 1985, 38(3): 365-379. |
| [9] |
林凡生, 邹志辉. 基于波形相似性的远震初至拾取方法进展与对比研究[J]. 地球物理学进展, 2017, 32(4): 1597-1606. LIN Fansheng, ZOU Zhihui. Review and comparative study of waveform-similarity based teleseismic first-arrival picking methods[J]. Progress in Geophysics, 2017, 32(4): 1597-1606. |
| [10] |
曹俊海, 顾汉明, 尚新民. 基于局部相关谱约束的多道匹配追踪算法识别微地震信号[J]. 石油地球物理勘探, 2017, 52(4): 704-714. CAO Junhai, GU Hanming, SHANG Xinmin. Microseismic signal identification with multichannel ma-tching pursuit based on local coherence spectrum constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 704-714. |
| [11] |
刘百红, 李建华, 郑四连, 等. 基于局部相似属性的初至自动拾取[J]. 石油地球物理勘探, 2018, 53(3): 449-453. LIU Baihong, LI Jianhua, ZHENG Silian, et al. Automatic first break picking based on local similarity attribute[J]. Oil Geophysical Prospecting, 2018, 53(3): 449-453. |
| [12] |
刁瑞, 吴国忱, 尚新民, 等. 地面微地震有源噪声自动识别与匹配压制方法[J]. 石油地球物理勘探, 2018, 53(2): 311-319. DIAO Rui, WU Guochen, SHANG Xinmin, et al. Microseismic active noise automatic identification and matching denoising[J]. Oil Geophysical Prospecting, 2018, 53(2): 311-319. |
| [13] |
Baer M, Kradolfer U. An automatic phase picker for local and teleseismic events[J]. Bulletin of the Seismological Society of America, 1987, 77(4): 1437-1445. |
| [14] |
陈金焕, 曹永生, 孙成龙, 等. 基于二分法的地震波初至自动拾取算法[J]. 地球物理学进展, 2015, 30(2): 688-694. CHEN Jinhuan, CAO Yongsheng, SUN Chenglong, et al. The algorithm for automatic first-breaks picking on seismic traces based on Dichotomy[J]. Progress in Geophysics, 2015, 30(2): 688-694. |
| [15] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [16] |
宋维琪, 李艳清, 刘磊. 独立分量分析与压缩感知微地震弱信号提取方法[J]. 石油地球物理勘探, 2017, 52(5): 984-989, 1041. SONG Weiqi, LI Yanqing, LIU Lei. Microseismic weak signal extraction based on the independent component analysis and compressive sensing[J]. Oil Geophysical Prospecting, 2017, 52(5): 984-989, 1041. |
| [17] |
Saragiotis C D. PAI-S/K:A robust automatic seismic P phase arrival identification scheme[J]. IEEE Tran-sactions on Geoscience and Remote Sensing, 2002, 40(6): 1395-1404. DOI:10.1109/TGRS.2002.800438 |
| [18] |
盛冠群, 李振春, 王维波, 等. 基于小波分解与高阶统计量的微地震初至拾取方法研究[J]. 石油物探, 2015, 54(4): 388-395. SHENG Guanqun, LI Zhenchun, WANG Weibo, et al. A new automatic detection method of microseismic events based on wavelet decomposition and high-order statistics[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 388-395. DOI:10.3969/j.issn.1000-1441.2015.04.004 |
| [19] |
Coppens F. First arrival picking on common offset trace collections for automatic estimation of static correction[J]. Geophysical Prospecting, 1985, 33(8): 1212-1213. DOI:10.1111/gpr.1985.33.issue-8 |
| [20] |
邹红星.地下核爆炸和天然地震自动识别研究[D].陕西西安: 第二炮兵工程学院, 1995. ZOU Hongxing.On Automatic Recognition of Underground Nuclear Explosion and Natural Earthquake[D].The Second Artillery Institute of Engineering, Xi'an, Shaanxi, 1995. |
| [21] |
贾瑞生, 谭云亮, 孙红梅, 等. 低信噪比微地震P波震相初至自动拾取方法[J]. 煤炭学报, 2015, 40(8): 1845-1852. JIA Ruisheng, TAN Yunliang, SUN Hongmei, et al. Method of automatic detection on micro-seismic P-arrival time under low signal to noise ratio[J]. Journal of China Coal Society, 2015, 40(8): 1845-1852. |
| [22] |
蔡剑华, 王先春. EMD在大地电磁信号分析中的问题及解决方法[J]. 石油地球物理勘探, 2016, 51(1): 204-210. CAI Jianhua, WANG Xianchun. Problems and solutions of EMD in magnetotelluric signal analysis[J]. Oil Geophysical Prospecting, 2016, 51(1): 204-210. |
| [23] |
谭玉阳, 于静, 冯刚, 等. 微地震事件初至拾取SLPEA算法[J]. 地球物理学报, 2016, 59(1): 185-196. TAN Yuyang, YU Jing, FENG Gang, et al. Arrival picking of microseismic events using the SLPEA algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 185-196. |
| [24] |
Wu Z, Huang N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [25] |
郭明威, 倪世宏, 朱家海, 等. 振动信号中HHT/EMD端点延拓方法研究[J]. 振动与冲击, 2012, 31(8): 62-66. GUO Mingwei, NI Shihong, ZHU Jiahai, et al. HHT/EMD end extension method in vibration signal analy-sis[J]. Journal of Vibration and Shock, 2012, 31(8): 62-66. DOI:10.3969/j.issn.1000-3835.2012.08.012 |
| [26] |
曲建岭, 王小飞, 高峰, 等. 基于复数据经验模态分解的噪声辅助信号分解方法[J]. 物理学报, 2014, 63(11): 9-17. QU Jianling, WANG Xiaofei, GAO Feng, et al. Noise assisted signal decomposition method based on complex empirical mode decomposition[J]. Acta Physics Sinica, 2014, 63(11): 9-17. |



 胡瑞卿, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100089。Email:
胡瑞卿, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100089。Email: