在三维地震勘探中,受地表障碍物、观测设备、施工条件等因素的限制,采集到的数据往往出现不规则、缺道、坏道等现象。地震数据的这种不规则性会严重影响后续的多次波压制[1]、偏移成像[2]、四维地震监测[3]等环节。为了消除地震数据不规则的影响,一般采用地震数据规则化方法重建缺失数据。但是,由于数据规则化本质上是一个欠定的反演问题,因此一直以来都是地震数据处理领域十分具有挑战性的研究课题。
目前,地震数据规则化方法主要分为三类:第一类是在信号变换域引入稀疏约束恢复地震数据,如Radon变换[4]、傅里叶变换[5-8]、小波变换[9]、曲波变换[10-11]等;第二类是基于褶积算子的预测滤波器方法,根据已知数据提取局部地震属性(如局部倾角),再扩展该信息以恢复缺失数据[12-18];第三类是模型驱动方法,利用已知的地下模型信息,采用积分延拓算子重建缺失数据,常见的延拓算子包括炮检距延拓[19]、炮点延拓[20]、方位角延拓[21]等。其中前两类方法属于数据驱动的规则化方法,
以往基于模型驱动的数据规则化方法虽然利用了已知的地下模型信息,但是处理精度往往过度依赖于模型的准确性。当地下模型存在一定误差时,规则化结果不理想。本文采用叠前时间偏移和反偏移算子作为积分延拓算子,在成像空间保留了一个维度的冗余信息(如地表炮检距),使映射到成像空间的过程中不丢失模型的误差信息;再通过引入更加稳定的预条件算子,可以在成像空间更好地提取和应用反射波同相轴特征,从而改善数据规则化质量。最后通过理论模型和实际资料处理验证本文方法能否够有效改善数据规则化效果,改进最终成像质量。
1 方法原理 1.1 最小二乘偏移理论基于一阶Born近似理论,反射地震数据d可以通过地下反射系数模型m线性映射得到
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Lm}} $ | (1) |
式中L为线性映射算子,也称为Born正演算子,可以是叠前/叠后反时间偏移算子,也可以是叠前/叠后反深度偏移算子。该算子与速度模型有关,由于规则化过程中速度模型固定,因此式(1)忽略了速度这个参数。最小二乘偏移最小化目标函数为
| $ J\left( \mathit{\boldsymbol{m}} \right) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{Lm}} - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|^2} + \frac{\mu }{2}{\left\| {\mathit{\boldsymbol{Dm}}} \right\|^2} $ | (2) |
式中:dobs为观测数据;D为正则化算子;μ为阻尼因子。式(2)的显式解为
| $ \mathit{\boldsymbol{m}} = {({\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}} + \mu {\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}})^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (3) |
定义一个新的向量p,满足
| $ \mathit{\boldsymbol{m}} = \mathit{\boldsymbol{Pp}} $ | (4) |
则式(2)变为
| $ J\left( \mathit{\boldsymbol{p}} \right) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{LPp}} - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|^2} + \frac{\mu }{2}{\left\| \mathit{\boldsymbol{p}} \right\|^2} $ | (5) |
式中P=D-1为预条件算子。上式的解为
| $ \mathit{\boldsymbol{p}} = {({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{LP}} + \mu \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (6) |
式中I为单位矩阵。将式(6)代入式(4),可得
| $ \mathit{\boldsymbol{m}} = \mathit{\boldsymbol{P}}{({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{LP}} + \mu \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (7) |
Clearbout[22]指出,合理的预条件算子比对应的正则化算子可以更快地加速迭代反演的收敛速度。
由于Born正演(或反偏移)算子L一般无法用矩阵显式表达,而且模型和数据的规模很大,因此一般采用共轭梯度法近似求解式(7),得到分辨率更高、振幅保真度更好的反射系数模型。在相同的理论框架下,选择不同的反偏移算子,可以构建不同的最小二乘偏移算法,如最小二乘叠前时间偏移[23-24]、最小二乘逆时偏移[25-26]等。
1.2 地震数据规则化当观测数据不规则时,式(5)可以修改为
| $ J\left( \mathit{\boldsymbol{p}} \right) = \frac{1}{2}{\left\| {\mathit{\boldsymbol{KLPp}} - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|^2} + \frac{\mu }{2}{\left\| \mathit{\boldsymbol{p}} \right\|^2} $ | (8) |
式中K为Mask算子,该算子的作用是将缺失地震道置0,非缺失地震道保持不变。通过共轭梯度法最小化目标函数式(8)得到最优解popt,再应用预条件算子和反偏移算子,则可以重建缺失地震数据
| $ {\mathit{\boldsymbol{d}}_{{\rm{reg}}}} = \mathit{\boldsymbol{LP}}{\mathit{\boldsymbol{p}}_{{\rm{opt}}}} $ | (9) |
重建后的地震数据可以表示为
| $ {\mathit{\boldsymbol{d}}_{{\rm{reg}}}} = \mathit{\boldsymbol{LP}}{({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{KLP}} + \mu \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (10) |
分三种情况分析式(10)中各项对数据规则化的影响。
第一种情况,忽略Hessian矩阵求逆过程(式(10)中的求逆项),即直接采用偏移+反偏移进行数据重建,式(10)变为
| $ {\mathit{\boldsymbol{d}}_{{\rm{reg}}}} = \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (11) |
这种做法虽然也能够起到数据插值的作用,但是振幅信息不可靠。通过设计一个匹配滤波器可以在一定程度上解决这个问题,但是匹配滤波器的估计本身也是一个欠定的反问题,存在多解性。
第二种情况,忽略预条件项,即直接采用最小二乘偏移+反偏移进行数据重建,式(10)变为
| $ {\mathit{\boldsymbol{d}}_{{\rm{reg}}}} = \mathit{\boldsymbol{L}}{({\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{KL}})^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (12) |
这种做法可以解决偏移+反偏移中存在的振幅匹配问题,但是无法消除数据缺失带来的成像噪声,该噪声反投影到数据域,会降低插值数据的信噪比。
第三种情况,完整地求解式(10),即采用预条件最小二乘偏移+反偏移进行数据重建,这种做法既考虑了振幅不匹配的问题,又可以压制数据不规则带来的噪声。
实际上,预条件算子的选取对数据规则化效果的影响很大。本文采用因果积分算子作为预条件算子,该算子的作用是使振幅随炮检距平滑变化。当速度比较准确时,共成像点道集拉平,满足振幅平滑变化的条件;当速度误差较大时,相邻道之间的振幅差异也不会太大,因此也基本能满足条件;当速度误差很大时,需要进一步采用更加合适的预条件算子,以保留原始数据中的剩余旅行时信息。
1.3 叠前时间偏移/反偏移综合考虑算子的灵活性、计算效率以及预处理阶段对规则化的需求,本文采用Kirchhoff叠前时间反偏移作为线性正演算子L,该算子可以表示为
| $ \mathit{\boldsymbol{d}}\left( {y, H, t} \right) = \mathop \sum \limits_{x, h} w\left( {x, y, H, \tau } \right)\mathit{\boldsymbol{m}}\left( {x, h, \tau } \right) $ | (13) |
式中:m(x,h,τ)为时间偏移共炮检距道集;d(y,H,t)为叠前共炮检距数据;x和h分别为成像域中心点坐标和炮检距;τ为成像域双程旅行时;y和H分别为数据域中心点坐标和炮检距,且H∈[h-Δh, h+Δh], Δh为炮检距间隔;w为加权函数,合适的加权函数可以加快反演的收敛速度。在各向同性介质和直射线假设下,双程旅行时满足双平方根方程
| $ t = \sqrt {\frac{{{\tau ^2}}}{4} + \frac{{{{\left( {y - x - h} \right)}^2}}}{{{v^2}}}} + \sqrt {\frac{{{\tau ^2}}}{4} + \frac{{{{\left( {y - x + h} \right)}^2}}}{{{v^2}}}} $ | (14) |
式中v为均方根速度。
正演算子式(13)的共轭转置LT为Kirchhoff叠前时间偏移,其表达式为
| $ \mathit{\boldsymbol{m}}\left( {x, h, \tau } \right) = \mathop \sum \limits_{y, H} w\left( {x, y, H, \tau } \right)\mathit{\boldsymbol{d}}\left( {y, H, t} \right) $ | (15) |
叠前时间偏移共成像点道集属于扩展模型的一种,该模型除了和物理位置有关,还允许模型随炮检距变化。因此,不论背景速度是否正确,使用该模型均可以模拟出和观测数据相同的反射波旅行时信息,都可以在不发生周波跳跃的前提下正确地匹配波形信息[27],即不论速度正确与否,随着迭代次数的增加,目标函数式(2)中的第一项(数据拟合项)总是可以逐渐趋近于零。但是,如果速度模型不准确,式(2)中的正则化算子需要适应速度不准确带来的旅行匹配误差。
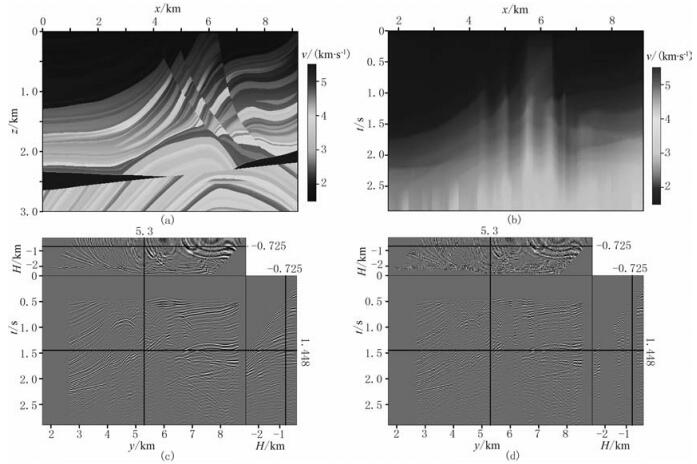
2 数值试验 2.1 Marmousi模型测试图 1a为深度域Marmousi层速度模型,图 1b为Dix公式转换后的时间域均方根速度模型。图 1c是公开的波动方程有限差分正演共炮点道集[28]经过炮检距分选后的(时间,中心点,炮检距)域的叠前数据体。图 1d为图 1c数据随机剔除50%地震道后的叠前数据体。
|
图 1 Marmousi模型及其正演数据体 (a)深度域层速度场;(b)时间域均方根速度场;(c)经过炮检距分选后的正演数据体;(d)随机剔出50%地震道的正演数据体 |
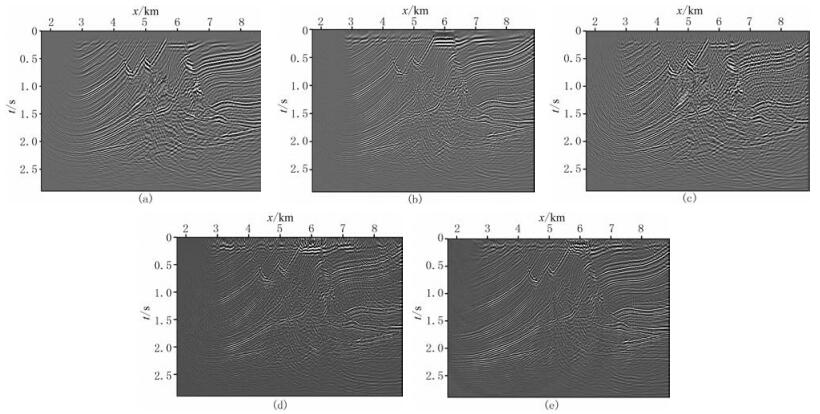
使用均方根速度场(图 1b)和不同的叠前数据体进行叠前时间偏移和最小二乘叠前时间偏移试验。首先对比炮检距为-0.325km的共炮检距成像剖面。图 2a和图 2b为使用完整的地震数据(图 1c)分别进行常规叠前时间偏移和最小二乘叠前时间偏移得到的共炮检距成像剖面,可以看出:尽管Marmousi模型构造复杂,速度横向变化剧烈,但是时间偏移仍然可以大致准确地对地下构造形态进行成像;经过最小二乘反演之后的成像结果分辨率得到显著提高。图 2c、图 2d和图 2e为使用不完整数据(图 1d)分别进行常规叠前时间偏移、最小二乘叠前时间偏移和预条件最小二乘叠前时间偏移得到的共炮检距成像剖面,可以看出,数据缺失给成像结果带来许多噪声,降低了信噪比,经过最小二乘反演,虽然可以提高分辨率,但是并不能消除数据缺失的影响。通过加入合理的先验信息(比如本文所采用的共成像点道集同相轴沿炮检距平滑变化),既可以提高成像分辨率,又可以压制成像噪声。
|
图 2 Marmousi模型完整数据和不完整数据不同偏移方法的共炮检距(炮检距为-0.325km)成像剖面对比 (a)完整数据常规叠前时间偏移;(b)完整数据最小二乘叠前时间偏移;(c)不完整数据常规叠前时间偏移;(d)不完整数据最小二乘叠前时间偏移;(e)不完整数据预条件最小二乘叠前时间偏移 |
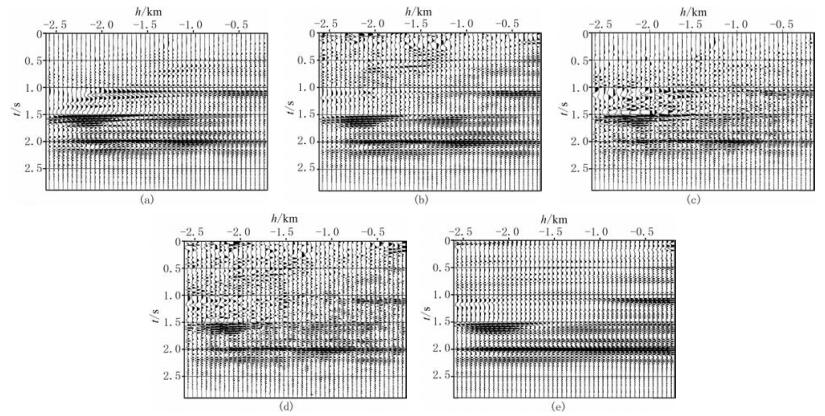
图 3a和图 3b为采用完整数据分别进行常规叠前时间偏移和最小二乘叠前时间偏移的共成像点道集,可以看出:尽管模型复杂,速度横向变化剧烈,但是采用Dix公式转化而来的均方根速度场(图 1b),共成像点道集基本可以被拉平,该信息可以作为先验信息约束反演成像;另外,经过最小二乘反演,成像分辨率有一定的提升,而且浅层大炮检距的拉伸效应也在一定程度上得到压制。图 3c、图 3d、图 3e为采用不完整地震数据分别进行常规叠前时间偏移、最小二乘叠前时间偏移和预条件最小二乘叠前时间偏移的共成像点道集,可以看出,和共炮检距成像剖面类似,数据缺失在成像道集中也引入噪声,通过最小二乘反演能够提高分辨率,但是无法压制这类噪声,利用共成像点道集同相轴沿炮检距平滑变化这个先验信息,再进行预条件最小二乘叠前时间偏移,不仅能够提高分辨率,而且能够有效压制数据缺失带来的噪声。
|
图 3 Marmousi模型完整数据和不完整数据不同偏移方法的3.350km处的炮检距域共成像点道集对比 (a)完整数据常规叠前时间偏移;(b)完整数据最小二乘叠前时间偏移;(c)不完整数据常规叠前时间偏移;(d)不完整数据最小二乘叠前时间偏移;(e)不完整数据预条件最小二乘叠前时间偏移 |
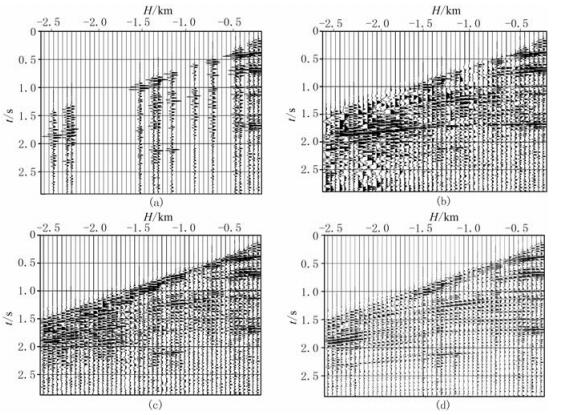
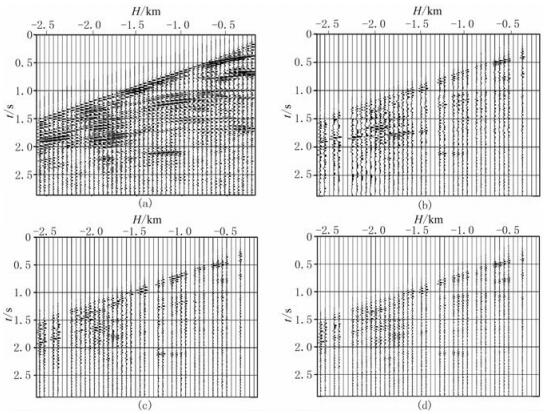
对上述成像结果应用叠前时间反偏移即可以进行数据规则化。图 4为5.300km位置处的CMP道集规则化结果,图 5为规则化结果与原始道集误差。由图 4和图 5可以看出,直接采用常规偏移方法也可以对数据进行插值,但是,由于没有考虑Hessian矩阵的影响,插值结果的振幅信息不准确,需要考虑振幅匹配问题,而这个问题也是一个欠定问题,存在多解性。通过最小二乘反演可以解决振幅匹配问题,但是在数据缺失严重的区域,没有先验信息做约束,容易将成像结果中的噪声反投影到数据空间,使插值结果信噪比较低。预条件最小二乘偏移规则化可以同时解决振幅不匹配和信噪比的问题,使得插值结果振幅属性更加可靠、信噪比更高。
|
图 4 Marmousi模型不同方法数据规则化的5.300km处CMP道集对比 (a)数据缺失的CMP道集;(b)常规叠前时间偏移插值结果;(c)最小二乘叠前时间偏移插值结果;(d)预条件最小二乘叠前时间偏移插值结果 |
|
图 5 Marmousi模型不同方法数据规则化的5.300km处CMP道集误差对比 (a)数据完整的CMP道集;(b)常规叠前时间偏移的插值误差;(c)最小二乘叠前时间偏移的插值误差;(d)预条件最小二乘叠前时间偏移的插值误差 |
需要注意的是,对于本文方法,如果均方根速度比较准确,可以采用沿着炮检距方向的平滑算子作为预条件算子,但是如果均方根速度不准确,则需要采用更加复杂的预条件算子,比如双曲Radon变换、非稳态平面波构建滤波器[8]等。尽管如此,通过偏移算子的作用,成像空间依然会比数据空间更简单,因此有助于简化预条件算子的设计,这也是模型驱动类数据规则化方法的意义所在。
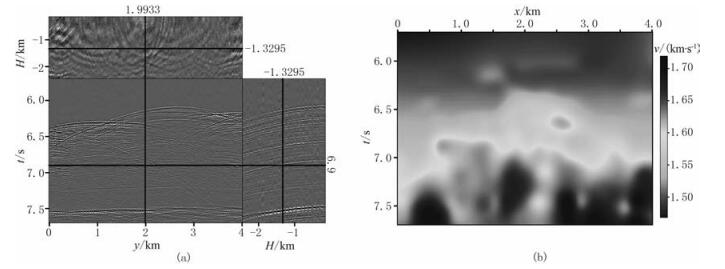
2.2 实际资料处理为了进一步验证本文方法的有效性,对海上实际不规则地震数据进行规则化处理。图 6a为海上实际观测的叠前数据体,受拖缆漂移等因素的影响,观测数据中存在明显的地震道缺失;图 6b为叠加速度分析得到的速度场,本文使用该速度场进行时间域成像,并将其作为模型先验信息进行数据规则化处理。
|
图 6 海上实际观测叠前数据体(a)及其叠加速度场(b) |
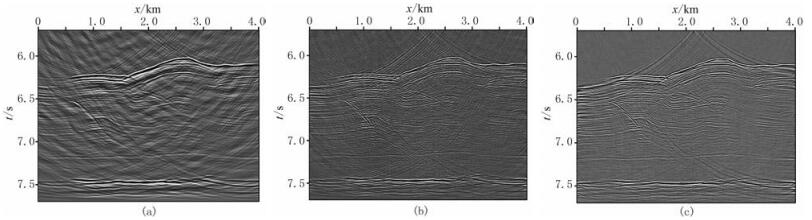
使用图 6b所示的速度场,采用常规叠前时间偏移、最小二乘叠前时间偏移、预条件最小二乘叠前时间偏移进行成像。图 7是炮检距为-0.425km的三种方法共炮检距成像剖面,可以看出,受数据不规则的影响,常规偏移结果中存在明显的成像噪声。经过最小二乘反演,成像分辨率得到显著提高,但是信噪比依然较低。通过在共成像点道集引入平滑约束,进行预条件最小二乘反演之后,不仅可以提高成像分辨率,而且可以有效压制成像噪声。
|
图 7 海上实际数据炮检距为-0.425m的不同方法共炮检距偏移剖面 (a)常规叠前时间偏移;(b)最小二乘叠前时间偏移;(c)预条件最小二乘叠前时间偏移 |
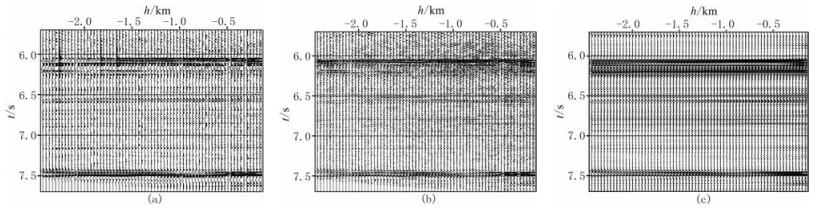
图 8为常规叠前时间偏移、最小二乘叠前时间偏移、预条件最小二乘叠前时间偏移后得到的位于2.360km处的炮检距域共成像点道集,可以看出,共成像点道集基本拉平,说明图 6b所示的速度场比较准确。另外,也能够明显的看出,受数据缺失的影响,常规叠前时间偏移成像道集的信噪比较低(图 8a)。通过最小二乘反演进行成像,虽然可以提高分辨率,但是无法压制数据缺失带来的噪声(图 8b)。进一步在成像道集引入同相轴沿炮检距方向平滑变化这一先验信息,可以显著提高道集的信噪比,同时也能够保持反演带来的分辨率(图 8c)。
|
图 8 2.360km处的不同方法的炮检距域共成像点道集 (a)常规叠前时间偏移;(b)最小二乘叠前时间偏移;(c)预条件最小二乘叠前时间偏移 |
最后,应用叠前时间反偏移对缺失数据进行重建。图 9a为2.360km处的CMP道集,该道集存在明显的数据缺失。图 9b~图 9d分别为采用常规叠前时间偏移、最小二乘叠前时间偏移和预条件最小二乘叠前时间偏移的规则化结果。从结果可以看出,对常规叠前时间偏移结果进行反偏移,虽然也可以起到数据插值的作用,但是由于没有考虑Hessian矩阵的影响,插值出来的振幅信息不可靠。经过最小二乘反演,虽然可以解决振幅信息不匹配的问题,但是受不规则数据引入噪声的影响,插值结果的信噪比较低。通过预条件化技术既可以恢复振幅信息,又能够提高规则化后数据的信噪比。
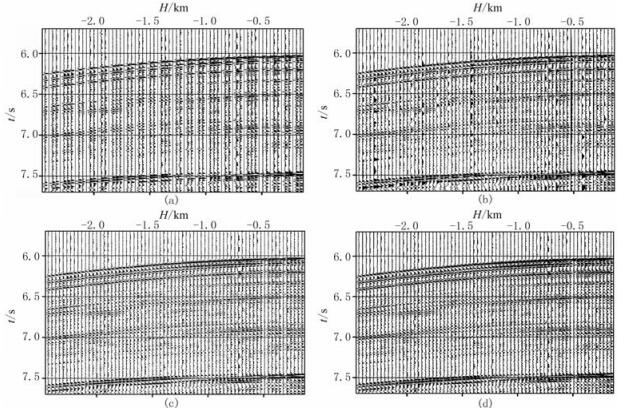
|
图 9 海上实际数据不同方法数据规则化的CMP道集 (a)原始的含缺失地震道的CMP道集;(b)常规叠前时间偏移规则化CMP道集;(c)最小二乘叠前时间偏移规则化结果;(d)预条件最小二乘叠前时间偏移规则化结果 |
本文在最小二乘反演的理论框架下,采用最小二乘叠前时间偏移进行数据规则化,利用合理的预条件算子改善数据规则化的处理效果。从理论模型和实际资料处理结果可以得到如下几点结论及认识:
(1) 叠前时间偏移共成像点道集是一种扩展模型,可以缓解模型驱动类数据规则化方法对模型的过度依赖;
(2) 最小二乘叠前时间偏移可以提高成像分辨率,改善振幅保真度,是本文规则化方法的中间结果,可以用作质量监控和后续的成像结果分析;
(3) 成像空间比数据空间的信息更加简单,更有利于设计预条件算子;
(4) 合理的预条件算子可以改善规则化的效果。当然,在复杂地表、复杂地质条件下,也可以采用更加复杂的成像算子,以简化成像空间预条件算子的设计,从而进一步改善规则化效果,但是相应地计算成本会增加,对速度模型的依赖性也会变强。
| [1] |
Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, part Ⅱ:Practical aspects and examples[J]. Geophysics, 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [2] |
Biondi B L.3-D Seismic Imaging[R].Stanford Exploration Project, 2004.
|
| [3] |
Morice S, Ronen S, Canter P, et al.The impact of positioning differences on 4D repeatability[C].SEG Technical Program Expanded Abstracts, 2000, 19: 1611-1614. https://www.researchgate.net/publication/249857145_The_impact_of_positioning_differences_on_4D_repeatability
|
| [4] |
Trad D, Ulrych T, Sacchi D. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [5] |
Liu B, Sacchi D. Minimum weighted norm interpola-tion of seismic records[J]. Geophysics, 2004, 69(4): 1560-1568. |
| [6] |
Xu S, Zhang Y, Pham D, et al. Antileakage Fourier transform for seismic data regularization[J]. Geophysics, 2005, 70(4): V87-V95. DOI:10.1190/1.1993713 |
| [7] |
王伟, 陈双廷, 王宝彬, 等. 五维规则化技术研究与应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 28-33. WANG Wei, CHEN Shuangting, WANG Baobin, et al. Application of 5D regularization in seismic data processing[J]. Oil Geophysical Prospecting, 2017, 52(S1): 28-33. |
| [8] |
段文胜, 王鹏, 党青宁, 等. 应用匹配追踪傅里叶插值技术实现OVT域连片处理[J]. 石油地球物理勘探, 2017, 52(4): 669-677. DUAN Wensheng, WANG Peng, DANG Qingning, et al. 5D data regularization based on matching pursuit Fourier interpolation for the OVT domain data merging processing[J]. Oil Geophysical Prospecting, 2017, 52(4): 669-677. |
| [9] |
崔兴福, 刘东奇, 张关泉. 小波变换实现地震道内插[J]. 石油地球物理勘探, 2003, 38(增刊1): 93-97. CUI Xingfu, LIU Dongqi, ZHANG Guanquan. Seismic interpolation via wavelet transform[J]. Oil Geophysical Prospecting, 2003, 38(S1): 93-97. |
| [10] |
刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237-246. LIU Guochang, CHEN Xiaohong, GUO Zhifeng, et al. Missing seismic data rebuilding by interpolation based on Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(2): 237-246. |
| [11] |
王本锋, 陆文凯, 陈小宏, 等. 基于3D Curvelet变换的频率域高效地震数据插值方法研究[J]. 石油物探, 2018, 57(1): 65-71. WANG Benfeng, LU Wenkai, CHEN Xiaohong, et al. Efficient seismic data interpolation using three-dimensional Curvelet transform in the frequency domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 65-71. |
| [12] |
Spitz S. Seismic trace interpolation in the f-x domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [13] |
Fomel S.Three Dimension Seismic Data Regulariza-tion[D].Stanford University, 2001.
|
| [14] |
刘洋, 张鹏, 刘财, 等. 地震数据Bregman整形迭代插值方法[J]. 地球物理学报, 2018, 61(4): 1400-1412. LIU Yang, ZHANG Peng, LIU Cai, et al. Seismic data interpolation based on Bregman shaping iteration[J]. Chinese Journal of Geophysics, 2018, 61(4): 1400-1412. |
| [15] |
陈双全, 王尚旭, 季敏. 基于信号保真的地震数据插值[J]. 石油地球物理勘探, 2005, 40(5): 515-517. CHEN Shuangquan, WANG Shangxu, JI Min. Seismic data interpolation based on signal hi-fi[J]. Oil Geophysical Prospecting, 2005, 40(5): 515-517. DOI:10.3321/j.issn:1000-7210.2005.05.006 |
| [16] |
李海山, 吴国忱, 印兴耀. 形态分量分析在地震数据重建中的应用[J]. 石油地球物理勘探, 2012, 47(2): 236-243. LI Haishan, WU Guochen, YIN Xingyao. Morphological component analysis in seismic data reconstruction[J]. Oil Geophysical Prospecting, 2012, 47(2): 236-243. |
| [17] |
刘玉金, 李振春. 局部平面波模型约束下的迭代加权最小二乘反演三维地震数据规则化[J]. 石油地球物理勘探, 2012, 47(3): 418-424. LIU Yujin, LI Zhenchun. Three dimensional data re-gularization by iteratively re-weighted least-squares inversion based on the local plane wave model[J]. Oil Geophysical Prospecting, 2012, 47(3): 418-424. |
| [18] |
祖绍环, 周辉, 陈阳康, 等. 不规则采样的多震源数据整形正则化分离方法[J]. 石油地球物理勘探, 2016, 51(2): 247-253. ZU Shaohuan, ZHOU Hui, CHEN Yangkang, et al. Irregularly sampled multi-source data deblending based on shaping regularization[J]. Oil Geophysical Prospecting, 2016, 51(2): 247-253. |
| [19] |
辛可锋, 王华忠, 王成礼, 等. 叠前地震数据的规则化[J]. 石油地球物理勘探, 2002, 37(4): 311-317. XIN Kefeng, WANG Huazhong, WANG Chengli, et al. Regularization of pre-stack seismic data[J]. Oil Geophysical Prospecting, 2002, 37(4): 311-317. DOI:10.3321/j.issn:1000-7210.2002.04.002 |
| [20] |
Bagaini C, Spagnolini U. 2-D continuation operators and their applications[J]. Geophysics, 1996, 61(6): 1846-1858. DOI:10.1190/1.1444100 |
| [21] |
Biondi B, Fomel S, Chemingui N. Azimuth moveout for 3-D prestack imaging[J]. Geophysics, 1998, 63(2): 574-588. DOI:10.1190/1.1444357 |
| [22] |
Claerbout J F. Earth Soundings Analysis:Processing Versus Inversion[M]. Blackwell Scientific Publications, 2004.
|
| [23] |
Wu D, Wang Y, Liu Y.Least-squares seismic data mapping with prestack time migration and demigration[C].SEG Technical Program Expanded Abstracts, 2015, 34: 3931-3935.
|
| [24] |
刘玉金, 李振春, 吴丹, 等. 局部倾角约束最小二乘偏移方法研究[J]. 地球物理学报, 2013, 56(3): 1003-1011. LIU Yujin, LI Zhenchun, WU Dan, et al. The research on local slope constrained least-squares migration[J]. Chinese Journal of Geophysics, 2013, 56(3): 1003-1011. |
| [25] |
Dai W, Boonyasiriwat C, Schuster G T.3D multi-source least-squares reverse time migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3120-3124. https://www.ingentaconnect.com/content/bsc/gpro/2012/00000060/00000004/art00009
|
| [26] |
Wong M, Ronen S, Biondi B.Least-squares reversetime migration/inversion for ocean bottom data: A case study[C].SEG Technical Program Expanded Abstracts, 2011, 30: 3578-3583.
|
| [27] |
Symes W. Migration velocity analysis and waveform inversion[J]. Geophysical Prospecting, 2008, 56(6): 765-790. DOI:10.1111/gpr.2008.56.issue-6 |
| [28] |
Bourgeois A, Bourget M, Lailly P, et al.Marmousi model and data[C].EAGE Workshop of Practical Aspects of Seismic Data Inversion, 1991, 5-16.
|



 吴丹, 北京市海淀区花园北路环星大厦D座3层中国石油勘探开发研究院西北分院计算机研究所, 100191。
吴丹, 北京市海淀区花园北路环星大厦D座3层中国石油勘探开发研究院西北分院计算机研究所, 100191。