② 闽南师范大学物理与信息工程学院, 福建漳州 363000;
③ 电子科技大学信息地学研究中心, 四川成都 610054
② School of Physics and Information Engineering, Minnan Normal University, Zhangzhou, Fujian 363000, China;
③ Center for Information Geosciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 610054, China
实际地震信号中存在大量随机噪声,这给地震资料的处理和解释带来较大的干扰。目前,去除地震信号随机噪声的方法主要有基于全变分模型的正则化去噪方法[1-4]、基于稀疏表示和字典学习的随机噪声去除方法[5-7]和基于变换域的滤波去噪方法[8-9]等。其中,基于稀疏表示和字典学习的去噪方法需观察数据进行字典训练,在获得较好去噪效果的同时,要耗费大量时间在字典学习上,只要数据量稍大就会引起较大计算量。基于变换域的滤波去噪方法通常需将地震信号从空域映射到变换域中进行截断滤波,易产生吉布斯效应。
全变分(Total variation,TV)模型被证明是一种可有效去除随机噪声的模型,自从它被Rudin等[1]提出之后,就引起学者们的广泛关注[10-16]。TV模型充分挖掘了二维图像的横向纵向梯度信息,较好地契合了自然图像的局部光滑和梯度稀疏等先验知识。该模型被广泛应用于地震图像去噪[10-11]、地震波阻抗反演[12-13]、地震波全波形反演[14]、弱小目标检测[15]和超分辨率分析[16]等众多领域。
由于TV模型假设图像是分片光滑常数,导致TV去噪模型存在较为严重的阶梯效应。为抑制阶梯效应和提高TV模型的去噪效果,Bredies等[17]提出广义全变分(Total generalized variation,TGV)模型。该模型是全变分模型的推广,具有凸性、下半连续性、旋转不变性等众多优秀的数学性质,并能逼近任意多项式[18]。TGV模型同时约束了图像的一阶梯度与二阶梯度,因此有效缓解了全变分模型的阶梯效应。Knoll等[18]将广义全变分模型用于核磁共振成像,取得较好的应用效果。随后,Guo等[19]提出一种基于TGV和剪切波变换的细节保留方法,用于MRI图像重构中。Qin等[20]将这种多约束正则项用于图像解卷积。Kong等[11]则将Shearlet和TGV正则项用于地震信号去噪。
近年来,Liu等[21]和Chen等[22-23]提出了交叠组稀疏正则项。该正则项是一种非分离正则项[24]。它不仅考虑了图像差分域的稀疏性,还挖掘了每个点邻域差分信息,因此可利用图像梯度的结构化稀疏特性。通过交叠组合梯度可提高平滑区域与边界区域的差异,从而抑制TV模型的阶梯效应。Liu等[25]借鉴Chen等[22-23]的成果,将一维交叠组稀疏正则项推广到二维领域,并将其引入各向异性全变分模型,用于椒盐噪声的去噪和解卷积问题。Liu等[26]将交叠组稀疏正则项用于Speckle噪声的去除。
上述工作全部是基于各向异性全变分模型做的推广,然而各向异性全变分模型没有二阶差分的约束,交叠组稀疏梯度的引入对阶梯效应的抑制能力有限。需指出的是,TGV和交叠组稀疏收敛算子对阶梯效应的抑制机理并不一样,前者利用图像一阶、二阶差分约束缓解阶梯效应,后者则通过图像梯度的结构特性抑制阶梯效应。目前,TGV模型与交叠组稀疏收敛算子的交叉研究仍处于起步阶段。
由于经典的TGV模型未考虑图像梯度的邻域结构特性,受Liu等[25]的启发,本文提出一种基于交叠组稀疏收敛算子的改进广义全变分模型(简称为TGV-OGS),并将其应用于地震信号去噪中。鉴于该模型的复杂性,采用交替乘子迭代法(Alternating direction method of multipliers,ADMM)[27-28]对其求解。为提高算法效率,假定处理图像满足周期性边界条件,并采用快速解卷积方法[29-31],巧妙地避免了大型差分矩阵的相乘运算,将差分操作理解为卷积,再利用卷积定理,从频域恢复图像。
在后续实验中,将对比常规各向异性全变分方法(Anisotropic total variation,ATV)[32]、各向异性组稀疏方法(Anisotropic total variation based on overlapping group sparsity,ATV-OGS)[25]、TGV去噪方法及本文去噪方法,并从峰值信噪比(Peak signal to noise ratio,PSNR)、结构相似性(Structural similarity,SSIM)[33]、信噪比(Signal to noise ratio,SNR)[7]及运算时间等指标客观地对比这几种算法。从实验结果可见,本文提出的算法及所构建的模型能进一步改进TGV的去噪性能。
1 预备知识经典的二阶TGV模型[34]定义为
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{S}},{\mathit{\boldsymbol{V}}_h},{\mathit{\boldsymbol{V}}_v}} \left[ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + \mu {\rm{TG}}{{\rm{V}}_2}\left( \mathit{\boldsymbol{S}} \right)} \right]\\ \;\; = \mathop {\min }\limits_{\mathit{\boldsymbol{S}},{\mathit{\boldsymbol{V}}_h},{\mathit{\boldsymbol{V}}_v}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + \mu \left[ {{\alpha _0}\left( {{{\left\| {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}} \right\|}_1} + } \right.} \right.} \right.\\ \;\;\;\;\;\left. {{{\left\| {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}} \right\|}_1}} \right) + {\alpha _1}\left( {{{\left\| {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_h}} \right\|}_1} + } \right.\\ \;\;\;\;\;\left. {\left. {\left. {{{\left\| {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_v}} \right\|}_1} + {{\left\| {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_h} + {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_v}} \right\|}_1}} \right)} \right]} \right\} \end{array} $ | (1) |
这里假定处理图像为方阵;使用傅里叶变换以提高算法速度,假定图像满足周期性边界条件,并将TGV模型写成矩阵卷积形式。式(1)中:S∈RN×N表示待去噪地震信号图像的列向量形式;G∈RN×N为观测地震信号图像的列向量形式;Vh, Vv∈RN×N为TGV正则项中间变量;
假定V0为待收敛矩阵,则其交叠组稀疏邻近算子记为
| $ \begin{array}{l} P\left( \mathit{\boldsymbol{V}} \right) = {\rm{prox}}\gamma \varphi \left( {{\mathit{\boldsymbol{V}}_0}} \right)\\ \;\;\;\;\;\;\;\;\; = \mathop {\min }\limits_\mathit{\boldsymbol{V}} \left[ {\frac{1}{2}\left\| {\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_0}} \right\|_2^2 + \gamma \varphi \left( \mathit{\boldsymbol{V}} \right)} \right] \end{array} $ | (2) |
式中:prox表示迫近算子;
| $ \begin{array}{l} {{\mathit{\boldsymbol{\tilde V}}}_{i,j,K,K}}\\ \;\;\;\; = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{i - {K_l},j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i - {K_l},j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i - {K_l},j + {K_r}}}}\\ {{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j + {K_r}}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{V}}_{i + {K_r},j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i + {K_r},j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i + {K_r},j + {K_r}}}} \end{array}} \right] \end{array} $ | (3) |
式中:
|
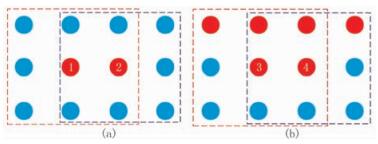
图 1 二维交叠组稀疏示意图 (a)含噪平滑区域纵向梯度场;(b)无噪边界区域纵向梯度场 蓝圈表示灰度值较低像素点,红圈表示灰度值较高像素点 |
假设图 1a表示图像的平滑区域的纵向梯度,且①、②两点被噪声重度污染;图 1b表示图像中边缘区域的纵向梯度,且无噪声污染。为方便讨论,假定蓝色区域灰度值为0,红色区域灰度值为1。由于所选区域为平滑区域,所以红色圈同时表示被噪声重度污染的点。如果采用传统的TV去噪方法,由于图 1a中①、②两个像素点灰度值与边界处③、④两个像素点梯度值相当,这两点就易被误判为图像边缘而保留下来,噪声就无法有效去除。在传统TV模型中,讨论的4个点具有完全相同的横向差分和纵向差分。无论阈值取多大,讨论的4个点梯度都将有一致的变化规律。注意到平滑区域中,连续几个点同时被高噪声污染的概率极小,可以利用这种结构相似性对噪声加以去除。显然,根据式(3)得到的①、②像素的组合梯度为
利用优化—最小化方法(Majorization-minimization,MM)[36]可有效计算式(2)。根据MM算法,最小化P(V)需首先找到一个函数Q(V, U)(U为辅助变量),该函数对所有V, U,都有Q(V, U)≥P(V),并且当且仅当U=V时等号成立。据此,每次计算的Q(V, U)最小值为P(V)的优化值,式(2)的计算可转化为如下迭代运算
| $ {\mathit{\boldsymbol{V}}^{\left( {k + 1} \right)}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{V}} Q\left( {\mathit{\boldsymbol{V}},{\mathit{\boldsymbol{V}}^{\left( k \right)}}} \right) $ | (4) |
考虑到组稀疏正则项的特殊性,并注意到下列不等式的存在
| $ \frac{1}{2}\left( {\frac{{\left\| \mathit{\boldsymbol{V}} \right\|_2^2}}{{{{\left\| \mathit{\boldsymbol{U}} \right\|}_2}}} + {{\left\| \mathit{\boldsymbol{U}} \right\|}_2}} \right) \ge {\left\| \mathit{\boldsymbol{V}} \right\|_2} $ | (5) |
式中,当且仅当U=V时,等号成立。
观察式(2),结合式(5),可以得到
| $ \begin{array}{l} S\left( {\mathit{\boldsymbol{V}},\mathit{\boldsymbol{U}}} \right) = \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left( {\frac{{\left\| {{{\mathit{\boldsymbol{\tilde V}}}_{i,j,K,K}}} \right\|_2^2}}{{{{\left\| {{{\mathit{\boldsymbol{\tilde U}}}_{i,j,K,K}}} \right\|}_2}}} + } \right.} } \\ \;\;\;\;\left. {{{\left\| {{{\mathit{\boldsymbol{\tilde U}}}_{i,j,K,K}}} \right\|}_2}} \right) \ge \varphi \left( \mathit{\boldsymbol{V}} \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\left\| {{{\mathit{\boldsymbol{\tilde V}}}_{i,j,K,K}}} \right\|}_2}} } \end{array} $ | (6) |
将S(V, U)重写为
| $ S\left( {\mathit{\boldsymbol{V}},\mathit{\boldsymbol{U}}} \right) = \frac{1}{2}\left\| {\mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{U}} \right)\mathit{\boldsymbol{v}}} \right\|_2^2 + C\left( \mathit{\boldsymbol{U}} \right) $ | (7) |
式中:v是矩阵V的向量形式;C(U)与V无关,可视为关于V的常数项;D(U)∈RN2×N2,是一个对角矩阵,其对角元素定义为
| $ \begin{array}{l} {\left[ {\mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{U}} \right)} \right]_{m,m}}\\ \;\;{\rm{ = }}\sqrt {\sum\limits_{i = - {K_l}}^{{K_r}} {\sum\limits_{j = - {K_l}}^{{K_r}} {{{\left( {\sum\limits_{{k_1} = - {K_l}}^{{K_r}} {\sum\limits_{{k_2} = - {K_l}}^{{K_r}} {{{\left| {{\mathit{\boldsymbol{U}}_{m - i + {k_1},m - j + {k_2}}}} \right|}^2}} } } \right)}^{\frac{1}{2}}}} } } \end{array} $ | (8) |
结合式(4)、式(7)和式(8),可将式(2)转化为如下迭代优化问题
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}^{\left( {k + 1} \right)}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{V}} \left[ {\frac{1}{2}\left\| {\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_0}} \right\|_2^2 + \gamma \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{V}},{\mathit{\boldsymbol{V}}^{\left( k \right)}}} \right)} \right]\\ \;\;\;\;\;\;\;\; = \mathop {\arg \min }\limits_\mathit{\boldsymbol{V}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_0}} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\gamma \left[ {\frac{1}{2}\left\| {\mathit{\boldsymbol{D}}\left( {{\mathit{\boldsymbol{V}}^{\left( k \right)}}} \right)\mathit{\boldsymbol{v}}} \right\|_2^2 + \mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{V}}^{\left( k \right)}}} \right)} \right]} \right\} \end{array} $ | (9) |
该式为二次规划问题,其迭代最优解为
| $ {\mathit{\boldsymbol{V}}^{\left( {k + 1} \right)}} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \gamma {\mathit{\boldsymbol{D}}^2}\left( {{\mathit{\boldsymbol{V}}^{\left( k \right)}}} \right)} \right]}^{ - 1}}{\mathit{\boldsymbol{v}}_0}} \right\} $ | (10) |
式中:I∈RN2×N2,表示单位矩阵;v0是V0的向量形式;mat表示向量矩阵化运算。
2 模型构建及其求解方法 2.1 基于交叠组稀疏的改进TGV模型将TGV中的L1约束项改进为交叠组稀疏约束项,从而更好地挖掘图像一阶梯度与二阶梯度的差分信息,建模如下
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{S}},{\mathit{\boldsymbol{V}}_h},{\mathit{\boldsymbol{V}}_v}} \left[ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + \mu {\rm{TG}}{{\rm{V}}_{2{\rm{ - OGS}}}}\left( \mathit{\boldsymbol{S}} \right)} \right]\\ \;\; = \mathop {\min }\limits_{\mathit{\boldsymbol{S}},{\mathit{\boldsymbol{V}}_h},{\mathit{\boldsymbol{V}}_v}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + \mu \left\{ {{\alpha _0}\left[ {\varphi \left( {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}} \right) + } \right.} \right.} \right.\\ \;\;\;\;\;\left. {\varphi \left( {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}} \right)} \right] + {\alpha _1}\left[ {\varphi \left( {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_h}} \right) + } \right.\\ \;\;\;\;\;\left. {\left. {\left. {\varphi \left( {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_v}} \right) + \varphi \left( {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_h} + {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_v}} \right)} \right]} \right\}} \right\} \end{array} $ | (11) |
对比经典的TGV模型,本文构建的模型将一阶梯度与二阶梯度矩阵的每个像素点邻域K2个信息点交叠组合,从而更充分挖掘一阶梯度矩阵和二阶梯度矩阵结构特性。显然,每个像素点的邻域梯度与二阶邻域梯度存在一定相似性,该结构稀疏先验知识被交叠组稀疏模型较好地刻画。
2.2 构建模型的ADMM求解为求解式(11)定义的改进TGV模型,利用ADMM框架求解模型。令
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Z}}_1} = {\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}\\ {\mathit{\boldsymbol{Z}}_2} = {\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}\\ {\mathit{\boldsymbol{Z}}_3} = {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_h}\\ {\mathit{\boldsymbol{Z}}_4} = {\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_v}\\ {\mathit{\boldsymbol{Z}}_5} = {\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_h} + {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_v} \end{array} \right. $ |
则根据ADMM原理,可将式(11)的增广拉格朗日函数表达为
| $ \begin{array}{l} J = \mathop {\max }\limits_{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1} \sim {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_5}} \left\{ {\mathop {\min }\limits_{\mathit{\boldsymbol{S}},{\mathit{\boldsymbol{V}}_h},{\mathit{\boldsymbol{V}}_v},{\mathit{\boldsymbol{Z}}_1} \sim {\mathit{\boldsymbol{Z}}_5}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + } \right.} \right.\\ \;\;\;\;{\mu _0}\left[ {\varphi \left( {{\mathit{\boldsymbol{Z}}_1}} \right) + \varphi \left( {{\mathit{\boldsymbol{Z}}_2}} \right)} \right] + {\mu _1}\left[ {\varphi \left( {{\mathit{\boldsymbol{Z}}_3}} \right) + } \right.\\ \;\;\;\;\left. {\varphi \left( {{\mathit{\boldsymbol{Z}}_4}} \right) + \varphi \left( {{\mathit{\boldsymbol{Z}}_5}} \right)} \right] - \\ \;\;\;\;\left\langle {{\beta _0}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1},{\mathit{\boldsymbol{Z}}_1} - \left( {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}} \right)} \right\rangle - \\ \;\;\;\;\left\langle {{\beta _0}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2},{\mathit{\boldsymbol{Z}}_2} - \left( {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}} \right)} \right\rangle - \\ \;\;\;\;\left\langle {{\beta _1}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_3},{\mathit{\boldsymbol{Z}}_3} - \left( {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_h}} \right.} \right\rangle - \left\langle {{\beta _1}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_4},{\mathit{\boldsymbol{Z}}_4} - {\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_v}} \right\rangle - \\ \;\;\;\;\left\langle {{\beta _1}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_5},{\mathit{\boldsymbol{Z}}_5} - \left( {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_h} + {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_v}} \right)} \right\rangle + \\ \;\;\;\;\frac{{{\beta _0}}}{2}\left[ {\left\| {{\mathit{\boldsymbol{Z}}_1} - \left( {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}} \right)} \right\|_2^2 + } \right.\\ \;\;\;\;\left. {\left\| {{\mathit{\boldsymbol{Z}}_2} - \left( {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}} \right)} \right\|_2^2} \right] + \\ \;\;\;\;\frac{{{\beta _1}}}{2}\left[ {\left\| {{\mathit{\boldsymbol{Z}}_3} - {\mathit{\boldsymbol{D}}_{\rm{h}}} * {\mathit{\boldsymbol{V}}_h}} \right\|_2^2 + \left\| {{\mathit{\boldsymbol{Z}}_4} - {\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_v}} \right\|_2^2 + } \right.\\ \;\;\;\;\left. {\left. {\left\| {{\mathit{\boldsymbol{Z}}_5} - \left( {{\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{V}}_h} + {\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{V}}_v}} \right)} \right\|_2^2} \right]} \right\} \end{array} $ | (12) |
式中:μ0=μα0;μ1=μα1;Λi(i=1, 2, …, 5)是拉格朗日乘子;〈X, Y〉表示两个矩阵X与Y的内积。
在ADMM框架下,分离变量及其对偶变量之间与三元组S、Vh、Vv是去耦合的。而三元组中三个变量是相互耦合的,因此需要建立关于三个变量的三元一次方程组。对于S子问题,其子目标函数为
| $ \begin{array}{l} {J_1} = \mathop {\min }\limits_\mathit{\boldsymbol{S}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\frac{{{\beta _0}}}{2}\left[ {\left\| {\left( {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_h}} \right) - \mathit{\boldsymbol{Z}}_1^{\left( k \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1^{\left( k \right)}} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\left. {\left. {\left\| {\left( {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{V}}_v}} \right) - \mathit{\boldsymbol{Z}}_2^{\left( k \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2^{\left( k \right)}} \right\|_2^2} \right]} \right\} \end{array} $ | (13) |
本文假定处理数据满足周期性边界条件,因此可以利用快速傅里叶变换进行卷积计算。
根据卷积定律,两个矩阵在空域卷积,对应到频域,卷积结果的频谱为两个矩阵频谱的点乘。将式(13)做傅里叶变换
| $ \begin{array}{l} {J_1} = \mathop {\min }\limits_{\mathit{\boldsymbol{\bar S}}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{\bar S}} - \mathit{\boldsymbol{\bar G}}} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\frac{{{\beta _0}}}{2}\left[ {\left\| {\left( {{{\mathit{\boldsymbol{\bar D}}}_h} \circ \mathit{\boldsymbol{\bar S}} - {{\mathit{\boldsymbol{\bar V}}}_h}} \right) - \mathit{\boldsymbol{\bar Z}}_1^{\left( k \right)} + \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_1^{\left( k \right)}} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\left. {\left. {\left\| {\left( {{{\mathit{\boldsymbol{\bar D}}}_v} \circ \mathit{\boldsymbol{\bar S}} - {{\mathit{\boldsymbol{\bar V}}}_v}} \right) - \mathit{\boldsymbol{\bar Z}}_2^{\left( k \right)} + \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_2^{\left( k \right)}} \right\|_2^2} \right]} \right\} \end{array} $ | (14) |
式中:·表示·变量的傅里叶变换;符号“。”表示点乘算子。令J1关于S的导数为零,就有
| $ \begin{array}{l} \frac{{\partial {J_1}}}{{\partial \mathit{\boldsymbol{\bar S}}}} = \mathit{\boldsymbol{\bar S}} - \mathit{\boldsymbol{\bar G}} + {\beta _0}\left\{ {{{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)}^ * } \circ \left[ {{{\mathit{\boldsymbol{\bar D}}}_h} \circ \mathit{\boldsymbol{\bar S}} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left( {{{\mathit{\boldsymbol{\bar V}}}_h} + \mathit{\boldsymbol{\bar Z}}_1^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_1^{\left( k \right)}} \right)} \right] + {\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ \\ \;\;\;\;\;\;\;\;\;\left. {\left[ {{{\mathit{\boldsymbol{\bar D}}}_v} \circ \mathit{\boldsymbol{\bar S}} - \left( {{{\mathit{\boldsymbol{\bar V}}}_h} + \mathit{\boldsymbol{\bar Z}}_2^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_2^{\left( k \right)}} \right)} \right]} \right\} = 0 \end{array} $ | (15) |
整理可得
| $ {\mathit{\boldsymbol{K}}_{11}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{12}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{13}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_1} $ | (16) |
其中
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{11}} = {\bf{1}} + {\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_h} + {\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_v}\\ {\mathit{\boldsymbol{K}}_{12}} = - {\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * }\\ {\mathit{\boldsymbol{K}}_{13}} = - {\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * }\\ {\mathit{\boldsymbol{B}}_1} = {\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_1^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_1^{\left( k \right)}} \right) + \\ \;\;\;\;\;\;\;{\beta _0}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_2^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_2^{\left( k \right)}} \right) + \mathit{\boldsymbol{\bar G}} \end{array} \right. $ |
式中:1是元素全为1的矩阵;上角“*”表示共轭运算。
同理,对Vh子目标函数关于Vh求导为零,可得Vh子问题的约束方程为
| $ {\mathit{\boldsymbol{K}}_{21}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{22}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{23}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_2} $ | (17) |
其中
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{21}} = - {\beta _0}{{\mathit{\boldsymbol{\bar D}}}_h}\\ {\mathit{\boldsymbol{K}}_{22}} = {\beta _0}{\bf{1}} + {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_h} + {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_v}\\ {\mathit{\boldsymbol{K}}_{23}} = {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_h}\\ {\mathit{\boldsymbol{B}}_2} = {\beta _0}\left( {\mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_1^{\left( k \right)} - \mathit{\boldsymbol{\bar Z}}_1^{\left( k \right)}} \right) + {\beta _1}\left[ {{{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)}^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_3^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_3^{\left( k \right)}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)}^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_5^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_5^{\left( k \right)}} \right)} \right] \end{array} \right. $ |
详细推导过程不再赘述。
同理,对Vv的子目标函数关于Vv求导为零,可得Vv子问题的约束方程为
| $ {\mathit{\boldsymbol{K}}_{31}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{32}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{33}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_3} $ | (18) |
其中
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{31}} = - {\beta _0}{{\mathit{\boldsymbol{\bar D}}}_v}\\ {\mathit{\boldsymbol{K}}_{32}} = {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_v}\\ {\mathit{\boldsymbol{K}}_{33}} = {\beta _0}{\bf{1}} + {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_h}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_h} + {\beta _1}{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)^ * } \circ {{\mathit{\boldsymbol{\bar D}}}_v}\\ {\mathit{\boldsymbol{B}}_3} = {\beta _0}\left( {\mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_2^{\left( k \right)} - \mathit{\boldsymbol{\bar Z}}_2^{\left( k \right)}} \right) + {\beta _2}\left[ {{{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)}^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_4^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_4^{\left( k \right)}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {{{\mathit{\boldsymbol{\bar D}}}_v}} \right)}^ * } \circ \left( {\mathit{\boldsymbol{\bar Z}}_5^{\left( k \right)} - \mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}_5^{\left( k \right)}} \right)} \right] \end{array} \right. $ |
得到关于S, Vh, Vv三个变量的方程组,即
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{11}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{12}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{13}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_1}\\ {\mathit{\boldsymbol{K}}_{21}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{22}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{23}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_2}\\ {\mathit{\boldsymbol{K}}_{31}} \circ \mathit{\boldsymbol{\bar S}} + {\mathit{\boldsymbol{K}}_{32}} \circ {{\mathit{\boldsymbol{\bar V}}}_h} + {\mathit{\boldsymbol{K}}_{33}} \circ {{\mathit{\boldsymbol{\bar V}}}_v} = {\mathit{\boldsymbol{B}}_3} \end{array} \right. $ | (19) |
该式可用克莱姆法则和快速反傅里叶变换求解
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} = {{\rm{F}}^{ - 1}}\left\{ {{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{B}}_2}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{B}}_3}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|}_ * }/{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|}_ * }} \right\}\\ \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} = {{\rm{F}}^{ - 1}}\left\{ {{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{B}}_2}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{B}}_3}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|}_ * }/{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|}_ * }} \right\}\\ \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} = {{\rm{F}}^{ - 1}}\left\{ {{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{B}}_2}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{B}}_3}} \end{array}} \right|}_ * }/{{\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|}_ * }} \right\} \end{array} \right. $ | (20) |
式中:除法都为按元素点除运算;F-1表示二维逆快速傅里叶变换算子;定义矩阵行列式算子为
| $ \begin{array}{l} {\left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}}}&{{\mathit{\boldsymbol{K}}_{13}}}\\ {{\mathit{\boldsymbol{K}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}}}&{{\mathit{\boldsymbol{K}}_{23}}}\\ {{\mathit{\boldsymbol{K}}_{31}}}&{{\mathit{\boldsymbol{K}}_{32}}}&{{\mathit{\boldsymbol{K}}_{33}}} \end{array}} \right|_ * } = {\mathit{\boldsymbol{K}}_{11}} \circ {\mathit{\boldsymbol{K}}_{22}} \circ {\mathit{\boldsymbol{K}}_{33}} + \\ \;\;\;{\mathit{\boldsymbol{K}}_{12}} \circ {\mathit{\boldsymbol{K}}_{23}} \circ {\mathit{\boldsymbol{K}}_{31}} + {\mathit{\boldsymbol{K}}_{13}} \circ {\mathit{\boldsymbol{K}}_{21}} \circ {\mathit{\boldsymbol{K}}_{32}} - {\mathit{\boldsymbol{K}}_{13}} \circ {\mathit{\boldsymbol{K}}_{22}} \circ {\mathit{\boldsymbol{K}}_{31}} - \\ \;\;\;{\mathit{\boldsymbol{K}}_{12}} \circ {\mathit{\boldsymbol{K}}_{21}} \circ {\mathit{\boldsymbol{K}}_{33}} - {\mathit{\boldsymbol{K}}_{11}} \circ {\mathit{\boldsymbol{K}}_{32}} \circ {\mathit{\boldsymbol{K}}_{23}} \end{array} $ |
对于Z1子问题,其目标子函数为
| $ \begin{array}{l} {J_2} = \mathop {\min }\limits_{{\mathit{\boldsymbol{Z}}_1}} \left\{ {{\mu _0}\varphi \left( {{\mathit{\boldsymbol{Z}}_1}} \right) + \frac{{{\beta _0}}}{2}\left[ {\left\| {{\mathit{\boldsymbol{Z}}_1} - \left( {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} - } \right.} \right.} \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {\left. {\left. {\mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)}} \right) - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1^{\left( k \right)}} \right\|_2^2} \right]} \right\} \end{array} $ | (21) |
根据式(10),可得Z1的更新公式为
| $ \mathit{\boldsymbol{Z}}_{1\left( {n + 1} \right)}^{\left( {k + 1} \right)} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \frac{{{\mu _0}}}{{{\beta _0}}}{\mathit{\boldsymbol{D}}^2}\mathit{\boldsymbol{Z}}_{1\left( n \right)}^{\left( {k + 1} \right)}} \right]}^{ - 1}}\mathit{\boldsymbol{z}}_{1\left( 0 \right)}^{\left( {k + 1} \right)}} \right\} $ | (22) |
式中:Z1(n)(k)表示第k次外循环、第n次内循环(组稀疏收敛迭代循环)迭代更新后的Z1,且有Z1(0)(k+1)=Dh*S(k+1)-Vk(k+1)+Λ1(k),z1表示Z1的列向量形式。
同理,Z2、Z3、Z4和Z5的更新公式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{Z}}_{2\left( {n + 1} \right)}^{\left( {k + 1} \right)} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \frac{{{\mu _0}}}{{{\beta _0}}}{\mathit{\boldsymbol{D}}^2}\mathit{\boldsymbol{Z}}_{2\left( n \right)}^{\left( {k + 1} \right)}} \right]}^{ - 1}}\mathit{\boldsymbol{z}}_{2\left( 0 \right)}^{\left( {k + 1} \right)}} \right\}\\ \mathit{\boldsymbol{Z}}_{3\left( {n + 1} \right)}^{\left( {k + 1} \right)} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \frac{{{\mu _1}}}{{{\beta _1}}}{\mathit{\boldsymbol{D}}^2}\mathit{\boldsymbol{Z}}_{3\left( n \right)}^{\left( {k + 1} \right)}} \right]}^{ - 1}}\mathit{\boldsymbol{z}}_{3\left( 0 \right)}^{\left( {k + 1} \right)}} \right\}\\ \mathit{\boldsymbol{Z}}_{4\left( {n + 1} \right)}^{\left( {k + 1} \right)} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \frac{{{\mu _1}}}{{{\beta _1}}}{\mathit{\boldsymbol{D}}^2}\mathit{\boldsymbol{Z}}_{4\left( n \right)}^{\left( {k + 1} \right)}} \right]}^{ - 1}}\mathit{\boldsymbol{z}}_{4\left( 0 \right)}^{\left( {k + 1} \right)}} \right\}\\ \mathit{\boldsymbol{Z}}_{5\left( {n + 1} \right)}^{\left( {k + 1} \right)} = {\rm{mat}}\left\{ {{{\left[ {\mathit{\boldsymbol{I}} + \frac{{{\mu _1}}}{{{\beta _1}}}{\mathit{\boldsymbol{D}}^2}\mathit{\boldsymbol{Z}}_{5\left( n \right)}^{\left( {k + 1} \right)}} \right]}^{ - 1}}\mathit{\boldsymbol{z}}_{5\left( 0 \right)}^{\left( {k + 1} \right)}} \right\} \end{array} \right. $ | (23) |
且有
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{Z}}_{2\left( 0 \right)}^{\left( {k + 1} \right)} = {\mathit{\boldsymbol{D}}_v} * {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} - \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2^{\left( k \right)}\\ \mathit{\boldsymbol{Z}}_{3\left( 0 \right)}^{\left( {k + 1} \right)} = {\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_3^{\left( k \right)}\\ \mathit{\boldsymbol{Z}}_{4\left( 0 \right)}^{\left( {k + 1} \right)} = {\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_4^{\left( k \right)}\\ \mathit{\boldsymbol{Z}}_{5\left( 0 \right)}^{\left( {k + 1} \right)} = {\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} + {\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_5^{\left( k \right)}\\ \mathit{\boldsymbol{Z}}_{i\left( 0 \right)}^{\left( {k + 1} \right)} = {\rm{vec}}\left( {\mathit{\boldsymbol{Z}}_{i\left( 0 \right)}^{\left( {k + 1} \right)}} \right)\;\;\;\;\;\left( {i = 1,2, \cdots ,5} \right) \end{array} \right. $ |
式中vec(·)表示将矩阵列向量化。
Λ1的目标子函数为
| $ {J_3} = \mathop {\max }\limits_{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}} \left[ {{\beta _0}\left\langle {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1} + ,{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} - \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} - \mathit{\boldsymbol{Z}}_1^{\left( {k + 1} \right)}} \right\rangle } \right] $ | (24) |
利用梯度上升法可得其更新公式
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1^{\left( {k + 1} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1^{\left( k \right)} + \gamma {\beta _0}\left[ {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} - \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} - \mathit{\boldsymbol{Z}}_1^{\left( {k + 1} \right)}} \right] $ | (25) |
其中γ为学习率。
类似地,拉格朗日乘子变量Λ2、Λ3、Λ4和Λ5的更新公式对应为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2^{\left( {k + 1} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2^{\left( k \right)} + \gamma {\beta _0}\left[ {{\mathit{\boldsymbol{D}}_h} * {\mathit{\boldsymbol{S}}^{\left( {k + 1} \right)}} - \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} - \mathit{\boldsymbol{Z}}_2^{\left( {k + 1} \right)}} \right]\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_3^{\left( {k + 1} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_3^{\left( k \right)} + \gamma {\beta _1}\left[ {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} - \mathit{\boldsymbol{Z}}_3^{\left( {k + 1} \right)}} \right]\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_4^{\left( {k + 1} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_4^{\left( k \right)} + \gamma {\beta _1}\left[ {{\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{V}}_v^{\left( {k + 1} \right)} - \mathit{\boldsymbol{Z}}_4^{\left( {k + 1} \right)}} \right]\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_5^{\left( {k + 1} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_5^{\left( k \right)} + \gamma {\beta _1}\left[ {{\mathit{\boldsymbol{D}}_h} * \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} + {\mathit{\boldsymbol{D}}_v} * \mathit{\boldsymbol{V}}_h^{\left( {k + 1} \right)} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{Z}}_5^{\left( {k + 1} \right)}} \right] \end{array} \right. $ | (26) |
至此,本文构建模型的所有子问题都得以解决。将该算法总结为表 1。
|
|
表 1 TGV-OGS算法伪代码 |
将本文算法应用于地震信号,并通过峰值信噪比、结构相似性指示系数、信噪比及运行时间客观评价该算法的去噪性能,并与ATV、ATV-OGS方法以及TGV去噪方法做全面对比。
3.1 评价指标去噪领域最常用评价指标有:峰值信噪比、结构相似性指标、信噪比和运行时间。其中峰值信噪比、结构相似性指标[33]为
| $ {\rm{PSNR}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = 10\lg \frac{{{{\left[ {\max \left( \mathit{\boldsymbol{X}} \right)} \right]}^2}}}{{\frac{1}{{{N^2}}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\left( {{\mathit{\boldsymbol{X}}_{ij}} - {\mathit{\boldsymbol{Y}}_{ij}}} \right)}^2}} } }} $ | (27) |
| $ \begin{array}{l} {\rm{SSIM}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right)\\ \;\; = \frac{{\left[ {2{u_\mathit{\boldsymbol{X}}}{u_\mathit{\boldsymbol{Y}}} + {{\left( {L{k_1}} \right)}^2}} \right]\left[ {2{\sigma _{\mathit{\boldsymbol{XY}}}} + {{\left( {L{k_2}} \right)}^2}} \right]}}{{\left[ {u_\mathit{\boldsymbol{X}}^2 + u_\mathit{\boldsymbol{Y}}^2 + {{\left( {L{k_1}} \right)}^2}} \right]\left[ {\left( {\sigma _\mathit{\boldsymbol{X}}^2 + \sigma _\mathit{\boldsymbol{Y}}^2 + {{\left( {L{k_2}} \right)}^2}} \right.} \right]}} \end{array} $ | (28) |
式中:X是原图;Y是重建图像;max(X)表示原图中最大的灰度值;uX、uY分别是X、Y的平均值;σX2、σY2、σXY2对应地是X、Y、X和Y的协方差;L=512,实验中取L=255;k1=0.05,k2=0.05。
为更好地表征去噪效果,还选用了信噪比参数,定义[7]如下
| $ {\rm{SNR}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = 10\lg \frac{{\left\| \mathit{\boldsymbol{X}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}} \right\|_2^2}} $ | (29) |
本节给出合成地震记录,该记录由20 Hz雷克子波与人工合成反射系数卷积获得。图 2为截取的前50道合成记录,可清晰观察到去噪效果。

|
图 2 合成地震信号 |
为验证交叠组稀疏正则项的有效性,在合成记录中加入0均值、标准差为σ的高斯白噪声,且设定K=3。ATV、ATV-OGS、TGV以及本文方法的测试结果如表 2所示,最优指标用粗体标出。
|
|
表 2 合成地震信号算法性能测试表 |
从表 2中可看到,交叠组稀疏正则项不仅对经典的各向异性TV模型算法性能有所改进,而且对TGV去噪方法有较好的改进。为直观反映其效果,以伪彩色形式(图 3)展示σ=30时上述四种算法的去噪效果。
|
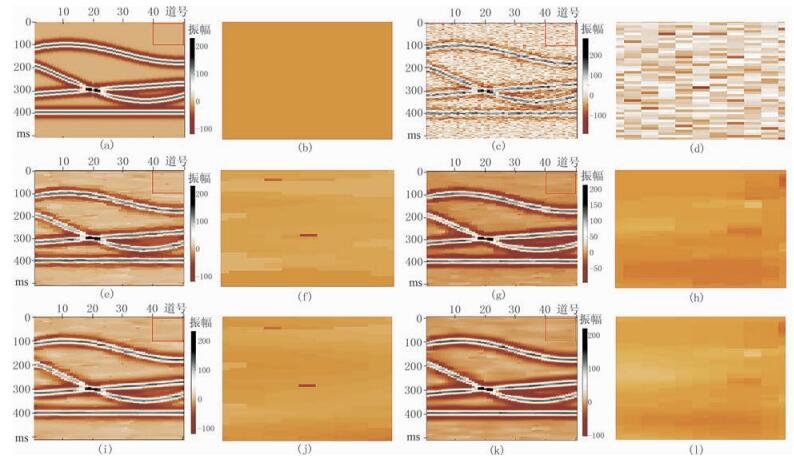
图 3 四种算法去噪效果对比 (a)原图;(b)图a的局部放大;(c)带噪声图;(d)图c的局部放大;(e)ATV去噪结果;(f)图e的局部放大;(g)ATV-OGS去噪结果;(h)图g的局部放大图;(i)TGV去噪结果;(j)图i的局部放大图;(k)TGV-OGV(K=3)去噪结果;(l)图k的局部放大 |
观察图 3中由矩形红色框圈定区域(图 3d),显然是平滑区域,在放大区域中可以看到若干个被重噪声污染的像素;ATV去噪方法在该区域有较明显的块效应。从放大图(图 3f)中可见,仍然有两个像素被重噪声干扰。从图 3h可见,利用交叠组稀疏正则项则非常好地抑制了块效应,且两个重噪声点被去除得较为干净。值得指出的是,各向异性交叠组稀疏方法并未完全抑制ATV的块效应。再观察TGV的去噪结果(图 3i、图 3j),可见TGV去噪方法也对ATV的块效应有较好的抑制作用,在平滑区域获得更加光滑的重构信号。但从图 3j可见,TGV去噪方法对于重噪声污染点也是无能为力的。而本文提出的方法则将交叠组稀疏和TGV的优点结合起来,获得比ATV-OGS和TGV更好的去噪效果。观察图 3l可以看到,本文算法获得的去噪结果在该区域更接近原图。值得注意的是,设定K=3时,算法性能尚未达到最优。
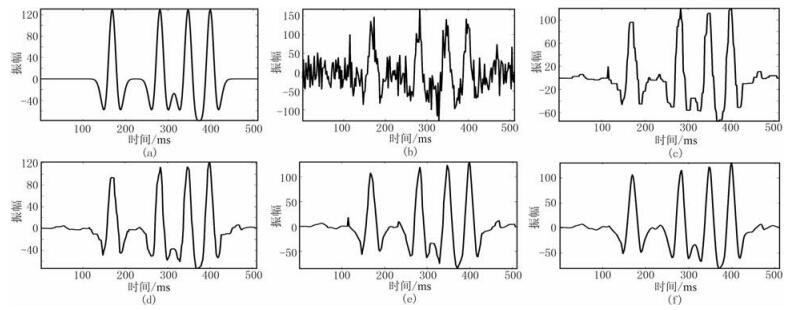
为进一步观察去噪效果,将图 3中六个子图的第40道抽出进行观察(图 4)。从图 4可见ATV存在明显的阶梯效应,而ATV-OGS去噪方法(图 4d)较好地缓解了ATV的阶梯效应,但是去噪结果仍然不够光滑。传统TGV方法也存在类似问题。本文提出的方法在TGV理论框架上结合了组稀疏收敛方法,从而挖掘了数据邻域梯度的结构信息,将两者的优点充分结合,大幅提高了信号的重构质量。在图 4b中50~100ms区间,地震信号被一强幅度噪声严重干扰。该强噪声污染在图 4c和图 4e中依然存在,这反映传统ATV和TGV方法的重大缺陷,即两种算法都是以单一像素点为处理对象,孤立地迭代,这样就无法充分考虑到信号邻域的梯度相似信息。而ATV-OGS方法和本文提出方法则不存在这种问题,观察图 4d和图 4f可知,基于交叠组稀疏收敛方法的ATV-OGS和TGV-OGS都能有效去除50~100ms存在的尖峰干扰。显然,本文提出方法充分利用了地震信号的邻域相似性,这对去除大幅度的噪声污染尤其有效。通过上述实验,得出如下结论,各向异性交叠组稀疏去噪方法能有效利用图像一阶梯度的结构特性,而广义全变分模型中存在一阶和二阶图像梯度,这些梯度同样含有邻似性,将交叠组稀疏正则项与TGV模型充分结合,进一步提升了TGV模型的去噪能力。
|
图 4 四种算法单道去噪效果对比 (a)原图;(b)带噪声图;(c)ATV去噪结果;(d)ATV-OGS去噪结果;(e)TGV去噪结果;(f)TGV-OGV(K=3)去噪结果 |
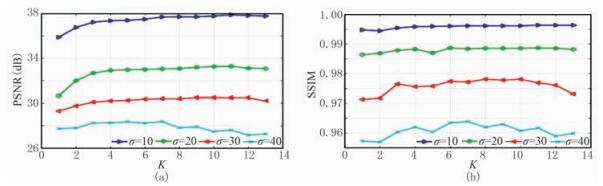
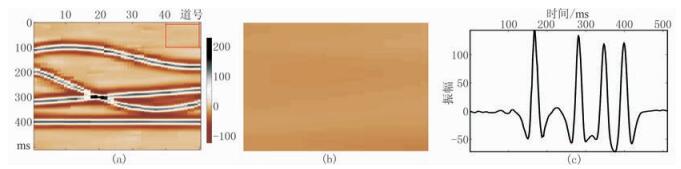
对本文算法的交叠组合数K进行测试对比,以评价其对算法的整体效果。采用PSNR和SSIM两个指标对算法进行客观评价,针对不同高斯噪声水平,将K从1到13连续变化,并记录PSNR和SSIM值,详见图 5。从图 5可以看到,随着K的增大,在不同噪声下,K对PSNR和SSIM起到的作用是不一样,显然,在低噪声的时候(例如σ=10),K取11时,PSNR和SSIM都达到峰值,若K继续加大,PSNR则下降。当σ=10时,本文算法的PSNR达到最高值37.7846 dB,高出TGV算法1.905 dB。从图 5可见,当噪声较低的时候,图像的邻域信息对算法性能起到了正面作用。然而,K也不宜取得过大,否则可能会取到邻域中图像变化剧烈的区域,这种情况下,PSNR和SSIM就要下降。而当噪声较大时,邻域梯度的结构特性被破坏得比较严重,这种情况下,K稍大就会导致算法性能下降,例如当σ=40时,K=7时获得了PSNR和SSIM的最高值。从图 5a中可见,当标准差为30时,设定K=9可以令PSNR值达到最高。图 6展示了在标准差为30时,算法参数K=9的去噪效果,其PSNR为30.4824dB,SSIM为0.9789,SNR为15.8382dB,均远超过经典TGV去噪模型。对比图 6b与图 4l可见,当K设置得足够合理,恢复出来的地震信号将更加符合梯度的稀疏先验知识。再对比图 6c与图 4f可知,当K取值合适时,本文算法的保护边缘能力及对重噪声的抗噪能力更强。
|
图 5 不同σ值的PSNR(a)和SSIM(b)随K值变化曲线的对比 |
|
图 6 TGV-OGV(K=9)去噪效果图 (a)TGV-OGV(K=9)去噪结果;(b)图a的局部放大;(c)图a的第40道地震信号 |
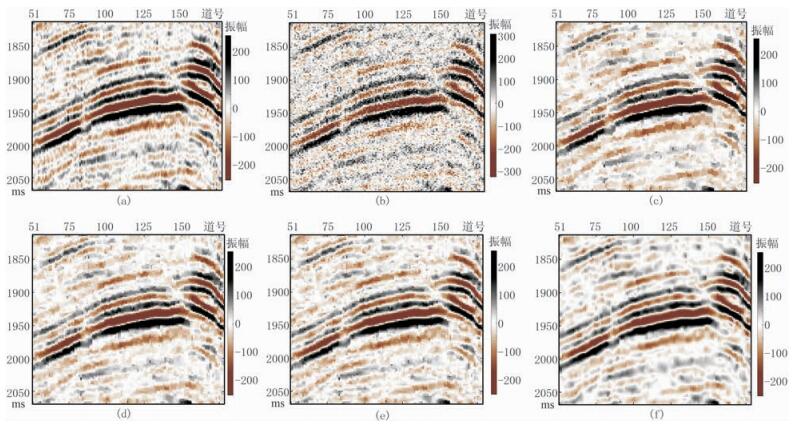
以二维地震信号作为测试信号(图 7a)。该地震信号为叠后地震信号,已经去除了噪声。为客观评价算法性能,在地震信号中加入σ=10,20,30,40的高斯白噪声,对比ATV、ATV-OGS、TGV以及TGV-OGS等算法的去噪性能指标,各项指标被记录在表 3中。表 3显示,对于实际地震信号,本文提出算法的去噪效果最好。
|
图 7 四种算法去噪效果对比 (a)二维地震信号;(b)带噪数据;(c)ATV去噪结果;(d)ATV-OGS去噪结果;(e)TGV去噪结果;(f)TGV-OGV去噪结果 |
|
|
表 3 实际地震信号算法性能测试表 |
图 7展示了σ=30时各种算法的二维地震信号去噪效果,可见本文算法有效去除了人为增加的高斯噪声。对比原地震信号可以发现,本文方法将地震信号中的高频干扰去除得较彻底,不存在ATV方法的块效应问题,且同相轴具有较好的横向连续性。
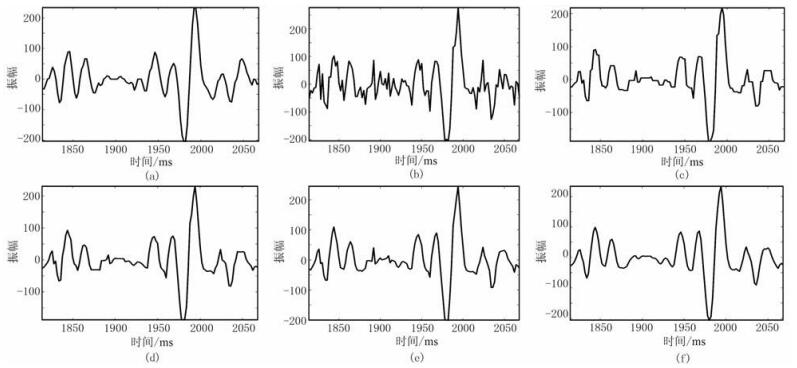
图 8展示了图 7中各个子图中道号为70的单道地震信号。从图 8b可以观察到,在1850~1900ms区间内,地震信号被一个大幅度噪声污染,显然,基于逐点迭代的ATV和TGV方法都无法有效去除该位置的噪声(图 8c和图 8e)。而基于交叠组稀疏收敛方法的ATV-OGS和TGV-OGS方法则非常好地去除了该位置的噪声(图 8d和图 8f)。对比图 8d与图 8f可见,本文提出方法恢复的地震信号更接近原地震信号。从图 8还可知,交叠组稀疏正则项对于平滑区域的高噪声污染有较为显著的效果。
|
图 8 四种算法单道去噪效果对比 (a)原数据;(b)带噪数据;(c)ATV去噪结果;(d)ATV-OGS去噪结果;(e)TGV去噪结果;(f)TGV-OGV(K=7)去噪结果 |
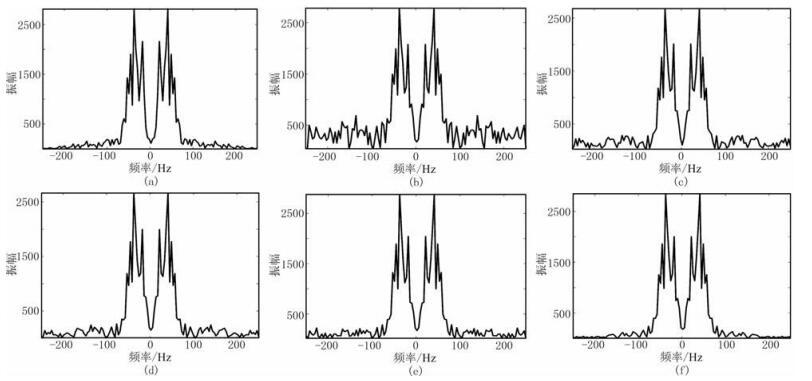
图 9给出图 8各个子图的频谱,可见加噪地震信号存在大量高频干扰,而经过各种去噪方法去噪后的地震信号频谱则一定程度压制了高频干扰。从图 9f可见,在大于100Hz范围,本文方法压制噪声的效果明显好于ATV、ATV-OGS、TGV方法。
|
图 9 图 8数据对应的频谱 |
图 10显示图 7b中加入的噪声(σ=30)和各种方法去除的噪声剖面的对比。观察图 10a的色标可发现,实际加入噪声的幅度范围是[-120, 120];而从图 10b可知,ATV方法估计的噪声范围是[-60, 60],显然低估了噪声幅度;从图 10c可见,ATV-OGS方法估计的噪声范围是[-70, 70],结果更准确些;观察图 10d可知,TGV方法估计的噪声范围是[-50, 50];而本文提出方法(图 10e)估计的噪声范围是[-100, 100],最接近实际加入噪声的幅度。因此,从噪声分布来看,本文方法估计的噪声范围是最接近实际添加噪声的。

|
图 10 四种算法去除噪声的对比 (a)含噪剖面;(b)ATV方法;(c)ATV-OGS方法;(d)TGV方法;(e)TGV-OGV方法 |
本文从交叠组稀疏正则项出发,结合广义全变分定义,在ADMM框架下提出一种改进广义全变分去噪算法,并将其应用于地震信号去噪。该算法充分利用图像一阶、二阶梯度的邻域相似性,提高平滑区域与边界区域的差异性,从而提高去噪的鲁棒性,获得相比于经典TGV更好的去噪性能。
将本文方法与ATV、ATV-OGS、TGV算法进行比较,从实验结果得出如下结论和认识:
(1) 将差分算子视为卷积算子,并结合ADMM能将复杂的模型转换为一系列简单的数学问题,并估计出较为准确的地震信号。
(2) 本文算法去噪能力高于其他各类全变分去噪算法,尤其对平滑区域的大幅度噪声污染有显著的去噪效果,因此,提出算法对噪声更加鲁棒。
(3) 取适当的K值可以有效提升整体去噪性能,在实际应用中需要调节参数取值,若K值取得过小,则邻域信息利用不够充分;反之,若取值过大,则会引入过多不相似的图像块,导致去噪性能下降。
值得注意的是,本文方法提出的通用正则项同样适用于其他各类图像重构问题,如地震波阻抗反演、自然图像去噪、椒盐噪声去除、图像解卷积,核磁共振图像重构等反问题的求解中,针对此于问题有待于深入研究。另外,由于引入MM算法,导致涉及两重循环,运算效率较低,因此算法的效率优化无疑是未来研究热点。
| [1] |
Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D:Nonlinear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
| [2] |
屈勇, 曹俊兴, 朱海东, 等. 一种改进的全变分地震图像去噪技术[J]. 石油学报, 2011, 32(5): 815-819. QU Yong, CAO Junxing, ZHU Haidong, et al. An improved total variation based seismic image denoising techonology[J]. Acta Petrolei Sinica, 2011, 32(5): 815-819. |
| [3] |
Wu L, Chen Y, Jin J, et al. Four-directional fractional-order total variation regularization for image denoising[J]. Journal of Electronic Imaging, 2017, 26(5): 053003. |
| [4] |
Chen Y, Wu L, Peng Z, et al.Fast overlapping group sparsity total variation image denoising based on fast Fourier transform and split Bergman iterations[C].The 7th International Workshop on Computer Science and Engineering, Beijing, 2017, 278-282.
|
| [5] |
张岩, 任伟建, 唐国维. 利用多道相似组稀疏表示方法压制随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 442-450. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression based on sparse representation of multi-trace similarity group[J]. Oil Geophysical Prospecting, 2017, 52(3): 442-450. |
| [6] |
张广智, 常德宽, 王一惠, 等. 基于稀疏冗余表示的三维地震数据随机噪声压制[J]. 石油地球物理勘探, 2015, 50(4): 600-606. ZHANG Guangzhi, CHANG Dekuan, WANG Yihui, et al. 3D seismic random noise suppression with sparse and redundant representation[J]. Oil Geophy-sical Prospecting, 2015, 50(4): 600-606. |
| [7] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-660. ZHOU Yatong, WANG Lili, PU Qingshan. Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-660. |
| [8] |
宋炜, 邹少峰, 欧阳永林, 等. 快速匹配追踪三参数时频特征滤波[J]. 石油地球物理勘探, 2013, 48(4): 519-525. SONG Wei, ZOU Shaofeng, OUYANG Yonglin, et al. Three parameter time-frequency characteristics filter based on fast matching pursuit[J]. Oil Geophysical Prospecting, 2013, 48(4): 519-525. |
| [9] |
魏海涛, 陆文凯, 郑晓东. 基于F-X域预测和全变分的串行滤波器[J]. 石油地球物理勘探, 2011, 46(5): 700-704. WEI Haitao, LU Wenkai, ZHENG Xiaodong. Cascaded filter based on F-X prediction and total variation filter[J]. Oil Geophysical Prospecting, 2011, 46(5): 700-704. |
| [10] |
Kong D, Peng Z, Fan H, et al. Seismic random noise attenuation using directional total variation in the shearlet domain[J]. Journal of Seismic Exploration, 2016, 25(4): 321-338. |
| [11] |
Kong D, Peng Z. Seismic random noise attenuation using shearlet and total generalized variation[J]. Journal of Geophysics and Engineering, 2015, 12(6): 1024-1035. DOI:10.1088/1742-2132/12/6/1024 |
| [12] |
Li S, Peng Z. Seismic acoustic impedance inversion with multi-parameter regularization[J]. Journal of Geophysics and Engineering, 2017, 14(3): 520-532. DOI:10.1088/1742-2140/aa5e67 |
| [13] |
王治强, 曹思远, 陈红灵, 等. 基于TV约束和Toeplitz矩阵分解的波阻抗反演[J]. 石油地球物理勘探, 2017, 52(6): 1193-1199. WANG Zhiqiang, CAO Siyuan, CHEN Hongling, et al. Wave impedance inversion based on TV regularization and Toeplitz-sparse matrix factorization[J]. Oil Geophysical Prospecting, 2017, 52(6): 1193-1199. |
| [14] |
张盼, 韩立国, 巩向博, 等. 基于各向异性全变分约束的多震源弹性波全波形反演[J]. 地球物理学报, 2018, 61(2): 716-732. ZHANG Pan, HAN Liguo, GONG Xiangbo, et al. Multi-source elastic full waveform inversion based on the anisotropic total variation constraint[J]. Chinese Journal of Geophysics, 2018, 61(2): 716-732. |
| [15] |
Wang X, Peng Z, Kong D, et al. Infrared dim target detection based on total variation regularization andprincipal component pursuit[J]. Image and Vision Computing, 2017, 63: 1-9. DOI:10.1016/j.imavis.2017.04.002 |
| [16] |
Huang L L, Xiao L, Wei Z H. Efficient and effective total variation image super-resolution:A preconditioned operator splitting approach[J]. Mathematical Problems in Engineering, 2011, 44-48. |
| [17] |
Bredies K, Kunisch K, Pock T. Total generalized variation[J]. SIAM Journal on Imaging Sciences, 2010, 3(3): 492-526. DOI:10.1137/090769521 |
| [18] |
Knoll F, Bredies K, Pock T, et al. Second order total generalized variation(TGV) for MRI[J]. Magnetic Resonance in Medicine, 2011, 65(2): 480-491. DOI:10.1002/mrm.22595 |
| [19] |
Guo W, Qin J, Yin W. A new detail-preserving regularization scheme[J]. SIAM Journal on Imaging Sciences, 2014, 7(2): 1309-1334. DOI:10.1137/120904263 |
| [20] |
Qin J, Yi X, Weiss S, et al.Shearlet-TGV based fluorescence microscopy image deconvolution[R].CAM Report, University of California, Los Angeles (UCLA), 2014, 14-32.
|
| [21] |
Liu J, Huang T Z, Selesnick I W, et al. Image restoration using total variation with overlapping group sparsity[J]. Information Sciences, 2015, 295: 232-246. DOI:10.1016/j.ins.2014.10.041 |
| [22] |
Chen P Y, Selesnick I W. Group-sparse signal denoising:non-convex regularization, convex optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(13): 3464-3478. DOI:10.1109/TSP.2014.2329274 |
| [23] |
Chen P Y, Selesnick I W. Translation-invariant shrinka-ge/thresholding of group sparse signals[J]. Signal Processing, 2014, 94: 476-489. DOI:10.1016/j.sigpro.2013.06.011 |
| [24] |
Selesnick I, Farshchian M. Sparse signal approximation via nonseparable regularization[J]. IEEE Tran-sactions on Signal Processing, 2017, 65(10): 2561-2575. DOI:10.1109/TSP.2017.2669904 |
| [25] |
Liu G, Huang T Z, Liu J, et al. Total variation with overlapping group sparsity for image deblurring under impulse noise[J]. Plos One, 2015, 10(4): e0122562. DOI:10.1371/journal.pone.0122562 |
| [26] |
Liu J, Huang T Z, Liu G, et al. Total variation with overlapping group sparsity for speckle noise reduction[J]. Neurocomputing, 2016, 216: 502-513. DOI:10.1016/j.neucom.2016.07.049 |
| [27] |
Boyd S. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1-122. |
| [28] |
Gabay D, Mercier B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation[J]. Computers & Mathematics with Applications, 1976, 2(1): 17-40. |
| [29] |
Wang Y, Yang J, Yin W, et al. A new alternating mini-mization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences, 2008, 1(3): 248-272. DOI:10.1137/080724265 |
| [30] |
Yang J, Zhang Y, Yin W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise[J]. SIAM Journal on Scientific Computing, 2009, 31(4): 2842-2865. DOI:10.1137/080732894 |
| [31] |
Yang J, Yin W, Zhang Y, et al. A fast algorithm for edge-preserving variational multichannel image restoration[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 569-592. DOI:10.1137/080730421 |
| [32] |
Goldstein T, Osher S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. DOI:10.1137/080725891 |
| [33] |
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [34] |
彭真明, 陈颖频, 蒲恬, 等. 基于稀疏表示及正则约束的图像去噪方法综述[J]. 数据采集与处理, 2018, 33(1): 1-11. PENG Zhenming, CHEN Yingpin, PU Tian, et al. Ima-ge denoising based on sparse representation and re-gularization constraint:A review[J]. Journal of Data Acquisition and Processing, 2018, 33(1): 1-11. |
| [35] |
林凡, 程祝媛, 陈颖频, 等. 基于交叠组合稀疏全变分的图像去噪方法[J]. 科学技术与工程, 2018, 18(18): 67-73. LIN Fan, CHENG Zhuyuan, CHEN Yingpin, et al. Animage denoising method based on overlapping groupsparsity total variation[J]. Sceience Technology andEngineering, 2018, 18(18): 67-73. DOI:10.3969/j.issn.1671-1815.2018.18.010 |
| [36] |
Sun Y, Babu P, Palomar D P. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Transactions on Signal Processing, 2016, 65(3): 794-816. |



 彭真明, 四川省成都市成华区建设北路二段4号电子科技大学信息与通信工程学院, 610054。Email:
彭真明, 四川省成都市成华区建设北路二段4号电子科技大学信息与通信工程学院, 610054。Email: