地质体深度是重磁数据解释的常规目的之一。有很多方法可完成该任务,如特征点法[1]、线性反演法[2]、解析信号法[3-4]、局部波数法[5]、维纳反褶积法[6]、欧拉反褶积法[7-8]等,这些方法主要采用以下两种方式计算深度:一是利用异常函数与地质体的分形对应关系;二是建立异常函数与地质体位置参数的线性反演方程。特征点法、局部波数法、解析信号法均是根据原始异常或变换后的异常、在给定构造指数的情况下计算地质体深度[9-15]。构造指数描述的是地质体类型,但实际数据解释时地质体类型是未知的,因此该类方法在实际应用中存在一定的限制。为此,人们提出了无需构造指数参与计算的新方法,但这类方法大多需要计算异常的二阶甚至更高阶的垂直导数[16-21],无疑会增大噪声的干扰,降低解释结果的精度。因此,有地质体先验信息时,构造指数的方法更加实用。维纳反褶积法和欧拉反褶积法依据原始异常及其不同方向的梯度计算地质体的位置参数[22-23],并且需要人为给定构造指数。后来有人利用高阶导数、解析信号导数、局部波数等构建欧拉方程计算深度[24-32], 有效地避免了对构造指数的要求,并制定了相应的筛选准则获得更准确的结果。
本文定义了一种计算重/磁异常体深度的梯度比值函数,即计算重力异常场或磁力异常场的一阶水平导数与原始异常场的比值,并证明该函数的极值点间水平距离等于地质体深度的2倍,因而该方法无需构造指数参与计算,且仅需计算一阶水平导数,不会明显地放大噪声。此外,还计算了多个上延高度的结果,并通过上半空间极值点连线的交点位置确定地质体的空间位置。磁异常体深度计算采用解析信号水平导数与解析信号的比值,可有效降低倾斜磁化的干扰。理论模型和实际数据计算结果验证了梯度比值函数的应用效果。
1 重磁梯度比值函数二维重力异常场[2]可以表示为
| $ g\left( {x, z} \right) = \frac{{\partial V}}{{\partial z}} = \frac{{k({z_0} - z)}}{{{{[{{(x - {x_0})}^2} + {{(z - {z_0})}^2}]}^{\frac{{N + 1}}{2}}}}} $ | (1) |
式中:V表示重力位; k为与地质体密度和万有引力常数相关的参数;(x0, z0)为场源的中心坐标;N为构造指数,其值与地质体类型的对应关系见表 1[33]。
|
|
表 1 不同类型地质体对应的构造指数 |
通过式(1),可以推导出重力异常水平导数
| $ \frac{{\partial g\left( {x, z} \right)}}{{\partial x}} = \frac{{k\left( {N + 1} \right)(z - {z_0})(x - {x_0})}}{{{{[{{(x - {x_0})}^2} + {{(z - {z_0})}^2}]}^{\frac{{N + 3}}{2}}}}} $ | (2) |
据式(2),地质体重力异常水平导数存在两个极值点,通过公式
| $ {x_{1, 2}} = {x_0} \pm \sqrt {\frac{{{z_0}}}{{N + 2}}} $ | (3) |
传统的地质体深度是在给定构造指数情况下依据式(3)计算的,但在实际数据解释中构造指数信息
难以预知,且构造指数是变化的。本文定义了一种梯度比值函数法,即异常场的一阶水平导数与异常场的比值
| $ \frac{{\partial g\left( {x, z} \right)/\partial x}}{{g\left( {x, z} \right)}} = - \frac{{\left( {N + 1} \right)(x - {x_0})}}{{{{(x - {x_0})}^2} + {{(z - {z_0})}^2}}} $ | (4) |
该函数也存在两个极值点,其水平坐标为
| $ {x_{1, 2}} = {x_0} \pm {z_0} $ | (5) |
由式(5)可以看出,梯度比值函数极值点水平坐标与构造指数无关,且两极值点间水平距离等于2z0,即两个极值点的中点对应地质体质心的水平位置,因此可在无先验信息的情况下获得地质体的位置参数。磁异常的梯度比值函数采用解析信号(总梯度模)的水平导数与解析信号的比值,利用解析信号进行数据处理可有效地避免倾斜磁化的干扰[3]。解析信号AS的表达式为
| $ {A_{\rm{S}}}\left( {x, z} \right) = \frac{K}{{{{[{{(x - {x_0})}^2} + {{(z - {z_0})}^2}]}^{\frac{{N + 1}}{2}}}}} $ | (6) |
式中K为与磁化强度相关的常数。
磁异常的梯度比值函数为
| $ \frac{{\partial {A_{\rm{S}}}\left( {x, z} \right)/\partial x}}{{{A_{\rm{S}}}\left( {x, z} \right)}} = - \frac{{\left( {N + 1} \right)(x - {x_0})}}{{{{(x - {x_0})}^2} + {{(z - {z_0})}^2}}} $ | (7) |
该函数两个极值点的水平坐标为
| $ {x_{1, 2}} = {x_0} \pm {z_0} $ | (8) |
图 1a为x=0、埋深为5m岩脉所引起的磁异常,磁倾角为60°,数据点距为1m。由图 1b可以看出,梯度比值函数存在两个极值点,其x坐标分别约为-5m和5m,因此可得到地质体的深度为5m,与模型深度一致。实际数据解释时,由于环境等干扰,采用单条曲线计算的结果精度较低,因而对不同上延高度的磁异常求梯度比值,并通过极值点连线的交点可更加准确地确定地质体的位置。

|
图 1 磁异常的梯度比值函数计算结果 (a)原始磁异常; (b)解析信号及梯度比曲线; (c)不同上延高度的梯度比曲线; (d)上半空间上延异常场的梯度比等值线 |
利用向上延拓技术获得不同高度h的梯度比值,梯度比值函数的极值点x坐标为
| $ {x_{1, 2}} = {x_0} \pm (h + {z_0}) $ | (9) |
根据式(9)得到地质体深度的平均值(图 1c中的A点)为5m,与实际深度吻合。
由式(9)可以发现,不同上延高度磁异常场的梯度比值函数极值点坐标与上延高度呈线性关系,因此对梯度比值函数成像(图 1d)。在地质体左侧和右侧极值点连线分别满足
| $ y = - x + \left( {{x_0} - {z_0}} \right) $ | (10) |
| $ y = x - \left( {{x_0} + {z_0}} \right) $ | (11) |
图 1c中红色虚线是不同上延高度曲线极值点的连线,这两条直线的交点坐标为(x0, -z0),即图 1c中的交点A,其坐标为(0, -5m),与模型中异常体的位置完全吻合。从图 1d也可以看出,两条极值点连线的交点A坐标为(0, -5m),与地质体实际位置一致。
2 理论模型试验假设在x=30m、70m处分别存在一个埋深为5m的圆柱体,其引起的重力异常如图 2a所示。图 2b为不同上延高度的重力梯度比值函数曲线,可以看出由于异常之间的相互干扰,梯度比值函数曲线并不是在各自水平位置对称分布。采用梯度比值函数极值点的坐标和通过不同上延高度的曲线均能得到地质体的深度为5m,而采用极值点坐标计算地质体深度,即使曲线不对称,其结果也是准确的,并不会明显地受到周围地质体的干扰。

|
图 2 双圆柱体模型无噪重力异常计算结果 (a)地面重力异常; (b)地面异常场的梯度比曲线; (c)上延异常场的梯度比曲线及极值点; (d)上半空间上延异常场的梯度比等值线 |
图 2c为不同上延高度重力异常场梯度比值函数极值点水平坐标的连接线图,根据连线的交点坐标可以获得两个地质体的坐标分别为(30m,-5m)和(70m,-5m)。图 2d为不同上延高度重力异常场的梯度比值曲线形成的剖面等值线图,根据极值点连线可以获得交点坐标分别为(30m,-5m)和(70m,-5m),与地质体的实际位置一致。说明本文方法能快速、准确地获得地质体的空间位置,且无需任何先验信息。
噪声在实际数据解释中不可避免,图 3a为在图 2a所示异常场中加入信噪比为30的高斯噪声后的重力异常场。图 3b为图 3a的梯度比值函数曲线,通过图中曲线极值点连线可以获得两个地质体的横坐标,通过极值点间的水平距离可获得地质体的埋深(即纵坐标),最终得到两个地质体的坐标分别为(30m,-4.8m)和(70m,-4.8m),接近于真实值,但依然受噪声的干扰。根据图 3c得到两个地质体的坐标分别为(30m,-4.93m)和(70m,-4.94m),而根据图 3d得到的交点坐标(即地质体坐标)分别为(30m,-4.95m)和(70m,-4.95m),说明这两种方法均能提高解释的准确性,但根据平面等值线求取交点坐标的方式精度更高,且由于该方法利用极值点横坐标的变化直接获得地质体的位置,计算简便,在实际数据解释中会得到更多应用。

|
图 3 双圆柱体模型含噪重力异常计算结果 (a)含噪地面重力异常剖面; (b)地面重力异常场的梯度比曲线; (c)不同上延高度的梯度比曲线; (d)上半空间上延异常场的梯度比等值线 |
将本文方法应用于埃及Hamrawien地区实测磁异常场的解释。图 4a为实测磁异常剖面,点距为50m。根据图 4b所示的磁异常解析信号,可以看出解析信号受倾斜磁化的影响较小,其异常形态较规则。
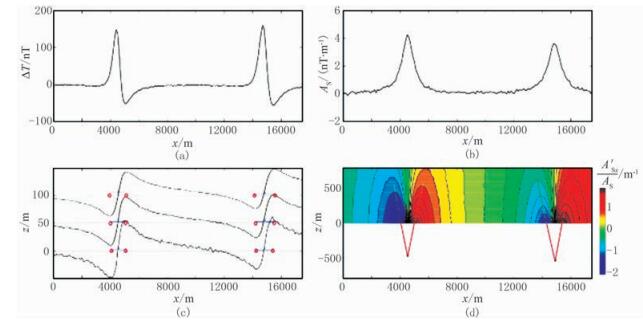
|
图 4 实测磁异常场的计算结果 (a)地面异常剖面; (b)磁异常解析信号; (c)不同上延高度的异常梯度比曲线及极值点横坐标连线; (d)上半空间上延异常场的梯度比等值线 |
根据图 4c可以得到地质体的坐标分别为(4542m, -485m)和(14861m, -556m),根据图 4d中极值点连线的交点得到地质体坐标分别为(4542m, -484m)和(14862m, -555m)。可见根据不同方式计算得到的结果基本一致。
4 结论本文定义了一种重/磁异常场的梯度比值函数(即重力异常场或磁力异常场的一阶水平导数与原始异常场的比值)计算地质体深度。根据此函数可知,不同类型地质体均具有极值点水平距离等于地质体深度2倍的关系。对多个高度的上延场按照本文方法求取地质体的坐标,并求其平均值,通过上半空间极值成像手段获得更加准确的结果。磁异常解释时,为了降低倾斜磁化的影响,采用解析信号构建梯度比值函数。理论模型试验和实际数据应用均证明本文方法能快速、准确地获得地质体的深度信息,且不会产生干扰,具有较高的抗噪性。该方法无需复杂的运算,通过极值点可直接获得地质体的深度,在实际数据解释中应用十分便利。
| [1] |
Atchuta R D, Ram B, Sanker N. Interpretation of magnetic anomalies due to dikes:The complex gradient method[J]. Geophysics, 1981, 46(11): 1572-1578. DOI:10.1190/1.1441164 |
| [2] |
Blakely R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge University Press, 1995.
|
| [3] |
Debeglia N, Corpel J. Automatic 3-D interpretation of potential field data using analytic signal derivatives[J]. Geophysics, 1997, 62(1): 87-96. DOI:10.1190/1.1444149 |
| [4] |
MacLeod I N, Jones K, Dai T F. 3-D analytic signal in the interpretation of total magnetic field data at low magnetic latitudes[J]. Exploration Geophysics, 1993, 24(3): 679-688. |
| [5] |
谷文彬, 陈清礼, 王余泉, 等. 饶阳凹陷虎8北潜山重力三维松约束反演[J]. 石油地球物理勘探, 2016, 51(6): 1219-1226. GU Wenbin, CHEN Qingli, WANG Yuquan, et al. Part-constrained 3D gravity inversion for the Hubabei buried hill in Raoyang Sag[J]. Oil Geophysical Prospecting, 2016, 51(6): 1219-1226. |
| [6] |
李婧, 崔永谦, 宋景明, 等. 重力-地震联合建模正演技术在SH地区潜山勘探中的应用[J]. 石油地球物理勘探, 2016, 51(增刊1): 152-160. LI Jing, CUI Yongqian, SONG Jingming, et al. Gravity forward modeling with model built based on drilling and seismic data:an example of buried hill exploration in area SH[J]. Oil Geophysical Prospecting, 2016, 51(S1): 152-160. |
| [7] |
耿美霞, 杨庆节. 应用RBF神经网络反演二维重力密度分布[J]. 石油地球物理勘探, 2013, 48(4): 651-657. GENG Meixia, YANG Qingjie. 2D density inversion with the RBF neural network method[J]. Oil Geophysical Prospecting, 2013, 48(4): 651-657. |
| [8] |
林宝泽, 肖锋, 王明常. 二维重力数据径向反演及应用[J]. 石油地球物理勘探, 2018, 53(2): 403-409. LIN Baoze, XIAO Feng, WANG Mingchang. 2D gravity data radial inversion[J]. Oil Geophysical Prospecting, 2018, 53(2): 403-409. |
| [9] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:Its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [10] |
Nabighian M N. Additional comments on the analytic signal of two-dimensional magnetic bodies with poly-gonal cross-section[J]. Geophysics, 1974, 39(1): 85-92. |
| [11] |
Nabighian M N. Toward a three-dimensional automa-tic interpretation of potential-field data via generalized Hilbert transforms:Fundamental relations[J]. Geophysics, 1984, 49(5): 780-786. |
| [12] |
Roest W R, Verhoef J, Pilkington M. Magnetic interpretation using 3-D analytic signal[J]. Geophy-sics, 1992, 57(1): 116-125. DOI:10.1190/1.1443174 |
| [13] |
Thurston J B, Smith R S. Automatic conversion of magnetic data to depth, dip, and susceptibility contrast using the SPI method[J]. Geophysics, 1997, 62(3): 807-813. DOI:10.1190/1.1444190 |
| [14] |
Thurston J B, Smith R S, Guillon J. A multi-model method for depth estimation from magnetic data[J]. Geophysics, 2002, 67(2): 555-561. |
| [15] |
Salem A, Ravat D, Gamey T J, et al. Analytic signal approach and its applicability in environmental magnetic investigations[J]. Journal of Applied Geophy-sics, 2002, 49(4): 231-244. DOI:10.1016/S0926-9851(02)00125-8 |
| [16] |
Hsu S K, Sibuet J C, Shyu C T. High-resolution detection of geologic boundaries from potential ano-malies:An enhanced analytic signal technique[J]. Geophysics, 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [17] |
Hsu S K, Coppens D, Shyu C T. Depth to magne-tic source using the generalized analytic signal[J]. Geophysics, 1998, 63(6): 1947-1957. DOI:10.1190/1.1444488 |
| [18] |
Bastani M, Pedersen L B. Automatic interpretation of magnetic dike parameters using the analytic signal technique[J]. Geophysics, 2001, 66(2): 551-561. DOI:10.1190/1.1444946 |
| [19] |
Smith R S, Thurston J B, Dai T F, et al. ISPI:the improved source parameters imaging method[J]. Geophysical Prospecting, 1998, 46(2): 141-151. DOI:10.1046/j.1365-2478.1998.00084.x |
| [20] |
Salem A, Ravat D, Mushayandebvu M F, et al. Linea-rized least-squares method for interpretation of potential-field data from sources of simple geometry[J]. Geophysics, 2004, 69(3): 783-788. DOI:10.1190/1.1759464 |
| [21] |
Salem A. Interpretation of magnetic data using analy-tic signal derivatives[J]. Geophysical Prospecting, 2005, 53(1): 75-82. DOI:10.1111/gpr.2005.53.issue-1 |
| [22] |
Thompson D T. EULDPH:A new technique for ma-king computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37. DOI:10.1190/1.1441278 |
| [23] |
Reid A N, Allsop J M, Granser H. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 1990, 55(1): 80-91. DOI:10.1190/1.1442774 |
| [24] |
Ma G, Du X. An improved analytic signal technique for the depth and structural index from 2D magnetic anomaly data[J]. Pure and Applied Geophysics, 2012, 169(8): 2193-2200. |
| [25] |
Cooper G R J. The automatic determination of the location and depth of contacts and dykes from aeromagnetic data[J]. Pure and Applied Geophysics, 2014, 171(9): 2417-2423. DOI:10.1007/s00024-014-0789-8 |
| [26] |
Cooper G R J. Using the analytic signal amplitude to determine the location and depth of thin dykes from magnetic data[J]. Geophysics, 2015, 80(1): J1-J6. |
| [27] |
马国庆, 黄大年, 李丽丽, 等. 重磁异常解释的归一化局部波数法[J]. 地球物理学报, 2014, 57(4): 1300-1309. MA Guoqing, HUANG Danian, LI Lili, et al. A normalized local wave number method for interpretation of gravity and magnetic anomalies[J]. Chinese Journal of Geophysics, 2014, 57(4): 1300-1309. |
| [28] |
马国庆, 杜晓娟, 李丽丽. 改进的位场相关成像方法[J]. 地球科学——中国地质大学学报, 2013, 38(5): 1121-1127. MA Guoqing, DU Xiaojuan, LI Lili. Improved potential field correlation imaging method[J]. Earth Science:Journal of China University of Geosciences, 2013, 38(5): 1121-1127. |
| [29] |
Ma Guoqing, Liu Cai, Xu Jiashu, et al. Correlation ima-ging method based on local wave number for interpreting magnetic data[J]. Journal of Applied Geophysics, 2017, 138(1): 17-22. |
| [30] |
Ma Guoqing, Liu Cai, Li Lili. Balanced horizontal derivative of potential field data to recognize the edges and estimate location parameters of the source[J]. Journal of Applied Geophysics, 2014, 108(9): 12-18. |
| [31] |
Salem A, Ravat D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data[J]. Geophysics, 2003, 68(6): 1952-1961. DOI:10.1190/1.1635049 |
| [32] |
Wen B D, Hsu S K, Yeh Y C. A derivative-based interpretation approach to estimating source parameters of simple 2D magnetic sources from Euler deconvolution, the analytic-signal method and analytical expressions of the anomalies[J]. Geophysical Prospecting, 2007, 55(1): 255-264. |
| [33] |
Stavrev P, Reid A. Degrees of homogeneity of potential fields and structural indices of Euler deconvolution[J]. Geophysics, 2007, 72(1): L1-L12. |



 马国庆, 吉林省长春市西民主大街938号地质宫517室, 130021。Email:
马国庆, 吉林省长春市西民主大街938号地质宫517室, 130021。Email: