② 西南石油大学博士后科研流动站, 四川成都 610500
② Post-Doctoral Mobile Station, Southwest Petroleum University, Chengdu, Sichuan 610500, China
目前有很多三维地震几何属性可以检测地震数据中的断层等不连续性地质边界。相干体属性是一种常用的描述三维不连续性的地震几何属性,因其能够检测地震资料中空间相邻地震道之间的相似性,进而可以很好地刻画断层等不连续性地质边界。第一代相干体属性(C1)是由Bahorich等[1]提出的。该属性基于二阶统计量(SOS)算法,参加计算的地震道只有三道,所以C1算法计算效率很高,但是它对地震资料中的噪声非常敏感,抗噪能力较差。Marfurt等[2]提出了第二代相干体属性(C2),该属性利用空间多道进行计算,求取相邻地震道之间的相似性系数。C2算法虽然抗噪能力很强,但是由于在分析时窗内参与计算的地震道数较多,所以不仅降低了横向分辨率,而且还增加了相干体计算时间。Gersztenkorn等[3]提出了基于特征结构的第三代相干体属性(C3),该属性在分析时窗内考虑了空间相邻的多道地震数据,并利用这些地震数据构建了协方差矩阵,通过求取协方差矩阵的特征值和特征向量检测地层中的不连续特征。C3算法不仅具有很强的抗噪能力,横向分辨率较高,而且比C2算法具有更强的识别不连续性边界的能力。但是C3算法并没有考虑地质构造中倾角和方位角的影响,因此在地层倾角较大的地区,C3算法的效果难尽人意。Marfurt等[4]结合C2和C3算法,提出了一种可以检测地层倾角的相干体算法,令人遗憾的是其计算效率非常低。Cohen等[5]提出了一种基于局部结构熵(LSE)的相干体算法,不仅能有效检测大的断层和裂缝,而且能检测数据体中细微、缓变的不连续性结构。不过因其未考虑局部倾角和方位角信息,抗噪能力较弱。
Lu等[6]提出了超级地震道(ST)的概念,并将ST与高阶累积量(HOS)和C1相干结合起来,提出了ST-C1和ST-HOS相干算法。Li等[7]将基于特征结构的C3算法与ST相结合,并利用倾角扫描技术获取了原始地震数据中的最佳倾角信息,由于这种新的相干体属性(ST-C3)只构建了4×4阶的协方差矩阵,计算效率很高。杨葆军等[8]分析了常规相干体属性在采用固定时窗长度时存在的不足,提出了自适应时窗长度相干体属性,即通过地震数据波形自适应确定时窗,利用该时窗计算的相干值作为时窗内各点的相干值。王静波等[9]基于多道互相关以及C1、C2相干算法的思想,提出了多道局部复值相关的改进相干算法。该算法无需进行相似性扫描、倾角扫描或迭代求解等复杂运算,能同时提供用于相干分析的相关系数属性和与地层视倾角有关的相移属性,大大提高了地震信号边缘检测结果的可信度。尹川等[10]利用小波变换进行地震数据的分频重构,在不同频率的窄带地震数据基础上计算相干属性,并与倾角约束相干属性相结合,很好地解决了含陡倾地层的复杂断裂带成像问题,有效地抑制了陡倾地层产生的背景噪声,分频倾角相干切片信噪比更高,断裂信息更加清晰、分辨率更高。Ahmed等[11]利用Hessian矩阵的谱分解法突出三维相干数据体的低相干值,不但比原始相干体更能突出地质体的边界,而且在复杂构造区域显示的不连续性信息更清晰。Gabriel等[12]在三维相干数据体中利用基于高斯函数的拉普拉斯滤波器对断层进行进一步的导向处理,经过处理后的断层分布特征更加明显,断层的连续性和清晰度得到了很大的提高。李军等[13]提出了一种基于魔方矩阵的断层检测方法,能够有效检测复杂区块的断层、裂缝等地质现象,具有较好的抗噪特性。王清振等[14]利用梯度结构张量属性检测断层和盐丘,克服了陡倾地层引起的不连续性假象,有效识别了真实的断层信息和盐丘发育范围。
与此同时,基于倾角和方位角属性的地震数据不连续性检测技术得到迅猛发展[15]。利用倾角和方位角属性可以进一步计算体曲率[16-17]、相干体[18]、地震纹理体[19]、结构导向滤波[20]或边缘保持滤波[21-22]。所有这些新的属性体为断层检测提供了丰富的基础数据。Lawrence[23]利用倾角方位角体和相干体检测了沙特阿拉伯布盖格地区的断层。Neves等[24]在结构导向滤波处理后,通过计算倾角方位角属性和相干属性以及谱分解属性预测了裂缝发育带和断层。
目前计算倾角属性和方位角属性的方法大致有3种。Barnes[25]在Taner研究复数地震道的基础上,提出了利用复数道的三维扩展形式计算地震数据的倾角体,因计算量较大,且计算结果受地震频率影响很大,实际应用效果欠佳。Marfurt等[2]提出了利用本征相干倾角扫描的方法计算地层视倾角体,但是该方法不但花费的计算时间较长,而且不适用于较陡的地层倾角计算。Bakker[26]提出了一种利用梯度结构张量的方法计算倾角体和方位角体,不仅计算速度快,而且适用于任何陡倾地层。隋京坤等[27]引入并改进了一种在频率域内的地层倾角估算法,总结出了一套融合时间域倾角搜索和频率域倾角估计的层拉平算法流程。与传统相干属性中只使用时间域倾角搜索的算法相比,该时间域—频率域层拉平算法能更彻底地消除地层倾角对相干值的影响。
笔者在前人研究工作的基础上,将基于梯度结构张量的倾角属性计算与基于梯度能量的熵值计算相结合,发展一种新的倾角导向梯度能量熵(Dip Oriented Gradient Energy Entropy,DOGEE)的相干分析方法,为断层等不连续地质边界的检测提供一种新的途径。
1 方法理论倾角导向梯度能量熵(DOGEE)算法的第一步是构建梯度能量数据体。首先将地震数据进行平滑滤波处理,u′(x, y, t)是原始地震数据u(x, y, t)经过三维高斯平滑滤波器G(x, y, t, σg)滤波后的地震数据,即
| $ u'\left( {x,y,t} \right) = u\left( {x,y,t} \right) \otimes G\left( {x,y,t,{\sigma _g}} \right) $ | (1) |
| $ G\left( {x,y,t,{\sigma _g}} \right) = \frac{1}{{2{{\rm{ \mathsf{ π} }}^{3/2}}\sigma _{\rm{g}}^3}}\exp \left( { - \frac{{{x^2} + {y^2} + {t^2}}}{{2\sigma _g^2}}} \right) $ | (2) |
式中:σg为噪声尺度参数,一般取0.1~3.0之间的数值;x、y和t分别表示三维地震数据中沿线方向、道方向和时间方向的变量。
由于原始地震数据中存在随机噪声,梯度计算是对数据做微分处理,往往对随机噪声很敏感,所以有必要在计算梯度向量体之前对地震数据进行高斯平滑滤波处理,然后分别沿着地震数据的x、y和t方向,利用中心差分法计算三个方向的梯度向量体gx、gy和gt
| $ {g_x}\left( {x,y,t} \right) = \frac{{u'\left( {x + \Delta x,y,t} \right) - u'\left( {x - \Delta x,y,t} \right)}}{{2\Delta x}} $ | (3) |
| $ {g_y}\left( {x,y,t} \right) = \frac{{u'\left( {x,y + \Delta y,t} \right) - u'\left( {x,y - \Delta y,t} \right)}}{{2\Delta y}} $ | (4) |
| $ {g_t}\left( {x,y,t} \right) = \frac{{u'\left( {x,y,t + \Delta t} \right) - u'\left( {x,y,t - \Delta t} \right)}}{{2\Delta t}} $ | (5) |
式中:Δx和Δy分别为地震数据在x方向和y方向的道间距;Δt为时间方向的采样间隔。
由此,可以通过式(3)~式(5)计算得到的三个梯度向量体合并而成梯度能量数据体
| $ g\left( {x,y,t} \right) = g_x^2\left( {x,y,t} \right) + g_y^2\left( {x,y,t} \right) + g_t^2\left( {x,y,t} \right) $ | (6) |
将计算得到的三个梯度向量体gx(x, y, t)、gy(x, y, t)和gt(x, y, t)做并矢运算,构建每一个地震数据对应的梯度结构张量矩阵。利用构造尺度平滑地震数据中的梯度结构张量矩阵可以达到有效的方向性平滑,具有结构导向滤波的效果,因此对三维高斯平滑滤波器卷积梯度结构张量矩阵中的每一个元素,经过高斯平滑滤波后得到每一个地震数据的梯度结构张量矩阵
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar T}} = \left[ {{g_x},{g_y},{g_t}} \right] \cdot {{\left[ {{g_x},{g_y},{g_t}} \right]}^{\rm{T}}} \otimes G\left( {x,y,t,{\sigma _{\rm{p}}}} \right)}\\ { = G\left( {x,y,t,{\sigma _{\rm{p}}}} \right) \otimes \left[ {\begin{array}{*{20}{c}} {g_x^2}&{{g_x}{g_y}}&{{g_x}{g_t}}\\ {{g_y}{g_x}}&{g_y^2}&{{g_y}{g_t}}\\ {{g_t}{g_x}}&{{g_t}{g_y}}&{g_t^2} \end{array}} \right]} \end{array} $ | (7) |
式中σp为构造尺度参数。噪声尺度参数与构造尺度参数之间满足3σg<σp<10σg[26]。由于通过计算梯度结构张量矩阵的特征值和特征向量能够获取局部地震数据的方向信息,利用式(7)得到的每一个地震数据的梯度结构张量矩阵做矩阵的谱分解,可以得到矩阵中每一个地震数据对应的三个特征值和特征向量
| $ \begin{array}{l} \mathit{\boldsymbol{\bar T}} = \left[ {\begin{array}{*{20}{c}} {\overline {g_x^2} }&{\overline {{g_x}{g_y}} }&{\overline {{g_x}{g_t}} }\\ {\overline {{g_y}{g_x}} }&{\overline {g_y^2} }&{\overline {{g_y}{g_t}} }\\ {\overline {{g_t}{g_x}} }&{\overline {{g_t}{g_y}} }&{\overline {g_t^2} } \end{array}} \right]\\ \;\;\; = \left[ {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2},{\mathit{\boldsymbol{v}}_3}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0\\ 0&{{\lambda _2}}&0\\ 0&0&{{\lambda _3}} \end{array}} \right]{\left[ {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2},{\mathit{\boldsymbol{v}}_3}} \right]^{\rm{T}}} \end{array} $ | (8) |
式中:vi和λi(i=1, 2, 3)分别为梯度结构张量矩阵对应的三个特征向量和特征值;上划线表示对梯度结构张量矩阵中每个元素卷积得到的结果。
梯度结构张量矩阵是一个对称半正定矩阵,因此特征值都是非负的。对这三个特征值排序,满足λ1>λ2>λ3,得到最大特征值λ1。其中,最大特征值λ1对应的特征向量v1(x, y, t)通常表现为分析时窗内法线方向所指示的最大变化率,包含了丰富的方向信息。
将式(8)中得到的最大特征值λ1对应的特征向量v1(x, y, t)分别在x、y和z方向上的三个元素v1x(x, y, t)、v1y(x, y, t)和v1t(x, y, t)进行数学计算,得到每一个地震数据对应的倾角和方位角
| $ p\left( {x,y,t} \right) = \frac{{{v_{1x}}\left( {x,y,t} \right)}}{{{v_{1t}}\left( {x,y,t} \right)}} $ | (9) |
| $ q\left( {x,y,t} \right) = \frac{{{v_{1y}}\left( {x,y,t} \right)}}{{{v_{1t}}\left( {x,y,t} \right)}} $ | (10) |
将三维分析时窗在整个梯度能量数据体g(x, y, t)中按照倾角和方位角导向进行滑动,并构建梯度向量序列
| $ g\left( {t,p,q} \right) = g\left( {t - p{x_j} - q{y_j}} \right) $ | (11) |
式中:xj和yj为第j道地震数据分别沿x方向和y方向距离时窗中心点的空间距离;p和q分别为x方向和y方向的倾角和方位角。
然后将滑动过程中包含在分析时窗内的梯度能量数据分为4组梯度向量序列{gi|i=1, …, 4},每一个梯度向量序列包含有L1×L2×N个梯度能量元素(L1×L2个地震道,N为地震数据时间方向的采样点数),这4组梯度向量序列都是将分析时窗内的地震道依次首尾连接合并成为一个序列。
最后,利用4组梯度向量序列构建局部梯度能量相关矩阵,通过对梯度能量相关矩阵内的每组梯度向量序列{gi|i=1, …, 4}进行自相关和互相关运算,得到三维地震数据中每一点对应的梯度能量熵值
| $ H\left( {x,y,t} \right) = - \frac{{\sum\limits_{i = 1}^4 {\left( {\mathit{\boldsymbol{g}}_i^{\rm{T}}{\mathit{\boldsymbol{g}}_i}} \right)} }}{{\sqrt {\sum\limits_{i,j = 1}^4 {{{\left( {\mathit{\boldsymbol{g}}_i^{\rm{T}}{\mathit{\boldsymbol{g}}_j}} \right)}^2}} } }}\ln \left[ {\frac{{\sum\limits_{i = 1}^4 {\left( {\mathit{\boldsymbol{g}}_i^{\rm{T}}{\mathit{\boldsymbol{g}}_i}} \right)} }}{{\sqrt {\sum\limits_{i,j = 1}^4 {{{\left( {\mathit{\boldsymbol{g}}_i^{\rm{T}}{\mathit{\boldsymbol{g}}_j}} \right)}^2}} } }}} \right] $ | (12) |
H(x, y, t)能够增强得到分析时窗的不连续性信息,很好地检测三维地震数据中断层等不连续性边界信息。在计算梯度能量熵过程中,三维分析时窗在x、y和z方向上一般是由奇数地震道构成,如3×3×5或者为5×5×7,三维分析时窗的大小决定了检测地质目标体的类型。
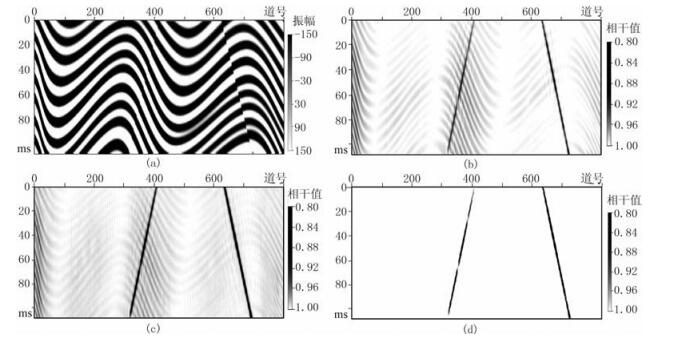
2 理论模型分析为了验证本文方法对断层不连续性信息的检测效果,开展了二维S型理论模型试验对比分析。图 1a所示的地震正演模型是采用褶积方法得到的合成地震记录。模型长度为800m,深度为200m,采样间隔为2ms。模型中设置了两个不同断距的断层,左侧断层的断距为10m,右侧断层的断距为20m。图 1b~图 1d分别为C1相干、LSE相干和DOGEE相干的检测效果。
|
图 1 二维S型理论模型的试验对比 (a)地震正演模型; (b)C1相干; (c)LSE相干; (d) DOGEE相干 |
从图 1b~图 1d中可以看出,虽然C1相干和LSE相干都能检测出两个断层,但是它们没有倾角导向的功能,都受到了S型地层结构的影响。DOGEE相干的检测效果则没有受到S型地层结构的影响,两个断层的检测清晰度更高。
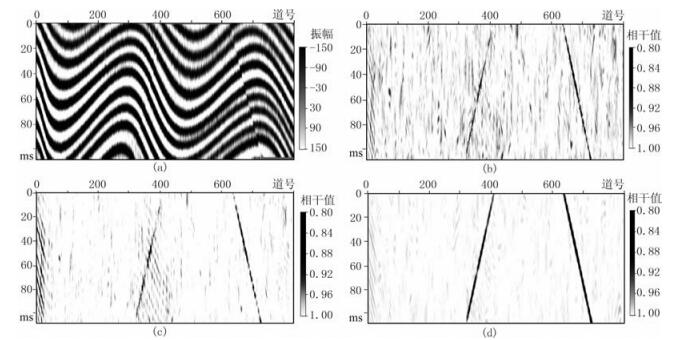
为了验证DOGEE相干的抗噪能力,在上述模型记录中加入20%的随机噪声,分别进行同样的相干计算,结果如图 2所示。显然,C1相干和LSE相干的检测效果都受到了随机噪声的影响,模型左侧10m断距的断层检测效果均不清晰,DOGEE相干的检测效果受随机噪声的影响很小,两个断层均得到了清晰呈现。这说明DOGEE相干方法的抗噪声能力很强,可提高断层不连续性信息的检测精度。
|
图 2 二维S型理论模型加入20%随机噪声的试验对比 (a)地震正演模型; (b)C1相干; (c)LSE相干; (d)DOGEE相干 |
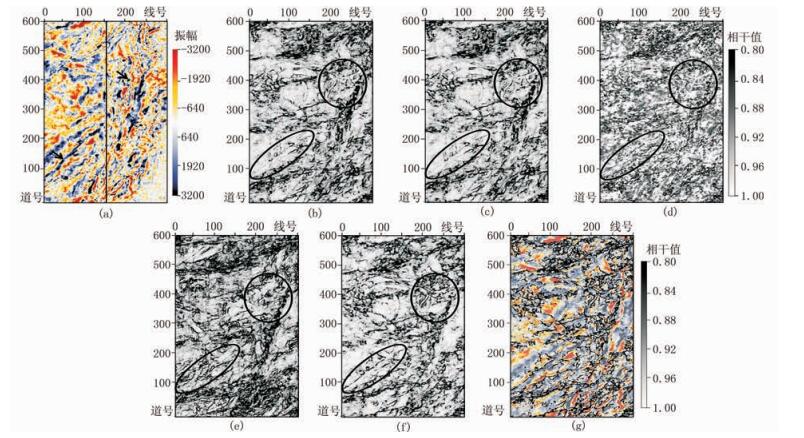
为了说明方法的实际应用效果,选取某区实际三维地震数据体进行方法测试和对比分析。三维数据体样点数为300×610×225,时间采样间隔为4ms,空间纵横向采样间隔均为25m。图 3a为从原始三维地震数据体中抽取的Inline方向地震剖面,用黑色箭头指示3个不清晰的断层。图 3b~图 3f分别为利用ST-C1相干、ST-C3相干、ST-HOS相干、LSE相干和DOGEE相干计算结果抽取的同一测线属性剖面,用椭圆形圈出的区域分别与3个断层对应。显然,图 3b~图 3e中椭圆形圈区域内断层并不清晰,而图 3f所计算的DOGEE相干属性却能够检测出清晰的断层。为了说明断层检测结果与地震剖面的一致性,图 3g将DOGEE相干剖面与原始地震剖面叠合显示,不难发现,众多地震同相轴间断点与DOGEE相干剖面所揭示的不连续性边界或断层边界具有很好的一致性,二者吻合良好。

|
图 3 实际三维地震数据剖面的试验对比 (a)原始地震数据剖面; (b) ST-C1相干剖面; (c)ST-C3相干剖面; (d)ST-HOS相干剖面; (e)LSE相干剖面; (f)DOGEE相干剖面; (g)DOGEE相干融入到原始地震剖面 |
在图 3b~图 3f中用圆形圈出的区域为平行于地震同相轴的“低相干”假象,这是由于在计算相干时没有考虑局部地震数据的倾角和方位角信息而引起的。尽管ST-C3相干方法考虑了反射同相轴的局部结构倾角,但并不能反映局部地震数据的倾角和方位角信息,而LSE相干方法没有考虑局部倾角和方位角信息,所以在ST-C1相干、ST-C3相干和LSE相干剖面中均存在明显的“低相干”假象,且受地震数据随机噪声的影响较大。ST-HOS相干因对随机噪声非常敏感,整体成像效果极差,甚至断层检测都异常困难。相比之下,DOGEE相干剖面中这种“低相干”假象被极大地削弱,剖面信噪比得到了明显改善,断层等不连续边界更清晰。这一点可以通过对比各剖面中方框内的相干结果得到更好诠释。
图 4给出了原始地震数据体和5种不同相干体在t=600ms处的时间切片。图 4a中的黑线即为图 3相应剖面的位置。图 4b~图 4f中黑色椭圆形区与图 4a中黑色箭头指示的不连续性地质特征相对应。不难看出,DOGEE相干方法比其他4种相干方法能检测出更多细微的地质边界特征,且边界的连续性更高。
|
图 4 实际三维地震数据切片的试验对比 (a)原始地震数据时间切片; (b)ST-C1相干时间切片; (c)ST-C3相干时间切片; (d)ST-HOS相干时间切片; (e)LSE相干时间切片; (f)DOGEE相干时间切片; (g)DOGEE数据与地震时间切片叠合显示 |
本文将基于梯度结构张量的倾角属性计算和基于梯度能量的熵值计算相结合,提出了一种新的倾角导向梯度能量熵(DOGEE)相干方法。DOGEE相干方法不但增强了检测不连续性边界的清晰度,而且抗噪能力很强,还能够提高断层边界的连续性。实际应用效果表明,通过DOGEE相干方法计算的相干剖面中“低相干”假象得到了极大的削弱,剖面的信噪比得到了明显改善,计算的相干切片中能够检测出更多细微的地质边界特征。但是DOGEE相干与ST-C1相干和ST-C3相干一样,存在计算效率较低的问题,并没有LSE相干计算效率高。因此,对于断层等不连续性边界的检测,需要根据实际情况综合考虑选择适用的相干体计算方法。
| [1] |
Bahorich M S, Farmer S L. 3-D seismic discontinuity for faults and stratigraphic features[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [2] |
Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attributes using a semblance-based coherence algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [3] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [4] |
Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherence calculations in the presence of strong structural dip[J]. Geophysics, 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [5] |
Cohen I, Coifman R R. Local discontinuity measures for 3-D seismic data[J]. Geophysics, 2002, 67(6): 1933-1945. DOI:10.1190/1.1527094 |
| [6] |
Lu W K, Li Y D, Xiao H Q, et al. Higher-order-statistics and supertrace-based coherence-estimation algorithm[J]. Geophysics, 2005, 70(3): P13-P18. DOI:10.1190/1.1925746 |
| [7] |
Li Y D, Lu W K, Xiao H Q, et al. Dip-scanning coherence algorithm using eigenstructure analysis and supertrace technique[J]. Geophysics, 2006, 71(3): V61-V66. DOI:10.1190/1.2194899 |
| [8] |
杨葆军, 杨长春, 陈雨红, 等. 自适应时窗相干体计算技术及其应用[J]. 石油地球物理勘探, 2013, 48(3): 436-442. YANG Baojun, YANG Changchun, CHEN Yuhong, et al. Coherence calculation with adaptive windows and its application[J]. Oil Geophysical Prospecting, 2013, 48(3): 436-442. |
| [9] |
王静波, 王尚旭, 袁三一, 等. 基于多道局部复值相关的地震信号边缘检测[J]. 石油地球物理勘探, 2014, 49(1): 190-196. WANG Jingbo, WANG Shangxu, YUAN Sanyi, et al. Seismic data edge detection using multichannel local complex-valued correlation[J]. Oil Geophysical Prospecting, 2014, 49(1): 190-196. |
| [10] |
尹川, 杜向东, 赵汝敏, 等. 小波分频倾角相干在复杂断裂解释中的应用[J]. 石油地球物理勘探, 2015, 50(2): 346-350. YIN Chuan, DU Xiangdong, ZHAO Rumin, et al. Dip-steering similarity based on wavelet decomposition in complex fault interpretation[J]. Oil Geophysical Prospecting, 2015, 50(2): 346-350. |
| [11] |
Ahmed A, Hameer A, Arsalan S.Enhancement of subtle features in coherence volumes[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 1707-1710.
|
| [12] |
Gabriel M, Abdulmohsen A, Bryce H. Display and enhancement of volumetric fault images[J]. Interpretation, 2016, 4(1): SB51-SB61. DOI:10.1190/INT-2015-0104.1 |
| [13] |
李军, 张军华, 龚明平, 等. 基于魔方矩阵的断层检测方法[J]. 石油地球物理勘探, 2018, 53(3): 552-557. LI Jun, ZHANG Junhua, GONG Mingping, et al. Fault detection based on magic matrix[J]. Oil Geophysical Prospecting, 2018, 53(3): 552-557. |
| [14] |
王清振, 张金淼, 姜秀娣, 等. 利用梯度结构张量检测盐丘与断层[J]. 石油地球物理勘探, 2018, 53(4): 826-831. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. Salt dome and fault detection based on the gradient-structure-tensor[J]. Oil Geophysical Prospecting, 2018, 53(4): 826-831. |
| [15] |
Marfurt K J. Robust estimates of 3D reflector dip and azimuth[J]. Geophysics, 2006, 71(4): 29-40. |
| [16] |
Al-Dossary S, Marfurt K J. 3-D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): 41-51. DOI:10.1190/1.2242449 |
| [17] |
王清振, 姜秀娣, 翁斌, 等. 高抗噪性三维体曲率分析技术及其在高陡地层发育区的应用[J]. 石油物探, 2017, 56(4): 559-566. WANG Qingzhen, JIANG Xiudi, WENG Bin, et al. A 3D curvature attribute analysis method with excellent anti-noise property suitable for high steep formation[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 559-566. DOI:10.3969/j.issn.1000-1441.2017.04.012 |
| [18] |
Marfurt K J, Kirlin R L. 3-D broadband estimates of reflector dip and amplitude[J]. Geophysics, 2000, 65(1): 304-320. DOI:10.1190/1.1444721 |
| [19] |
Gao D. Volume texture extraction for 3-D seismic visualization and interpretation[J]. Geophysics, 2003, 68(4): 1294-1302. DOI:10.1190/1.1598122 |
| [20] |
Hocker C, Fehmers G. Fast structural interpretation with structure-oriented filtering[J]. The Leading Edge, 2002, 21(3): 238-243. DOI:10.1190/1.1463775 |
| [21] |
Bakker P L, Vliet J V, Verbeek P W.Edge-preserving orientation adaptive filtering[C]. Proceedings of the IEEE-CS Coherence on Computer Vision and Pattern Recognition, 1999, 1535-1540.
|
| [22] |
Luo Y, Al-Dossary S, Alfaraj M. Edge-preserving smoothing and application[J]. The Leading Edge, 2002, 21(2): 136-158. DOI:10.1190/1.1452603 |
| [23] |
Lawrence P. Seismic attributes in the characterization of small-scale reservoir faults in Abqaiq Field[J]. The Leading Edge, 1998, 17(4): 521-525. DOI:10.1190/1.1438004 |
| [24] |
Neves F A, Zahrani M S, Bremkamp S W. Detection of potential fractures and small faults using seimic attributes[J]. The Leading Edge, 2004, 23(9): 903-906. DOI:10.1190/1.1803500 |
| [25] |
Barnes A E. Theory of two-dimensional complex seismic trace analysis[J]. Geophysics, 1996, 61(1): 264-272. DOI:10.1190/1.1443947 |
| [26] |
Bakker P.Image Structure Analysis for Seismic interpretation[D]. Delft University of Technology, 2003.
|
| [27] |
隋京坤, 郑晓东, 李艳东, 等. 一种精确消除倾斜地层对相干值影响的方法[J]. 石油地球物理勘探, 2015, 50(4): 691-698. SUI Jingkun, ZHENG Xiaodong, LI Yandong, et al. A precise algorithm to eliminate effects of slope on seismic coherence[J]. Oil Geophysical Prospecting, 2015, 50(4): 691-698. |



 彭达, 四川省成都市高新区天府大道北段12号石油科技大厦10楼1015室, 610041。Email:
彭达, 四川省成都市高新区天府大道北段12号石油科技大厦10楼1015室, 610041。Email: