基于散射矩阵分解的反射系数二阶近似
① 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580
② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580
本文于2018年2月11日收到，最终修改稿于同年10月26日收到。
本项研究受国家科技重大专项子课题“基于宽方位叠前地震反演的中深层复杂储层表征及油气检测技术”（2016ZX05024-001-008）、国家自然科学基金联合基金项目“非常规油气富集机制与地球物理甜点识别”（U1562215）联合资助。
吴国忱, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:guochenwu@upc.edu.cn。
摘要：常规AVO反演利用精确Zoeppritz方程的一阶近似式，更加适用于弱介质变化的反射界面、小角度或小炮检距反射问题，其假设条件导致计算误差，不利于准确提取密度参数，不能很好地预测复杂储层或中深部储层，且无法充分利用近临界角数据；基于反射/透射系数精确表达式进行高阶近似过于繁琐，利用上、下行波特征向量矩阵及矩阵对称性对反射/透射系数进行泰勒二阶展开，其过程物理意义不够明确，且得到的二阶近似式亦不够完善。为此，直接从P-SV平面波入射/散射矩阵出发，给出了一种求取散射矩阵高阶近似的方法，即利用扰动思想将散射矩阵分解为背景矩阵与一阶、二阶扰动矩阵，求取纵波反射系数背景项与一阶、二阶扰动项，推得纵波反射系数的二阶近似公式。模型对比分析表明，所推公式在中高角度乃至近临界角入射情况下具有较高的精度，对密度参数的敏感性更高，为充分利用大炮检距地震数据准确地反演物性参数提供了基础。
关键词：散射矩阵 二阶近似 反射系数 密度
Second-order approximation of reflection coefficient based on decomposition of scattering matrix
① School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China
Abstract: The first-order approximation of the exact Zoeppritz equation is widely used in conventional AVO inversions, which is more suitable for the interface with weak medium variations and the problem of small angle or short offset.The assumptions will lead to calculation errors, which are not conducive to accurate inversion of density and prediction of complex reservoirs and medium-deep reservoirs.And seismic data near the critical angle cannot be fully used.The high-order approximation method based on the exact equation of reflection/transmission coefficients is too complicated.The physical meaning of the process of second-order Taylor expansion of the reflection/transmission coefficients based on the eigenvector matrices of up-and-down waves and matrix symmetry is not clear enough.And the second-order approximation is also not perfect enough.In this paper, a high-order approximation of the scattering matrix based on the incident/scattering matrix of P-SV plane wave is presented.The scattering matrix can be decomposed into the background matrix, the first-and second-order perturbation matrices, and the background term based on the theory of perturbations.The background term, first-and second-order perturbation terms can be derived respectively and the second-order approximation of P wave reflection coefficient can be further obtained.The model comparison analysis shows that the second-order approximation obtained in this paper has higher accuracy in the case of medium-high angle and even near-critical angle incidence and more sensitive to the density variations.It provides a basis for making full use of large-angle or long-offset seismic data and the accurate inversion of physical parameters.
Keywords:
scattering matrix second order approximation reflection coefficient density
0 引言
3 密度敏感性分析
AVO技术利用振幅信息研究岩性、检测油气，经过数十年的发展，已经形成了一套完整而严谨的理论体系。Zoeppritz[1]研究了平面波入射在水平界面上的纵横波反射、透射情况，建立了Zoeppritz方程。如何利用地震反射振幅随入射角变化的信息检测油气成为地球物理学家关注的问题，但是由于Zoeppritz方程的结构过于复杂且物理含义并不直观，不易进行数值计算，一直没有得到很好的应用。Muskat等[2]首先提出了AVO概念，即“平面波的反射和透射系数是入射角的函数”；Koefoed[3]将泊松比与反射系数相联系，给出了精确Zoeppritz方程的近似公式，使AVO技术得到快速发展；Bortfeld[4]在界面两侧岩性参数变化小的假设下得到了区分流体、固体的近似公式；Richards等[5]在假设介质参数变化小的情况下根据位移和应力连续条件推导出较直观的反射/透射系数近似表达式；Aki等[6]给出了反射/透射系数精确表达式，并利用射线参数与角度的关系给出了弱参数变化下的反射/透射系数近似式。Ostrander[7]利用AVO技术识别“亮点”型含油气砂岩，使AVO技术用于实际生产。在前人的基础上，人们从不同角度推导出各类近似表达式，表征纵波反射系数与不同岩石物理参数间的关系。如Shuey[8]给出了具有不同角度项的关于泊松比的纵波反射系数近似式；Smith等[9]利用Gardner公式，采用加权分析提出了速度随密度变化的经验公式；Hilterman[10]在Shuey近似的基础上，给出了关于泊松比的另一种近似式；郑晓东[11]、杨绍国等[12]推出了Zoeppritz方程的近似幂级数表达式；Fatti等[13]发布了关于相对波阻抗的纵波反射系数近似式；Goodway等[14]提出了关于拉梅参数的纵波反射系数近似式；Xu等[15]引入剪切模量、体积模量和压缩模量简化了纵波反射系数；Gray等[16]给出了关于剪切模量、体积模量和压缩模量相对变化量的近似表达式；Russell等[17]在多孔流体饱和岩石的前提下提出了关于Russell流体因子的纵波反射系数近似表达式；宗兆云等[18]推出了关于杨氏模量和泊松比纵波反射系数近似方程。
常规AVO反演利用精确Zoeppritz方程的一阶近似式，更加适用于弱介质变化的反射界面、小角度或小炮检距反射问题，其假设条件导致计算误差[19]，不利于准确提取密度参数[20]，不能很好地预测复杂储层或中深部储层，且无法充分利用近临界角数据。因此，针对复杂储层或中深部储层，需要改进反射系数近似方程，使其适应近临界角入射，充分利用大角度地震数据提高反演精度。Xu等[21]基于Aki-Richards近似方法给出了具有归一化速度、密度二阶项的近似公式；Wang[22]对纵波反射系数精确方程的射线参数表达形式进行泰勒展开，得到了关于垂直慢度、射线参数的二阶近似公式；Ramos[23]对纵波反射系数精确方程进行三阶泰勒展开，给出了适用于强反射界面的横波反射系数近似公式；Ursin等[24]利用上、下行波特征向量矩阵及矩阵对称性对反射/透射系数进行泰勒二阶展开，得到二阶近似公式；Charles[25]提出最优Zoeppritz近似，通过研究纵波反射系数精确值与纵横波速度和密度相对变化量各阶泰勒展开的关系得到拟线性近似，提高了近临界角处的反射系数反演精度。
基于反射系数精确表达式利用Aki-Richards近似方法进行高阶近似过于繁琐[22-23]，利用特征向量化简物理意义不够明确[24]。为此，本文直接从P-SV平面波入射/散射矩阵出发，给出了一种求取散射矩阵高阶近似的方法，即利用扰动思想将散射矩阵分解为背景矩阵与一阶、二阶扰动矩阵，求取纵波反射系数背景项与一阶、二阶扰动项，推得纵波反射系数的二阶近似公式。模型对比分析表明，所推公式在中高角度乃至近临界角入射情况下具有较高的精度，对密度参数的敏感性更高，为充分利用大炮检距地震数据准确地反演物性参数提供了基础。
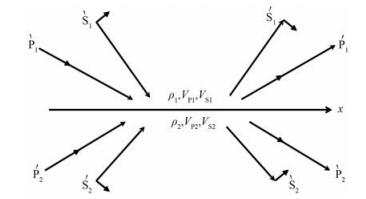
1 基于散射矩阵分解的高阶近似 1.1 散射矩阵分解Aki等[6]研究了P-SV平面波在固体—固体分界面上的反射与透射问题，得到了入射与散射P-SV平面波完整系统(图 1)，并基于此系统推导了完整的散射矩阵。
| $ \left( {\begin{array}{*{20}{c}} {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{P}}\limits^/ }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{S}}\limits^/ }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{P}}\limits^\backslash }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{S}}\limits^\backslash } \end{array}} \right) = {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{N}} = \mathit{\boldsymbol{R}} $ | (1) |
|
图 1 入射与散射的P-SV平面波完整系统 假设同时存在下行P波、下行SV波、上行P波、上行SV波等四种入射波，水平界面两侧半空间介质均为固体，上层介质密度为ρ1，纵波速度为VP1，横波速度为VS1，下行P波入射角为θP1，下行SV波入射角为θS1。下层介质密度为ρ2，纵波速度为VP2，横波速度为VS2，上行P波入射角为θP2，上行SV波入射角为θS2。 |
式中：M、N分别为与散射波、入射波相关的系数矩阵；矩阵内的元素表示相应上、下行P-SV波产生的反射/透射系数，如
| $ \mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{M}}^1} + \Delta {\mathit{\boldsymbol{M}}^2} $ | (2) |
| $ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{N}}^1} + \Delta {\mathit{\boldsymbol{N}}^2} $ | (3) |
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{R}}^1} + \Delta {\mathit{\boldsymbol{R}}^2} $ | (4) |
式中：Mb、Nb、Rb分别为M、N、R的背景矩阵，由各向同性介质参数构成；ΔM1、ΔN1、ΔR1分别为M、N、R的一阶扰动矩阵，由介质参数的一阶变化构成；ΔM2、ΔN2、ΔR2分别为M、N、R的二阶扰动矩阵，由介质参数的二阶变化构成。
1.2 纵波反射系数二阶近似定量表达(附录A)对式(1)变形得到如下矩阵表达式
| $ \mathit{\boldsymbol{MR}} = \mathit{\boldsymbol{N}} $ | (5) |
首先，仅考虑系数矩阵M、N的背景项Mb、Nb时，可以推得散射矩阵的背景项Rb
| $ {\mathit{\boldsymbol{R}}^{\rm{b}}} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}}} \right)^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{b}}} = \left( {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1\\ 1&0&0&0\\ 0&1&0&0 \end{array}} \right) $ | (6) |
当某种波型入射时，由于背景介质均为各向同性，故背景介质中不存在该波型的反射以及其他波型的反射与透射，在Rb中相同波型的透射系数为1，其他波型的反射、透射系数为0。
假设M、N与R仅由背景矩阵与一阶扰动矩阵构成，则式(5)可表示为
| $ \left( {{\mathit{\boldsymbol{M}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{M}}^1}} \right)\left( {{\mathit{\boldsymbol{R}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{R}}^1}} \right) = \left( {{\mathit{\boldsymbol{N}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{N}}^1}} \right) $ | (7) |
对式(7)进行整理，忽略一阶以上高阶项，得
| $ \Delta {\mathit{\boldsymbol{R}}^1} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}}} \right)^{ - 1}}\left( {\Delta {\mathit{\boldsymbol{N}}^1} - \Delta {\mathit{\boldsymbol{M}}^1}{\mathit{\boldsymbol{R}}^{\rm{b}}}} \right) $ | (8) |
式(8)即为散射矩阵的一阶扰动形式。当仅有纵波入射时，即取背景项中的R11b与一阶扰动项的ΔR111，两项相加可得到Aki-Richards近似公式。
假设M、N与R由背景矩阵与一阶扰动矩阵、二阶扰动矩阵共同构成，则式(5)可表示为
| $ \begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{M}}^1} + \Delta {\mathit{\boldsymbol{M}}^2}} \right)\left( {{\mathit{\boldsymbol{R}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{R}}^1} + \Delta {\mathit{\boldsymbol{R}}^2}} \right)}\\ { = {\mathit{\boldsymbol{N}}^{\rm{b}}} + \Delta {\mathit{\boldsymbol{N}}^1} + \Delta {\mathit{\boldsymbol{N}}^2}} \end{array} $ | (9) |
对式(9)进行整理，忽略二阶以上高阶项，得
| $ \Delta {\mathit{\boldsymbol{R}}^2} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}}} \right)^{ - 1}}\left( {\Delta {\mathit{\boldsymbol{N}}^2} - \Delta {\mathit{\boldsymbol{M}}^1}{\mathit{\boldsymbol{R}}^{\rm{1}}} - \Delta {\mathit{\boldsymbol{M}}^2}{\mathit{\boldsymbol{R}}^{\rm{b}}}} \right) $ | (10) |
整理二阶扰动矩阵及其内部参数，经过计算可以得到ΔN2=ΔM2Rb，则式(10)可以进一步简化为
| $ \Delta {\mathit{\boldsymbol{R}}^2} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}}} \right)^{ - 1}}\left( { - \Delta {\mathit{\boldsymbol{M}}^1}\Delta {\mathit{\boldsymbol{R}}^{\rm{1}}}} \right) $ | (11) |
式(11)即为散射矩阵的二阶扰动形式，其中的ΔR112为固体—固体分界面处仅有下行纵波入射产生的纵波反射系数的二阶扰动项。展开式(11)并对ΔR112项进行整理，得
| $ \begin{array}{l} \Delta R_{11}^2 = \left( {{M^{\rm{b}}}} \right)_{11}^{ - 1}\left( {\Delta M_{11}^1\Delta R_{11}^1 + \Delta M_{12}^1\Delta R_{21}^1 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\Delta M_{13}^1\Delta R_{31}^1 + \Delta M_{14}^1\Delta R_{41}^1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\left( {{M^{\rm{b}}}} \right)_{12}^{ - 1}\left( {\Delta M_{21}^1\Delta R_{11}^1 + \Delta M_{22}^1\Delta R_{21}^1 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\Delta M_{23}^1\Delta R_{31}^1 + \Delta M_{24}^1\Delta R_{41}^1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\left( {{M^{\rm{b}}}} \right)_{13}^{ - 1}\left( {\Delta M_{31}^1\Delta R_{11}^1 + \Delta M_{32}^1\Delta R_{21}^1 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\Delta M_{33}^1\Delta R_{31}^1 + \Delta M_{34}^1\Delta R_{41}^1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\left( {{M^{\rm{b}}}} \right)_{14}^{ - 1}\left( {\Delta M_{41}^1\Delta R_{11}^1 + \Delta M_{42}^1\Delta R_{21}^1 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\Delta M_{43}^1\Delta R_{31}^1 + \Delta M_{44}^1\Delta R_{41}^1} \right) \end{array} $ | (12) |
分别计算散射矩阵的背景项、一阶扰动项、二阶扰动项并相加，整理可得入射、散射P-SV平面波完整系统下的纵波反射系数RPP关于纵、横波速度与密度的二阶近似定量表达式
| $ \begin{array}{l} {R_{{\rm{PP}}}} = R_{11}^{\rm{b}} + \Delta R_{11}^{\rm{1}} + \Delta R_{11}^{\rm{2}}\\ \;\;\;\;\;\; = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4V_{\rm{S}}^2{p^2}\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {1 - 4V_{\rm{S}}^2{p^2}} \right)\frac{{\Delta \rho }}{\rho } + {p^2}V_{\rm{S}}^4\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}} \times \\ \;\;\;\;\;\;\;\;\;{\left( {\frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)^2} - \frac{{{V_{\rm{P}}}}}{{\cos {\theta _{\rm{P}}}}}\frac{{{V_{\rm{S}}}}}{{\cos {\theta _{\rm{S}}}}} \times \\ \;\;\;\;\;\;\;\;\;{p^2}{\left[ {\left( {{p^2}v_{\rm{S}}^2 - \frac{1}{2}} \right)\frac{{\Delta \rho }}{\rho } + 2{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right]^2} \end{array} $ | (13) |
式中：Δρ、ΔVP、ΔVS分别为界面两侧介质密度、纵波速度、横波速度的差值；ρ、VP、VS分别为界面两侧介质密度、纵波速度、横波速度的平均值；θP、θS分别为界面两侧下、上行纵(θP1、θP2)、横波入射角(θS1、θS2)的平均值；p为射线参数。
1.3 横波因子cosθS观察式(13)发现，基于散射矩阵得到的纵波反射系数的二阶项受横波入射角、透射角的平均值θS影响，但在实际纵波反演方法中不存在θS。因此，文中将cosθS称为横波因子，并由反射界面的弹性参数近似表示。
由Snell定律可知
| $ p = \frac{{\sin {\theta _{{\rm{S1}}}}}}{{{V_{{\rm{S1}}}}}} = \frac{{\sin {\theta _{{\rm{S2}}}}}}{{{V_{{\rm{S2}}}}}} = \frac{{\sin {\theta _{{\rm{P1}}}}}}{{{V_{{\rm{P1}}}}}} = \frac{{\sin {\theta _{{\rm{P2}}}}}}{{{V_{{\rm{P2}}}}}} $ | (14) |
假设界面两侧介质参数变化较小，入射角、反射角与透射角均为实数，则界面两侧介质参数可由p的一阶扰动项及其平均值的形式表示，即
| $ {V_{{\rm{S1}}}} = {V_{\rm{S}}} - \Delta {V_{\rm{S}}}/2 $ |
| $ {V_{{\rm{S2}}}} = {V_{\rm{S}}} + \Delta {V_{\rm{S}}}/2 $ |
| $ {V_{{\rm{P1}}}} = {V_{\rm{P}}} - \Delta {V_{\rm{P}}}/2 $ |
| $ {V_{{\rm{P2}}}} = {V_{\rm{P}}} + \Delta {V_{\rm{P}}}/2 $ |
| $ {\theta _{{\rm{S1}}}} = {\theta _{\rm{S}}} - \Delta {\theta _{\rm{S}}}/2 $ |
| $ {\theta _{{\rm{S2}}}} = {\theta _{\rm{S}}} + \Delta {\theta _{\rm{S}}}/2 $ |
| $ {\theta _{{\rm{P1}}}} = {\theta _{\rm{P}}} - \Delta {\theta _{\rm{P}}}/2 $ |
| $ {\theta _{{\rm{P2}}}} = {\theta _{\rm{P}}} + \Delta {\theta _{\rm{P}}}/2 $ |
将各参数代入式(14)，得
| $ \begin{array}{l} p = \frac{{\sin \left( {{\theta _{\rm{S}}} - \Delta {\theta _{\rm{S}}}/2} \right)}}{{{V_{\rm{S}}} - \Delta {V_{\rm{S}}}/2}} = \frac{{\sin \left( {{\theta _{\rm{S}}} + \Delta {\theta _{\rm{S}}}/2} \right)}}{{{V_{\rm{S}}} + \Delta {V_{\rm{S}}}/2}}\\ \;\;\; = \frac{{\sin \left( {{\theta _{\rm{P}}} - \Delta {\theta _{\rm{P}}}/2} \right)}}{{{V_{\rm{P}}} - \Delta {V_{\rm{P}}}/2}} = \frac{{\sin \left( {{\theta _{\rm{P}}} + \Delta {\theta _{\rm{P}}}/2} \right)}}{{{V_{\rm{P}}} + \Delta {V_{\rm{P}}}/2}} \end{array} $ | (15) |
进一步化简并忽略高阶扰动项，得
| $ p \approx \frac{{\sin {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}} = \frac{{\sin {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}} $ | (16) |
横波因子可由实测纵、横波速度与入射角定量表示为
| $ \cos {\theta _{\rm{S}}} = \sqrt {1 - {{\sin }^2}{\theta _{\rm{S}}}} = {\left( {1 - \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)^{\frac{1}{2}}} $ | (17) |
将式(17)代入式(13)，可得到纵波反射系数的另一种表达形式
| $ \begin{array}{l} {R_{{\rm{PP}}}} = R_{11}^{\rm{b}} + \Delta R_{11}^{\rm{1}} + \Delta R_{11}^{\rm{2}} = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - \\ \;\;4\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{\sin ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \left( {\frac{1}{2} - 2\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)\frac{{\Delta \rho }}{\rho } + \\ \;\;{\left( {1 - \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)^{\frac{1}{2}}}{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)^3}\cos {\theta _{\rm{P}}}{\sin ^2}{\theta _{\rm{P}}} \times \\ \;\;{\left( {\frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)^2} - \frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}\sin {\theta _{\rm{P}}}\tan {\theta _{\rm{P}}}{\left( {1 - \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)^{ - \frac{1}{2}}} \times \\ \;\;{\left[ {\left( {\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}} - \frac{1}{2}} \right)\frac{{\Delta \rho }}{\rho } + 2\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right]^2} \end{array} $ | (18) |
式(18)为化简后的关于纵、横波速度以及密度的纵波反射系数二阶近似式。与式(13)相比，用横纵波速度比的形式表示射线参数p与横波因子cosθS，使近似公式的参数形式得到统一，便于选取实际反演参数，更加适用于AVO反演。
2 纵波反射系数二阶近似方程精度分析 2.1 二阶项对精度的影响若忽略式(18)中的二阶扰动项，便得到关于纵、横波速度以及密度的纵波反射系数一阶近似方程
| $ \begin{array}{l} {R_{{\rm{PP}}}} = R_{11}^{\rm{b}} + \Delta R_{11}^{\rm{1}} = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\frac{1}{2}\left( {1 - 4{p^2}V_{\rm{S}}^2} \right)\frac{{\Delta \rho }}{\rho } \end{array} $ | (19) |
式中纵、横波速度以及密度的反射系数均为线性项，等价于Aki-Richards[6]一阶线性近似式。若忽略式(18)中的
| $ \begin{array}{l} {R_{{\rm{PP}}}} = {R^{\rm{b}}} + \Delta R_{11}^{\rm{1}} + \Delta R_{11}^{\rm{2}}\\ \;\;\;\;\;\; = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{\sin ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\;\left( {\frac{1}{2} - 2\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)\frac{{\Delta \rho }}{\rho } + \\ \;\;\;\;\;\;\;\;\;\frac{{V_{\rm{S}}^3}}{{V_{\rm{P}}^3}}\cos {\theta _{\rm{P}}}{\sin ^2}{\theta _{\rm{P}}}{\left( {\frac{{\Delta \rho }}{\rho } + 2\frac{{{V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)^2} \end{array} $ | (20) |
本文借鉴Wang[22]的四种模型，分别利用不同近似表达式给出了不同岩石界面下的纵波反射系数曲线。这四种模型分别表示页岩/砂岩、页岩/石灰岩(或白云岩)、硬石膏/砂岩和硬石膏/石灰岩(或白云岩)界面，模型参数如表 1所示。
|
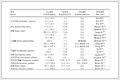
表 1 模型参数 |
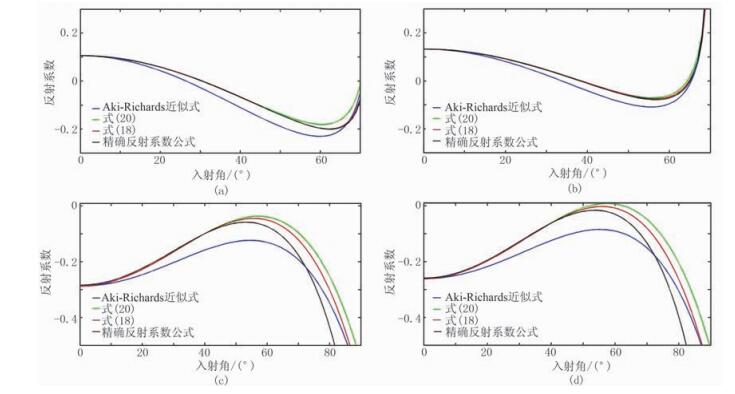
图 2为RPP曲线(未考虑横波因子)。由图可见：①当为页岩/砂岩(图 2a)、页岩/石灰岩(或白云岩)(图 2b)界面时，上层介质的波阻抗小于下层介质(正阻抗界面)，Aki-Richards近似方程仅在小角度入射时得到的RPP具有较高精度，在中高角度处会产生明显误差，而二阶近似方程在中高角度仍能取得很好的近似效果，且本文得到的二阶近似方程(式(18))在近临界角处仍能取得很高的近似效果；②由于页岩/砂岩(图 2a)界面两侧密度与纵波速度变化小、横波速度变化大，页岩/石灰岩(或白云岩)(图 2b)界面两侧密度与速度变化趋势相反，因此后者的二阶近似方程精度更高，表明二阶RPP反映了横波的影响，即变化小的横波速度提高了二阶RPP的精度；③当为硬石膏/砂岩(图 2c)、硬石膏/石灰岩(或白云岩)(图 2d)界面时，上层介质波阻抗大于下层介质(负阻抗界面)，在小角度入射时三种近似方程得到的RPP均具很高的精度，但在中高角度处仅有二阶近似方程可以满足精度要求，且本文推导的二阶近似方程(式(18))所产生的误差最小；④由于硬石膏中的密度、纵波速度、横波速度远大于砂岩与石灰岩，介质参数变化大，进行射线参数与横波因子处理时，在大角度情况下会产生较大误差，二阶近似方程的精度随着入射角的增大而逐渐变低。
|
图 2 RPP曲线(未考虑横波因子) (a)页岩/砂岩界面；(b)页岩/石灰岩(或白云岩)界面；(c)硬石膏/砂岩界面；(d)硬石膏/石灰岩(或白云岩)界面 |
综上所述，由于Aki-Richards近似方程忽略了二阶扰动项，其结果仅在很小的角度范围内与精确方程曲线吻合，随着入射角的增大，Aki-Richards近似方程曲线与精确方程曲线的误差趋于明显，二阶近似式的精度明显高于Aki-Richards近似方程，与精确Zoeppritz方程对应曲线的拟合程度更好。本文提出的二阶近似方程(式(18)，暂未考虑横波因子)与Wang的二阶近似方程((式20))相比，仅在定量表达形式上增加了
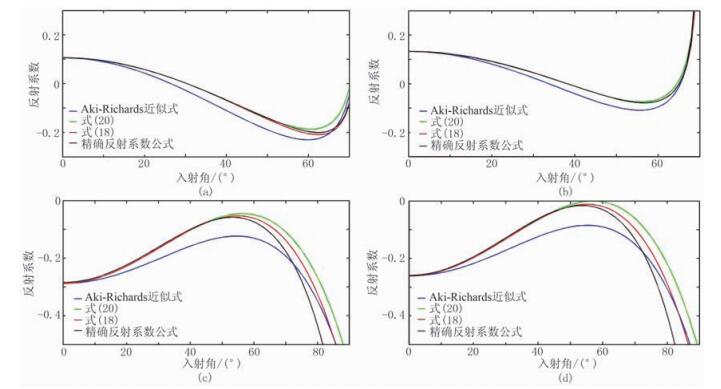
将横波因子表达式(式(17))代入式(13)与式(20)，可得到RPP曲线(考虑横波因子)(图 3)。对比未考虑横波因子(图 2)与考虑横波因子(图 3)的RPP曲线可知，后者的精度较高，确保了近似方程在入射角增大情况下的适用性，如本文提出的二阶近似方程(式(18))曲线与精确方程曲线在近临界角处几乎完全拟合。当界面两侧物性差异较大时(图 3c、图 3d)，考虑横波因子明显提高了近似方程的精度。
|
图 3 RPP曲线(考虑横波因子) (a)页岩/砂岩界面；(b)页岩/石灰岩(或白云岩)界面；(c)硬石膏/砂岩界面；(d)硬石膏/石灰岩(或白云岩)界面 |
基于AVO反演可以从地震数据中获取相应介质参数，小炮检距(小入射角)地震振幅数据主要与地震波速度相关，密度参数对中高炮检距(中高入射角)地震振幅数据更敏感[26-29]，但是由于纵波反射系数一阶近似方程在中高入射角时无法获得很高的近似效果，因此基于此类方程的AVO反演方法的密度反演精度相对有限[30]。Fatti等[13]提出了相对波阻抗的概念，并在Aki-Richards的反射系数近似式的基础上推导了关于纵波阻抗、横波阻抗、密度的Fatti近似式。由于纵、横波阻抗及纵、横波速度都与密度直接相关，其中密度对阻抗的影响最大[31]。因此为了更清晰地体现本文所提近似方程(式(18))在中高角度地震数据密度反演中的优势，将式(18)改写为关于纵波阻抗、横波阻抗、密度的近似方程
| $ \begin{array}{l} {R_{{\rm{PP}}}} = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {I_{\rm{P}}}}}{{{I_{\rm{P}}}}} - 4\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{\sin ^2}{\theta _{\rm{P}}}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}} + \\ \;\;\;\;\;\left( {2\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}} - \frac{1}{2}{{\tan }^2}{\theta _{\rm{P}}}} \right)\frac{{\Delta \rho }}{\rho } + {\left( {1 - \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)^{\frac{1}{2}}} \times \\ \;\;\;\;\;{\left( {\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}} \right)^3}\cos {\theta _{\rm{P}}}{\sin ^2}{\theta _{\rm{P}}}{\left( {2\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}} - \frac{{\Delta \rho }}{\rho }} \right)^2} - \\ \;\;\;\;\;\frac{{{V_{\rm{S}}}}}{{{V_{\rm{P}}}}}\sin {\theta _{\rm{P}}}\tan {\theta _{\rm{P}}}{\left( {1 - \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}} \right)^{ - \frac{1}{2}}} \times \\ \;\;\;\;\;{\left[ {2\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}} - \left( {\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}{\theta _{\rm{P}}} + \frac{1}{2}} \right)\frac{{\Delta \rho }}{\rho }} \right]^2} \end{array} $ | (21) |
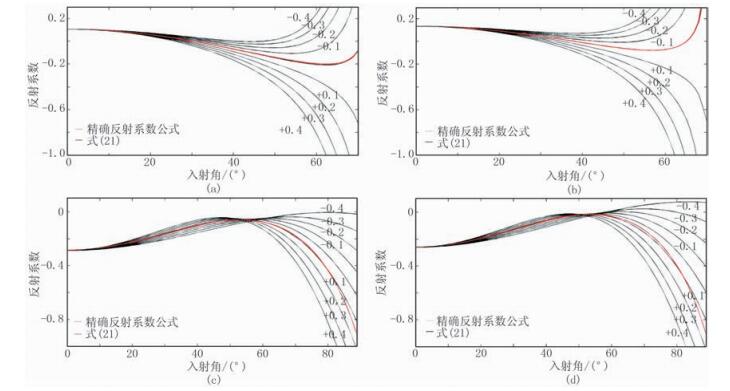
为了研究Fatti近似式与式(21)对密度变化的敏感性差异，进一步基于Wang[22]的四种模型进行分析，控制
|
图 4 Fatti近似公式RPP曲线 (a)页岩/砂岩界面(临界角约72°)；(b)页岩/石灰岩(或白云岩)界面(临界角约69°)；(c)硬石膏/砂岩界面；(d)硬石膏/石灰岩(或白云岩)界面 |
|
图 5 式(21)RPP曲线 (a)页岩/砂岩界面(临界角约72°)；(b)页岩/石灰岩(或白云岩)界面(临界角约69°)；(c)硬石膏/砂岩界面；(d)硬石膏/石灰岩(或白云岩)界面 |
由图可见：①在小角度入射时，随着Δρ/ρ变化，纵波反射系数基本保持不变，随着入射角进一步增加，反射系数曲线产生明显变化，表明纵波反射系数在小角度入射时对密度变化不敏感，在中高角度乃至大角度入射时对密度变化敏感。②对于Fatti近似方程，在入射角小于25°时，反射系数曲线几乎没有变化，当入射角大于30°时反射系数曲线产生明显变化(图 4a、图 4b)；对于式(21)，当入射角等于10°时反射系数曲线开始变化，当入射角达到30°时反射系数曲线变化极为明显(图 5a、图 5b)。③Fatti近似公式反射系数曲线(图 4c、图 4d)在
本文基于P-SV平面波入射与散射完整系统下的散射矩阵，给出了一种利用矩阵分解推导反射/透射系数高阶近似的方法，将散射矩阵分解为背景矩阵与不同阶数扰动矩阵，得到了基于入射角的纵波反射系数二阶近似公式。与常规AVO分析中的Aki-Richards线性近似[6]、Wang[22]的二阶近似表达式相比，文中所提反射系数二阶近似公式在中高角度入射时与精确方程具有良好的吻合性，且在近临界角入射情况下也具有较高的精度，当界面两侧横波速度与密度变化差异适中时，近似效果可以达到最佳。因此利用本文的近似公式可以充分利用大炮检距地震振幅数据，解决了一阶近似公式未能充分利用临界角数据的问题，提高了中高入射角的反射系数反演精度，并且为近临界角反演提供了一种方法。利用AVO反演可以提取各种弹性、物性参数，其中密度参数对小入射角地震响应的影响弱，在大炮检距地震振幅数据中富含更精细的信息，常规地震方法很难获得稳定的密度参数估计。本文的近似公式增强了对密度的敏感性，提高了富含密度信息的大炮检距地震振幅数据的利用程度，为准确而稳定地密度反演提供了基础。
附录A 基于散射矩阵分解的纵波反射系数二阶近似公式推导Aki等[6]研究了P-SV平面波在固体—固体分界面上的反射与透射问题，得到了完整的散射矩阵
| $ \left( {\begin{array}{*{20}{c}} {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{P}}\limits^/ }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{P}}\limits^/ }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{S}}\limits^/ }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{S}}\limits^/ }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{P}}\limits^\backslash }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{P}}\limits^\backslash }\\ {\mathop {\rm{P}}\limits^\backslash \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{S}}\limits^\backslash \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{P}}\limits^/ \mathop {\rm{S}}\limits^\backslash }&{\mathop {\rm{S}}\limits^/ \mathop {\rm{S}}\limits^\backslash } \end{array}} \right) = {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{N}} = \mathit{\boldsymbol{R}} $ | (A-1) |
式中M、N分别为与散射波、入射波相关的系数矩阵，分别为
| $ \mathit{\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}} { - {V_{{\rm{P1}}}}p}&{ - \cos {\theta _{{\rm{S1}}}}}&{{V_{{\rm{P2}}}}p}&{\cos {\theta _{{\rm{S2}}}}}\\ {\cos {\theta _{{\rm{P1}}}}}&{ - {V_{{\rm{S1}}}}p}&{\cos {\theta _{{\rm{P2}}}}}&{ - {V_{{\rm{P2}}}}p}\\ {2{\rho _1}V_{{\rm{S1}}}^2p\cos {\theta _{{\rm{P1}}}}}&{{\rho _1}{V_{{\rm{S1}}}}\left( {1 - 2V_{{\rm{S1}}}^2{p^2}} \right)}&{2{\rho _2}V_{{\rm{S2}}}^2p\cos {\theta _{{\rm{P2}}}}}&{{\rho _2}{V_{{\rm{S2}}}}\left( {1 - 2V_{{\rm{S2}}}^2{p^2}} \right)}\\ { - {\rho _1}{V_{{\rm{P1}}}}\left( {1 - 2V_{{\rm{S1}}}^2{p^2}} \right)}&{2{\rho _1}V_{{\rm{S1}}}^2p\cos {\theta _{{\rm{S1}}}}}&{{\rho _2}{V_{{\rm{P2}}}}\left( {1 - 2V_{{\rm{S2}}}^2{p^2}} \right)}&{ - 2{\rho _2}V_{{\rm{S2}}}^2p\cos {\theta _{{\rm{S2}}}}} \end{array}} \right) $ | (A-2) |
| $ \mathit{\boldsymbol{N}} = \left( {\begin{array}{*{20}{c}} {{V_{{\rm{P1}}}}p}&{\cos {\theta _{{\rm{S1}}}}}&{ - {V_{{\rm{P2}}}}p}&{ - \cos {\theta _{{\rm{S2}}}}}\\ {\cos {\theta _{{\rm{P1}}}}}&{ - {V_{{\rm{S1}}}}p}&{\cos {\theta _{{\rm{P2}}}}}&{ - {V_{{\rm{P2}}}}p}\\ {2{\rho _1}V_{{\rm{S1}}}^2p\cos {\theta _{{\rm{P1}}}}}&{{\rho _1}{V_{{\rm{S1}}}}\left( {1 - 2V_{{\rm{S1}}}^2{p^2}} \right)}&{2{\rho _2}V_{{\rm{S2}}}^2p\cos {\theta _{{\rm{P2}}}}}&{{\rho _2}{V_{{\rm{S2}}}}\left( {1 - 2V_{{\rm{S2}}}^2{p^2}} \right)}\\ {{\rho _1}{V_{{\rm{P1}}}}\left( {1 - 2V_{{\rm{S1}}}^2{p^2}} \right)}&{ - 2{\rho _1}V_{{\rm{S1}}}^2p\cos {\theta _{{\rm{S1}}}}}&{ - {\rho _2}{V_{{\rm{P2}}}}\left( {1 - 2V_{{\rm{S2}}}^2{p^2}} \right)}&{2{\rho _2}V_{{\rm{S2}}}^2p\cos {\theta _{{\rm{S2}}}}} \end{array}} \right) $ | (A-3) |
直接将参数扰动形式代入矩阵表达式，各参数的扰动形式为
| $ \Delta {V_{\rm{P}}} = {V_{{\rm{P2}}}} - {V_{{\rm{P1}}}} $ |
| $ {V_{\rm{P}}} = \frac{{{V_{{\rm{P2}}}} + {V_{{\rm{P1}}}}}}{2} $ |
| $ \Delta {V_{\rm{S}}} = {V_{{\rm{S2}}}} - {V_{{\rm{S1}}}} $ |
| $ {V_{\rm{S}}} = \frac{{{V_{{\rm{S2}}}} + {V_{{\rm{S1}}}}}}{2} $ |
| $ \Delta \rho = {\rho _2} - {\rho _1} $ |
| $ \rho = \frac{{{\rho _2} + {\rho _1}}}{2} $ |
| $ \Delta {\theta _{\rm{P}}} = {\theta _{{\rm{P2}}}} - {\theta _{{\rm{P1}}}} $ |
| $ {\theta _{\rm{P}}} = \frac{{{\theta _{{\rm{P2}}}} + {\theta _{{\rm{P1}}}}}}{2} $ |
| $ \Delta {\theta _{\rm{S}}} = {\theta _{{\rm{S2}}}} - {\theta _{{\rm{S1}}}} $ |
| $ {\theta _{\rm{S}}} = \frac{{{\theta _{{\rm{S2}}}} + {\theta _{{\rm{S1}}}}}}{2} $ |
由散射理论，将矩阵分解为背景矩阵Mb、Nb、Rb，一阶扰动矩阵ΔM1、ΔN1、ΔR1和二阶扰动矩阵ΔM2、ΔN2、ΔR2。其中背景矩阵为
| $ {\mathit{\boldsymbol{M}}^{\rm{b}}} = \left( {\begin{array}{*{20}{c}} { - {V_{\rm{P}}}p}&{ - \cos {\theta _{\rm{S}}}}&{{V_{\rm{P}}}p}&{\cos {\theta _{\rm{S}}}}\\ {\cos {\theta _{\rm{P}}}}&{ - {V_{\rm{S}}}p}&{\cos {\theta _{\rm{P}}}}&{ - {V_{\rm{P}}}p}\\ {2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{P}}}}&{\rho {V_{\rm{S}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{P}}}}&{\rho {V_{\rm{S}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}\\ { - \rho {V_{\rm{P}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{S}}}}&{\rho {V_{\rm{P}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{ - 2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{S}}}} \end{array}} \right) $ | (A-4) |
| $ {\mathit{\boldsymbol{N}}^{\rm{b}}} = \left( {\begin{array}{*{20}{c}} {{V_{\rm{P}}}p}&{\cos {\theta _{\rm{S}}}}&{ - {V_{\rm{P}}}p}&{ - \cos {\theta _{\rm{S}}}}\\ {\cos {\theta _{\rm{P}}}}&{ - {V_{\rm{S}}}p}&{\cos {\theta _{\rm{P}}}}&{ - {V_{\rm{P}}}p}\\ {2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{P}}}}&{\rho {V_{\rm{S}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{P}}}}&{\rho {V_{\rm{S}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}\\ {\rho {V_{\rm{P}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{ - 2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{S}}}}&{ - \rho {V_{\rm{P}}}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)}&{2\rho V_{\rm{S}}^2p\cos {\theta _{\rm{S}}}} \end{array}} \right) $ | (A-5) |
当某种波型入射时，由于背景介质均为各向同性，故背景介质中不存在该波型的反射以及其他波型的反射与透射，在Rb中相同波型的透射系数为1，其他波型的反射、透射系数为0，即
| $ {\mathit{\boldsymbol{R}}^{\rm{b}}} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{b}}}} \right)^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{b}}} = \left( {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1\\ 1&0&0&0\\ 0&1&0&0 \end{array}} \right) $ | (A-6) |
其中R11b表示纵波反射系数背景项RPPb。
取各参数的一阶近似项进行整理，得到的一阶扰动矩阵为
| $ \Delta {\mathit{\boldsymbol{M}}^1} = \left( {\begin{array}{*{20}{c}} {\Delta M_{11}^1}&{\Delta M_{12}^1}&{\Delta M_{13}^1}&{\Delta M_{14}^1}\\ {\Delta M_{21}^1}&{\Delta M_{22}^1}&{\Delta M_{23}^1}&{\Delta M_{24}^1}\\ {\Delta M_{31}^1}&{\Delta M_{32}^1}&{\Delta M_{33}^1}&{\Delta M_{34}^1}\\ {\Delta M_{41}^1}&{\Delta M_{42}^1}&{\Delta M_{43}^1}&{\Delta M_{44}^1} \end{array}} \right) $ | (A-7) |
| $ \Delta {\mathit{\boldsymbol{N}}^1} = \left( {\begin{array}{*{20}{c}} { - \Delta M_{11}^1}&{ - \Delta M_{12}^1}&{ - \Delta M_{13}^1}&{ - \Delta M_{14}^1}\\ {\Delta M_{21}^1}&{\Delta M_{22}^1}&{\Delta M_{23}^1}&{\Delta M_{24}^1}\\ {\Delta M_{31}^1}&{\Delta M_{32}^1}&{\Delta M_{33}^1}&{\Delta M_{34}^1}\\ { - \Delta M_{41}^1}&{ - \Delta M_{42}^1}&{ - \Delta M_{43}^1}&{\Delta M_{44}^1} \end{array}} \right) $ | (A-8) |
其中
| $ \Delta M_{11}^1 = \Delta M_{13}^1 $ |
| $ \Delta M_{12}^1 = \Delta M_{14}^1 $ |
| $ \Delta M_{21}^1 = - \Delta M_{23}^1 $ |
| $ \Delta M_{22}^1 = - \Delta M_{24}^1 $ |
| $ \Delta M_{31}^1 = - \Delta M_{33}^1 $ |
| $ \Delta M_{32}^1 = - \Delta M_{34}^1 $ |
| $ \Delta M_{41}^1 = \Delta M_{43}^1 $ |
| $ \Delta M_{42}^1 = \Delta M_{44}^1 $ |
| $ \Delta M_{11}^1 = \frac{1}{2}p\Delta {V_{\rm{P}}} $ |
| $ \Delta M_{12}^1 = - \frac{1}{2}\cos {\theta _{\rm{S}}}\Delta {\theta _{\rm{S}}} $ |
| $ \Delta M_{21}^1 = \frac{1}{2}\cos {\theta _{\rm{P}}}\Delta {\theta _{\rm{P}}} $ |
| $ \Delta M_{22}^1 = \frac{1}{2}p\Delta {V_{\rm{S}}} $ |
| $ \begin{array}{l} \Delta M_{31}^1 = - V_{\rm{S}}^2p\cos {\theta _{\rm{P}}}\Delta \rho - 2\rho {V_{\rm{S}}}p\cos {\theta _{\rm{P}}}\Delta {V_{\rm{S}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\rho V_{\rm{S}}^2p\sin {\theta _{\rm{P}}}\Delta {\theta _{\rm{P}}} \end{array} $ |
| $ \begin{array}{l} \Delta M_{32}^1 = - \frac{1}{2}\left( {1 - 2V_{\rm{S}}^2{p^2}} \right)\left( {\rho \Delta {V_{\rm{S}}} + {V_{\rm{S}}}\Delta \rho } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;2V_{\rm{S}}^2{p^2}\rho \Delta {V_{\rm{S}}} \end{array} $ |
| $ \begin{array}{l} \Delta M_{41}^1 = \frac{1}{2}\left( {1 - 2V_{\rm{P}}^2{p^2}} \right)\left( {\rho \Delta {V_{\rm{P}}} + {V_{\rm{P}}}\Delta \rho } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;2{V_{\rm{P}}}{V_{\rm{S}}}{p^2}\rho \Delta {V_{\rm{S}}} \end{array} $ |
| $ \begin{array}{l} \Delta M_{42}^1 = - V_{\rm{S}}^2p\cos {\theta _{\rm{S}}}\Delta \rho - 2\rho {V_{\rm{S}}}p\cos {\theta _{\rm{S}}}\Delta {V_{\rm{S}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\rho V_{\rm{S}}^2p\sin {\theta _{\rm{S}}}\Delta {\theta _{\rm{S}}} \end{array} $ |
同理，取各参数的二阶近似项进行整理，得到的二阶扰动矩阵为
| $ \Delta {\mathit{\boldsymbol{M}}^2} = \left( {\begin{array}{*{20}{c}} 0&{\Delta M_{12}^2}&0&{\Delta M_{14}^2}\\ {\Delta M_{21}^2}&0&{\Delta M_{23}^2}&0\\ {\Delta M_{31}^2}&{\Delta M_{32}^2}&{\Delta M_{33}^2}&{\Delta M_{34}^2}\\ {\Delta M_{41}^2}&{\Delta M_{42}^2}&{\Delta M_{43}^2}&{\Delta M_{44}^2} \end{array}} \right) $ | (A-9) |
| $ \Delta {\mathit{\boldsymbol{N}}^2} = \left( {\begin{array}{*{20}{c}} { - \Delta M_{11}^2}&{ - \Delta M_{12}^2}&{ - \Delta M_{13}^2}&{ - \Delta M_{14}^2}\\ {\Delta M_{21}^2}&{\Delta M_{22}^2}&{\Delta M_{23}^2}&{\Delta M_{24}^2}\\ {\Delta M_{31}^2}&{\Delta M_{32}^2}&{\Delta M_{33}^2}&{\Delta M_{34}^2}\\ { - \Delta M_{41}^2}&{ - \Delta M_{42}^2}&{ - \Delta M_{43}^2}&{ - \Delta M_{44}^2} \end{array}} \right) $ | (A-10) |
其中
| $ \Delta M_{12}^2 = - \Delta M_{14}^2 $ |
| $ \Delta M_{33}^2 = \Delta M_{31}^2 $ |
| $ \Delta M_{34}^2 = \Delta M_{32}^2 $ |
| $ \Delta M_{21}^2 = \Delta M_{23}^2 $ |
| $ \Delta M_{43}^2 = - \Delta M_{41}^2 $ |
| $ \Delta M_{44}^2 = - \Delta M_{42}^2 $ |
| $ \Delta M_{12}^2 = \frac{1}{8}\cos {\theta _{\rm{S}}}{\Delta ^2}{\theta _{\rm{S}}} $ |
| $ \Delta M_{12}^2 = - \frac{1}{8}\cos {\theta _{\rm{P}}}{\Delta ^2}{\theta _{\rm{P}}} $ |
| $ \begin{array}{l} \Delta M_{31}^2 = p\left( {{V_{\rm{S}}}\cos {\theta _{\rm{P}}}\Delta \rho {V_{\rm{S}}} - \frac{1}{2}V_{\rm{S}}^2\sin {\theta _{\rm{P}}}\Delta \rho \Delta {\theta _{\rm{P}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\rho {V_{\rm{S}}}\sin {\theta _{\rm{P}}}\Delta {V_{\rm{S}}}\Delta {\theta _{\rm{P}}} + \frac{1}{2}\rho \cos {\theta _{\rm{P}}}{\Delta ^2}{V_{\rm{S}}} - \\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{4}\rho V_{\rm{S}}^2\cos {\theta _{\rm{P}}}{\Delta ^2}{\theta _{\rm{P}}}} \right) \end{array} $ |
| $ \Delta M_{32}^2 = - \frac{3}{2}{p^2}\rho {V_{\rm{S}}}{\Delta ^2}{V_{\rm{S}}} + \frac{1}{4}\left( {1 - 6{p^2}V_{\rm{S}}^2} \right)\Delta \rho \Delta {V_{\rm{S}}} $ |
| $ \begin{array}{l} \Delta M_{41}^2 = \frac{1}{2}{p^2}\rho {V_{\rm{P}}}{\Delta ^2}{V_{\rm{S}}} + {p^2}{V_{\rm{P}}}{V_{\rm{S}}}\Delta \rho \Delta {V_{\rm{S}}} + \\ \;\;\;\;\;\;\;\;\;\;\;{p^2}\rho {V_{\rm{S}}}\Delta {V_{\rm{P}}}\Delta {V_{\rm{S}}} - \frac{1}{4}\left( {1 - 2{p^2}V_{\rm{S}}^2} \right)\Delta \rho \Delta {V_{\rm{P}}} \end{array} $ |
| $ \begin{array}{l} \Delta M_{42}^2 = p\left( {{V_{\rm{S}}}\cos {\theta _{\rm{S}}}\Delta \rho \Delta {V_{\rm{S}}} - \frac{1}{2}V_{\rm{S}}^2\sin {\theta _{\rm{S}}}\Delta \rho \Delta {\theta _{\rm{S}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\rho {V_{\rm{S}}}\sin {\theta _{\rm{S}}}\Delta {V_{\rm{S}}}\Delta {\theta _{\rm{S}}} + \frac{1}{2}\rho \cos {\theta _{\rm{S}}}{\Delta ^2}{V_{\rm{S}}} - \\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{4}V_{\rm{S}}^2\cos {\theta _{\rm{S}}}{\Delta ^2}{\theta _{\rm{S}}}} \right) \end{array} $ |
根据式(A-6)、式(A-9)、式(A-10)及其二阶参数关系，整理计算可以得到
| $ \Delta {\mathit{\boldsymbol{N}}^2} = \Delta {\mathit{\boldsymbol{M}}^2}{\mathit{\boldsymbol{R}}^{\rm{b}}} $ | (A-11) |
将式(A-4)、式(A-6)~式(A-8)代入式(8)，经计算整理得散射矩阵的一阶扰动形式，其中第一列的四项为
| $ \begin{array}{l} \Delta R_{11}^1 = \frac{1}{2}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {1 - 4{p^2}V_{\rm{S}}^2} \right) + \frac{1}{2}\tan {\theta _{\rm{P}}}\Delta {\theta _{\rm{P}}} \end{array} $ | (A-12) |
| $ \begin{array}{l} \Delta R_{21}^1 = - \frac{{p{V_{\rm{P}}}}}{{2\cos {\theta _{\rm{S}}}}} \times \\ \;\;\;\;\;\;\left( {1 - 2{p^2}V_{\rm{S}}^2 + 2V_{\rm{S}}^2\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)\frac{{\Delta \rho }}{\rho } \end{array} $ | (A-13) |
| $ \Delta R_{31}^1 = - \frac{1}{2}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - \frac{1}{2}\frac{{\Delta \rho }}{\rho } + \frac{1}{2}\tan {\theta _{\rm{P}}}\Delta {\theta _{\rm{P}}} $ | (A-14) |
| $ \begin{array}{l} \Delta R_{41}^1 = - \frac{{p{V_{\rm{P}}}}}{{2\cos {\theta _{\rm{S}}}}}\left[ {\left( {1 - 2{p^2}V_{\rm{S}}^2 - 2V_{\rm{S}}^2\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right) \times } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\Delta \rho }}{\rho } - \left( {4{p^2}V_{\rm{S}}^2 + 4V_{\rm{S}}^2\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right] \end{array} $ | (A-15) |
对θP、θS泰勒展开，得
| $ \Delta {\theta _{\rm{P}}} = {\theta _{{\rm{P2}}}} - {\theta _{{\rm{P1}}}} = \tan {\theta _{\rm{P}}}\left( {\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}}} \right) $ |
| $ \Delta {\theta _{\rm{S}}} = {\theta _{{\rm{S2}}}} - {\theta _{{\rm{S1}}}} = \tan {\theta _{\rm{S}}}\left( {\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right) $ |
代入式(A-11)便可得到Aki-Richards近似，即纵波反射系数RPP的一阶近似式
| $ \begin{array}{l} {R_{{\rm{PP}}}} = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {1 - 4{p^2}V_{\rm{S}}^2} \right)\frac{{\Delta \rho }}{\rho } \end{array} $ | (A-16) |
将式(A-4)、式(A-7)、式(A-12)~式(A-15)代入式(12)，计算整理得到RPP的二阶扰动项
| $ \begin{array}{l} \Delta R_{11}^2 = {p^2}V_{\rm{S}}^4\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}}{\left( {\frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)^2} - \\ \;\;\;{p^2}\frac{{{V_{\rm{P}}}}}{{\cos {\theta _{\rm{P}}}}}\frac{{{V_{\rm{S}}}}}{{\cos {\theta _{\rm{S}}}}}{\left[ {\left( {{p^2}V_{\rm{S}}^2 - \frac{1}{2}} \right)\frac{{\Delta \rho }}{\rho } + 2{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right]^2} \end{array} $ | (A-17) |
将RPP的背景项、一阶扰动项(式(A-12))、二阶扰动项(式(A-17))相加、整理可得入射、散射P-SV平面波完整系统下的RPP关于纵波速度、横波速度与密度的二阶近似表达式
| $ \begin{array}{l} {R_{{\rm{PP}}}} = {R^{\rm{b}}} + \Delta R_{11}^1 + \Delta R_{11}^2\\ \;\;\;\;\;\; = \frac{1}{2}{\sec ^2}{\theta _{\rm{P}}}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} + \\ \;\;\;\;\;\;\frac{1}{2}\left( {1 - 4{p^2}V_{\rm{S}}^2} \right)\frac{{\Delta \rho }}{\rho } + \\ \;\;\;\;\;\;{p^2}V_{\rm{S}}^4\frac{{\cos {\theta _{\rm{P}}}}}{{{V_{\rm{P}}}}}\frac{{\cos {\theta _{\rm{S}}}}}{{{V_{\rm{S}}}}}{\left( {\frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right)^2} - \\ \;\;\;\;\;\;{p^2}\frac{{{V_{\rm{P}}}}}{{\cos {\theta _{\rm{P}}}}}\frac{{{V_{\rm{S}}}}}{{\cos {\theta _{\rm{S}}}}}{\left[ {\left( {{p^2}V_{\rm{S}}^2 - \frac{1}{2}} \right)\frac{{\Delta \rho }}{\rho } + 2{p^2}V_{\rm{S}}^2\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}} \right]^2} \end{array} $ | (A-18) |
参考文献
| [1] |
Zoeppritz K. On the reflection and penetration of seismic waves through unstable layers[J]. Goettinger Nachr, 1919, 66-84. |
| [2] |
Muskat M, Merest M W. Reflection and transmission coefficients for plane waves in elastic media[J]. Geophysics, 1940, 5(2): 115-124. DOI:10.1190/1.1441797 |
| [3] |
Koefoed O. On the effect of Poisson's ratio of rock strata on the reflection coefficients of plane waves[J]. Geophysical Prospecting, 1995, 43(4): 381-387. |
| [4] |
Bortfeld R. Approximation to the reflection and transmission coefficients of the plane longitudinal and transverse waves[J]. Goephysical Prospecting, 1961, 9(4): 485-502. DOI:10.1111/gpr.1961.9.issue-4 |
| [5] |
Richards P G, Frasier C W. Scattering of elastic waves from depth-dependent inhomogeneities[J]. Geophy-sics, 1976, 41(3): 441-458. DOI:10.1190/1.1440625 |
| [6] |
Aki K, Richards P G.Quantitative Seismology: Theory and Methods[M]. W H Freeman and Co Cambridge, 1980.
|
| [7] |
Ostrander W J. Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J]. Geophysics, 1984, 49(10): 1637-1648. DOI:10.1190/1.1441571 |
| [8] |
Shuey R T. A simplification of the Zoeppritz equa-tions[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [9] |
Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas[J]. Goephy-sical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/gpr.1987.35.issue-9 |
| [10] |
Hilterman F. Is AVO the seismic signature of lithology? A case history of Ship Shoal-South addition[J]. The Leading Edge, 1990, 9(6): 15-22. DOI:10.1190/1.1439744 |
| [11] |
郑晓东. Zoeppritz方程的近似及其应用[J]. 石油地球物理勘探, 1991, 26(2): 129-144. ZHENG Xiaodong. Approximation and application of Zoeppritz equations[J]. Oil Geophysical Prospecting, 1991, 26(2): 129-144. |
| [12] |
杨绍国, 周熙襄. Zoeppritz方程的级数表达式及近似[J]. 石油地球物理勘探, 1994, 29(4): 399-412. YANG Shaoguo, ZHOU Xixiang. The series expressions and approximations of the Zoeppritz equations[J]. Oil Geophysical Prospecting, 1994, 29(4): 399-412. |
| [13] |
Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [14] |
Goodway B, Chen T, Downton J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters: "λρ, μρ, λμ fluid stack", from P and S inversions[C]. SEG Technical Program Expanded Abstracts, 1997, 16: 183-186.
|
| [15] |
Xu Y, Bancroft J C.AVO case study: extraction of Lame's parameters from vertical component seismic data[R]. CREWES Project, Canada, 1998.
|
| [16] |
Gray D, Goodway B, Chen T.Bridging the gap: Using AVO to detect changes in fundamental elastic constants[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 852-855.
|
| [17] |
Russell B H, Gray D, Hampson D P. Linearized AVO and poroelasticity[J]. Geophysics, 2011, 76(3). |
| [18] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [19] |
邓炜, 印兴耀, 宗兆云, 等. 基于逆算子估计的高阶AVO非线性反演[J]. 石油地球物理勘探, 2016, 51(5): 955-964. DENG Wei, YIN Xingyao, ZONG Zhaoyun, et al. High-order nonlinear AVO inversion based on estimated inverse operator[J]. Oil Geophysical Prospecting, 2016, 51(5): 955-964. |
| [20] |
黄捍东, 王彦超, 郭飞, 等. 基于佐普里兹方程的高精度叠前反演方法[J]. 石油地球物理勘探, 2013, 48(5): 740-749. HUANG Handong, WANG Yanchao, GUO Fei, et al. High precision prestack inversion algorithm based on Zoeppritz equations[J]. Oil Geophysical Prospecting, 2013, 48(5): 740-749. |
| [21] |
Xu Y, Bancroft J C.Joint AVO analysis of PP and PS data[R]. Crewes Research Reports, 1997, 1-44.
|
| [22] |
Wang Y H. Approximations to Zoeppritz equations and their use in AVO analysis[J]. Geophysics, 1999, 64(6): 1920-1927. DOI:10.1190/1.1444698 |
| [23] |
Ramos C B. Useful approximations for converted-wave AVO[J]. Geophysics, 2001, 66(6): 1721-1734. DOI:10.1190/1.1487114 |
| [24] |
Ursin B, Stovas A. Second-order approximations of the reflection and transmission coefficients between two visco-elastic isotropic media[J]. Journal of Seismic Exploration, 2001, 9(3): 223-233. |
| [25] |
Charles P.Ursenbach.Optimal Zoeppritz approximations[R]. CREWES Research Report, 2002, 14, 1-10.
|
| [26] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
| [27] |
Behural J, Kabir N, Crlder R, et al.Density extraction from P-wave AVO inversion: Tusealoosa Trend example[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 1466-1470.
|
| [28] |
郭强, 张宏兵, 曹呈浩, 等. Zoeppritz方程叠前多参数反演及密度敏感性分析[J]. 石油地球物理勘探, 2017, 52(6): 1218-1225. GUO Qiang, ZHANG Hongbing, CAO Chenghao, et al. Density-sensitivity analysis about prestack multi-parameter inversion based on the exact Zoeppritz equation[J]. Oil Geophysical Prospecting, 2017, 52(6): 1218-1225. |
| [29] |
印兴耀, 王慧欣, 曹丹平, 等. 利用三参数AVO近似方程的深层叠前地震反演[J]. 石油地球物理勘探, 2018, 53(1): 129-135. YIN Xingyao, WANG Huixin, CAO Danping, et al. Three term AVO approximation of Kf-fm-ρ and prestack seismic inversion for deep reservoirs[J]. Oil Geophysical Prospecting, 2018, 53(1): 129-135. |
| [30] |
Lavaud B, Kabir N, Chavent G. Pushing AVO inversion beyond linearized approximation[J]. Journal of Seismic Exploration, 1999, 8(11): 279-302. |
| [31] |
石玉梅, 姚逢昌, 孙虎生, 等. 地震密度反演及地层孔隙度估计[J]. 地球物理学报, 2010, 53(1): 197-204. SHI Yumei, YAO Fengchang, SUN Husheng, et al. Density inversion and porosity estimation using seismic data[J]. Chinese Journal of Geophysics, 2010, 53(1): 197-204. DOI:10.3969/j.issn.0001-5733.2010.01.022 |