② 山西省煤炭地质物探测绘院, 山西晋中 030600;
③ 华北水利水电大学资源与环境学院, 河南郑州 450046
② Shanxi Provincial Coal Geological Exploration, Geophysical Prospecting, Surveying and Mapping Institute, Jinzhong, Shanxi 030600, China;
③ School of Resources and Environment, North China University of Water Resources and Electric Power, Zhengzhou, Henan 450046, China
由于表层激发条件的限制以及其他各种不可抗干扰因素的影响,仅在野外采集阶段完全压制随机噪声不太现实,需要在室内用有效的数学去噪方法提高叠前地震资料的信噪比,以满足不同处理环节的需求[1-4]。目前,有许多行之有效的随机噪声压制方法,其中稀疏变换应用较为广泛,包括傅里叶变换[5-8]、小波变换[9-10]、Radon变换[11-12]、Contourlet变换[13]、曲波变换[14]以及Seislet变换[15]等。该类方法根据随机噪声和有效波在稀疏变换域中能量分配的差异,对稀疏系数采用适当的阈值去除随机噪声的影响。为了取得较好的去噪效果,稀疏基需要尽可能地捕获地震波的有效信息,并且少数较大的稀疏系数能够代表信号的主要特征,而大部分较小、被滤除的系数不影响原始数据的主要特征[16]。曲波变换能够有效地表示地震数据的尺度性和方向性,更加稀疏地表示地震波场局部细节特征,所以许多学者选用曲波变换方法去噪,且效果显著[17-20]。
现有曲波变换去噪方法的前提是地震数据为均匀网格采样,而对于非均匀网格采样的含噪数据则效果不佳。由于野外地形条件及施工环境的制约,在很多情况下,地震数据常为非均匀采样[21]。如果在去噪过程中将非均匀采样视为均匀采样进行处理,就得不到连续的地震波场,自然也不能充分压制噪声干扰,从而会影响到后续其他处理方法的应用。Hennenfent等[22]提出基于非均匀采样的曲波变换重建方法,但未讨论该方法在噪声压制中的应用。
本文在前人研究的基础上,针对非均匀采样地震数据,在传统曲波变换的基础上,引入非均匀傅里叶变换,建立均匀曲波系数与空间非均匀采样地震道之间的规则化反演算子;然后选择合适的噪声估计值,使用线性Bregman方法反演,在迭代过程中采用软阈值对曲波系数去噪,由反演得到无噪声的均匀曲波系数;再进行常规曲波反变换,得到去噪后的地震数据,由此形成基于非均匀曲波变换和线性Bregman方法的随机噪声压制方法。模型数据和实际数据的实验结果表明了本文方法的有效性。
1 非均匀曲波变换Candès等[23]提出了第二代曲波变换,从而使曲波变换更容易被理解、运算效率更高、实现更简单,能够为地震信号提供最优的稀疏表示方式。实际上,实现快速离散曲波变换主要包括两个步骤:①对地震数据应用二维傅里叶变换,得到频率—波数域系数;②在频率—波数域形成角度楔形,将每一个楔形围绕到原点重新装配,并对每一个装配好的楔形应用二维傅里叶反变换,得到离散曲波系数。参考文献[22]定义曲波正变换算子为
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{TF}} $ | (1) |
式中:F实现了上述离散曲波变换第①步:T则实现了第②步。
定义曲波反变换算子为
| $ {\mathit{\boldsymbol{A}}^{\rm{H}}} = {\mathit{\boldsymbol{F}}^{\rm{H}}}{\mathit{\boldsymbol{T}}^{\rm{H}}} $ | (2) |
式中:上标“H”表示共轭转置;FH表示二维傅里叶反变换,将频率—波数域转换到时间—空间域中;TH表示曲波平铺算子,即将曲波系数变换到频率—波数域的过程。
式(1)中,由于傅里叶变换要求数据均匀采样,所以常规的二维曲波变换不能处理非均匀采样数据,否则会严重扭曲原始地震数据的真实位置,使地震同相轴不连续,得不到正确的频率—波数域系数。用FxH代表沿着空间轴的一维傅里叶反变换算子,FtH表示沿着时间轴的一维傅里叶反变换算子,则二维傅里叶反变换可以表示为两个维度变换的克罗内克乘积,即
| $ {\mathit{\boldsymbol{F}}^{\rm{H}}} = \mathit{\boldsymbol{F}}_x^{\rm{H}} \otimes \mathit{\boldsymbol{F}}_t^{\rm{H}} $ | (3) |
式中“⊗”表示克罗内克乘积。在这个分解变换中,时间方向是均匀理想采样,不需要重建。因此,可以用非均匀快速傅里叶反变换Nx代替一维傅里叶反变换算子FxH,则非均匀曲波反变换算子可以定义为
| $ \mathit{\boldsymbol{C}} = ({\mathit{\boldsymbol{N}}_x} \otimes \mathit{\boldsymbol{F}}_t^{\rm{H}}){\mathit{\boldsymbol{T}}^{\rm{H}}} $ | (4) |
该算子描述了非均匀采样下离散曲波系数与地震数据之间的关系。
由于快速离散曲波变换具有紧支撑性,正、反曲波变换前、后能量无损失,即
| $ \mathit{\boldsymbol{A}}\;{\mathit{\boldsymbol{A}}^{\rm{H}}} = \mathit{\boldsymbol{I}} $ | (5) |
式中I为单位矩阵。对于新的非均匀曲波反变换算子C,由于包含非均匀快速傅里叶变换,那么算子C就不满足式(5)。为此定义非均匀曲波正变换算子C+为
| $ \begin{array}{l} {\mathit{\boldsymbol{C}}^ + }:\mathit{\boldsymbol{d}} \to \mathit{\boldsymbol{\tilde x}} = \arg \min \left\| {{x}} \right\|_1\\ \;\;\;\;\;\;\;满足\;\;\;\;\;\;\;{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Cx}}} \right\|_2} \le \sigma \end{array} $ | (6) |
式中:d表示非均匀含噪地震数据;σ为大于零的噪声均方根估计值,主要根据噪声能量计算该值的大小,该值的选择尤为关键,直接决定去噪效果。如果σ=0,则表示仅对非均匀含噪数据进行规则化,不进行噪声压制。从式(6)可知,C+将非均匀含噪数据d非线性映射到曲波系数向量
式(6)最优化问题可转为求解下述基追踪规则化问题[25]
| $ \begin{array}{l} \mathop {\min }\limits_x \left( {\lambda {{\left\| \mathit{\boldsymbol{x}} \right\|}_1} + \frac{1}{2}\left\| \mathit{\boldsymbol{x}} \right\|_2^2} \right)\\ \;\;\;\;\;\;满足\frac{1}{2}\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Cx}}} \right\|_2^2 \le {\sigma ^2} \end{array} $ | (7) |
式中λ是一个阈值权衡因子,平衡L1范数和L2范数的比重,可以在第一次迭代过程计算。线性Bregman方法求解迭代式为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{z}}_{k + 1}} = {\mathit{\boldsymbol{z}}_k} - {l_k}\mathit{\boldsymbol{C}}_k^{\rm{H}}({\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{d}}_k})\\ {\mathit{\boldsymbol{x}}_{k + 1}} = {S_\lambda }({\mathit{\boldsymbol{z}}_{k + 1}}) \end{array} \right. $ | (8) |
式中:zk表示第k次迭代得到的曲波系数向量;lk为动态步长,定义为
| $ {l_k} = \frac{{\left\| {{\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{d}}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{C}}_k^{\rm{H}}({\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{d}})} \right\|_2^2}} $ | (9) |
软阈值函数为
| $ {S_\lambda }\left( \mathit{\boldsymbol{x}} \right) = {\rm{sign}}\left( \mathit{\boldsymbol{x}} \right)\max \left( {\left| \mathit{\boldsymbol{x}} \right| - \lambda , 0} \right) $ | (10) |
式(8)只能进行规则化重建,而不能够同时压制噪声。在式(8)中引入新的投影函数
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{z}}_{k + 1}} = {\mathit{\boldsymbol{z}}_k} - {l_k}\mathit{\boldsymbol{C}}_k^{\rm{H}}\mathop \prod \limits_\sigma ({\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{d}}_k})\\ {\mathit{\boldsymbol{x}}_{k + 1}} = {S_\lambda }({\mathit{\boldsymbol{z}}_{k + 1}}) \end{array} \right. $ | (11) |
投影函数
| $ \begin{array}{l} \mathop \prod \limits_\sigma ({\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{d}}_k})\\ = \max \left( {0, 1 - \frac{\sigma }{{{{\left\| {{\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{d}}_k}} \right\|}_2}}}} \right)({\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{d}}_k}) \end{array} $ | (12) |
该式可以保证在每次迭代过程中对含噪地震数据进行噪声压制,从中也可以看出线性Bregman方法实现非常简单,没有过多的调节参数。
3 噪声压制原理一个含噪声二维地震信号模型可以表示成为
| $ d(i, j) = s(i, j) + e(i, j) $ | (13) |
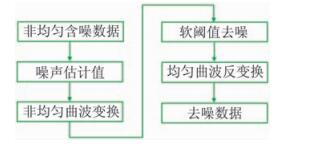
式中:s为真实信号;e为噪声。去噪过程就是从非均匀含噪地震信号d中提取真实信号s,去除噪声干扰信号e(图 1)。
|
图 1 非均匀曲波变换噪声压制流程 |
非均匀曲波变换依赖于式(6)中的曲波系数。对于随机干扰噪声的去除,在采用线性Bregman方法求解式(6)的过程中,由于较大曲波系数代表有效信号本身,通过对曲波系数进行软阈值处理[27-28],经过多次迭代就可以得到无噪声的均匀曲波系数估计值
| $ \mathit{\boldsymbol{\tilde s}} = {\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{\tilde x}} $ | (14) |
式中AH是常规的曲波反变换算子。通过对反演后的无噪声均匀曲波系数应用常规曲波反变换,可得到均匀采样后的去噪地震数据。
4 数值模拟信噪比定义为[29]
| $ R = - 10\lg \frac{{{{\left\| {\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}_0}} \right\|}_2}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_0}} \right\|}_2}}} $ | (15) |
式中:s0表示原始均匀不含噪声数据;s表示去噪后的均匀地震数据。R越高,表示去噪效果越好。
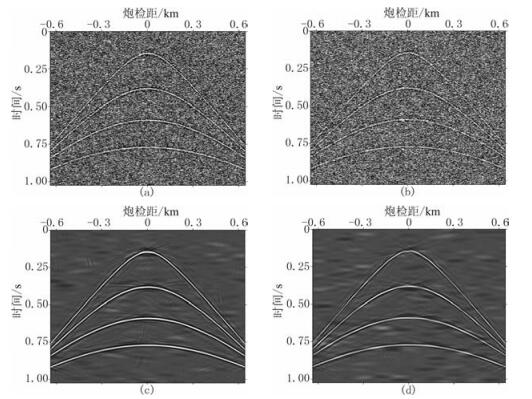
图 2a为合成的256道地震数据,有4个反射波同相轴,各反射同相轴能量有差异,采样间隔为1ms,道间距为5m,每道1024个采样点。加入标准差为0.05的高斯白噪声,如图 2b所示,其信噪比为-5.11dB。对含噪数据进行空间均匀傅里叶变换,然后再进行空间非均匀傅里叶反变换,得到新的空间非均匀采样下的256道地震数据,如图 2c所示,信噪比为-5.25dB,道间距范围为0~10m。如果直接用均匀曲波变换法对图 2c数据去噪,则扭曲的同相轴得不到校正,导致去噪后的地震记录误差较大。因此首先采用非均匀曲波变换方法对图 2c进行规则化处理,此时噪声估计值σ=0,曲波变换所选择的尺度数为5,在第二个最粗尺度上的角度数为32。规则化结果如图 2d所示,可以看见规则化后的地震波场非常连续,几乎没有视觉上的差异,并且从误差剖面(图 2e)也可以看出规则化前后几乎没有误差,说明非均匀曲波变换方法规则化效果好。

|
图 2 合成地震数据规则化结果 (a)合成理论地震数据;(b)加噪地震数据;(c)非均匀采样含噪数据;(d)规则化数据;(e)图d与图b数据的差 |
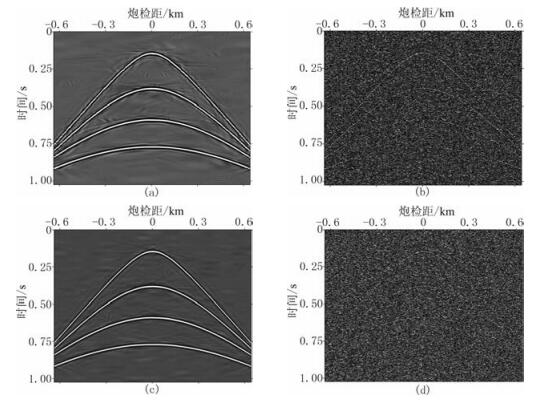
采用均匀曲波变换方法对非均匀含噪数据(图 2c)直接去噪,对分解后的曲波系数进行软阈值处理,将保留下来的曲波系数进行曲波反变换,从而得到最终的去噪结果,如图 3a所示,其信噪比为4.45dB。图 3b为去除的噪声干扰,可以看出,其中含有部分有效波信号,主要原因是常规曲波变换不能直接处理非均匀采样数据,而是把非均匀采样数据当成均匀采样数据进行处理。根据噪声能量计算出噪声估计值σ=2.5,采用本文方法在非均匀采样数据规则化过程中同时去噪,结果如图 3c所示,其信噪比为5.11dB。去除的噪声如图 3d所示。可以看出,本文方法不仅可以将非均匀采样地震数据内插为均匀采样数据,还可以同时有效地去除随机噪声干扰,去噪后的地震同相轴更加连续、清晰,大幅度地提高了信噪比,且去除的噪声中几乎不含有效波能量,表明对于非均匀采样地震数据本文方法具有较好的去噪效果。
|
图 3 非均匀地震数据不同噪声压制法结果对比 (a)常规曲波变换方法的去噪结果;(b)常规曲波变换方法去除的噪声;(c)本文方法的去噪结果;(d)本文方法去除的噪声 |
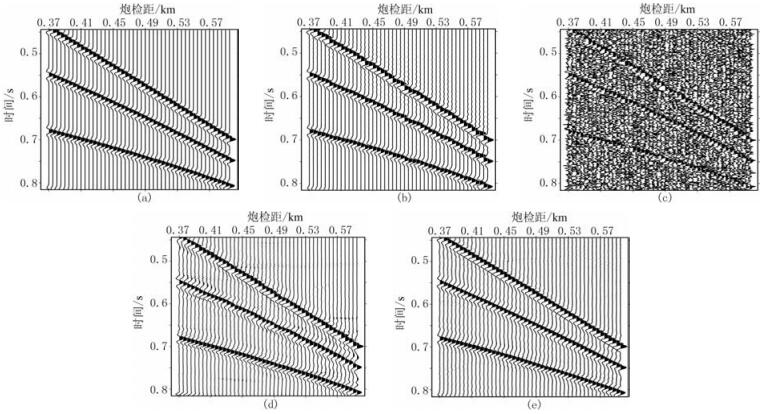
为了详细对比去噪效果,将原始理论地震数据、非均匀地震数据、含噪非均匀地震数据、常规曲波变换去噪结果和本文方法去噪结果分别进行局部放大,如图 4所示。可以看到非均匀地震数据显示在均匀网格上使有效波同相轴扭曲错动明显,再加上噪声的影响,这种扭曲现象更为严重,使有效波能量和噪声能量相互缠绕在一起,降低了整个地震数据的信噪比。从去噪结果的局部放大显示来看,由于常规曲波变换的去噪前提条件是均匀采样,所以在压制非均匀地震数据噪声时不能有效调整非均匀采样点位置,使去噪后的有效波同相轴仍然扭曲错动,并且噪声压制也不彻底。而本文方法去噪后的有效波与原始地震数据有效波非常接近,去噪后的同相轴光滑连续,这进一步说明本文方法在去除随机噪声的同时,也可以将非均匀地震数据调整为均匀采样数据。
|
图 4 非均匀地震数据去噪前、后局部放大 (a)合成地震数据;(b)无噪声非均匀地震数据;(c)含噪声非均匀地震数据;(d)常规曲波变换去噪结果;(f)本文方法去噪结果 |
为了对比不同噪声水平下本文方法的去噪效果,对原始理论数据加入标准差分别为0.075和0.100的高斯白噪声,然后采用非均匀傅里叶反变换获得非均匀地震数据,如图 5a和图 5b所示,信噪比分别为-6.99dB和-8.23dB。可以看出有效波信号被噪声淹没,难以识别,并且有效波同相轴局部扭曲,模糊不清,尤其是图 5b,几乎看不出有效信号。采用本文方法同时进行数据规则化和噪声压制,噪声估计值分别为σ=3.8和σ=5.1,结果如图 5c和图 5d所示。去噪后的信噪比分别为3.34dB和1.99dB,可以看出本文方法能够有效地去除非均匀采样数据中的随机噪声,并且将其内插为均匀采样,极大地提高了原始含噪数据的信噪比,但随着噪声能量大幅度增强,有效波损伤也会增加。
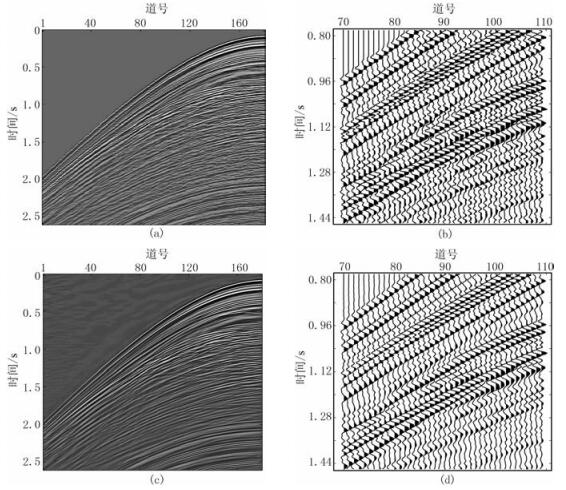
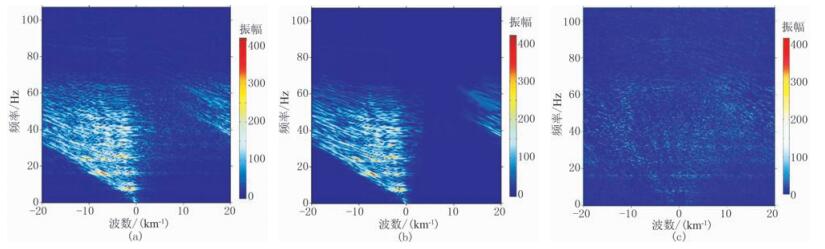
5 应用实例图 6a为海上单炮地震数据,数据采集时设计道距为12.5m,然而由于海上拖缆的羽状漂移导致采集道距不均匀,道距范围为6~20m。图 6b为其局部放大,可以看出随机噪声较为发育,并且非均匀采样扭曲了部分有效波同相轴。采用本文方法进行去噪,分解的尺度为5,在第二个最粗尺度上的角度数为16,噪声估计值σ=8.5。图 6c为本文方法去噪结果,图 6d为局部放大显示,可以看出绝大部分噪声能量得到了有效压制,去噪后的地震数据同相轴较为连续,几乎没有损失有效波。图 7a和图 7b分别为原始单炮数据和本文方法去噪结果所对应的二维频谱,也可以看出本文方法去噪相对彻底,并且将非均匀采样地震数据内插为均匀采样。从去噪前、后振幅谱差(图 7c)可以看出,去除了大部分随机噪声,有效波的损伤较小,大幅提高了信噪比。
|
图 6 海上非均匀采样数据去噪结果 (a)海上非均匀采样道集;(b)图a局部放大显示;(c)本文方法去噪结果;(d)图c局部放大显示 |
|
图 7 海上实际数据去噪前、后频谱对比 (a)原始数据;(b)本文方法去噪结果;(c)图a与图b数据的差 |
本文在多尺度多方向二维曲波变换基础上,提出了基于非均匀二维曲波变换和线性Bregman方法的地震数据随机噪声压制方法。由于非均匀曲波变换在正、反变换过程中具有能量无损性质,而这种性质特别适合在曲波域处理非均匀采样下的含噪地震数据,并且将其内插为均匀采样,在此过程中能有效地压制随机噪声。理论和实际资料的处理结果表明,该方法可以有效地压制地震数据中的随机噪声,且尽可能地保护了微弱的有效波信号,使反射波同相轴更加连续、清晰。
本文方法采用非均匀采样快速傅里叶变换,需要进行褶积和反褶积运算,计算速度远远低于均匀采样快速傅里叶变换,而且曲波变换实现过程复杂、冗余度高,因此本文所提出的非均匀曲波变换去噪方法计算效率相对较低。本文只进行了二维非均匀曲波变换,如推广到三维数据,则计算时间会进一步增加,需要发展其他快速算法提高本文方法的计算效率。
| [1] |
田彦灿, 王西文, 彭更新, 等. 宽方位角地震资料噪声压制技术[J]. 石油地球物理勘探, 2013, 48(2): 187-191. TIAN Yancan, WANG Xiwen, PENG Gengxin, et al. Noise attenuation technology on wide azimuth seismic data[J]. Oil Geophysical Prospecting, 2013, 48(2): 187-191. |
| [2] |
刘志刚, 谢言光, 陈峰. 地震数据处理中噪声衰减方法的探讨[J]. 石油地球物理勘探, 2009, 44(增刊1): 67-71. LIU Zhigang, XIE Yanguang, CHEN Feng. Discussion on noise attenuation methods in seismic data pro-cessing[J]. Oil Geophysical Prospecting, 2009, 44(S1): 67-71. |
| [3] |
邱淑芳, 刘西林, 刘胜兰. 一种基于PDE与结构-纹理分解的图像去噪方法[J]. 东华理工大学学报, 2013, 36(1): 90-94. QIU Shufang, LIU Xilin, LIU Shenglan. An image denoising method based on PDE and structure-texture[J]. Journal of East China Institute of Technology, 2013, 36(1): 90-94. DOI:10.3969/j.issn.1674-3504.2013.01.015 |
| [4] |
Liu Y, Fomel S, Liu C. Signal and noise separation in prestack seismic data using velocity-dependent seislet transform[J]. Geophysics, 2015, 80(6): WD117-WD128. DOI:10.1190/geo2014-0234.1 |
| [5] |
张胤彬, 张华, 刘松. 二维小波变换与中值滤波联合去噪方法研究[J]. 中国煤炭地质, 2011, 23(5): 38-42. ZHANG Yinbin, ZHANG Hua, LIU Song. A study on 2D wavelet transform and median filtering jointed denoising method[J]. Coal Geology of China, 2011, 23(5): 38-42. DOI:10.3969/j.issn.1674-1803.2011.05.10 |
| [6] |
Chen Y, Ma J, Fomel S. Double-sparsity dictionary for seismic noise attenuation[J]. Geophysics, 2016, 81(2): V17-V30. |
| [7] |
何旭莉, 刘素芹, 仝兆岐. 三维频率-波数域视速度去噪方法[J]. 中国石油大学学报, 2010, 34(4): 62-66. HE Xuli, LIU Suqin, TONG Zhaoqi. 3-D denoising method through visual speed in frequency-wavenumber domain[J]. Journal of China University of Petroleum, 2010, 34(4): 62-66. DOI:10.3969/j.issn.1673-5005.2010.04.011 |
| [8] |
Liu Y, Liu N, Liu C. Adaptive prediction filtering in t-x-y domain for random noise attenuation using regularized nonstationary autoregression[J]. Geophysics, 2015, 80(1): V13-V21. DOI:10.1190/geo2014-0011.1 |
| [9] |
张华, 陈小宏, 杨海燕. 地震信号去噪的最优小波基选取方法[J]. 石油地球物理勘探, 2011, 46(1): 70-75. ZHANG Hua, CHEN Xiaohong, YANG Haiyan. Optimistic wavelet basis selection in seismic signal noise elimination[J]. Oil Geophysical Prospecting, 2011, 46(1): 70-75. |
| [10] |
王清振, 张金淼, 姜秀娣, 等. 基于高维小波变换的高抗噪性边缘检测技术[J]. 石油地球物理勘探, 2016, 51(5): 889-893. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. A robust denoise edge detection method based on high-dimensional wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(5): 889-893. |
| [11] |
宋维琪, 刘太伟. 地面微地震资料τ-p变换噪声压制[J]. 石油地球物理勘探, 2015, 50(1): 48-53. SONG Weiqi, LIU Taiwei. Surface microseismic noise suppression with τ-p transform[J]. Oil Geophysical Prospecting, 2015, 50(1): 48-53. |
| [12] |
徐彦凯, 曹思远, 何元. 双曲Radon-ASVD方法压制叠前地震数据随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 451-457. XU Yankai, CAO Siyuan, HE Yuan. Prestack seismic random noise attenuation with a hyperbolic Radon-ASVD[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457. |
| [13] |
刘燕峰, 邹少峰, 居兴国. 基于Contourlet变换的K-L变换地震随机噪声自适应衰减方法[J]. 石油物探, 2017, 56(5): 676-683. LIU Yanfeng, ZOU Shaofeng, JU Xingguo. Seimic random noise self-adaptive attenuation method based on K-L transform in Contourlet domain[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 676-683. DOI:10.3969/j.issn.1000-1441.2017.05.008 |
| [14] |
Ramesh N, Domimique G, Mohamed T, et al. Coherent and random noise attenuation using the curvelet transform[J]. The Leading Edge, 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [15] |
刘洋, SERGEY F, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用[J]. 地球物理学报, 2009, 52(8): 2142-2151. LIU Yang, Sergey F, LIU Cai, et al. High-order seislet transform and its application of random noise attenuation[J]. Chinese Journal of Geophysics, 2009, 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 |
| [16] |
张广智, 常德宽, 王一惠, 等. 基于稀疏冗余表示的三维地震数据随机噪声压制[J]. 石油地球物理勘探, 2015, 50(4): 600-606. ZHANG Guangzhi, CHANG Dekuan, WANG Yihui, et al. 3D seismic random noise suppression with spare and redundant representation[J]. Oil Geophysical Prospecting, 2015, 50(4): 600-606. |
| [17] |
Lari H H, Gholami A. Curvelet-TV regularized Bregman iteration for seismic random noise attenuation[J]. Journal of Applied Geophysics, 2014, 109(2): 233-241. |
| [18] |
张之涵, 孙成禹, 姚永强, 等. 三维曲波变换在地震资料去噪处理中的应用研究[J]. 石油物探, 2014, 53(4): 421-430. ZHANG Zhihan, SUN Chengyu, YAO Yongqiang, et al. Research on the application of 3D curvelet transform to seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 421-430. DOI:10.3969/j.issn.1000-1441.2014.04.007 |
| [19] |
彭才, 常智, 朱仕军. 基于曲波变换的地震数据去噪方法[J]. 石油物探, 2008, 47(5): 461-464. PENG Cai, CHANG Zhi, ZHU Shijun. Noise elimination method based on curvelet transform[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 461-464. DOI:10.3969/j.issn.1000-1441.2008.05.006 |
| [20] |
Neelamani R, Baumstein A I, Gillard D G, et al. Coherent and random noise attenuation using the curvelet transform[J]. The Leading Edge, 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [21] |
Zhang H, Chen X H, Zhang L Y. 3D simultaneous seismic data reconstruction and noise suppression based on the curvelet transform[J]. Applied Geophy-sics, 2017, 14(1): 87-95. DOI:10.1007/s11770-017-0607-z |
| [22] |
Hennenfent G, Fenelon L, Herrmann F J. Nonequi-spaced curvelet transform for seismic data reconstruction:A sparsity-promoting approach[J]. Geophysics, 2010, 75(6): WB203-WB210. DOI:10.1190/1.3494032 |
| [23] |
Candès E, Demanet L, Donoho D, et al. Fast discrete curvelet transforms[J]. SIAM Multiscale Modeling and Simulation, 2006, 5(1): 861-899. |
| [24] |
Bregman L M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming[J]. USSR Computational Mathematics and Mathematical Physics, 1967, 7(3): 200-217. DOI:10.1016/0041-5553(67)90040-7 |
| [25] |
Yin W, Osher S, Goldfarb D, et al. Bregman iterative algorithms for L1-minimization with applications to compressed sensing[J]. SIAM Journal on Imaging Sciences, 2008, 1(1): 143-168. DOI:10.1137/070703983 |
| [26] |
Lorenz D A, Schöpfer F, Wenger S. The linearized Bregman method via split feasibility problems:analysis and generalizations[J]. SIAM Journal on Imaging Sciences, 2013, 7(7): 1237-1262. |
| [27] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [28] |
Górszczyk A, Adamczyk A, Malinowski M. Application of curvelet denoising to 2D and 3D seismic data-practical considerations[J]. Journal of Applied Geophysics, 2014, 105(3): 78-94. |
| [29] |
Herrmann F J. Randomized sampling and sparsity:Getting more information from fewer samples[J]. Geophysics, 2010, 75(6): WB173-WB187. DOI:10.1190/1.3506147 |



 白敏, 河南省郑州市北环路36号华北水利水电大学资源与环境学院, 450045。Email:
白敏, 河南省郑州市北环路36号华北水利水电大学资源与环境学院, 450045。Email: