② 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249;
③ 中国石油大学(北京)地球科学学院, 北京 102249;
④ 中国石油青海油田分公司采油四厂, 青海海西 816499;
⑤ 中海油研究总院, 北京 100027
② State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China;
③ College of Geosciences, China University of Petroleum(Beijing), Beijing 102249, China;
④ Oil Production Plant 4, Qinghai Oilfield Company, PetroChina, Haixi, Qinghai 816499, China;
⑤ CNOOC Research Institute, Beijing 100027, China
储层地质模型是油藏描述中具有代表性与综合性的成果,在油气勘探、开发中得到了广泛应用[1]。为提高储层地质建模精度、降低井间储层预测的不确定性,人们广泛研究了储层随机模拟新方法[2-6]、地质知识库的建立[7-10]、储层随机建模的约束条件[11-18]、融合多尺度资料参与建模[19-22]等方面,但对决定储层模型是否符合实际地质情况的随机模拟核心参数(变差函数)尚未引起足够的重视。
在一般情况下直井的测井资料采样间隔为0.125m,在垂向具有较高的采样密度,为变差函数选取提供了丰富的数据,因此垂向变差函数较易获取。而对于平面变差函数的求取,往往面临井数少、井距大、平面分布不均的问题,难以得到理想的平面变差函数,因此储层建模的重点在于求取可靠的平面变差函数。针对横向变差函数,前人主要研究了改进变差函数求取算法[23-24]、变差函数的模型拟合[25-26]、变差函数在储层建模中的应用[27],但对储层建模中如何获取合理的横向变差函数涉及较少。前人提出利用各井的垂向变程、横向与垂向方差比值估算井间的相关长度[28]。Bahar等[29]采用多井的垂向井点数据得出的横向变差函数确定真实横向变差函数的基台值,而用井垂向数据平均值的变差函数推断真实横向变差函数的变程和结构特征。贾爱林等[30]通过建立露头地质资料和油田储层地质知识库,探讨如何融合地层和露头地质资料获取油田砂体的横向变差函数,以提高井间储层预测精度。这些方法考虑了横向变差函数与垂向变差函数的关系,并尝试利用地质露头等资料克服直井测井资料求取变差函数的弊端,对变差函数的研究具有指导意义,但仍然存在一些不足[28-30]。为此,本文在分析现有变差函数求取方法适用性的基础上,研究了扶余油田平台12井区多尺度变差函数,总结多尺度变差函数与储层的对应关系,以期探讨利用不同资料获取地质统计学变差函数的规律。
1 多尺度变差函数求取思路 1.1 变差函数变差函数是地质统计学的基本参数,反映了空间变异程度随距离变化的特征,利用变差函数表征地质体空间相关性是经典随机建模的基础[31]。变差函数强调数据的空间结构,从而定量地描述区域化变量的空间相关性,即储层参数在空间上的相关性。假设N(h)是滞后距为h的所有点对的总数,则变差函数为
| $ r\left( h \right)=\frac{1}{2N\left( h \right)}\sum\limits_{i=1}^{N\left( h \right)}{{{[Z({{x}_{i}})-Z({{x}_{i}}+h)]}^{2}}} $ |
式中Z(xi)和Z(xi+h)分别为区域化随机变量x在位置xi和xi+h时的取值。
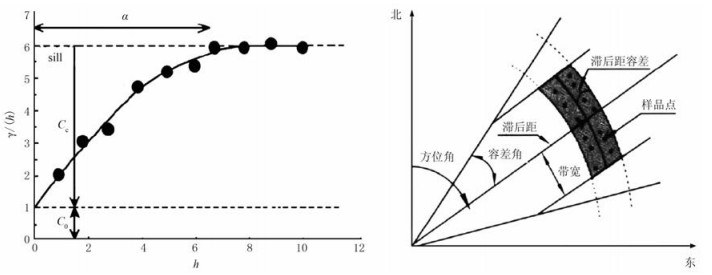
变差函数γ(h)中的几个主要参数分别为a、sill、C0及Cc(图 1左)。其中a为变程,反映区域化变量的空间相关性范围。C0表示块金效应,用以描述区域化变量在很小的距离内发生的突变程度,其大小可反映区域化变量的随机性。基台值sill反映变量在空间的总变异性。Cc为拱高,表示在取得有效数据的尺度上可观测到的变异性幅度。当C0=0时,sill即为Cc。在求取变差函数过程中要利用方位角、搜索半径、容差角、带宽、滞后距、滞后距容差等参数(图 1右)。其中搜索半径为两个采样点之间的最大搜索距离。为了将滞后距控制在有意义的研究范围内,通常将搜索半径限定为小于工区内相距最远的2个数据点的距离。最小滞后距可选为指定方向的平均井距,因为当小于平均井距时得不到足够的点对。
|
图 1 变差函数(左)和楔形搜索域示意图(右) |
多尺度变差函数是指三维空间中的地质采样数据常常存在不同尺度的变化,地质变量在不同尺度的变异规律不尽相同,具体表现为不同尺度的变差函数具有不同的形式,因此称某种地质变量具有多尺度变差函数结构。
储层表征研究分层次描述储层的性质、类型、分布,进而借助地质和数学方法以及计算机手段建立不同层次的储层模型,使不同层次的特征统一在一个体系中进行层次归一,从而达到预测的目的[32]。多尺度变差函数求取的必要性体现在:①储层的非均质性具有层次性。前人认为储层非均质性是按一定级别而相互联系的,储层结构极其复杂,它所包含的非均质性尺度可以从几千米到几米、几厘米到几毫米。Lake等[33]提出了在油田评价和开发阶段定量认识非均质性的分类体系。裘亦楠[34]把储层非均质性划分为五个不同级别,并深入描述了不同级别的非均质性。可见,在同一尺度上储层非均质性是绝对的,而不同尺度的储层非均质性是相对的。②在序贯指示模拟、序贯高斯模拟[35]等经典随机建模算法中都要用到描述区域化变量空间几何特征的变差函数,以研究储层空间结构的非均质性。既然非均质性以不同尺度存在于储层中,作为表征非均质性的空间结构参数(变差函数)也具有尺度关联性。同时,某一尺度的非均质性应有对应的变差函数,即变差函数的获取需要明确非均质研究尺度。因此,求取多尺度变差函数非常必要。
1.3 多种资料求取多尺度变差函数的适用性变差函数作为描述区域化变量空间结构以及随机性的重要数学工具,在储层地质建模中起重要作用,储层建模变差函数的研究重点在于求取可靠的平面变差函数。研究人员利用露头资料、密井网直井测井资料、现代沉积研究成果和水平井测井资料获取横向变差函数。本文通过分析前人的变差函数求取方法,为利用不同资料求取多尺度变差函数提供一种思路。
(1) 露头资料。通过对露头的详细描述、观测、取样分析、剖面数字化,分析沉积露头不同井距、不同微相的变差函数以及相应的水平主变程的变化范围,并为相似环境中的地下储层变差函数提供类比[31]。该方法求取的变差函数的精度高且观测方便,不足之处在于求取的水平变程远小于目前密井网的井距,同时还存在露头特征与实际地下储层地质特征是否匹配的问题,难以用于油藏地质建模,并且解剖露头成本较高,采样点数量也受限。
(2) 直井密井网资料。在开发中后期,在井网密度较大的情况下,普遍利用测井曲线解释的储层岩性、物性参数求取水平变差函数。该方法的不足之处在于:出于经济效益的考虑,多数井部署在区块的有利储层区域内,导致直井的分布极不均匀,由这种井点数据求取的平面变差函数的可信度不高。此外,在开发初期井网密度较小的情况下,此方法也不具备普适性。
(3) 地震资料。由于地震资料较丰富,在开发初期也不受钻井数量的限制,因此将地震数据转换为储层岩性、物性的平面分布属性研究平面变差函数[36]。该方法的优点在于地震数据的平面采样密度大于直井测井资料,且采样点分布均匀,具有较好的横向连续性,可反映大尺度横向地质变化特征。需要注意的是,地震属性应与储层岩性及物性具有较好相关性,能够真实地反映岩性、物性的平面分布。
(4) 水平井测井资料。在水平井控制区,利用水平井测井曲线解释储层岩性、物性参数分析水平变差函数[37]。该方法的优点在于当具有较长的水平井段时,其横向采样密度很大,所提供的横向信息是常规露头、现代沉积和密井网资料无法替代的。不足之处为变差函数搜索范围受水平井段长度的限制,无法反映大尺度非均质性的变异特征。同时由于斜井或水平井轨迹在储层中穿行时具有一定的斜度,导致采样点测井数据并非严格反映垂向变异特征,引起变差函数的精度不高。因此,斜井或水平井资料不适合求取垂向变差函数。
综上所述,不同尺度储层非均质性的变差函数具尺度关联性,需要针对各类资料的优、缺点,尝试利用不同资料求取多尺度变差函数。
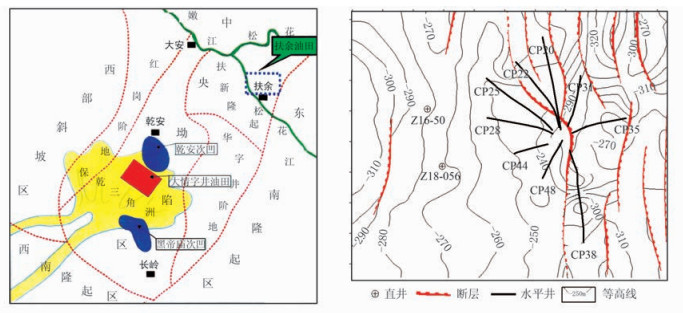
2 地质概况平台12井区位于扶余油田西南部城区,区内发育NS和NE-SW向断层,地层倾角约为4°,构造平缓(图 2左)。泉头组四段扶余油层分4个砂组(13个小层),地层厚度为70~110m,埋深为310~450m(图 3)。储层主要为浅水三角洲前缘沉积,发育水下分流河道、河口坝、水下分流间湾等微相类型,主要为一套砂、泥岩互层夹薄层灰岩地层。其孔隙度和渗透率主要分布在10.9%~30.6%、10~700mD,均值分别为25.0%、201mD,属于中孔、中渗储层。该区有直井86口、大斜度井9口、水平井23口。
|
图 2 扶余油田区域位置图(左)和平台水平井区扶余油层顶面构造图(右) |

|
图 3 扶余油层地层单元划分(黄色为砂岩) |
研究目的层为6号小层,岩石碎屑主要由石英、长石和岩屑组成,石英平均含量为26.80%,长石平均含量为39.70%,岩屑以火成岩为主,平均含量为11.33%。胶结物以泥质为主,含少量的钙质胶结物,泥质平均含量为19.45%。岩石组分呈次棱角—次圆状分布,分选性中等,为中深风化程度,主要为孔隙胶结类型。在岩心上普遍见到槽状交错层理、斜层理、平行层理,搅混构造发育。
6号小层自然伽马曲线主要呈齿化的箱型或钟型,砂岩厚度为6~17m(图 3)。砂体平面分布较稳定,延伸一般大于2km,连续性好。5口水平井钻遇6号小层,目的层地震资料主频为40Hz,道间距为25m,地震波阻抗数据能够较好地区分岩性,如砂岩的伽马值较低(小于16API)、阻抗值较高(大于7000g·cm-3·m·s-1)。
3 多尺度变差函数分析 3.1 利用直井测井资料求取平面变差函数扶余油田平台12井区的直井测井资料的垂向采样密度为0.125m,利用直井测井资料能够获得较高精度的垂向变差函数。在平面上直井井距为90~250m,通过统计井点数据,不断变换变差函数主方向的角度,利用现有井网分析变差函数,可知研究区6号小层的主变程为144.54m,次变程为100.03m,垂向变程为5.32m,基台值为0.94,方向为46°。
需要注意的是:对于平面变差函数而言,当数据点较多、且数据点在实验区域内均匀分布时,求取的实验变差函数更为合理[38];当模拟区的砂体尺度大于井控范围或者小于井距时,则由井点数据计算的平面变差函数不能很好地反映储层参数的变异性。研究区井点分布不均匀,井网分布范围不能控制砂体分布。因此,由研究区直井测井资料求取的平面变差函数结果的可信度不高。
3.2 利用地震资料求取平面变差函数求取平面变差函数包括以下步骤:①通过波阻抗反演求取目的层段的地震波阻抗数据体;②依据岩石物理分析结果将波阻抗数据体转换为岩相体;③分析不同采样密度的平面变差函数。
3.2.1 数据准备对平台12井区测井曲线进行岩石物理分析可知:扶余油层自然伽马(GR)曲线与波阻抗曲线交会图能够较好地区分岩性,即GR与波阻抗呈负相关,波阻抗随着GR的升高而减低。砂岩表现为低伽马值(小于16API)、高阻抗值(大于7000g·cm-3·m·s-1)。应用砂、泥岩的波阻抗门槛值将波阻抗数据体转换为岩相属性体,通过在岩相属性体上设置不同井距(井距由50m开始逐渐增加至400m)的虚拟井以达到不同采样密度[39]。
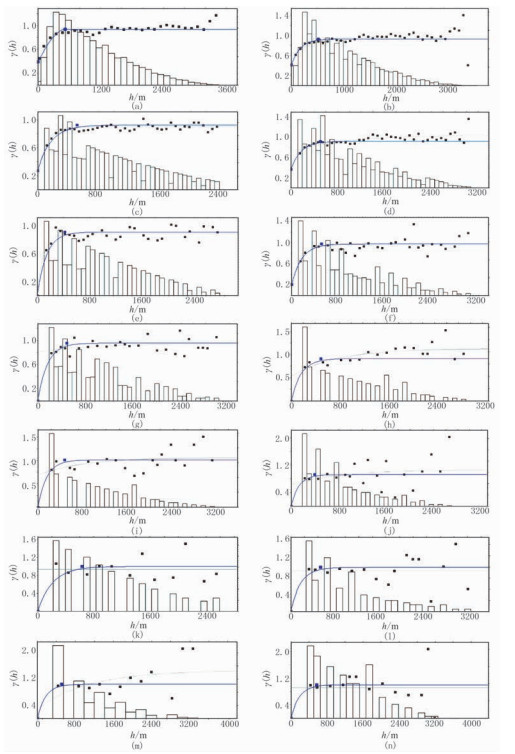
3.2.2 平面变差函数求取为了精确地估计变差函数,根据经验将搜索半径控制在小于工区内相距最远的数据点距离范围内,同时为了得到足够的点对,最小滞后距取平均井距,带宽为两倍井距,滞后距容差取平均井距的一半,求取主、次方向的变程。图 4为6号小层不同井距的砂岩主方向变差函数拟合图,表 1为6号小层不同井距砂岩变差函数拟合参数表。分析图 4及表 1可知:①当井距较小时,可较准确地确定变差函数的拟合参数(图 4a~图 4f);随着井距增大,实验变差函数点对的个数减少,当井距增大到一定程度(大于225m)时,靠近原点处的点对很少,难以准确估计变程。然而,离原点越近的点对对变差函数拟合结果影响越大,即大井距下变程估计的可靠性较低(图 4g~ 图 4n)。②当井距小到一定程度时,再继续减小井距变差函数变化不大(图 4a~图 4f)。因此,选取合适的采样密度即可求取合理的拟合参数,故选用75m井距。③变差函数结构类型为指数模型(表 1),表明三角洲前缘水下分流河道岩性变化相对较大,具有较强的非均质性。④小井距采样时普遍存在块金效应[40](表 1)。⑤在不同井距下6号小层变差函数的主、次变程分别为471~632m和354~561m,与研究区现有直井变差函数拟合的变程相差较大,说明不同的数据类型对求取变差函数的影响较大。
|
图 4 6号小层不同井距砂岩主方向变差函数拟合图 (a)50m; (b)75m; (c)100m; (d)125m; (e)150m; (f)175m; (g)200m; (h)225m; (i)250m; (j)275m; (k)300m; (l)325m; (m)350m; (n)400m |
|
|
表 1 6号小层不同井距砂岩变差函数拟合参数表 |
利用水平井测井资料求取平面变差函数主变程方向以及平面变程。有5口水平井钻遇6号小层,水平井段长度通常为150~550m,且水平井轨迹起伏较小。在求取过程中校正了孔、渗数据,最终得到水平井的实验变差函数,经过模型拟合建立了相应的结构模型。
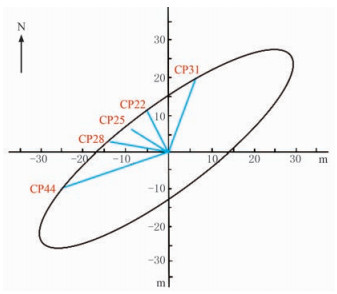
分析平台12井区6号小层5口水平井的砂岩变差函数拟合参数(表 2)可知:①水平变差函数结构类型以指数型为主,表明6号小层三角洲平原分流河道砂体内部岩性变化较剧烈;②水平井变差函数最小变程为9.14m,最大变程为30.16m。6号小层砂岩水平变程平面图(图 5)表明,分流河道砂体的主方向为NE-SW向(方位为51°),与前期直井、地震资料研究得到的变化方位相符,其中变程椭圆的长、短轴分别约为39.71m和11.22m,两者之比为3.7:1.0,指示了单个分流河道内砂体的长度和宽度。
|
|
表 2 6号小层水平井测井资料砂岩变差函数拟合参数汇总表 |
|
图 5 6号小层砂岩水平变程平面图 |
对比6号小层不同资料砂岩平面变差函数拟合结果(表 3)可知,主、次变程在取值范围上存在较大差异。为确定不同变差函数对地质建模结果的影响,采用序贯指示方法对6号小层进行随机建模,除主、次方向变程以及基台值之外,三种变差函数的参数设置都基本相同。
|
|
表 3 6号小层不同资料砂岩平面变差函数拟合参数汇总表 |
图 6为不同资料得到的6号小层平面变差函数模拟结果。由图可见:由地震资料求取的变差函数的模拟结果(图 6b)的砂体展布趋势符合地质规律,与6号小层井插值砂岩厚度图(图 6d)相似,表明由地震资料求取的变差函数反映了小层级别大尺度砂体的变异趋势;利用水平井测井资料求得的水平变程过小,井间的随机性增强,砂体不连续,不能反映研究区范围内小层级别砂体的变异情况(图 6c);利用常规直井测井资料求取的平面变差函数模拟结果显示砂体连续性稍差(图 6a),与6号小层井插值砂岩厚度图(图 6d)差别较大,无法表征小层级别大尺度的砂体变异趋势。由此可知,利用地震资料求取的平面变差函数反映了小层级别大尺度的砂体变异特征。

|
图 6 不同资料得到的6号小层平面变差函数模拟结果 (a)直井测井;(b)地震;(c)水平井测井;(d)6号小层井插值砂岩厚度图 |
以孔隙度建模为例,利用前述方法求取不同资料的孔隙度平面变差函数(表 4)。由于本区地震波阻抗数据体与孔隙度相关性较弱,无法由地震资料获取大尺度孔隙度平面变差函数,仅可由直井、水平井测井资料获取大尺度孔隙度平面变差函数。因此,仅仅针对6号小层内部的单砂体进行随机建模,采用序贯高斯方法,除主、次方向变程以及基台值之外,两种变差函数的参数设置都基本相同。
|
|
表 4 6号小层不同资料孔隙度平面变差函数拟合参数汇总表 |
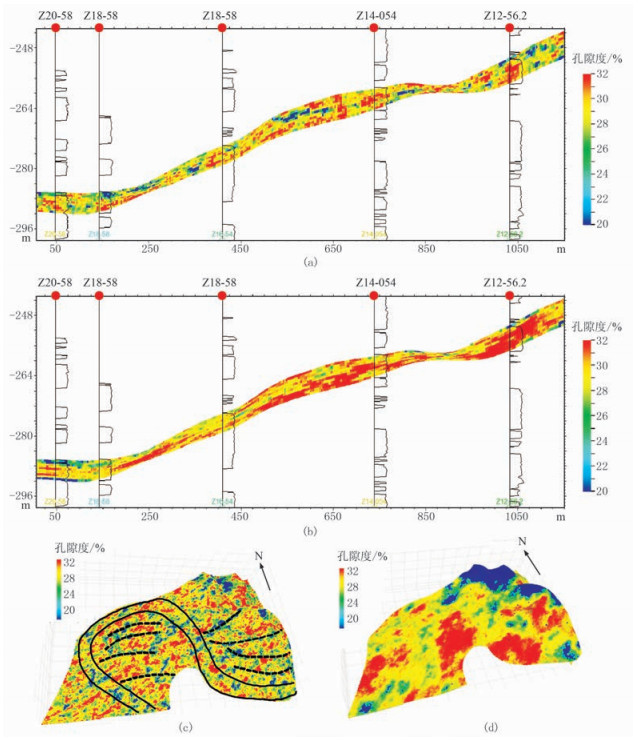
图 7为6号层不同资料的孔隙度模型平、剖面。由图可见:利用水平井测井资料获取的小尺度变差函数参与属性模拟(图 7a、图 7c),随机模型可在一定程度上预测单一点坝砂体内部的物性分布,可精确表征点坝内部夹层的非均质密度特征;直井测井资料的模拟孔隙度结果在横向上掩盖了侧积层发育特征,随机模型不能预测单砂体尺度的非均质性(图 7b、图 7d)。综上所述,由水平井资料获取的变差函数反映了小层内单砂体的小尺度变异特征,利用200m井距的常规直井资料求取的变差函数在大、小尺度上都不能很好地表征空间变异性。
|
图 7 6号层不同资料的孔隙度模型平、剖面 (a)水平井测井资料孔隙度模型剖面;(b)直井测井资料孔隙度模型剖面;(c)水平井测井资料孔隙度平面图;(d)直井测井资料孔隙度平面图 |
非均质性以不同尺度存在于储层中,作为表征非均质性的空间结构参数,变差函数具有尺度关联性。因此最合理的储层建模结果必然满足储层尺度与变差函数尺度相匹配,即不同的储层尺度有对应的变差函数。对于研究区而言,可以采用分层次储层地质建模的方法,分别建立小层尺度和单砂体尺度的储层地质模型。每一尺度的地质模型都可用于后期的数值模拟,从而进行小层与单砂体尺度的数值模拟,分别研究小层及单砂体的剩余油分布规律,这是分析不同尺度储层剩余油分布规律的一种思路。
(1) 不同尺度的储层具有不同的变差函数,受资料条件限制,仅由常规直井测井资料求取的变差函数可能不尽准确,即单一直井的平面变差函数并不适合多层次储层地质模型。因此,可由地震和水平井测井等多种资料获取多尺度的平面变差函数。
(2) 利用直井资料求取的研究区6号小层的主变程为144.54m、次变程为100.03m。采用地震波阻抗数据体求取的砂岩主变程为533.82m、次变程为409.10m,变差函数为指数型,表明三角洲平原分流河道岩性变化相对较大,具有较强的非均质性。由水平井测井资料求取的砂岩主变程为39.71m、次变程为11.22m。
(3) 利用地震波阻抗数据体求取的变差函数反映了大尺度(小层级次)砂体的变异特征,利用多方向水平井测井资料求取的变差函数反映了小尺度砂体(小层内单砂体)的变异特征,本区利用200m井距的常规直井测井资料求取的变差函数在大、小尺度上都不能很好地表征空间变异性。
| [1] |
贾爱林. 中国储层地质模型20年[J]. 石油学报, 2011, 32(1): 181-188. JIA Ailin. Research achievements on reservoir geologi-cal modeling of China in the past two decades[J]. Acta Petrolei Sinica, 2011, 32(1): 181-188. |
| [2] |
王家华, 张团峰. 油气储层随机建模[M]. 北京: 石油工业出版社, 2001.
|
| [3] |
李宇鹏, 吴胜和. 储集层构型分级套合模拟方法[J]. 石油勘探与开发, 2013, 40(5): 630-635. LI Yupeng, WU Shenghe. Hierarchical nested simulation approach in reservoir architecture modeling[J]. Petroleum Exploration and Development, 2013, 40(5): 630-635. |
| [4] |
李少华, 刘显太, 王军, 等. 基于沉积过程建模算法Alluvsim的改进[J]. 石油学报, 2013, 34(1): 140-144. LI Shaohua, LIU Xiantai, WANG Jun, et al. Improvement of the Alluvsim algorithm modeling based on depositional processes[J]. Acta Petrolei Sinica, 2013, 34(1): 140-144. |
| [5] |
尹艳树, 张昌民, 石书缘, 等. 综合随机游走过程与多点统计的河流相建模新方法[J]. 石油天然气学报, 2011, 33(8): 44-47. YIN Yanshu, ZHANG Changmin, SHI Shuyuan, et al. Modeling on integrating random walk process and multiple-point geostatistics to fluvial reservoirs[J]. Journal of Oil and Gas Technology, 2011, 33(8): 44-47. DOI:10.3969/j.issn.1000-9752.2011.08.010 |
| [6] |
王志章, 韩海英. 现代油藏描述关键技术[J]. 地学前缘, 2011, 37(7): 296-302. WANG Zhizhang, HAN Haiying. The key technologies of advanced reservoir characterization[J]. Earth Science Frontiers, 2011, 37(7): 296-302. |
| [7] |
石书缘, 胡素云, 冯文杰, 等. 基于Google Earth软件建立曲流河地质知识库[J]. 沉积学报, 2012, 30(5): 869-878. SHI Shuyuan, HU Suyun, FENG Wenjie, et al. Buil-ding geological knowledge data-base based on Google Earth software[J]. Acta Petrolei Sinica, 2012, 30(5): 869-878. |
| [8] |
尹太举, 张昌民, 樊中海, 等. 双河油田井下地质知识库的建立[J]. 石油勘探与开发, 1997, 24(6): 95-99. YIN Taiju, ZHANG Changmin, FAN Zhonghai, et al. Founding subsurface geological data bank for Shuanghe oil field[J]. Petroleum Exploration & Development, 1997, 24(6): 95-99. DOI:10.3321/j.issn:1000-0747.1997.06.023 |
| [9] |
贾爱林, 陈亮, 穆龙新, 等. 扇三角洲露头区沉积模拟研究[J]. 石油学报, 2000, 21(6): 107-110. JIA Ailin, CHEN Liang, MU Longxin, et al. A study on sedimentary simulation of fan-delta outcrop[J]. Acta Petrolei Sinica, 2000, 21(6): 107-110. DOI:10.3321/j.issn:0253-2697.2000.06.020 |
| [10] |
Deutsch C V. Geostatistical Reservoir Modeling[M]. London: Oxford University Press, 2002.
|
| [11] |
冯文杰, 吴胜和, 夏钦禹, 等. 基于地质矢量信息的冲积扇储层沉积微相建模——以克拉玛依油田三叠系克下组为例[J]. 高校地质学报, 2015, 21(3): 449-460. FENG Wenjie, WU Shenghe, XIA Qinyu, et al. Micro-facies modeling of alluvial fan reservoir based on geological vector information:A case study on the Triassic Lower Karamay Formation, Yizhong Area, Karamay Oilfield, NW China[J]. Geological Journal of China Universities, 2015, 21(3): 449-460. |
| [12] |
刘太勋, 陶自强. 界面约束法在曲流河储层构型建模中的应用[J]. 中国石油大学学报(自然科学版), 2011, 35(3): 26-30. LIU Taixun, TAO Ziqiang. Application of bounding surface restriction to meandering river reservoir architecture modeling[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011, 35(3): 26-30. DOI:10.3969/j.issn.1673-5005.2011.03.005 |
| [13] |
李宇鹏, 吴胜和, 耿丽慧, 等. 基于空间矢量的点坝砂体储层构型建模[J]. 石油学报, 2013, 34(1): 133-139. LI Yupeng, WU Shenghe, GENG Lihui, et al. Spatial-vector-based reservoir architecture modeling of meandering point bar sand[J]. Acta Petrolei Sinica, 2013, 34(1): 133-139. |
| [14] |
许丽, 刘磊, 吴长双. 应用井间地震资料建立砂泥岩薄互层地质模型[J]. 石油地球物理勘探, 2006, 41(1): 58-61. XU Li, LIU Lei, WU Changshuang. Application of cross-hole seismic data to create thin-interbedded sandstone mudstone geologic model[J]. Oil Geophysical Prospecting, 2006, 41(1): 58-61. DOI:10.3321/j.issn:1000-7210.2006.01.012 |
| [15] |
刘文岭. 地震约束储层地质建模技术[J]. 石油学报, 2008, 29(1): 64-68. LIU Wenling. Geological modeling technique for reservoir constrained by seismic data[J]. Acta Petrolei Sinica, 2008, 29(1): 64-68. DOI:10.3321/j.issn:0253-2697.2008.01.011 |
| [16] |
陈恭洋, 胡勇, 周艳丽, 等. 地震波阻抗约束下的储层地质建模方法与实践[J]. 地学前缘, 2012, 19(2): 67-73. CHEN Gongyang, HU Yong, ZHOU Yanli, et al. Methods and practices of reservoir geologic modeling constrained by seismic impedance[J]. Earth Science Frontiers, 2012, 19(2): 67-73. |
| [17] |
陈文浩, 董少群, 王志章, 等. 致密砂岩地震储层质量评价方法研究[J]. 中国石油大学学报:自然科学版, 2016, 40(3): 63-68. CHEN Wenhao, DONG Shaoqun, WANG Zhizhang, et al. Seismic reservoir quality evaluation in tight sandstone reservoirs[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016, 40(3): 63-68. |
| [18] |
罗亚能, 黄捍东, 王玉梅, 等. 地震波形反演与测井联合的三维建模方法[J]. 石油地球物理勘探, 2016, 51(5): 947-954. LUO Yaneng, HUANG Handong, WANG Yumei, et al. Three-dimensional modeling based on integration of full wave inversion and well logging data[J]. Oil Geophysical Prospecting, 2016, 51(5): 947-954. |
| [19] |
胡向阳, 袁向春, 侯加根, 等. 多尺度岩溶相控碳酸盐岩缝洞型油藏储集体建模方法[J]. 石油学报, 2014, 35(2): 340-346. HU Xiangyang, YUAN Xiangchun, HOU Jiagen, et al. Modeling method of carbonate fractured-cavity reservoirs using multiscale karst facies-controlling[J]. Acta Petrolei Sinica, 2014, 35(2): 340-346. |
| [20] |
夏吉庄, 张玉晓, 吕德灵. 多资料匹配融合储层建模技术[J]. 石油地球物理勘探, 2016, 51(2): 350-354. XIA Jizhuang, ZHANG Yuxiao, LV Deling. Reservoir model building with multi-data fusion[J]. Oil Geophysical Prospecting, 2016, 51(2): 350-354. |
| [21] |
董少群, 曾联波, Xu Chaoshui, 等. 储层裂缝随机建模方法研究进展[J]. 石油地球物理勘探, 2018, 53(3): 625-641. DONG Shaoqun, ZENG Lianbo, XU Chaoshui, et al. Some progress in reservoir fracture stochastic modeling research[J]. Oil Geophysical Prospecting, 2018, 53(3): 625-641. |
| [22] |
印兴耀, 刘永社. 储层建模中地质统计学整合地震数据的方法及研究进展[J]. 石油地球物理勘探, 2002, 37(4): 423-430. YIN Xingyao, LIU Yongshe. Methods and development of integrating seismic data in reservoir model-building[J]. Oil Geophysical Prospecting, 2002, 37(4): 423-430. DOI:10.3321/j.issn:1000-7210.2002.04.020 |
| [23] |
王仁铎, 胡光道. 线性地质统计学[M]. 北京: 地质出版社, 1988.
|
| [24] |
孙洪泉. 地质统计学及应用[M]. 徐州: 中国矿业大学出版社, 1990.
|
| [25] |
张小艳, 谭勇. 变差函数球状模型的自动拟合与实现[J]. 物探与化探, 2010, 34(2): 253-257. ZHANG Xiaoyan, TAN Yong. The automatic fitting and implementation of the spherical model of variogram[J]. Geophysical and Geochemical Exploration, 2010, 34(2): 253-257. |
| [26] |
胡小荣, 俞茂宏. 理论变异函数球状模型的加权线性规划法拟合[J]. 地质与勘探, 2001, 37(5): 45-48. HU Xiaorong, YU Maohong. Regression of spherical model and its nugget structure of theoretic variogram using weighted linear programming method[J]. Geo-logy and Prospecting, 2001, 37(5): 45-48. DOI:10.3969/j.issn.0495-5331.2001.05.011 |
| [27] |
王云专, 付检刚, 曲忠勇, 等. 变差函数在储层地质建模中的应用[J]. 科学技术与工程, 2010, 10(29): 7147-7150. WANG Yunzhuan, FU Jiangang, QU Zhongyong, et al. The application of variogram in reservoir geological modeling[J]. Science Technology and Engineering, 2010, 10(29): 7147-7150. DOI:10.3969/j.issn.1671-1815.2010.29.008 |
| [28] |
理查 德A, 约翰F著; 乔月译. 储层表征新进展[M]. 北京: 石油工业出版社, 2002: 32-52.
|
| [29] |
Bahar A, Kelkar M. Journey from well logs/cores to integrated geological and petrophysical properties simulation:a methodology and application[J]. SPE Reservoir Evaluation & Engineering, 1998, 3(5): 444-456. |
| [30] |
贾爱林, 何东博, 何文祥, 等. 应用露头知识库进行油田井间储层预测[J]. 石油学报, 2003, 24(6): 51-53. JIA Ailin, HE Dongbo, HE Wenxiang, et al. Application of outcrop geological knowledge database to prediction of inter-well reservoir in oilfield[J]. Acta Petrolei Sinica, 2003, 24(6): 51-53. DOI:10.3321/j.issn:0253-2697.2003.06.010 |
| [31] |
印森林, 吴胜和, 冯文杰, 等. 基于辫状河露头剖面的变差函数分析与模拟[J]. 中南大学学报(自然科学版), 2013, 44(12): 4988-4994. YIN Senlin, WU Shenghe, FENG Wenjie, et al. Variogram analysis and simulation on sedimentary outcrop profile of braided river[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 4988-4994. |
| [32] |
张昌民. 储层研究中的层次分析法[J]. 石油与天然气地质, 1992, 13(3): 344-350. ZHANG Changmin. Hierarchy analysis in reservoir researches[J]. Oil & Gas Geology, 1992, 13(3): 344-350. DOI:10.3321/j.issn:0253-9985.1992.03.013 |
| [33] |
Lake L W, Carroll Jr.H B. Reservoir Characterization[M]. New York: Academic Press, 1986: 487-544.
|
| [34] |
裘亦楠. 储层地质模型[J]. 石油学报, 1991, 12(4): 55-62. QIU Yinan. Geological models of petroleum reservoir[J]. Acta Petrolei Sinica, 1991, 12(4): 55-62. |
| [35] |
吴胜和, 李宇鹏. 储层地质建模的现状与展望[J]. 海相油气地质, 2007, 12(3): 53-60. WU Shenghe, LI Yupeng. Reservoir modeling:Current situation and development prospect[J]. Marine Origin Petroleum Geology, 2007, 12(3): 53-60. DOI:10.3969/j.issn.1672-9854.2007.03.009 |
| [36] |
陈恭洋, 胡勇, 周艳丽, 等. 地震波阻抗约束下的储层地质建模方法与实践[J]. 地学前缘, 2012, 19(2): 67-73. CHEN Gongyang, HU Yong, ZHOU Yanli, et al. Methods and practices of reservoir geologic modelling constrained by seismic impedance[J]. Earth Science Frontiers, 2012, 19(2): 67-73. |
| [37] |
杨勇, 吴蕾, 郭凯, 等. 河口砂坝变差函数研究——以印尼某气田为例[J]. 新疆石油地质, 2006, 27(4): 422-424. YANG Yong, WU Lei, GUO Kai, et al. A study on variation function of channel mouth bar:An example of a gas filed in Indonesia[J]. Xinjiang Petroleum Geology, 2006, 27(4): 422-424. DOI:10.3969/j.issn.1001-3873.2006.04.009 |
| [38] |
吴胜和. 储层表征与建模[M]. 北京: 石油工业出版社, 2010.
|
| [39] |
甘利灯, 张昕, 王峣钧, 等. 从勘探领域变化看地震储层预测技术现状和发展趋势[J]. 石油地球物理勘探, 2018, 53(1): 214-225. GAN Lideng, ZHANG Xin, WANG Yaojun, et al. Current status and development trends of seimic re-servoir prediction viewed from the exploration industry[J]. Oil Geophysical Prospecting, 2018, 53(1): 214-225. |
| [40] |
周游, 程时清, 张敏. 储层建模中变差函数参数的设置[J]. 西安石油大学学报(自然科学版), 2010, 25(5): 25-27, 32. ZHOU You, CHENG Shiqing, ZHANG Min. Setting of variogram parameters in reservoir modeling[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2010, 25(5): 25-27, 32. DOI:10.3969/j.issn.1673-064X.2010.05.006 |



 王志章, 北京市昌平区府学路18号中国石油大学(北京)石油工程学院, 102249。Email:
王志章, 北京市昌平区府学路18号中国石油大学(北京)石油工程学院, 102249。Email: