② 成都理工大学地球物理学院, 四川成都 610059;
③ 云南建投第一勘察设计有限公司, 云南昆明 650000
② College of Geophysics, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
③ Yunnan Construction Investment First Investigation and Design Co., LTD, Kunming, Yunnan 650000, China
随着浅层、常规油气资源获取难度的增大,针对深层、超深层与非常规油气储层的地震勘探技术越来越成为人们关注的热点[1-2]。非常规油气资源之一的页岩油气的开采通常需要压裂,因此岩石的易压裂程度成为页岩油气储层评价中非常重要的指标[3]。岩石物理研究表明[4],杨氏模量和泊松比能够较好地表征岩石压裂的难易程度,为寻找储层脆性区提供了基础。
叠前AVO反演可以充分利用叠前地震资料包含的地质、岩性和流体信息,获取丰富的地下介质弹性参数。叠前反演的核心是地震波传播的物理基础和描述地震波传播过程的数理方程。Koefoed[5]通过详细对比泊松比在17组不同参数的横向各向同性介质模型中对反射系数的影响,首次给出了将泊松比与反射系数直接联系起来的Zoeppritz近似方程。Shuey[6]整理了另一种版本的Zoeppritz近似方程,指出泊松比的变化对反射系数的决定性影响。Smith等[7]通过PP波数据的加权叠加计算纵、横波波阻抗及其他弹性参数。Vestrum等[8]利用Gardner经验公式,用纵波速度的变换式替换Aki-Richards公式里的密度项,形成了加权联合反演公式。Fatti[9]消除了多波反射系数公式中的密度项,得到纵、横波阻抗两参数叠前联合反演方法。郑晓东[10]以幂级数形式表示Zoeppritz公式,消除了横波角度在方程中的影响,促进了线性AVO反演的发展。Ursenbach[11]基于Gardner公式,推导出针对砂泥岩地层的两项反射系数近似式。蔡涵鹏等[12]总结前人两参数AVO反演公式之间的关系,优化了适用于较大角度的两项AVO分析方法。高刚等[13]引入Tikhonov正则化方法,推导了以纵、横波阻抗表示的两项弹性波阻抗公式。宗兆云等[14-15]分别建立了杨氏模量、泊松比与纵、横波模量的叠前反演方法,在识别页岩气“甜点”方面进行了非常有价值的探索。张广智等[16]推导了基于杨氏模量、泊松比和密度的反射系数近似方程,为页岩气储层含流体性识别提供了可靠方法。苏建龙等[17]探讨了针对页岩气层段的叠前弹性参数反演技术。李超等[18]推导了包含Gassmann流体项和剪切模量项的两项地震反射系数近似方程,发展了针对深部储层的流体识别反演方法。
本文在叠前反演理论的基础上,通过讨论岩石弹性参数关系与拟合条件,推导新的AVO反演两项式近似方程,建立了可直接获取描述超深储层岩体脆性特征的两项式叠前反演方法。利用数值模型分析新方法与Aki-Richards正演结果的精度差异,并且完成实际地震资料的叠前AVO反演,检验了方法的合理性。
1 反射系数近似公式推导过程完整的Zoeppritz方程精确描述了反射系数随入射角变化的函数关系与反射、透射纵横波能量随入射角变化的分配机制,因此成为反射波地震勘探AVO分析的理论基础。但由于其数学形式太过复杂而不易用,故Akis等[19]于1980年对Zoeppritz公式进行近似推导,提出了目前广泛使用的Aki-Richards反射系数近似方程。该方程易被用于地震反演问题的求解,第一次给出了能够满足实际解释需要的近似反射系数的计算途径,为AVO方法应用提供了数理基础。
Aki-Richards近似方程为
| $ \begin{array}{l} R\left( \theta \right) = \frac{1}{2}\left( {1 - 4\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{{\sin }^2}\theta } \right)\frac{{\Delta \rho }}{\rho } + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{{\sec }^2}\theta }}{2}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} - 4\frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}}{\sin ^2}\theta \frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} \end{array} $ | (1) |
式中:VP、VS分别为纵、横波速度;ρ为密度;θ为入射角;
密度项是一个与泊松比等信息相关的非独立参数[20],且相对于其他参数,变化范围不大,因此可以与纵波速度建立关系。Gardner等[21]针对碎屑岩建立了密度与纵波速度的数学联系,给出幂指数的经验参数为0.25,Gardner公式为由岩石密度拟合纵波速度的经典公式。朱广生等[22]通过实测资料证明了Gardner经验公式对不同岩性的适用性较差,故本文采用幂指数拟合的方式,引入参数可变的关系式消除密度项,以此保证对实际资料拟合的准确性。推导过程如下
| $ \rho = FV_{\rm{P}}^L $ | (2) |
式中系数F、幂指数L均为常数,可根据工区纵波速度与密度数据拟合求出。由密度与纵波速度的微商关系
| $ {\rm{d}}\rho = FLV_{\rm{P}}^{L - 1}{\rm{d}}{V_{\rm{P}}} $ | (3) |
可得
| $ \frac{{\Delta \rho }}{\rho } = L\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} $ | (4) |
纵横波模量反射系数与纵横波速度、密度反射系数的关系为
| $ \frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} = \frac{1}{2}\left( {\frac{{\Delta M}}{M} - \frac{{\Delta \rho }}{\rho }} \right) $ | (5) |
| $ \frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} = \frac{1}{2}\left( {\frac{{\Delta \mu }}{\mu } - \frac{{\Delta \rho }}{\rho }} \right) $ | (6) |
式中:M为纵波模量;μ为横波模量。将式(4)代入式(5)、式(6)得
| $ \frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} = \frac{1}{{2 + L}}\frac{{\Delta M}}{M} $ | (7) |
| $ \frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} = \frac{1}{2}\left( {\frac{{\Delta \mu }}{\mu } - \frac{L}{{2 + L}}\frac{{\Delta M}}{M}} \right) $ | (8) |
令
| $ k = \frac{{V_{\rm{S}}^2}}{{V_{\rm{P}}^2}} $ | (9) |
整理杨氏模量E、泊松比σ关于纵横波速度VP、VS的关系,并融合以上各式,得
| $ \frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} = \frac{1}{{2 + L}}\frac{{\Delta E}}{E} - \frac{1}{{2 + L}}\left[ {\frac{{{{\left( {2k - 1} \right)}^2}\left( {2k - 3} \right)}}{{\left( {3 - 4k} \right)k}}} \right]\frac{{\Delta \sigma }}{\sigma } $ | (10) |
| $ \begin{array}{l} \frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} = \frac{1}{{2 + L}}\frac{{\Delta E}}{E} - \\ \;\;\;\frac{1}{2}\left[ {\frac{{1 - 2k}}{{3 - 4k}} - \frac{{L{{\left( {2k - 1} \right)}^2}\left( {2k - 3} \right)}}{{\left( {2 + L} \right)\left( {3 - 4k} \right)k}}} \right]\frac{{\Delta \sigma }}{\sigma } \end{array} $ | (11) |
| $ \frac{{\Delta \rho }}{\rho } = \frac{L}{{2 + L}}\frac{{\Delta E}}{E} - \frac{{L{{\left( {2k - 1} \right)}^2}\left( {2k - 3} \right)}}{{\left( {2 + L} \right)\left( {3 - 4k} \right)k}}\frac{{\Delta \sigma }}{\sigma } $ | (12) |
将式(10)~式(12)代入式(1),得到新的两项式近似方程
| $ \begin{array}{l} R\left( \theta \right) = \left( {\frac{{L + {{\sec }^2}\theta }}{{4 + 2L}} - 2k{{\sin }^2}\theta } \right)\frac{{\Delta E}}{E} + \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {\frac{{\left( {1 - 2k} \right)2{k^2}{{\sin }^2}\theta }}{{\left( {3 - 4k} \right)k}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{\left( {L + {{\sec }^2}\theta } \right){{\left( {2k - 1} \right)}^2}\left( {2k - 3} \right)}}{{\left( {4 + 2L} \right)\left( {3 - 4k} \right)k}}} \right]\frac{{\Delta \sigma }}{\sigma } \end{array} $ | (13) |
在此笔者沿用宗兆云等[14]对三项近似式的命名方法,将上式称为YP近似方程,该式建立了杨氏模量反射率、泊松比反射率与反射系数的直接、线性关系。
2 精度分析四川元坝气田是一个埋藏很深的海相气田,选择元坝气田实际测井资料及构造地质模型对精确Zoeppritz方程、Aki-Richards近似方程与YP近似方程的计算精度进行实验对比、分析。YP方程中的参数k=0.2599,L=0.5339,模型参数如表 1所示。
|
|
表 1 元坝地区实测地震模型参数(据文献[23]) |
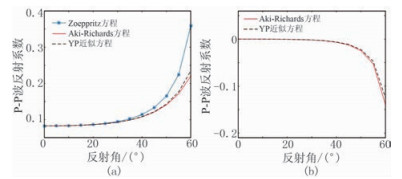
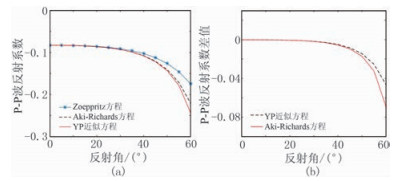
地震波速度与密度的乘积被称为波阻抗,正波阻抗界面的入射介质的波阻抗小于透射介质,负波阻抗界面则相反。在本模型中,上覆地层与气层的分界面为负波阻抗界面,气层与下伏地层的分界面为正波阻抗界面。分别用精确的Zoeppritz方程、Aki-Richard近似方程、YP近似方程计算上述模型不同界面处的反射系数及近似方程与精确方程的残差(图 1、图 2),可见基于YP近似方程计算的反射系数与精确Zoeppritz方程有一定误差,其精度优于Aki-Richard近似方程的计算结果。Aki-Richard近似方程对Zoeppritz方程的残差在入射角为50°时开始急剧增大。相对而言,YP近似方程的误差较小,说明在一定情况下,YP近似方程具有与Aki-Richard近似方程相似、甚至更小的误差。根据选用的地震模型不同,其计算误差会在小范围内变动。
|
图 1 正波阻抗界面不同方程反射系数(a)和反射系数差值(b)对比 |
|
图 2 负波阻抗界面界面不同方程反射系数(a)和反射系数差值(b)对比 |
影响误差的主要因素是密度与纵波速度的拟合方程是否得当,即参数L、k的取值是否合适。当L、k取值得当,通过纵、横波速度拟合得到的密度就较为准确,由方程计算得到的反射系数精度高;当参数L、k取值不当,实际效果相当于三参数反演中密度项的取值不准确,可见L、k的取值较为关键。因此,在实际反演中,应尽量使用目标层段的测井数据进行幂指数拟合计算,求取准确的参数L、k。
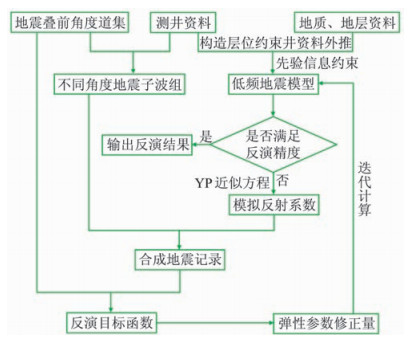
3 反演流程基于YP近似方程的两项AVO反演流程包含叠前地震资料预处理、测井资料预处理、地质层位解释、多角度子波提取等主要环节,最终通过反演获得杨氏模量和泊松比数据体。主要反演流程如图 3。
|
图 3 YP近似方程地震叠前反演流程图 |
在进行杨氏模量与泊松比反演计算之前,需从先验信息中求得参数L、k。为确保参数拟合结果准确、可靠,针对目的层段可采用测井资料的纵、横波速度与密度确定L、k,其中k为测井资料中横、纵波速度比的平方,L则通过密度与纵波速度的幂指数拟合计算得到。
待反演参数的计算可简化为求解
| $ \left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}\left( {t,{\theta _1}} \right)}\\ {{R_{{\rm{PP}}}}\left( {t,{\theta _2}} \right)}\\ \vdots \\ {{R_{{\rm{PP}}}}\left( {t,{\theta _i}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_E}\left( {t,{\theta _1}} \right)}&{{C_\sigma }\left( {t,{\theta _1}} \right)}\\ {{C_E}\left( {t,{\theta _2}} \right)}&{{C_\sigma }\left( {t,{\theta _2}} \right)}\\ \vdots&\vdots \\ {{C_E}\left( {t,{\theta _i}} \right)}&{{C_\sigma }\left( {t,{\theta _i}} \right)} \end{array}} \right]\left[ \begin{array}{l} {R_E}\left( t \right)\\ {R_\sigma }\left( t \right) \end{array} \right] $ | (14) |
式中:RPP是反射纵波的反射系数;CE和Cσ与角度有关;RE和Rσ分别是杨氏模量、泊松比的反射系数时间序列。
| $ {C_E}\left( {{\theta _i}} \right) = \frac{{L + {{\sec }^2}{\theta _i}}}{{4 + 2L}} - 2k{\sin ^2}{\theta _i} $ | (15) |
| $ \begin{array}{l} {C_\sigma }\left( {{\theta _i}} \right) = \frac{{2{k^2}\left( {1 - 2k} \right){{\sin }^2}{\theta _i}}}{{\left( {3 - 4k} \right)k}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\left( {L + {{\sec }^2}{\theta _i}} \right){{\left( {2k - 1} \right)}^2}\left( {2k - 3} \right)}}{{\left( {4 + 2L} \right)\left( {3 - 4k} \right)k}} \end{array} $ | (16) |
| $ {R_E}\left( t \right) = \frac{{\Delta E\left( t \right)}}{{E\left( t \right)}} $ | (17) |
| $ {R_\sigma }\left( t \right) = \frac{{\Delta \sigma \left( t \right)}}{{\sigma \left( t \right)}} $ | (18) |
反射系数与某一角度子波卷积形成一个固定角度的地震合成记录。将式(14)等号两边同时与子波卷积
| $ {S_{{\rm{PP}}}}\left( {t,{\theta _i}} \right) = \int_0^t {{R_{{\rm{PP}}}}\left( {\tau ,{\theta _i}} \right) * {W_{t,i}}\left( {t - \tau } \right){\rm{d}}\tau } $ | (19) |
| $ \mathit{\boldsymbol{W}}\left( {t,{\theta _i}} \right) = \int_0^t {C\left( {\tau ,{\theta _i}} \right) * {W_{t,i}}\left( {t - \tau } \right){\rm{d}}\tau } $ | (20) |
式中:Wt, i为不同角度的子波;SPP(t,θi)是入射角为θi的角道集;W(t,θi)是一个子波核矩阵。
卷积运算之后可得
| $ \left[ {\begin{array}{*{20}{c}} {{S_{{\rm{PP}}}}\left( {t,{\theta _1}} \right)}\\ {{S_{{\rm{PP}}}}\left( {t,{\theta _2}} \right)}\\ \vdots \\ {{S_{{\rm{PP}}}}\left( {t,{\theta _i}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{W_E}\left( {t,{\theta _1}} \right)}&{{W_\sigma }\left( {t,{\theta _1}} \right)}\\ {{W_E}\left( {t,{\theta _2}} \right)}&{{W_\sigma }\left( {t,{\theta _2}} \right)}\\ \vdots&\vdots \\ {{W_E}\left( {t,{\theta _i}} \right)}&{{W_\sigma }\left( {t,{\theta _i}} \right)} \end{array}} \right]\left[ \begin{array}{l} {R_E}\left( t \right)\\ {R_\sigma }\left( t \right) \end{array} \right] $ | (21) |
若设D = Gm,D表示包含向量SPP的叠前角度道集,WE和Wσ构成核矩阵G,m是包含RE和Rσ的反射率项。
反演的目标函数为
| $ f\left( \mathit{\boldsymbol{V}} \right) = \left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{D}}} \right\| \to \min $ | (22) |
式中:V为待反演弹性参数构成的参数向量;S(t)=W*R为初始低频模型在各角度下的合成地震记录,其中W为一组不同角度地震子波,R为计算得到的低频地震模型的反射系数。
构造f(V)的Jacobian矩阵J,通过对J进行求解得到对V的修正量ΔV0 [24],将V0=V+ΔV0作为新的反演参数向量代入式(22),反复迭代求解f(V)的极小值,直至求得使f(V)达到允许误差的ΔVn,此时认为Vn=Vn-1+ΔVn为最优解。
4 模型试算为验证YP近似方程两项AVO反演的可行性与稳定性,本文采用层状模型进行反演信噪比试验与模型依赖性试验。
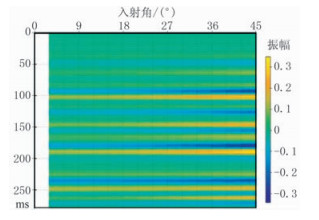
设置一个共16层、每层具有一定厚度、水平层状介质模型,赋予其纵、横波速度与密度(图 4)。子波采用主频为40Hz的雷克子波,采用精确Zoeppritz方程进行正演得到角度域叠前角道集,并对角道集分别添加信噪比10dB、5dB、2dB、1dB、0.5dB的高斯白噪声,采用本文所述YP近似方程进行杨氏模量、泊松比反演,结果如图 5所示。
|
图 4 多层水平层状介质角道集 |
|
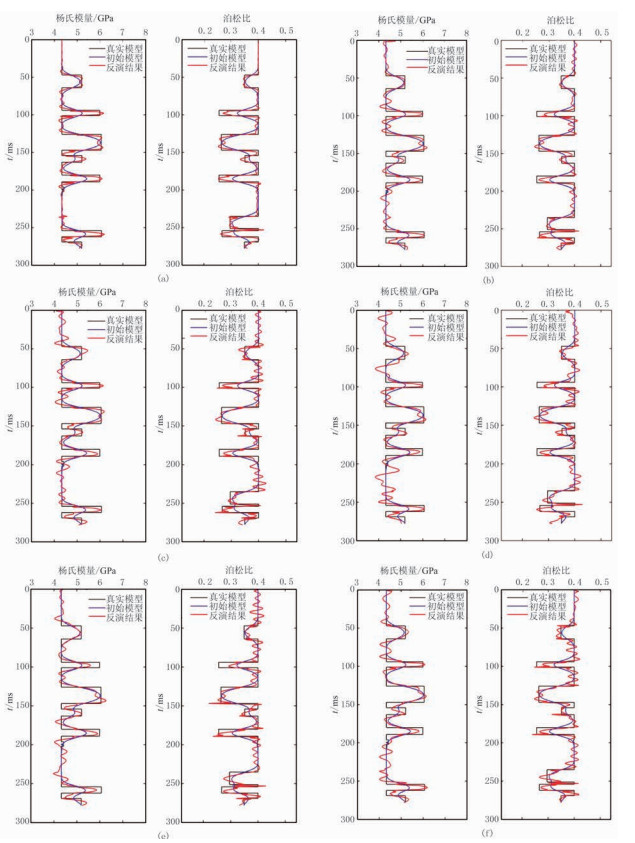
图 5 信噪比试验反演结果 (a)无噪声;(b)10dB;(c)5dB;(d)2dB;(e)1dB;(f)0.5dB |
由反演结果可见,反演曲线受信噪比影响较大。模型信噪比降低,反演结果的波动也相应加大,且使反演精确度降低,但反演曲线的变化趋势与模型吻合,能够反映真实杨氏模量与泊松比的相对大小。
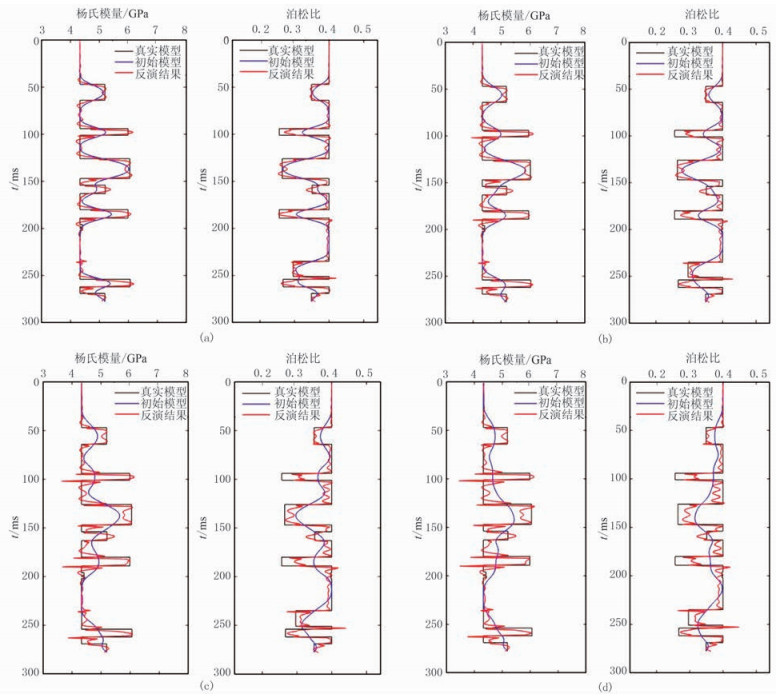
对真实模型进行不同程度的平滑处理,以各组平滑曲线作为初始模型进行模型依赖性实验(图 6),可见初始模型中高频成分的缺失,将使反演结果在地层分界处出现异常值;初始模型越准确,反演效果越好。总体而言,通过YP反演可以将反演值归位到真实值附近,获得体现杨氏模量、泊松比有效信息的反演结果。
|
图 6 不同初始模型试验结果 (a)10均值平滑;(b)20均值平滑;(c)35均值平滑;(d)50均值平滑 |
使用A区实测地震数据与测井资料进行分析。A区地层相对平缓,发育NW向展布的裂缝带,构造规模普遍较小。目的层为须四上亚段(顶界面为TT3-4顶),发育辫状河三角洲前缘水下分流河道,岩性主要为细粒、中粒碎屑砂岩。孔隙度为1.2~4.6%,渗透率为0.005~0.050mD,属典型的致密砂岩储层。目的层埋藏深度约4550m,地震时间深度约2400ms,属深层—超深层。研究区气层受岩性与裂缝联合控制,储层类型为裂缝—孔隙型,伽马测井曲线可用于区分岩性。W173井获高产工业气流。本文所用地震资料横向CDP共603道,道间距为25m;纵向时间为0~4000ms,采样间隔为1ms。
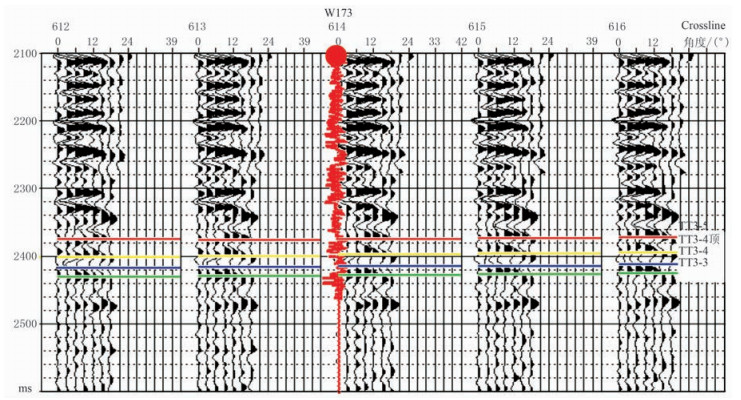
记录地震波振幅数据的角道集有效角度范围为0°~26°,缺失26°以上大角度地震数据(图 7),因此不具备开展三参数叠前反演的数据基础。本区采用YP近似反演方法进行杨氏模量、泊松比反演。
|
图 7 叠前角道集地震数据 |
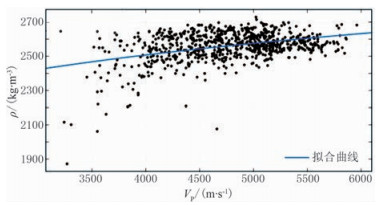
根据测井资料中纵波速度与密度曲线进行幂指数拟合,得到拟合曲线图(图 8),参数L=0.1202,修正了Gardner公式对砂泥岩的经验参数。
|
图 8 W173井纵波速度与密度拟合曲线图 |
充分考虑地层沉积模式和接触关系,使用目标层段的测井资料,构建目标层段的地质模型,之后对模型层位进行平滑,得到满足反演需要的初始模型(图 9)。利用YP近似反演得到杨氏模量、泊松比反演数据。
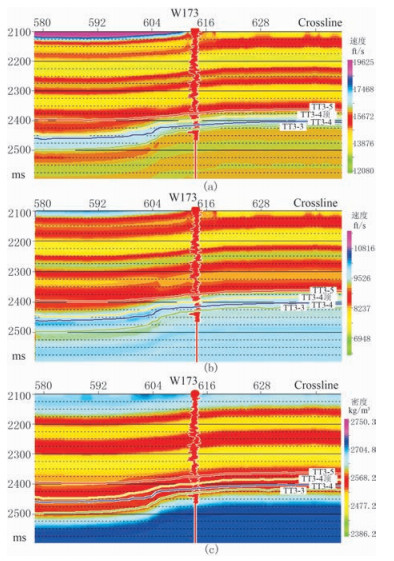
|
图 9 叠前反演低频模型剖面 (a)纵波速度;(b)横波速度;(c)密度 |
过W173井的杨氏模量、泊松比反演剖面如图 10所示。含气层为杨氏模量局域高值、泊松比局部低值,表征天然气储集岩层脆性较高,易于产生作为页岩气运移通道的随机裂缝,因此具有改造成为商业页岩气优质产区的有利条件。反演结果与实际勘探情况相吻合。

|
图 10 过井反演剖面 (a)主测线杨氏模量;(b)主测线泊松比;(c)联络测线杨氏模量;(d)联络测线泊松比 |
本文针对优质页岩气储层具有高杨氏模量、低泊松比的特点,以岩石物理分析为基础,由Aki-Richard近似方程出发,推导了直接反演杨氏模量、泊松比的两参数反射系数近似方程,进而总结了一套适用于超深储层、能够直接反演岩石脆性参数的叠前反演方法。该方法考虑到Gardner经验公式的不完备性,在替换密度项时引入参数可变公式,使密度的近似更加合理。模型反演结果能够较好反映真实杨氏模量、泊松比的相对大小,为刻画页岩气储层甜点区提供了较为有效的途径。需要指出的是,超深层储层地震资料的品质通常较低,对于反演结果的稳定性与准确度影响较大。未来在提高地震资料品质的同时,应尝试引入多种数理方法改进反演计算的稳定性,以期获得更好的反演效果。
| [1] |
赵波, 王赟, 芦俊. 多分量地震勘探技术新进展及关键问题探讨[J]. 石油地球物理勘探, 2012, 47(3): 506-516. ZHAO Bo, WANG Yun, LU Jun. Recent advances of multi-component seismic and some of its key issues[J]. Oil Geophysical Prospecting, 2012, 47(3): 506-516. |
| [2] |
王海龙, 杨午阳, 李海亮, 等. 塔东古城地区深层油气藏岩溶储层预测[J]. 石油地球物理勘探, 2017, 52(增刊2): 116-122. WANG Hailong, YANG Wuyang, LI Hailiang, et al. Deep karst reservoir prediction in the Gucheng area, Tarim Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 116-122. |
| [3] |
任岩, 曹宏, 姚逢昌, 等. 吉木萨尔致密油储层脆性及可压裂性预测[J]. 石油地球物理勘探, 2018, 53(3): 511-519. REN Yan, CAO Hong, YAO Fengchang, et al. Brittleness and fracability prediction for tight oil reservoir in Jimsar Sag, Junggar Basin[J]. Oil Geophysical Pro-specting, 2018, 53(3): 511-519. |
| [4] |
Sena A, Castillo G, Chesser K, et al. Seismic reservoir characterization in resource shale plays:"Sweet Spot" discrimination and optimization of horizontal well placement[J]. SEG Technical Program Expanded Abstracts, 2011, 30: 1744-1748. |
| [5] |
Koefoed O. Reflection and transmission coefficients for plane longitudinal incident waves[J]. Geophysical Prospecting, 1962, 10(3): 304-351. DOI:10.1111/gpr.1962.10.issue-3 |
| [6] |
Shuey R T. A simplification of the Zoeppritz-equations[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [7] |
Smith G C, Gidlow M.The fluid factor angle and the crossplot angle[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 2452.
|
| [8] |
Vestrum R W, Stewart R R.Joint P and P-SV Inversion: Application and Testing[R]. Crewes Research Report, 1993, 13(5): 1-7.
|
| [9] |
Fatti J L. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [10] |
郑晓东. Zoeppritz方程的近似及其应用[J]. 石油地球物理勘探, 1991, 26(2): 129-144. ZHENG Xiaodong. Approximation of Zoeppritz equation and its application[J]. Oil Geophysical Prospecting, 1991, 26(2): 129-144. |
| [11] |
Ursenbach C.Two new approximations for AVO inversion[C]. 2004 CSEG National Convention, 2004.
|
| [12] |
蔡涵鹏, 贺振华, 李瑞, 等. 两项AVO反演研究及应用[J]. 成都理工大学学报(自然科学版), 2011, 38(5): 581-587. CAI Hanpeng, HE Zhenhua, LI Rui, et al. Study and application of two-term AVO inversion[J]. Journal of Chengdu University of Technology, 2011, 38(5): 581-587. DOI:10.3969/j.issn.1671-9727.2011.05.015 |
| [13] |
高刚, 贺振华, 曹俊兴, 等. 两项式弹性波阻抗反演方法在深层碳酸盐岩储层预测中的应用[J]. 石油地球物理勘探, 2013, 48(3): 450-457. GAO Gang, HE Zhenhua, CAO Junxing, et al. The new two-term elastic impedance inversion and its application to predict deep gas-bearing carbonate reserviors[J]. Oil Geophysical Prospecting, 2013, 48(3): 450-457. |
| [14] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [15] |
宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 2012, 55(1): 284-292. ZONG Zhaoyun, YIN Xingyao, WU Guochen. Fluid identification method based on compressional and shear modulus direct inversion[J]. Chinese Journal of Geophysics, 2012, 55(1): 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
| [16] |
张广智, 杜炳毅, 李海山, 等. 页岩气储层纵横波叠前联合反演方法[J]. 地球物理学报, 2014, 57(12): 4141-4149. ZHANG Guangzhi, DU Bingyi, LI Haishan, et al. The method of joint pre-stack inversion of PP and P-SV waves in shale gas reservoirs[J]. Chinese Journal ofGeophysics, 2014, 57(12): 4141-4149. DOI:10.6038/cjg20141225 |
| [17] |
苏建龙, 屈大鹏, 陈超, 等. 叠前地震反演方法对比分析——焦石坝页岩气藏勘探实例[J]. 石油地球物理勘探, 2016, 51(3): 581-588. SU Jianlong, QU Dapeng, CHEN Chao, et al. Application of pre-stack inversion technique for shale gas in Jiaoshiba Gas Field[J]. Oil Geophysical Prospecting, 2016, 51(3): 581-588. |
| [18] |
李超, 张金淼, 朱振宇. 深部储层流体因子直接反演方法[J]. 石油物探, 2017, 56(6): 827-834. LI Chao, ZHANG Jinmiao, ZHU Zhenyu. Direct inversion for fluid factor of deep reservoirs[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 827-834. DOI:10.3969/j.issn.1000-1441.2017.06.008 |
| [19] |
Aki K, Richards P G. Quantitative Seismology[M]. San Francisco: W.H.Freeman, 1980: 5-43.
|
| [20] |
Lu S. Elastic impedance inversion of multichannel seismic data from unconsolidated sediments containing gas hydrate and free gas[J]. Geophysics, 2004, 69(1): 164-179. DOI:10.1190/1.1649385 |
| [21] |
Gardner G H F, Gardner L W, Gregory A R, et al. Formation velocity and density:The diagnostic basis for stratigraphic traps[J]. Geophysics, 1974, 39(6): 777-780. |
| [22] |
朱广生, 桂志先, 熊新斌, 等. 密度与纵横波速度关系[J]. 地球物理学报, 1995, 38(增刊1): 260-264. ZHU Guangsheng, GUI Zhixian, XIONG Xinbin, et al. Relationships between density and P-wave, S-wave velocities[J]. Chinese Journal of Geophysics, 1995, 38(S1): 260-264. |
| [23] |
文晓涛, 黄德济. 礁滩储层地震识别[M]. 北京: 科学出版社, 2014.
|
| [24] |
王家映. 地球物理反演理论[M]. 北京: 高等教育出版社, 2002.
|



 张瑞, 四川省成都市成华区成都理工大学地球物理学院, 610059。Email:
张瑞, 四川省成都市成华区成都理工大学地球物理学院, 610059。Email: