② 中国石油大学(华东)地球科学与技术学院, 山东青岛, 266580;
③ 青岛海洋科学与技术试点国家实验室, 山东青岛, 266237
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ National Pilot Laboratory for Marine Sciences and Technology(Qingdao), Qingdao, Shandong 266237, China
传统地震反演是基于褶积模型,也就意味着地震道是平稳的,实际上由于吸收衰减和噪声干扰等因素的影响,地震数据往往是非平稳的。因而,常子波假设不适用于实际地震道。为了解决这个问题,目前已经发展多种方法建立时变子波或非平稳褶积模型,以满足地震数据的非平稳性质。Van der Baan等[1-2]利用最大峰度提出了一种时变子波估计方法;Margrave等[3]考虑到地层的衰减提出非平稳褶积模型,并基于此模型实现了高分辨率地震反褶积;Dai等[4]利用广义S变换对地震道进行时频分解,并基于局部相似度估计时变子波,通过反褶积验证了时变子波的适用性,继而又提出时频分析与自适应分段结合的时变子波提取方法[5]。为了获得符合实际的混合相位子波,孔德辉等[6]提出一种基于在线字典学习的时变子波估计方法;Zhang等[7]基于局部谱时频分析提取了时变子波,并将其用于地震反演,得到了更准确的波阻抗反演结果;Wang[8]提出了广义地震子波解析式,能更好地表征地震数据频谱的不对称性,用于更精确的地震子波构建。
时频分解技术能刻画时间与瞬时频率之间的非平稳关系,已逐渐成为地震信号处理和解释的有力工具,广泛用于地震薄层厚度分析、气藏低频阴影检测等方面。经典的短时傅里叶变换(STFT)用窗函数截取信号,展示信号的局部频率特征[9],但存在固有的窗口效应,易引起频谱模糊。将STFT的正弦基函数改为小波函数,以克服窗口效应,就形成了目前广泛使用的基于小波的频谱分解方法[10]。该类方法在描述微幅构造和储层特征方面都体现出良好的性能,常见的有连续小波变换[11]和匹配追踪技术[12-13]。Liu等[14]和Liu等[15]发展了一种基于局部属性的S变换方法[16],通过正则化的非平稳回归[17]实现频谱分解。这种基于局部属性的谱分解技术已成功应用于地滚波压制、多分量数据匹配和地层解释[15, 18]。以上谱分解技术都各有其优点,但都不可避免地在时间分辨率与频率分辨率之间进行权衡。经验模式分解(EMD)[19]算法能将信号分离成局部常频率分量,同时获得较高的时间和频率分辨率。随后很多种改进算法被提出,如EEMD和CEEMD[20]。近年来,基于算法结合(如同步压缩变换SST[21-22])和反演方案(如基追踪[23])的时频分解技术在改善时频分辨率方面呈现越来越大的潜能。
本文基于基追踪谱分解提取时变广义地震子波,并将其应用于非平稳地震道的基追踪反演,提高了反演结果的分辨率,增强了反演结果的地质连续性。首先对非平稳地震道做基追踪谱分解,将其映射到时频空间,于各时间采样点处获得局部功率谱;然后采用广义地震子波构建方法,提取时变子波并构建时变子波核矩阵;继而基于时变奇偶反射波形字典,最终实现非平稳地震道的基追踪反演。对比常子波基追踪地震道反演结果,说明了时变子波基追踪反演对反演结果分辨率和地质连续性的改善,也证明了提取时变子波的必要性。
1 基本理论与技术流程 1.1 基追踪谱分解基追踪(BP)与匹配追踪(MP)谱分解[12]的基本原理类似,都是试图将地震信号分解到预先定义的波形字典的各个基函数上,求得基函数表示系数,经尺度到频率的映射,最终得到高分辨率谱分解结果。基追踪谱分解有两个典型特点:一是引入了一个最小化项减少重构基函数的数量和幅值,以期得到地震信号的稀疏表示[23];二是在匹配追踪谱分解过程中,采用逐步压缩的方法,也就是依据内积最大原则逐次识别并移除基函数,而基追踪谱分解是同时鉴别所有基函数,通过将识别和移除两个步骤融入到一个反演问题中予以实现[24-25]。
地震道s(t)可被表示为一族基函数ψ(t, n)与其对应的系数序列a(t, n)的卷积
| $ s\left( t \right) = \sum\limits_{n = 1}^N {\left[ {\psi \left( {t,n} \right) * a\left( {t,n} \right)} \right]} $ | (1) |
式中:N是基函数的个数;n是控制基函数频率特征的尺度参数。采用矩阵记法,式(1)写作
| $ \mathit{\boldsymbol{s}} = \left( {{\mathit{\boldsymbol{\psi }}_1}\;{\mathit{\boldsymbol{\psi }}_2}\; \cdots \;{\mathit{\boldsymbol{\psi }}_N}} \right)\left( {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_N}} \end{array}} \right) + \mathit{\boldsymbol{\eta }} = \mathit{\boldsymbol{Da}} + \mathit{\boldsymbol{\eta }} $ | (2) |
式中:s是地震道s(t)的向量记法;Ψn表示基函数ψ(t, n)的卷积矩阵;an表示对应Ψn的系数;D为波形字典;a是由an组成的列向量,也即由全部系数a(t, n)按列排布形成的列向量;η是随机噪声。这样谱分解结果就是地震道映射在波形字典D中的权系数a(t, n)于时间—频率空间的分布。
式(2)中权系数a的求解问题即为典型的基追踪去噪问题。设定目标函数为
| $ J = \min \left( {\frac{1}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Da}}} \right\|_2^2 + \lambda {{\left\| \mathit{\boldsymbol{a}} \right\|}_1}} \right) $ | (3) |
式中λ是权衡因子。J的第一项代表基于L2范数的数据误差项,也就是地震道与重构数据之间的最小二乘误差;J的第二项即为L1范数约束正则化项,λ控制数据误差和解稀疏度的相对强弱。可用多种方法求解式(2),使目标泛函(式(3))最小化[26-28]。
与匹配追踪不同,基追踪是一种非贪婪算法,它从一个初始模型出发,通过不断迭代,调整波形字典基函数,最终收敛到一个局部最优解。与匹配追踪类似,方程解的精度在一定程度上依赖于波形字典的选择,波形字典越完备,解越精确,但同时会增加计算时间,降低计算效率[23, 29]。
1.2 广义地震子波的提取在地震反演中,子波提取非常关键,子波估计的精度会直接影响地震反演的效果。当有井信息时,往往通过井震标定实现子波提取;当没有井信息时,往往假设反射系数序列是白色的或者近似是白色的,也就是有一个平稳的功率谱,进而可以采用谱比法或者相关法进行子波估计。为了更好地表示实际地震道特征,Wang[8]构建了广义地震子波解析式,该式广泛适用于多种非对称振幅谱。广义地震波解析表达式被定义为高斯函数的导数。广义地震波的频谱具有如下的解析形式
| $ \begin{array}{l} W\left( \omega \right) = {\left( {\frac{u}{2}} \right)^{ - u/2}}\frac{{{\omega ^u}}}{{\omega _0^u}}\exp \left( { - \frac{{{\omega ^2}}}{{\omega _0^2}} + \frac{u}{2}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ { - {\rm{i}}\omega {\tau _0} + {\rm{i \mathsf{ π} }}\left( {1 + \frac{u}{2}} \right)} \right] \end{array} $ | (4) |
式中:τ0为对称中心的时间位置;u为分数阶,取值范围为0.4~2.2,它控制了频谱的对称性质;ω0是参考角频率,控制子波的带宽和主频。当u=2.0时,广义地震子波就变成经典的雷克子波。广义地震子波频谱W(ω)的平均频率及其标准差分别为
| $ {\omega _{\rm{m}}} = \frac{{\sum\limits_\omega {\omega {{\left| {A\left( \omega \right)} \right|}^2}} }}{{\sum\limits_\omega {{{\left| {A\left( \omega \right)} \right|}^2}} }} $ | (5) |
| $ {\omega _\sigma } = \left[ {\frac{{\sum\limits_\omega {{{\left( {\omega - {\omega _{\rm{m}}}} \right)}^2}{{\left| {A\left( \omega \right)} \right|}^2}} }}{{\sum\limits_\omega {{{\left| {A\left( \omega \right)} \right|}^2}} }}} \right] $ | (6) |
式中|A(ω)|2是实值地震信号的功率谱。分数阶数u可以通过平均频率ωm与其标准差ωσ的比值唯一地给出
| $ \frac{{\omega _{\rm{ \mathsf{ σ} }}^2}}{{\omega _{\rm{m}}^2}} = \left( {\frac{1}{{2u}} + 1} \right){\left[ {\frac{{\mathit{\Gamma }\left( {u + \frac{1}{2}} \right)}}{{\sqrt u \mathit{\Gamma }\left( u \right)}}} \right]^2} - 1 $ | (7) |
式中Γ(u)是Gamma函数。
对于这个单变量的非线性方程,式中的两个Gamma函数的比值可被表示为渐进级数序列[30]
| $ \begin{array}{*{20}{c}} {\frac{{\mathit{\Gamma }\left( {u + \frac{1}{2}} \right)}}{{\sqrt u \mathit{\Gamma }\left( u \right)}} = 1 - \frac{1}{{8u}} + \frac{1}{{128{u^2}}} + \frac{5}{{1024{u^3}}} - }\\ {\frac{{21}}{{32768{u^4}}} + \cdots } \end{array} $ | (8) |
基于该级数可以确定一个最佳的分数阶数u。然后,基于ωm2和ωσ2之和,可求出参考角频率ω0
| $ {\omega _0} = 2\sqrt {\frac{{\omega _{\rm{m}}^2 + \omega _{\rm{ \mathsf{ σ} }}^2}}{{1 + 2u}}} $ | (9) |
当确定分数阶数u和参考角频率ω0之后,即可求得广义地震子波的频谱W(ω),然后再做反傅里叶变换,并最终得到时间域子波。
1.3 时变子波核矩阵的构建在地震反演中,褶积模型[31]被广泛使用,即地震道是地震子波与反射率的褶积
| $ s\left( t \right) = w\left( t \right) * r\left( t \right) + \eta \left( t \right) $ | (10) |
式中:w(t)表示地震子波;r(t)表示反射系数序列;η(t)表示随机噪声。
地震子波与反射率的卷积运算等价于矩阵与向量相乘,即
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Wr}} + \mathit{\boldsymbol{\eta }} $ | (11) |
式中:s、r和η分别代表地震记录向量、反射系数向量和随机噪声向量。假设W代表子波核矩阵,该矩阵通过子波w(t)沿着方阵主对角线方向平移构建而成,W在反演问题中即为映射矩阵。
基于褶积模型假设,采用统计方法[32-36]或者井震标定的方法[37-38],可以从地震数据中估计得到一个常子波w(t)。
考虑到吸收衰减以及噪声干扰造成的地震道的非平稳性,首先对地震道做基追踪谱分解,然后逐时间点提取广义地震子波,再用时变的广义地震子波逐列取代子波核矩阵W的常子波w(t),形成时变子波核矩阵,用于后续的地震反演。
2.4 时变子波基追踪反演基追踪是一种L1范数约束的优化方法,考虑到地下地层的稀疏性,近年来该方法逐渐被应用于地震反演[39-43],提高了反演结果的分辨率,其中目标函数被定义为
| $ \min \left[ {{{\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Gr}}} \right\|}_2} + {{\left\| \mathit{\boldsymbol{r}} \right\|}_1}} \right] $ | (12) |
式中G是映射矩阵,可选为常子波核矩阵或时变子波核矩阵。
为了表征地层的层稀疏,而不是反射率稀疏,Zhang等[39]采用奇偶反射脉冲对代替地层反射率
| $ \begin{array}{*{20}{c}} {r\left( t \right) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\left[ {{a_{n,m}}{r_{\rm{e}}}\left( {t,m,n,\Delta t} \right) + } \right.} } }\\ {\left. {{b_{n,m}}{r_{\rm{o}}}\left( {t,m,n,\Delta t} \right)} \right]} \end{array} $ | (13a) |
或写为矩阵形式
| $ \mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{D}}_{\rm{r}}}\mathit{\boldsymbol{x}} $ | (13b) |
式中:ro(t, m, n, Δt)和re(t, m, n, Δt)分别为奇、偶反射对分量;an, m和bn, m分别为对应奇、偶反射对的系数;Δt为采样间隔;m、n分别为层顶、底界面所对应的采样点位置;M为单道地震道的采样点数;N为最大地层数,根据实际地震资料选定;Dr为反射系数字典;x为反射系数字典基函数的稀疏表示系数向量。
求反射系数序列r(t)与地震子波w(t)的卷积,得到地震道
| $ \begin{array}{*{20}{c}} {s\left( t \right) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\left\{ {{a_{n,m}}\left[ {w\left( t \right) * {r_{\rm{e}}}\left( {t,m,n,\Delta t} \right)} \right] + } \right.} } }\\ {\left. {{b_{n,m}}\left[ {w\left( t \right) * {r_{\rm{o}}}\left( {t,m,n,\Delta t} \right)} \right]} \right\}} \end{array} $ | (14a) |
或写为矩阵形式
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{D}}_{\rm{s}}}\mathit{\boldsymbol{x}} $ | (14b) |
即地震数据是奇、偶反射对波形的叠加。式中Ds为奇、偶反射对波形字典。考虑到地震数据的非平稳性,将常子波w(t)替换为时变子波w(t, m, n),可得
| $ \begin{array}{*{20}{c}} {s\left( t \right) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\left\{ {{a_{n,m}}\left[ {w\left( {t,m,n} \right) * {r_{\rm{e}}}\left( {t,m,n,\Delta t} \right)} \right] + } \right.} } }\\ {\left. {{b_{n,m}}\left[ {w\left( {t,m,n} \right) * {r_{\rm{o}}}\left( {t,m,n,\Delta t} \right)} \right]} \right\}} \end{array} $ | (15a) |
或写为矩阵形式
| $ \mathit{\boldsymbol{s}} = {{\mathit{\boldsymbol{D'}}}_{\rm{s}}}\mathit{\boldsymbol{x}}\begin{array}{l} \end{array} $ | (15b) |
反演过程中,目标函数变为
| $ \min {\left\| {\mathit{\boldsymbol{s}} - {{\mathit{\boldsymbol{D'}}}_{\rm{s}}}\mathit{\boldsymbol{x}}} \right\|_2} + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_1} $ | (16) |
采用基追踪优化算法求解上述方程,即可得到优化稀疏表示系数向量x,然后利用式(13)重构得到反射系数的最终反演结果。
2 非平稳基追踪反演模型测试为了说明非平稳基追踪反演的重要性,建立如图 1a所示的声波阻抗模型,计算对应的反射系数如图 1b所示。为了获得非平稳地震道,对反射系数分段采用主频为60Hz和100Hz两种雷克子波进行褶积(图 1c)。
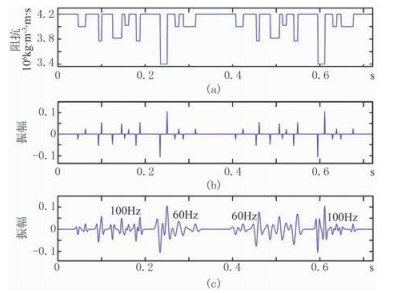
|
图 1 模型及合成地震记录 (a)阻抗模型; (b)反射系数序列; (c)合成地震记录 |
分别采用60Hz、100Hz雷克子波波形字典以及由60Hz、100Hz雷克子波形成的时变子波波形字典,进行基追踪反演,得到反射系数反演结果(图 2)。可以看出,采用60Hz雷克子波波形字典时,地震道中采用100Hz雷克子波褶积形成的部分不能被有效地反演出来,反之亦然。总的来说,低频成份高频子波反演结果使反射率变“胖”,分辨率降低,高频成份低频子波反演结果的反射率个数增多,出现虚假界面信息。采用时变子波字典时,基追踪地震反演能获得准确的反射率序列。
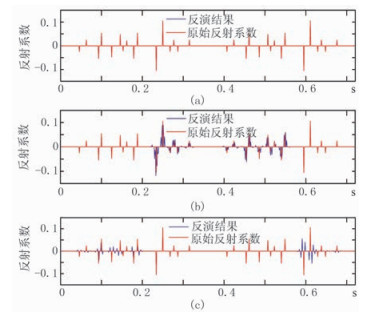
|
图 2 基追踪反射系数反演结果 (a)基于时变子波字典; (b)基于100Hz子波字典; (c)基于60Hz子波字典 |
因此,基追踪地震反演中,子波字典的正确性和完备性至关重要,故对于实际的非平稳地震数据,时变子波的有效估计也是地震反演精度的有力保障。
3 实际资料测试 3.1 基追踪时频分解本文采用来自荷兰北海F3区块的实际地震数据体和测井数据,阐述基追踪谱分解时变子波提取与地震反演的技术流程。图 3为过F06井(位于Crossline387)的Inline244地震剖面。对该地震剖面逐道进行基追踪谱分解(图 4),可以看出时频谱分解能量团具有较高的分辨率,与地震波形吻合较好,随着时间增加,时频谱主频整体变小,但局部有明显错动。图 5为整个地震剖面基追踪谱分解结果的三维展示,可以看出,地震记录的谱分解结果不仅随时间轴变化,还沿着Crossline方向变化,在整个地震剖面每一道的每个时间点处都提取一个广义地震子波,则对整个地震剖面而言,提取到的地震子波不仅是时变的,还是空变的。

|
图 3 过F06井的Inline244地震剖面 |
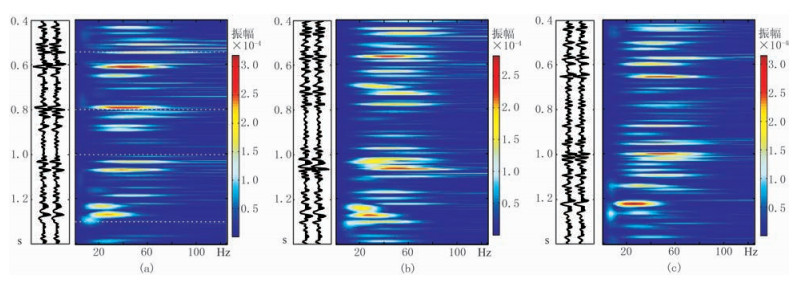
|
图 4 Inline244单道地震记录(左)及其基追踪谱分解结果(右) (a)Crossline400; (b)Crossline600; (c)Crossline800 |
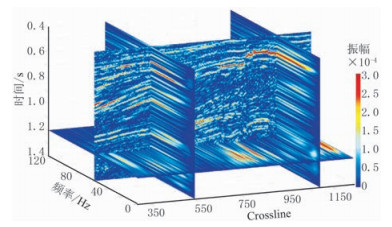
|
图 5 Inline244地震剖面基追踪谱分解结果 |
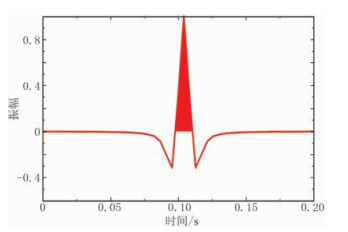
传统地震子波的估计是基于一些假设,包括卷积模型、随机反射率以及最小相位等[32-34]。如Inline244地震剖面,采用测井数据和井旁地震道做井震标定,利用谱除法获得常地震子波(图 6)。该地震子波在传统的地震反演中用于整条地震剖面,距井越远的地震道反演结果误差越大,且在单地震道内,未考虑地震道的非平稳特征,因此常子波地震反演不能精确地捕获地层的局部特征。
|
图 6 经井震标定提取的常地震子波 |
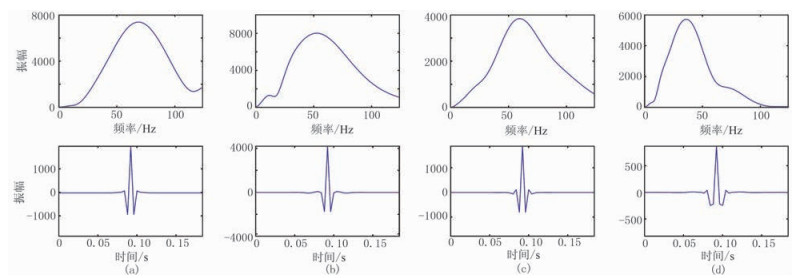
从图 4和图 5可以清晰地观测到地震数据时频谱沿着时间轴和空间水平轴的变化特征。基追踪谱分解结果代表地震数据沿时间和频率的能量分布,可以看作是每个地震道在每个采样点的局部功率谱。基于单点功率谱,采用广义地震子波构建方法,提取整个地震剖面的时变子波。沿图 4a中的四条白色虚线提取功率谱(图 7上),从而得到时间点0.52、0.80、1.00、1.30s处的广义地震子波(图 7下)。可以看出,地震子波从浅到深逐渐变化,对0.12s以上的中新世—更新世地层,广义地震子波的主瓣基本一致,旁瓣有差异;而对于0.12s以下的大型河流相基底,广义地震子波主频降低,子波长度有所增大。
|
图 7 四个时间点处的局部谱(上)及提取的时变子波(下) (a)0.52s; (b)0.80s; (c)1.00s; (d)1.30s |
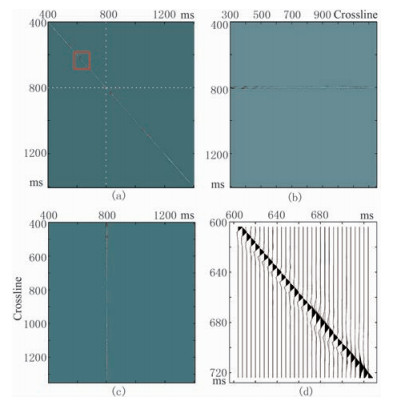
传统地震反演将常地震子波沿方阵主对角线方向设定获得的子波核矩阵,作为联系地震记录与反射系数序列的映射算子。用逐点提取的时变子波替换常子波,形成时变子波核矩阵(图 8),形成非平稳地震道反演的基本映射关系。从图 8a可见,通过对Inline244地震剖面的每一道提取时变广义地震子波,可以得到空变的子波核矩阵;图 8b和图 8c所示的子波核矩阵切片分别对应图 8a中水平和垂直白色虚线。从图 8可以清晰地观察广义地震子波沿时间和Crossline方向的变化特征,这也验证了基于基追踪谱分解进行子波估计的可行性。获得时变子波矩阵之后,对应每个时间点上,在下一个波长范围内构建楔形体奇、偶波形字典,即将传统的反射系数稀疏变成层稀疏,继而求解目标函数(式(16)),最终反演得到反射系数。
|
图 8 时变子波核矩阵 (a)Crossline400地震记录时变子波核矩阵; (b)沿Crossline方向水平时间0.80s处的时变子波核矩阵切片; (c)沿Crossline方向垂直时间0.80s处的时变子波核矩阵切片; (d)图a中红色实线矩形区域的细节展示 |
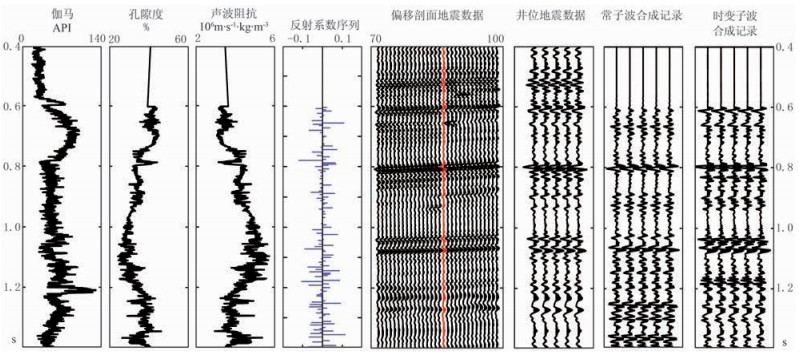
从图 9可见,采用常地震子波合成地震记录时,深层部分与原始地震记录不能很好地匹配,若采用时变地震子波,整道地震记录与原始地震记录匹配较好。采用常地震子波时,合成地震记录与原始地震记录的相关系数为0.31,而采用时变子波时,其相关系数为0.52。因此,采用时变地震子波能有效地改善井震标定效果,为后续地震反演提供保障。
|
图 9 测井数据及井震标定 |
为了比较基追踪谱分解时变地震子波与井震标定常地震子波的差别,用实际地震数据进行测试。反演采用相同的初始模型、收敛条件及最大迭代次数。对比图 10a与图 10b可以看出,采用时变子波可提高反演结果的分辨率,尤其对深部地层的构造细节(图中方框区域)展现得更清晰,连续性(图中椭圆形区域)得到明显增强。
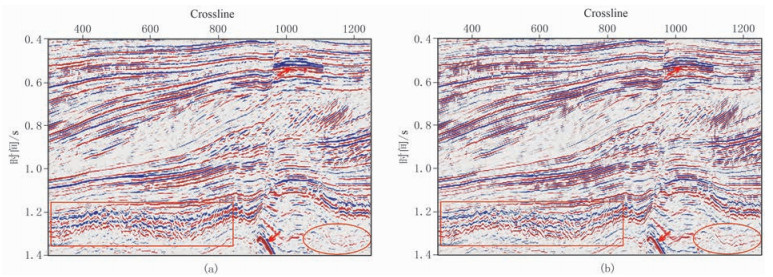
|
图 10 采用不同子波Inline244地震剖面反射系数反演剖面 (a)常子波; (b)时变子波 |
(1) 基于基追踪的谱分解法将时频分解问题融入反演框架,并结合L1范数稀疏约束,能同时获得较高的时间和频率分辨率,克服了传统时频分解方法中时间与频率高分辨率之间的矛盾。
(2) 广义地震子波被定义为高斯函数的分数阶导数,基于地震道谱分解的时间点谱可唯一地估计广义地震子波,它能更好地表征地震数据的局部属性和非平稳特征。基于时变广义地震子波构建的非平稳波形字典更精确和完备,为后续的基追踪地震反演提供了保障。
(3) 实际资料测试表明,采用本文提出的基追踪谱分解广义时变子波提取方法,能实现高效井震标定,基于时变子波的非平稳基追踪地震反演结果有更高的分辨率、更强的连续性和更清晰的地质细节展示。
| [1] |
Van der Baan M. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geophy-sics, 2008, 73(2): V11-V18. DOI:10.1190/1.2831936 |
| [2] |
Van der Baan M, Fomel S. Nonstationary phase estimation using regularized local kurtosis maximization[J]. Geophysics, 2009, 74(6): A75-A80. DOI:10.1190/1.3213533 |
| [3] |
Margrave G F, Lamoureux M P, Henley D C. Gabor deconvolution:Estimating reflectivity by nonstationa-ry deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [4] |
Dai Y S, Wang R R, Li C, et al. A time-varying wavelet extraction using local similarity[J]. Geophysics, 2016, 81(1): V55-V68. |
| [5] |
王蓉蓉, 戴永寿, 李闯, 等. 时频分析与自适应分段相结合的时变子波提取方法[J]. 石油地球物理勘探, 2016, 51(5): 850-862. WANG Rongrong, DAI Yongshou, LI Chuang, et al. Time-varying wavelet extraction based on time-frequency analysis and adaptive segmentation[J]. Oil Geophysical Prospecting, 2016, 51(5): 850-862. |
| [6] |
孔德辉, 彭真明. 利用改进的在线字典学习估计时变子波[J]. 石油地球物理勘探, 2016, 51(5): 901-908. KONG Dehui, PENG Zhenming. Time-varying wavelet estimation based on improved online dictionary learning[J]. Oil Geophysical Prospecting, 2016, 51(5): 901-908. |
| [7] |
Zhang R, Fomel S. Time-variant wavelet extraction with a local-attribute-based time-frequency decomposition for seismic inversion[J]. Interpretation, 2017, 5(1): SC9-SC16. DOI:10.1190/INT-2016-0060.1 |
| [8] |
Wang Y H. Generalized seismic wavelets[J]. Geo-physical Journal International, 2015, 203(2): 1172-1178. DOI:10.1093/gji/ggv346 |
| [9] |
Allen J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1977, 25(3): 235-238. DOI:10.1109/TASSP.1977.1162950 |
| [10] |
Chakraborty A, Okaya D. Frequency-time decomposition of seismic data using wavelet-based method[J]. Geophysics, 1995, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
| [11] |
Sinha S, Routh P S, Anno P D, et al. Spectral decomposition of seismic data with continuous-wavelet transform[J]. Geophysics, 2005, 70(7): P19-P25. |
| [12] |
Liu J, Marfurt K J. Instantaneous spectral attributes to detect channels[J]. Geophysics, 2007, 72(2): P23-P31. |
| [13] |
Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [14] |
Liu G, Fomel S, Chen X. Time-frequency analysis of seismic data using local attributes[J]. Geophysics, 2011, 76(6): P23-P24. DOI:10.1190/geo2010-0185.1 |
| [15] |
Liu Y, Fomel S. Seismic data analysis using local time-frequency decomposition[J]. Geophysical Prospecting, 2013, 61(3): 516-525. DOI:10.1111/gpr.2013.61.issue-3 |
| [16] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum:The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [17] |
Fomel S. Shaping regularization in geophysical-esti-mation problems[J]. Geophysics, 2005, 24(1): R29-R36. |
| [18] |
Cai Y H, Fomel S, Zeng H L. Automated spectral recomposition with application in stratigraphic interpretation[J]. Interpretation, 2013, 1(1): SA109-SA116. DOI:10.1190/INT-2013-0035.1 |
| [19] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society of London Series, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [20] |
Tary J B, Herrera R H, Han J, et al. Spectral estimation:What is new? What is next?[J]. Reviews of Geophysics, 2014, 52(4): 723-749. DOI:10.1002/2014RG000461 |
| [21] |
Daubechies I, Lu J, Wu H T. Synchrosqueezed wavelet transforms:An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. |
| [22] |
刘晗, 张建中, 黄忠来. 基于同步挤压S变换的地震信号时频分析[J]. 石油地球物理勘探, 2017, 52(4): 689-695. LIU Han, ZHANG Jianzhong, HUANG Zhonglai. Time-frequency analysis of seismic data using synchro-squeezing S transform[J]. Oil Geophysical Prospecting, 2017, 52(4): 689-695. |
| [23] |
Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. Siam Review, 2001, 43(1): 129-159. DOI:10.1137/S003614450037906X |
| [24] |
Bonar D C, Sacchi M D. Complex spectral decomposition via inversion strategies[J]. SEG Technical Program Expanded Abstracts, 2010, 29(1): 1408-1412. |
| [25] |
Vera Rodriguez I, Bonar D, Sacchi M D. Microseismic data denoising using a 3C group sparsity constrained time-frequency transform[J]. Geophysics, 2012, 77(2): V21-V29. DOI:10.1190/geo2011-0260.1 |
| [26] |
Figueiredo M, Nowak R D, Wright S J. Gradient projection for sparse reconstruction:Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 568-598. |
| [27] |
Van den B, Friedlander M P. Probing the Pareto frontier for basis pursuit solutions[J]. Siam Journal on Scientific Computing, 2008, 31(2): 890-912. |
| [28] |
Beck A, Teboulle M. A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Science, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [29] |
Rubinstein R, Bruckstein A M, Elad M. Dictionaries for sparse representation modeling[J]. Proceedings of the IEEE, 2010, 98(6): 1045-1057. DOI:10.1109/JPROC.2010.2040551 |
| [30] |
Graham RL, Knuth D E, Patashnik O. Concrete Mathe-matics:A Foundation for Computer Science[M]. Massachusetts: Addison-Wesley Professional, 1994.
|
| [31] |
Oldenburg D W, Scheuer T, Levy S. Recovery of the acoustic impedance from reflection seismograms[J]. Geophysics, 1983, 48(10): 1318-1337. DOI:10.1190/1.1441413 |
| [32] |
White R E, O'Brien P. Estimation of the primary seismic pulse[J]. Geophysical Prospecting, 1974, 22(4): 627-651. DOI:10.1111/gpr.1974.22.issue-4 |
| [33] |
Bednar J B. Applications of median filtering to deconvolution, pulse estimation, and statistical editing of seismic data[J]. Geophysics, 1983, 48(2): 1598-1610. |
| [34] |
Walden A, White R. Seismic wavelet estimation:A frequency domain solution to a geophysical noisy input-output problem[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 287-297. DOI:10.1109/36.655337 |
| [35] |
Sacchi M D, Ulrych T J. Nonminimum-phase wavelet estimation using higher order statistics[J]. The Lea-ding Edge, 2000, 19(1): 80-83. DOI:10.1190/1.1438466 |
| [36] |
Misra S, Chopra S. Mixed-phase wavelet estimation:A case study[J]. CSEG Recorder, 2011, 36(1): 33-35. |
| [37] |
Danielsen V, Karlsson T V. Extraction of signatures from seismic and well data[J]. First Break, 1984, 2(4): 15-21. |
| [38] |
Lines L R, Treitel S. Wavelets, well logs and Wiener filters[J]. First Break, 1985, 3(8): 9-14. |
| [39] |
Zhang R, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [40] |
Yuan S, Wang S. Spectral sparse Bayesian learning reflectivity inversion[J]. Geophysical Prospecting, 2013, 61(4): 735-746. DOI:10.1111/gpr.2013.61.issue-4 |
| [41] |
Zhang R, Sen M K, Srinivasan S. A prestack basis pursuit seismic inversion[J]. Geophysics, 2013, 78(1): R1-R11. |
| [42] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于基追踪弹性阻抗反演的深部储层流体识别方法[J]. 地球物理学报, 2016, 59(1): 277-286. LIU Xiaojing, YIN Xingyao, WU Guochen, et al. Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance[J]. Chinese Journal of Geophysics, 2016, 59(1): 277-286. |
| [43] |
张丰麒, 金之钧, 盛秀杰, 等. 基于低频软约束的叠前AVA稀疏层反演[J]. 石油地球物理勘探, 2017, 52(4): 770-782. ZHANG Fengqi, JIN Zhijun, SHENG Xiujie, et al. AVA sparse layer inversion with the soft-low frequency constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 770-782. |



 姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地学楼B512, 330013。Email:
姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地学楼B512, 330013。Email: