2. 甘肃省牦牛繁育工程重点实验室,兰州 730050;
3. 青海省海西州动物疫病预防控制中心,德令哈市 817099;
4. 青海省大通种牛场,西宁 810102
2. Key Laboratory of Yak Breeding Project in Gansu Province, Lanzhou 730050;
3. Animal disease prevention and control center of Haixi prefecture in Qinghai Province, Delingha 817099;
4. Datong Cattle Farm in Qinghai Province, Xining 810102
体尺和体重性状是牦牛(Bos grunniens)遗传育种的重要选育指标,体重更是决定牦牛产肉性能最为主要的指标,也是最直接的育种选择参数之一。由于牦牛的野性较强,生产过程中体重的称量存在很大难度,而体尺性状的测定相对简洁准确。另外,仅依靠体重指标进行育种选择不够全面和准确,所以还需要借助其他的形态性状进行间接选择,以便选留出具有优良遗传潜质且体形优美的牦牛个体。因此,利用多元统计和通径分析估计体尺性状对体重的影响,对提高牦牛育种效果具有重要指导意义。
近年来,通过分子标记的方法对动物的性状与基因型间相关性的研究得到了广范的报道。然而,动物的生产性状往往受成百上千个基因所调控,鉴于分子标记成本的限制,最多只能对十几个基因同时进行标记,这便产生了标记基因的数量与真实控制性状的基因的数量不对等的矛盾。如果控制动物性状的基因相对较少,或者能够在众多基因中确定控制性状的主效基因,这种分子标记的方法在动物选育过程中也能发挥很大的指导作用[1]。另外,全基因组关联分析也可应用于动物的选育工作,但限于该技术成本较高,在短期内还不适用于大范围的动物育种工作。
在生产实践中,传统的育种方式仍发挥着主导的作用,虽然对动物的系谱记录和性状的测定有较高的要求,但目前该方法却是最可行和最经济的方法,而分子标记选择主要作为动物育种的一种辅助手段。建立体尺与体重性状的多元线性回归方程,可通过动物体尺对体重进行较为准确的估计,通径分析还可将体尺对体重的影响(相关系数)分解为直接作用(直接通径系数)和间接作用(间接通径系数),两者对于动物的传统育种工作是不可或缺的。目前,多元线性回归和通径分析被广泛应用于动物形态性状的统计分析中,如罗非鱼[2]、舌鳎[3]、厚蟹[4]、大鲵[5]、鹌鹑[6]、猪[7]、驴[8]、山羊[9-11]和绵羊[12-14]等动物。然而,将通径分析应用于牛品种各性状的研究相对较少,更多的研究只集中在对牛性状的多元线性回归分析上[15-20]。对于牦牛多元统计的研究也主要集中于对其体重与体尺指标相关回归系数的分析上[21-23],未见对牦牛体重和体尺性状进行通径分析的报道。
无角牦牛是继“大通牦牛”后,经中国农业科学院兰州畜牧与兽药研究所几代人的辛苦努力,育种出的又一牦牛新品种(定于近期申报国家品种)。该牦牛主要分布于青海省大通县达板山地区,适应能力强、生产性能好、遗传参数稳定,因无角特征而便于饲养管理。本研究以无角牦牛为研究对象,利用相关分析、多元线性回归分析、通径分析,对其体重与体尺性状进行了相关性检验,建立了多元线性回归方程,解析出影响无角牦牛体重的主要体尺性状,旨在为无角牦牛选育工作提供理想的选择指标。
1 材料与方法 1.1 材料无角牦牛选自青海省大通县达板山。随机抽取247头健康8-10月龄无角牦牛个体进行实验研究,其中包含155头公牛和92头母牛,每个个体处于相同的放牧和饲养管理条件。用测杖和皮尺测量各牦牛的体长(X1)、体高(X2)、胸围(X3)和管围(X4)4个体尺指标,并称量其体重(Y)。
1.2 方法由于公牦牛和母牦牛在体型上存在一定的差异,分别对其各自的体尺和体重数据进行统计分析。体尺性状及体重数据借助Excel和SPSS软件进行整理和初步统计分析,获得各项表型参数值。对各性状分别进行表型相关分析和逐步回归分析,建立体尺对体重的多元回归方程;对体重进行正态分布检验,判定其是否适合用于通径分析;进行形态性状各指标对体重的通径分析和决定系数计算,剖析这些性状对体重的直接作用和间接影响。
2 结果 2.1 性状的数据整理对牦牛各体尺性状和体重性状的数据进行整理和简单的统计分析,所测公牦牛和母牦牛体尺和体重性状的数据资料经初步整理后得到表型描述性统计量(表 1)。
由表 1可知,无角牦牛公牛和母牛体尺和体重指标较为接近,两群体各性状变异系数由大到小的顺序均为体重>管围>体长>胸围>体高。公牛和母牛变异系数最大的都是体重,公牛为12.49,母牛为13.27。在体尺性状中,公牛和母牛变异系数最大的都为管围,分别是8.94和9.70。
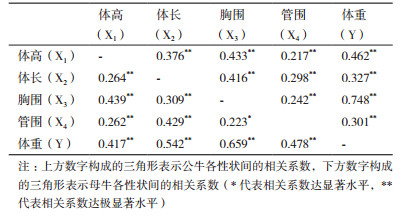
2.2 性状间的相关分析为研究各体尺和体重性状的相关关系,采用皮尔逊法对无角牦牛各性状进行相关分析,得出各性状间的相关系数(表 2)。
由表 2可知,体高、体长、胸围分别对体重的相关关系均达到极显著水平(P<0.01),各形态性状对公牛体重的相关系数大小依次为胸围>体高>体长>管围,母牛为胸围>体长>管围>体高。除母牛胸围和管围的相关系数表现为显著性水平(P<0.05)外,体重与所测定的各体尺指标间的相关系数均达到了极显著水平(P<0.01)。对于公牛,只有胸围与体重之间的相关属于强相关(相关系数>0.5),对于母牛,胸围和体长对体重有强相关作用。以上结果表明,公牦牛和母牦牛的体尺性状与其各自体重的相关性存在一定的差异,这种差异可能是由其不同的体型构造决定的。
2.3 数据检验及建立逐步回归方程选取体重为依变量,其他体尺性状参数为自变量进行逐步回归分析。回归方程可表示为Y=b0+b1X1+b2X2+b3X3+b4X4,其中b0、b1、b2、b3和b4为常数,Y为体重(kg),X1为体高(cm),X2为体长(cm),X3为胸围(cm),X4为管围(cm)。根据显著性检验,公牛的体高、胸围和管围3个体尺性状被保留,而体长性状被剔除,建立回归方程:Y=-86.969+0.338X1+1.082X3+0.905X4。母牛的体长、胸围和管围3个体尺性状被保留,体高性状被剔除,建立回归方程:Y=-85.693+0.440X2+0.860X3+1.972X4。
经多元回归关系的显著性检验和各个偏回归系数的显著性检验(表 3)表明,除公牛的管围指标外,所有的偏回归系数均达到极显著水平(P<0.01)。
为获得较为可靠的多元线性回归方程,用SPSS软件对各线性回归方程进行R2值检测,检测结果见表 4。对于公牛,模型的R2值为0.594,说明该模型是公牛较为理想的回归方程;对于母牛,模型的R2值为0.609,说明模型是母牛较为理想的回归方程。所得两个多元线性方程的R2值均大于0.4,表明方程可用于后续研究。经回归预测,估计值与实际观察值之间有较好的线性关系,说明该方程可以简便可靠的应用于生产实际中。
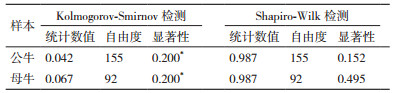
在进行通径分析前需对因变量体重进行正态分布检验,Kolmogorov-Smirnov检验适用于大样本检验,而Shapiro-Wilk检验适用于小样本检验。本实验的样本数公牛155,母牛为92,属于大样本,因此,对因变量体重进行正态性检验后采用Kolmogorov-Smirnov方法的检验结果。公牛和母牛的统计检验的显著性均为0.200,P>0.05(表 5),所以公牛和母牛的体重都符合态分布,即可以对体重进行通径分析。对公牛和母牛两群体的体重性状作正态分布图(图 1)。

|
| 图 1 体重性状的正态分布图 A和B分别代表公牛和母牛的正态检测结果,横坐标为回归标准化残差,纵坐标为体重频数 |
由表 3可以得出公牛自变量X1、X3、X4对Y的直接作用分别为P1Y=0.155、P3Y=0.654、P4Y=0.110,显著性检验结果表明,X4的偏回归系数的显著性小于0.05,X1、和X3的偏回归系数的显著性均小于0.01。母牛自变量X2、X3、X4对Y的直接作用分别为P2Y=0.277、P3Y=0.519、P4Y=0.243,显著性检验结果表明,X2、X3、X4的偏回归系数的显著性均小于0.01。以上结果说明无角牦牛自变量(体尺指标)与因变量(体重)之间的回归系数存在显著性差异,有统计学意义,因此保留在方程中,并且可进行通径分析。
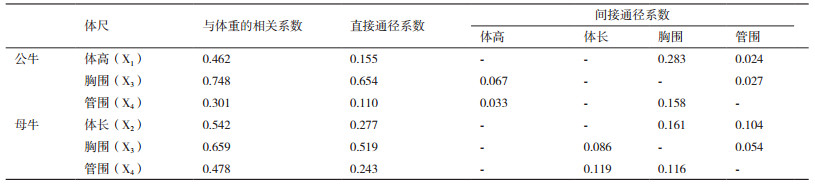
相关系数可以剖分为直接通径系数和间接通径系数,可用图 2来表示各性状间的通径关系。无角牦牛体尺与体重性状间的相关分析见表 2,对于公牛,自变量体高X1与胸围X3和管围X4之间的相关系数分别为r13=0.433、r14=0.217。自变量体高X1与因变量体重Y之间的直接通径系数P1Y为0.155(表 3中的β值),通过胸围X3的间接通径系数为r13×P3Y=0.433×0.654=0.283,通过管围X4的间接通径系数为r14×P4Y = 0.217×0.110=0.024,体高X1与体重Y之间的相关系数r1Y=P1Y+r13×P3Y+r14×P4Y = 0.155+0.433×0.654+0.217×0.110 = 0.462,结果与相关系数一致(表 2),同理可以计算出公牛胸围X3和管围X4对体重Y的间接通径系数,母牛相应的通径系数计算方法相同(表 6)。

|
| 图 2 体尺与体重性状的通径分析图 A和B分别为公牛和母牛的通径分析示意图 |
对无角牦牛通径系数的部分示意图见图 2。对于公牛,在所保留的3个体尺性状对体重的直接影响中,胸围对体重的直接作用最大,体高次之,管围最小;对于母牛,在所保留的3个自变量对体重的直接影响中,胸围对体重的直接作用大于体高和管围(表 6)。除胸围外,公牛各形态性状通过其他体尺性状的间接作用均大于其直接作用,说明这些体尺对对体重的作用是通过胸围的间接影响达到的。而对于母牛来说,胸围在其他体尺上的这种间接作用则不及其各自的直接作用。通过分析各个间接通径系数发现,无论公、母牛,只有胸围对体重的直接通径系数大于0.5,且胸围通过各体尺对体重的间接通径系数均较小,因此,胸围是影响体重的主要因素,对体重的增加具有重要作用。
3 讨论 3.1 多元回归方程的建立牦牛主要以放牧的形式进行采食,由于其活动范围比较广范,同时又具有一定的野性,致使不易对其进行聚集和捕捉,使称重工作变得异常困难。然而,无论是品种资源调查、选种选配,还是计算日粮、用药量都需要对牦牛的体重进行测定。牦牛的体尺测量相对容易,通过测量牦牛体尺性状来测算体重是比较方便可行的方法。多元回归分析对于弄清形态性状与体重之间的关系,确定合适的测量指标,提高选择育种准确性具有重要的现实意义。该方法被广泛用于各牛品种的数量性状间的相关分析[15-16, 24],并对育种实践中选择指标的确立具有重要的参考价值,但应用该方法对牦牛性状进行的育种选择却鲜有报道。
在所建立的多元回归方程中保留了主要体尺性状指标,其原因在于表型相关未排除其他变量的干扰,体尺指标间存在不同程度的共线性问题。为确定和量化形态指标与体重的真实关系,本实验借助多元逐步回归的方法排除了形态性状间的共线性问题和回归方程中检验不显著的自变量,在公牛的回归方程中排除了体长变量,在母牛的回归方程中排除了体高变量,建立了回归方程,量化了体长、体高、胸围和管围的相关关系。判断回归模型好坏的标准是多方面的,根据回归模型来计算拟合值与实测值之间的决定系数(R2),R2值越大模型的相关程度越高、拟合效果也就越好,从而作为回归模型选择的标准。本研究获得了较大的回归方程R2值,暗示利用逐步回归法所筛选的体尺测定值来建立体重估测模型是可行的。
无角牦牛胸围在线性方程中对体重的影响为正线性关系,且胸围的回归系数大于其他体尺的回归系数,这与前人的研究结果相似[15, 25-26]。造成这种现象的原因可能是胸围的增加能反应出动物的膘情,膘情对体重必然产生直接的影响。将本研究的结果与前人对牦牛体尺与体重性状的相关研究进行对比,发现本研究中的线性回归方程与成年牦牛相比存在较大差异[22, 27],而与牦牛犊牛的线性方程相比具有较为接近的回归系数[23, 28],这说明成年牦牛和牦牛牛犊的体尺性状对体重的影响存在一定的差异,不难理解,这是由于成年牦牛和牦牛牛犊具有不同的体型特征所造成的。公牛和母牛具有不同的线性回归方程,反映出公牛和母牛在体型结构上存在明显的差异,这与生产实践中观察到的结果相符。另外,本研究还将管围性状指标纳入到多元线性方程中,这在之前的研究中是没有报道的。牦牛的管围指标能在一定程度上影响体重,是因为管围的大小能反应出牦牛骨骼的生长状况,管围较粗的个体其骨骼的总量可能较大,这也必然使其体重有所增加。
3.2 通径系数的剖分牦牛是一个复杂的有机整体,其各指标之间存在千丝万缕的关系,仅从数据表面难以得到其本质关系。相关系数虽然可以表示自变量和因变量之间的关系紧密度,但是借助于相关系数不能完全体现自变量与因变量之间的关系,从而使结果产生片面性。通径系数是变量标准化的偏回归系数,既可以反映出自变量与因变量的直接关系,又能体现出通过其他自变量作用于因变量影响的间接关系[7]。有时自变量与因变量的相关系数很大,但对因变量的直接影响并不一定也很大,因为相关系数包含了两者的直接关系和通过其他自变量的间接关系,是自变量间相互关系的综合表现,而只有直接作用才能反映出自变量与因变量间的本质关系。
本研究通过对无角牦牛的通径分析将表型相关分为直接相关(通径系数)和间接相关(间接通径系数)两部分,反向验证了回归方程的量化关系。在本研究中,公牛和母牛的胸围对体重的直接通径系数都是最大的,影响的相对程度分别为0.654和0.519,说明胸围对无角牦牛体重具有根本性作用。公牛的体长和管围与体重的相关系数分别为0.462和0.301,但是,胸围的间接作用带来的影响就分别达到0.283和0.153,说明体长和管围主要通过胸围间接影响公牛的体重。对于母牛,胸围的这两个性状则没有这么强的间接作用。
3.3 本研究对无角牦牛选择育种的意义体尺和体重指标是牦牛生产能力表现的重要指征,体重更是其产肉能力最直接的相关因素,如何有效的选择具有体重优势的优良个体是无角牦牛选育的关键。然而,体重的变异系数在本实验所测定的性状中是最大的(公牛12.485%,母牛13.270%),而体高、体长、胸围、管围指标的变异系数相对较小(<10%)。因此,选育中如果直接根据体重进行选择,往往会因为其他因素的影响而产生较大的选择误差,从而影响选育的效率。量化和筛选变异系数较小且与体重具有重要直接关系的形态性状,借助这些形态指标进行间接选择可有效降低其他因素的影响,提高体重选育的准确性。本研究中公牛和母牛胸围对体重的直接作用均大于其他各体尺指标,同时,公牛和母牛胸围的变异系统都是倒数第二小,仅大于体高。因此,当以牦牛的体重为主要选择指标进行育种工作时,胸围可做为重要的体尺选择性状。在以提高牦牛生产性能为主的选育过程中,以体重为目标的同时注重胸围指标,兼顾体高和体长这两个指标,也要注意管围性状带来的限制性作用。
同时,我们应该注意在育种实践中如果只以体重作为主要选择指标,难免有失偏颇。例如,体重往往和脂肪沉积有很大的相关性,而乳房易沉积大量脂肪会使乳腺不发达,导致泌乳量减少,这必然不能达到选择优良品种的目的。因此,在牦牛的育种过程中,虽然可以将体重指标纳入重要的选择参数,但不能单方面的只顾及体重指标的选择,应兼顾体尺性状和其他重要经济状态,以达到可加快牦牛选种速度的目的。
4 结论影响无角公牦牛体重的主要体尺性状有体高、胸围和管围,而影响无角母牦牛体重的主要体尺性状为体长、胸围和管围;管围可做为选育牦牛体尺性状的选择指标;相比其他体尺性状,胸围对牦牛体重的直接影响最大,在以体重为主要选育性状的牦牛选择育种过程中,可将胸围作为最主要的体尺性状进行选择。
| [1] |
陈昌嫱, 覃道攀, 张志罡. 分子标记育种在我国的研究进展[J]. 生物技术通报, 2008(S1): 22-24. |
| [2] |
Conti ACM, Oliveira CA L de, Martins EN, et al. Genetic parameters for weight gain and body measurements for Nile tilapias by random regression modeling[J]. Semina-Ciencias Agrarias, 2014, 35(5): 2843-2858. DOI:10.5433/1679-0359.2014v35n5p2843 |
| [3] |
李玉全. 线性回归法实现半滑舌鳎幼鱼表型性状与体重的通径分析[J]. 生物数学学报, 2014(1): 185-191. |
| [4] |
平洪领, 李玉全. 逐步线性回归法实现天津厚蟹(Helice tientsinensis)表型性状与体重的通径分析[J]. 海洋与湖沼, 2013(5): 1353-1357. |
| [5] |
王启军, 赵虎, 张红星, 等. 人工养殖大鲵全长与体重关系的回归分析[J]. 基因组学与应用生物学, 2012(4): 381-384. |
| [6] |
庞有志, 赵淑娟, 员银现, 等. 蛋用黄羽鹌鹑体重与体尺相关及回归分析[J]. 中国畜禽种业, 2009(9): 137-139. |
| [7] |
Machebe NS, Ezekwe AG, Okeke GC, et al. Path analysis of body weight in grower and finisher pigs[J]. Indian Journal of Animal Research, 2016, 50(5): 794-798. |
| [8] |
肖海霞, 托乎提·阿及德, 石国庆, 等. 疆岳驴体重和体尺性状的相关和回归分析[J]. 中国奶牛, 2012(23): 27-31. DOI:10.3969/j.issn.1004-4264.2012.23.011 |
| [9] |
俄木曲者, 范景胜, 陈天宝, 等. 简阳大耳羊黑色类群成年母羊体重与体尺指数回归分析[J]. 中国草食动物科学, 2012(5): 13-16. |
| [10] |
陈永军, 赵中权, 张家骅, 等. 成年大足黑山羊体重与体尺通径分析及最优回归模型的建立[J]. 草食家畜, 2008(3): 71-74. |
| [11] |
徐铁山, 王东劲, 刘小林, 等. 海南黑山羊体尺与体重的通径分析及最优回归模型的建立[J]. 家畜生态学报, 2005(1): 49-53. |
| [12] |
高志英, 乌云毕力克, 艾尔肯江, 等. 德国美利奴成年母羊体尺与体重相关回归分析[J]. 草食家畜, 2012(4): 31-33, 36. |
| [13] |
韩卫杰, 陈玉林, 冯涛, 等. 道寒F1羔羊体尺与体重的通径分析及回归模型[J]. 湖北农业科学, 2006(3): 357-359. |
| [14] |
白俊艳, 庞有志, 王永伟. 大尾寒羊体重与体尺的回归分析[J]. 安徽农业科学, 2007(15): 4537-4538. DOI:10.3969/j.issn.0517-6611.2007.15.071 |
| [15] |
曹丹. 辽育白牛体重与体尺指标的相关与回归分析[J]. 黑龙江畜牧兽医, 2016(13): 109-110. |
| [16] |
王志军, 董万福, 张喜才, 等. 夏洛来公牛体尺同体重相关与回归探讨[J]. 吉林畜牧兽医, 2013(9): 39+42. |
| [17] |
周振勇, 张杨, 蔺宏凯, 等. 基于主成分逐步回归法的新疆褐牛体重预测模型研究[J]. 中国牛业科学, 2012(1): 1-4. |
| [18] |
Baldi F, Albuquerque LG, Alencar MM. Random regression models on Legendre polynomials to estimate genetic parameters for weights from birth to adult age in Canchim cattle*[J]. Journal of Animal Breeding and Genetics, 2010, 127(4): 289-299. DOI:10.1111/jbg.2010.127.issue-4 |
| [19] |
Selapa NW, Nephawe KA, Maiwashe A, et al. Genetic analysis of body weights of individually fed beef bulls in South Africa using random regression models[J]. Genetics and Molecular Research, 2012, 11(1): 271-276. DOI:10.4238/2012.February.8.2 |
| [20] |
Speidel SE, Peel RK, Crews DH, et al. Random regression models for the prediction of days to weight, ultrasound rib eye area, and ultrasound back fat depth in beef cattle[J]. Journal of Animal Science, 2016, 94(2): 471-482. DOI:10.2527/jas.2015-9581 |
| [21] |
王伟. 6月龄大通牦牛母牛体重与体尺指标的相关回归分析[J]. 黑龙江动物繁殖, 2012(6): 39-41. |
| [22] |
刘更寿. 2. 5岁大通牦牛母牛体重与体尺指标的相关回归分析[J]. 黑龙江动物繁殖, 2016(5): 57-59. |
| [23] |
罗海青, 赵寿保. 大通牦牛体重与体尺指标的相关回归分析[J]. 黑龙江动物繁殖, 2016(1): 11-12. |
| [24] |
王志军, 董万福, 付延军, 等. 西门塔尔公牛体尺与体重相关与回归探讨[J]. 吉林畜牧兽医, 2013(6): 36+45. |
| [25] |
张守词, 刘翠侠, 田红军. 阜阳市改良F_1黄牛体尺体重回归分析[J]. 黑龙江动物繁殖, 2001(2): 9-10. |
| [26] |
马存寿. 杂种荷斯坦成年母牛体重与体尺指标的相关回归分析[J]. 青海畜牧兽医杂志, 2012(1): 28-29. |
| [27] |
穷达, 彭措巴姆. 西藏嘉黎成年母牦牛体重与体尺指标的相关与回归分析[J]. 畜牧与饲料科学, 2011(6): 11-12. |
| [28] |
赵寿保, 夏宗军. 13月龄母牦牛体重与体尺指标的相关回归分析[J]. 湖北畜牧兽医, 2013(7): 8-9. |