b. Research Center of Quantitative Ecology, Nanjing Forestry University, Nanjing 210037, China;
c. University of Chinese Academy of Sciences, Beijing, 100049, China;
d. Guangzhou Climate and Agro-meteorology Center, Guangzhou 511430, China;
e. Guangdong Ecological Meteorological Center, Guangzhou 510640, China
Ecology, the study of relationships between organisms and their environments, often requires analyzing complex datasets that capture linear or nonlinear variability in ecological processes. Classical linear regressions may not always effectively capture the nonlinear relationships characteristic of ecological systems. Generalized Additive Models (GAMs) provide a flexible framework capable of modeling these nonlinearities, enabling ecologists to gain deeper insights into ecological patterns and processes (Zuur et al., 2009; Wood, 2017). Consequently, GAMs are extensively used in environmental and ecological research (Sun et al., 2018; Liu et al., 2019; Pedersen et al., 2019; Gao et al., 2023; Singh et al., 2024).
As extension of the Generalized Linear Models (GLMs) framework, GAMs can be expressed as:
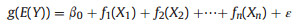
|
(1) |
where, E(Y) represents the expected value of the response variable Y, modeled with an appropriate distribution and link function g. β0 is the intercept, while ε denotes an error term. fi(Xi) represents the smooth function that characterizes the relationship between the transformed mean response Y and the predictor variables Xi. These smooth functions, typically employing splines (De Boor, 1978), can be chosen to be either parametric or nonparametric and thus allow the capture of a broad spectrum of relationships (Ramsay et al., 2003), establishing GAMs as an effective tool for exploring and interpreting complex data patterns (Wood et al., 2016). In GAMs, parameter estimation typically utilizes penalized maximum likelihood estimation techniques (Wood and Augustin, 2002; Wood, 2017) (see Appendix I in Supplementary file for details). After parameter estimation, GAMs enable the prediction or inference of the response variable based on predictor values.
In regression analysis with multiple predictors, researchers strive to understand the relative importance of each predictor on the response variable (Healy, 1990). This understanding often depends on quantifying the contribution of each predictor to the model's goodness-of-fit, typically measured by R2 (Johnson and LeBreton, 2004). In GAMs featuring multiple predictors, researchers are interested in determining the relative importance of these predictors to response variables (e.g., Damalas et al., 2007; Feng et al., 2019; Liu et al., 2019; Ma et al., 2020). Despite the effectiveness of GAMs in modeling nonlinear relationships between the response variable and predictors, the predictors' relative importance can be obscured by concurvity, which is analogous to collinearity in GLMs (Zuur et al., 2010; Ramsay et al., 2003). Collinearity, which occurs when two or more predictors are highly correlated, can obscure the individual influence of each predictor, complicating the determination of their relative importance in models (Graham, 2003; Dormann et al., 2013; Ray-Mukherjee et al., 2014; Cammarota and Pinto, 2020). This is because collinear predictors share overlapping variance (i.e., shared R2) with regard to the response, obscuring their individual contributions (Peres-Neto et al., 2006; Murray and Conner, 2009). In ecological studies, where predictor correlation is frequent, allocating shared R2 to specific predictors poses a complex challenge (Graham, 2003; Murray and Conner, 2009).
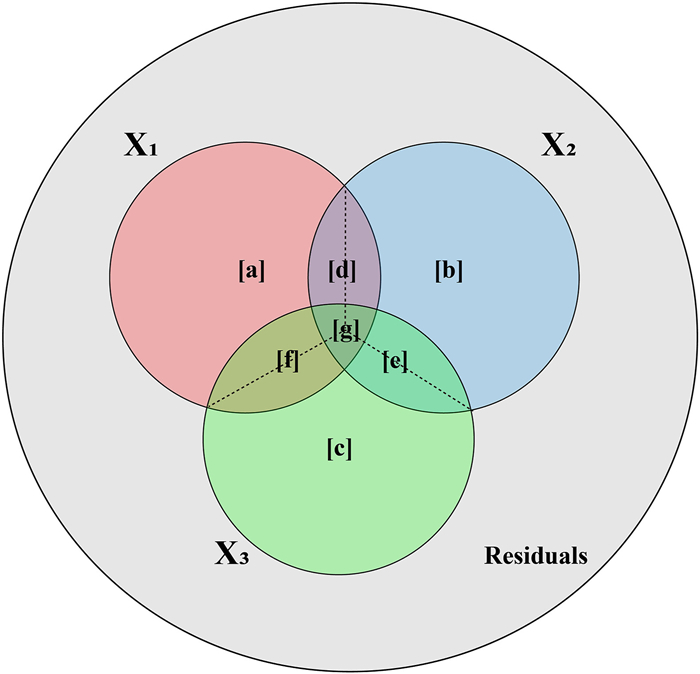
Lai et al. (2022a) introduced the 'average shared variance' concept for assessing the relative importance of predictors in multiple regression and canonical analyses. This method proposes dividing the shared R2 among related predictors evenly, allowing for a straightforward estimation of each predictor's relative importance. This is achieved by calculating the individual R2 for each predictor, represented by the sum of its own unique R2 and the allocated shared R2 values (see Fig. 1). Remarkably, the outcomes from this approach are consistent with previously established methodologies, such as 'averaging over orderings' (Lindeman et al., 1980; Kruskal and Majors, 1989), 'hierarchical partitioning' (Chevan and Sutherland, 1991), and 'dominance analysis' (Budescu, 1993), despite these methods being independently introduced across different disciplines and involving distinct computational processes. Lai et al. (2022a) initially established a mathematical link between the method and 'commonality analysis', a variance-partitioning technique widely utilized in multiple regression (Ray-Mukherjee et al., 2014). Consequently, the new concept of 'average shared variance' enables researchers to understand the fundamental principles of this technique quickly and intuitively (Lai et al., 2022a, Lai et al., 2022b) (see Fig. 1).
|
| Fig. 1 The Venn diagram illustrates the distribution of variation components within a Generalized Additive Model. The large circle represents the total variation, while three smaller, intersecting circles represent the explained variation attributed to three predictors with concurvity (analogous to collinearity). Dashed lines within these intersections indicate fractions are evenly allocated into the contributing predictors. |
This 'average shared variance' concept has led to the creation of two R packages: rdacca.hp package for canonical analysis (Lai et al., 2022a) and glmm.hp package for generalized linear mixed models (Lai et al., 2022b, 2023b). These tools have been extensively utilized in ecological research and related fields, with rdacca.hp garnering more than 400 citations and glmm.hp accumulating over 100 citations to date, according to the Web of Science (http://www.webofknowledge.com). This highlights the acknowledged effectiveness of the methodology and its significant contributions to enhancing data analysis capabilities.
In this study, we extended the 'average shared variance' methodology to the GAMs framework and introduced gam.hp, an R package designed for its implementation. Our research focuses on the implementation of GAMs using the mgcv R package (Wood, 2011). The mgcv package is distinguished for its comprehensive range of GAM structures and model-fitting methodologies, making it popular in the analysis of ecological data (Lai et al., 2019) and conservation biology (Lai et al., 2023a). The mgcv package provides two metrics for evaluating the goodness-of-fit of GAMs: adjusted R2 and explained deviance. To understand these two metrics, one can refer to the help document of summary.gam() in the mgcv package. As suggested in the help document, adjusted R2 may be more suitable for normal errors, whereas explained deviance may be more appropriate for non-normal errors (Wood, 2017). Currently, gam.hp is designed to decompose the adjusted R2 and explained deviance provided by mgcv package. This gam.hp provides a significant advantage by decomposing the overall adjusted R2 and explained deviance into individual contributions from each predictor, allowing for the evaluation of their relative importance.
Here we demonstrate how the gam.hp package can be used by analyzing air quality data from London (UK) obtained from the openair package (Carslaw and Ropkins, 2012). Specifically, we used the gam.hp package to assess the relative importance of emission sources and meteorological factors in explaining ozone concentration variability.
2. MethodsThe concept of 'average shared variance', as introduced by Lai et al. (2022a), suggests that the shared R2 can be equitably allocated among the contributing predictors. To illustrate, consider a scenario in a GAM involving three predictors with concurvity, labeled X1, X2, and X3 (Fig. 1). The fractions [a], [b], and [c] represent the unique R2 of X1, X2, and X3, respectively. The fractions [d], [e], and [f] indicate the shared R2 jointly attributed to pairs of these predictors, and [g] represents the shared R2 for all three predictors collectively. The calculation of individual R2 for each predictor involves summing its average allocated shared R2 with its unique R2, as shown in the following equations:
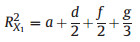
|
(2) |
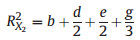
|
(3) |
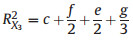
|
(4) |
Here 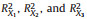
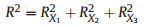
|
(5) |
This method offers a significant advantage by decomposing the overall R2 into individual contributions from each predictor (Lai et al., 2022b). This decomposition is achieved through commonality analysis, which calculates the fractions from [a] to [g] based on all possible subset models (Ray-Mukherjee et al., 2014). In GAMs, the importance of each predictor to the response variable is assessed based on its individual R2. However, as the number of predictors (N) increases, the count of fractions representing both unique and shared R2 expands following an exponential pattern of 2N-1 segments. Consequently, this exponential increase leads to a rapid surge in computational volume, as highlighted by Lai et al. (2022a).
3. Package descriptionDeveloped in the R programming language (R Development Core Team, 2023), the gam.hp package is accessible on the Comprehensive R Archive Network (CRAN) at http://cran.r-project.org/web/packages/gam.hp/ or GitHub at https://github.com/laijiangshan/gam.hp. The package comprises one primary function: gam.hp() for computing the individual R2 of each predictor within GAMs. Additionally, the package provides an S3 method for graphing, plot.gamhp(), which enables the visualization of individual R2 using bar charts, based on the ggplot2 package (Wickham, 2016). The gam.hp package depends on mgcv package (Wood, 2011) to calculate adjusted R2 and explained deviance of GAMs.
The gam.hp() requires three input arguments: mod, type, and commonality. mod refers to a GAM model object fitted using gam() from mgcv package. type allows users to select between 'adjR2' for adjusted R2 and 'dev' for explained deviance, depending on their analysis needs. commonality, when set to TRUE, shows the outcome of the commonality analysis, listing all shared and unique contributions of predictors through 2N-1 fractions for N predictors, with its default setting as FALSE.
plot.gamhp() takes two arguments: x and plot.perc. x refers to an object generated by gam.hp(). plot.perc is a logical variable that determines the type of visualization: when set to TRUE, it generates a bar chart showing the proportional contribution of each individual R2 to the total R2, whereas the default setting (FALSE) produces a chart displaying the original individual R2 values.
4. A working exampleGiven the widespread use of GAMs in atmospheric science (Ravindra et al., 2019), we illustrate the utility of gam.hp package using air quality data from the openair package (Carslaw and Ropkins, 2012). The dataset, named 'mydata', comprises hourly records of nine continuous air quality and meteorological variables collected from London (UK) from January 1, 1998, to June 23, 2005. Various studies have indicated that the concentration of ozone is primarily influenced by emission sources and meteorological factors (Wang et al., 2009; Li et al., 2023; Liu et al., 2023). However, analyses determining the relative importance of these emission sources and meteorological factors on ozone variations, through the use of GAMs, lack a clear and effective approach. To address this issue in GAMs, several studies have assessed the relative importance of individual predictors by measuring the reduction in R2 (termed unique or part R2) following the exclusion of a predictor from the model (e.g., Liu et al., 2019), or by the incremental increase of R2 (referred to as sequential or conditional R2) as predictors are sequentially added to the model (e.g., Damalas et al., 2007; Feng et al., 2019; Ma et al., 2020; Li et al., 2023). When predictors are correlated, both methods may not accurately represent the contribution of shared R2. The unique R2 method entirely overlooks the contribution of the shared R2, whereas the sequential R2 approach depends on the order in which predictors are added to the model, unfairly allocating the entire shared R2 to earlier input predictors. Our analysis aims to enhance the understanding and interpretation of the relative importance of predictors in GAMs, facilitated by individual R2 from gam.hp package.
In this case we select four variables—O3 (ozone concentration), WS (wind speed), NOx (nitrogen oxides), and CO (carbon monoxide)—to construct a GAM with O3 as the response variable and others as predictors. WS is considered a proxy for meteorological influences on O3 concentration, while NOx and CO are regarded as emission factors. The GAM is fitted using gam() function with splines smooth in mgcv package (in Appendix II in Supplementary file). Concurvity among predictors was assessed using the concurvity() in mgcv package. Concurvity measures the degree to which one smooth term can be approximated by a combination of other smooth terms in the model (Wood, 2017). If the level of concurvity exceeds 0.5, steps should be taken to eliminate or reduce this issue (Ramsay et al., 2003). In this case, the three indices of NOx and CO provided by concurvity() are all over 0.6, indicating severe concurvity (See Appendix II in Supplementary file).
The output from the summary.gam() function in the mgcv package indicates non-linear relationships between O3 and the predictors, as evidenced by the estimated degrees of freedom (edf) for the smoothed variables (an edf greater than 1 indicates a non-linear relationship) (Zuur et al., 2009; Wood, 2017) (See Appendix II in Supplementary file). The adjusted R2 and explained deviance values for this model were 0.5052 and 0.5054, respectively.
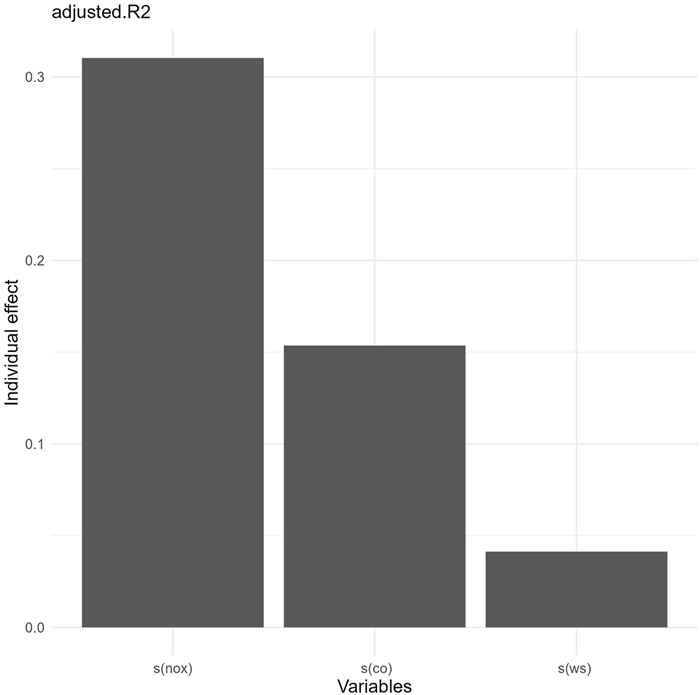
We utilized the gam.hp() function to decompose adjusted R2 for GAMs, assuming a default Gaussian distribution, noting that the difference between adjusted R2 and explained deviance is negligible in this instance (refer to Appendix II in Supplementary file). The core output from gam.hp() is a matrix containing the unique, average shared, and individual R2 for each predictor (see Table 1 and Appendix II in Supplementary file). In this case, the individual R2 value for NOx, CO, and WS, were 0.310, 0.154, and 0.041, respectively, cumulatively accounting for the total adjusted R2 (0.505). The individual R2 is the sum of both the unique R2 and the averaged shared R2 allocated to each predictor.
| Predictor variables | Concurvitya | Sequential R2 | Unique R2 | Average.shared R2 | Individual R2 | I.perc (%) |
| NOx | 0.742 | 0.462 | 0.152 | 0.158 | 0.310 | 61.4 |
| CO | 0.673 | 0.003 | 0.003 | 0.150 | 0.154 | 30.4 |
| WS | 0.046 | 0.040 | 0.038 | 0.003 | 0.041 | 8.2 |
| Total | – | 0.505 | 0.193 | 0.311 | 0.505 | 100.0 |
| a Concurvity refers to "observed" value provided by concurvity() in mgcv package. | ||||||
If we focus solely on the unique R2 (e.g., Liu et al., 2019), the order of their relative importance influencing ozone concentration is NOx (0.152), WS (0.038), and CO (0.003), totaling 0.193. This accounts for just 38.4% of the total adjusted R2 (0.505), potentially offering limited insights. If we adopt sequential R2 (e.g., Damalas et al., 2007; Feng et al., 2019; Ma et al., 2020; Li et al., 2023), the ranking of their relative importance remains NOx (0.462), WS (0.040), and CO (0.003) (See Table 1 and Appendix II in Supplementary file). While the sum of all sequential R2s equals to the overall R2, the sequential R2 of NOx is notably high. This is primarily due to its initial inclusion in the model according to the sequential R2 rule, allowing it to absorb all its shared R2 with CO. This allocation seems particularly unfair to CO.
Upon analyzing the individual R2 (Table 1), the order shifts to NOx (0.310), CO (0.154), and WS (0.041) (Fig. 2). This change in rank is due to CO's significantly larger average allocated shared R2 (0.150) compared to WS (0.003), reflecting higher observed concurvity for NOx (0.742) and CO (0.673), but a lower observed concurvity for WS (0.046). The gam.hp() function, by providing both unique R2 and average shared R2, which together constitute the individual R2, facilitates a comprehensive quantitative analysis of each predictor's contribution to adjusted R2 (or explained deviance) of GAMs. In this illustrative case, the findings recommend prioritizing the control of NOx emissions during ozone pollution episodes in London, followed by efforts to reduce CO emissions and enhance the accuracy of wind speed (WS) forecasts. This methodology supports the formulation of more refined and effective strategies for ozone pollution control by government bodies, considering various influencing factors.
|
| Fig. 2 The relative importance of individual smoothed variables in explaining ozone concentration variability by gam.hp. |
Generalized Additive Models (GAMs) are non-parametric regression models designed to fit nonlinear relationships between a response variable and one or multiple predictors without restrictive assumptions (Zuur et al., 2009; Wood, 2017). This flexibility facilitates a deeper understanding of natural phenomena and environmental processes (Zuur et al., 2009), making GAMs a popular tool in environmental and ecological studies (Beale et al., 2010; Bininda-Emonds and Purvis, 2012; Sun et al., 2018).
In both GLMs and GAMs, collinearity (or concurvity) significantly influences the evaluation of each predictor's relative importance (Zuur et al., 2010). This interdependence among predictors complicates the model's ability to distinguish the individual contribution of variables to the response. The shared variance between correlated predictors can obscure their individual contribution. The 'average shared variance' concept, introduced by Lai et al. (2022a), presents a straightforward and acceptable approach to addressing issues related to the relative importance of collinear predictor variables.
We extend the 'average shared variance' concept to GAMs, resulting in the development of the gam.hp package. The tool decomposes the overall R2 into individual contributions of each predictor in GAMs, which automatically sum to the overall R2. Based on the examples presented in this paper, individual R2 values may offer a more intuitive and user-friendly alternatives to evaluate relative importance than do traditional methods such as unique and sequential R2. However, it is crucial to recognize that GAMs are extremely complex models, and the gam.hp package merely presents a new solution to the issue of concurvity in GAMs.
We encourage researchers to incorporate the gam.hp package into their studies, emphasizing the importance of domain-specific expertise for a comprehensive interpretation of results. Utilize this package if its outcome meets your analytical expectations; otherwise, its usage is not mandatory. It is essential to understand that collinearity remains a fundamental challenge in both linear and nonlinear models. Ecologists should be aware that no perfect solution exists for collinearity (Gilbert et al., 2024). The concept of 'average shared variance' serves as an acceptable solution to mitigate collinearity's impact rather than resolving it entirely.
The parameter fitting process in GAMs are inherently iterative, which demands substantial computational time. The gam.hp() function performs fitting for all possible subset models within a commonality analysis framework, also requiring considerable computational effort. Furthermore, while there may be other packages capable of fitting GAMs, currently gam.hp focuses exclusively on the mgcv package. Moving forward, we are dedicated to continuously enhancing the gam.hp package's functionalities and improving its computational efficiency to better address the evolving needs of users.
AcknowledgmentsThis research was supported by the National Natural Science Foundation of China (32271551), National Key Research and Development Program of China (2023YFF0805803) and the Metasequoia funding of Nanjing Forestry University.
Data availability statement
The gam.hp package is available for installation from the Comprehensive R Archive Network (CRAN) at http://cran.r-project.org/web/packages/gam.hp/ or GitHub at https://github.com/laijiangshan/gam.hp.
The data "mydata" in our example is in the package openair, which is available on CRAN: https://cran.r-project.org/web/packages/openair/index.html. The R code in this paper is available on Supplementary data.
CRediT authorship contribution statement
Jiangshan Lai: Writing original draft, Data curation, Conceptualization. Jing Tang: Writing original draft, Formal analysis, Data curation. Tingyuan Li: Formal analysis, Data curation. Aiying Zhang: Writing original draft, Data curation. Lingfeng Mao: Writing review & editing, Investigation.
Declaration of competing interest
The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.pld.2024.06.002.
Beale, C.M., Lennon, J.J., Yearsley, J.M., et al., 2010. Regression analysis of spatial data. Ecol. Lett., 13: 246-264. DOI:10.1111/j.1461-0248.2009.01422.x |
Bininda-Emonds, O.R.P., Purvis, A., 2012. Comment on "impacts of the cretaceous terrestrial revolution and KPg extinction on mammal diversification". Science, 337: 34. DOI:10.1126/science.1220012 |
Budescu, D.V., 1993. Dominance analysis: a new approach to the problem of relative importance of predictors in multiple-regression. Psychol. Bull., 114: 542-551. DOI:10.1037/0033-2909.114.3.542 |
Cammarota, C., Pinto, A., 2020. Variable selection and importance in presence of high collinearity: an application to the prediction of lean body mass from multi-frequency bioelectrical impedance. J. Appl. Stat., 48: 1644-1658. |
Carslaw, D.C., Ropkins, K., 2012. Openair – an R package for air quality data analysis. Environ. Modell. Softw., 27: 52-61. |
Chevan, A., Sutherland, M., 1991. Hierarchical partitioning. Am. Stat., 45: 90-96. DOI:10.1080/00031305.1991.10475776 |
Damalas, D., Megalofonou, P., Apostolopoulou, M., 2007. Environmental, spatial, temporal and operational effects on swordfish (Xiphias gladius) catch rates of eastern Mediterranean Sea longline fisheries. Fish. Res., 84: 233-246. DOI:10.1016/j.fishres.2006.11.001 |
De Boor, C., 1978. A Practical Guide to Splines. Switzerland: Springer.
|
Dormann, C.F., Elith, J., Bacher, S., et al., 2013. Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography, 36: 27-46. DOI:10.1111/j.1600-0587.2012.07348.x |
Feng, Y.J., Cui, L., Chen, X.J., et al., 2019. Impacts of changing spatial scales on CPUE-factor relationships of Ommastrephes bartramii in the northwest Pacific. Fish. Oceanogr., 28: 143-158. DOI:10.1111/fog.12398 |
Gao, Z., Ivey, C.E., Blanchard, C.L., et al., 2023. Emissions and meteorological impacts on PM2.5 species concentrations in Southern California using generalized additive modeling. Sci. Total Environ., 891: 164464. DOI:10.1016/j.scitotenv.2023.164464 |
Gilbert, N.A., Amaral, B.R., Smith, O.M., et al., 2024. A century of statistical ecology. Ecology, 105: e4283. DOI:10.1002/ecy.4283 |
Graham, M.H., 2003. Confronting multicollinearity in ecological multiple regression. Ecology, 84: 2809-2815. DOI:10.1890/02-3114 |
Healy, M.J.R., 1990. Measuring importance. Stat. Med., 9: 633-637. DOI:10.1002/sim.4780090609 |
Johnson, J.W., LeBreton, J.M., 2004. History and use of relative importance indices in organizational research. Organ. Res. Methods, 7: 238-257. DOI:10.1177/1094428104266510 |
Kruskal, W., Majors, R., 1989. Concepts of relative importance in recent scientific literature. Am. Stat., 43: 2-6. DOI:10.1080/00031305.1989.10475596 |
Lai, J.S., Lortie, C.J., Muenchen, R.A., et al., 2019. Evaluating the popularity of R in ecology. Ecosphere, 10: e02567. DOI:10.1002/ecs2.2567 |
Lai, J.S., Zou, Y., Zhang, J.L., et al., 2022a. Generalizing hierarchical and variation partitioning in multiple regression and canonical analyses using the rdacca. hp R package. Methods Ecol. Evol., 13: 782-788. DOI:10.1111/2041-210x.13800 |
Lai, J.S., Zou, Y., Zhang, S., et al., 2022b. glmm.hp: an R package for computing individual effect of predictors in generalized linear mixed models. J. Plant Ecol., 15: 1302-1307. DOI:10.1093/jpe/rtac096 |
Lai, J.S., Cui, D.F., Zhu, W.J., et al., 2023a. The use of R and R Packages in biodiversity conservation Research. Diversity, 15: 1202. DOI:10.3390/d15121202 |
Lai, J.S., Zhu, W.J., Cui, D.F., et al., 2023b. Extension of the glmm.hp package to zero-inflated generalized linear mixed models and multiple regression. J. Plant Ecol., 16: rtad038. DOI:10.1093/jpe/rtad038 |
Li, T.Y., Wu, N.G., Chen, J.Y., et al., 2023. Vertical exchange and cross-regional transport of lower-tropospheric ozone over Hong Kong. Atmos. Res., 292: 106877. DOI:10.1016/j.atmosres.2023.106877 |
Lindeman, R.H., Merenda, P.F., Gold, R.Z., 1980. Introduction to Bivariate and Multivariate Analysis. Scott Foresman, Glenview, IL.
|
Liu, X., Feng, J., Wang, Y., 2019. Chlorophyll a predictability and relative importance of factors governing lake phytoplankton at different timescales. Sci. Total Environ., 648: 472-480. DOI:10.1016/j.scitotenv.2018.08.146 |
Liu, X.Y., Gao, H., Zhang, X.M., et al., 2023. Driving forces of meteorology and emission changes on surface ozone in the Huaihe River Basin, China. Water Air Soil Pollut., 234: 355. DOI:10.1007/s11270-023-06345-1 |
Ma, Y.X., Ma, B.J., Jiao, H.R., et al., 2020. An analysis of the effects of weather and air pollution on tropospheric ozone using a generalized additive model in Western China: Lanzhou, Gansu. Atmos. Environ., 224: 117342. DOI:10.1016/j.atmosenv.2020.117342 |
Murray, K., Conner, M.M., 2009. Methods to quantify variable importance: implications for the analysis of noisy ecological data. Ecology, 90: 348-355. DOI:10.1890/07-1929.1 |
Pedersen, E.J., Miller, D.L., Simpson, G.L., et al., 2019. Hierarchical generalized additive models in ecology: an introduction with mgcv. PeerJ, 7: e6876. DOI:10.7717/peerj.6876 |
Peres-Neto, P.R., Legendre, P., Dray, S., et al., 2006. Variation partitioning of species data matrices: estimation and comparison of fractions. Ecology, 87: 2614-2625. DOI:10.1890/0012-9658(2006)87[2614:VPOSDM]2.0.CO;2 |
R Development Core Team, 2023. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
|
Ramsay, T.O., Burnett, R.T., Krewski, D., 2003. The effect of concurvity in generalized additive models linking mortality to ambient particulate matter. Epidemiology, 14: 18-23. DOI:10.1097/00001648-200301000-00009 |
Ravindra, K., Rattan, P., Mor, S., et al., 2019. Generalized additive models: building evidence of air pollution, climate change and human health. Environ. Int., 132: 104987. DOI:10.1016/j.envint.2019.104987 |
Ray-Mukherjee, J., Nimon, K., Mukherjee, S., et al., 2014. Using commonality analysis in multiple regressions: a tool to decompose regression effects in the face of multicollinearity. Methods Ecol. Evol., 5: 320-328. DOI:10.1111/2041-210X.12166 |
Singh, P.D., Klamerus-Iwan, A., Hawrylo, P., et al., 2024. Possibility of spatial estimation of soil erosion using Revised Universal Soil Loss Equation model and generalized additive model in post-hard coal mining spoil heap. Land Degrad. Dev., 35: 923-935. DOI:10.1002/ldr.4961 |
Sun, J.M., Lu, L., Liu, K.K., et al., 2018. Forecast of severe fever with thrombocytopenia syndrome incidence with meteorological factors. Sci. Total Environ., 626: 1188-1192. DOI:10.1016/j.scitotenv.2018.01.196 |
Wang, Y., Hao, J., McElroy, M.B., et al., 2009. Ozone air quality during the 2008 Beijing Olympics: effectiveness of emission restrictions. Atmos. Chem. Phys., 9: 5237-5251. DOI:10.5194/acp-9-5237-2009 |
Wickham, H., 2016. Elegant Graphics for Data Analysis. New York: Springer-Verlag.
|
Wood, S.N., 2011. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. Roy. Stat. Soc. B-Stat. Methodol., 73: 3-36. DOI:10.1111/j.1467-9868.2010.00749.x |
Wood, S.N., 2017. Generalized Additive Models: an Introduction with R. Second ed.. Boco Raton: CRC Press.
|
Wood, S.N., Augustin, N.H., 2002. GAMs with integrated model selection using penalized regression splines and applications to environmental modelling. Ecol. Model., 157: 157-177. DOI:10.1016/S0304-3800(02)00193-X |
Wood, S.N., Pya, N., Saefken, B., 2016. Smoothing parameter and model selection for general smooth models. J. Am. Stat. Assoc., 111: 1548-1563. DOI:10.1080/01621459.2016.1180986 |
Zuur, A., Ieno, E., Walker, N., et al., 2009. Mixed Effects Models and Extensions in Ecology with R. New York: Springer.
|
Zuur, A.F., Ieno, E.N., Elphick, C.S., 2010. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol., 1: 3-14. DOI:10.1111/j.2041-210X.2009.00001.x |



