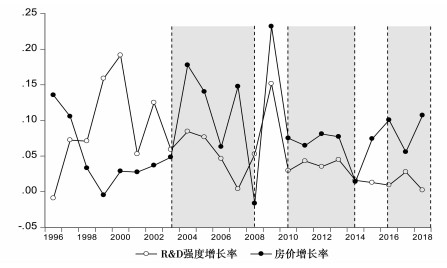
随着中国经济进入新常态发展阶段,原有的粗放式经济增长模式已经难以持续,社会经济亟待向高质量发展方式转变。高质量发展着眼于生产要素的优化配置,力图将经济增长转换到全要素生产率(Total Factor Productivity,TFP)驱动式的轨道上,从而实现经济可持续发展。然而,我们注意到中国背景下房地产投资快速增长以及房价持续上涨,房地产开发投资从1998年的3614亿元增长至2018年的12万亿元,百城新建商品房平均销售价格从当年的2063元/m2上涨至2018年的12800元/m2,年均上涨24.8%,房地产已成为传统经济增长的重要驱动力,同时高房价也对社会创新、经济可持续发展造成不可忽略的负面冲击。具体而言,高房价会挤压企业的创新投入(荣昭、王文春,2014)、形成企业家精神的错配(Li and Wu, 2014)、削弱高房价地区对优秀人才的吸引力(赵锋、樊正德,2019),进而降低了全要素生产率(陈斌开等,2015)。但房地产作为国民经济的重要构成,合理的房价能够推动房地产市场的可持续发展,为企业提供生产活动所需的厂房,为家庭提供高品质的住所进而吸引人才集聚,因此合理房价可能有助于提升TFP。图 1显示了1996-2018年全国R&D强度增长率和房价增长率间的关系,灰色区域为房地产调控紧缩期,经验观察发现2010年前后两者分别呈大致的正向和负向关系,表明房价可能对TFP具有差异性影响。但现有文献并未对合理房价和高房价进行区分,而是将研究样本期的房价先验地设定为高房价,这种处理方法将导致研究结论出现偏差。因此,如何准确地辨析房价对TFP的差异性影响就成为本文的研究方向。
|
图 1 R & D强度增长率和房价增长率,灰色区域为房地产调控紧缩期 数据来源:中经网数据库。 |
2003年以来,中央政府认识到高房价带来的巨大风险,并密集出台多项房地产调控政策,如2005年3月和8月先后发布的新旧“国八条”、2006年5月的“国六条”以及2007年9月的“房贷新政”等。总体来看,2010年以前的调控政策注重住房供给端调控,通过加大普通商品房土地供应,强化经济适用房建设,严格房地产开发贷款管理等措施增加住房供给,并辅之以住房信贷政策来调控住房需求,但面对当时公众旺盛的房产投资(投机)需求,供给侧管理为主的调控效果并不明显。因此,随着2010年国务院“新国十条”的出台,政府部门开始重视住房限购、差异化信贷政策等需求侧调控措施的运用。需求侧调控能够有效抑制不合理的房地产需求,但由于在调控政策搭配、调控强度把握等方面缺乏理论支撑,调控部门在需求侧施行严厉的限购政策,并在供给侧加强保障房建设与住宅供地,导致2014-2015年产生房地产高库存风险,并在2015-2016年的“去库存”周期过度放松调控,造成同时期房价大幅上涨,再次形成“灰犀牛”式的宏观经济风险。基于已有的研究成果以及可观察到的事实,我们发现房地产调控的效果并不是太好(丁杰等,2015)。部分学者开始关注此类问题,并对房地产调控效果展开了大量研究(黄昕等,2018),但现有文献还存在着如下不足:首先,在当前“因城施策”的调控思路下,各城市实行差异化调控措施,但学者们主要采取对调控政策进行虚拟变量赋值的做法,难以准确评估具体城市的政策效果。其次,现有文献仅针对限购、限售、限价和限贷中的某类措施进行效果分析,缺少研究房地产调控的整体视角,且对调控措施分类及政策搭配缺乏关注。房地产调控是多项政策的同时实施,单一的政策效果研究导致调控部门不能对调控综合措施的效果进行预估,容易造成总体调控力度“偏弱”或“偏强”的后果。鉴于此,本文将在房地产差异化调控背景下,理论探讨房价和房地产调控对TFP的不对称影响,并从供给侧和需求侧两个维度构建房地产调控强度指标,实证检验房价和房地产调控对TFP的门槛效应,以及房地产调控对TFP的影响是否存在房价预期传导机制,以期为我国房地产调控政策的制定与实施提供参考。
本文可能的贡献:①探讨合理房价与高房价对TFP的差异性影响,进一步丰富了现有研究结论。②从供给侧和需求侧两个维度构建房地产调控强度指数,研究房地产调控强度“偏弱”和“偏强”状态下对TFP的差异性影响,为提升房地产调控效果提供经验支持。③探讨房地产调控影响TFP的房价预期传导机制,为构建房地产调控政策体系提供理论支撑。
二、理论分析与研究假说现有文献关于房地产与TFP关系的研究成果还较为有限。陈斌开等(2015)发现过高的房价降低了资源再配置效率,进而降低全要素生产率,即房价上涨1%,全要素生产率下降0.045%。刘程、王仁曾(2019)发现房价上涨导致产业间资源错配和挤占企业研发投入,进而不利于地区产业结构优化升级。房地产对TFP的影响机制方面,房地产泡沫会引发投机行为(Abraham and Hendershott, 1996)、挤占其他行业的信贷资源(Chen et al., 2015)、驱逐高房价地区的研发活动(李昊洋等,2018)、向实体经济传染风险(杨海生、杨祯奕,2019),从而抑制了TFP增长。一些学者还从高房价影响技术进步的角度展开研究。①房价的过快上涨会产生资产泡沫(郭文伟,2017),资产泡沫导致储蓄不能顺利转化为生产性资本,从而阻碍了技术进步(Futagami and Shibata, 2000)。Miao and Wang(2014)通过构建两部门内生增长模型,发现企业将有限的资金投入资产泡沫部门,其主业的技术进步会受到抑制。徐妍、郭品(2019)采用H-P滤波测算我国29个省级地区房地产定价的效率因素和非效率因素,发现房价非效率因素的增加阻碍了企业创新。上述研究主要关注房地产泡沫对TFP的不利影响,但房地产作为国民经济的重要组成部门,房价上涨产生的财富效应促进了居民消费,消费规模的扩大能够提升企业创新能力(Benito,2007);房价温和上涨还能增加企业成本,所形成的倒逼机制提升了出口企业的TFP和新产品销售比重(任志成、戴翔,2015);合理房价产生的资产负债表效应有助于企业获得更多的外部融资(Caballero and Krishnamerthy, 2006),企业将扩大投资规模并增加创新支出(Gan,2007)。因此合理房价可能有助于社会创新,本文提出假说1:
① 部分文献直接将全要素生产率视为技术创新,如苏治、徐淑丹(2015)。
H1:高房价对TFP的影响为负,合理房价对TFP的影响为正。
房地产调控已经成为宏观调控的重要组成,对市场经济产生着愈加深刻的影响,近年来国内学者开始关注调控对房地产市场的影响。王鹤等(2014)发现调控政策对区域房价的影响显著,因此政府在制订房价调控政策时应充分考虑市场反应。叶剑平、李嘉(2018)从“住房-土地-财税-金融”四个维度探讨房地产调控长效机制构建,发现供给端的土地政策和财税政策效果长期来看效果显著,但需求端的金融政策效果长期效果不显著。李嘉(2019)从需求侧和供给侧角度对我国房地产调控措施进行梳理,发现2016年以前的调控措施主要针对于需求端,直到2016年6月提出“发展住房租赁市场”及2017年房地产供给侧政策推进,房地产供给侧调控才重新受到重视。黄昕等(2018)构建了限购、限贷、限售、土地供给四个维度的房地产调控指标,探讨四种房地产调控措施对房价增速的差异性影响。房地产调控通过稳定公众房价预期,从而抑制投机和市场过热(丁如曦、倪鹏飞,2018);削弱房价上涨对实体企业的信贷挤占效应(安磊等,2018),有助于减缓高房价对TFP的抑制作用。但经验证据表明我国房地产调控的效果不佳,根源在于房地产调控如果不能改变房价上涨预期,则市场投机对社会创新的负面冲击难以减缓。房地产调控通过房价预期传导机制对全要素生产率将产生差异性影响,由此提出假说2:
H2:房地产调控强度较小(大)时对TFP的影响为负(正),且房地产调控对TFP的影响存在房价预期传导机制。
三、理论模型借鉴Miao and Wang(2014)的两部门内生增长模型,假定某个经济体包含房地产部门和最终产品部门,金融市场为两个部门提供用于资本投入的信贷总额Cr,房地产部门和最终产品部门获得信贷的比例分别为k和(1-k)。房地产部门投入资本和劳动后的产出为房屋H,最终产品部门购置房地产并作为生产要素投入生产的产出为Y,房地产具有金融属性,两部门都可能基于房价上涨预期而持有更多的房地产,表现为房地产企业“捂盘惜售”式的房地产存货投资和最终产品生产企业的房地产投资,目的是预期收益最大化。一旦政府认为房地产市场过热,就会通过经济和行政手段调节信贷资源在房地产部门和最终产品部门间的分配,设定房地产调控强度为RC,则房地产部门获得的信贷比例k=υ0-υ1RC,即调控强度增加,房地产部门信贷会以υ1比例减少。
(一) 房地产部门假定房地产开发所需资本全部通过信贷市场获取,基于C-D生产函数给出房地产产出函数。其中,Ah为房地产生产技术,kCr为信贷资本投入,Lh为劳动投入,α为资本产出弹性并设定生产函数的规模报酬不变。
| $ H = {A_h}{(kCr)^\alpha }{L_h}^{1 - \alpha }\quad 0 < \alpha < 1 $ | (1) |
房地产具有金融属性,房地产企业可能会进行房屋存货投资以达到期望收益Ehπ的最大化。其中,Ph为房地产价格,设定η为最终产品部门企业将信贷资金分配在房地产资产上的比例,则η(1-k)Cr/Ph为最终产品生产企业向房地产企业购买的房地产数量,(1-η)(1-k)Cr为最终产品部门企业的资本设备投入,此时房地产企业的存货投资为H-[η(1-k)Cr/Ph],EPh-Ph为房地产企业对存货投资的期望收益,wLh和rkCr分别为房地产企业的工资支出和资本利息支出,则房地产企业的期望利润表达式:
| $ {E_h}\pi = {P_h}[\eta (1 - k)Cr/{P_h}] + \{ H - [\eta (1 - k)Cr/{P_{\rm{h}}}]\} (E{P_h} - {P_h}) - w{L_h} - rkCr $ | (2) |
房地产部门通过定价达到期望利润最大化,由式(2)房价Ph的一阶条件:
| $ {\partial {E_h}\pi /\partial {P_h} = - H + \eta (1 - k)Cr * E{P_h}/P_h^2 = 0} $ | (3) |
| $ {{\rm{求得}}:E{P_h} = H * P_h^2/(1 - k)\eta Cr} $ | (4) |
现有研究对生产活动所需的房地产资本和设备资本不加以区分,将两者作为同类固定资产纳入生产函数,但企业将房地产作为生产要素投入,还会基于金融投资目的持有房地产。本文将房地产与资本设备进行区分,得到最终产品生产企业的生产函数Y。其中,A代表全要素生产率,η(1-k)Cr/Ph为购买的房地产数量,(1-η)(1-k)Cr为生产设备资本投资,Ls为劳动投入,为简化分析本文假定生产设备资本的折旧率为1,β和γ分别为生产设备资本和劳动的产出弹性,由于生产函数的规模报酬不变,房地产生产要素的产出弹性为1-β-γ。
| $ Y = {A_s}{[(1 - \eta )(1 - k)Cr]^\beta }{L_s}^\gamma {[\eta (1 - k)Cr/{P_h}]^{1 - \beta - \gamma }}\quad 0 < \beta ,\gamma < 1 $ | (5) |
房地产具有金融属性,最终产品生产企业除生产最终产品Y获取利润,还投资于房地产获取升值收益,目的在于期望收益最大化。本文设定期望收益函数Esπ,其中Ps为最终产品价格,wLs和r(1-k)Cr分别为工资支出和资本利息支出,Ht-1和Px分别为持有的前期房地产数量及成本。
| $ {E_s}\pi = {P_s}Y - w{L_s} - r(1 - k)Cr + [\eta (1 - k)Cr/{P_h}](E{P_h} - {P_h}) + {{\rm{H}}_{t - 1}}(E{P_h} - {P_x}) $ | (6) |
在式(6)期望利润最大化条件下,信贷配置比例k的一阶条件:
| $ \frac{{\partial {E_s}\pi }}{{\partial k}} = - \frac{{{P_s}{A_s}{\eta ^{1 - \beta - \gamma }}{{(1 - \eta )}^\beta }(1 - \gamma ){{(1 - k)}^{ - \gamma }}C{r^{1 - \gamma }}{L_s}^\gamma }}{{P_h^{1 - \beta - \gamma }}} + rCr - \frac{{\eta Cr}}{{{P_h}}}(E{P_h} - {P_h}) $ | (7) |
| $ {\rm{求得}}:{A_s} = \frac{{{{(1 - k)}^\gamma }[r - \eta (E{P_h} - {P_h})/{P_h}]P_h^{1 - \beta - \gamma }}}{{{P_s}(1 - \gamma ){{(1 - \eta )}^\beta }{\eta ^{1 - \beta - \gamma }}C{r^\gamma }{L_s}^\gamma }} $ | (8) |
将k=υ0-υ1RC代入式(8)后对RC求偏导:
| $ \frac{{\partial {A_s}}}{{\partial k}}\frac{{\partial k}}{{\partial RC}} = \frac{{\gamma {v_1}{{(1 - k)}^{\gamma - 1}}[r - \eta (E{P_h} - {P_h})/{P_h}]P_h^{1 - \beta - \gamma }}}{{{P_s}(1 - \gamma ){{(1 - \eta )}^\beta }{\eta ^{1 - \beta - \gamma }}C{r^\gamma }{L_s}^\gamma }} $ | (9) |
由于式(9)中0 < k, γ, η < 1,因此
将式(4)代入式(8)并对Ph求一阶偏导:
| $ \frac{{\partial {A_s}}}{{\partial {P_h}}} = \frac{{{{(1 - k)}^\gamma }[(1 - \beta - \gamma )r + (1 - \beta - \gamma )\eta - (2 - \beta - \gamma )H * {P_h}/(1 - k)Cr]P_h^{ - \beta - \gamma }}}{{{P_s}(1 - \gamma ){{(1 - \eta )}^\beta }{\eta ^{1 - \beta - \gamma }}C{r^\gamma }{L_s}^\gamma }} $ | (10) |
同理由于0 < k, γ, η < 1,因此
为了检验本文提出的理论假说,我们构建基于Hansen(1999)的面板门槛计量模型如下:
| $ TF{P_{it}} = {\alpha _0} + {\alpha _1}H{P_{it}}(H{P_{it}} \le {\gamma _1}) + {\alpha _2}H{P_{it}}(H{P_{it}} > {\gamma _1}) + {\rm{ }}Cont{r_{it}} + {\varepsilon _{it}} $ | (11) |
| $ TF{P_{it}} = {\beta _0} + {\beta _1}R{C_{it}}(R{C_{it}} \le {\gamma _2}) + {\beta _2}R{C_{it}}(R{C_{it}} > {\gamma _2}) + {\rm{ }}Cont{r_{it}} + {\mu _{it}} $ | (12) |
模型中TFP为全要素生产率,HP为房价,Contr为控制变量,RC为房地产调控强度。模型(11)和模型(12)分别以房价HP和调控强度RC作为门槛变量,γ为门槛变量的阈值,i和t为地区与年份,ε和μ为随机干扰项。
(二) 变量选取和定义1.全要素生产率(TFP)
本文采用数据包络分析法(Data Envelopment Analysis,DEA)测算152个地级市的全要素生产率。其中,产出是以2000年为基期,将地级市GDP对所在省份的GDP平减指数进行平减,最终调整为不变价产出;要素投入为资本存量和劳动,资本存量使用永续盘存法进行计算,其核算方式为Kt=It/Pt+Kt-1(1-δ),Kt与Kt-1代表t和t-1时期的资本存量;It为t时期的资本投资额;Pt为t时期的价格指数,资本存量的计算以1991年为基期,将1991年的资本存量按照省级资本存量乘以当年各地级市占所在省份固定资产投资的比重予以确定,并将固定资产折旧率取值9.6%;劳动投入采用全社会从业人员数,包括单位从业人员、私营和个体从业人员总和。
2.房地产价格(HP)
采用(商品房销售总额/商品房销售面积)并取自然对数作为房价指标,同时将(当期房价/上期房价)取自然对数衡量房价增速。
3.房地产调控强度(RC)
参考黄昕等(2018)对限购、限售、限贷的测度方法,本文从供给侧和需求侧两个角度测算调控强度。房地产调控可区分为中央调控和地方调控,体现为地方政府在中央政府的统一政策框架下拥有“因城施策”的调控主动权,承担调控主体责任并接受中央调控部门的考核问责。本文先对地方调控强度进行评价,没有地方调控政策的地区以正在施行的中央调控政策进行评价。如果某项调控政策RC在年中第m月发布,RCt为新发布调控政策的强度,RCt-1为前项调控政策的强度,则当年该项调控政策的强度为RCt-1*(m/12)+RCt*(12-m)/12;个人住房贷款利率为5年以上贷款基准利率,如果在年中第m月调整基准利率,it为调整后的利率,it-1为调整前的利率,则当年的房贷利率为it-1*(m/12)+it*(12-m)/12。需求侧房地产调控包括限购强度和限贷强度,供给侧房地产调控包括限售强度、限价强度、房地产开发强度3个二级指标,并进一步划分为三级指标后进行测算。各项指标的具体测算方法见表 1。
| 表 1 房地产调控强度测算 |
表 1中各项原始指标的差异性较大,采用专家打分法难以控制主观偏差,且指标间独立性较强和指标数量有限,运用主成分分析或因子分析法难以提取公因子。房地产调控主要通过改变市场主体的房价预期,推动市场主体调整自身的经济行为,最终对全要素生产率产生影响,即房价预期是房地产调控影响全要素生产率的中间变量。借鉴钟少颖等(2016)将房价预期设定为适应性预期,根据过去五期房价上涨率的均值作为下一期房价预期的做法,分别将需求侧调控的三级指标,以及供给侧调控的三级指标对房价预期EHP回归,结果如下:
| $ {EH{P_{it}} = {{0.399}^{***}} - {{1.706}^{**}}H{R_{it}} - {{0.846}^{**}}I{R_{it}} - {{2.893}_{it}}M{P_{it}}} $ |
| $ {EH{P_{it}} = {{0.560}^{***}} - {{2.109}^{***}}R{H_{it}} + 0.641L{P_{it}} - {{4.092}^*}L{S_{it}}} $ |
将各系数绝对值占三个系数绝对值之和的比重作为权重赋值,如住房限购变量的权重为1.706/(1.706+0.846+2.893),通过确定三级指标的权重后计算得到需求侧调控强度DRC,采用同样的方法测算供给侧调控强度SRC,并最终得到房地产调控强度RC,表 2为2018年部分重点城市的房地产调控强度。
| 表 2 2018年部分重点城市房地产调控强度 |
4.控制变量
参考现有文献的做法,选取FDI比重、科教投入、财政自主、人均产出取对数、进出口比重、产业结构作为控制变量。其中,FDI比重反映了外商投资带来的技术扩散效应,科教投入为研发与教育投入对产出效率的影响,财政自主、人均产出、进出口比重和产业结构能够控制经济发展程度、产业结构等因素对TFP的影响。
(三) 变量统计描述本文采用2008-2018年地级市层面的面板数据进行分析,房地产调控强度是通过检索各城市人民政府网站、住建部门网站、REICO房地产市场报告、国信房地产信息网获取原始数据测算得到,其中二手房价数据来源于房地产行业大数据平台(www.creprice.cn),土地出让面积来源于前瞻数据库(www.qianzhan.com),其他数据来源于历年的《中国城市统计年鉴》和《中国区域经济统计年鉴》,通过对异常样本的剔除,最终整理得到152个地级市共1672个样本的平衡面板数据,各变量的统计性描述见表 3。
| 表 3 各变量的统计性描述 |
表 4为房价和房地产调控强度影响TFP的门槛效应检验。①模型(1)为房价HP影响TFP的单门槛效应,当HP低于门槛值9.03时房价对TFP的影响显著为正,可能的原因是合理区间的房价上涨能增加企业抵押品价值,有助于缓解企业融资约束从而增加研发投入,形成TFP的增长效应。HP高于门槛值9.03时房价的回归系数显著为负,表明房价处于过高区间时,企业会将信贷资源大量投入房地产业,形成对企业生产投入和研发投入的挤占效应,最终阻碍了TFP。模型(2)为房地产调控强度RC对TFP的双门槛效应回归,当RC低于0.82时,调控强度对TFP的影响为-0.3214,本文的解释是调控强度较弱时,公众的房价上涨预期未发生扭转,从而不利于TFP的增长;调控强度RC处于0.82到1.64之间时,调控强度对TFP的回归系数为0.5072,而当调控强度RC高于1.64时回归系数下降为0.3516,这表明调控强度在0.82到1.64之间时能够对TFP产生“事半功倍”的最佳效果。因此,多年来房地产调控效果“事与愿违”的可能原因在于调控强度较弱,但调控强度过高也不利于达到最佳的调控效果。模型(3)为需求侧调控强度DRC对TFP的单门槛回归,当DRC低于1.89时对TFP的影响显著为负,高于1.89时对TFP的影响转变为正。模型(4)为供给侧调控强度SRC对TFP的门槛回归,当SRC低于1.35时回归系数为0.1388但不显著,SRC高于1.35时回归系数为0.3426,供给侧调控强度SRC对TFP的影响始终为正,表明本文样本期间供给侧调控未出现“事与愿违”的调控效果。
① bootstrap次数设定为500,每个门槛区间的样本值不低于50。
| 表 4 房价和房地产调控强度影响TFP的门槛效应检验 |
房价预期对房价具有重要作用(赵胜民、罗琦,2015),因此房地产调控的关键在于房价预期管理。房价看涨预期会造成社会资本过度流向房地产业,导致供给端的创新投入和需求端的消费升级受到抑制,最终阻碍TFP的增长。借鉴Baron and Kenny(1986)的做法,本文将建立房价预期传导机制模型,检验是否存在房地产调控影响TFP的房价预期传导机制,设定如下的实证模型:
| $ {EH{P_{it}} = {\alpha _0} + {\alpha _1}R{C_{it}} + {\rm{ }}Cont{r_{it}} + {\varepsilon _{it}}} $ | (13) |
| $ {TF{P_{it}} = {\beta _0} + {\beta _1}EH{P_{it}} + {\rm{ }}Cont{r_{it}} + {\mu _{it}}} $ | (14) |
表 5为房地产调控强度RC影响TFP的房价预期传导机制检验,房价预期EHP是将过去五期房价上涨率的均值作为下一期房价预期,并根据调控强度影响TFP的门槛值0.82将样本划分为两个区间分别回归。模型(1)至模型(3)为调控强度低于0.82时的传导机制检验,其中模型(1)调控强度RC对房价预期EHP的影响系数显著为正,模型(2)房价预期EHP对TFP的影响为-0.1397,则调控强度对TFP的房价预期传导机制影响为负,表明调控强度较弱时将不利于扭转房价上涨预期,最终阻碍了TFP增长。模型(3)将调控强度和房价预期同时纳入模型,调控强度RC对TFP的回归系数为-0.1795,说明除了房价预期传导变量外,可能还存在其他因素导致调控强度阻碍了TFP增长。模型(4)至模型(6)为调控强度高于0.82时的传导机制检验,其中模型(4)调控强度对房价预期的影响显著为负,模型(5)房价预期对TFP的回归系数为-0.1572,说明较高的调控强度能够扭转房价预期,并通过房价预期下降推动TFP增长。模型(6)将调控强度和房价预期同时纳入模型,调控强度RC的回归系数为0.1635,房价预期在5%显著水平的回归系数为-0.4458,说明存在着调控强度影响TFP的房价预期传导机制。
| 表 5 房地产调控强度影响TFP的中间传导机制检验 |
为了保证房价和房地产调控影响TFP的门槛效应结论的可靠性,本文采用两种方法进行稳健性检验。一是借鉴余泳泽、张少辉(2017)的做法将发明专利授权量比单位从业人员数衡量地区创新(PIP),将地区创新代替TFP后进行稳健性回归;二是建立包含核心解释变量一次项和二次项的模型进行稳健性回归,采用二手房价上涨率作为房价预期进行传导机制稳健性检验。
(一) 门槛效应稳健性检验表 6报告了房价和调控强度对地区创新PIP的回归结果,模型(1)房价低于8.61时的回归系数为正但不显著,高于8.61时影响系数显著为负,说明高房价抑制了TFP的结论是可靠的。模型(2)和模型(3)中调控强度RC和需求侧调控强度DRC对TFP的影响都存在由负转正的门槛效应,模型(4)供给侧调控强度SRC的回归系数都为正但在低门槛区间不显著。表 6的稳健性回归表明房价和调控强度影响TFP的门槛效应结论是可靠的。
| 表 6 房价和房地产调控强度影响TFP的门槛效应稳健性检验 |
本文将地区创新PIP作为TFP的替代变量,以过去五期房价上涨率的均值作为房价预期进行传导机制稳健性检验,回归结果见表 7。模型(1)至模型(3)为调控强度RC低于1.17时的房价预期传导机制检验,其中模型(1)调控强度对房价预期EHP的回归系数为正且通过1%显著性检验,模型(2)房价预期对地区创新PIP的影响显著为负,说明调控强度较低时的房价预期传导机制为负;模型(3)将调控强度和房价预期同时纳入模型,房价预期的回归系数为负但不显著。模型(4)至模型(6)为调控强度RC高于1.17时的房价预期传导机制检验,模型(4)调控强度对房价预期的回归系数显著为负,模型(5)房价预期对PIP的回归系数显著为负,表明调控强度较高时的房价预期传导机制为正;模型(6)将调控强度和房价预期同时纳入模型,房价预期的回归系数为负并有所降低。其他控制变量的回归系数未发生显著性改变,证明本文关于房价预期传导机制的结论是可靠的①。
① 本文还将房地产调控RC与RC2项同时对TFP回归,RC2的回归系数显著为正,RC的回归系数显著为负,说明房地产调控对TFP的影响呈先减后增关系;我们还将二手房价格上涨率作为房价预期进行传导机制的稳健性检验,各变量的回归系数未发生显著变化,再次表明本文结论稳健。回归结果限于篇幅未在文中显示,感兴趣的读者可以联系获取。
| 表 7 房地产调控强度影响TFP的房价预期传导机制稳健性检验 |
本文基于2008-2018年152个地级及以上城市面板数据,从理论和实证两个角度探讨房价和房地产调控对TFP增长的门槛影响。研究表明合理区间的房价能够推动TFP增长,过高的房价会阻碍TFP增长;房地产调控强度较弱时不利于TFP增长,房地产调控强度适中时促进TFP增长的效果最好。进一步的研究表明,房地产调控通过改变房价预期从而对TFP产生影响,形成房地产调控影响TFP的房价预期传导机制。基于上述结论,本文从房价与房地产调控角度提出推动TFP增长的政策性建议:
(1) 努力抑制房价过快增长。研究表明高房价会阻碍TFP增长,当前房价已进入高房价区间并显著抑制了TFP增长。因此,应该将“房子是用来住的、不是用来炒的”作为房地产调控的中长期指导思想,建议严格控制房地产市场的投资性需求,让房地产居住性功能得到发挥。微观角度要限制信贷资金大量流入房地产市场,加大土地供应和保障房建设力度;宏观角度要管住货币的投放规模,构建多层次的直接融资市场并引导房地产投机资本流向证券市场,同时在合适时机出台房产税和房屋空置税。
(2) 构建房地产调控长效机制。本文研究发现房地产调控强度较弱时会“事与愿违”地阻碍TFP增长,当调控处于合适强度区间时能够发挥“事倍功半”的最佳效果。多年来我国房地产调控效果不佳的原因之一在于调控力度较弱,建议房地产泡沫较大的地区要保持合适的调控强度。同时,房地产宏观调控部门应该建立调控强度测度体系,厘清房地产调控与房价、公众房价预期和社会创新之间的关系,通过优化调控措施减缓高房价对社会创新的抑制作用。
(3) 完善房地产调控结构体系。房地产调控政策可以区分为需求侧调控和供给侧调控。需求侧调控通过影响房价预期对TFP产生影响,不足之处在于对中间传导变量——房价预期难以准确测度,导致需求侧调控的效果难以提前研判,且需求侧调控还容易“误伤”合理的住房需求;供给侧调控的对象为房地产企业与多套房持有者,调控效果相对容易实现,本文的研究结果也支持上述观点。因此应该建立科学的房地产调控结构体系,重视供给侧调控抑制高房价的作用发挥,建立更加科学的需求侧和供给侧调控措施搭配体系。
(4) 引导公众建立房价理性预期。多年来的房价持续上涨已经形成公众强烈的房价上涨预期,房地产市场平稳发展的关键在于稳定公众房价预期、引导公众形成房价理性预期。当前房价预期波动较大且难以准确测度,公众的房价理性预期不足都制约着房地产调控效果的发挥,建议房地产调控部门充分借助大数据技术,建立包含新建房和存量房的房价预期监控体系,并以此为基础构建包含房地产调控工具、中间传导变量和调控目标的科学调控体系,推动房地产调控理论和实践的更好融合。
| [] |
安磊、沈悦、徐妍, 2018, “房价上涨如何影响实体企业债务融资——兼论房地产调控政策的实施效果”, 《当代经济科学》, 第 9 期, 第 47-61 页。 |
| [] |
陈斌开、金箫、欧阳涤非, 2015, “住房价格、资源错配与中国工业企业生产率”, 《世界经济》, 第 4 期, 第 77-98 页。 |
| [] |
丁如曦、倪鹏飞, 2018, “房地产市场调控优化及深化改革:目标原则与路径找寻”, 《改革》, 第 10 期, 第 28-38 页。 |
| [] |
丁杰、李仲飞、郑军, 2015, “房地产调控政策的连续性与有效性——基于信贷资源再配置的视角”, 《经济评论》, 第 4 期, 第 96-108 页。 |
| [] |
郭文伟, 2017, “中国房地产市场泡沫分层测度及时变溢出效应研究”, 《现代财经》, 第 4 期, 第 51-65 页。 |
| [] |
黄昕、董兴、平新乔, 2018, “地方政府房地产限购限贷限售政策的效应评估”, 《改革》, 第 5 期, 第 107-118 页。 |
| [] |
李昊洋、程小可、高升好, 2018, “高房价驱逐了公司的研发活动吗?——来自创业板的经验证据”, 《中国软科学》, 第 12 期, 第 95-109 页。 |
| [] |
李嘉, 2019, “长效调控机制构建背景下的宏观经济对住房市场供需双侧影响研究”, 《经济问题探索》, 第 3 期, 第 19-31 页。 |
| [] |
刘程、王仁曾, 2019, “房价上涨会抑制地区产业结构升级吗”, 《产业经济研究》, 第 2 期, 第 102-113 页。 |
| [] |
荣昭、王文春, 2014, “房价上涨和企业进入房地产:基于我国非房地产上市公司数据的研究”, 《金融研究》, 第 4 期, 第 158-173 页。 |
| [] |
任志成、戴翔, 2015, “劳动力成本上升对出口企业转型升级的倒逼作用——基于工业企业数据实证研究”, 《中国人口科学》, 第 1 期, 第 48-58 页。 |
| [] |
苏治、徐淑丹, 2015, “中国技术进步与经济增长收敛性测度——基于创新与效率的视角”, 《中国社会科学》, 第 7 期, 第 4-25 页。 |
| [] |
王鹤、潘爱民、陈湘州, 2014, “经济环境、调控政策与区域房价——基于面板数据同期强相关视角”, 《南方经济》, 第 6 期, 第 56-74 页。 |
| [] |
徐妍、郭品, 2019, “房价、资源错配与企业创新——基于房价效率因素和非效率因素的分析”, 《经济问题》, 第 7 期, 第 16-28 页。 |
| [] |
杨海生、杨祯奕, 2019, “把握脱虚向实力度——房地产与实体经济的风险传染机制研究”, 《中山大学学报(社会科学版)》, 第 4 期, 第 184-196 页。 |
| [] |
叶剑平、李嘉, 2018, “住房-土地-财税-金融:四位一体房地产调控长效机制构建研究”, 《中国软科学》, 第 12 期, 第 67-86 页。 |
| [] |
余永泽、张少辉, 2017, “城市房价、限购政策与技术创新”, 《中国工业经济》, 第 6 期, 第 98-116 页。 |
| [] |
钟少颖、王蕊、陈锐, 2016, “货币政策, 市场预期与房地产价格”, 《管理评论》, 第 5 期, 第 13-22 页。 |
| [] |
赵胜民、罗琦, 2015, “动态随机一般均衡模型视角下的预期冲击与住房价格波动”, 《南方经济》, 第 2 期, 第 37-52 页。 |
| [] |
赵锋、樊正德, 2019, “高房价对大城市人口流入的抑制效应——来自北上广深四城市的实证证据”, 《城市发展研究》, 第 3 期, 第 41-48 页。 |
| [] |
Abraham J., Hendershott P., 1996, "Bubbles in Metropolitan Housing Markets". Journal of Housing Research, 79(2), 191–207.
|
| [] |
Benito, A., 2007, "Housing Equity as a Buffer: Evidence from UK Households", Bank of England Working Paper, No.324.
|
| [] |
Baron M., Kenny A., 1986, "The Moderator-mediator Variable Distinction in Social Psychological Research:Conceptual, Strategic, and Statistical Considerations". Journal of Personality and Social Psychology, 51(6), 1173–1198.
DOI:10.1037/0022-3514.51.6.1173 |
| [] |
Chen, T., Liu, L. and Zhou, L., 2015, "The Crowding Out Effects of Real Estate Shocks-Evidence from China", Available at SSRN 2584302.
|
| [] |
Caballero J., Krishnamurthy A., 2006, "Bubbles and Capital Flow Volatility:Causes and Risk Managreement". Journal of Monetary Economics, 53(1), 35–53.
DOI:10.1016/j.jmoneco.2005.10.005 |
| [] |
Futagami K., Shibata A., 2000, "Growth Effects of Bubbles in an Endogenous Growth Model". Japanese Economic Review, 51(6), 221–235.
|
| [] |
Gan J., 2007, "Collateral, Debt Capacity, and Corporate Investment:Evidence from a Natural Experiment". Journal of Financial Economics, 85(3), 709–734.
|
| [] |
Hansen E., 1999, "Threshold Effects in Non-dynamic Panels:Estimation, Testing, and Inference". Journal of Econometrics, 93(12), 345–368.
|
| [] |
Li L., Wu X., 2014, "Housing Price and Entrepreneurship in China". Journal of Comparative Economics, 42(2), 436–49.
DOI:10.1016/j.jce.2013.09.001 |
| [] |
Miao J., Wang P., 2014, "Sectoral Bubbles, Misallocation, and Endogenous Growth". Journal of Mathematical Economics, 53(8), 153–163.
|




