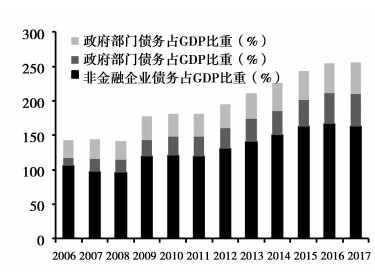
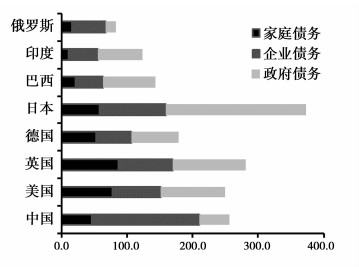
2011年以来,我国实体经济杠杆率①不断攀升,根据国际清算银行数据库,2017年一季度我国实体经济债务占GDP比重为255.9%,已经超过美国(249.5%),与英国(281.0%)较为接近,远超其他新兴市场国家。同时我国经济的高杠杆问题呈现显著的结构性特征,非金融企业部门债务②占GDP比重由2008年的96.3%迅速上升至同时2017年上半年的163.4%。非金融企业债务已成为“中国经济的阿喀琉斯之踵” ③,高杠杆成为新常态下经济运行机制的重要特征之一。
|
图 1 我国债务占GDP比重的构成 |
|
图 2 2017年世界主要国家债务占GDP比重(%) |
① 采用实体经济债务总量比GDP衡量实体经济中的杠杆率。
② 包括银行贷款与债券。
③ 观点摘自2016年4月复旦大学经济学院举办的第8期“RICE-CCES”沙龙。
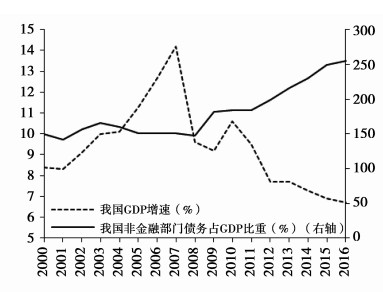
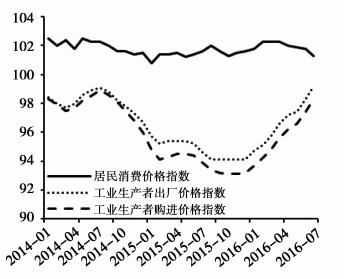
随着债务占GDP比例的不断上升,2013年我国经济增速出现趋势性下降,2015年我国GDP增速降至6.9%,2016年进一步降至6.7%,经济增长不确定性增大。同时经济增速下降伴随着社会价格水平的下降,PPI自2014年至2016年9月以来连续54个月下降,经济出现通缩风险。以史为鉴,经济体中债务杠杆与通缩并存隐含着巨大的“债务-通缩”风险,例如美国1929-1933年大萧条中出现了严重的“债务-通缩”(Fisher,1933),债务水平不断上涨伴随价格水平下跌,通缩导致全社会实际债务规模上升29%,产出下降30%,投资锐减90%。我国经济运行中呈现出日益显著的高杠杆特征,高杠杆隐藏的巨大风险也成为决策层关注的焦点,2016年党中央和国务院提出“加强供给侧结构性改革”的重要经济战略,其中去杠杆是供给侧改革“三去一降一补”的重要组成部分。2017年全国金融工作会议中再次强调去杠杆与防范系统性风险。在上述经济背景与政策背景下,理解高杠杆经济的运行机制并分析其潜在风险具有重要的理论与现实意义。
|
图 3 我国GDP与债务走势分析 |
|
图 4 社会价格水平走势分析 |
杠杆率包括微观与宏观两种范畴。从微观上看,杠杆率是指企业资产负债率,即总负债比总资产,但仅研究资产负债表无法全面衡量债务问题的结构特征与可持续性。李扬等(2015)认为债务偿付的主要来源是经济体的总收入,故宏观范畴内用债务收入比来衡量债务负担动态变化(陆婷、余永定,2015;潘英丽、黄益平,2016)。
公司金融领域的经典理论“MM定理”认为理想市场状态下企业资本结构与企业价值无关(Mldigliani and Miller, 1958),但金融摩擦使企业债务杠杆成为影响微观企业发展与宏观经济运行的关键变量之一。引入金融摩擦的主流范式之一是金融加速器模型(Bernanke, 1999),模型认为金融市场摩擦表现为借贷市场的信息不对称,银行通过观测企业资产负债表确定借贷利率,负向经济冲击导致企业资产负债表恶化,银行将要求更高的风险升水,形成“杠杆上升-外部融资溢价上升”的金融加速器。之后Christensen and Dib (2008)与Gelain(2010)分别在模型中引入名义债务框架与名义粘性,证明金融加速器机制的存在。我国学者对金融加速器机制进行了重要探索。杜清源、龚六堂(2005)建立一个实际价格计价的RBC模型,首次证明我国存在金融摩擦导致的外部融资溢价;崔光灿(2006)认为金融加速器机制将加剧资产价格与宏观经济的波动;刘兰凤、袁申国(2012)在DSGE模型中证明了我国经济存在金融加速器效应;袁申国、陈平(2011)运用上市公司数据建立动态面板模型,证明我国上市公司的投资支出受到资产负债表的显著影响,为我国的金融加速器机制提供实证证据;马家进(2016)运用金融加速器模型证明了银行“晴天送伞、雨天收伞”的顺周期信贷行为。
刻画金融摩擦的另一范式是名义“债务-通缩”机制,Fisher(1933)认为1933年大萧条的原因在于“债务-通缩”,高债务使企业陷入偿债危机,迫使企业出售资产,导致资产价格下降与通缩,加剧真实债务负担并形成“债务-通缩”恶性循环。陈小亮、马啸(2016)认为我国目前高债务运行的经济系统存在“债务-通缩”风险,需要宏观政策体系谨慎应对。“债务-通缩”机制的重要因素之一是债务合约形式,分为名义债务合约与实际债务合约:名义债务合约中企业借贷合约以名义值计价,真实债务负担将受到通胀的影响,而实际债务合约中债务以实际价格水平计价。Christensen and Dib(2008)在金融加速器模型中引入名义债务框架,但并未涉及两种框架的比较。Iacoviello(2005)在一个包含信贷抵押约束的DSGE模型中分别设置名义债务模型与实际债务模型,对比发现名义债务模型中货币政策冲击与负向通胀冲击对经济的影响更为显著。
杠杆阈值也具有两个层面的意义:从微观企业角度看,杠杆阈值是指企业杠杆率超过一定值时可能导致企业价值或经济增速下降,Cecchetti et al.(2011)运用OECD国家1980年至2010年的债务数据证明非金融企业部门债务超过GDP的90%①时将阻碍经济增速,不同行业企业的杠杆阈值不同。从宏观经济角度看,杠杆阈值是指经济体债务量超过一定水平时将导致经济增速下降,甚至触发金融危机。从经济现实看,宏观债务增加可能导致金融危机,Reinhart and Rogoff (2009)总结了全球金融发展历程,发现危机的共同主题是“过度负债”;IMF(2015)则认为新兴市场国家许多金融危机发生前都出现了杠杆率的快速攀升;Jorda et al.(2011)证明危机前经济中杠杆越高,危机中经济受损越大。在理论研究中,Mendoza(2006)和宋潇(2015)建立内嵌信贷抵押约束的DSGE模型,设信贷抵押约束偶尔触及上限(occasionally binding),一旦债务过高触及上限将导致资产价格大幅下降并触发“债务-通缩”,而触及条件则有赖于模型的参数设定。有学者认为债务杠杆的风险阈值是不稳定的,Cuorpo et al.(2013)认为欧盟各国杠杆可持续性受到各国经济发展状况的影响存在异质性,Azzimonti et al.(2014)证明经济体债务的可持续性受到资本全球流动和金融资产全球配置的影响,纪敏等(2017)指出高杠杆的系统性风险阈值存在非稳定性与时变性,可能与新兴经济体的发展特点、产出增速、债务增速有关。本文拓展了这一思路,在金融加速器模型中用代表性企业的杠杆率分析经济体的债务杠杆水平①,进而证明杠杆阈值的内生性。
① 门限效应在政府债务与家庭部门债务中也存在,政府债务超过GDP的85%、家庭部门债务超过GDP的85%时将抑制经济增长。
① 借鉴Bernanke(1999)、Christensen and Dib(2008)的研究思路,鉴于模型设定经济体只有一个代表性企业,且只有代表性企业具有借贷行为,故微观企业的杠杆率可用来分析经济体的债务杠杆水平。
在总结文献的基础上,本文的边际贡献有以下几点:
第一,金融加速器与名义“债务-通缩”理论已经是宏观金融领域较为常见的分析工具,本文的创新点在于在金融加速器模型中分别设置了名义债务框架与实际债务框架,在模型中通过名义债务框架与实际债务框架的区别证明了名义“债务-通缩”机制的存在性,进一步将二者统一于同一个分析框架内,分析高杠杆经济的运行机制。
第二,之前关于杠杆率阈值的研究以实证研究与定性分析为主,纪敏等(2017)证明了杠杆风险阈值“并不稳健”,本文拓展了这一思路,在DSGE模型中引入金融加速器机制与名义“债务-通缩”机制,证明了不同金融市场信息效率、不同债务合约下相同杠杆率将导致不同的宏观经济波动。进一步证明了杠杆阈值内生于经济系统中,与金融市场信息效率与债务合约结构相关。
第三,在总结高杠杆经济运行机制的基础上,本文提出去杠杆一方面需要降低宏观杠杆率,另一方面要提升杠杆承担能力,即抵御金融风险的能力,包括提升金融市场效率、完善多层次资本市场等,为供给侧改革与去杠杆提供理论支持。
二、DSGE分析框架本文借鉴Bernanke(1999)和Christensen and Dib(2008),建立包含金融加速器与名义“债务-通缩”的DSGE模型。基准模型中共存在三种粘性设定:名义债务计价刻画了企业融资面临的价格粘性、投资调整成本描述了固定资产形成时的实际刚性、零售商部门导致的社会总价格水平的粘性。
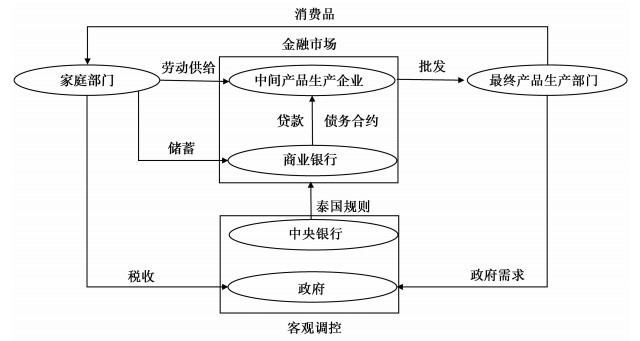
|
图 5 DSGE模型结构 |
家庭部门向企业提供劳动力、获得工资进行消费,同时持有现金并向商业银行储蓄,服从效用函数:
| $ {E_0}\sum\limits_{t = 0}^\infty {{\beta ^t}\left\{ {\frac{{\varpi \exp \left( {{j_t}} \right)}}{{\varpi - 1}}\log \left[ {c_t^{\frac{{\varpi - 1}}{\varpi }} + \exp {{\left( {m{p_t}} \right)}^{1/\varpi }}{{\left( {\frac{{{M_t}}}{{{P_t}}}} \right)}^{\frac{{\varpi - 1}}{\varpi }}}} \right] + \eta \log \left( {1 - {l_t}} \right)} \right\}} $ | (1) |
其中,
| $ \begin{array}{l} {j_{t + 1}} = {\rho _j}{j_t} + {e_{j,t + 1}},{e_{j,t + 1}} \sim N\left( {0,{\varepsilon _j}} \right)\\ m{p_{t + 1}} = {\rho _{mp}}m{p_t} + {e_{mp,t + 1}},{e_{mp,t + 1}} \sim N\left( {0,{\varepsilon _{mp}}} \right) \end{array} $ | (2) |
家庭部门的预算约束为:
| $ {c_t} + \left( {{M_t} - {M_{t - 1}}} \right)/{P_t} + {d_t} = {w_t}{l_t} + {R_{t - 1}}{d_{t - 1}}/{\pi _t} - {T_t} + {\Pi _t} $ | (3) |
ct为当期消费,dt为家庭当期储蓄,Rt-1dt-1/πt为按照名义值计价的上期储蓄本息,πt=pt/pt-1表示通胀率。名义债务计价意味着企业的实际利率由名义利率与通胀率决定,通缩时将加重实际债务负担,构成名义“债务-通缩”机制的基础。wtlt为当期劳动收入,(Mt-Mt-1)/Pt为当期增持货币,Tt, Πt分别为转移支付净额、零售商转移的利润。家庭在预算约束下进行消费、储蓄、劳动决策以达到效用最大化,分别对消费、劳动、储蓄、现金求一阶条件,得到:
| $ {\lambda _t} = \frac{{\exp \left( {{j_t}} \right){c_t}{ - ^{\frac{1}{\varpi }}}}}{{\exp {{\left( {m{p_t}} \right)}^{\frac{1}{\varpi }}}m_t^{\frac{{\varpi - 1}}{\varpi }} + c_t^{\frac{{\varpi - 1}}{\varpi }}}} $ | (4) |
| $ {w_t}{\lambda _t} = \frac{\eta }{{1 - {l_t}}} $ | (5) |
| $ \frac{{{\lambda _t}}}{{{R_t}}} = \beta {E_t}\left( {\frac{{{\lambda _{t + 1}}}}{{{\pi _{t + 1}}}}} \right) $ | (6) |
| $ {\lambda _t} - \beta {E_t}\left( {\frac{{{\lambda _{t + 1}}}}{{{\pi _{t + 1}}}}} \right) = \frac{{\exp \left( {{j_t}} \right)\exp {{\left( {m{p_t}} \right)}^{1/\varpi }}m_t^{ - 1/\varpi }}}{{\exp {{\left( {m{p_t}} \right)}^{\frac{1}{\varpi }}}m_t^{\frac{{\varpi - 1}}{\varpi }} + c_t^{\frac{{\varpi - 1}}{\varpi }}}} $ | (7) |
λt是(3)式的拉格朗日乘子,mt=Mt/pt表示实际货币持有量。(6)式的均衡形式可得到均衡利率与贴现率的关系。
(二) 企业部门企业将资产与劳动力按照C-D生产函数投入生产Aexp(at)ktαlt1-α,面临随机技术冲击at+1=ρaat+ea, t+1, ea, t+1~N(0, εa)。企业将中间产品出售给零售商,中间产品与最终产品的相对价格等于生产边际成本ζt,分别对资本与劳动力求一阶条件,得到:
| $ M{K_t} = \alpha {\zeta _t}\frac{{{y_t}}}{{{k_t}}},{w_t} = \left( {1 - \alpha } \right){\zeta _t}\frac{{{\gamma _t}}}{{{l_t}}} $ | (8) |
企业通过投资积累固定资产,在每期面临一个投资效率冲击exp(invt),服从AR(1)过程,invt+1=ρinvinv+einv, t+1, einv, t+1~N(0, εinv)。一单位投资将新增exp(invt)invt单位资本,但同时面临调整成本
| $ {q_t} = \frac{1}{{\exp \left( {in{v_t}} \right)}}\left[ {1 + \chi \left( {\frac{{{i_t}}}{{{k_t}}} - \delta } \right)} \right] $ | (9) |
企业资本演化方程为:
| $ {k_{t + 1}} = {i_t}\exp \left( {{\rm{in}}{{\rm{v}}_t}} \right) - \left( {1 - \delta } \right){k_t} $ | (10) |
企业在t期结束时积累得到下一期资产存量kt+1,资产价格为qt,权益资本为nt+1。为保证资产负债表平衡,企业需向商业银行借款bt=kt+1qt-nt+1,杠杆率为levt=bt/kt+1qt。企业获取资金的实际外部融资成本等于资本的预期边际回报率,后者由两部分组成,分别是资本边际产出率和增值收益:
| $ {E_t}\left\{ {R_{t + 1}^k} \right\} = {E_t}\left\{ {\frac{{M{K_{t + 1}} + \left( {1 + \delta } \right){q_{t + 1}}}}{{{q_t}}}} \right\} $ | (11) |
借鉴Bernanke(1999)引入信贷市场摩擦,银行与企业间存在信息不对称,银行通过观测资产负债表决定借贷利率,企业的资产负债状况决定了银行要求的风险升水:
| $ {E_t}\left\{ {R_{t + 1}^k} \right\} = {E_t}\left\{ {L\left( {le{v_t}} \right)\frac{{{R_t}}}{{{\pi _{t + 1}}}}} \right\},L'\left( \cdot \right) > 0 $ | (12) |
(12) 式是金融加速器机制的核心,表示企业实际外部融资成本Rt+1k与无风险利率Rt之间存在一定的风险溢价,定义为外部融资溢价,其大小由企业杠杆率决定。L′(·)>0表示企业杠杆升高导致外部融资溢价增加,而融资成本上升将抑制企业投资和产出导致杠杆率被迫提高,进一步提升融资成本、抑制投资与产出,形成金融加速器机制。设每期企业的存活概率为ν,留存企业的净利润将积累成为企业的净资产nt+1:
| $ {n_{t + 1}} = \nu \left[ {R_t^k{q_{t - 1}}{k_t} - {E_{t - 1}}R_t^k\left( {{q_{t - 1}}{k_t} - {n_t}} \right)} \right] $ | (13) |
参照DSGE文献的标准设置,引入零售商作为名义价格粘性的来源①。零售商在完全竞争市场中以ζt为价格向企业购买中间产品,在不消耗固定成本的情况下生产成为差异化的最终产品,并服从Calvo定价原则,每一期有(1-θ)的概率收到一个可以重新设定价格的随机信号。求解零售商部门的一阶条件可得到对数线性化后的菲利普斯曲线:
| $ {{\hat \pi }_t} = \beta {E_t}{{\hat \pi }_{t + 1}} + \frac{{\left( {1 - \beta \theta } \right)\left( {1 - \theta } \right)}}{\theta }{{\hat \zeta }_t} $ | (14) |
① 关于零售商部门的设定已成为DSGE文献的标准设置,故不再赘述。
商业银行以无风险利率从家庭部门吸收存款,并以一定的风险溢价贷给企业,银行资产负债表平衡需满足以下条件:
| $ {d_t} = {b_t} $ | (15) |
参照Ireland(2003)设中央银行采用混合型货币政策规则,参考产出缺口、通胀缺口与货币供应量增速mut=Mt/Mt-1制定名义利率,πss, yss, muss分别表示通胀目标、均衡产出水平与稳态时的货币供应量增速,ρR, ρπ, ρy, ρmu分别为货币政策的利率、通胀、产出与货币供应量反应系数,并面临货币政策随机冲击exp(eRt),货币政策制定规则为:
| $ \frac{{{R_t}}}{R} = {\left( {\frac{{{R_{t - 1}}}}{R}} \right)^{{\rho _R}}}{\left( {\frac{{{\pi _t}}}{{{\pi _{ss}}}}} \right)^{{\rho _\pi }}}{\left( {\frac{{{Y_t}}}{{{Y_{ss}}}}} \right)^{{\rho _Y}}}{\left( {\frac{{m{u_t}}}{{m{u_{ss}}}}} \right)^{{\rho _{mu}}}}\exp \left( {{e_{{R_t}}}} \right),{e_{{R_t}}} \sim N\left( {0,{\varepsilon _R}} \right) $ | (16) |
政府财政平衡要求政府支出等于净税收与铸币税之和,同时面临财政支出效率随机冲击exp(gt), gt+1=ρggt+eg, t+1, eg, t+1~N(0, εg),政府资产负债表平衡条件为:
| $ {G_t} = {T_t} + \frac{{{M_t} - {M_{t - 1}}}}{{{p_t}}} $ | (17) |
模型设六个外生冲击,分别为技术冲击、投资效率冲击、消费偏好冲击、现金偏好冲击货币政策冲击、财政政策冲击。模型均衡解包括分配向量{yt, ct, it, mt, lt, kt}与价格向量{wt, MKt, Rt, Rtk, qt, λt, ζt},满足家庭、企业、零售商、中央银行、政府部门的一阶条件,同时满足商品市场、劳动力市场、贷款存贷款市场出清。上述经济均衡状态表示为:
| $ {{\hat S}_{t + 1}} = {{\hat \Gamma }_t} + {\rm{H}}{\varepsilon _{t + 1}},{{\hat \Upsilon }_t} = \Psi {S_t} $ | (18) |
其中
DSGE模型的估计采用2001年一季度至2015年四季度的季度数据,本文引入了包括技术冲击、货币政策冲击在内的6个随机冲击,故需要6个观测变量,分别为产出、消费、投资、利率、通胀、货币供应量。与之分别对应的实际经济数据分别为GDP、全社会消费品零售总额、固定资产投资总额、一年期人民币贷款基准利率、CPI、M2,数据来源为《中国统计年鉴》与国泰安数据库。为了使观测变量与模型中变量的经济意义一致,采用以下处理方法:首先对上述经济数据取对数,发现产出与投资等数据存在显著的季节性特征,故利用Eviews对对数数据进行Census X12季节性调整。同时模型求解使采用对数线性化的方法刻画了经济变量偏离稳态的波动,故利用平滑因子为1600的HP滤波分离观测变量的趋势项与扰动项,将扰动项作为观测变量。上述实际数据处理方法是DSGE模型实际数据的标准处理方法。通过上述处理后,以Δ代表一阶差分算子,得到的模型观测变量为:
| $ O{\rm{b}}{{\rm{s}}_t} = \left[ {\mathit{\Delta log}{Y_t},\mathit{\Delta log}{C_t},\mathit{\Delta log}{I_t},\mathit{\Delta log}{R_t},\mathit{\Delta log}{\pi _t},\mathit{\Delta log}{M_{2t}}} \right] $ | (19) |
根据已有文献与实际数据对模型进行参数校准与参数估计。部分参数利用标准校准技术基于稳态目标进行校准,其余参数利用贝叶斯估计法进行估计。首先考察家庭部门参数:借鉴王国静、田国强(2014),利用一年期贷款基准利率得到样本期内年度平均利率为4.98%,折算为稳态时季度利率为1.24%,由β=1/(1+R)计算得到家庭部门贴现因子为0.988;通过贝叶斯估计得到家庭部门劳动厌恶系数、消费与现金持有替代弹性的估计值分别为1.315和0.059。
其次是企业部门参数:根据七日同业拆借利率相对于名义利率的风险升水,得到均衡时的外部融资溢价参数S为1.008,高于Christensen and Dib(2008)设定的企业融资溢价,说明从整体上看我国企业面临更高的风险升水。鉴于权益乘数与杠杆率成同向变动,故模型中将权益乘数作为杠杆率的代理变量,计算我国主板上市公司2015年权益乘数均值为2.01,故模型中权益乘数的稳态值设为2。①利用索洛残差法计算得到我国资本产出份额为0.45,与王国静、田国强(2014)的取值较为接近。为了使模型更符合我国实际情况,借鉴仝冰(2010)和刘晓光、张杰平(2016)将企业存活概率设为0.975。通过贝叶斯估计得到资本折旧率估计值为0.025,与王国静、田国强(2014)的取值一致。贝叶斯估计得到外部融资溢价弹性为0.04,说明资产负债表恶化将导致企业外部融资溢价上升,本文在DSGE模型模拟中也将设置不同的外部融资溢价弹性代表不同的金融市场信息效率。投资调整成本的贝叶斯估计值为0.575,略高于Bernanke(1999)设定的0.25,体现出我国企业的资本价格对投资资本的弹性更大。参照DSGE标准的Calvo定价法则将零售商定价参数设为θ=0.75。
① 权益乘数与杠杆率成同向变动,且在对数线性化中采用权益乘数在计算上更为简便,可作为杠杆率的代理变量,这也是金融加速器模型中的标准处理方法(Bernanke,1999;Christensen and Dib, 2008;崔光灿,2006)等。
下面讨论随机冲击的调整系数与标准差。设随机冲击的调整系数服从均值为0.5的Beta分布,标准差服从均值为0.01的逆伽马分布。表 1结果显示,各项随机冲击的自相关冲击系数与标准差的贝叶斯估计结果均与先验分布显著不同,说明观测数据包括了经济中变量间的真实关系,在先验分布这一维度上稳健性较强。货币政策采用混合型,其中通胀反应系数为0.985,与陈小亮、马啸(2016)的估计值较为接近,说明我国目前的货币政策规则注重熨平通胀波动;货币供应量反映系数为0.07,说明货币供应量调整在我国货币政策调整中具有重要作用。同时模型中其余5个随机冲击系数均大于0.5,说明随机冲击的持续性较强。
| 表 1 模型参数及随机冲击估计结果 |
为在统一框架内深入分析高杠杆对宏观经济的影响机制,本文根据经济系统与金融市场的不同运行特征对经济体进行分类:其一,参数校准部分得到2015年我国上市公司的权益乘数均值为2.01,故设实际经济体中权益乘数稳态值为2,为了分析不同企业杠杆率下经济运行的不同规律,设为2.5和1.5①以刻画高杠杆经济体与低杠杆经济体。其二,金融市场信息效率决定金融加速器大小,经济中信息不对称程度越严重,一单位杠杆率的上升对融资溢价的影响更大。根据参数校准得到目前我国外部融资溢价杠杆弹性为0.04,为了刻画信息不对称与信息完全优化状态,设定外部融资溢价的杠杆弹性为0.06和0。其三,按照金融债务合约的形式设定名义债务框架与实际债务框架,上述理论模型部分描述的是名义债务合约。而实际债务合约的关键在于债务负担按照当期实际价格计算,预算约束变为:
| $ {c_t} + {M_t}/{P_t} + {d_t} = {w_t}{l_t} + {R_{t - 1}}{d_{t - 1}} + {M_{t - 1}}/{P_t} - {T_t} + {\Pi _t} $ | (20) |
① 我国主板上市公司的权益乘数2.01对应的企业的资产负债率为50%,更高的权益乘数2.5对应企业的资产负债率为60%,用来衡量杠杆率更高的经济体。
企业外部融资溢价与企业杠杆之间的关系变为:
| $ {E_t}\left\{ {R_{t + 1}^k} \right\} = {E_t}\left\{ {L\left( {le{v_t}} \right){R_t}} \right\} $ | (21) |
对比(21)与(12)式,发现名义框架内企业的融资成本溢价受到杠杆率与通缩的双重影响,当出现通缩时名义债务框架(12)将产生更高的融资成本,加重企业融资负担,这也是之后检验名义“债务-通缩”机制的基础。
(二) 模型适用性分析:杠杆率、金融市场效率、债务合约与宏观经济波动从杠杆率、金融信息效率、债务合约形式等三个维度出发(根据表 2设定),将经济系统分为18种情况,基本可以涵盖所有的金融市场运行特征。基于DSGE模型,分别模拟上述模型的宏观经济波动,并与实际经济运行对比,判断模型的适用性。在实际杠杆率、基准信息效率与名义债务框架共同刻画的基准模型1中,模型运行的波动结果与实际经济波动较为接近,准确刻画了投资波动(6.45%)2-3倍于产出波动(2.95%)、消费(3.08%)略大于产出波动的经验事实,K-P方差比①、相关系数也与实际值较为接近,证明基准模型基本刻画了企业杠杆率对宏观经济波动的影响,构建了联系微观企业与宏观经济的分析框架,模型适用性较强。
| 表 2 不同模型的参数设定 |
① K-P方差比指的是投资与消费相对于产出的波动幅度。
根据表 3,进一步分析不同经济结构特征对宏观经济波动的影响:
| 表 3 不同杠杆率与金融特征下宏观经济的波动特征 |
首先,企业杠杆率越高经济体的宏观经济波动越大。对比相同信息效率与债务合约,但杠杆率不同的模型(例如模型1、7与13①),发现更高的杠杆率将显著增大宏观经济波动,尤其是产出与投资,高杠杆模型7的产出与投资波动分别为5.07%和11.91%,初步证明了高杠杆可能放大金融风险、增大经济不确定性,而低杠杆经济体(模型13)的稳定性更强。同时,相较于实际杠杆模型1与低杠杆模型13的差距,高杠杆模型7中同等幅度的杠杆率上升导致了更大的宏观经济波动,产出与投资波动几乎二倍于实际杠杆模型1,证明杠杆上升对宏观经济的波动率呈现显著的凸性影响,即杠杆越高,提升杠杆将导致更大的宏观经济波动。杠杆率“风险凸性”可以通过企业资本结构的动态演变解释:负向冲击导致资产价格下降,资产价格下降将同时引起资产波动与资本波动,一单位资产价格波动将导致资本下降幅度大于资产,从而导致杠杆率的提升;而杠杆越高资本相对于资产的下降幅度越大,杠杆率的提升更快,将进一步加剧金融加速器效应并增大宏观经济波动,说明杠杆率对金融风险的累积具有凸性加速影响。
① 模型的编号参见表 3的第一列。
其次,金融市场信息效率越低、信息不对称程度越高,宏观经济波动越大。对比相同杠杆率与债务合约,但信息效率不同的模型(模型1、3和5),发现信息不对称状态下(模型3)企业杠杆的外部融资溢价较高、金融加速器机制最大,产出波动为3.63%。而信息效率优化(模型5)意味着信息完全对称,将切断金融加速器机制,即杠杆率的高低不影响宏观经济波动,模型5、11和17的产出波动相同,均为1.89%,在DSGE框架内证明了MM定理,即在完美信息下资本结构(杠杆率)与企业价值无关,不影响产出波动。
再次,名义债务合约下宏观经济波动更大。对比相同杠杆率与相同市场信息效率,但债务合约不同的模型(模型1、2),发现名义债务模型中主要经济变量的波动均高于实际债务合约,证明名义债务框架加剧了宏观经济波动。原因在于企业的实际债务利率等于名义利率负担除以通胀(12与21式),通缩冲击将增大融资成本并增大宏观经济波动。
总结上述宏观经济波动的证据,发现高杠杆在金融风险累积过程中存在显著的凸性,同时高杠杆将通过金融加速器与名义“债务-通缩”两种机制影响经济波动,以下将结合DSGE模型证据与我国的实际经济情况对上述两种影响机制进行分析。
(三) 高杠杆对宏观经济的影响机制分析:金融加速器机制金融加速器机制刻画了企业资产负债表与融资溢价的内在联系:当经济受到负向冲击时,资产价格下降,导致资产负债表失衡、杠杆上升、破产风险增加,银行要求更高的风险溢价,融资成本上升、企业投资产出下降,进一步恶化资产负债表、杠杆被迫上升,经济进入“杠杆上升-外部融资溢价”的正向加速循环。当经济受到正向冲击时,资产价格上升、杠杆率下降,外部融资溢价下降刺激投资与产出,进入“杠杆下降-外部融资溢价下降”的负向加速循环。金融加速器机制导致了企业金融活动存在显著的顺周期性,即“晴天送伞、雨天收伞”的信贷行为。而金融市场信息效率是决定金融加速器机制的关键,金融市场信息越不对称,金融加速器机制越大,杠杆上升将导致更大程度的融资成本上升。
为了证明上述金融加速器模型,在DSGE模型中分析模型1、3和5(基准杠杆率、名义债务合约,但信息效率不同)中负向产出冲击的脉冲应函数,分别对应三种金融市场信息效率:基准信息效率(金融加速器模型)、信息效率较低(超金融加速模型)、信息效率优化(无金融加速器) ①。
① 外部融资溢价杠杆弹性分别设置为0.06, 0.04和0,信息效率完全优化模型假设企业与银行信息完全对称,资产负债表情况将不影响企业借贷利率。鉴于模型中施加的是标准差为0.01的负向技术冲击,故在进行脉冲响应分析时对模型数据其进行10倍放大,经济意义为0.1个标准差对经济系统的影响。
根据图 6,当金融市场信息效率较低时0.1标准差的技术冲击将导致价格波动幅度降低接近10%,信息效率优化时资产价格降幅最小;图 7显示了企业资本结构的动态演变,技术冲击带来的资本相对于资产的下降幅度更大,从而证明了杠杆率的“风险凸性”;图 8显示信息效率较低时外部融资溢价将提升0.16%;图 9显示金融市场信息效率越低,技术冲击带来的投资与产出波动越大。
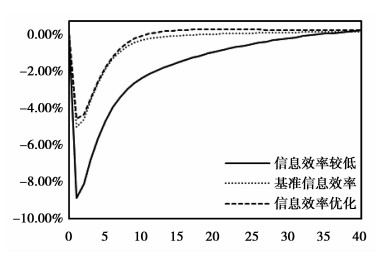
|
图 6 负向技术冲击对资产价格 |
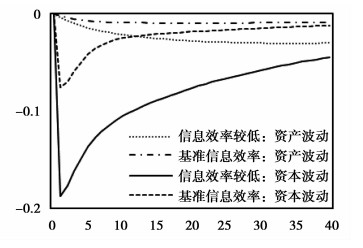
|
图 7 负向技术冲击对资本结构的影响 |
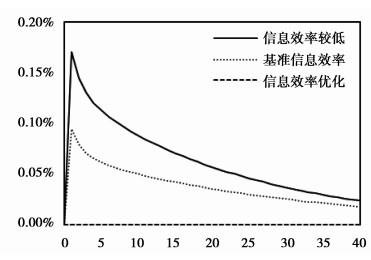
|
图 8 负向技术冲击对融资成本的影响 |
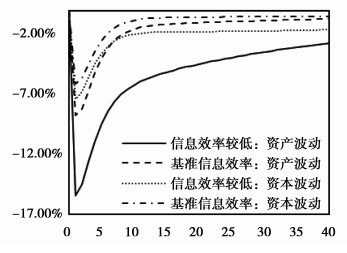
|
图 9 负向技术冲击对产出与投资的影响 |
从国际经验看,日本20世纪90年代“失去的二十年”的重要原因是资产价格泡沫破裂导致企业资产负债表恶化,从而影响企业投资与经济恢复。而2014年后我国企业部门杠杆率不断提升,导致企业盈利下降、融资困难,2015年中央经济会议中提出供给侧改革“去杠杆与降成本”。根据金融加速器理论,杠杆的高低决定了融资成本,故去杠杆是改善企业资产负债表、释放企业活力、降低融资成本的必由之路,只有“去杠杆”才能“降成本”。
(四) 高杠杆对宏观经济的影响机制分析:名义“债务-通缩”机制名义“债务-通缩”机制是指高债务与通缩之间的相互加速循环:一方面,高债务经济体一旦面临流动性缺口或偿债危机将抛售资产或商品,导致社会总价格水平下降,同时高杠杆企业活力不足也加剧了通缩预期;另一方面,当出现通缩时,名义债务计价合约使得企业仍需按照合约价格偿还债务,增大实际债务负担(对比12、21式),从而进一步抑制投资与产出。名义“债务-通缩”效应通过价格和收入两个渠道影响经济:价格层面,通缩增大实际债务负担,恶化资产负债表,加剧金融加速器机制;收入层面,“债务-通缩”意味着财富由债务人转移至债权人,由于债权人边际消费倾向较低,财富转移将降低整体消费倾向,降低总产出。
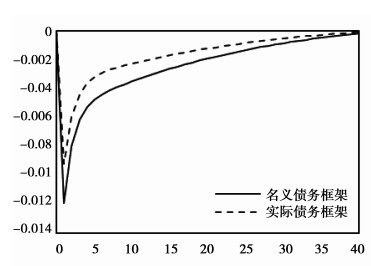
|
图 10 货币政策紧缩对资产价格的影响 |
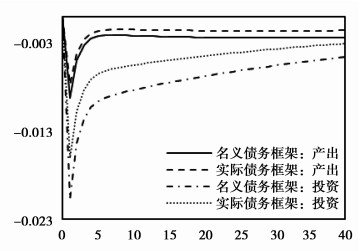
|
图 11 货币政策紧缩对投资与产出的影响 |
为了证明名义“债务-通缩”机制的存在,在DSGE模型中分析模型1和2中(相同杠杆率、相同信息效率,但债务合约不同)紧缩货币政策冲击对经济系统的影响。紧缩货币政策可能带来通缩环境,在名义债务框架内,通缩将导致实际债务负担上升、资产价格更大幅度下降,同时产出与投资下降。美国1933年大萧条是“债务-通缩”的典型案例,危机前债务杠杆不断积累、资产价格持续上涨,外部经济因素与美联储加息使房地产价格暴跌,同时经济出现通缩,酿成经济大萧条。2014年至2016年9月,我国GDP平减指数与PPI连下降,PPI持续下跌时间超过亚洲金融危机与2008年金融危机,经济中出现了“债务-通缩”压力,之后随着去杠杆带动钢铁等上游部门价格上涨,PPI转负为正,但对CPI的传导力度有限,经济仍未完全摆脱通缩压力,2016年底银行间同业拆放利率连续上涨30个交易日,出现“钱荒”,也是通缩压力在资本市场的表现之一,需谨慎应对。
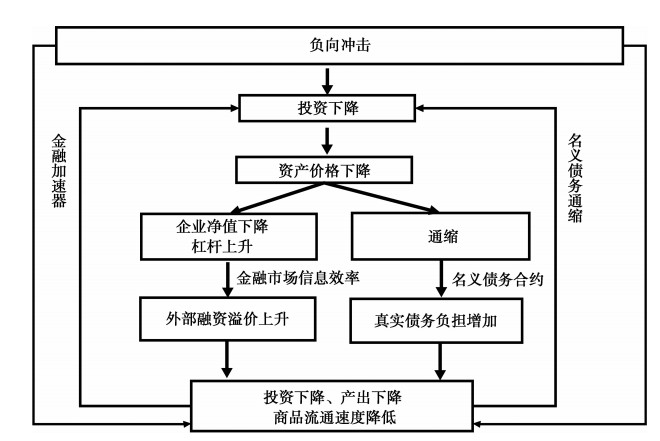
|
图 12 高杠杆对经济的影响机制:金融加速器与名义“债务-通缩” |
上节证明了高杠杆对经济的影响机制,以及其可能蕴含的风险。下面需要思考的是我国经济究竟能够承担多高的杠杆率?换言之,当杠杆超过何种水平时将引发资产价格断崖式下跌甚至金融危机?这一问题的定量回答涉及具体经济现状与结构特征,不考虑经济运行特征的单一数字显然没有经济意义。纪敏等(2017)指出不同经济环境下杠杆的可持续性不同,认为杠杆率阈值存在非稳定性与时变性,本文拓展这一思路,着重分析了杠杆率阈值的内生性。关于金融危机的定义主要集中在定性层面,潘英丽(2016)将金融危机定义为“银行危机、货币危机与泡沫经济破灭”,我国现实经济中多大幅度的产出波动可以定义为金融危机,目前尚无明确结论。故本文采用HP滤波法分离出我国GDP数据的波动项与趋势项①,发现2001年之后我国经济最为严重的负向波动出现在2008年金融危机时,计算2008年-2009年之间产出波动项的标准差为4.336%,故本文将同等幅度的负向产出波动定义为一次金融危机,将触发金融危机时的杠杆率即定义为杠杆阈值。
① 首先对产出数据去对数,之后进行季节调整,采用HP滤波分离出波动项。
(一) 杠杆阈值的内生性:模型证据与分析在DSGE模型的基准杠杆率下设置四种不同的金融市场信息效率,分别是基准模型、信息不对称较为严重、信息效率较为优化、信息效率完全优化①,同时在基准模型中设置实际债务框架与名义债务框架。分别分析在上述模型下,多高的杠杆率会导致经济体出现2008年金融危机引致的宏观经济负向波动。
① 外部融资溢价杠杆弹性分别设为0.04,0.06,0.02和0。为了更准确地衡量金融市场信息效率对宏观经济波动的影响,在这里增加外部融资溢价等于0.02的情况,以描述信息效率较为优化的经济状态。
表 4证明杠杆率阈值内生于经济系统中,经济中最高能够承受的杠杆率是由经济系统内生决定的,相同杠杆的经济体可能由于市场信息效率不同、债务合约等因素导致不同的金融风险:
| 表 4 杠杆阈值的内生性 |
第一,金融信息效率越高,杠杆率阈值越高。在基准模型中,实际权益乘数2对应的产出波动为2.95%,当杠杆率上升至58.30%时,宏观经济波动为4.49%;在信息不对称较强的模型中,杠杆率54.5%就会导致4.91%的宏观经济波动,杠杆阈值下降了4个百分点;当信息效率提升时,经济中可以容忍的杠杆率阈值提升至66.7%;在信息效率完全优化的理想状态下,宏观经济波动仅决定于外生技术冲击,杠杆率将不影响宏观经济波动。
第二,实际债务框架下杠杆阈值大于名义债务框架。在基准信息结构模型中发现实际债务框架内杠杆阈值为61.50%,比名义债务框架(58.30%)提升了3.2%。
第三,经济中的储蓄率越高,杠杆阈值越高。储蓄率高意味着经济中间接融资比重越高,银行信贷在经济系统中的作用更强,使经济能够承受较高的杠杆率;同时,储蓄率越高,投资对债权融资的依赖性越强,客观上需要高杠杆支撑投资与产出。目前我国经济呈现高投资与高储蓄并存的特征,相较于直接融资占比较高的经济体,我国经济能够承受更高的杠杆率,杠杆率阈值更高。
第四,经济上升期杠杆阈值高于经济下行时期,经济下行时期杠杆可持续性受到更大挑战。从经济周期视角出发,当经济处于复苏期时,边际产出上升,企业对未来增长预期较为乐观,将主动增加杠杆以扩大产出规模,此时杠杆的上升具有盈利能力的支持,债务可持续性强,杠杆阈值较高。当技术进步或改革红利逐渐衰退,边际产出下降,企业盈利能力下降,债务可持续性受到挑战,杠杆阈值降低。同时,从宏观层面看,宏观杠杆率等于债务水平比产出水平,杠杆率增速等于债务增速减去产出增速,故产出水平与产出增速较高时,经济中杠杆阈值较高。我国自2013年之后经济增速出现周期性下降,产出下降导致债务杠杆率上升,而杠杆率上升进一步增大宏观经济波动,债务杠杆的可持续性受到挑战。
我们可以从国际比较中进一步理解杠杆率阈值的内生性。20世纪80年代拉美地区发生严重的债务危机导致经济停滞、社会混乱,但1980年拉美各国债务占GDP比重均不超过50%,负债最严重的智利与秘鲁债务占GDP比重分别为40.7%和40.3% ②;而欧债危机中2012年希腊债务占GDP比重达到283.9%。当然由于发展阶段与时间区间不一致,仅对比两组数字意义不大,但可以确定的是一个经济体能够承担多大的杠杆率是由经济体内部决定的,例如拉美地区银行业呈现出高度垄断性,一旦出现流动性危机将影响银行信贷,进而影响宏观经济,故经济体系对杠杆的容忍程度很低,防御风险的能力较差。
② 数据来自《21世纪拉丁美洲发展大趋势》,世界知识出版社,2002。
(二) 提升抵御金融风险的能力鉴于杠杆阈值存在内生性,高杠杆经济体的运行逻辑并不在于一个外生的杠杆率是否能够被接受,而在于经济系统内生决定了自身能够承担多大的杠杆率、能够化解何种程度的金融风险。在经济新常态背景下,供给侧改革与去杠杆旨在“将杠杆率控制在风险可控的范围内”,具有两个层面的内涵:一方面需要控制杠杆率的过快上升,另一方面则需要主动提升经济系统抵御金融风险的能力,提升“风险可控的范围”。具体的,可以通过以下途径提升经济系统内生抵御金融风险的能力:
第一,金融市场信息效率衡量了经济体中金融摩擦的程度,决定了经济体对金融风险的抵御能力。这启示我们可以通过提升金融市场信息效率、降低信息不对称增强抵御金融风险的能力、提升杠杆阈值。目前我国金融市场信息效率的主要问题在于“融资二元化”特征(邓建平等,2011;孙灵燕,2012),已有研究证明国有企业受惠于“预算软约束”,信贷条件更为优越(钟宁桦等,2016),而民营企业则面临更为严重的信息不对称。这一问题表现为国有企业的经营风险没有被充分定价,而资质优良的民营企业也无法得到相应的融资支持,本质上是一种金融资源的错配,导致了金融效率较低,经济结构恶化。所以目前我国降低金融市场信息不对称的关键在于降低民营企业的信贷歧视,缓解国企的隐性担保与预算软约束。
第二,实际债务合约占比上升意味着企业能够迅速根据通胀水平调整债务负担,将增大经济应对外生冲击的能力。在实际操作中发行通胀指数化债券能够使债务负担随实际物价水平调整,降低物价水平变动产生的债权人与债务人收入的相对扭曲,从而降低宏观经济波动。第三,金融信息效率的提升需要建设和完善多层次资本市场,发展股权融资渠道。目前我国股权融资占社会融资规模不超过3%,发展直接融资体系将提升股权融资市场的资源配置效率,为实体经济提供流动性支持,分散金融风险。
六、研究结论与政策建议本文主要解决了以下两个问题:
第一,高杠杆通过何种机制影响宏观经济波动?本文在一个DSGE框架中分析了高杠杆经济体运行机制,发现企业杠杆将通过两种机制扩大外生冲击、增大经济波动,一方面,当经济下行并面临负向冲击时,资产价格下降,外部融资溢价上升,抑制企业投资,进入恶性循环;另一方面,过高的企业杠杆隐藏着名义“债务-通缩”的风险,可能导致“通缩--资产价格下降--实际债务负担增大”的恶性循环。
第二,在明确了高杠杆对宏观经济的影响机制后,本文尝试回答“我国经济最多能够承受多高的杠杆率”这一问题,通过在DSGE模型中设置不同的结构性特征证明债务杠杆阈值存在内生性,经济对债务杠杆的承担能力内生于经济系统中,信息不对称程度越低、实际债务合约占比越高、储蓄率越高,经济中对杠杆的承受能力越强,杠杆风险阈值越高。
基于上述结论本文提出以下政策建议:
第一,本文为供给侧改革与去杠杆提供了理论支持,鉴于高杠杆隐藏的巨大经济风险,去杠杆成为宏观审慎背景下重要的经济战略,也是长期经济稳定的必由之路。同时去杠杆也要重视债务杠杆的结构性特征,目前我国非金融企业部门债务主要集中于国有企业,2017年全国金融工作会议中强调去杠杆工作重点在于“降低国有企业杠杆率”。
第二,鉴于杠杆阈值的内生性,当前经济的主要任务不是单纯从数字上将降低债务与产出的比例,而是需要从宏观上提升经济系统抵御金融风险的能力、强债务可持续性,包括金融市场信息效率提升、降低信贷歧视与信息不对称、发展通胀指数化债券、控制银行坏账率、经济结构调整等,其中提升金融市场信息效率的关键是改变国有企业预算软约束、降低银企借贷市场信息不对称程度。
第三,去杠杆需要避免骤然紧缩信贷导致的流动性风险。去杠杆是一个复杂的过程,宜将保持经济稳定、降低杠杆阈值与去杠杆过程统筹考虑,增大经济潜力并化解金融风险:从经济增长层面看,化解金融风险、提升债务可持续性的关键在于降低经济增长对投资的高度依赖,需要扩大有效需求,包括国内需求与外需出口。从企业层面看,保障杠杆的可持续性需破解“借新还旧”的恶性循环,提升投资效率与盈利能力,从而提升资产收益率;其三,紧缩货币政策将导致通缩,增大企业实际债务负担,甚至直接触发“债务-通缩”,所以去杠杆需要保证稳定温和的货币环境。
| [] |
陈小亮、马啸, 2016, “'债务-通缩'风险与货币政策财政政策协调”, 《经济研究》, 第 12 期, 第 28-42 页。 |
| [] |
崔光灿, 2006, “资产价格、金融加速器与经济稳定”, 《世界经济》, 第 11 期, 第 59-69 页。 |
| [] |
邓建平、曾勇, 2011, “金融关联能否缓解民营企业的融资约束”, 《金融研究》, 第 8 期, 第 78-92 页。 |
| [] |
马家进, 2016, “晴天送伞, 雨天收伞:对金融摩擦、信贷周期和企业融资难问题的分析”, 《南方经济》, 第 7 期, 第 63-77 页。 DOI:10.3969/j.issn.1000-6249.2016.07.010 |
| [] |
李扬、张晓晶、常欣, 2015, 《中国国家资产负债表 2015-杠杆调整与风险管理》, 北京: 中国社会科学出版社。 |
| [] |
刘晓光、张杰平, 2016, “中国杠杆率悖论——兼论货币政策'稳增长'和'降杠杆'真的两难吗”, 《财贸经济》, 第 8 期, 第 5-19 页。 |
| [] |
刘兰凤、袁申国, 2012, “中国经济金融加速器效应的DSGE模型分析”, 《南方经济》, 第 8 期, 第 102-114 页。 DOI:10.3969/j.issn.1000-6249.2012.08.008 |
| [] |
陆婷、余永定, 2015, “中国企业债对GDP比的动态路径”, 《世界经济》, 第 5 期, 第 3-16 页。 |
| [] |
宋潇, 2015, “信贷约束、资产价格与通货紧缩——基于动态一般均衡模型的分析”, 《经济管理》, 第 9 期, 第 1-10 页。 |
| [] |
孙灵燕, 2012, “所有制信贷歧视对中国民营企业出口的影响:基于融资的视角”, 《南方经济》, 第 7 期, 第 43-56 页。 DOI:10.3969/j.issn.1000-6249.2012.07.004 |
| [] |
仝冰, 2010, 《货币、利率与资产价格——基于DSGE模型的分析和预测》, 北京大学。 |
| [] |
潘英丽、黄益平, 2016, 《激辩去杠杆:如何避免债务通缩》, 北京: 中国社会科学出版社。 |
| [] |
袁申国、陈平, 2010, “资产负债表、金融加速器与企业投资”, 《经济学家》, 第 4 期, 第 61-67 页。 |
| [] |
吴国平, 2002, 《21世纪拉丁美洲经济发展大趋势》, 世界知识出版社。 |
| [] |
王国静、田国强, 2014, “金融冲击和中国经济波动”, 《经济研究》, 第 3 期, 第 20-34 页。 |
| [] |
纪敏、严宝玉、李宏瑾, 2017, “杠杆率结构、水平和金融稳定——理论分析框架和中国经验”, 《金融研究》, 第 2 期, 第 11-25 页。 |
| [] |
钟宁桦、刘志阔、何嘉鑫, 2016, “我国企业债务的结构性问题”, 《经济研究》, 第 7 期, 第 102-117 页。 |
| [] |
Fisher I., 1933, "The debt-deflation theory of great depressions". Econometrica:Journal of the Econometric Society, 337–357.
|
| [] |
Azzimonti M., De Francisco E. and Quadrini V., 2014, "Financial globalization, inequality, and the rising public debt". The American Economic Review, 104(8), 2267–2302.
DOI:10.1257/aer.104.8.2267 |
| [] |
Bernanke B.S., Gertler M. and Gilchrist S., 1999, "The financial accelerator in a quantitative business cycle framework". Handbook of Macroeconomics, 1, 1341–1393.
DOI:10.1016/S1574-0048(99)10034-X |
| [] |
Cecchetti S.G., Mohanty M.S. and Zampolli F., 2011, "The Real Effects of Debt". Bis Working Papers, 68(3), 145–196.
|
| [] |
Christensen I., Dib A., 2008, "The financial accelerator in an estimated New Keynesian model". Review of Economic Dynamics, 11(1), 155–178.
DOI:10.1016/j.red.2007.04.006 |
| [] |
Cuerpo, C., Drumond, I., and Lendvai, J., 2013, "Indebtedness, deleveraging dynamics and macroeconomic adjustment", European Commission, Directorate-General for Economic and Financial Affairs.
|
| [] |
Gelain P., 2010, "The external finance premium in the euro area:A dynamic stochastic general equilibrium analysis". The North American Journal of Economics and Finance, 21(1), 49–71.
DOI:10.1016/j.najef.2009.11.004 |
| [] |
Iacoviello M., 2005, "House prices, borrowing constraints, and monetary policy in the business cycle". The American Economic Review, 95(3), 739–764.
DOI:10.1257/0002828054201477 |
| [] |
Jordà Ò., Schularick M.H.P. and Taylor A.M., 2011, "When credit bites back:leverage, business cycles, and crises". National Bureau of Economic Research.
|
| [] |
Mendoza E.G., Smith K.A., 2006, "Quantitative implications of a debt-deflation theory of Sudden Stops and asset prices". Journal of International Economics, 70(1), 82–114.
|
| [] |
Modigliani F., Miller M., 1958, "The Cost of Capital, Corporation Finance and the Theory of Investment". American Economic Review, 48(3), 261–297.
|
| [] |
Reinhart C.M., Rogoff K.S., 2010, "Growth in a time of debt". American Economic Review, 100(2), 573–578.
DOI:10.1257/aer.100.2.573 |
| [] |
Reinhart C.M., Rogoff K.S., 2009, This time is different:Eight centuries of financial folly, Princeton University Pres.
|




