2. 西北工业大学 航空学院, 西安 710072;
3. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000
2. School of Aeronautic, Northwestern Polytechnical University, Xi'an 710072, China;
3. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
CFD在国内外航空航天领域中的地位日益重要,成为飞行器研制中不可或缺的重要手段。这不仅表现在对CFD越来越多的依赖,一些时候,如在极端气动力/热环境、流动结构或流动机理剖析、紧急任务或复杂事故分析等情况下,CFD是唯一可以依赖的手段。
CFD历经百年,但真正实用化只有约40年。40年来,CFD在应用上的普及和发展速度如此之快,几乎超出了所有人的意料。但CFD在计算方法和物理模型等核心理论上的进步却是步履蹒跚、甚至止步不前,这也几乎超出了所有人的意料。例如,1979年, 美国工程院院士、NASA Ames研究中心航天部主任Chapman预测[1]LES将于20世纪90年代应用于飞行器全机的计算,可事实是:距他预测的时间过去近30年了,这个预测至今还没有实现,而且在可预见的未来也不太可能实现。虽然每年都有数以千计的CFD论文等成果发表,但真正被大家接受、甚至走入应用的却很少。
为了进一步论证上述可能引起争议的观点,这里简述一下国内外的CFD现状。
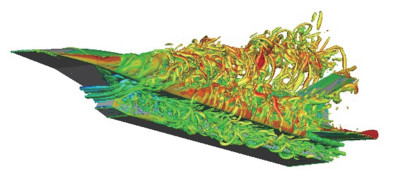
在国内,众所周知,CFD的应用无论是深度还是广度,都有了飞速的发展,一些十年前我们甚至想都不敢想的复杂CFD计算,也许今天新入门的研究生都可以轻松完成。这里给出一个实例:图 1是笔者硕士研究生在2017年完成的复杂飞行器全机非定常湍流DES模拟,全模7000万网格,湍流能谱平均误差2%。十年前,这样的CFD计算是不可想象的。
|
图 1 复杂飞行器全机非定常湍流瞬时涡结构的精细模拟(Q=300,Ma染色,Ma=2.5,H=20 km,α=10°) Fig.1 Highly accurate unsteady turbulence simulation over a complex aircraft (Q=300, Contour color: Ma, Ma =2.5, H=20 km, α=10°) |
但是,CFD真的大踏步进步了吗?不妨简单考察一下CFD的核心理论也就是它的计算方法和物理模型的现状:
(1) 计算方法:目前航空航天领域应用最广的Roe格式是1981年发表的,39年了,但它早被人知的原始缺陷依然存在;
(2) 物理模型:目前应用最广的湍流模型之一k-ε模型(它也是另一个应用最广的湍流模型之一——SST模型——的组成部分)出现在1972年,48年了,但它早被人知的原始缺陷也依然存在。
也就是说,在CFD核心方法上,我们已经陷入了长达40年没有本质进步的困境。更让我们忧虑的是,目前,仍然很难看到走出这些困境的曙光。
2017年至2019年,中国空气动力研究与发展中心等多家单位联合开展了“第一届航空CFD可信度研讨会”[2],公开发布了计算模型、基础网格和试验数据,对多家单位提供的计算结果进行了统计分析,并与相关风洞试验结果进行了对比。会议认为:国内自主研发的CFD软件与美国先进CFD软件计算结果精度相当,CFD计算结果与风洞试验结果定性吻合较好, 定量方面距离精细化设计尚有不小的差距。
为了全面了解和评估航空航天中CFD的现状、梳理存在的问题,美国、欧洲等的政府部门、科研机构、企业、高校等开展了很多的国际合作、项目研究、专题讨论、系列研讨会等,比较知名的如:The European Research Community on Flow, Turbulence, and Combustion (ERCOFTAC)、Workshops on CFD Uncertainty Analysis、CFDVAL2004 Workshop、The Drag Prediction Workshop (DPW)、High Lift Prediction Workshop (HiLiftPW) series、A European Project on the Development of Adaptive Higher-Order Variational Methods for Aerospace Applications(ADIGMA)、Advanced Turbulence Simulation for Aerodynamic Application Challenges(ATAAC)。这其中DPW影响最大,DPW参与者几乎包含了国际上所有知名的航空航天单位,其大量CFD结果的数据统计、分类归纳和物理分析等成果非常珍贵、意义重大,因为本文的部分观点也基于这些成果,因此这里先简单介绍DPW。
DPW起源始于1998-1999年AIAA会议的走廊讨论,这些走廊讨论的几位成员在AIAA应用空气动力学技术委员会的赞助下,于2000年1月正式成立了第一届DPW组织委员会。此后,经过二十年的不懈努力和六次国际研讨会,DPW取得了出乎意料的成功。与会者和组织者都认为DPW是绝对的成功,因为它是CFD研究者、软件开发者、航空航天CFD使用者等“一线基层”集体努力的计算分析、公开诚实的交流讨论。DPW通过广泛、长期、充分、公开、多角度、多层次的国际合作和研讨,评估CFD的实用性能(尤其关注阻力)、公正评价CFD软件的有效性、发现需要进一步研究的问题并探索其解决方法,DPW因此成为航空航天CFD领域影响最大的国际活动。会议发布了大量的几何构型、各种网格、数据统计、结果对比分析和建议等,这些均在公共可访问的网站上发布,包括数据库、研讨会记录、大量公开发表的论文、相关出版物和演示文稿等。
DPW的成果太丰富,本文只能根据笔者自己的阅读理解,简单地浓缩其要点(为简洁,以下用DPW后面加数字N表示第N次DPW会议)[3]:
1) 普遍对CFD结果失望,这主要表现在不同软件的CFD结果散布较大,超出了预期。虽然通过不断提高网格质量和数量、强化收敛性等,降低了散布程度,但仍然大于飞机设计者对CFD的期望,而且俯仰力矩总体上并没有显示出随着网格分辨率的提高而趋于收敛的明显趋势。整体说来,CFD置信度仍未降到可与实验相竞争的水平。
2) 网格问题(网格质量、网格分辨率、网格收敛性)一直是DPW研究的焦点,数据统计证实了网格质量和网格分辨率的重要性。网格数量也从最初的250万平均基准网格、到后来最大24亿个网格。但最终并没有给出明确的或指导性结论,计算结果散布问题仍然存在。比如:对于类似的网格分辨率,DPW6结果的变化通常比DPW5更高,DPW6俯仰力矩的变化也高于DPW3的结果。
3) 会议通过设计各种独特的网格集合,以尽量消除网格变化对计算结果的影响。但结果是,数据仍然存在较大的散布,所以会议认为湍流模型、软件、边界条件和迎风格式等其他因素也很重要。因为工作量大、协调困难等原因,对这些问题没有开展深入的研究。
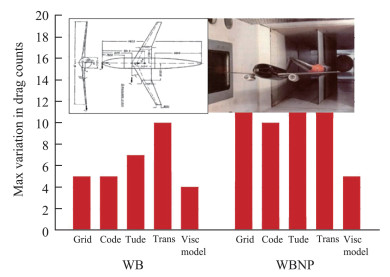
4) 统计分析DPW2会议的结果,在网格、程序、湍流模型、转捩模型、黏性模型等影响CFD计算结果的因素中,发现湍流模型、转捩模型以及网格对CFD计算结果的影响位居前三强,如图 2所示,分别占到约15%、11%和11%,这也是世界上第一次量化认识了CFD结果的影响因素。
5) 从DPW2开始,就有一个共识:关键区域的流动分离使得很难对网格收敛性和阻力预测得到有意义的结论。很遗憾,后来的会议虽然针对这一问题设计了多种方法,这一共识最后也没有得到确认或否定,因为影响因素多且复杂。例如,网格细化后,分离区变大还是变少?对于这一个看似简单的问题,几个世界知名的CFD软件,给出了令人困惑的结论:变小(CFL3D, OVERFLOW)、变大(UPACS, TAS, FUN3D, ONERA-elsA,BCFD)、不变(Edge,DLR-TAU)。
实际上,HiLiftPW和国内“第一届航空CFD可信度研讨会”[2]也有类似的结论:网格规模的增加并没有明显提高计算结果之间的数据散布度;应该加强CFD方法、湍流模型和可信度分析方法研究。
CFD在应用上的飞速前进和理论上的步履蹒跚,让我们有必要认真地审视他的现状、筹划他的未来。确实,近些年来,美国、欧洲、日本等陆续发表了一些这方面的研究报告。其中,特别要提到的是,2014年NASA组织了185名有关领域的资深专家,进行了150多次调查和讨论,发表了研究报告“CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences” (以下简称CFD2030)[5]。该报告评估了航空航天领域CFD的成就与不足、需求与差距,对CFD在2030年应具备的能力进行了规划、给出了实现的具体建议。这是一份在CFD发展史上具有重要意义的指导性文件。显然,我国也有必要思考类似的问题,很高兴国内的一些单位已经开始这样有意义的工作。
本文试图对航空航天领域CFD应用的关键问题,进行一点梳理和思考。鉴于CFD涉及的面太广,很难在一篇期刊论文中面面俱到地论述清楚,如NASA的CFD2030共58页,虽然作者十年前也曾做过这样的努力[6],但是十年后的今天,为了论述得更深入,本文欲聚焦一下重点:面向航空航天领域的CFD应用,针对其核心问题即CFD计算方法和物理模型,叙述、评论其发展的现状、存在的问题以及面临的挑战,以期认识现状、展望未来、推动应用。
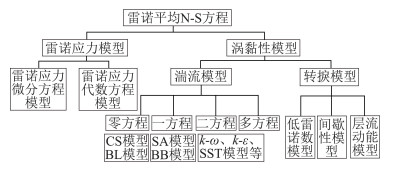
1 物理模型无论是在实际工程应用、还是在科学研究领域,目前广泛使用的CFD方法是基于物理模型的雷诺平均N-S方程(Reynolds Averaged Navier-Stokes Equations, 简称RANS方程)方法。其基本分类如图 3所示。即:雷诺应力模型(Reynolds-Stress Model, RSM)和涡黏性模型(Eddy Viscosity Model, EVM)两大阵营组成了RANS CFD的物理模型。目前广泛使用的物理模型几乎都是线性EVM,尽管它有一些“致命的弱点”,但因为其简单、经济、鲁棒性好、容易实现、历史悠久、性能特点了解较多、使用者众多等原因,因此本文重点讨论线性EVM,主要包括湍流模型和在湍流模型基础上通过补充经验关系式或输运方程发展而来的转捩模型。
|
图 3 RANS方法分类 Fig.3 Classification of RANS models |
在CFD长期的发展、研究和应用中,越来越认识到湍流模型的重要性。Spalart[7]在湍流模型综述论文指出“湍流模型是CFD的决定因素”;2018年,Durbin[8]在Annu. Rev. Fluid Mech.中明确“湍流模型是大量应用CFD的核心”。
但是,湍流模型一般被认为是CFD中最大的误差源、最薄弱的环节、“最不靠谱”,多次被称为是CFD的Achilles heel(原指荷马史诗中英雄阿喀琉斯的脚跟,现在一般指致命的弱点、要害)[9-10]。因此当CFD结果与实验结果不一致时,湍流模型很容易成为替罪羊[10]。事实上,本文开头介绍的DPW2的统计分析结果也表明:湍流模型对CFD计算精度的影响最大。因此,湍流模型成为制约CFD发展和应用的主要瓶颈。
即便在目前热门的RANS/LES混合类方法中,湍流模型仍然是成功的基础:因为一般湍流主要在近壁产生、输运、耗散等,因此混合方法强烈依赖近壁区湍流特性模拟的准确性,这些都是由湍流模型决定的。
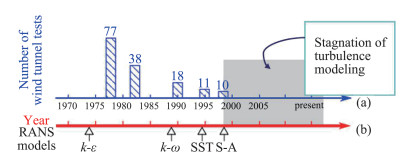
图 4表示的是在过去五十年中,商业飞行器设计一个循环中所需的试验模型数随时间变化。图中蓝色轴线表示在过去五十年中,在商业飞行器设计一个循环中所需的试验模型数随时间的变化,红色的是常用湍流模型发展的时间轴。由图可见,湍流模型在近二十多年中,没有取得显著的进展。结合下面红色的常用湍流模型发展时间轴来看,模型发展之初,在应用中成就斐然,试验模型数显著下降。但是近二十多来来,该数据并没有发生大的变化,导致这一瓶颈的主要原因是湍流模型的预测精度不足。
|
图 4 商业飞行器设计一个循环中所需的试验模型数随时间变化[11] Fig.4 History of number of wind tunnel test during one design period of commercial airplanes[11] |
2010年美国航空航天局(AIAA)下属的湍流模型基准测试工作小组针对湍流模型的应用和未来发展进行了深刻的讨论[12],结论之一即是:尽管对于许多工程流动的模拟不尽完美,RANS将在未来20~50年内依旧得到广泛的使用。目前,国内外CFD界普遍认为:在未来的20~50年,基于湍流模型的RANS方法仍然是CFD的主流。
近20多年来,随着计算机能力的普遍提升,可以通过使用数量更多、质量更好的网格来提高计算格式方面的精度。但是湍流模型的问题来自本身固有的缺陷,改善网格对湍流模型并没有本质的帮助,因此,湍流模型的问题愈加突出。
首先,这里先简单讨论一下Boussinesq线性涡黏性湍流模型的基本原理和特点:Boussinesq基于涡黏性假设,认为湍流脉动引起的动量交换与分子热运动引起的动量交换存在可以类比的关系,引入涡黏性系数将雷诺应力与平均速度应变率联系起来,建立了线性涡黏性模型的本构关系:
| $ - \overline {{u_i}{u_j}} = 2{\nu _t}{S_{ij}} - \frac{2}{3}{\rm{ }}k{\delta _{ij}} $ | (1) |
式中:
线性涡黏性模型建立了雷诺应力——平均速度应变率之间的线性关系(应力和应变之间用一个标量的涡黏性系数,而不是张量联系),这导致了诸多缺陷:
· 各向同性:涡黏性系数的各向同性或标量特性;
· 坐标不变性:雷诺应力依赖于应变率张量;
· 雷诺应力张量与平均速度应变率之间瞬时平衡;
· 雷诺应力与平均场应变率方向相同;
……
各向同性是EVM的致命缺点之一,如航空航天领域最关心的壁湍流,由于壁面的抑制作用而具有非常明确的各向异性。
这些缺陷导致了很多后果,如无法正确预测分离流动、角区二次流、旋转效应、曲率效应等等。大量的理论分析和数值实验表明:一般说来,涡黏性模型只有对二维剪切主导、正应力不重要的简单流动才能给出可靠的结果;对于高速、转捩、流线弯曲、旋转、逆压梯度,尤其是分离流动等复杂湍流,涡黏性模型存在很大缺陷。
最常见的湍流是边界层等壁湍流,在航空航天领域尤其如此。湍流模型的近壁区处理是一个重要、而又常被忽视的问题。由于近壁区流动梯度非常大,而且该区也是湍流产生、输运、耗散、扩散等效应最强烈的区域,模型中的近壁区处理方法对最终的湍流模拟精度如摩擦系数、热流等影响很大,因此是一个非常重要、不幸又是一个非常困难的问题,更严重的是很多湍流模型的使用者对这个关键、复杂而又困难的问题认识不足,因此,它又常常成为湍流模型中的“替罪羊”。
按照近壁区处理方式的不同,一般把湍流模型分为低雷诺数湍流模型和高雷诺数湍流模型,前者可以直接积分到壁面,后者一般使用壁函数等桥接方法。
低雷诺数湍流模型,依赖引入一些以湍流雷诺数和壁面距离等表达的阻尼函数,借此考虑对模化输运方程中各项的近壁影响,这方面的研究是湍流模型经久不息的研究热点之一。实际上,目前广泛使用的k-ε模型自1972年提出后,近50年来的发展主要就是关于黏性阻尼函数和耗散率方程的修正。
目前,低雷诺数模型的使用者较少,这是因为存在以下问题:(1)一些方程系数和函数需要调整且有一定的任意性,对大压力梯度流动等缺乏普适性;(2)近壁大梯度等带来的数值刚性困难;(3)网格量多、计算步长约束大、计算量大。
高雷诺数湍流模型不使用壁阻尼或壁修正等方法,而多是使用壁函数。壁函数就是放弃紧邻壁区域的计算,而在该区域的顶部(壁上第一个网格点处)施加边界条件。在紧邻壁区域内,假定湍流和平均速度遵循指定的关系,如对数律。这就避免了对网格要求很高的紧邻壁区域的求解,大大减少了近壁区的网格量,增大了时间步长,因此有效提高了计算效率。但其缺点也很明显:所指定的关系缺乏普适性,尤其是复杂流动,因此计算精度和可靠性较差。而且,在应用中,实际生成的网格常常不能满足壁函数关于y+等较苛刻的要求,这会带来明显的误差、而且不容易被重视和发现。
回顾湍流模型的发展历史,不难发现,人们在更经济的壁函数和更精细可靠的直接积分到壁面方法之间徘徊、曲折前进。但目前,大多数计算者都更喜欢使用壁函数,因为其简单、经济、鲁棒,当然这是以牺牲精度和普适性等为代价的。也因此可以推论:对壁函数进行进一步改进和通用化是当前CFD最急迫的任务之一。
湍流模型给使用者带来的困难不仅是理论上的缺陷,还包括认识上的困惑。这种困惑一方面来自湍流模型本身的种类很多、假设条件和适用范围复杂、各种经验性系数繁多等等,另一方面来自湍流模型本身性能表现的模糊不清甚至是自相矛盾[10],令人困惑的是,同一种模型在不同的软件上得出的结论也常不一致[10]、甚至一些知名软件也是这样。另外,研究和应用实践也发现:无论是k-ε、k-ω还是SST湍流模型,其中封闭参数的微小改变可能会导致模式性能的显著改善或恶化。近年来的不确定度量化分析也证实了这一结论。
准确、系统地认识湍流模型的性能是研究者和使用者都非常关心的问题。但如前所述,虽然长期以来这方面开展了大量的研究、分析、评估等等,但直到今天,即便对于最简单或最常用的湍流模型,我们也无法给出严格、明确的性能结论。尽管如此,一般说来,经过几十年的不断实践、总结和摸索,对各种湍流模型的性能还是有了一些粗略的认识,这里笔者根据自己的理论认识和实践经验给出航空航天领域常用湍流模型的一些一般性的认识:
1) SA模型:该模型从经验和量纲分析出发得到了关于涡黏性的输运方程,模型中的常数通过大量、广泛的实验数据进行了精细标定,是一个强调应用的实用化模型。突出的优点是鲁棒性非常好、计算效率高、简单实用,是航空航天领域应用最广的模型之一,尤其在航空领域受到普遍欢迎,对附着边界层等较简单的流动效果很好。例如在上述的DPW、HiLiftPW等活动中,SA的使用者数量远超其他模型。但是,一般说来,SA模型的普适性、精度(如涡黏性有时偏大)、对分离等复杂流动的模拟能力等有待进一步提高。
2) k-ε模型:这是RANS历史上第一个实用化的、完备的两方程模型,历史悠久、发展和演化的类型多、使用者众、应用广泛,发展了很多种针对各种情况的修正方法等,但该模型的边界条件处理困难、数值刚性大、稳定性较差,对逆压梯度、分离等模拟效果欠佳,需要普适性差、经验性强的阻尼函数或桥函数等。尤其是在一些较复杂的边界层中,因为ε的扩散模型性能不佳,会高估湍流长度尺度等,这将导致分离抑制或延迟、回流区短、表面摩擦系数和热流过大等难以克服的缺陷。相比SA、SST等模型,现在的趋势是问题较多、应用偏少,在最近的一些大型湍流模型的性能评估中,甚至没有进入评估名单,在DPW、HiLiftPW等系列活动中,使用者也越来越少。
3) k-ω模型:该模型的发展历史悠久,种类很多,这其中应用最成功、最受欢迎的是不同时期、不同版本的Wilcox k-ω两方程模型。该模型数值稳定性好,壁面处可以使用Dirichlet型边界条件,处理难度低、精度高、数值刚性小;因为不需要计算到壁面的最小距离,可以直接积分到壁面,不需要显式壁面衰减函数,因此便于应用在复杂外形流动中;对逆压梯度、分离等问题的模拟性能良好。因此,总体上说来是一个性能优秀、特点鲜明的模型。但其缺点也较明显:对ω的自由来流边界条件过分敏感、湍流近壁渐近特性欠佳等。需要说明的是,近些年该模型的不断完善也在努力改进这些缺点。
4) SST k-ω模型:剪切应力输运(Shear-Stress-Transport,SST)模型,是目前广泛使用的EVM模型中评价性能最好一个,无论是模型研究者还是有经验的实战使用者对它都比较推崇。SST的基本原理是:在近壁处采用k-ω模型、在边界层边缘和自由剪切层采用k-ε模型,并通过Bradshaw假设(剪应力正比于湍动能τ=ρa1k)引入了雷诺剪切应力输运的影响。因此它巧妙结合了k-ω、k-ε和JK模型的优点。除了具有上述k-ω的稳定性好、精度高等优点外,还可以较好地处理湍流剪切应力在逆压梯度和分离边界层内的输运,故SST模型能更好地预测逆压梯度和边界层分离等较复杂的流动情况。因此,SST模型以其精度高、鲁棒性好、适用性较广而成为航空航天领域应用最广的湍流模型之一。
5) 雷诺应力模型RSM:目前CFD界对RSM认识和使用者都很少,但不少人看好RSM的应用前景,甚至认为是未来的主力模型,因此这里较详细地讨论一下。
RSM通过求解由N-S方程严格推导来的、完整的传输方程,从而提供额外的湍流动量通量,在RANS框架下是对湍流最全面的描述。因此被认为是最自然、最符合逻辑的模型,它可以克服涡黏性模型的一些严重缺陷,如各向同性等。但是长期以来的评估分析认为:虽然一般情况下RSM模型比EVM模型具有更高的精度、更广的普适性,尤其是对曲率、旋转、分离等复杂流动情况,但这种优势并不是全面的、明确的。
RSM的主要问题在于:1)雷诺应力方程的建模问题,尤其是压力应变项的建模复杂、困难;2)数值刚性问题较严重;3)计算量较大。但近十多年来,RSM模型在建模和计算方法等方面都取得了较大的进展:模化精度进步较大,数值方法进步明显:计算量已不是大问题,鲁棒性得到改善。例如:使用RSM模型,成功地计算出几个复杂的涡轮机械流动,所用的计算时间与k-ε模型相比仅多了30%[13]。
遗憾的是,至今愿意使用RSM模型的人还是不多,分析原因如下:
1) 一般认为,相比EVM,虽然RSM的性能有改善,尤其对复杂流动,但并没有显示出普遍性、压倒性的优势;
2) CFD界普遍对RSM模型的进展认识不足,习惯用过去的眼光看待今天的RSM;
3) 使用者的习惯或者惯性,也就是说不太愿意接触新的、更加复杂难用的模型;
4) 软件开发和推广困难,因为RSM虽然性能上有优势,但仍然不如EVM使用方便,也还可能包括商业上利益驱动不足。
长期以来,美国、欧洲等开展了多次针对湍流模型的专题研究、性能评估、分析研讨等,近些年来,尤其关注EVM和RSM的对比分析和评估。这是因为一方面EVM在目前的CFD占主导地位、而RSM有希望成为未来的主流;另一方面,RSM在建模方法、数值刚性、计算效率等方面取得了较大的进步,而EVM的表现不尽如人意。
为了对EVM和RSM的性能有一个直观的认识,也为了介绍上述的性能评估,作为示例,这里给出一个比较严谨的湍流模型性能研究。
文献[14]使用多个经典标模,系统深入地对比研究了4个经典湍流模型:EVM(SA、SST)和RSM(SSG /LRR-ω、JHh-v2)。这4个湍流模型是目前学术界公认的、具有代表性的优秀湍流模型。计算结果分析表明:对于简单标模如小压力梯度平板边界层,4个模型计算结果非常一致;随着标模复杂性的增加,一般情况下,RSM表现出了有更大的适用性和更高的精度,但这种结果的改善常常不是很明显,也不是很普遍。
这里较详细地讨论一个计算结果改善明显的标模算例:ONERA M6机翼。这是一个经典的湍流模型验证标模,常用来检验湍流模型的跨声速性能,尤其激波诱导分离的模拟水平。使用DLR TAU软件计算,流动参数:Ma=0.84,Re=11.72×106,0.03°≤ α ≤ 6.06°。
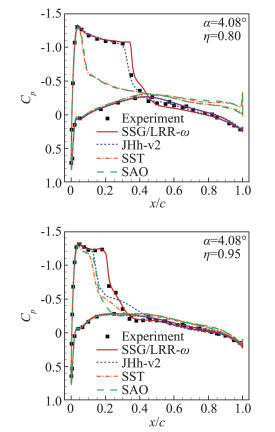
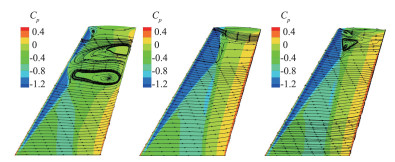
α=3.06°之前的计算结果表明,不同湍流模型的预测之间几乎没有任何差异。但α= 4.08°时,在机翼外侧,RSM模型的结果部分同EVM模型结果大相径庭。图 5显示了两个机翼外侧展向截面站位分别为80%和95%的压力分布。可以看到,SA和SST模型的预测与实验结果明显不同,而SSG/LRR-ω模型所预测的压力分布与测量结果都非常吻合,JHh-v2 RSM预测的激波位置在80%展向截面处同实验更加吻合、但在95%展向截面时偏差明显。图 6显示了机翼上表面的摩擦线图,可以看到,SST模型预测的机翼外半部有很大的分离,而SSG/LRR-ω模型预测的分离仅限于激波根部后面的小区域,根据压力分布,这个结果与实验吻合得更好,JHh-v2模型预测的分离流展向延伸得更小。
|
图 5 ONERA M6不同展向站位的压力分布[14] Fig.5 Pressure distribution at different spanwise locations of ONERA M6[14] |
|
图 6 ONERA M6机翼上表面摩擦线和压力分布(α= 4.08°)SST模型(左),SSG /LRR-ω模型(中)和JHh-v2模型(右)[14] Fig.6 Wall friction lines and pressure distribution of the supper surface of ONERA M6 (α=4.08°). Left: SST, middle: SSG/LRR-ω, right: JHh-v2[14] |
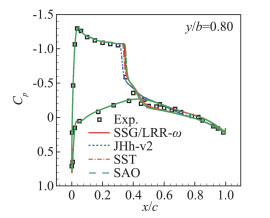
进一步的研究还发现了另一个不希望的结果:除了SSG/LRR-ω外,其他3个模型显示出了对网格质量的高度敏感性,只有SSG/LRR-ω模型在两套网格上都与实验结果一致吻合。在上述计算网格的基础上,保持网格总量基本不变、重点在激波附近加密网格,结果4个湍流模型都给出了非常好的结果,如图 7,对比图 5,网格效应明显,显然这个结果不是使用者希望的。
|
图 7 ONERA M6 η=0.8展向站位的压力分布[14] Fig.7 ressure distribution at the spanwise location of η=0.8 for ONERA M6[14] |
其他较复杂的经典标模的计算结果表明:在翼尖涡旋、弯管流动等算例中,RSM的优势更明显,这是因为线性涡黏性模型无法考虑流线曲率等效应。
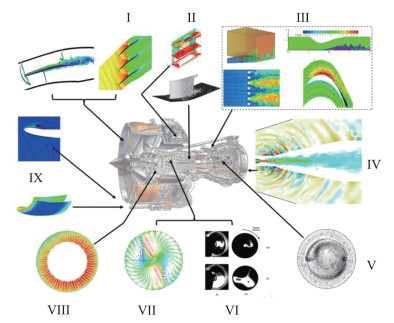
1.2 转捩模型转捩是流动从分层稳定的层流状态演化为混沌紊乱的湍流状态的连续物理过程。由于内在演化机制高度复杂,转捩流动被认为是经典物理学遗留的最具有挑战性的问题之一,具有重要的理论研究意义。同时,转捩现象与社会经济发展和科技进步的重大科学问题密切相关。国务院2018年印发的《“十三五”国家科技创新规划》部署了面向2030年的一批重大科技项目,其中的航空发动机及燃气轮机项目重点攻关的多类复杂流动与转捩密不可分(如图 8所示)。以涡轮叶片为例,受自由来流湍流度、来流雷诺数、流动分离和非定常尾流等多类因素影响,涡轮叶片的流动大多涉及边界层转捩现象,包括但不限于旁路转捩、分离诱导转捩、逆转捩(再层流化)以及上游叶片尾流导致的周期性转捩等。早期研究认为尾流诱导的转捩会增加涡轮叶片流动损失,但随着认知深入,人们发现上游尾流效应还可以被用来控制叶片吸力侧的边界层转捩过程,从而抑制流动分离,在不牺牲效率的情况下提升低压涡轮叶片的升力、节约成本。由此可见,深入开展转捩研究、准确预测转捩对现代涡轮设计和性能评估有重要指导意义。此外,边界层转捩还将显著影响高超声速飞行器的壁面摩擦阻力、气动热环境、流动分离位置和进气道流场品质等,是发展高超声速飞行器技术必须攻克的瓶颈问题。
|
图 8 高涵道比涡扇发动机中的湍流/转捩现象[15] Fig.8 Modern bypass engine section and examples of CFD simulation zones considered[15] |
目前针对边界层转捩/湍流的数值模拟研究方法主要包括DNS、LES、转捩准则、稳定性理论和基于RANS的湍流/转捩模型方法。这其中,基于RANS的转捩模型方法由于优越的经济性和鲁棒性,是现有条件下最有可能应用于工程复杂外形边界层转捩预测的数值模拟方法。
经过二十余年的快速发展,转捩模型方法的研究取得了长足的进步,截止到目前,文献公开发表的基于RANS方程的转捩模型就已多达几十种,其宗旨都是合理预测转捩起始位置(即转捩判据的建立)和转捩区长度。同时,转捩模型的发展伴随着人们对转捩物理机理认知的日益丰富也在不断进步。这方面里程碑式的工作是转捩流动间歇性和层流脉动(或称非湍流脉动)的发现。这两个转捩流动关键特征的提出,为转捩模型的发展和改进提供了重要的理论依据和指导价值,由此发展出一系列面向工程应用背景的转捩数值预测手段。根据所构造的转捩模型对这两个重要概念的模化程度,本文将现有涡黏性RANS转捩模型分为低雷诺数湍流模型、基于间歇因子的转捩模型和基于层流动能的转捩模型三类。
1.2.1 低雷诺数湍流模型低雷诺数湍流模型既没有考虑转捩的间歇现象,也没有描述层流动能,其核心思想是通过阻尼函数限制黏性子层湍动能的生成,从而在一定程度上达到模拟边界层转捩的效果。比较著名的工作是Wilcox的研究,他在k-ω湍流模型的封闭参数和涡黏性中引入了一个关于湍流雷诺数的人工阻尼函数[16]。湍流雷诺数表达式为ReT=ρk/ωμ,通过变换可表示为涡黏性系数μt和分子黏性系数μ的黏性比ReT=μt/μ。流动为层流时,湍流雷诺数远小于1(ReT≪1)。当流动接近转捩起始位置时ReT近似为1,从而导致湍动能k迅速增长。随着k增长,涡黏性和壁面摩阻开始增大,ReT随之变大,一旦ReT≫1湍动能比耗散率ω开展增长,直到k方程的生成项和耗散项达到平衡,此时层流到湍流的转捩过程结束,流动转捩为湍流。基于ReT构造的低雷诺数湍流模型还有很多,例如Jones和Launders的k-ε模型[17],Hadzic和Hanjalic的SMC模型[18]等。Langtry和Sjolander的模型也可归为此类,不同的是,其用涡雷诺数ReV代替ReT作为转捩起始位置的判定因子[19]。通过上述描述可发现,低雷诺数湍流模型对转捩现象的模拟纯粹由模型的数值特性引起,并无物理背景。Zheng等[20]的研究发现,Wilcox的k-ω低雷诺数模型预测的转捩起始位置过于提前,且不能正确预测分离诱导转捩。Rumsey [21]通过深入分析认为低雷诺数模型对转捩的预测只是一种巧合,并将其称之为“伪转捩”。越来越多的研究指出“只应用湍流模型而不考虑转捩现象的间歇性,对转捩过程的模拟是脆弱且不可靠的”[22]。因此,尽管低雷诺数湍流模型作为早期的转捩研究工具,对转捩模型的发展意义重大,但建立基于转捩物理机理的转捩模型刻不容缓。
1.2.2 间歇因子转捩模型这类模型考虑了转捩物理过程中的间歇现象,从而将层流、转捩和湍流等不同发展阶段的求解解耦。转捩区域流动的间歇现象最早由Emmon[23]发现,自此转捩问题的理论研究有了实质性突破。所谓间歇现象是指在转捩过程中,同一空间位置层、湍流交替出现的现象,通常用间歇因子γ来描述。对于γ的求解,目前主要有两种方法:第一种方法也是最简单直接的方法,是根据实验数据拟合出代数经验公式;第二种方法是根据拟合公式构造γ输运方程。
首先介绍第一种方法,Dhawan和Narasimha[24]最早根据平板边界层的实验数据给出了γ沿流向分布的经验拟合式:
| $ \gamma = {\rm{ }}\left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x < {x_t}\\ 1 - {\rm{exp}}\left[ { - \frac{{{\rm{ }}{{(x - {x_t})}^2}n\sigma }}{U}} \right]{\rm{ }},\;\;x \ge {x_t} \end{array} \right. $ | (2) |
其中,n代表展向单位距离的湍斑生成速率,σ表示湍斑扩散参数,xt为转捩起始点。上式可无量纲化为以下两种形式:
| $ \begin{array}{l} \gamma = 1 - {\rm{exp}}\left[ { - {{\left( {\frac{{{\rm{ }}x - {x_t}}}{{{\theta _t}}}} \right)}^{2{\rm{ }}}}\frac{N}{{R{e_{\theta t}}}}} \right]{\rm{ }},N = n\sigma {\rm{ }}\frac{{\theta _t^3}}{\nu }\\ \gamma = 1 - {\rm{exp}}\left[ { - {{\left( {\frac{{{\rm{ }}x - {x_t}}}{{{\theta _t}}}} \right)}^{2{\rm{ }}}}\hat n\sigma Re_{\theta t}^2} \right],\hat n = n{\rm{ }}\frac{{{\nu ^2}}}{{{U^3}}} \end{array} $ | (3) |
式中N是无量纲的破碎参数,
| $ \begin{array}{*{20}{l}} {\gamma \left( y \right) = 0.5{\rm{ }}\left[ {1 - {\rm{erf}}\left( \zeta \right)} \right]{\rm{ }},}\\ {\zeta = 5\left( {y/{\delta ^*} - 0.78} \right)/8} \end{array} $ | (4) |
其中,δ*为边界层位移厚度。Addison和Hodson[28-29]提出了Prescribed Unsteady Intermittency Model (PUIM)方法以使γ在流向和法向的分布均吻合实验数据。PUIM中γ是一个关于壁面Emmon斑(湍斑)发展特征的积分表达式,其只对自然转捩和旁路转捩有效。此外,基于代数经验公式的方法还有Steelant和Dick[30]提出的γ模型,Fürst等[31]建立的模型等,在此不一一赘述。这种通过代数经验拟合式求解γ的方法应用范围有限,其严重依赖于来流和外形条件,无法反映转捩区间歇现象的非当地效应和历史效应。
为克服这一缺陷,人们尝试引入γ输运方程来求解三维流动中的γ分布规律。Libby[32-33]在1975年构造了间歇因子输运方程,Dopazo[34]、Chevray和Tutu[35]在其基础上对输运方程进行了改进和发展。Cho和Chung[36]将γ输运方程与k-ε湍流模型相耦合,开创性地提出了k-ε-γ转捩模型,并将其成功应用于平面射流、圆射流和尾流等剪切流的转捩预测。以上输运方程均针对自由剪切流发展而来,不适用于边界层流动中的转捩模拟。Savill[37]在Cho和Chung[36]模型的基础上发展了适用于边界层转捩的γ输运方程。Steelant和Dick则[38]借鉴Dhawan和Narasimha经验拟合式[24]构造了新的γ输运方程。比较代表性的工作还包括Suzen和Huang[39],Suzen等[40]和Pecnik等[41]发展的边界层流动γ输运方程,这些模型在特定三维流场计算中都获得了满意的结果。
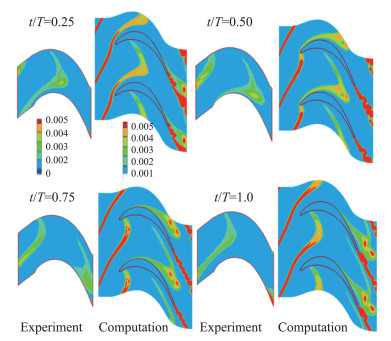
然而,间歇因子只描述转捩过程,为实现流动的转捩预测,往往还需要一个与之分离的转捩起始位置判据。转捩起始位置受众多因素影响,加剧了预测难度[42]。目前转捩起始位置判据通常基于经验公式发展而来,以动量厚度雷诺数Reθ最为常见。首先积分求解层流流场中每个流向位置Reθ值,一旦判定当地Reθ超过经验确定的临界值,即可认为转捩发生。然而需要积分求解的非当地变量的引入,限制了这类转捩模型在非结构并行求解器中的应用。为此,阎超等[43-44]提出了适用于大规模并行计算的网格重排序循环盒子法来识别边界层参数。Menter和Langtry等[45-46]通过使用应变率为底的雷诺数Rev代替动量厚度雷诺数Reθ,创新性地提供了一个将转捩判据进行完全当地化处理的框架,进而提出了γ-Reθ转捩模型。该工作具有十分重要的借鉴意义,在学术研究和工程应用方面受到了广泛关注。大量算例验证表明,γ-Reθ模型在涡轮机、风力发电机以及其他工业应用中都可得到满意的预测结果[46]。图 9给出了γ-Reθ模型计算的T106涡轮叶片在不同尾迹周期的湍动能分布与实验值的对比,可见计算与实验结果吻合良好。但需要指出的是,γ-Reθ模型的构造完全依赖于低速流动实验数据的经验拟合,并不反映边界层转捩过程中的物理机制,导致适用范围有限,尤其在应用于拟合数据适用范围之外的其他转捩问题时,如高速边界层转捩,其模型构造往往需要进行重新拟合与标定。郝子辉和阎超等[47]构造了适用于高超声速流动的涡雷诺数Rev与边界层动量厚度雷诺数Reθ的拟合关系,实现了γ-Reθt转捩模型的高超声速修正。
|
图 9 T106涡轮叶片不同尾迹周期(t/T)湍动能分布云图(左:实验,右:γ-Reθ模型)[46] Fig.9 Contours of turbulent kinetic energy at various wake passing periods (t/T) of T106 turbine blade cascade (left: Experimental data, right: γ-Reθ model)[46] |
此外,γ-Reθ模型还需要一个额外的动量厚度雷诺数Reθ输运方程将自由来流中经验拟合的当地动量厚度雷诺数
总体而言,基于间歇因子的转捩模型可较为合理地描述转捩过程,但通常需要额外构造一个转捩起始位置判据,且目前该判据的建立高度依赖于实验数据的经验拟合,而对转捩前区域的物理机制考虑不足,极大地限制了该类转捩模型的适用流动范围。
1.2.3 层流动能转捩模型随着对边界层转捩机理认知的不断深入,人们发现通过对转捩前层流动能的刻画即可实现转捩起始位置的自动判断,为此发展出一系列层流动能转捩模型。顾名思义,这类模型考虑了转捩物理过程中层流动能的发展,当边界层转捩流动前的层流动能发展到一定程度时判定转捩发生,因此又被称为基于物理机理的转捩模型(Physics-Based Transition Models)。
实验研究发现,转捩起始点前的层流区域中的流动并不是稳定的,其存在类似湍流脉动的结构,Mayle和Schulz[51]将其称为“层流脉动”或“非湍流脉动”。层流脉动与湍流脉动有着显著的区别,具体表现在以下三个方面:首先,从能量分布的角度来看,层流脉动的能量几乎全部包含在流向分量上;其次,从动力学特性的角度来看,层流脉动不存在经典湍流脉动中能量由大尺度向小尺度输运的能量级串过程;最后,层流脉动频率相对较低,除了壁面附近,其耗散也较低。层流脉动结构的发现对转捩预测极具吸引力,并由此开辟了一个新的转捩模型研究思路。就目前而言,边界层层流脉动发展的物理机制还未被完全揭示,不过主流思想认为:边界层对自由来流中特定尺度涡的选择性以及边界层内低频扰动被流动剪切作用放大的过程对层流脉动的发展影响显著。Bradshaw[52]提出了Splat机制来揭示层流脉动的演化发展过程。Splat机制认为,壁面的约束作用强迫边界层内法向脉动方向发生改变,导致当地局部压力梯度的出现,进而诱导层流脉动的产生和发展。尽管如此,层流脉动的发展规律和频率选择性仍尚未被完全揭示。
目前层流脉动的主流计算方法包括两种,一是建立层流脉动动能kL的输运方程,二是比拟湍流涡黏性系数μt对层流脉动黏性系数μnt进行模化。
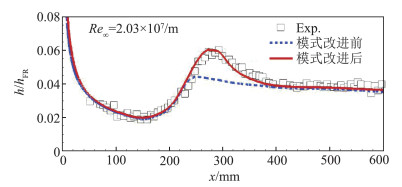
层流脉动动能kL输运方程的建模关键是层流脉动的产生和能量由层流脉动向湍流脉动的输运。Mayle和Schulz[51]首次通过类比湍动能kT的输运方程构造了kL的输运方程,不同的是将kT方程产生项的应力/应变替换成了压力脉动。这也反映了层流脉动不同于湍流脉动的产生机制。Walters等基于Splat机制,将边界层内的脉动能量分为有壁面约束的层流动能kL和无壁面约束的湍动能动能kT,由此构建了kL输运方程,并分别基于k-ε和k-ω湍流模型发展了kT-kL-ε[53]和kT-kL-ω[54]转捩模型,成功实现了对转捩起始点的自动判断。秦玉培和阎超等将kT-kL-ω转捩模型拓展至高超声速边界层的自然转捩[55]预测,并针对原始模型对转捩峰值位置“overshoot”现象预测不足的问题,通过分析湍动能扩散时间尺度与湍动能输运时间尺度之间的关系构造了新的代数型间歇因子,成功实现了对“overshoot”现象[56]的准确模拟(如图 10所示)。刘再接和阎超等[57]进一步拓展了kT-kL-ω模型对粗糙单元诱导转捩现象的预测功能。陈灿平等[58]通过引入分离敏感参数修正了小尺度涡黏性系数,改进了层流动能转捩模型对于流动分离区域数值预测的准确性。
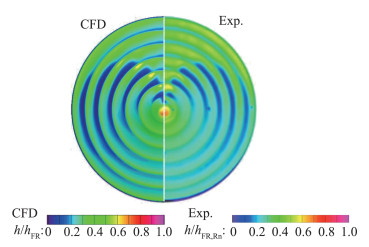
第二种描述层流脉动的方法是直接模化层流动能黏性系数μnt,该思路最初由Warren等[59]提出。他们以k-ζ湍流模型为基础,将其中的涡黏性系数μt替换为有效涡黏性系数μeff,从而在黏性系数中显示层流脉动的影响。μeff的表达式为μeff =(1-γ)μnt+γμt,其中μnt的构造利用了稳定性分析的模态理论结果。国内王亮和符松[60-61]借鉴Warren等[59]工作,发展了完全基于当地变量的k-ω-γ转捩模型。该模型的特色之处是对超/高超声速边界层转捩现象的预测。赵雅甜和阎超等[62-63]通过对比评估k-ω-γ和γ-Reθ、kT-kL-ω转捩模式在高超声速充气式柔性减速器外形转捩现象预测中的性能发现:γ-Reθ和kT-kL-ω模式预测的转捩位置严重偏离实验值,而k-ω-γ模型计算得到的转捩起始位置和转捩阵面均与实验值吻合良好(如图 11所示)。周玲和阎超等进一步对k-ω-γ转捩模型进行了雷诺数效应修正[64]、头部钝度修正[64]和横流拓展[65],并拓展应用于复杂工程外形的转捩预测,取得了较为满意的结果。
|
图 11 k-ω-γ模型(CFD)计算的高超声速充气式柔性减速器壁面热流分布云图与实验值(Exp.)对比[62] Fig.11 Surface heat flux contours of Hypersonic Inflatable Aerodynamic Decelerator predicted by k-ω-γ model (CFD) compared with experimental data(Exp.) [62] |
总体而言,层流动能转捩模型较为充分地考虑了转捩过程的物理机理,显示出了较大的应用潜质和优势。然而,由于目前层流动能的机制尚未被完全揭示,再加上多种不稳定扰动模态相互干扰的复杂性,现有基于层流动能的转捩模型依然难以解析地给出三维边界层流动的转捩起始位置和转捩过程。同时,无论是kL输运方程的建立,还是层流动能黏性μnt的构造,都不可避免地增加了转捩模型中经验参数的数量,从而导致预测结果的更大不确定性。针对这一现象,赵雅甜和阎超等[66-67]、张金程和符松[68]开展了相应的不确定度量化研究工作。
本文根据转捩模型构建思路和构造方式的差异将转捩模型分为三类,但需要注意的是各类方法间并没有明确清晰的界限。例如,王亮和符松提出的k-ω-γ模型[60-61]既考虑了转捩前的层流脉动动能,又建立了间歇因子输运方程,同时该模型以SST湍流模型为基础框架,因此还会受到低雷诺数模型中阻尼函数的影响。此外近年来还有一些新的方法不断涌现,他们并不属于这三类方法的范畴。例如,依据层湍流发展过程中的动力学近似发展的三维唯象V-model模型[69]以及基于机器学习的数据驱动湍流/转捩建模方法[70-71]等。这些新方法的提出丰富了转捩的模拟手段和求解思路,具有重要的研究价值。
2 计算方法在航空航天领域,CFD是通过数值求解流体动力学方程,来获取各种流动条件下的流场数据以及作用在绕流物体上的气动载荷的。因此,直接针对控制方程进行离散化求解的计算格式,如通量格式和高阶格式,就一直是学界研究的热点。它们通过模拟离散化控制方程所表征的流动演化,起着反映流动物理性质的作用。而CFD领域中的其他关键技术,如湍流模拟、转捩预测等方面的研究,都需要建立在方程物理性质能够被准确刻画的基础之上。所以,计算方法也一直被视作为CFD的基石之一。而NASA发表的CFD2030报告中也明确指出:计算格式是未来需要大力发展的关键技术之一。为此,本节将针对航空航天中通量格式和高阶格式的研究进展分别进行评述。
2.1 通量求解方法研究进展通量格式通常被大致分为两类:中心类通量格式和迎风类通量格式[72]。而较之于中心类通量格式,迎风通量格式是在精确Riemann解的基础上,通过近似求解Riemann问题,考虑了实际流动过程中波的传播方向、物理意义更加明确。此外,这类方法还具有计算效率和计算精度的综合优势,因此成为了当前CFD中应用最为广泛的计算方法。例如,工业界广泛使用的商业或in-house软件,如FLUENT、CFD++、CFL3D、FUN3D、OVERFLOW、BCFD等,均采用迎风类通量格式作为自己的核心算法。所以,本文将着重针对迎风类通量格式展开讨论。
目前,根据各自构造思想的不同,迎风类通量格式被分为三类。
第一类是基于近似求解Riemann问题的通量差分分裂类格式(Flux Difference Splitting, FDS)。其中,Roe格式因为其对接触间断与激波的高分辨率而应用最广。但是在模拟膨胀波时,Roe格式会因为违反熵条件而产生非物理解,需要引入熵修正。熵修正需要经验性人工参数的设置,不同的参数设置对流场计算精度的影响较大[73]。
第二类是矢通量分裂格式(Flux Vector Spliting, FVS)。它们基于特征值符号的信息对通量项进行分裂和定向离散,比较有代表性的是Steger and Warming格式和van Leer格式。这类方法有激波捕捉能力强、可靠性高,以及计算效率高等优点。但是该类格式无法精确捕捉接触间断,黏性区分辨率较差。
第三类是混合的AUSM(Advection Upstream Splitting Method)类格式。这类格式通过对压强通量和对流通量分别进行相应的通量分裂,结合了FVS类格式的高效率以及FDS类格式的高间断分辨率,并且克服了二者的缺点。其中,基于对流通量或者压强通量构造方式的不同,这类方法包括AUSM+、AUSMDV、AUSMPW+等一系列格式[74]。此外,还有一些方法采用了其它不同的通量分离模式,例如Zha-Bilgen通量分裂方法以及Toro通量分裂方法等[75-76]。
从上述三类迎风类通量格式的简要介绍可以看出,作为CFD领域所围绕的发展主线之一,通量格式无论在理论研究方面还是在工程应用方面,近几十年来都受到了广泛的关注并取得了一定的进展。然而正如本文引言部分所述,作为航空航天领域所广泛使用的通量计算方法,它们却一直没有取得太多本质上的进步,如下一些不足致使它们距离“完美”还非常遥远:
1) 在模拟强激波时,容易出现激波异常现象;
2) 在计算膨胀流动时容易出现非物理的“overheating”解;
3) 在模拟椭圆型的低速不可压流动时,会出现精度下降、收敛困难等问题,无法适用于全速域流动的高精度数值模拟;
4) 在针对流动分离、激波/边界层干扰这类多维复杂流动进行数值模拟时,会出现精度降低和计算稳定性下降等问题。
下面我们将针对这四个问题,就近年来国内外学者所取得的研究成果以及遇到的挑战进行简要概述。
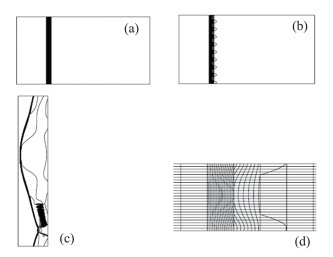
2.1.1 激波异常问题激波异常现象是指CFD在模拟高马赫数流动中的强激波问题时,容易因为出现非物理的激波不稳定解而得到错误的气动力/热载荷。1988年Perry等在使用Roe格式计算高超声速圆柱绕流问题时首先发现了该问题,并将其称之为“红玉”现象(图 12)[77]。在此之后,大量学者针对该问题开展了深入的研究,其中比较有代表性的工作可以参见文献[78,79]。但是,2010年Roe等通过计算一维/二维静驻激波问题指出,即使是公认的激波捕捉最为稳定的van Leer格式,在平行于激波方向的网格尺度过小时,也会出现非物理的激波异常现象(图 13)[80]。也就是说,现有的所有通量格式都无法完全避免激波异常现象的出现,而激波处的网格长细比显著影响着它们的激波稳定性。

|
图 12 激波异常现象 Fig.12 The shock anomaly phenomenon |
|
图 13 1.5D静驻激波问题中van Leer’s FVS格式在不同网格下计算得到的密度分布图[80] Fig.13 Density contours of the 1.5D steady shock problem obtained by van Leer's FVS[80] |
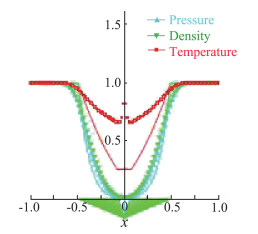
2011年,Liou在“Open Problems in Numerical Fluxes: Proposed Resolutions”的文章中首次明确指出,现有通量格式在计算膨胀流动或对撞流动时都会出现非物理的温度跳跃,即“overheating”现象(图 14)。而加密网格、增加时间迭代步数或者采用高阶重构方法均无法有效解决该问题[81]。针对这一不足,Liou开展了详细的理论分析并发现,造成“overheating”现象出现的直接原因是当前通量格式在计算无黏流动时无法保证熵守恒。基于该结论,他提出了一种熵守恒的通量计算方法。但遗憾的是,这种方法需要与时间推进强耦合,不适用于现有的CFD软件体系,因此在航空航天领域没有得到推广应用。
|
图 14 膨胀流动模拟中的“overheating”现象[81] Fig.14 The 'overheating' phenomenon in simulating the receding flow problem [81] |
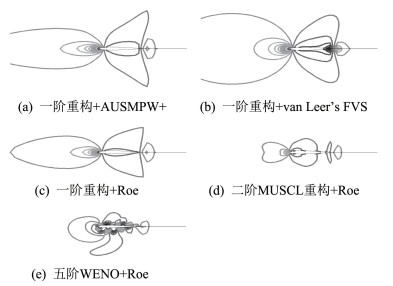
特征分析表明,描述无黏流动的Euler方程在不同速域中的数学特性差别较大。例如,描述低速近不可压流动时,Euler方程为椭圆型;描述超声速流动时,Euler方程为双曲型。理论上针对不同特性的微分方程组应采用不同的空间离散方法[82]。因此,上述基于可压缩Euler方程求解进行构造的通量格式难以实现对低速流动的高精度模拟。甚至在很多情况下,即使加密网格或者采用高阶重构方法,它们也依旧无法给出令人满意的结果(图 15)[83]。
|
图 15 低速无黏NACA0012翼型等密度分布图(Ma=0.05)[83] Fig.15 Density contours of inviscid flow over the NACA0012 airfoil[83] |
针对该问题,Guillard等通过对可压缩Euler方程开展低速渐近性分析发现,在低速近不可压流动中,流场中压强扰动的幅值与马赫数满足如下的关系式:
| $ \Delta p = p\left( {x,t} \right) - {P_0}\left( t \right) = {M^2}_ * {p_2}\left( {x,t} \right) $ | (5) |
而传统的通量格式在模拟低速流动时得到的流场解无法满足式(5)。因此,它们难以高精度模拟低速流动[84]。为了改善这一缺陷,Weiss与Turkel等在特征分析可压缩Euler方程的基础上,通过引入预处理矩阵,有效改善了离散化可压缩Euler方程在低速近不可压流动中的刚性问题,提高了通量格式在低速近不可压流动区域的模拟精度[85]。然而,这类预处理方法存在如下不足:自由来流条件为超声速时,预处理方法完全失效,如果此时流场存在低速流动区域,该区域的计算精度难以保证;需要设置经验性人工参数,这种参数应该根据具体的流场变化,难以找到普适的量化准则。针对该问题,李雪松对Roe格式开展了低速渐近性分析。通过量纲分析他发现,Roe格式中压强耗散项系数过大导致其难以高精度求解低速流动。基于该结论,李雪松将无量纲化离散方程中压强耗散项的量级修正至O(M),改进了Roe格式的低速模拟精度[86]。Thornber、Rieper、FillionShima和Kitamura等也开展了类似的工作[87]。
但是,这些研究并没有关注格式在捕捉强激波时所遇到的稳定性问题。为此,笔者借鉴李雪松等的工作,针对Roe格式同时开展了高速的激波线性小扰动分析及其低速的渐近性分析,揭示了通量格式中各耗散项系数在低速流动模拟以及激波捕捉中应满足的构造准则是相互补充而非互相矛盾的。基于上述结论,笔者提出了一种适用于全速域流动模拟的RoeMAS格式[88]。此后,Tsoutsanis、Chen、Xie等也开展了类似的工作[89-91]。
下面展示几个全速域通量格式在航空航天中的应用实例。
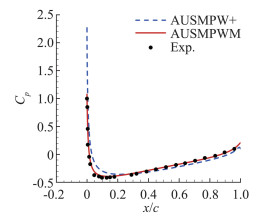
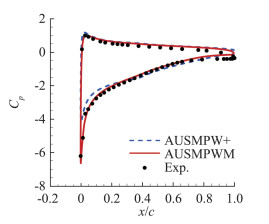
图 16和图 17分别对比了低速NACA0012和NACA0042翼型有黏绕流算例中不同格式计算得到的壁面压强系数分布[92]。其中,AUSMPWM格式是基于AUSMPW+格式,通过抑制低马赫数情况下的压强耗散而构造的一种全速域通量格式[93]。可以看到,在低速流动模拟中,全速域通量格式的模拟精度明显优于传统通量格式。
|
图 16 低速有黏NACA0012翼型壁面压强系数分布对比(Ma=0.15, Re∞=6×106)[92] Fig.16 Distributions of pressure coefficients along the wall in viscous flow over the NACA0012 airfoil (Ma=0.15, Re∞=6×106)[92] |
|
图 17 低速有黏NACA4412翼型壁面压强系数分布对比(Ma=0.09, Re∞=1.52×106)[92] Fig.17 Distributions of pressure coefficients along the wall in viscous flow over the NACA4412 airfoil (Ma=0.09, Re∞=1.52×106)[92] |
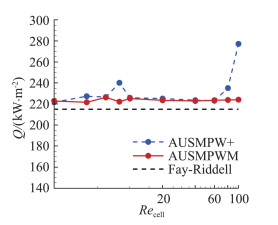
图 18展示了高超声速钝锥绕流问题中,不同格式计算得到的驻点热流值同网格雷诺数的对应关系[94]。从中可以看出,采用全速域通量格式可显著改善高超声速气动热预测精度对计算网格的依赖性,有利于降低使用者的技术门槛。但是遗憾的是,针对全速域通量格式在知名商业软件或者in-house工程CFD代码中的应用推广,尚没有相关公开报道。
|
图 18 高超声速钝锥扰流驻点热流值随网格雷诺数变化曲线对比[94] Fig.18 Schemes' stagnation heating values vs. the cell Reynolds number[94] |
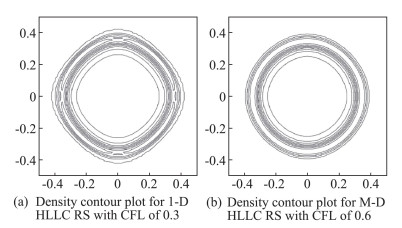
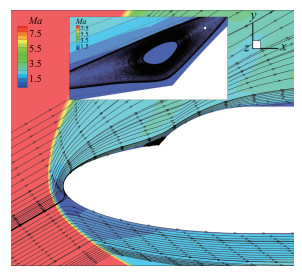
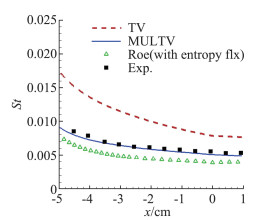
2017年Abgrall和Roe在Handbook of Numerical Analysis一书中先后指出,基于维度分裂思想进行构造的传统通量格式,在针对流动分离、激波/边界层干扰这类多维复杂流动进行数值模拟时,仅考虑了沿着网格界面法向传播的信息而忽略了沿着网格界面横向传播的信息,因此无法准确描述空间中不同维度之间的相互影响,容易出现精度降低和计算稳定性下降等问题。为了克服该缺陷,诸多学者开展了关于多维通量格式的相关研究。其中比较有代表性的工作包括文献[95-97]。但是,这些多维通量格式构造复杂,或针对定常流动求解只能显式推进、无法结合隐式时间推进方法实现求解加速,所以尚未在复杂流动模拟中得到广泛应用。为了解决这个问题,Balsara通过在网格角点处构造二维干扰波系,提出了一种形式简单的多维HLL通量求解方法[98]。图 19所展示的径向冲击波算例的计算结果表明,该方法在求解多维波传播时,可以基本实现流场解与网格分布的相互解耦[99]。基于该工作,Mandal等在Zha-Bilgen通量分裂思想的基础上,将流动控制方程中的无黏通量项分解成压强通量项及对流通量项,并通过直接采用Balsara所构造的多维干扰波模型,实现了可精确捕捉线性接触间断的多维GM-HLL-CPS-Z通量求解方法[100]。袁礼等基于TV格式的分裂思想,也提出了类似的多维HLL通量求解方法[101]。笔者基于坐标变化,将上述工作推广至一般曲线坐标系,提出了一种适用于复杂飞行器流动模拟的多维通量求解方法MULTV格式[102]。高超声速二维双椭球绕流算例的计算结果验证了该方法在多维复杂流场模拟中的精度优势(图 20、图 21)。然而,当前关于真正多维Riemann通量求解方法的研究仍比较初步,针对三维、宽速域流动问题的算法研究较为匮乏。
|
图 20 高超声速二维双椭球等马赫数云图[101] Fig.20 Mach contours of the hypersonic viscous flow over the two-dimensional double-ellipsoid[101] |
|
图 21 不同格式得到的壁面斯坦顿数分布(高超声速二维双椭球算例)[102] Fig.21 Distributions of the schemes' Stanton numbers along the meridians of the windward side[102] |
假设网格尺度为h、数值解的误差为e,如果e∝hk成立,则称数值格式为k阶精度。一般将离散精度高于二阶(即k≥3)的计算格式统称为高阶格式[103]。相比于低阶格式,高阶格式被认为在花费较低计算代价的前提下具备获得更高精度的巨大潜力,因而引起了CFD研究者和用户的广泛关注。国外方面,专注于高阶格式的研讨会“The International Workshop on High-Order CFD Methods”[104]已分别于2012年、2013年、2015年、2016年和2018年举办了五届。国内方面,已连续举办了两届(2018年和2019年)“计算流体力学中高精度数值方法及应用”(Trends of High Order Numerical Methods for Computational Fluid Dynamics and Their Applications)研讨会。
CFD发展到今天,出现了多种高阶格式,主要包括:
1) 有限差分类高阶格式:WENO(weighted essentially non-oscillatory)格式[105-106]、TENO(targeted ENO)格式[107]、紧致格式[108]、保单调格式[109]、WCNS格式[110]、ENN格式[111]等。这类方法最突出的优点是高精度、高效率,编程实现相对直观,较多应用于外形相对简单的湍流大涡模拟和直接数值模拟。然而,有限差分类格式只适用于结构网格,并且其数值解的质量与度量系数的计算精度相关,因此要求网格要足够光滑。这一要求很难在复杂构型的网格生成中得到满足,也限制了此类方法向实际工程问题的推广。
2) 有限体积类高阶格式:有限体积WENO格式[112]、高阶紧致重构格式[113]等。有限体积格式适用于非结构网格,因此,对于工业级CFD软件,二阶精度的有限体积格式是最常用的数值离散框架。然而有限体积法需要扩展重构模板来实现高阶精度和增强稳定性,而由于非结构网格的无序性,使得高阶有限体积法无论是算法设计还是程序编写都较为繁琐。同时,扩张的模板也给计算效率带来较为严重的负面影响。为应对上述问题,Wang等[113]通过引入相邻单元导数的信息来有效控制模板的范围。
3) 有限元类高阶格式:SD (Spectral Difference)[114]、SV (Spectral Volume)[115]、DG(Discontinuous Galerkin) [116]、FR(Flux Reconstruction) [117]、SUPG (Streamline upwind/Petrov-Galerkin) [118]等。这类格式与有限差分和有限体积类格式的最大差别是:有限差分和有限体积类格式通过扩张插值或重构模板,引入周围单元更多的信息来提高精度,而有限元类高阶格式则通过在一个网格单元内引入更多自由度来提高精度,而无需扩展模板。这一特征决定了有限元类格式可以较容易地在非结构网格上实现任意高阶精度,也是近年来获得较多关注的高阶格式。有限元类高阶格式在带来高精度的同时,也在网格生成、时间推进以及激波捕捉等方面迎来了挑战。本节后面将详细论述。
4) 其他衍生类型高阶格式:PnPm[119]、DG/FV混合格式[120]、BGK(Bhatnagar-Gross-Krook)[121]格式等。
本节以下将从应用现状、计算精度、时间推进、激波捕捉、计算成本、开源软件等方面进行评述。因篇幅限制,以下内容将重点关注发展历史较长、关注较多的两种高阶格式:WENO和DG。
2.2.1 高阶格式的应用现状高阶格式发展至今,已在多个方向得到了不同程度的应用。
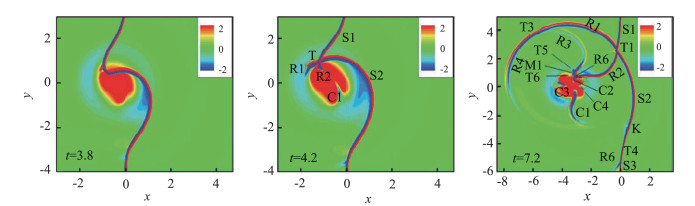
2.2.1.1 气动声学数值模拟中的应用1) 激波与旋涡的相互作用[122]。激波与旋涡相互作用是激波噪声的一个简化模型,通过研究激波与旋涡相互作用,可以深入了解激波噪声产生机制。张树海等采用五阶精度WENO格式,系统模拟了激波与强旋涡相互作用系统的模拟,发现激波与强旋涡相互作用存在多级干扰。第一级干扰是入射激波和初始旋涡的相互作用,第二级干扰是反射激波和变形旋涡的相互作用,第三级干扰是涡心附近产生的小激波串和变形旋涡的干扰,如图 22所示。与此同时,旋涡的变形也存在多级特征。在第一级干扰中,初始圆形旋涡被压成椭圆形;在第二级干扰中,椭圆形旋涡被压回成圆形旋涡;在第三级干扰中,圆形旋涡又被压缩成椭圆形。此外,这种多级干扰会引起旋涡在水平线附近做振荡运动。根据激波与强旋涡相互作用过程中的多级干扰过程,当时张树海等预测,这种多级干扰过程会产生更为复杂的声波。
|
图 22 激波与强旋涡的干扰过程(Ms=1.2, Mv=1.0) Fig.22 Interaction between a shock wave and strong vortex (Ms=1.2, Mv=1.0) |
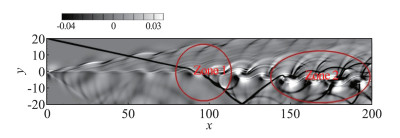
2) 激波与剪切层相互作用[123]。激波与剪切层相互作用是一个典型的问题,也可以看做是研究超声速喷流激波噪声的一个简化模型。为了了解超声速喷流激波噪声的产生机制,刘旭亮和张树海设计了一个激波与剪切层相互作用的模型。一道斜激波打到一个剪切层上,下边界是一个反射固壁,透射激波打到固壁上后,形成反射激波,反射激波再次与剪切层相互作用发生反射,形成类似于超声速喷流的激波串结构。通过较为系统的数值模拟,揭示了两种噪声产生机制,一是激波与旋涡相互作用,发生在图 23所示的区域1,另一是激波泄露机制,发生在图 23所示的区域2。
|
图 23 激波穿过剪切层的两个区域 Fig.23 Two zone of shock wave passing through supersonic shear layer |
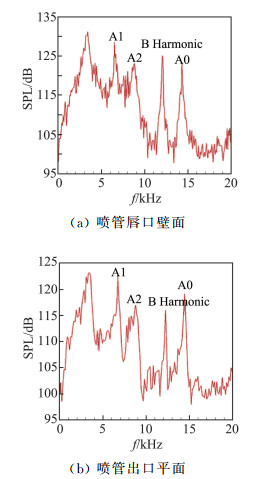
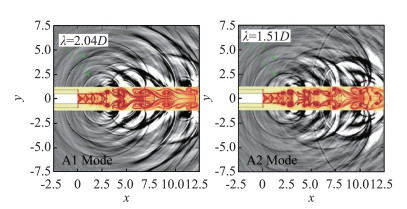
3) 轴对称超声速喷流噪声[124]。超声速喷流噪声是一种典型的激波噪声,与很多工程密切相关。采用五阶WENO格式直接求解轴对称Navier-Stokes方程,数值模拟了射流马赫数(完全膨胀)为Mj=1.19(啸声呈现轴对称模态,三维效应不明显)的轴对称欠膨胀射流,其对应的射流声速马赫数为Ma=1.05,雷诺数为Re=6.216×105,喷管直径为D=25.4 mm,喷管厚度为0.4D,环境温度为288.15 K。图 24给出了喷管唇口壁面和喷管出口平面上压力监测点处噪声信号的频谱信息, 包括频率和声压级。结果显示,在大于5000 Hz的频率区间内,有4个尖锐的声压级突起:前两个声压级突起的频率为65 657 Hz (128 dB)和8637 Hz (123 dB),分别是啸声A1模态和啸声A2模态;另外两个声压级突起的频率为12 087 Hz(125 dB)和14 310 Hz (123 dB),分别是啸声B模态的谐频和啸声A0模态。综合流场结构和声场信息可以得到的啸声模态的图像及其产生位置,其中流场结构用数值纹影(密度梯度的模)表示,声场由胀量场表示。根据啸声频率可以得到啸声的波长,利用波长可以在胀量场中清晰地分辨出啸声A1模态和A2模态, 相应的波长分别为λ=2.04D和λ=1.51D。从图 25中可以清晰地分辨出向上游传播的啸声,并且啸声产生位置都是在第三个激波栅格和第五个激波栅格之间的区域。
|
图 24 监测点处压力信号的谱分析 Fig.24 Sound pressure level |
|
图 25 喷管厚度为0.4D射流马赫数为1.19的射流啸声图像 Fig.25 Screech of supersonic jet with the diameter being 0.4D at Ma=1.19 |
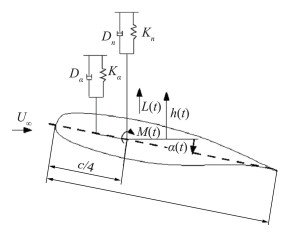
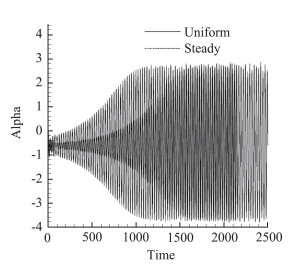
1) NLR7301翼型极限环振荡[125]。采用流固耦合方法结合五阶WENO差分格式计算NLR7301翼型极限环振荡问题。图 26是弹性支撑NLR7301翼型的模型。流动计算中黏性项采用四阶中心差分格式,湍流模型为Spalart-Allmaras模型。来流马赫数为0.753。时均迎角为-0.45°,初始流场分别采用了定常流计算的解和均匀来流。图 27给出了计算结果的极限环振荡的振幅,可以看到,尽管中间过程有所不同,两种初始条件达到了几乎同样的极限环。
|
图 26 弹性支撑NLR7301翼型的模型 Fig.26 Model of the elastically mounted NLR7301 airfoil |
|
图 27 弹性支撑NLR7301翼型的俯仰运动情况,Ma=0.753 Fig.27 Predicted plunge motion for the model of the elastically mounted NLR7301 airfoil |
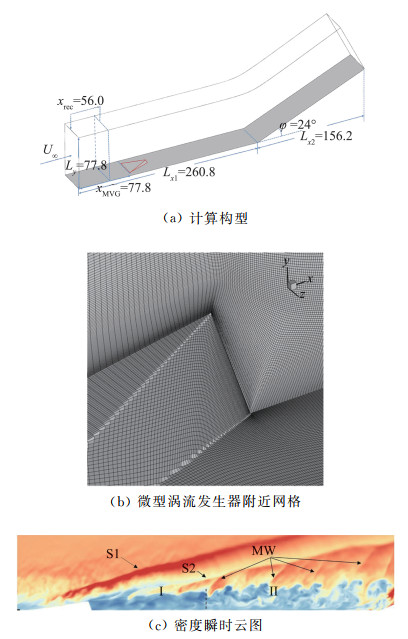
2) 涡流发生器高超声速绕流直接数值模拟。图 28为基于高阶有限差分WENO格式的高超声速可压缩流动直接数值模拟,计算构型为微型涡流发生器。这类问题的特点是外形相对简单,利于保证网格质量,同时对精度和效率要求较高,所以一般采用有限差分类高阶格式。
|
图 28 微型涡流发生器高超声速绕流直接数值模拟[126], Ma=5,四阶对称型WENO格式[127] Fig.28 Direct numerical simulation of hypersonic flow over the micro vortex generator[126], Ma=5, fourth-order symmetric WENO[127] |
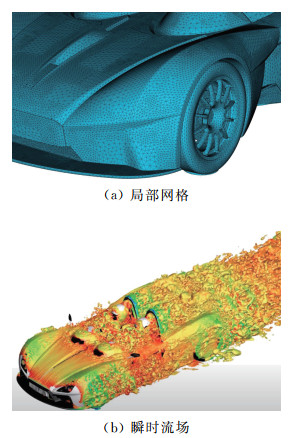
3) 整车大涡模拟。对于这类复杂几何构型的精细模拟,则需采用有限元类高阶格式,以便在非结构网格上实现高阶精度。图 29为采用五阶DG格式对整车开展大涡模拟的结果及网格示意图[128]。这类模拟的目的是对车身部件流场特征进行分析,优化汽车高速行驶的空气动力学性能,关键是要准确刻画漩涡结构的发展和相互作用,因而必须采用高阶格式。
|
图 29 汽车气动仿真[128], 五阶精度DG格式,10亿自由度 Fig.29 Aerodynamic simulation of an automobile[128], fifth-order DG, 1 billion degrees of freedom |
目前这类算例多见于运输机构型(如图 30所示)的气动力计算,这类构型能够获得高质量的结构网格,王运涛等[129]已成功地使用五阶WCNS格式对这类构型开展了计算。该问题对于有限元类格式带来的主要挑战是如何克服高阶离散的刚性使计算收敛到定常解,目前公开发表的文献中已经出现三阶DG格式的计算结果[130]。

|
图 30 运输机构型气动力特性计算模型示意图 Fig.30 Computational model for a transport aircraft |
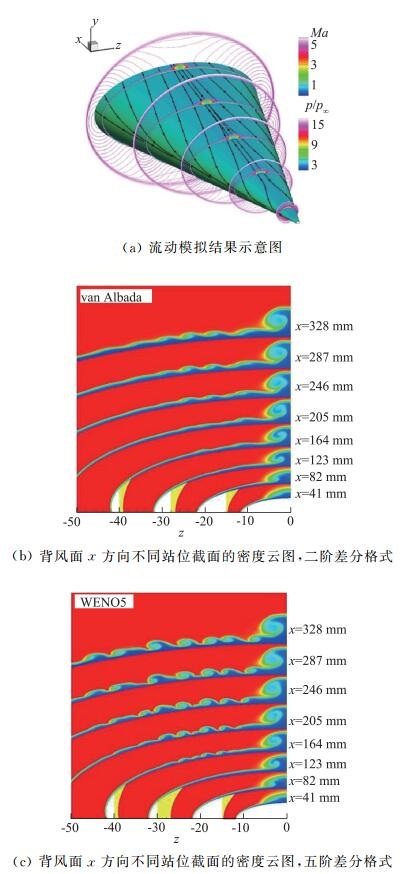
目前人们普遍的共识是与采用同样网格规模的二阶格式相比,无论是对于定常RANS计算还是多尺度求解问题,高阶格式的计算精度都将获得显著的提升。图 31对比了典型高超声速飞行器绕流在有限差分框架下二阶格式和五阶格式的计算结果,可以看出二阶格式得到的“二次涡”结构清晰程度明显弱于五阶格式,二阶格式过大的数值耗散抑制了边界层的不稳定发展,抹平了流场中的细节结构。此外,对于定常气动力/热计算,尽管湍流模型的误差常常起主导作用,高阶有限差分格式也体现出了显著的优势[131-132]。
|
图 31 高超声速飞行器HIFiRE-5数值模拟, Ma=6,层流计算 Fig.31 Numerical simulation of HIFiRE, Ma=6, laminar flow |
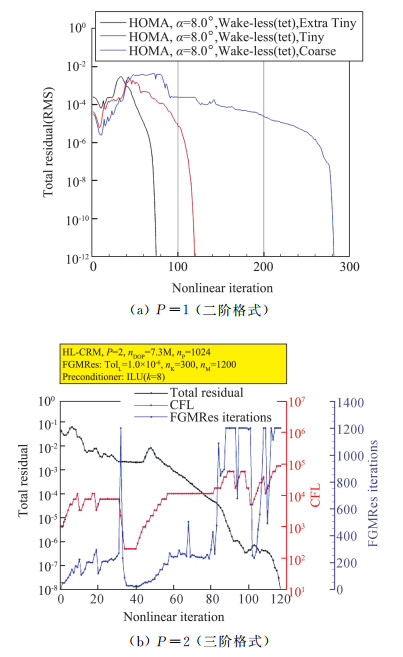
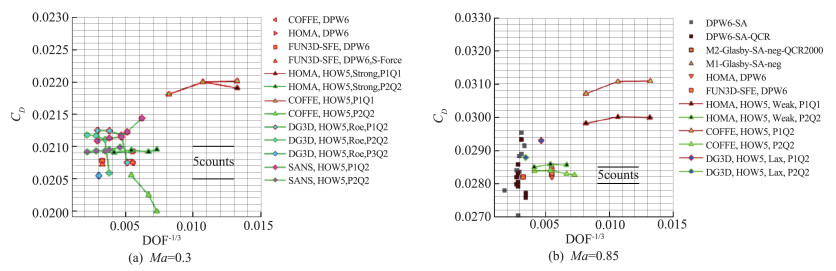
对于给定的网格,DG等有限元类格式提高近似阶数带来的精度提升要远高于有限差分类格式。这是因为有限元类格式提高阶数会增加自由度数,而有限差分离散通过扩展插值模板提升精度,其自由度数是固定的。因此,有限元类格式能够在较低自由度个数下获得更高的计算精度。这一结论在更复杂的问题中也得到了验证。图 32给出了CRM(Common Research Model)模型计算结果对比。从中可以看到,在采用相当甚至更少自由度的前提下,高阶SUPG和DG格式所得阻力系数落在了收敛区域内,而此时SUPG和DG所采用的网格要远稀疏于二阶有限体积法。对于P2(三阶格式)情况,计算的分散性大大改善,即在最粗的网格上也得到了比较精确的阻力系数值。
|
图 32 CRM模型阻力系数计算结果[133](HOMA和COFFE为SUPG方法,DG3D和SANS代表DG方法) Fig.32 Drag coefficients of the CRM model[133] (HOMA and COFFE use the SUPG method, DG3D and SANS use the DG method) |
如前所述,对于高阶有限差分格式,需要解决的问题主要是如何在复杂构型上生成高质量的结构化网格。而对于高阶有限元类格式,要实现上述高阶精度仍然面临诸多挑战。首先,如果近似解的多项式的阶数是P次,曲面边界需要采用P+1次近似才能使得DG类格式达到设计精度。而复杂外形的高阶网格生成仍极具挑战性,相关功能在网格生成软件中的集成也还处于起步阶段。其次,对于多尺度求解问题,高阶有限元格式存在因不能精确积分非线性通量而带来的混淆误差,导致数值计算不稳定,这一现象在“高阶精度+稀疏网格”的组合下尤其严重[134]。此外,高阶有限元类格式一个显著的特点是在高波数区域具备很强的耗散,这一般被看作是此类方法适用于隐式大涡模拟的主要依据。但高阶有限元类格式的多模态属性使得控制和调节格式的傅立叶特性变得困难(如DG格式的auto-correction机制[135]),这给格式性能的优化以及亚格子模型的构造都带来了挑战。
2.2.3 高阶格式的时间求解方法现代CFD方法一般都采用半离散形式,时间格式的构造不依赖具体的空间离散,有限差分与有限体积法所采用的时间格式一般不需随格式精度变化。因此,本部分主要关注有限元类高阶格式的时间求解。定常CFD计算常用的时间格式主要包括两大类:近似算子分裂方法和Newton-Krylov迭代法。对于有限元类格式,Block Lower-Upper Symmetric Gauss-Seidel (BLU-SGS)格式是典型的近似算子分裂方法,通过求解非线化方程,避免了方程线化带来的误差,能够取得更快的收敛,因而被推广到了诸如SD[136]、FR[137]、CPR[138]等方法中。另外,Nastase等[139]系统比较了线性Element Jacobi(EJ)、非线性Element Jacobi以及Linear Gauss-Seidel(LGS)格式。结果表明,LGS格式虽然需要额外存储非对角矩阵,但却能够取得最优收敛效果。
在基于Newton-Krylov的迭代法中,最常用的为广义最小残差法(GMRES)。对Newton-Krylov方法的研究首先集中在预处理技术上,Persson等[140]对比了多种预处理技术,认为线性多重网格以及不完全因子分解(incomplete lower-upper factorization,ILU)技术配合使用效果较佳。Diosady等[141]提出了基于张量积的预处理技术,并对比了与算子分裂预处理子的性能差异。迭代法涉及大型线性方程组求解,会导致计算量和存储量急剧增加。例如,采用DG格式求解三维Navier-Stokes方程,假设使用100 000个四面体单元,应用3次多项式,双精度计算,存储雅克比(Jacobian)矩阵非零块的内存消耗约为102.1 GB,除需要大量存储空间外,计算Jacobian矩阵本身也将花费大量的计算资源。Luo等[142]探讨了避免矩阵存储的技术,能够有效降低内存消耗。Xia等[143]对比了GMRES方法多种雅可比矩阵(Jacobian Matrix)计算方法的优劣,并评估了一系列隐式格式的计算效率。
高阶有限元类格式空间离散后得到的方程系统刚性往往较强(尤其是对于大长细比网格[144]、跨声速、复杂外形等情况),求解定常解的难度和代价都会急剧升高。这一点也已在评估近似算子分裂方法和GMRES迭代法两大类隐式方法的研究工作[145]中得到体现。计算结果表明,即使对于平板、翼型这类简单问题,BLUSGS也常常计算发散,GMRES类格式收敛性能更好,但也需要谨慎选择预处理方法。高阶格式定常计算的求解策略往往需要先用低阶格式计算获得初始解,随后再用高阶格式续算直到计算收敛。此外,此类方法的收敛速率严重依赖于网格,即随着网格的加密收敛性能迅速恶化(如图 33所示)。上述困难是目前在复杂构型问题中少有四阶或更高阶有限元类格式计算结果出现的主要原因。
对于非定常计算,高阶时间离散格式如隐式Runge-Kutta(Implicit Runge-Kutta, IRK)方法,已被推广应用于DG非定常算法的构造中[146]。Wang等[147]研究了从低阶到高阶一系列时间离散格式,发现在同样的误差要求下,高阶时间离散方法比低阶时间离散方法的效率更高,尤其是随着误差精度的进一步提高,高阶时间格式的优势将更加明显。Vermeire和Nadarajah[148]发展了一种显示-隐式混合时间推进方法。相比IRK方法,计算效率更高的高阶时间离散格式相继被提出[149-150],这类方法在每个时间步只需进行一次雅可比矩阵计算。
2.2.4 高阶格式的激波捕捉方法对于强可压缩流动,高阶格式面临的一大挑战是:以极小的数值耗散来分辨小尺度脉动,在光滑区保持格式的高精度特性不被破坏,同时光滑地捕捉流场中出现的各种间断。对于有限差分类格式、有限体积类格式以及有限元类格式,常用的激波捕捉策略是相似的,主要包括:限制器、WENO类插值/重构、人工黏性模型等。限制器类方法[151-152]以保证格式的TVD或TVB性质为目标,优点是稳定性好,常用于二阶格式,但往往因为耗散过大,不利于实现高精度,因而在各类高阶格式中应用较少。
在有限差分的框架下,WENO类方法成为最常用的可压缩流动高阶格式,获得了巨大的成功。其核心思想就是将格式的设计模板分成若干子模板,在每个子模板上重构一个低阶数值通量,通过某种光滑测试因子计算每个子模板的权,将所有子模板的数值通量非线性叠加,得到高阶或者最优精度的数值通量。WENO格式具有如下特点,在光滑区,格式可以达到最优精度,在激波区,基本选择了最光滑的子模板。而经典的WENO格式在面对各种不同的问题也逐渐暴露出一些不足之处,针对WENO格式的改进主要包括两类:1)针对WENO格式在极值点附近降阶的问题进行改进,如WENO-M[153]和WENO-Z[154]格式;2) WENO格式计算定常激波时,在激波下游会出现微弱的非物理波动,导致残差不能收敛到满意程度,对于激波噪声,这种微弱的非物理波动则非常大,有时比激波噪声的幅度高两个数量级。张树海等提出了两种方法消除这种微弱的非物理波动,主要包括一种适合于五阶WENO格式的光滑测试因子[155]和迎风型插值方法[156]。
而在有限体积的框架下,提高精度需要扩展模板,这使得WENO类方法的构造较为复杂,向高阶格式推广往往存在稳定性问题。当将此类方法推广到有限元框架下时,为了保证计算效率,需要依赖额外的激波指示器[157],先判断那些需要进行修正的单元(即包含间断的单元),然后在这些单元上采用WENO重构,而在其他单元处采用原始的高阶格式。因此,激波指示器的性能就很大程度上决定了基于WENO重构方法的计算精度和稳定性。在有限元的框架下引入WENO重构,初衷是为了利用WENO的高精度特性,有效保持有限元离散的精度,然而,实际应用发现,WENO重构很难推广到三阶精度以上。作者认为,这主要是因为WENO重构往往涉及多维高次多项式的内插或外插过程,容易导致计算结果的不稳定。Dumbser等[158-159]利用后验思想MOOD(Multi-dimensional Optimal Order Detection)来对包含激波的单元进行修正,修正时将一个DG单元划分成若干个子单元,在单元内部引入WENO等方法进行限制,所给出的算例最高精度达到10阶,很好地保留了DG格式的高阶特性。
捕捉激波的另外一种方法是人工黏性方法,即通过添加人工黏性项来抑制虚假振荡。人工黏性方法最早可以追溯到1950年von Neumann和Richtmyer的工作[160],随后Baldwin和MacCormack[161]以及Jameson[162]沿着这一方向均取得了杰出的成果。这些早期的工作大多采用低阶有限体积方法。而当格式精度提升后,有限差分和有限体积框架下的人工黏性方法则因耗散过大而较少采用。与之相反,人工黏性与高阶有限元类方法的结合能够在一个单元内分辨激波[163](即亚格子分辨率),使得人工黏性这一经典概念焕发新生,引起了人们的极大兴趣,也诞生了众多方法[164-167]。人工黏性方法的关键是人工黏性系数的计算,需要设计能够可靠衡量流场光滑性的指示器。目前常用的光滑性指示器大致有三种:1)流场关键参数(如密度)的导数;2)模态分解系数的衰减速率;3)熵增。研究表明[168],这三种模型都有各自的缺点:1)基于导数的模型需要根据流动特性结合开关机制来减少对于小尺度脉动等的耗散;2)基于模态分解的模型往往存在高估光滑性的情况;3)基于熵增的模型则耗散偏大,且对于经验参数的依赖性较强。而当格式阶数较高(一般大于4阶)的时候,各模型均能够得到分辨率较好的结果,并且不同模型之间的差别也逐渐减小。
2.2.5 高阶格式的计算代价分析计算代价方面,目前,对不同格式计算代价的评估大多停留在以相同自由度个数为基准的前提下。例如,文献[169]针对引擎内流的大涡模拟计算开展格式效率的对比,在误差相当时,四阶格式所需自由度数比二阶格式低约一个数量级,也显著低于基于二阶格式的LES/RANS混合方法。然而需要指出的是,真正严格的对比则应是在达到相同误差时衡量格式的计算效率。此外,评估计算代价还应考虑算法与硬件的结合。现代基于CPU的大规模并行计算集群虽然能够有效压缩计算周期,但计算成本仍然巨大。而DG、FR这类高阶格式使用的网格单元数少,局部计算量集中,更利于充分利用现代计算架构的浮点运算能力,更适合GPU计算。基于CPU并行策略的有限体积求解器一般只能使用并行集群性能峰值的5%~10%,而使用GPU计算的FR格式计算速度最高可以达到性能峰值的58%[170]。
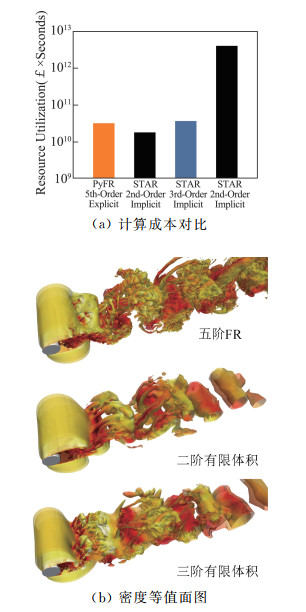
Vincent等[171]从误差和计算代价的角度系统对比了FR和基于二阶有限体积法的商用软件STAR-CCM+在湍流计算中的计算成本,图 34给出了计算所用的成本(硬件购置成本×计算时间)和流场结果的对比。在计算成本相当的前提下,5阶FR计算得到的结果更精细。
|
图 34 圆柱湍流绕流计算对比(Re=3900) Fig.34 Comparison on the numerical results of the cylinder flow (Re=3900) |
需要指出的是,上述计算成本对比选取的算例属于分离流动,更容易体现高阶格式的优势。而对于定常RANS计算,高阶格式的计算代价是否具有竞争力仍需进一步研究。发展h-p自适应方法将是进一步提高有限元类高阶格式在计算代价方面竞争力的有效途径。
2.2.6 软件实现高阶格式因为算法设计复杂,编程困难,在一定程度上也限制了其推广和应用。鉴于此,一些研究团队开发了高阶格式的开源软件,有助于帮助初学者快速完成基于高阶格式的研究和计算任务。以下列举部分开源软件:
1) 有限差分类:中科院力学所的OpenCFD(WENO格式、紧致格式等);
2) 有限元类:如英国帝国理工大学的Nektar++[172] (DG格式)和PyFR[173](FR格式),美国斯坦福大学的HiFiLES[174](FR格式),瑞士洛桑联邦理工大学的NUDG[175](DG格式),美国德克萨斯A&M大学的deal.II[176](有限元方法一般框架)等。
3 发展趋势及建议本文针对航空航天CFD应用中的物理模型和计算方法等核心问题,评述了其发展现状和面临的挑战。一方面,CFD的应用无论是深度和广度都有了快速发展,其作用也越来越大;另一方面,CFD在关键的核心理论等方面都还面临着诸多问题和困难,进展缓慢。这促使我们认真思考未来的CFD应该如何发展,这里将分别针对本文中的各个方向,给出一些思考、建议和意见,以期抛砖引玉,图画未来。
3.1 湍流模型1) 对于使用者来说,建议重视如下问题:通过相关文献等方式,了解湍流模型的基本性能和特点,注意模型中常数或参数的选择原则、边界条件正确的设置方法、对网格尤其是近壁网格和大流动梯度处等网格的限定和要求,尽量通过多种手段保证湍流模型的收敛性。
2) 继续改进、完善和发展现有的涡黏性湍流模型,提高预测精度、扩展适应性和预测能力:根据近二十年来国外湍流模型的新发展,选择评价较高、实用性较好、性能优越的新发展模型,如高鲁棒性的椭圆松弛法、K-KL模型等,促进其实用化发展和推广应用。对于现有经典两方程模型,重点研究长度尺度和近壁模拟方法的评估和改进。
3) 支持RSM模型的长期研究,大力推广其在航空航天领域的应用。
4) 在发展和验证新的湍流模型中,重视DNS和LES的作用,使其能提供宝贵的数据库、流动结构和机理模型,尤其是建模指导等。
5) 美国NASA等在2017年召开了Turbulence Modeling Symposium[177],会议主要讨论湍流模型的现状、新思想以及应对未来的问题。与会者充分讨论后,认为近期应该开展2个方面的研究:1)不确定性量化(UQ);2)数据驱动建模。
3.2 转捩模型随着对转捩物理机理认知的逐渐深入和实验数据的不断丰富,转捩模型已取得了丰硕的研究成果。目前已有数十种转捩模型被提出,这些模型对特定流动特征下的转捩预测具有较高的精度,特别是在二维简单转捩流动中。然而就目前的发展来看,这些转捩模型距离在工程三维复杂外形中的应用尚有一定差距。主要困难如下:
1) 边界层转捩路径的复杂化和影响因素的多样化导致尚无关于转捩系统完备的物理机制解释;
2) 转捩现象本身的高复杂性和强非线性,使得在基于物理的方程框架中对所有转捩机制进行完整建模十分困难,特别是涉及线性和非线性效应及其相互作用机制时。因此,如何将转捩内在机制合理准确地引入转捩模型仍是个难题;
3) 转捩模型的普适性严重不足,单类方法往往只适用于特定流动类型,对其他类型转捩流动的预测性能显著下降或完全失效;
4) 为使方程封闭,转捩模型均不可避免地引入了大量模化参数,从而导致预测结果的不确定度。
建议在后续研究中应重点关注以下几点:
1) 加强转捩机制研究和理论建模,使得转捩模型能够反映更本质的物理机制;
2) 充分利用飞行/风洞实验数据、DNS等高精度数值模拟手段、稳定性理论结论和机器学习等数据挖掘技术,校验转捩模型相关模型的正确性和准确性,实现转捩模型的预测能力提升;
3) 普适性本身就是一个值得探讨的问题,一方面可考虑针对性地发展特定流动类型转捩模型,实现术业有专攻,另一方面引入混合模型,通过提取不同转捩机制类型的特征参数,预先判定转捩主导机制,实现分区转捩预测;
4) 针对转捩模型在工程应用中所面临的普适性差、参数调整对经验依赖性强等问题,开展转捩模型的不确定度量化和敏感性分析。
3.3 通量求解通量格式作为CFD领域的热点问题在过去的几十年间取得了丰硕的研究成果。但是,在针对流动分离、激波边界层干扰等多维复杂流动开展数值模拟时,现有方法仍具有模拟精度不足、计算结果严重依赖于网格分布等缺陷。此外,尚无一种通量格式可以完全避免非物理的激波异常和“overheating”现象。为此,本文作者有如下建议:
1) 鉴于现有通量格式无法完全避免激波异常现象的出现,在模拟高速流动时,应尽量选取激波稳定性较佳的通量格式,并注意强激波附近网格长细比的合理设置,通过高质量的网格生成抑制求解过程中可能出现的非物理流场脉动。
2) 应深入挖掘膨胀流动模拟中非物理“overheating”现象出现的数学机制,从理论上找到改进这一缺陷的具体措施。
3) 推广全速域通量格式在航空航天领域的应用,改善当前主流软件在宽速域复杂流动模拟中的预测精度以及计算网格依赖性。
4) 针对当前通量格式在多维复杂流动模拟中精度不足的缺陷,大力发展真正多维全速域通量格式,进而提高CFD技术在航空航天领域的可靠性。
3.4 高阶格式1) 高阶格式框架的选取取决于求解的具体问题:a)几何外形简单的大涡模拟或直接数值模拟建议选择有限差分类格式;b)复杂构型的定常RANS计算,在能够生成高质量结构网格的前提下可采用高阶有限差分格式,如WCNS格式等。在几何构型更为复杂的情况下,可尝试选择三阶精度的DG格式,更高阶精度的DG格式会面临收敛性和鲁棒性等问题;c)复杂构型的湍流精细模拟可选择有限元类的高阶格式。
2) 高阶格式在向实际复杂问题推广过程中遇到的困难是全方位的,涉及网格生成、激波捕捉、时间推进、计算稳定性、计算效率等各方面,尤其亟需发展高效率、低存储、鲁棒性强的隐式时间格式。高阶格式面临的这些困难在二阶格式中已经存在,在高阶格式的框架下则变得更加突出。
3) CFD其他关键技术比如通量格式、物理模型等在高阶格式的框架下,性能也会发生不同程度的变化。因此,高阶格式的发展还应注意结合这些CFD的关键环节综合考虑。
4) 目前来看,大规模并行集群的性能并未得到充分的利用。在计算机硬件更新换代日新月异的今天,高阶格式要提高竞争力,在方法发展过程中应当重视与计算机硬件的紧密结合,充分发掘硬件资源的计算潜能。
| [1] |
CHAPMAN D R. Computational aerodynamics development and outlook[J]. AIAA Journal, 1979, 17(12): 1293-1313. DOI:10.2514/3.61311 |
| [2] |
王运涛, 刘刚, 陈作斌. 第一届航空CFD可信度研讨会总结[J]. 空气动力学学报, 2019, 37(2): 247-261, 246. WANG Y T, LIU G, CHEN Z B. Summary of the first aeronautical computational fluid dynamics credibility workshop[J]. Acta Aerodynamica Sinica, 2019, 37(2): 247-261, 246. (in Chinese) |
| [3] |
阎超, 席柯, 袁武, 等. DPW系列会议述评与思考[J]. 力学进展, 2011, 41(6): 776-784. YAN C, XI K, YUAN W, et al. Review of the drag prediction workshop series[J]. Advances in Mechanics, 2011, 41(6): 776-784. (in Chinese) |
| [4] |
RUMSEY C, RIVERS S M, MORRISON J. Study of CFD variation on transport configurations from the second drag-prediction workshop[C]//Proc of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2004. doi: 10.2514/6.2004-394
|
| [5] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences[R]. NASA/CR-2014-218178, 2014.
|
| [6] |
阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589. YAN C, YU J, XU J L, et al. On the achievements and prospects for the methods of computational fluid dynamics[J]. Advances in Mechanics, 2011, 41(5): 562-589. (in Chinese) |
| [7] |
SPALART P R. Strategies for turbulence modelling and simulations[J]. International Journal of Heat and Fluid Flow, 2000, 21(3): 252-263. DOI:10.1016/s0142-727x(00)00007-2 |
| [8] |
DURBIN P A. Some recent developments in turbulence closure modeling[J]. Annual Review of Fluid Mechanics, 2018, 50(1): 77-103. DOI:10.1146/annurev-fluid-122316-045020 |
| [9] |
HANJALI' K. Second-moment turbulence closures for CFD:needs and prospects[J]. International Journal of Computational Fluid Dynamics, 1999, 12(1): 67-97. DOI:10.1080/10618569908940816 |
| [10] |
Rumsey C L. Turbulence modeling verification and validation: AIAA-2014-0201[R]. Reston: AIAA, 2014.
|
| [11] |
JOHNSON F, TINOCO E, YU J. Thirty years of development and application of CFD at boeing commercial airplanes, Seattle[C]//16th AIAA Computational Fluid Dynamics Conference, Orlando, Florida. Reston, Virginia: AIAA, 2003 doi: 10.2514/6.2003-3439
|
| [12] |
RUMSEY C, SMITH B, HUANG G. Description of a website resource for turbulence modeling verification and validation[C]//Proc of the 40th Fluid Dynamics Conference and Exhibit, Chicago, Illinois. Reston, Virigina: AIAA, 2010. doi: 10.2514/6.2010-4742
|
| [13] |
HANJALIC' K. Will RANS survive LES? A view of perspectives[C]//Proceedings of ASME Conference on ASME 2004 Heat Transfer/Fluids Engineering Summer Conference, 2009: 715-725. doi: 10.1115/HT-FED2004-56356
|
| [14] |
CECORA R, RADESPIEL R, EISFELD B, et al. Differential Reynolds-stress modeling for aeronautics[J]. AIAA Journal, 2015, 53(3): 739-755. DOI:10.2514/1.J053250 |
| [15] |
TUCKER P G. Computation of unsteady turbomachinery flows:Part 1:Progress and challenges[J]. Progress in Aerospace Sciences, 2011, 47(7): 522-545. DOI:10.1016/j.paerosci.2011.06.004 |
| [16] |
WILCOX D A. Simulation of transition with a two-equation turbulence model[J]. AIAA Journal, 1994, 32(2): 247-255. DOI:10.2514/3.59994 |
| [17] |
JONES W P, LAUNDER B E. The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence[J]. International Journal of Heat and Mass Transfer, 1973, 16(6): 1119-1130. DOI:10.1016/0017-9310(73)90125-7 |
| [18] |
HADŽIĆ I, HANJALIĆ K. Separation-induced transition to turbulence:second-moment closure modelling[J]. Flow, Turbulence and Combustion, 2000, 63(1-4): 153-173. DOI:10.1023/A:1009980119240 |
| [19] |
LANGTRY R, SJOLANDER S. Prediction of transition for attached and separated shear layers in turbomachinery[C]//38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, Indiana. Reston, Virginia: AIAA, 2002 doi: 10.2514/6.2002-3641
|
| [20] |
ZHENG X Q, LIU C Q, LIU F, et al. Turbulent transition simulation using the k-ω model[J]. International Journal for Numerical Methods in Engineering, 1998, 42(5): 907-926. DOI:10.1002/(sici)1097-0207(19980715)42:5<907::aid-nme393>3.0.co;2-t |
| [21] |
RUMSEY C L. Apparent transition behavior of widely-used turbulence models[J]. International Journal of Heat and Fluid Flow, 2007, 28(6): 1460-1471. DOI:10.1016/j.ijheatfluidflow.2007.04.003 |
| [22] |
符松, 王亮. 湍流转捩模式研究进展[J]. 力学进展, 2007, 37(3): 409-416. FU S, WANG L. Progress in turbulence/transition modelling[J]. Advances in Mechanics, 2007, 37(3): 409-416. (in Chinese) |
| [23] |
EMMONS H W. The laminar-turbulent transition in a boundary layer-part I[J]. Journal of the Aeronautical Sciences, 1951, 18(7): 490-498. DOI:10.2514/8.2010 |
| [24] |
DHAWAN S, NARASIMHA R. Some properties of boundary layer flow during the transition from laminar to turbulent motion[J]. Journal of Fluid Mechanics, 1958, 3(4): 418-436. DOI:10.1017/S0022112058000094 |
| [25] |
GOSTELOW J P, BLUNDEN A R, WALKER G J. Effects of free-stream turbulence and adverse pressure gradients on boundary layer transition[J]. Journal of Turbomachinery, 1994, 116(3): 392-404. DOI:10.1115/1.2929426 |
| [26] |
MAYLE R E. The role of laminar-turbulent transition in gas turbine engines[C]//Proceedings of the ASME 1991 International Gas Turbine and Aeroengine Congress and Exposition. Orlando, Florida, USA: 1991. doi: 10.1115/91-GT-261
|
| [27] |
KLEBANOFF P S. Characteristics of turbulence in a boundary layer with zero pressure gradient[EB/OL]. 1954
|
| [28] |
ADDISON J S, HODSON H P. Modeling of unsteady transitional boundary layers[J]. Journal of Turbomachinery, 1992, 114(3): 580-589. DOI:10.1115/1.2929182 |
| [29] |
SCHULTE V, HODSON H P. Prediction of the becalmed region for LP turbine profile design[C]//Proceedings of ASME Conference on ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, 2014 doi: 10.1115/97-GT-398
|
| [30] |
STEELANT J, DICK E. Modelling of bypass transition with conditioned navier-stokes equations coupled to an intermittency transport equation[J]. International Journal for Numerical Methods in Fluids, 1996, 23(3): 193-220. DOI:10.1002/(SICI)1097-0363(19960815)23:3<193::AID-FLD415>3.0.CO;2-2 |
| [31] |
FVRST J, PŘÍHODA J, STRAKA P. Numerical simulation of transitional flows[J]. Computing, 2013, 95(1): 163-182. DOI:10.1007/s00607-012-0266-0 |
| [32] |
LIBBY P A. On the prediction of intermittent turbulent flows[J]. Journal of Fluid Mechanics, 1975, 68(2): 273-295. DOI:10.1017/S0022112075000808 |
| [33] |
LIBBY P A. Prediction of the intermittent turbulent wake of a heated cylinder[J]. Physics of Fluids, 1976, 19(4): 494-501. DOI:10.1063/1.861505 |
| [34] |
DOPAZO C. On conditioned averages for intermittent turbulent flows[J]. Journal of Fluid Mechanics, 1977, 81(3): 433-438. DOI:10.1017/S0022112077002158 |
| [35] |
CHEVRAY R, TUTU N K. Intermittency and preferential transport of heat in a round jet[J]. Journal of Fluid Mechanics, 1978, 88(1): 133-160. DOI:10.1017/S0022112078002025 |
| [36] |
CHO J R, CHUNG M K. A k-ε-γ equation turbulence model[J]. Journal of Fluid Mechanics, 1992, 237: 301-322. DOI:10.1017/s0022112092003422 |
| [37] |
Savill A M. The Savill-Launder-Younis (SLY) RST intermittency model for predicting transition[C]. ERCOFTAC Bulletin, 1995, 24: 37-41.
|
| [38] |
STEELANT J, DICK E. Modeling of laminar-turbulent transition for high freestream turbulence[J]. Journal of Fluids Engineering, 2001, 123(1): 22-30. DOI:10.1115/1.1340623 |
| [39] |
SUZEN Y B, HUANG P G. Modeling of flow transition using an intermittency transport equation[J]. Journal of Fluids Engineering, 2000, 122(2): 273-284. DOI:10.1115/1.483255 |
| [40] |
BOR Y, HUANG P, HULTGREN L, et al. Predictions of separated and transitional boundary layers under low-pressure turbine airfoil conditions using an intermittency transport equation[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. doi: 10.2514/6.2001-446
|
| [41] |
PECNIK R, SANZ W, GEHRER A, et al. Transition modeling using two different intermittency transport equations[J]. Flow, Turbulence and Combustion, 2003, 70(1-4): 299-323. DOI:10.1023/B:APPL.0000004983.49982.69 |
| [42] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. (in Chinese) |
| [43] |
周玲.高超声速边界层转捩模式研究[D].北京: 北京航空航天大学, 2013.
|
| [44] |
HAO Z H, YAN C, ZHOU L, et al. Development of a boundary layer parameters identification method for transition prediction with complex grids[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2017, 231(11): 2068-2084. DOI:10.1177/0954410016660872 |
| [45] |
LANGTRY R, MENTER F. Transition modeling for general CFD applications in aeronautics[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2005. doi: 10.2514/6.2005-522
|
| [46] |
LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906. DOI:10.2514/1.42362 |
| [47] |
HAO Z H, YAN C, QIN Y P, et al. Improved γ-Reθt model for heat transfer prediction of hypersonic boundary layer transition[J]. International Journal of Heat and Mass Transfer, 2017, 107: 329-338. DOI:10.1016/j.ijheatmasstransfer.2016.11.052 |
| [48] |
DURBIN P. An intermittency model for bypass transition[J]. International Journal of Heat and Fluid Flow, 2012, 36: 1-6. DOI:10.1016/j.ijheatfluidflow.2012.03.001 |
| [49] |
GE X, AROLLA S, DURBIN P. A bypass transition model based on the intermittency function[J]. Flow, Turbulence and Combustion, 2014, 93(1): 37-61. DOI:10.1007/s10494-014-9533-9 |
| [50] |
MENTER F R, SMIRNOV P E, LIU T, et al. A one-equation local correlation-based transition model[J]. Flow, Turbulence and Combustion, 2015, 95(4): 583-619. DOI:10.1007/s10494-015-9622-4 |
| [51] |
MAYLE R E, SCHULZ A. The path to predicting bypass transition[J]. Journal of Turbo machinery, 1997, 119(3): 405-411. DOI:10.1115/1.2841138 |
| [52] |
BRADSHAW P. Turbulence:the chief outstanding difficulty of our subject[J]. Experiments in Fluids, 1994, 16(3-4): 203-216. DOI:10.1007/BF00206540 |
| [53] |
WALTERS D K, LEYLEK J H. A new model for boundary-layer transition using a single-point RANS approach[C]//Proceedings of ASME Conference on ASME 2002 International Mechanical Engineering Congress and Exposition, 2008: 67-79. doi: 10.1115/IMECE2002-32740
|
| [54] |
KEITH WALTERS D, COKLJAT D. A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flow[J]. Journal of Fluids Engineering, 2008, 130(12): 121401. DOI:10.1115/1.2979230 |
| [55] |
QIN Y P, YAN C, HAO Z H, et al. A laminar kinetic energy transition model appropriate for hypersonic flow heat transfer[J]. International Journal of Heat and Mass Transfer, 2017, 107: 1054-1064. DOI:10.1016/j.ijheatmasstransfer.2016.11.012 |
| [56] |
QIN Y P, YAN C, HAO Z H, et al. An intermittency factor weighted laminar kinetic energy transition model for heat transfer overshoot prediction[J]. International Journal of Heat and Mass Transfer, 2018, 117: 1115-1124. DOI:10.1016/j.ijheatmasstransfer.2017.10.081 |
| [57] |
LIU Z J, ZHAO Y T, CHEN S S, et al. Predicting distributed roughness induced transition with a four-equation laminar kinetic energy transition model[J]. Aerospace Science and Technology, 2020, 99: 105736. DOI:10.1016/j.ast.2020.105736 |
| [58] |
CHEN C P, ZHAO Q J, SUN X L. Investigation on a improved laminar kinetic energy transition model[J]. Journal of Engineering Thermophysics, 2013, 34(8): 1424-1428. |
| [59] |
WARREN E S, HASSAN H. A transition closure model for predicting transition onset[J]. Journal of Aircraft, 1998, 35(5): 769-775. DOI:10.4271/975502 |
| [60] |
WANG L, FU S. Development of an intermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition[J]. Flow, Turbulence and Combustion, 2011, 87(1): 165-187. DOI:10.1007/s10494-011-9336-1 |
| [61] |
WANG L, FU S, CARNARIUS A, et al. A modular RANS approach for modelling laminar-turbulent transition in turbomachinery flows[J]. International Journal of Heat and Fluid Flow, 2012, 34: 62-69. DOI:10.1016/j.ijheatfluidflow.2012.01.008 |
| [62] |
ZHAO Y T, YAN C, LIU H K, et al. Assessment of laminar-turbulent transition models for Hypersonic Inflatable Aerodynamic Decelerator aeroshell in convection heat transfer[J]. International Journal of Heat and Mass Transfer, 2019, 132: 825-836. DOI:10.1016/j.ijheatmasstransfer.2018.11.025 |
| [63] |
ZHAO Y T, LIU H K, LIU Z J, et al. Numerical study of the cone angle effects on transition and convection heat transfer for hypersonic inflatable aerodynamic decelerator aeroshell[J]. International Communications in Heat and Mass Transfer, 2020, 110: 104406. DOI:10.1016/j.icheatmasstransfer.2019.104406 |
| [64] |
ZHOU L, YAN C, HAO Z H, et al. Improved k-ω-γ model for hypersonic boundary layer transition prediction[J]. International Journal of Heat and Mass Transfer, 2016, 94: 380-389. DOI:10.1016/j.ijheatmasstransfer.2015.11.048 |
| [65] |
ZHOU L, LI R F, HAO Z H, et al. Improved k-ω-γ model for crossflow-induced transition prediction in hypersonic flow[J]. International Journal of Heat and Mass Transfer, 2017, 115: 115-130. DOI:10.1016/j.ijheatmasstransfer.2017.08.013 |
| [66] |
ZHAO Y T, LIU H K, ZHOU Q, et al. Quantification of parametric uncertainty in k-ω-γ transition model for hypersonic flow heat transfer[J]. Aerospace Science and Technology, 2020, 96: 105553. DOI:10.1016/j.ast.2019.105553 |
| [67] |
ZHAO Y T, YAN C, LIU H K, et al. Uncertainty and sensitivity analysis of flow parameters for transition models on hypersonic flows[J]. International Journal of Heat and Mass Transfer, 2019, 135: 1286-1299. DOI:10.1016/j.ijheatmasstransfer.2019.02.071 |
| [68] |
ZHANG J C, FU S. An efficient Bayesian uncertainty quantification approach with application to k-ω-γ transition modeling[J]. Computers & Fluids, 2018, 161: 211-224. DOI:10.1016/j.compfluid.2017.11.007 |
| [69] |
VIZINHO R, MORGADO J, PÁSCOA J, et al. Analysis of transitional flow in 3D geometries using a novel phenomenological model[J]. Aerospace Science and Technology, 2015, 45: 431-441. DOI:10.1016/j.ast.2015.06.018 |
| [70] |
DURAISAMY K, DURBIN P A. Transition modeling using data driven approaches[R]//Proceedings of the Summer Program, Stanford CA: Center for Turbulence Research, 2014.
|
| [71] |
PARSH E J, DURAISAMY K, A paradigm for data-driven predictive modeling using field inversion and machine learning[J]. Journal of Computational Physics, 2016, 305: 758-774. doi: 10.1016/j.jcp.2015.11.012
|
| [72] |
BLAZEK J. Boundary conditions[M]//Computational Fluid Dynamics: Principles and Applications. Amsterdam: Elsevier, 2001: 267-297. doi: 10.1016/b978-008043009-6/50010-8
|
| [73] |
TORO E F. Riemann solvers and numerical methods for fluid dynamics[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2009. DOI:10.1007/b79761
|
| [74] |
LIOU M S. Ten years in the making-AUSM-family[C]//15th Computational Fluid Dynamics Conference, Anaheim, CA, United States: 2001. doi: 10.2514/6.2001-2521
|
| [75] |
ZHA G C. Low diffusion efficient upwind scheme[J]. AIAA Journal, 2005, 43(5): 1137-1140. DOI:10.2514/1.7726 |
| [76] |
TORO E F, VÁZQUEZ-CENDÓN M E. Flux splitting schemes for the Euler equations[J]. Computers & Fluids, 2012, 70: 1-12. DOI:10.1016/j.compfluid.2012.08.023 |
| [77] |
Peery K M, and Imlay S T. Blunt-Body Flow Simulations: AIAA-88-2904[R]. Reston: AIAA, 1988.
|
| [78] |
KIM S S, KIM C, RHO O H, et al. Cures for the shock instability:Development of a shock-stable Roe scheme[J]. Journal of Computational Physics, 2003, 185(2): 342-374. DOI:10.1016/S0021-9991(02)00037-2 |
| [79] |
PANDOLFI M, D'AMBROSIO D. Numerical instabilities in upwind methods:analysis and cures for the "carbuncle" phenomenon[J]. Journal of Computational Physics, 2001, 166(2): 271-301. DOI:10.1006/jcph.2000.6652 |
| [80] |
KITAMURA K, SHIMA EIJI, NAKAMURA Y, et al. Evaluation of Euler fluxes for hypersonic heating computations[J]. AIAA Journal, 2010, 48(4): 763-776. DOI:10.2514/1.41605 |
| [81] |
LIOU M S. Open problems in numerical fluxes: proposed resolutions[C]//20th AIAA Computational Fluid Dynamics Conference, Honolulu, Hawaii: 2011. AIAA 2011-3055.
|
| [82] |
陆金甫, 关治. 偏微分方程数值解(第三版)[M]. 北京: 清华大学出版社, 2016.
|
| [83] |
QU F, YAN C, YU J, et al. A study of parameter-free shock capturing upwind schemes on low speeds' issues[J]. Science China Technological Sciences, 2014, 57(6): 1183-1190. DOI:10.1007/s11431-014-5547-8 |
| [84] |
GUILLARD H, NKONGA B. On the behaviour of upwind schemes in the low Mach number limit: a review[J]. 2017, 18: 203-231. doi: 10.1016/bs.hna.2016.09.002
|
| [85] |
TURKEL E. Preconditioning techniques in computational fluid dynamics[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 385-416. DOI:10.1146/annurev.fluid.31.1.385 |
| [86] |
LI X S, GU C W. An All-Speed Roe-type scheme and its asymptotic analysis of low Mach number behaviour[J]. Journal of Computational Physics, 2008, 227(10): 5144-5159. DOI:10.1016/j.jcp.2008.01.037 |
| [87] |
LI X S, GU C W. Mechanism of Roe-type schemes for all-speed flows and its application[J]. Computers & Fluids, 2013, 86: 56-70. DOI:10.1016/j.compfluid.2013.07.004 |
| [88] |
QU F, YAN C, SUN D, et al. A new Roe-type scheme for all speeds[J]. Computers & Fluids, 2015, 121: 11-25. DOI:10.1016/j.compfluid.2015.07.007 |
| [89] |
SIMMONDS N, TSOUTSANIS P, ANTONIADIS A F, et al. Low-Mach number treatment for Finite-Volume schemes on unstructured meshes[J]. Applied Mathematics and Computation, 2018, 336: 368-393. DOI:10.1016/j.amc.2018.04.076 |
| [90] |
CHEN S S, YAN C, LIN B X, et al. A new robust carbuncle-free roe scheme for strong shock[J]. Journal of Scientific Computing, 2018, 77(2): 1250-1277. DOI:10.1007/s10915-018-0747-1 |
| [91] |
XIE W J, LI W, LI H, et al. On numerical instabilities of Godunov-type schemes for strong shocks[J]. Journal of Computational Physics, 2017, 350: 607-637. DOI:10.1016/j.jcp.2017.08.063 |
| [92] |
QU F, SUN D. Investigation into the influences of the low-speed flows' accuracy on RANS simulations[J]. Aerospace Science and Technology, 2017, 70: 578-589. DOI:10.1016/j.ast.2017.08.031 |
| [93] |
QU F, YAN C, SUN D, et al. A parameter-free upwind scheme for all speeds' simulations[J]. Science China Technological Sciences, 2015, 58(3): 434-442. DOI:10.1007/s11431-014-5759-y |
| [94] |
QU F, YAN C, SUN D. Investigation into the influences of the low speed's accuracy on the hypersonic heating computations[J]. International Communications in Heat and Mass Transfer, 2016, 70: 53-58. DOI:10.1016/j.icheatmasstransfer.2015.11.009 |
| [95] |
FEY M. Multidimensional upwinding. part II. decomposition of the Euler equations into advection equations[J]. Journal of Computational Physics, 1998, 143(1): 181-199. DOI:10.1006/jcph.1998.5959 |
| [96] |
WENDROFF B. A two-dimensional HLLE Riemann solver and associated Godunov-type difference scheme for gas dynamics[J]. Computers & Mathematics with Applications, 1999, 38(11-12): 175-185. DOI:10.1016/S0898-1221(99)00296-5 |
| [97] |
REN Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computers & Fluids, 2003, 32(10): 1379-1403. DOI:10.1016/S0045-7930(02)00114-7 |
| [98] |
BALSARA D S. Multidimensional HLLE Riemann solver:Application to Euler and magnetohydrodynamic flows[J]. Journal of Computational Physics, 2010, 229(6): 1970-1993. DOI:10.1016/j.jcp.2009.11.018 |
| [99] |
BALSARA D S. A two-dimensional HLLC Riemann solver for conservation laws:Application to Euler and magnetohydrodynamic flows[J]. Journal of Computational Physics, 2012, 231(22): 7476-7503. DOI:10.1016/j.jcp.2011.12.025 |
| [100] |
MANDAL J C, SHARMA V. A genuinely multidimensional convective pressure flux split Riemann solver for Euler equations[J]. Journal of Computational Physics, 2015, 297: 669-688. DOI:10.1016/j.jcp.2015.05.039 |
| [101] |
胡立军, 袁礼. 一种基于TV分裂的真正多维Riemann解法器[J]. 应用数学和力学, 2017, 38(3): 243-264. HU L J, YUAN L. A genuinely multidimensional Riemann solver based on the TV splitting[J]. Applied Mathematics and Mechanics, 2017, 38(3): 243-264. (in Chinese) |
| [102] |
QU F, SUN D, BAI J Q, et al. A genuinely two-dimensional Riemann solver for compressible flows in curvilinear coordinates[J]. Journal of Computational Physics, 2019, 386: 47-63. DOI:10.1016/j.jcp.2019.02.030 |
| [103] |
WANG Z J, FIDKOWSKI K, ABGRALL R, et al. High-order CFD methods:current status and perspective[J]. International Journal for Numerical Methods in Fluids, 2013, 72(8): 811-845. DOI:10.1002/fld.3767 |
| [104] |
Cenaero. 5th international workshop on high-Order CFD methods[EB/OL]. https://how5.cenaero.be/
|
| [105] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [106] |
DON W S, BORGES R. Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes[J]. Journal of Computational Physics, 2013, 250: 347-372. DOI:10.1016/j.jcp.2013.05.018 |
| [107] |
FU L, HU X Y, ADAMS N A. A family of high-order targeted ENO schemes for compressible-fluid simulations[J]. Journal of Computational Physics, 2016, 305: 333-359. DOI:10.1016/j.jcp.2015.10.037 |
| [108] |
LELE S K. Compact finite difference schemes with spectral-like res-olution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. DOI:10.1016/0021-9991(92)90324-r |
| [109] |
LI X L, LENG Y, HE Z W. Optimized sixth-order monotonicity-preserving scheme by nonlinear spectral analysis[J]. International Journal for Numerical Methods in Fluids, 2013, 73(6): 560-577. DOI:10.1002/fld.3812 |
| [110] |
DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44. DOI:10.1006/jcph.2000.6594 |
| [111] |
张涵信, 贺国宏.高精度差分求解气动方程的几个问题[J].空气动力学学报, 1993, 11(4): 347-356. ZHANG H X, HE G H, ZHANG L. Some important problems for high order accurate difference scheme solving gas dynamic equations[J]. Acta Aerodynamica Sinica, 1993, 11(4): 347-356. (in Chinese) |
| [112] |
TSOUTSANIS P, TITAREV V A, DRIKAKIS D. WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions[J]. Journal of Computati onal Physics, 2011, 230(4): 1585-1601. DOI:10.1016/j.jcp.2010.11.023 |
| [113] |
WANG Q, REN Y X, PAN J H, et al. Compact high order finite volume method on unstructured grids III:Variational reconstruction[J]. Journal of Computational Physics, 2017, 337: 1-26. DOI:10.1016/j.jcp.2017.02.031 |
| [114] |
WANG Z J, LIU Y, MAY G, et al. Spectral difference method for unstructured grids II:extension to the Euler equations[J]. Journal of Scientific Computing, 2007, 32(1): 45-71. DOI:10.1007/s10915-006-9113-9 |
| [115] |
LIU Y, VINOKUR M, WANG Z J. Spectral (finite) volume method for conservation laws on unstructured grids V:Extension to three-dimensional systems[J]. Journal of Computational Physics, 2006, 212(2): 454-472. DOI:10.1016/j.jcp.2005.06.024 |
| [116] |
COCKBURN B, HOU S, SHU C W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case[J]. Mathematics of Computation, 1990, 54(190): 545-581. doi: 10.1090/S0025-5718-1990-1010597-0
|
| [117] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous galerkin methods[C]//18th AIAA Computational Fluid Dynamics Conference, Miami, Florida. Reston, Virigina: AIAA, 2007. doi: 10.2514/6.2007-4079
|
| [118] |
BROOKS A N, HUGHES T J R. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 1982, 32(1-3): 199-259. DOI:10.1016/0045-7825(82)90071-8 |
| [119] |
DUMBSER M, BALSARA D S, TORO E F, et al. A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes[J]. Journal of Computational Physics, 2008, 227(18): 8209-8253. DOI:10.1016/j.jcp.2008.05.025 |
| [120] |
WEI L, HE L X, DENG X G, et al. A class of hybrid DG/FV methods for conservation laws II:Two-dimensional cases[J]. Journal of Computational Physics, 2012, 231(4): 1104-1120. DOI:10.1016/j.jcp.2011.03.032 |
| [121] |
XU K. A gas-kinetic BGK scheme for the navier-stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. DOI:10.1006/jcph.2001.6790 |
| [122] |
ZHANG S H, ZHANG Y T, SHU C W. Multistage interaction of a shock wave and a strong vortex[J]. Physics of Fluids, 2005, 17(11): 116101. DOI:10.1063/1.2084233 |
| [123] |
刘旭亮, 张树海. 二维激波与剪切层相互作用的直接数值模拟研究[J]. 力学学报, 2013, 45(1): 61-75. LIU X L, ZHANG S H. Direct numerical simulation of the interaction of 2D shock wave and shear layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 61-75. (in Chinese) |
| [124] |
李虎.轴对称超声速射流激波噪声数值模拟研究[D].绵阳: 中国空气动力研究与发展中心, 2016.
|
| [125] |
WANG B Y, ZHA G C. Numerical simulation of transonic limit cycle oscillations using high-order low-diffusion schemes[J]. Journal of Fluids and Structures, 2010, 26(4): 579-601. DOI:10.1016/j.jfluidstructs.2010.02.003 |
| [126] |
Sun D, Guo Q, Li C, et al. Direct numerical simulation of effects of a micro-ramp on a hypersonic shock wave/boundary layer interaction[J]. Physics of Fluids, 2019, 31(12): 126101. DOI:10.1063/1.5123453 |
| [127] |
LI Q, GUO Q L, SUN D, et al. A fourth-order symmetric WENO scheme with improved performance by new linear and nonlinear optimizations[J]. Journal of Scientific Computing, 2017, 71(1): 109-143. DOI:10.1007/s10915-016-0293-7 |
| [128] |
LCS FAST. Spectral/HP element methods[EB/OL]. http://www.lcs-fast.com/fifth_order/
|
| [129] |
王运涛, 孙岩, 孟德虹, 等. CRM翼身组合体模型高阶精度数值模拟[J]. 航空学报, 2017, 38(3): 98-105. WANG Y T, SUN Y, MENG D H, et al. High-order numerical simulation of CRM wing-body model[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 98-105. (in Chinese) |
| [130] |
HARTMANN R, HARLAN M M. Curved grid generation and DG computation for the DLR-F11 high lift configuration[C]//Eccomas Congress. Crete Island, Greece: 2016.
|
| [131] |
王运涛, 孙岩, 王光学, 等. DLR-F6翼身组合体的高阶精度数值模拟[J]. 航空学报, 2015, 36(9): 2923-2929. WANG Y T, SUN Y, WANG G X, et al. High-order accuracy numerical simulation of DLR-F6 wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2923-2929. (in Chinese) |
| [132] |
姜振华, 阎超. 高超声速热流高精度数值模拟方法[J]. 北京航空航天大学学报, 2011, 37(12): 1529-1533. JIANG Z H, YAN C. High order accurate methods in numerical simulation of hypersonic heat transfer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12): 1529-1533. DOI:10.13700/j.bh.1001-5965.2011.12.002 (in Chinese) |
| [133] |
MAVRIPLIS D J. Progress in CFD discretizations, algorithms and solvers for aerodynamic flows[C]//AIAA Aviation 2019 Forum, Dallas, Texas. Reston, Virginia: AIAA, 2019: 2944. doi: 10.2514/6.2019-2944
|
| [134] |
GASSNER G J, BECK A D. On the accuracy of high-order discretizations for underresolved turbulence simulations[J]. Theoretical and Computational Fluid Dynamics, 2013, 27(3-4): 221-237. DOI:10.1007/s00162-011-0253-7 |
| [135] |
YU J, YAN C, JIANG Z H. Effects of artificial viscosity and upwinding on spectral properties of the discontinuous Galerkin method[J]. Computers & Fluids, 2018, 175: 276-292. DOI:10.1016/j.compfluid.2018.07.014 |
| [136] |
SUN Y Z, WANG Z J, LIU Y. Efficient implicit non-linear LU-SGS approach for viscous flow computation using high-order spectral difference method[C]//18th AIAA Computational Fluid Dynamics Conference, Miami, Florida. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-4322
|
| [137] |
YU M L, WANG L. A high-order flux reconstruction/correction procedure via reconstruction formulation for unsteady incompressible flow on unstructured moving grids[J]. Computers & Fluids, 2016, 139: 161-173. DOI:10.1016/j.compfluid.2016.05.028 |
| [138] |
HAGA T, GAO H Y, WANG Z. Efficient solution techniques for high-order methods on 3-D anisotropic hybrid meshes[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2011: 45. doi: 10.2514/6.2011-45
|
| [139] |
NASTASE C R, MAVRIPLIS D J. High-order discontinuous Galerkin methods using an hp-multigrid approach[J]. Journal of Computational Physics, 2006, 213(1): 330-357. DOI:10.1016/j.jcp.2005.08.022 |
| [140] |
PERSSON P O, PERAIRE J. Newton-GMRES preconditioning for discontinuous galerkin discretizations of the navier-stokes equations[J]. SIAM Journal on Scientific Computing, 2008, 30(6): 2709-2733. DOI:10.1137/070692108 |
| [141] |
DIOSADY L T, MURMAN S M. Tensor-product preconditioners for higher-order space-time discontinuous Galerkin methods[J]. Journal of Computational Physics, 2017, 330: 296-318. DOI:10.1016/j.jcp.2016.11.022 |
| [142] |
LUO H, BAUM J D, LÖHNER R. A fast, matrix-free implicit method for compressible flows on unstructured grids[M]//Sixteenth International Conference on Numerical Methods in Fluid Dynamics. USA: Springer Berlin Heidelberg. 1998: 73-78. doi: 10.1007/bfb0106564
|
| [143] |
XIA Y D, LUO H, FRISBEY M, et al. A set of parallel, implicit methods for a reconstructed discontinuous Galerkin method for compressible flows on 3D hybrid grids[J]. Computers & Fluids, 2014, 98: 134-151. DOI:10.1016/j.compfluid.2014.01.023 |
| [144] |
JIANG Z H, YAN C, YU J. High-order discontinuous Galerkin solver on hybrid anisotropic meshes for laminar and turbulent simulations[J]. Applied Mathematics and Mechanics, 2014, 35(7): 799-812. DOI:10.1007/s10483-014-1834-9 |
| [145] |
ZHOU C, WANG Z J. An evaluation of implicit time integration schemes for discontinuous high order methods[C]//Proc of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-2688
|
| [146] |
LUO H, SEGAWA H, VISBAL M R. An implicit discontinuous Galerkin method for the unsteady compressible Navier-Stokes equations[J]. Computers & Fluids, 2012, 53: 133-144. DOI:10.1016/j.compfluid.2011.10.009 |
| [147] |
WANG L, MAVRIPLIS D J. Implicit solution of the unsteady Euler equations for high-order accurate discontinuous Galerkin discretizations[J]. Journal of Computational Physics, 2007, 225(2): 1994-2015. DOI:10.1016/j.jcp.2007.03.002 |
| [148] |
VERMEIRE B C, NADARAJAH S. Adaptive IMEX time-stepping for the correction procedure via reconstruction scheme[C]//Proc of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-2687
|
| [149] |
PAZNER W, PERSSON P O. Stage-parallel fully implicit Runge-Kutta solvers for discontinuous Galerkin fluid simulations[J]. Journal of Computational Physics, 2017, 335: 700-717. DOI:10.1016/j.jcp.2017.01.050 |
| [150] |
BASSI F, BOTTI L, COLOMBO A, et al. Linearly implicit Rosenbrock-type Runge-Kutta schemes applied to the Discontinuous Galerkin solution of compressible and incompressible unsteady flows[J]. Computers & Fluids, 2015, 118: 305-320. DOI:10.1016/j.compfluid.2015.06.007 |
| [151] |
VAN LEER B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method[J]. Journal of Computational Physics, 1979, 32(1): 101-136. DOI:10.1016/0021-9991(79)90145-1 |
| [152] |
BURBEAU A, SAGAUT P, BRUNEAU C H. A problem-independent limiter for high-order runge-kutta discontinuous galerkin methods[J]. Journal of Computational Physics, 2001, 169(1): 111-150. DOI:10.1006/jcph.2001.6718 |
| [153] |
HENRICK A K, ASLAM T D, POWERS J M. Mapped weighted essentially non-oscillatory schemes:Achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207(2): 542-567. DOI:10.1016/j.jcp.2005.01.023 |
| [154] |
BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227(6): 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [155] |
ZHANG S H, SHU C W. A new smoothness indicator for the WENO schemes and its effect on the convergence to steady state solutions[J]. Journal of Scientific Computing, 2007, 31(1-2): 273-305. DOI:10.1007/s10915-006-9111-y |
| [156] |
ZHANG S H, JIANG S F, SHU C W. Improvement of convergence to steady state solutions of Euler equations with the WENO schemes[J]. Journal of Scientific Computing, 2011, 47(2): 216-238. DOI:10.1007/s10915-010-9435-5 |
| [157] |
QIU J X, SHU C W. A comparison of troubled-cell indicators for runge:kutta discontinuous galerkin methods using weighted essentially nonoscillatory limiters[J]. SIAM Journal on Scientific Computing, 2005, 27(3): 995-1013. DOI:10.1137/04061372X |
| [158] |
DUMBSER M, ZANOTTI O, LOUBÈRE R, et al. A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws[J]. Journal of Computational Physics, 2014, 278: 47-75. DOI:10.1016/j.jcp.2014.08.009 |
| [159] |
LOUBERE R, DUMBSER M, DIOT S. A new family of high order unstructured MOOD and ADER finite volume schemes for multidimensional systems of hyperbolic conservation laws[J]. Communications in Computational Physics, 2014, 16(3): 718-763. DOI:10.4208/cicp.181113.140314a |
| [160] |
VONNEUMANN J, RICHTMYER R D. A method for the numerical calculation of hydrodynamic shocks[J]. Journal of Applied Physics, 1950, 21(3): 232-237. DOI:10.1063/1.1699639 |
| [161] |
BALDWIN B S, MACCORMACK R W. Interaction of strong-shock wave with turbulent boundary layer: AIAA-74-558[R]. Reston: AIAA, 1974.
|
| [162] |
JAMESON A, SCHMIDT W, TURKEL E. Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes[C]//14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA. Reston, Virigina: AIAA, 1981. doi: 10.2514/6.1981-1259
|
| [163] |
PERSSON P O, PERAIRE J. Sub-cell shock capturing for discontinuous galerkin methods[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006. doi: 10.2514/6.2006-112
|
| [164] |
HUGHES T J R, MALLET M. A new finite element formulation for computational fluid dynamics:IV. A discontinuity-capturing operator for multidimensional advective-diffusive systems[J]. . Computer Methods in Applied Mechanics and Engineering, 1986, 28(3): 329-336. DOI:10.1016/0045-7825(86)90153-2 |
| [165] |
ZINGAN V, GUERMOND J L, MOREL J, et al. Implementation of the entropy viscosity method with the discontinuous Galerkin method[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 253: 479-490. DOI:10.1016/j.cma.2012.08.018 |
| [166] |
BARTER G E, DARMOFAL D L. Shock capturing with PDE-based artificial viscosity for DGFEM:Part I. Formulation[J]. Journal of Computational Physics, 2010, 229(5): 1810-1827. DOI:10.1016/j.jcp.2009.11.010 |
| [167] |
MORO D, NGUYEN N C, PERAIRE J. Dilation-based shock capturing for high-order methods[J]. International Journal for Numerical Methods in Fluids, 2016, 82(7): 398-416. DOI:10.1002/fld.4223 |
| [168] |
HESTHAVEN J Y, JAN S. A study of several artificial viscosity models within the discontinuous galerkin framework[J]. Communications in Computational Physics, 2020, 27(5): 1309-1343. DOI:10.4208/cicp.oa-2019-0118 |
| [169] |
TYACKE J, VADLAMANI N R, TROJAK W, et al. Turbomachinery simulation challenges and the future[J]. Progress in Aerospace Sciences, 2019, 110: 100554. DOI:10.1016/j.paerosci.2019.100554 |
| [170] |
VINCENT P, WITHERDEN F, VERMEIRE B, et al. Towards green aviation with python at petascale[C]//SC'16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA. IEEE, 2016: 1-11. doi: 10.1109/SC.2016.1
|
| [171] |
VERMEIRE B C, WITHERDEN F D, VINCENT P E. On the utility of GPU accelerated high-order methods for unsteady flow simulations:a comparison with industry-standard tools[J]. Journal of Computational Physics, 2017, 334: 497-521. DOI:10.1016/j.jcp.2016.12.049 |
| [172] |
CANTWELL C D, MOXEY D, COMERFORD A, et al. Nektar++:an open-source spectral/hp element framework[J]. Computer Physics Communications, 2015, 192: 205-219. DOI:10.1016/j.cpc.2015.02.008 |
| [173] |
WITHERDEN F D, FARRINGTON A M, VINCENT P E. PyFR:an open source framework for solving advection-diffusion type problems on streaming architectures using the flux reconstruction approach[J]. Computer Physics Communications, 2014, 185(11): 3028-3040. DOI:10.1016/j.cpc.2014.07.011 |
| [174] |
LÓPEZ-MORALES M, BULL J R, CRABILL J, et al. Verification and Validation of HiFiLES: a High-Order LES unstructured solver on multi-GPU platforms[C]//AIAA Aviation. 2014. AIAA 2014-3168.
|
| [175] |
NUDG development team. Nodal unstructured discontinuous Galerkin methods (NUDG)[EB/OL]. http://www.nudg.org, 2015.
|
| [176] |
BANGERTH W, HARTMANN R, KANSCHAT G. deal.II:a general-purpose object-oriented finite element library[J]. ACM Transactions on Mathematical Software, 2007, 33(4): 24. DOI:10.1145/1268776.1268779 |
| [177] |
DURAISAMY K, SPALART P R, RUMSEY C L. Status, emerging ideas and future directions of turbulence modeling research in aeronautics[J]. NASA Technical Memorandum, 2017. |