由于建模误差、格式转换等一系列问题,模型往往存在法向错误、穿插、狭缝、贴合等一系列问题,我们将这类无法直接应用于数值计算的几何模型称为脏几何[1]。因此,在传统的网格生成流程中,网格生成前往往需要对几何进行清理操作,用户需要识别所有的几何错误,并依次修复[2]。这一修复过程往往需要大量人工交互,并借助复杂的图形界面,如CADfix[3]等专业的几何处理软件,且十分依赖于操作人员的经验。对于大量部件组成的复杂模型,人工修复的成本是难以忍受的。
Shephard等提出了一种基于八叉树的全自动网格生成方法[4],基于八叉树的网格生成方法可以一定程度上容忍几何错误,但仍存在一些固有的缺陷。模型的几何特征并非初始构造,该方法需要向基网格嵌入特征,使网格逼近真实几何[5],基网格的质量严重影响几何特征嵌入的效果。在嵌入过程中,往往需要引入大量的单元来捕捉细小的几何特征,导致单元数目的大幅上升。
刘等人基于混合曲面表征[2, 6-7]实现了装配体的“曲面嵌入”,可以解决多个部件之间可能存在的相交和重叠问题。其方法是在离散曲面上计算边界相交图,得到离散嵌入结果,之后根据连续-离散的映射关系完成连续曲面边界表征上的曲面自动嵌入[3]。该算法具有较高的时间效率,也保证了计算结果的几何精度,但其适用范围有限,鲁棒性不足,针对模型贯穿的问题,由于贯穿处缺少边界表征,曲面嵌入失效。
Hu 等通过将三角形-三角形求交升维至四面体-三角形求交,在初始三角形表面约束下生成纯四面体网格,并在有理数范围内实现了精确求交[8]。这种方法在一定程度上可以解决脏几何模型中出现的相交问题,但其局限性亦存在。一是相交计算十分耗时,二是此类方法仅能设定全局容差值,当缝隙间距大于其允许的容差值时,使用此方法不仅无法消除几何误差,反而可能急剧影响性能和网格质量,而容差值过大时,几何特征不能被完全保留。刘[9]也采用四面体化的方法来完成脏几何的网格生成,并创新性地引入了边界恢复算法[10],从而大幅减少相交计算量。两者的四面体化方法中均要求输入边界法向正确,对于存在法向错误的几何,仍然需要大量的手工交互调整输入模型的法向。
本文针对脏几何中可能出现的法向错误、穿插、狭缝、贴合问题,通过四面体化方法自动修复脏几何,并生成高质量的曲面网格。其核心思想是一个有效的四面体网格的表面一定是一个有效的曲面网格。本文在输入模型的离散表征的基础上直接生成四面体网格,通过离散边界切割四面体解决了模型中存在的穿插问题,基于四面体优化解决狭缝和贴合问题,此时该四面体网格的表面便是有效的曲面网格,提取该表面并应用曲面网格重构提升表面网格质量,得到最终的曲面网格。
相较于八叉树方法,本方法具有更高的几何精度,可以生成贴体的曲面网格;相较于基于混合曲面表征的曲面嵌入方法,本方法具有更强的普适性和健壮性;相较于Hu等的四面体化方法,本方法的主要优点有:
1)应用基于视图采样的方法完成法向修复,允许输入的脏几何中存在法向错误;
2)实现了基于容差场的局部修复与特征保持,避免四面体优化导致的特征丢失或修复不完全;
3)实现了基于多级Hausdorff距离[11]的网格重构技术,可以在修复的曲面网格的基础上进行高精度的网格重构,避免网格重构导致的表面自相交。
1 算法流程图1和图2给出了本文所提出的基于四面体化方法的面向脏几何曲面网格生成算法流程,该算法的输入为脏几何模型,输出为保形的高质量曲面网格。该算法主要包含以下步骤:

|
图 1 算法流程简图 Fig.1 Diagram for the algorithm illustration |
1)构建混合曲面表征。建立模型的离散-连续表征数据结构[2],采用B-rep表示模型的连续表征,采用三角网格表示模型的离散表征,同时维护连续模型和离散模型之间的映射关系。得到离散表征后,我们采用基于视图采样的方法,完成法向调整。
2)初始四面体化。本文采用Bowyer-Watson方法[6, 12]完成四面体化,我们提取离散表征中的所有点,作为B-W算法的输入,构造一个Delaunay三角化。单次B-W增量插点的过程为:(1)在当前Delaunay三角化中找到包含待插入点的基单元;(2)利用单元的相邻关系在基单元附近快速搜索所有打破外接圆准则的单元;(3)删除所有(2)中的单元,形成空腔,连接待插入点与空腔边界顶点,形成新的Delaunay三角化。

|
图 2 算法流程图 Fig.2 Flow chat of the algorithm |
3)边界恢复与相交计算。初始四面体化中并不保证包含所有的原始曲面边界,不能包含的边界单元可分为两类。第一类是由于Delaunay三角化只能保证点存在于三角化中,不能保证网格边和网格面也都存在于三角化中,这类边界可以通过边界恢复[9-10, 13-14]的策略来找回原始边界,第二类是由于脏几何模型本身存在相交或重叠的情形,得到的三角化必然无法包含此类边界,如图1(c)所示蓝色区域,这类边界需要通过相交计算对四面体进行裁剪以找回边界。
4)四面体网格质量优化。相交计算仅能解决部件相交的问题,但模型中仍可能存在狭缝等不必要的特征。我们采用四面体网格质量优化的方法,在容差范围内抹除此类特征。
5)曲面网格重构。提取上述四面体网格的表面得到修复后的表面网格,修复后的表面网格解决了原始模型的一系列错误,但网格质量与网格密度均难以达到数值计算的要求,因此需要对4)中得到的表面网格进行重构。
2 算法实现 2.1 法向调整本文算法的核心思想是生成有效的四面体网格,提取其表面得到最终有效的曲面网格。如图1所示,我们在输入模型的外部加入包围盒,在整个包围盒区域内生成四面体网格,我们计算每个四面体单元相对输入表面的绕卷数[15],筛选得到内部的四面体单元,从而方便地提取出有效的表面。绕卷数计算正确的前提是输入表面的法向是正确的,此外,在曲面网格重构中,也需要保持每个面上单元的法向一致。因此在完成混合曲面表征的构造后,我们需要对离散表征的面法向进行修复。
若离散表征中所有的三角单元都是相连的,即两个三角单元之间存在一条共享边,我们可以通过BFS算法[16]完成面法向调整,即锁定某一个三角单元的法向,以该单元为起点,不断搜索其邻居,使与其相连的单元的法向调整为与该起点单元同向。但考虑最坏情况下,若几乎所有的面片均不存在与其他面片的拓扑连接,此时我们无法通过BFS算法快速地完成法向调整。为了尽可能地解决脏几何中可能出现的法向问题,我们采用基于视图采样的法向调整策略。通过绘制该离散模型在各个方向上的视图,可以计算该模型中任意一个面片法向的可能性。理想情况下,我们在任意一个观测点
定义三角面片
| $ P\left({t}_{i}\right) = \frac{{O}_+\left({t}_{i}\right)}{{O}_+\left({t}_{i}\right)+{O}_-\left({t}_{i}\right)} $ | (1) |
若
为了恢复模型的所有原始边界,我们使用原始边界的三角面片所在的平面来切割四面体。非退化情况下四面体单元被原始表面单元所在平面切割如图4所示,被切割的四面体单元的侧面将会被截断为一个四边形和一个三角形,该四面体单元将形成一个四面体单元和一个五面体单元。首先对侧面的三个四边形分别进行Delaunay三角化,再对该五面体单元进行分割,在其重心处插入新点,与侧面的新三角形顶点连接后形成分裂后的新四面体单元。贴合问题将产生零体积的四面体单元,本算法中的三角形求交计算全部采用基于GMP的高精度有理数计算[18],退化情况下舍弃零体积的新单元即可。基于精确的求交计算,我们可以保证输入模型中的所有自相交问题可以得到修复。

|
图 3 法向调整效果 Fig.3 Meshes before and after the normal adjustment |

|
图 4 四面体单元切割的非退化情形 Fig.4 Non-degenerate case of tetrahedral cutting |
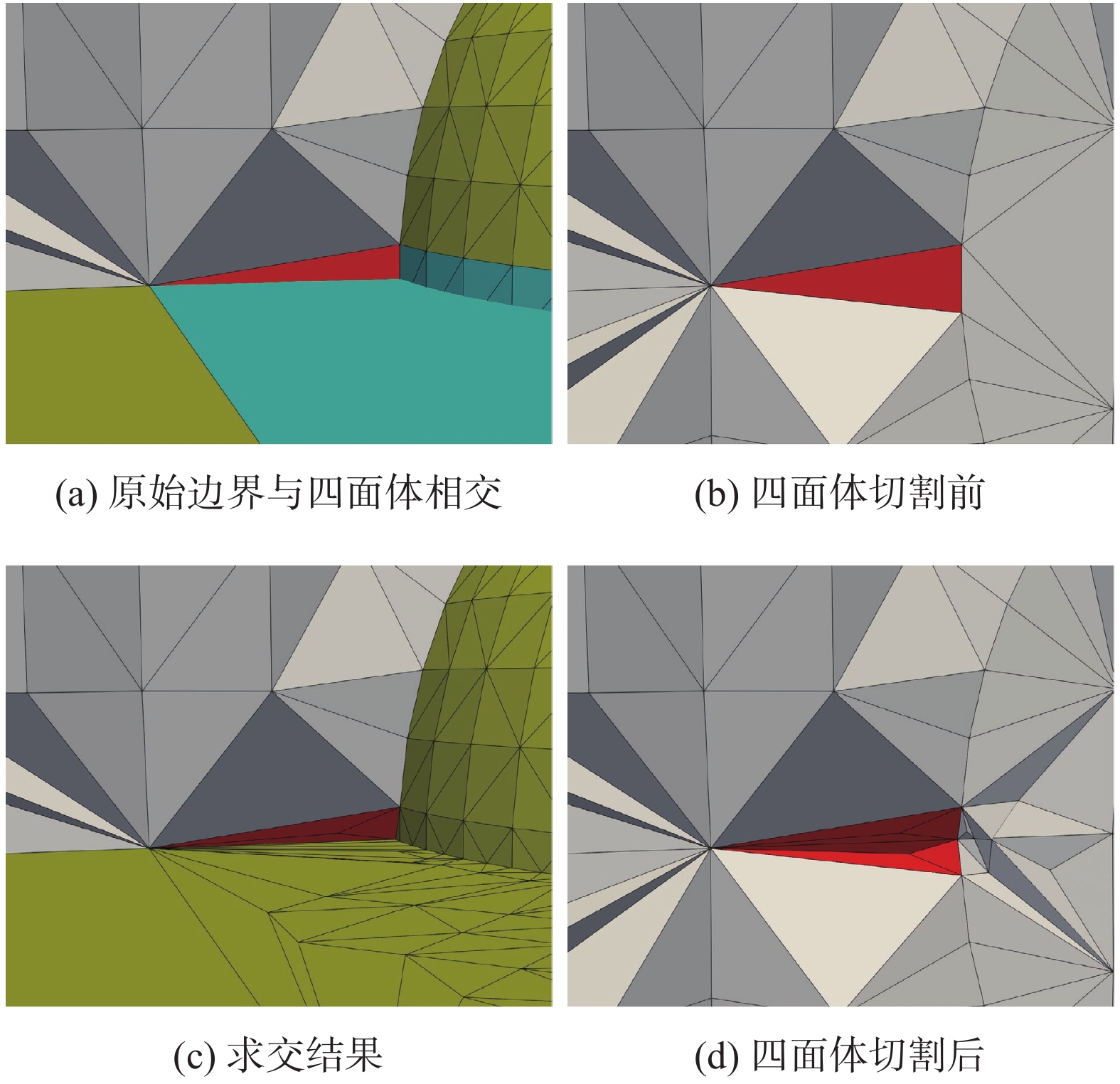
图5展示了利用原始边界切割四面体解决相交问题,图5(a)中红色四面体与蓝色的原始边界出现相交,图5(b)为该四面体的底面。利用原始边界切割四面体,其结果如图5(c)和图5(d)所示。
|
图 5 曲面求交过程 Fig.5 Surface intersection process |
上述四面体-平面求交可以在有理数的范围内修复脏几何的自相交问题,但模型仍可能存在狭缝等不必要的细小特征。由于前述步骤已经完成了输入模型原始表面的恢复,那么在狭缝处必然存在狭窄甚至是退化的四面体单元,因此优化此处的四面体单元质量,即可抹除此类特征。图6展示了通过四面体优化解决狭缝的详细过程。图示两圆柱之间存在狭缝需要被抹除,经过初始四面体化后,如图6(b)所示,狭缝处产生了图示红色的四面体单元,这类四面体单元的质量较差,经过四面体质量提升后,这类单元被抹去,得到的表面如图6(c)所示。

|
图 6 四面体网格优化解决狭缝问题 Fig.6 Tetrahedral mesh optimization for slits |
四面体单元质量的提升主要操作为边分裂、边折叠、面交换与点优化四种局部操作[19],其示意图如图7所示。本文通过循环执行这四种局部操作来逐步优化四面体单元。
本文采用Rabinovich等[8, 20]提出的能量函数作为四面体单元的质量标准,该函数具有天然的各向同性,可以有效地甄别出各向异性的和负体积的四面体单元,公式如下:
| $ {{ E}}_{t} = \dfrac{\mathrm{t}\mathrm{r}\left({\mathit{J}}_{t}^{{\;\rm{T}}}{\mathit{J}}_{t}\right)}{{\mathrm{det}\left({\mathit{J}}_{t}\right)}^{2/D}}$ | (2) |
其中,
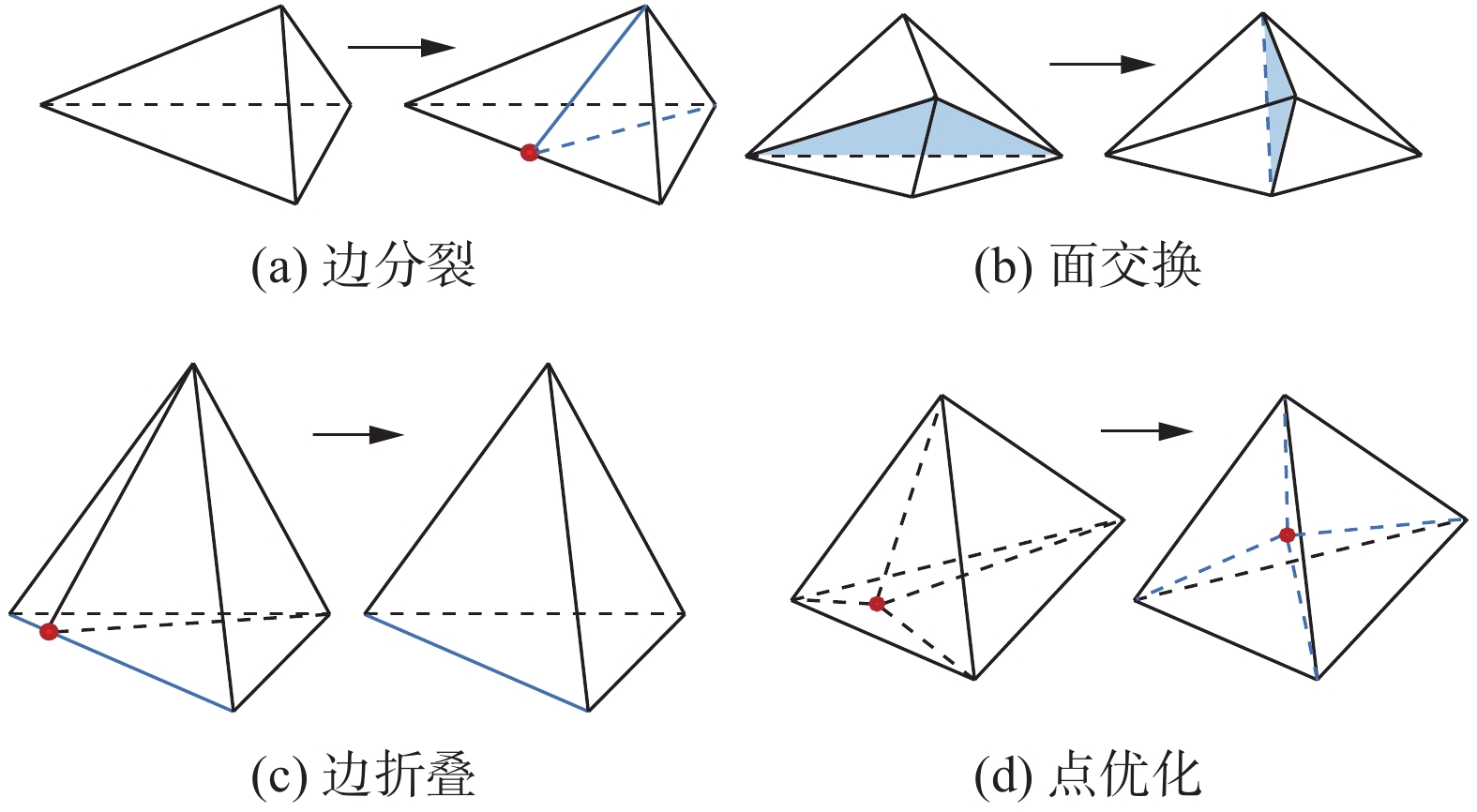
|
图 7 四面体单元质量提升 Fig.7 Quality improvement of tetrahedral elements |
定义理想单元尺寸为
四面体网格质量优化的目的是解决狭缝或重叠处产生的狭窄的或退化的四面体单元,对于空间中的四面体,其质量评判标准不同。为了加速优化效率,我们采用了多级能量阈值判别方案,即每个四面体单元优化的目标能量值不同,这里我们采用四面体单元至边界的距离来计算该单元的能量阈值。我们令原始表面附近的单元的目标能量值为
| $ {E}_{t} = \left[1+\frac{2{d}_{s}}{L}\left(k-1\right)\right]{E}_{ts} $ | (3) |
其中,
上述四面体网格质量优化方法中,边折叠与点优化涉及网格点的位移操作,若网格点的偏移量过大,可能导致网格与输入模型之间产生较大的偏差,我们将禁止这样的边折叠与点优化操作。为了确保本算法生成的表面网格与输入模型之间的误差在可控范围内,每次边折叠与点优化的操作执行后,需要进行包络检测以确保生成保形的表面网格,包络检测的方法如下。
记待检测的三角形为
由上述采样方法可知,实际采样点允许的容差值小于

|
图 8 包络检测的采样点 Fig.8 Sampling points for the envelope detection |
为解决上述问题,我们采用多级的包络检测[8],第
容差
曲面求交与四面体质量提升两个环节中均可能产生新的边界点,新的边界点都是由边分裂形成的,故新边界点的容差值应取其边分裂前的两端点处容差值的最小值。

|
图 9 局部容差实现特征保持 Fig.9 Feature preserving based on local tolerance |
本文中采用经典的网格重构策略完成曲面网格重构,其核心算法与四面体网格重构相同,对需要优化的单元依次执行边分裂、边折叠、边交换与点优化操作,直至所有的表面网格均满足质量要求。
本文中的尺寸场定义采用Liu等[21]提出的定义在离散边界上的尺寸场,并采用其全局光滑化策略[22]。曲面网格单元的衡量标准采用面积与边长之比的平方和,表面网格中的每个点都记录其理想边长
为了生成保形的表面网格,我们希望在重构过程中由于边分裂产生的新点、点优化后的点都能尽可能地贴近原始表面。网格重构中的误差估计通过计算Hausdorff距离[11-21]来衡量,我们要求所有的网格点距离输入边界的Hausdorff距离均小于
本算法采用C++语言实现,借助GMP库完成基于有理数的精确计算。测试平台为Intel Core i7-6700,3.4 GHz,内存24 GB。
3.1 网格生成效果本文选取了靶球、格栅鳍、F-16战斗机、AIM-54导弹、Ford发动机和某压气机六个典型的脏几何模型作为实验对象,模型网格如图10所示。

|
图 10 典型脏几何模型 Fig.10 Typical models for dirty geometries |
为验证本文算法的有效性,这里详细展示三个复杂脏几何的网格生成结果,分别为:靶球模型、格栅鳍模型和F-16战斗机模型。
图11展示了靶球模型的几何及其生成结果,该模型包含115个体部件,存在15177处相交,图11(a)为曲面离散后的局部放大结果,可以明显地看出该处存在部件之间的相交问题,经过本文的四面体化方法修复的表面网格如图11(b)所示,部件之间的相交问题已经得到处理。

|
图 11 靶球模型及其网格生成结果 Fig.11 Target ball model and its mesh generation |
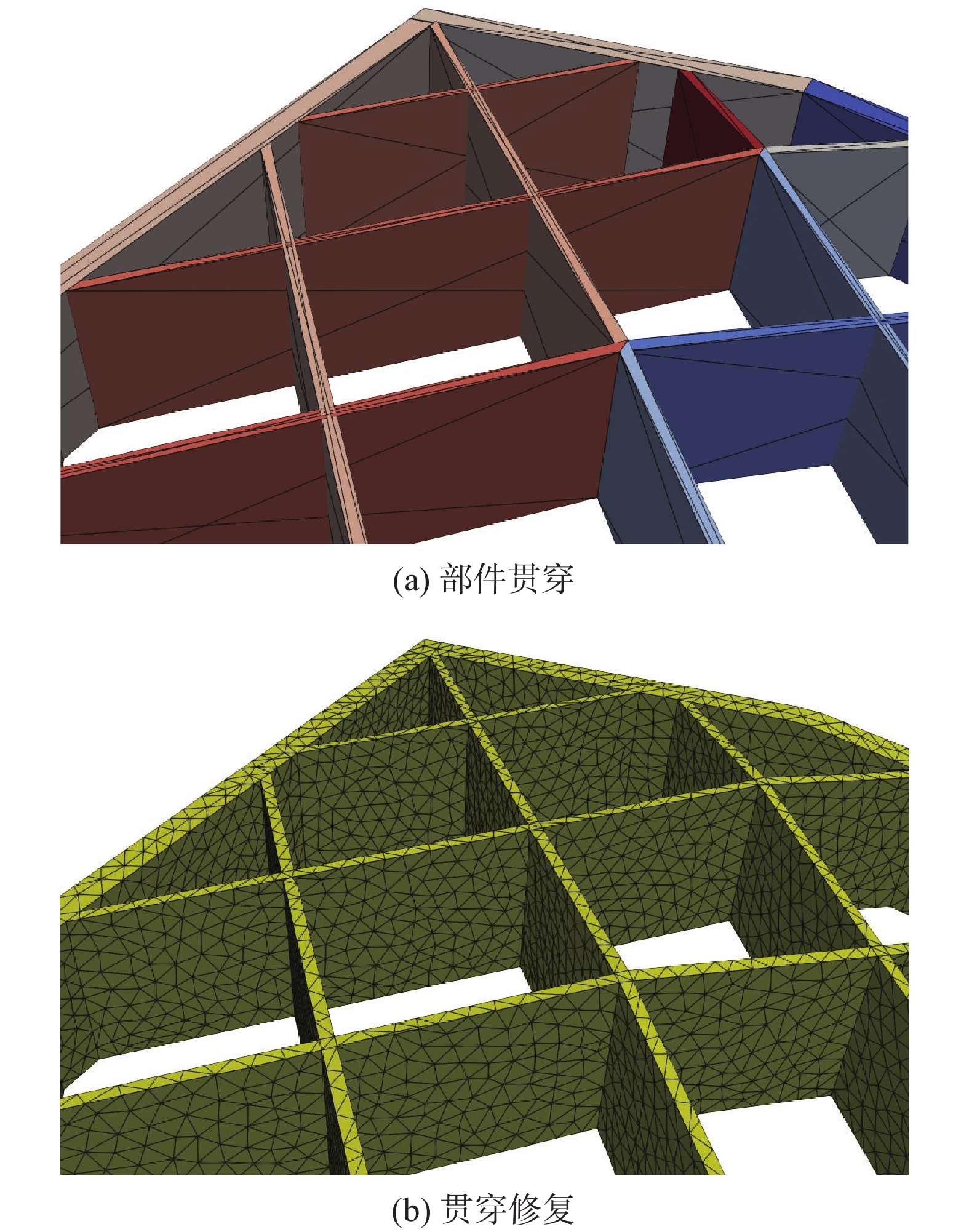
图12展示了格栅鳍模型的几何及其网格生成结果,该模型的各片格栅鳍之间存在大量的贯穿问题,如图12(a)所示,对于此类模型,曲面嵌入的算法由于贯穿处缺少对应的边界表征,故无法支持部件之间互相贯穿的情形。而本文算法由于不依赖原始的边界表征,可以很好地解决这一问题,网格生成结果如图12(b)所示。
|
图 12 格栅鳍模型及其网格生成结果 Fig.12 Grid fin model and its mesh generation |
图13展示了F-16战斗机模型的几何及其网格生成结果,该模型由8个部件组装而成,部件之间存在相交与狭缝等问题。如图13(a)展示了该模型存在的部件之间的相交问题,粉色尾鳍与淡蓝色机身之间存在部件相交问题,图13(b)为该处网格的生成结果。图13(c)展示了该模型部件之间存在的狭缝问题,深蓝色为该模型机翼,淡蓝色区域为该模型机身,机翼与机身之间存在狭缝,图13(d)为该处网格生成结果,可以看出狭缝已经被抹除。

|
图 13 F-16模型及其网格生成结果 Fig.13 F-16 aircraft model and its mesh generation |
F-16战斗机模型中存在一些特殊的几何特征在网格生成中需要得到保留,如图14所示机翼后缘,我们希望在此处能够保留直线特征,后缘处应用2.3.2节所述的局部容差可以实现该处的特征保留,在机翼后缘处设置较小的容差值,实现了该处特征保持的效果,TetWild[8]在此处生成的网格如图14(a)所示,无法保留此类特征。

|
图 14 F-16战斗机局部特征保持对比 Fig.14 Comparison of local feature preservation for the F-16 fighter |
此外,由于本文算法的网格重构过程中引入了尺寸场[21],可以根据曲率特征实现网格的局部加密,即在曲率较大的区域自动生成较密的网格,图14(b)中的机翼前后缘区域的网格受曲率特征的控制,网格尺寸较小,这一特征也使得该网格更能满足后续数值分析的需要。
AIM-54导弹、Ford发动机和某压气机的部分模型错误与修复结果如图15所示。图15(a)中AIM-54的机翼与机身之间,图15(c)中Ford发动机红圈处存在贴合错误,其修复结果如图15(b)和15(d)所示。图15(e)中压气机存在狭缝,修复结果如图15(f)所示。

|
图 15 AIM-54、Ford发动机、压气机模型与网格 Fig.15 Models and meshes of AIM-54, a Ford engine and a compressor |
常用的网格生成算法均不具备表面修复的能力,Hu等完成的TetWild[8]旨在任意离散表面上生成四面体网格,具备一定的表面修复能力,3.1节中的结果表明,本文算法具有更好的修复效果,并且由于本文加入了曲面网格重构的策略,可以在保形的基础上尽可能地生成高质量的表面网格。
我们将前述6个典型的脏几何模型作为实验对象,与TetWild[8]进行网格质量与时间效率对比。由于TetWild只能接受离散输入,且无法处理法向错误的情况,我们将混合曲面表征中已经完成法向调整的离散表征结果作为TetWild的输入。
我们选用平均最小角度和平均最大边长比作为网格质量对比项,平均最小角度为该网格所有单元中每个单元的最小角度的平均值,平均最大边长比为该网格所有单元中每个单元的最大边长比的平均值。前述6个模型分别采用TetWild与本文算法处理所得网格的质量统计与对比结果如表1所示。对比表明,本文算法生成的网格的平均最小角度与平均最大边长比均优于TetWild。
| 表 1 网格质量对比 Table 1 Comparison of mesh quality |
|
|
前述6个模型分别采用TetWild与本文算法处理所耗时间的数据统计与对比结果如表2所示。对比表明,TetWild所耗时间是本文算法的3倍及以上,本文算法在时间效率上领先TetWild。
| 表 2 时间效率对比 Table 2 Comparison of time efficiency |
|
|
本文针对脏几何存在的法向错误、穿插、狭缝、贴合问题,应用基于四面体化的曲面网格修复方法,开发了适用于脏几何的自动网格生成算法。本算法实现了以往四面体化方法无法完成的法向修复;应用边界恢复算法,可以大幅减少参与求交的三角形数量,提高求交性能;应用分级的误差检测,可以大幅提高包络检测精度,从而保证生成保形的曲面网格;引入容差场,实现了特征保持与特征消除;应用多级误差估计,避免曲面网格重构产生自相交,最终生成了高质量的表面网格。上述对比实验也展示了本算法在修复效果、时间效率与网格质量上的优势。
本文算法需要手动设置容差,从而达到好的修复效果,未来将持续探索更加简便与自动化的容差设置方式。此外,本文算法针对存在破洞的几何尚无法完成修复,需要进一步研究补面的算法。
| [1] |
WASSERMANN B, KOLLMANNSBERGER S, YIN S H, et al. Integrating CAD and numerical analysis: ‘Dirty geometry’ handling using the Finite Cell Method[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 351: 808-835. DOI:10.1016/j.cma.2019.04.017 |
| [2] |
曹秉万, 陈建军, 郑耀, 等. 面向混合曲面模型的自动拓扑生成算法[J]. 浙江大学学报(工学版), 2014, 48(5): 923-933. CAO B W, CHEN J J, ZHENG Y, et al.. Automatic topology generation algorithm for hybrid surface models[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(5): 923-933. DOI:10.3785/j.issn.1008-973X.2014.05.025 (in Chinese) |
| [3] |
刘智伟, 杨洋, 陈建军, 等. 面向错位装配体的自动曲面嵌入算法[J]. 空气动力学学报, 2022, 40(5): 166-174. LIU Z W, YANG Y, CHEN J J, et al.. Automatic surface imprinting for misaligned assembly CAD models[J]. Acta Aerodynamica Sinica, 2022, 40(5): 166-174. DOI:10.7638/kqdlxxb-2021.0005 (in Chinese) |
| [4] |
YERRY M A, SHEPHARD M S. Automatic three-dimensional mesh generation by the modified-octree technique[J]. International Journal for Numerical Methods in Engineering, 1984, 20(11): 1965-1990. DOI:10.1002/nme.1620201103 |
| [5] |
DE COUGNY H L, SHEPHARD M S. Parallel volume meshing using face removals and hierarchical repartitioning[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 174(3-4): 275-298. DOI:10.1016/S0045-7825(98)00300-4 |
| [6] |
郑耀, 陈建军. 非结构网格生成: 理论、算法和应用[M]. 北京: 科学出版社, 2016. ZHENG Y, CHEN J J. Unstructured mesh generation: theories, algorithms and applications[M]. Beijing: Science Press, 2016 (in Chinese). |
| [7] |
CHEN J J, CAO B W, ZHENG Y, et al. Automatic surface repairing, defeaturing and meshing algorithms based on an extended B-rep[J]. Advances in Engineering Software, 2015, 86: 55-69. DOI:10.1016/j.advengsoft.2015.04.004 |
| [8] |
HU Y X, ZHOU Q N, GAO X F, et al. Tetrahedral meshing in the wild[J]. ACM Transactions on Graphics, 2018, 37(4): 1-14. DOI:10.1145/3197517.3201353[LinkOut |
| [9] |
刘智伟. 脏几何非结构网格自动生成中的关键问题研究[D]. 浙江大学, 2021. LIU Z W. Automatic Generation of unstructured meshes on dirty geometry[D]. Zhejiang University, 2021 (in Chinese). |
| [10] |
CHEN J J, ZHAO D W, HUANG Z G, et al. Three-dimensional constrained boundary recovery with an enhanced Steiner point suppression procedure[J]. Computers & Structures, 2011, 89(5-6): 455-466. DOI:10.1016/j.compstruc.2010.11.016 |
| [11] |
GRÉGOIRE N, BOUILLOT M. Hausdorff distance between convex polygons[EB/OL]. [2021/11/17]. http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html
|
| [12] |
GEORGE P L. Improvements on Delaunay-based three-dimensional automatic mesh generator[J]. Finite Elements in Analysis and Design, 1997, 25(3-4): 297-317. DOI:10.1016/S0168-874X(96)00063-7 |
| [13] |
陈建军. 非结构化网格生成及其并行化的若干问题研究[D]. 杭州: 浙江大学, 2006. CHEN J J. Unstructured mesh generation and its paralleliz-ation[D]. Hangzhou: Zhejiang University, 2006 (in Chinese). |
| [14] |
郑建靖. 面向并行计算流体动力学模拟的非结构动网格生成的若干问题研究[D]. 杭州: 浙江大学, 2016. ZHENG J J. Some issues on dynamic unstructured grid generation for parallel CFD simulations[D]. Hangzhou: Zhejiang University, 2016 (in Chinese). |
| [15] |
CHENG S, DEY T K, SHEWCHUK J, et al. Delaunay mesh generation[M]. CRC Press Boca Raton, FL, 2013.
|
| [16] |
CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to algorithms[M]. MIT press, 2009.
|
| [17] |
FOLEY J D, VAN F D, Van DAM A, et al. Computer graphics: principles and practice[M]. Addison-Wesley Professional, 1996.
|
| [18] |
JESSE R, RONALD C. GNU multiple precision arithmetic library[M]. Book on Demand Ltd., ISBN: 9785511971391
|
| [19] |
CHEN J J, ZHENG J J, ZHENG Y, et al. Tetrahedral mesh improvement by shell transformation[J]. Engineering With Computers, 2017, 33(3): 393-414. DOI:10.1007/s00366-016-0480-z |
| [20] |
RABINOVICH M, PORANNE R, PANOZZO D, et al. Scalable locally injective mappings[J]. ACM Transactions on Graphics, 2017, 36(4): 1. DOI:10.1145/3072959.3126782 |
| [21] |
LIU Z W, CHEN J J, XIA Y F, et al. Automatic sizing functions for unstructured mesh generation revisited[J]. Engineering Computations, 2021, 38(10): 3995-4023. DOI:10.1108/ec-12-2020-0700 |
| [22] |
CHEN J J, LIU Z W, ZHENG Y, et al. Automatic sizing functions for 3D unstructured mesh generation[J]. Procedia Engineering, 2017, 203: 245-257. DOI:10.1016/j.proeng.2017.09.804 |
 2022, Vol. 40
2022, Vol. 40


