经济的发展需要能源作为支撑。根据国际能源局(International Energy Agency)的公开统计结果[1],自2000年来,全球能源需求的年增长速率约为2%,与全球GDP近20年的平均增长率(3%)基本持平。每年为了实现GDP增长所消耗的所有能源中,化石能源占比85%以上,所带来的温室气体排放、环境污染、气候变化等问题依然很突出[2]。针对该问题,国际社会制定了一系列政策目标,来推广包括风能、太阳能、水电、清洁生物能源等在内的可再生能源,提高使用比例。如,欧洲和中国计划在2030年分别达到32%和25%的可再生能源使用比例目标(2020年全球占比仅为11%[3]);作为世界风能资源开发强国,丹麦承诺截止2050年,该国100%的电能均由可再生能源产生。回顾2020年,全球新冠疫情爆发,交通运输业对化石能源需求萎缩,受优先入网、财税补贴等政策引导,全球可再生能源的使用总量同比2019年增加了3%,幅度相当可观[1]。
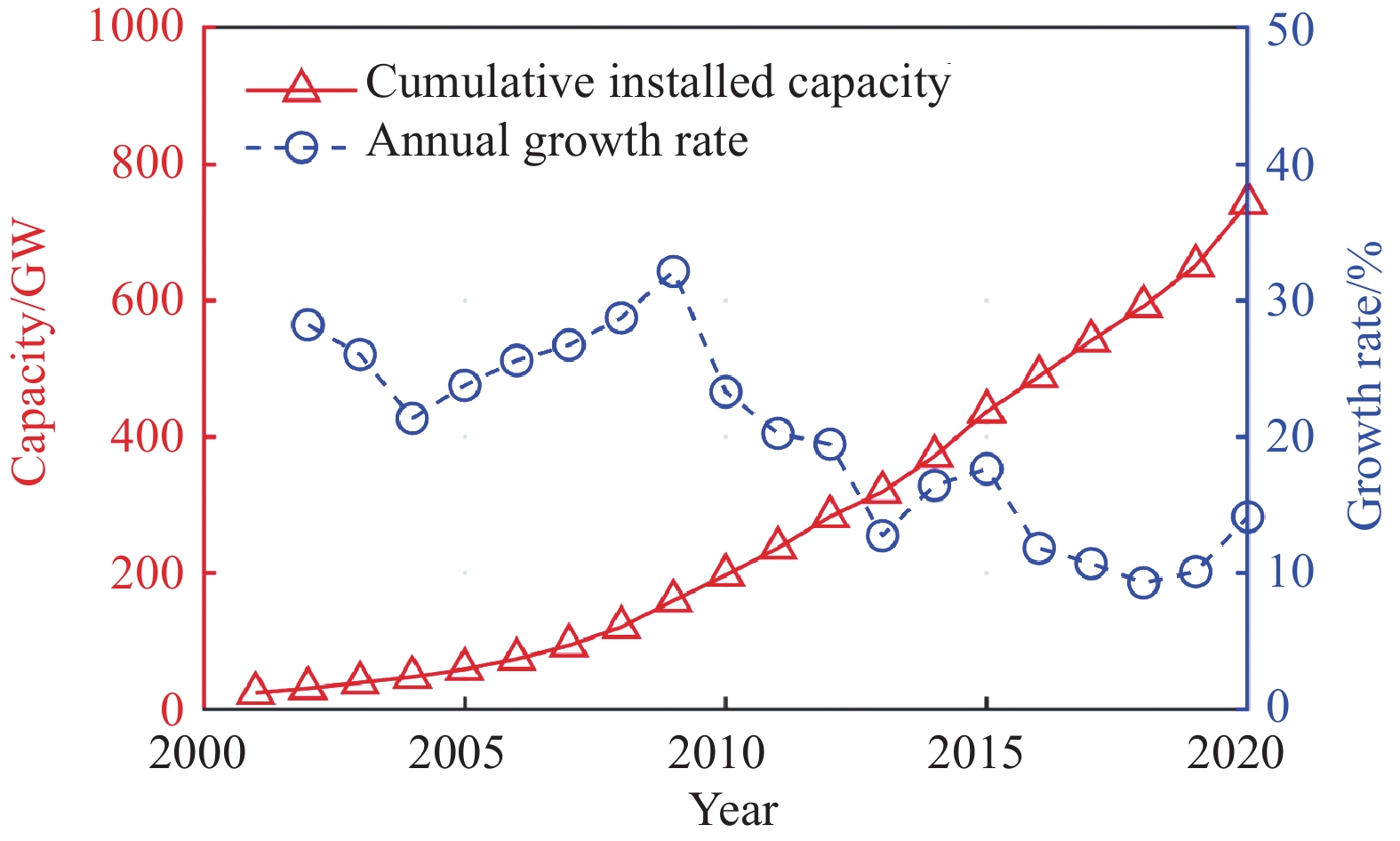
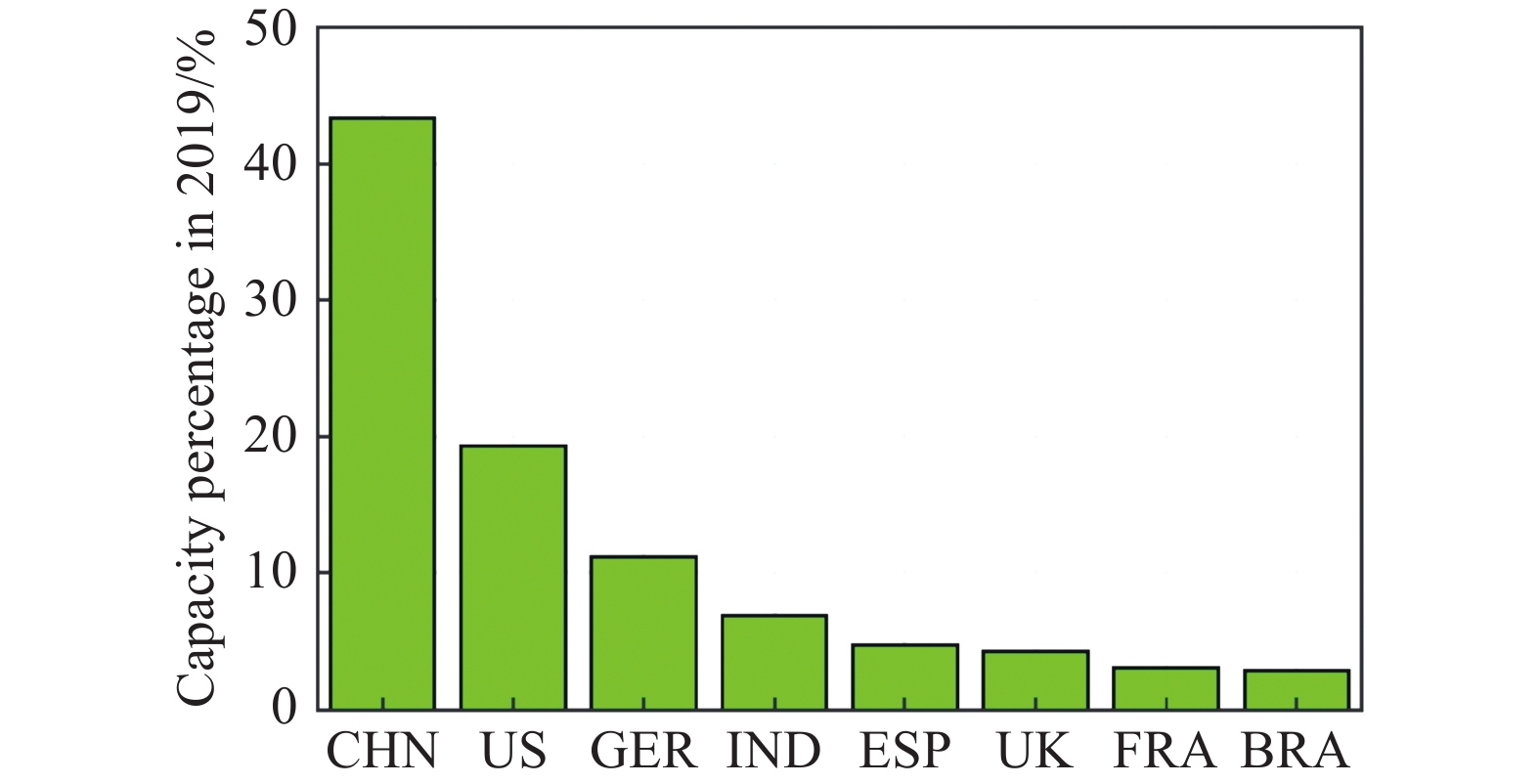
与太阳能和水电等可再生能源类型相比,风能的发展趋势尤为迅猛。图1展示了statista统计网站所公布的自2000年至今全球风能累计总装机容量和年增长速率的变化趋势[4]。可以看出,总装机容量随着时间呈现出一种指数增长的趋势,目前已经达到了740 GW。近10年的年均增长速率约为16%,远高于其他类型能源增长速率。进一步,从不同国家的风能装机容量占世界比例来看(图2),中国已经成为当之无愧的风电大国。2019年,中国总装机容量占比为43%,约为世界的一半。占比排名第二至第八的国家分别为美国(19%)、德国(11%)、印度(7%)、西班牙(4.7%)、英国(4.3%)、法国(3%)和巴西(2.8%)。
|
图 1 全球风能累计总装机容量(左)和年增长率(右)的变化趋势[4] Fig.1 Annual variations of the global cumulative wind power installed capacity (left) and its growth rate (right)[4] |
|
图 2 2019年各风能大国装机容量占世界总装机容量比重[4] Fig.2 Top eight wind power countries and their corresponding percentages[4] |
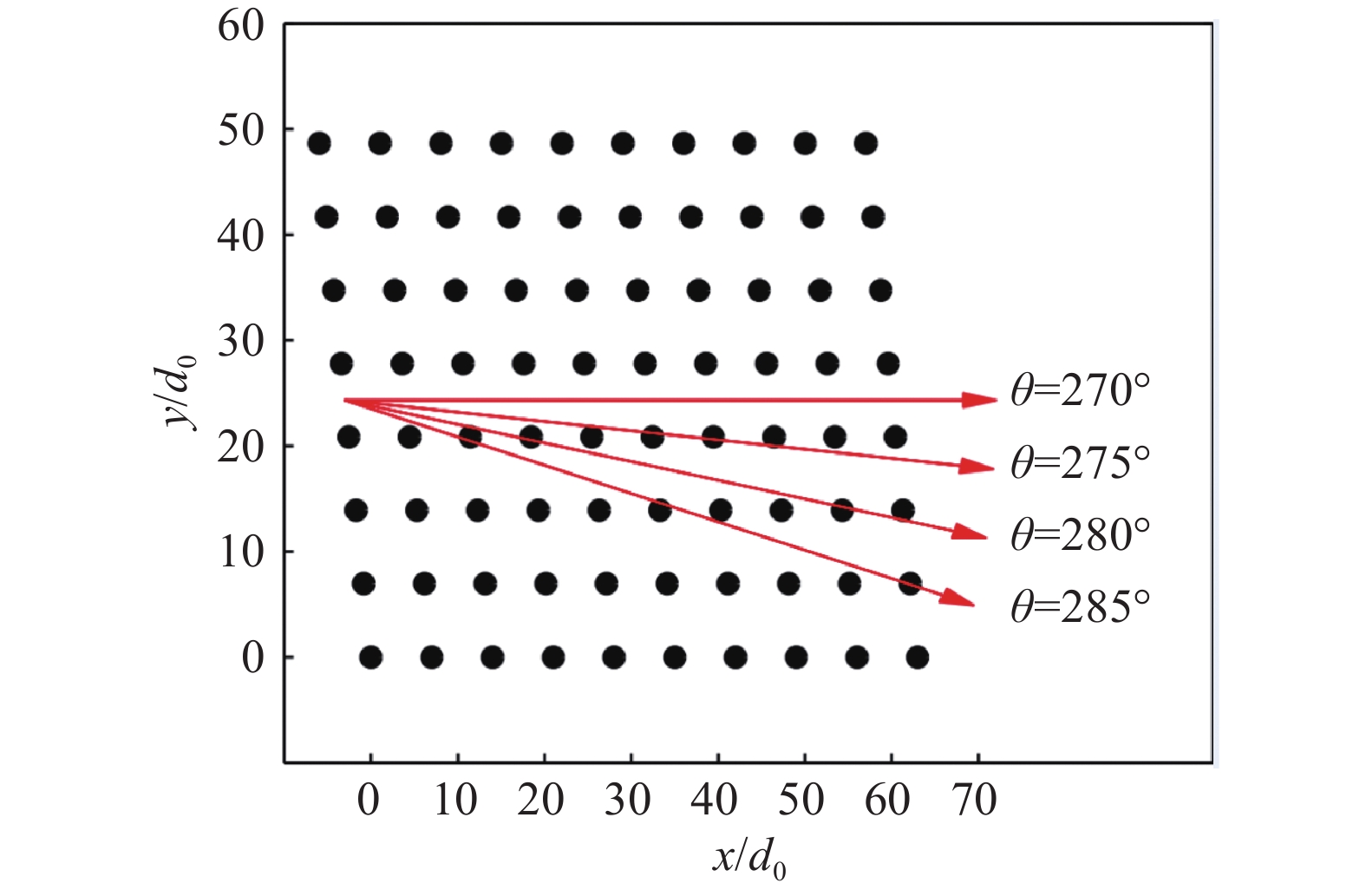
大规模风电场一般由几十或者上百个风力机并网组成阵列,单机平均功率处于兆瓦量级[5-6]。以全球第一个大型海上风电场丹麦Horns-Rev一期为例(图3),80个2 MW风力机按照8行、10列的方式排成平行四边形阵列,行的方向沿着东向,列的方向与北向呈7°夹角[7-8]。为了尽量减少上游风力机尾流对下游风力机产能的影响,海上风电场内部的风力机间隔一般选为5~7倍的风轮直径(d0)。Horns-Rev也不例外,其行和列间距均为7d。但即便如此,风力机在特殊风向下仍然不可避免地存在强烈尾流干扰现象[8-9]。
|
图 3 Horns Rev一期风电场总体布局 (θ代表风向)[2] Fig.3 The planform of Horns Rev-1 Wind Farm (θ denotes the wind direction)[2] |
图4为Hasager等在风向θ = 270°时通过航拍得到的Horns-Rev一期风电场内部尾流干扰图片[10]。此时,后排风力机完全沉浸在前排风力机的尾流中。由于风力机在运转过程中对外界气流施加的阻力作用,风轮尾流中的风速明显低于风电场上游的自由来流风速。因此,在每一行内部,风力机的产能随着列数的增加而逐渐降低。在图4所示的极端全尾流干扰情况下,第4至第10列风力机的产能只有第一列风力机的60%[7-8]。其他三个典型风向下(275°、280°和285°),由尾流干扰所引起的产能降低也不容忽视,最后一列风力机的产能仅为第一列风力机产能的70%。

|
图 4 Horns Rev一期风电场内部的风力机尾流干扰现象[10] Fig.4 Full wake interaction of wind turbines in Horns Rev-1 wind farm visualized by clouds and fog[10] |
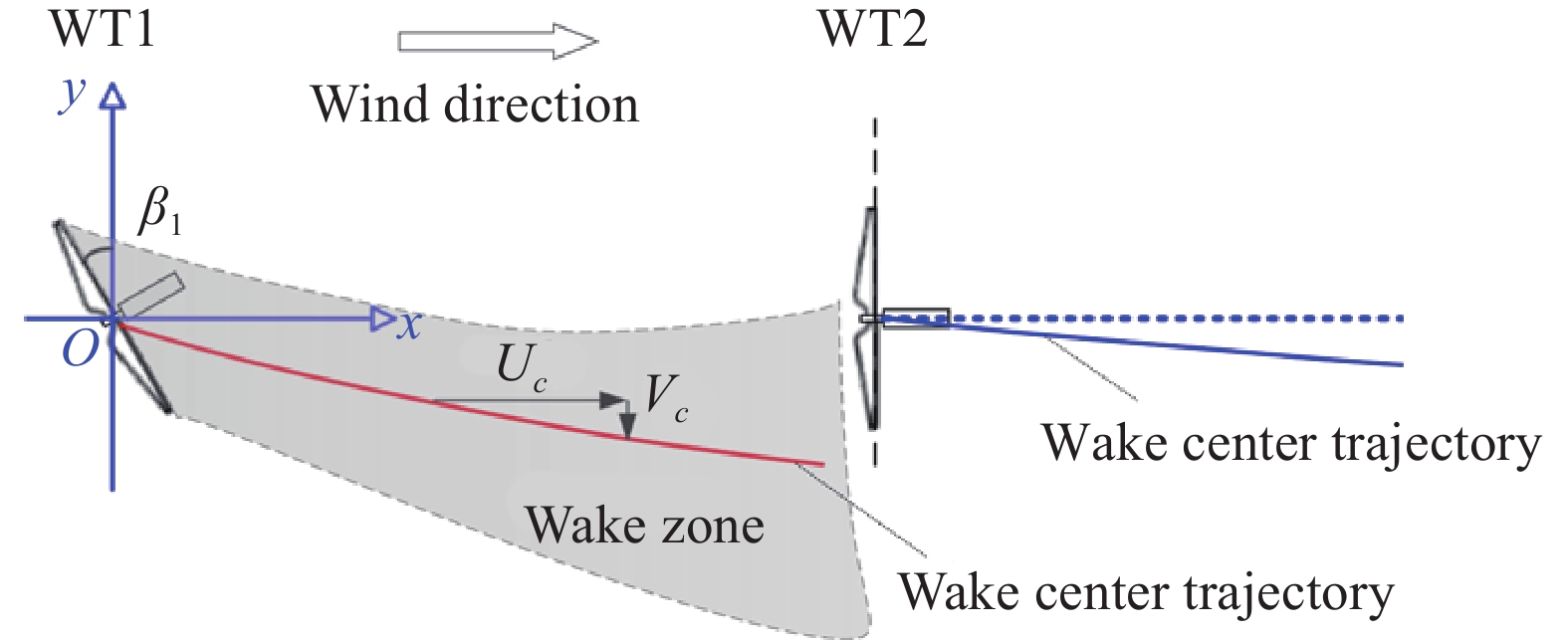
为了克服风力机尾流干扰导致风电场产能下降这一严重问题,瑞典风能研究中心的Dahlberg和瑞典皇家理工大学(KTH)的Medici于2003年在欧洲风能会议上提出采用主动尾流控制技术(Active Wake Control,AWC)对风电场产能进行优化,得到了研究人员的广泛关注[11-15]。后续文献也将AWC技术表述为“Wake Steering”。其基本原理如图5所示:在强烈尾流干扰情况下,通过主动偏航控制,使上游风轮与风向之间处于非垂直状态,产生一个偏航角β;一方面,由于上游风力机WT1(全称:wind turbine 1)的偏航,其有效风能捕获面积减小,产能减低;另一方面,偏航状态的风力机对来流存在一个非零的侧向力,在该侧向力作用下,上游风力机WT1的尾流中心偏向下游风力机,使得WT2(全称:wind turbine 2)的捕获风速提高、产能增加。一系列的实验和仿真研究结果表明,只要合理选取上游风力机的偏航角度,就可以提高整个风电场的产能。对于全尾流干扰这一极端风向下,应用主动偏航控制(Active Yaw Control,AYC)后,风电场产能可优化提升10%~20%[16-18]。在一年时间尺度内,经过各个风向平均后,平均产能有望提升2%~3%[19]。
|
图 5 用于风电场产能优化的主动偏航控制技术原理示意图 Fig.5 A sketch of the active yaw control technique for wind farm power optimization |
实际上,为了减弱尾流干扰所带来的不利影响,还可以采用周期性变桨距、风轮仰角控制等[20-23]。但这些方法较静态偏航控制而言,工程实现难度大,尾流偏转效率低,同时还极大地增大了叶片的动载荷[24-26],因而相关研究较少。
目前,包括洛桑联邦理工大学[18-19]、斯坦福大学[17]、慕尼黑工业大学[16]、挪威科技大学[12]、美国可再生能源实验室(NREL)[27-29]、荷兰能源研究中心(ECN)[13]、中南大学[30]等在内的多家单位都已经参与到了AWC技术的研究中,以期能够早日实现工程应用。该技术理论研究的最终目标是在风向、湍流度等大气参数和风电场几何布局等参数已知的情况下,快速(秒量级内)为所有风力机找到一个最佳的偏航角组合,实现整个风电场尾流干扰最弱、总产能最高。正因为主动偏航控制的时效性要求,整个风场产能的估算必须采用简单解析理论模型。雷诺平均湍流模拟(RANS)、大涡模拟(LES)和直接数值模拟(DNS)等计算流体力学方法虽然精度高,但由于耗时在小时量级,因此无法应用。
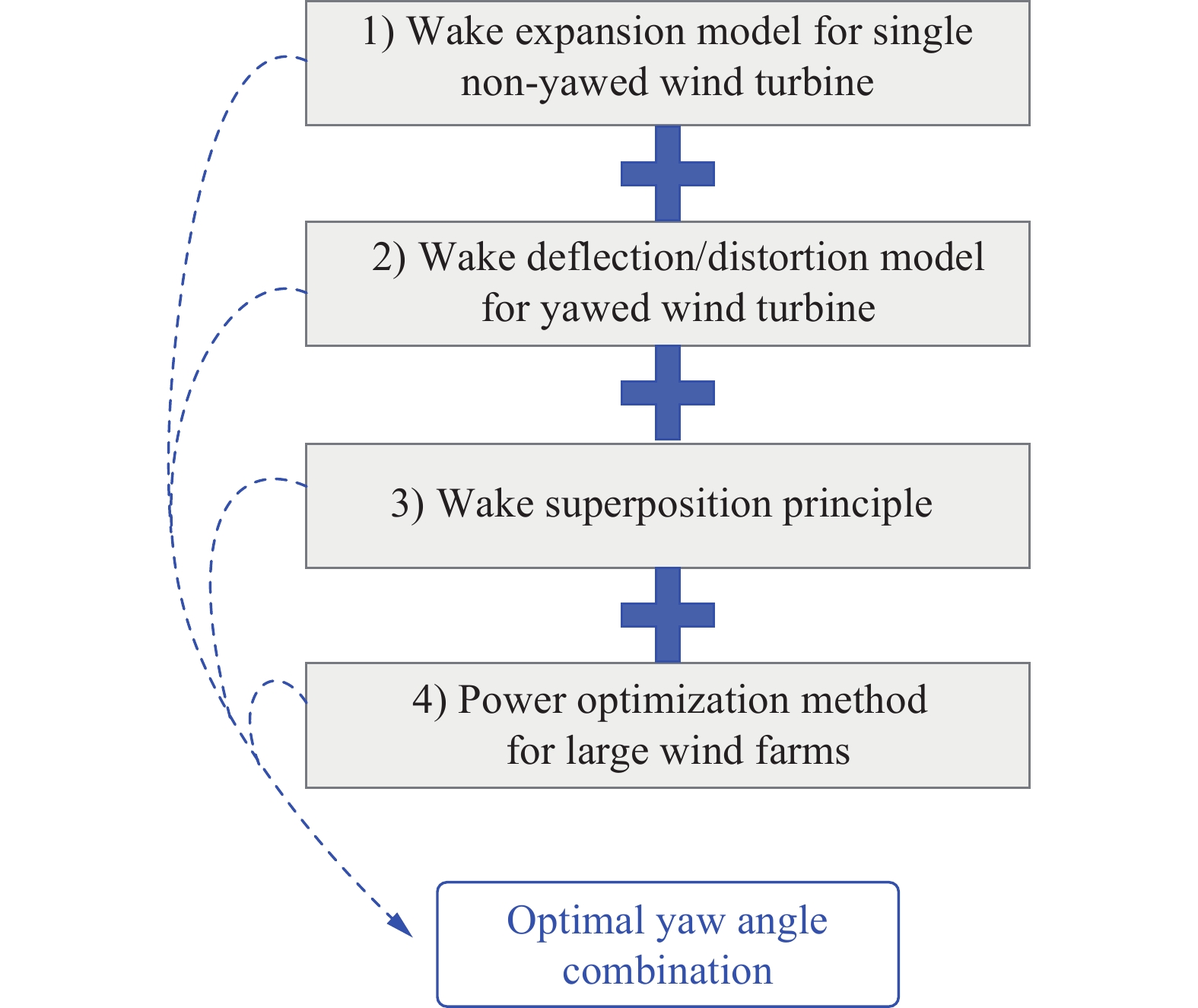
如图6所示,为了获得最佳的偏航角组合,需要开展以下几个方面的研究:1)单个风力机尾流演化解析模型;2)偏航风力机尾流偏转/变形解析模型;3)多个风力机的尾流迭加原理;4)风电场产能优化算法。本文遵循相同的理论框架,对AWC四个支撑内容的研究现状和主要成果进行综述,并在文章最后对制约该项技术走向工程应用的几个问题进行了探讨。而关于风轮叶片气动设计等问题,请参见其他综述[5,31-32]。
|
图 6 主动偏航技术研究理论框架 Fig.6 Theoretical framework for active yaw control research |
如图7所示,在风力机运转过程中,其上下游流动可以划分三个区域:上游诱导区、近场尾流区、远场尾流区[2,32]。Medici和Bastankhah等的研究结果表明[33-34],上游诱导区域的流向影响范围大致为−2d0<x<0,其中d0为叶轮直径。

|
图 7 风力机的上游诱导区、近场尾流区、远场尾流区示意图[2] Fig.7 Sketch of the induction region, near-wake, and far-wake in wind turbine flow[2] |
在诱导区内,受叶尖涡诱导效应影响,中心轴线上的流向压力梯度为负值,主流速度u呈现出随x增加而逐渐减小的变化趋势。两者之间的数学表达式可以由涡面理论推导出来,如下所示:
| $ \frac{{{{\bar u}_c}(x)}}{{{U_\infty }}} = 1 - a\left( {\left. {1 + \frac{x}{{\sqrt {0.25{d_0}^2 + {x^2}} }}} \right)} \right. $ | (1) |
其中:
风力机近场尾流区包含的主要流动特征有叶尖涡、轮毂涡、机舱尾流、塔杆尾流等[32,35-36]。由于不同风力机设计叶尖速度比差异较大,且塔杆和机舱的几何形状又不尽相同,因此近场尾流流动呈现出强三维特征、缺乏自相似性。近场尾流区所占据的流向范围约为2~4倍的叶轮直径,并随着大气湍流度的增加而减小[37]。近场尾流在流向演化过程中,一方面,与上游诱导区域类似的也受到流向逆压梯度作用,呈现出随x增加而逐步减小的趋势;另一方面,在湍流卷吸效应下,近场尾流低速气流与外界未受干扰流动在交界面上进行掺混,使得剪切层增厚、尾流核心区收缩(图7中的黑色虚线)。当核心区完全消失后,尾流速度亏损剖面由叶轮下游的平顶型演化为远场尾流的高斯型。整个过程与自由射流的速度剖面演化基本类似[38]。
从时均速度场来看,远场尾流区的一个重要特征是尾流亏损速度剖面(
从瞬时速度场来看,远场尾流中心在向下游传播的过程中,呈现出沿着展向来回震荡的蜿蜒行为[2,40]。研究人员普遍认为该蜿蜒效应与大气边界层内部的大尺度相干结构有关。具体来讲,这些大尺度结构存在于边界层内的对数区,其流向长度最多可达10~20倍的边界层厚度[41]。当该大尺度结构经过风力机时,尾流速度亏损就像是一个被动输运量,被这些非定常大尺度结构所扭曲,呈现出蜿蜒行为[42]。由于地面的束缚效应,边界层内部展向脉动比垂直方向脉动要强烈,因此远场尾流的展向蜿蜒幅度要比垂向蜿蜒幅度大很多[43]。这种蜿蜒效应对于尾流速度亏损的快速恢复具有重要意义。
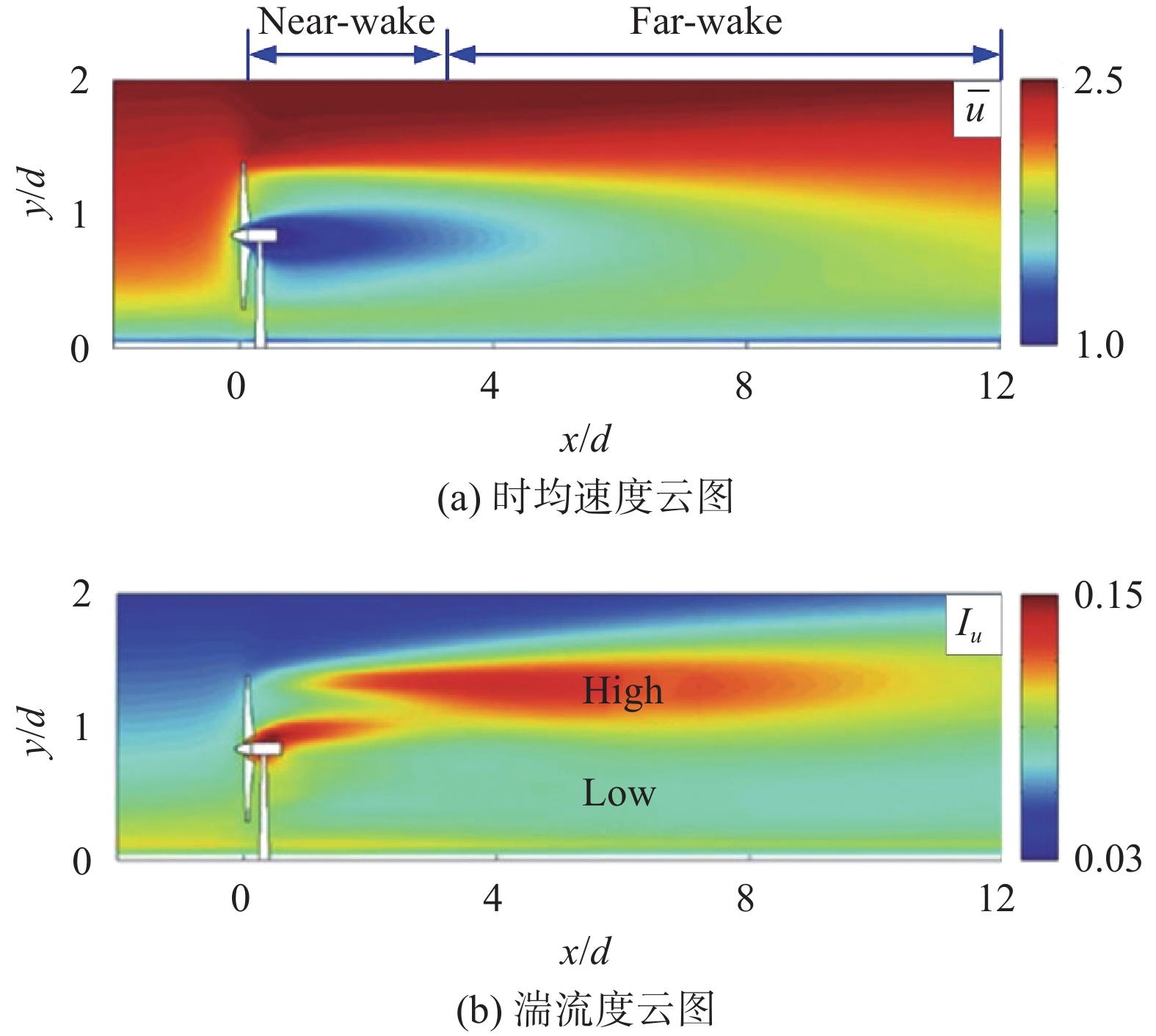
轴对称尾流和自相似性速度剖面是目前所有尾流简化建模的基础假设。但需要说明的是,在大气边界层中,受风剪切和风向顺变等因素影响,这两个假设并不严格成立。图8所示为Wu和Porte-Agel通过LES得到的风力机尾流速度云图和湍流度云图[44]。在垂直平面内,受壁面约束,尾流只能朝着上边界扩张。此外,受大气边界层内风剪切效应影响,尾流上边界剪切层内的速度梯度要明显高于下边界剪切层内的。根据湍动能平衡方程,速度梯度与雷诺应力的乘积决定了湍动能的生成速率[38]。因此,风力机尾流上边缘剪切层内的湍流度要远远高于下边缘剪切层内的,这进一步加剧了垂直面内的速度不对称。在现有的尾流建模中,上述风剪切效应的考虑还不够。绝大部分尾流模型均认为风剪切效应下的尾流速度亏损演化与均匀来流速度下基本相同。
|
图 8 大气边界层中典型风力机尾流流场的LES结果[44] Fig.8 LES results of the wind turbine wake flow in an atmospheric boundary layer[44] |
目前在风电场产能优化中应用较多的风力机尾流模型有Jensen模型[45]、Frandsen模型[46]、EPFL高斯尾流模型[39]等。虽然推导过程各异,但基本假设都是均匀来流,最终目标都是获得不同流向和径向位置处的尾流速度分布表达式,核心参数为尾流宽度和最大尾流亏损速度。表1对比了不同尾流扩张模型的主要特点。下文进一步对各个模型的推导思路和尾流速度表达式进行逐一介绍。
| 表 1 非偏航风力机尾流扩张模型对比 Table 1 Comparisons of wake expansion models for non-yawed wind turbines |
|
|
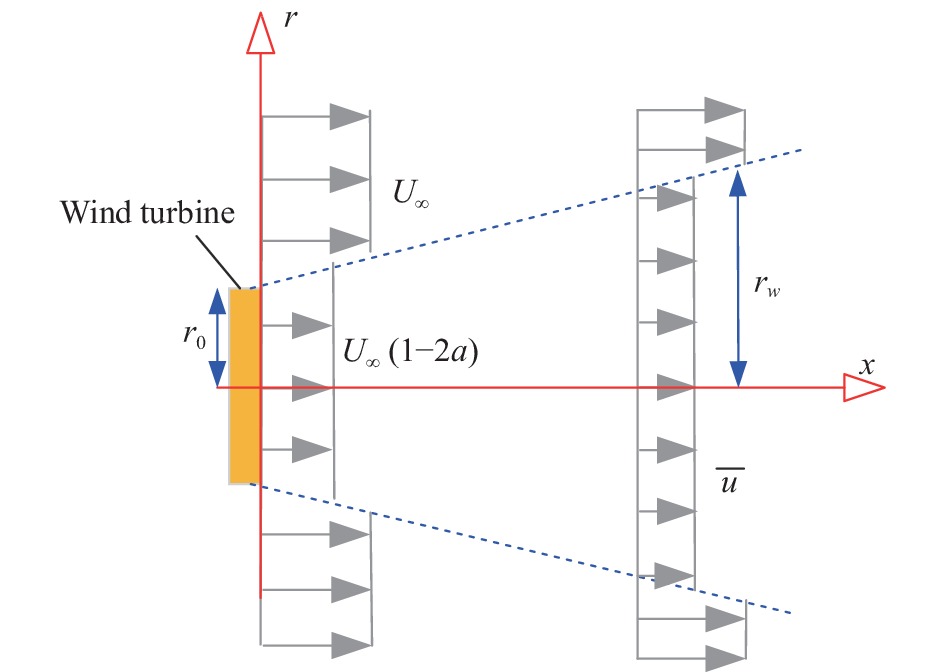
如图9所示,Jensen模型[45]假定尾流速度剖面是平顶型的,尾流半径rw随x线性增加,表达式为:
|
图 9 Jensen尾流模型示意图 Fig.9 Sketch of the Jensen’s wake model |
| $ {r_w} = {r_0} + {k_w}x $ | (2) |
其中,r0为风轮半径,kw为尾流扩张速率(~0.1)。
进一步,选取尾流区域为控制体,应用“动量守恒定律”,可得任一位置x处的尾流动量等于风轮位置处的尾流动量与边界处的卷吸动量之和:
| $ \text{π} r_w^2 \bar u = \text{π} r_0^2 {U_\infty }(1 - 2a) + \text{π} (r_w^2 - r_0^2) {U_\infty } $ | (3) |
将式(2)代入式(3)中,进行化简后即可推导出Jensen尾流模型:
| $ \dfrac{\Delta u}{{U}_{\infty }} = \left\{\begin{array}{*{20}{l}}0 &,\;{r}^{2} > {r}_{w}^{2}\\ \dfrac{2a}{{\Bigg(1+{k}_{w} \dfrac{x}{{r}_{0}}\Bigg)}^{2}} &,\;{r}^{2}\leqslant {r}_{w}^{2}\end{array}\right. $ | (4) |
其中,轴向诱导系数a由风力机推力系数CT决定[31,47]:
尽管Jensen模型自称应用了“动量守恒定律”,但式(3)中速度的阶数仅为一阶,其实质为流量守恒,并非动量守恒。
Frandsen模型[46]与Jensen模型类似,均假设尾流速度亏损为平顶型剖面。在推导过程中,Frandsen模型从经典湍流理论的动量表达式出发,进一步应用流量守恒,得到的尾流亏损速度表达式如下:
| $ \dfrac{{\Delta u}}{{{U_\infty }}} = \left\{ \begin{array}{*{20}{l}} 0 & {,}{{r^2} > r_w^2} \\ {\dfrac{1}{2}\left( {1 - \sqrt {1 - 2\dfrac{{r_0^2}}{{r_w^2}}{C_T}} }\; \right)} & {,}{{r^2} \leqslant r_w^2} \end{array} \right. $ | (5) |
式(5)中的尾流宽度rw也改为流向坐标x的非线性函数,
| $ {r_w} = {r_0}\sqrt {\beta + \frac{\alpha }{{2{r_0}}} x} $ | (6) |
其中,α是一个与尾流扩张速率相关的常数,约等于10倍的kw。β代表了当风轮后部尾流压力恢复到大气压时,尾流直径与风轮直径的比值,具体表达式如下:
| $ \beta = \frac{1}{2} \cdot \frac{{1 + \sqrt {1 - {C_T}} }}{{\sqrt {1 - {C_T}} }} $ | (7) |
Frandsen模型中的一个不合理假设是认为风力机的尾流压力恢复到大气压力时所对应的流向位置可以近似为x = 0。实际上,该位置大约为x = 0.5D[46]。
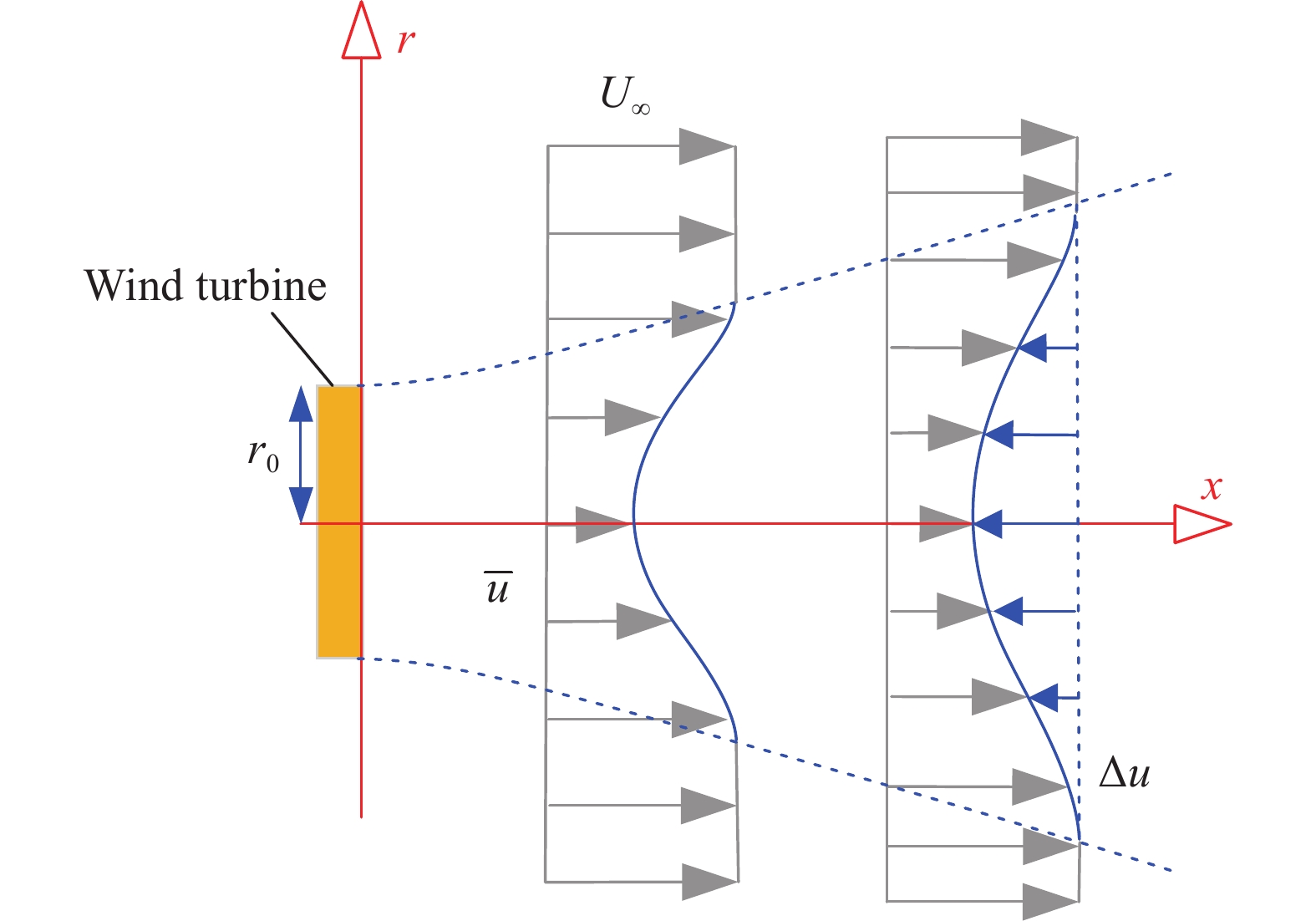
2014年,瑞士洛桑联邦理工大学(EPFL)的Bastankhah和Porté-Agel提出了高斯尾流模型[39]。如图10所示,与Jensen和Frandsen模型不同,该模型采用高斯函数来描述远场尾流的速度剖面,精度更高。经过多年的扩展,该模型已经包含了流向压力梯度[48]、垂直风向顺变[49-50]等各个因素的影响,正在成为风电场产能估算的标准尾流模型。
高斯模型推导的出发点是尾流流动中的动量守恒关系。即,当尾流压力恢复至大气压力后,对于任意一个横截面,有如下关系成立[38]:
| $ T = \iint {\bar u}({U_\infty } - \Delta u){\rm{d}}A $ | (8) |
其中,T为风力机的推力系数。
|
图 10 EPFL高斯尾流模型示意图 Fig.10 Sketch of EPFL’s Gaussian wake model |
进一步,假设尾流速度亏损剖面是自相似的高斯函数
| $ \frac{{\Delta u}}{{{U_\infty }}} = \left[ {1 - \sqrt {1 - \frac{{{C_T}}}{{8\Bigg(\dfrac{\sigma}{d_0}\Bigg)^2}}} } \right]{{\rm{e}}^{ - \frac{{{r^2}}}{{2{\sigma ^2}}}}} $ | (9) |
在该式中,σ代表了尾流的特征宽度,可以直观理解为高斯速度剖面的标准差。
Bastankhah等沿用了Jensen模型中的线性尾流扩张假设,将σ表示成x的一次函数:
| $ \sigma {\text{ = }}{k_w} x + 0.2{d_0}\sqrt \beta $ | (10) |
其中,kw和β的含义已在式(2)和式(7)中进行了解释。
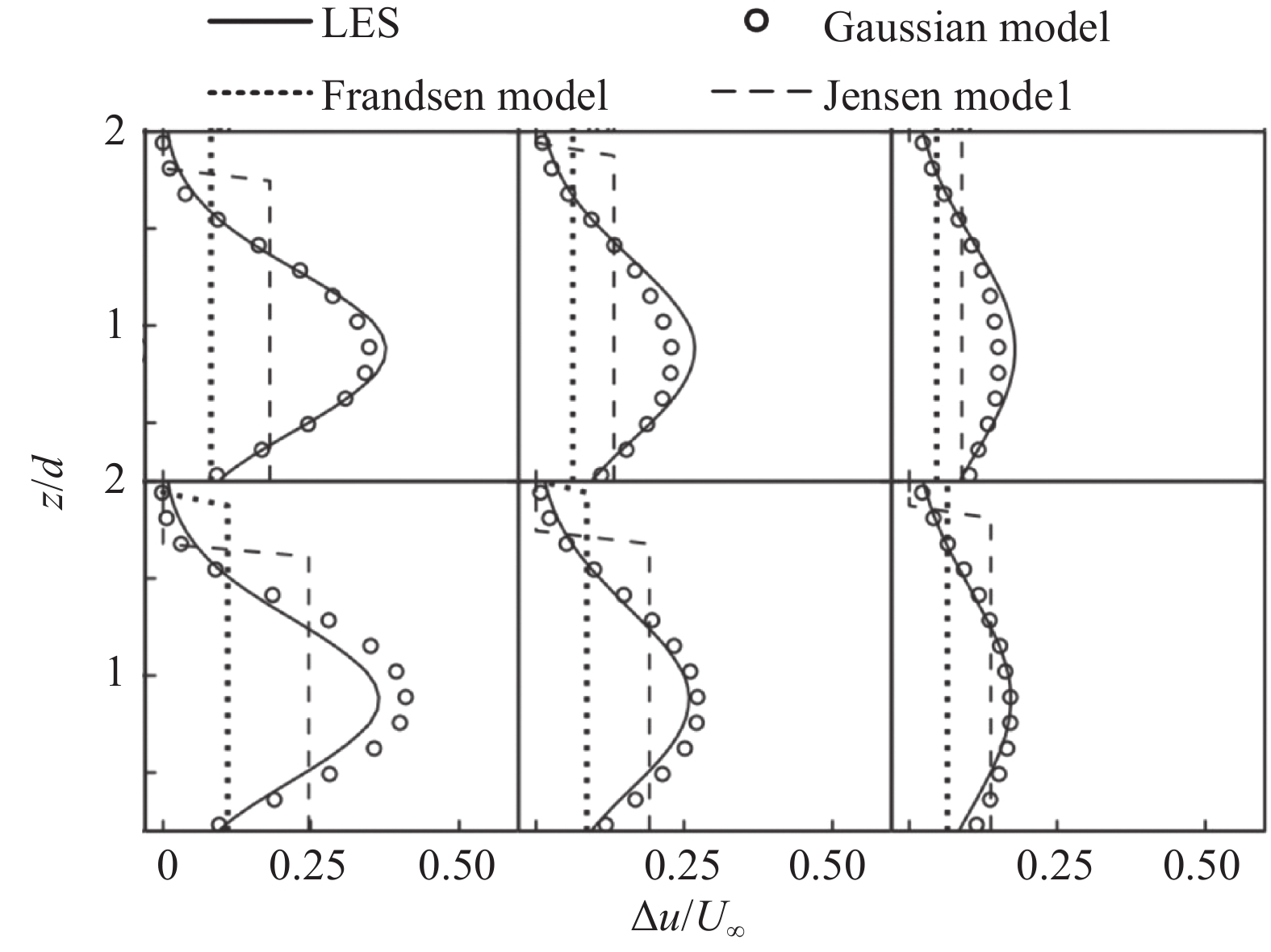
文献[39]和[51]中对比了不同解析模型所预测出的尾流速度亏损剖面。如图11所示,高斯模型的预测结果与LES仿真结果吻合较好,而Jensen和Frandsen模型所预测出来的最大尾流速度均偏低。
|
图 11 不同解析模型所预测的尾流速度亏损剖面[39] Fig.11 Wake velocity deficit profiles predicted by different analytical models[39] |
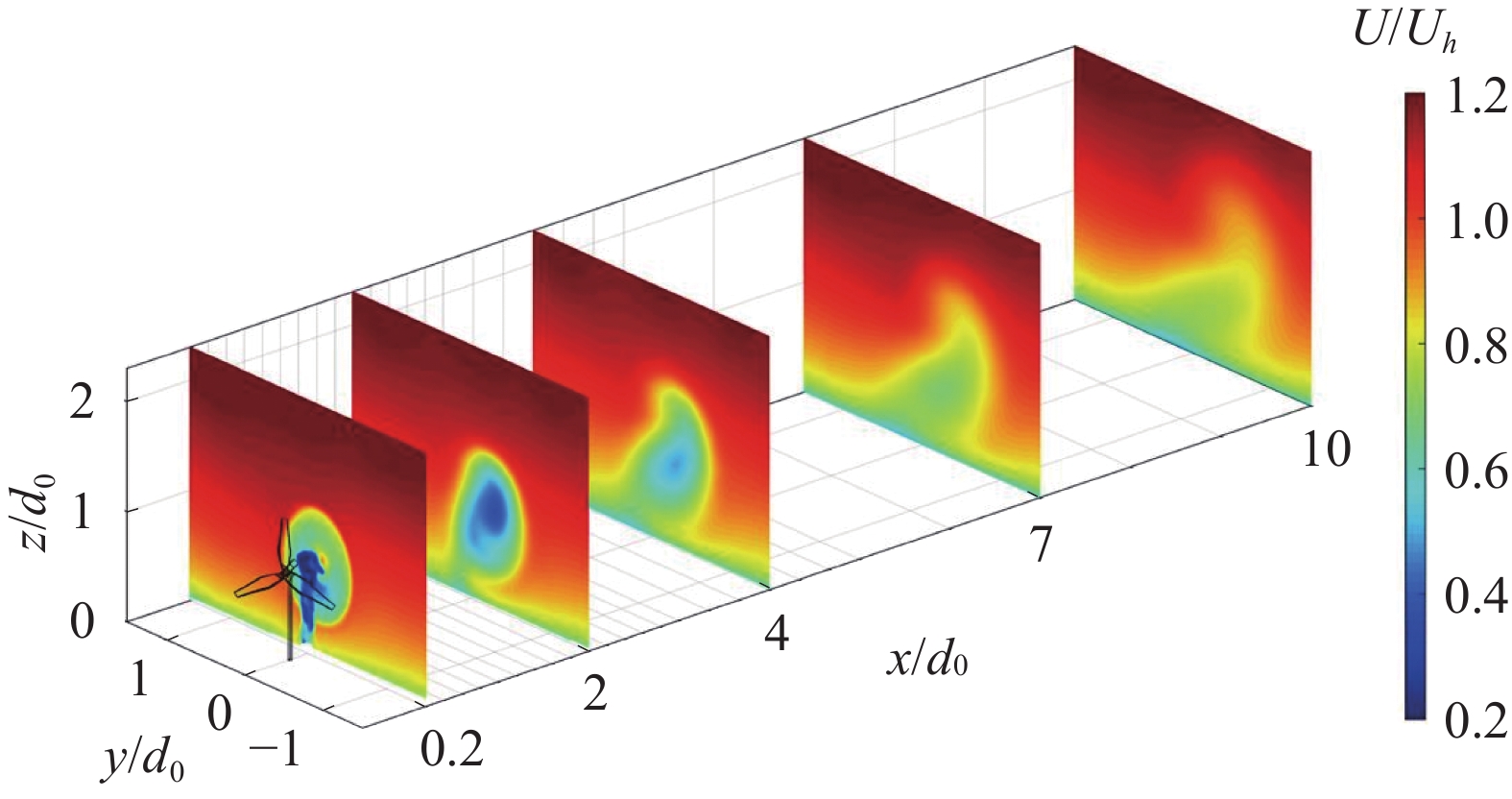
在传统风电场中,各个风力机的偏航控制系统无交联。每个风力机均根据自身所测得的短时平均风向去实时调整风轮朝向,以最小化偏航误差、最大化来流捕获面积。但即便如此,受控制系统响应速度和偏航调整频率约束,在风力机正常运行过程中,仍存在着4°~10°的偏航误差[52]。因此,研究偏航风力机尾流特征不仅仅是发展AWC技术的需要,更是提升现有风电场产能预测精度的必然要求。图12为EPFL的Zong等在风洞中测量得到的偏航风力机尾流剖面演化过程(偏航角β = 30°,偏转方向正负定义见图5)。风洞中边界层厚度大约为2倍的风轮直径(2d0 = 0.3 m),轮毂中心线高度处的湍流度为5.5%。与非偏航风力机相比,偏航风力机尾流呈现出三大典型特征:中心线偏移、肾型速度亏损剖面、对转涡对。
|
图 12 采用体视粒子图像测速仪(SPIV)测量得到的偏航风力机尾流演化(β = 30°)[53] Fig.12 Streamwise evolution of the wake velocity profiles behind a yawed wind turbine (β = 30°)[53] |
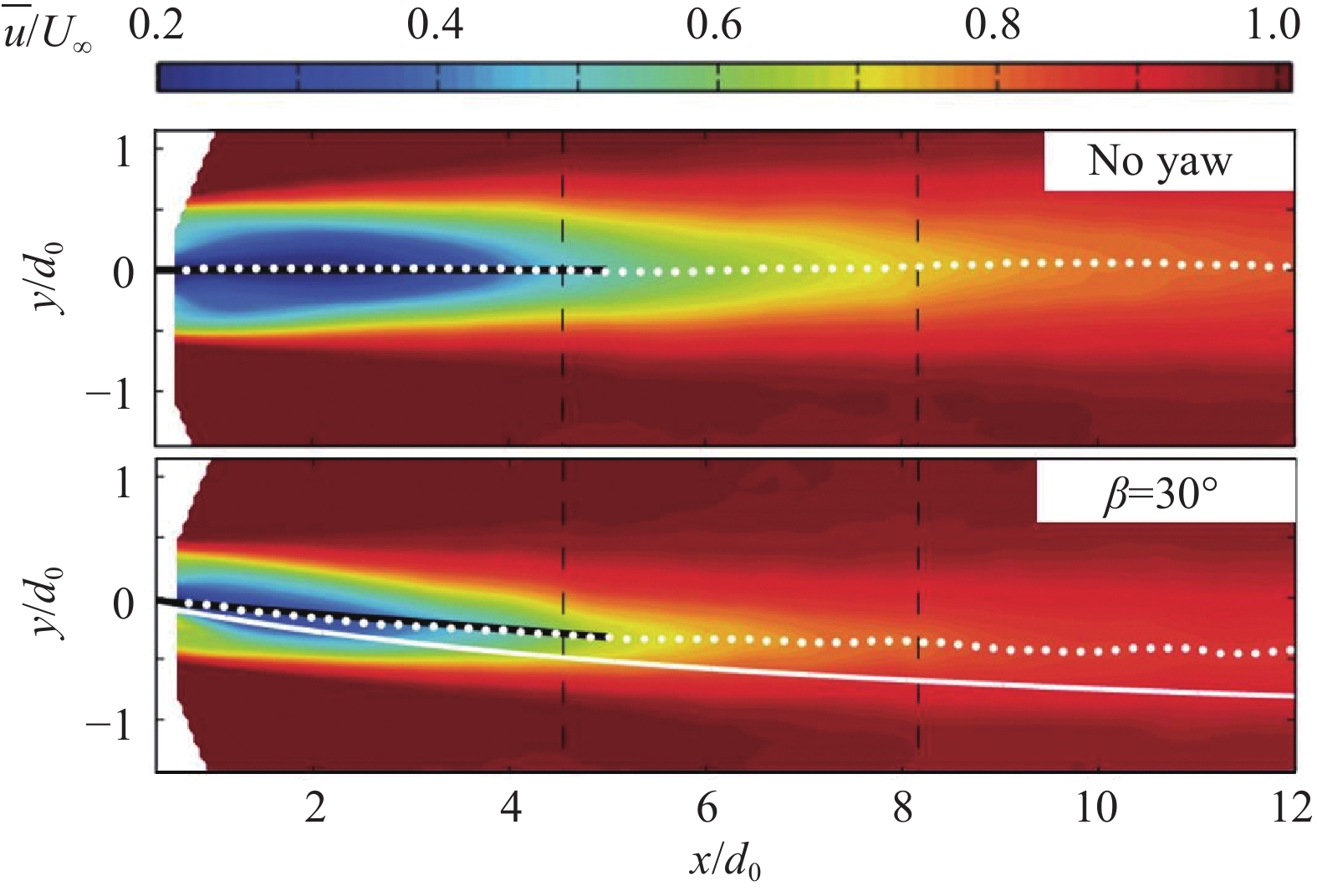
图13给出了实验所测得的轮毂中心高度处尾流速度分布云图[54]。如白色虚线所示,非偏航风力机尾流轨迹基本上沿着风轮中心轴线,而偏航风力机尾流的中心轨迹则随着向下游传播距离的增加而逐渐向一侧飘移。这种偏移的最根本原因是偏航风力机所诱导的非零侧向力和展向速度[25]。由于尾流扩张效应,风轮所诱导的展向速度会沿流向逐渐减小,因此尾流中心偏移量(定义为yd)并不会随着x的增加而一直增加,存在一个渐进极限[55]。以图13中的30°偏航风力机为例,当x>10d0时,尾流中心偏移量基本保持不变,极限值约为−0.5d0。
|
图 13 非偏航与偏航风力机尾流中心轨迹对比[54] Fig.13 Comparison of the wake center trajectories between yawed and non-yawed wind turbines[54] |
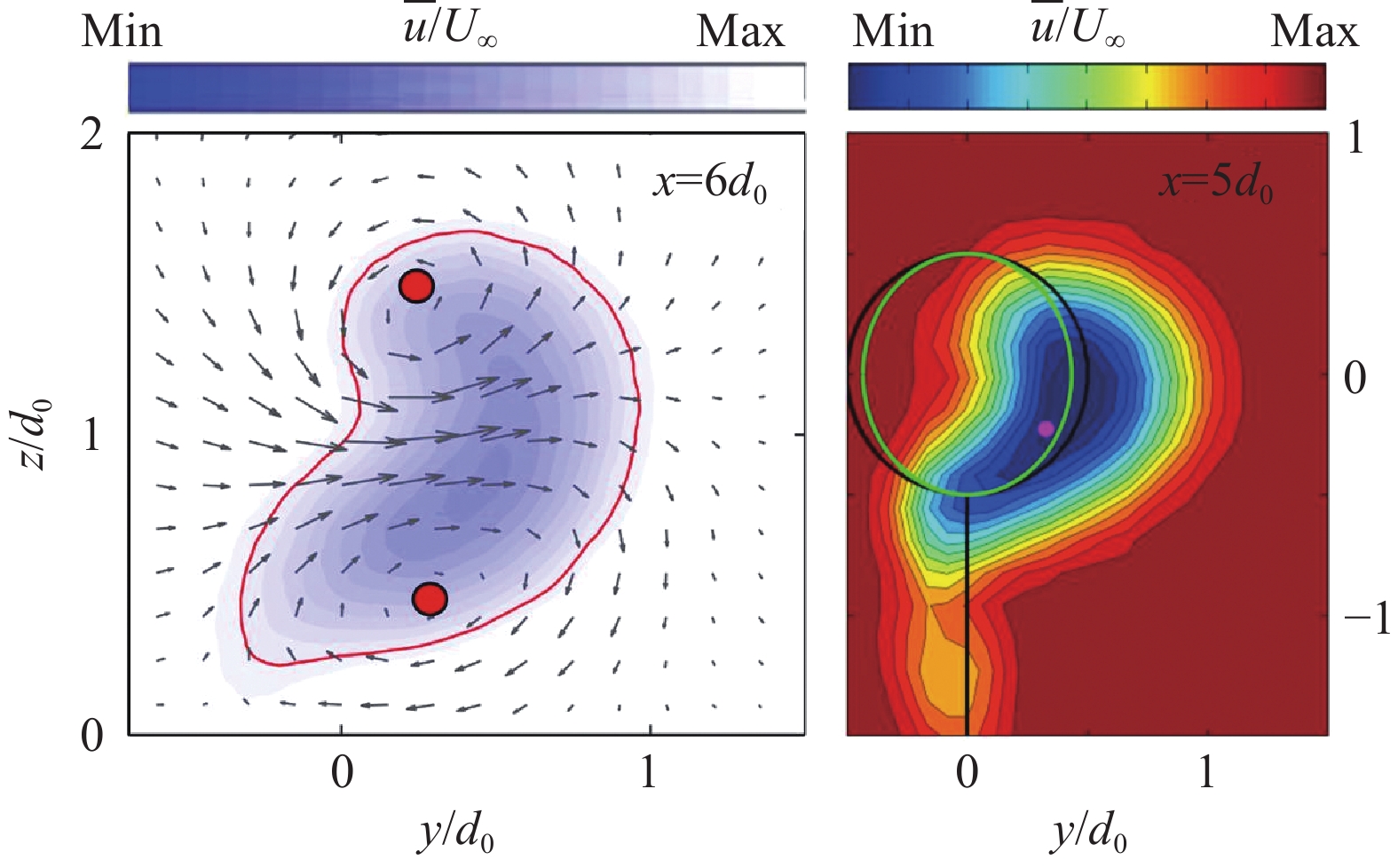
偏航风力机的速度亏损剖面与非偏航风力机存在着明显不同,表现为上下不对称的肾型(图14左)[53],其形成机理一度存在争议。Bastankhah等[54]认为非零的侧向力在尾流剖面内诱导了横向速度,横向速度输运的流体由上部和下部补充,构成了对转涡对结构。这一个对转涡对和轮毂涡相互诱导演化,形成了上下非对称的尾流剖面。Howland等[55]则通过对比偏航多孔阻力圆盘的尾流测量结果(图14右),发现叶轮的旋转不是形成肾型尾流剖面的必要条件。只要处于偏航状态,就会在圆盘/风轮的上下两端形成一个对转涡对。该对转涡对在尾流中心处诱导了一个非均匀的横向速度,并将高速度亏损区域输运到一侧,形成了向内“卷曲”的尾流剖面,因此也被成为“curled wake”。
|
图 14 偏航风力机尾流速度亏损剖面与偏航多孔阻力圆盘尾流速度亏损剖面对比[53,55] Fig.14 Comparison of the wake deficit velocity profiles pertaining to a yawed wind turbine and a porous drag disk [53,55] |
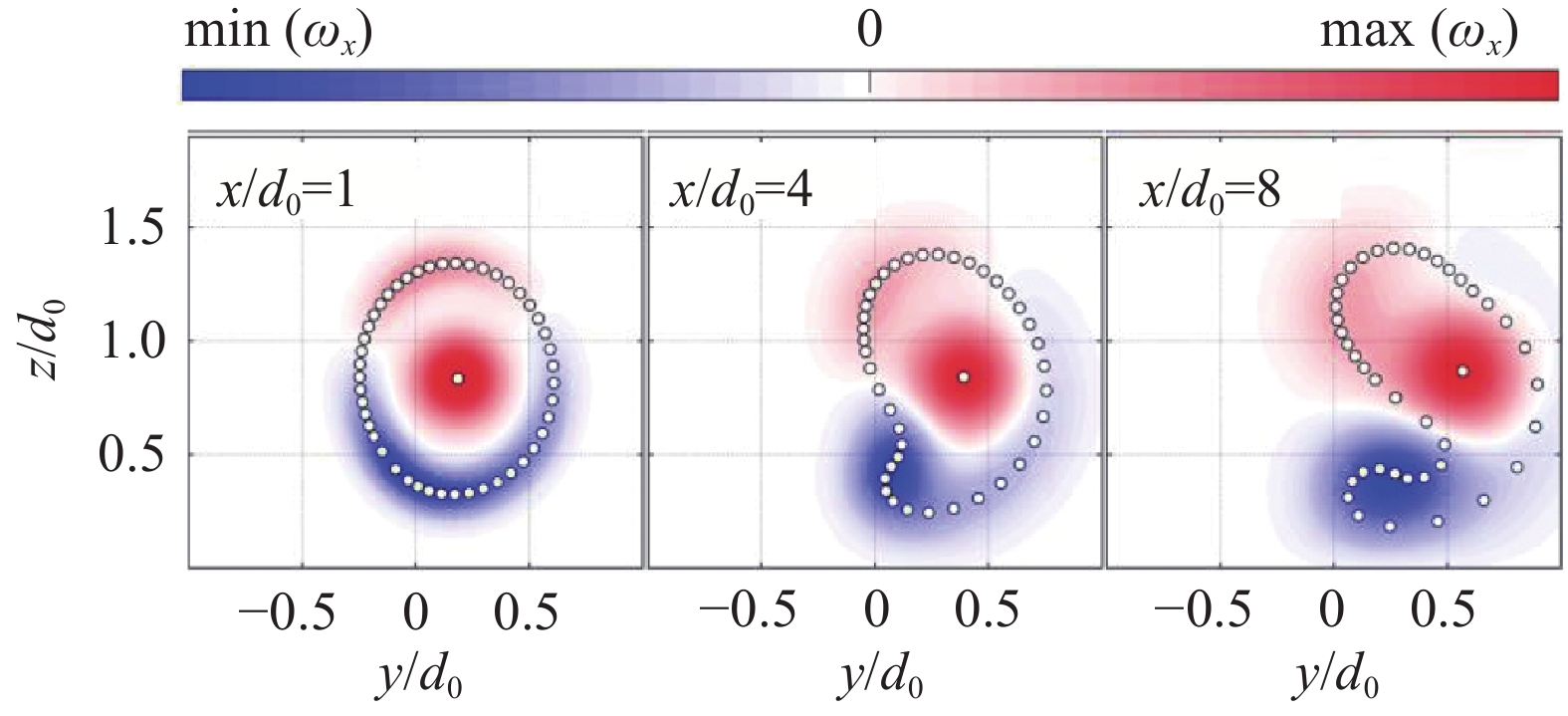
以上两种机理解释,均将肾型尾流剖面的成因归结到非均匀展向速度的输运效应上。但在展向速度与旋涡体系的关系上存在不同认识。Bastankhah机理解释的核心是“力诱导横向速度,横向速度诱导‘对转涡对+轮毂涡’”;而Howland的核心思想为“力诱导对转涡对,对转涡对诱导横向速度,与轮毂涡无关”。为了澄清这种争议,Zong和Porté-Agel在Martinez等所发展的卷曲尾流模型基础上,引入涡动力学理论和流向动量方程抛物化求解方法,发展了描述偏航风力机尾流演化的点涡输运(Point Vortex Transportation,PVT)模型[53,56-57]。结果表明,尾流中的轮毂涡并不是存在于对转涡对之外的一个独立旋涡,而是与叶尖涡的流向涡量相互诱导融合,共同构成了一个对转涡包(图15)。该对转涡包的正负涡量分散在风轮边缘和轮毂中心,因而诱导的展向速度是不均匀的,经过输运之后形成的肾型尾流剖面也是上下不对称的。简而言之,“叶尖涡的流向涡量+轮毂涡 = 对转涡对,对转涡对诱导横向速度,横向速度输运导致肾型速度亏损剖面+尾流中心偏移”。
|
图 15 偏航风力机尾流中流向涡的演化过程[53] Fig.15 Spatial evolution of streamwise vortices behind a yawed wind turbine[53] |
风力机处于偏航工作状态时,尾流中心线的偏移会直接影响到下游风力机的功率输出。因此,偏航风力机尾流建模的首要问题便是计算不同偏航状态下的尾流中心偏移量。目前广泛采用的尾流偏转模型有Jiménez模型、Bastankhah模型、Shapiro模型等[54,58-60]。虽然推导过程各异,但大致思路都是先得到初始横流速度,然后假设该速度随尾流扩张而渐进衰减,最后对该横流速度进行积分即可得到偏移量。表2对比了三大尾流偏转模型的特点。
| 表 2 偏航风力机尾流偏转模型对比 Table 2 Comparison of wake deflection models for yawed wind turbines |
|
|
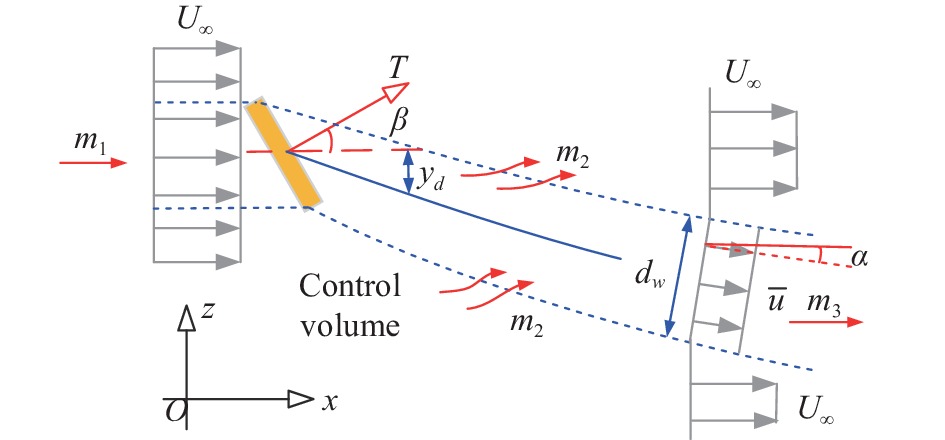
下文对尾流偏转模型进行逐一介绍。如图16所示,Jiménez等假设尾流速度亏损是平顶型的[58]。在任一流向位置处,尾流中心线的轨迹由尾流速度方向α决定。选取图中蓝色虚线所包含的开口区域作为控制体,应用流量和动量守恒方程,并在尾流偏转角度足够小(
|
图 16 Jiménez尾流偏转模型推导示意图 Fig.16 Sketch of Jiménez wake deflection model |
| $ T\sin (\beta ) \approx - \rho U_\infty ^2\frac{{{\text{π}}d_w^2}}{4}\alpha $ | (11) |
对于偏航风力机而言,风轮所捕获的有效风速为来流速度的法向分量U∞ cos(β),故推力T可以写为如下形式:
| $ T = 0.5\rho {({U_\infty }\cos \beta )^2}{\text{π}}r_0^2{C_T} $ | (12) |
联立式(11)式(12),可以推导出尾流速度方向角:
| $ \alpha = \frac{1}{2}{C_T}{\cos ^2}\beta \; \sin \beta {\left( {\frac{{{r_0}}}{{{r_w}}}} \right)^2} $ | (13) |
进一步,将Jensen模型的线性尾流扩张假设(rw = r0+kwx)代入上式,并对x进行积分,即可得偏航风力机尾流中心偏转公式:
| $ {y_d} = \int_0^x {\tan } \alpha \; {\rm{d }}x \approx \frac{1}{2}{C_T}{\cos ^2}\beta \; \sin \beta \frac{{{r_0}x}}{{{r_0} + {k_w}x}} $ | (14) |
根据该式,随着偏航角
| $ {y_{d,{\text{limit}}}} = \frac{{{C_T}{{\cos }^2}\beta \; \sin \beta }}{{2{k_w}}}{r_0} $ | (15) |
尽管在文献[58]中,式(15)所预测的结果与LES结果吻合较好,但在后续使用过程中,研究人员普遍发现根据Jiménez模型所计算出的尾流偏转量与实验值相比偏大[53-54,59-61]。
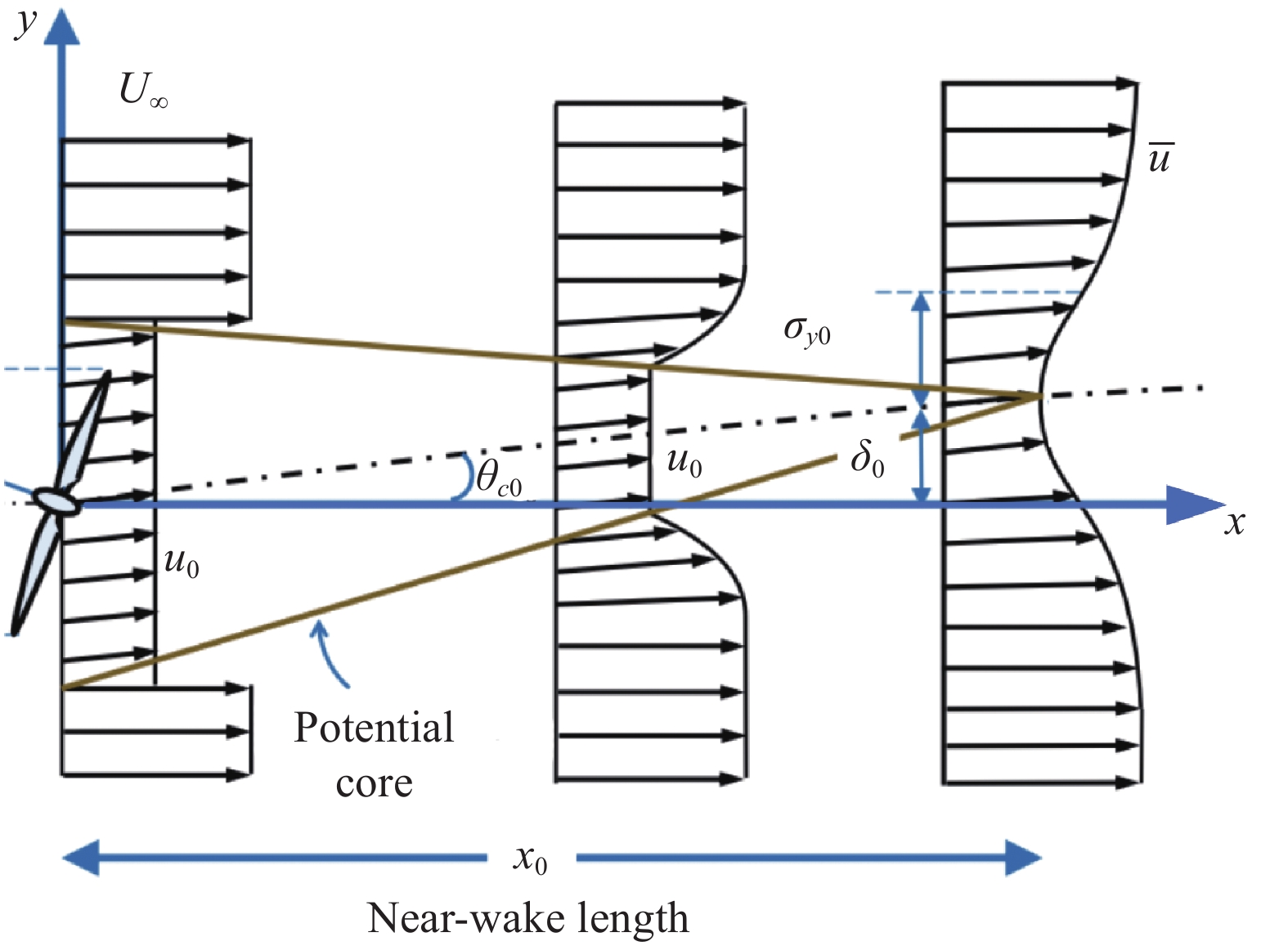
Bastankhah模型将尾流偏转分为两个阶段进行考虑—近场尾流的线性偏转和远场尾流的渐进偏转(如图17所示)。依据偏航风力机的经典涡面理论[62]和射流核心区长度估算公式,可以分别得出近场尾流轨迹角
| $ {\theta _{c0}} \approx \frac{{0.3\beta }}{{\cos \beta }}(1 - \sqrt {1 - {C_T}\cos \beta } ) $ | (16) |
| $ \frac{{{x_0}}}{{{d_0}}} = \frac{{\cos \beta (1 + \sqrt {1 - {C_T}} )}}{{3.28 {I_0} + 0.22 (1 - \sqrt {1 - {C_T}} )}} $ | (17) |
其中,I0为来流湍流度。故当x<x0时(近场),尾流中心偏转的表达式为:
| $ {y_d} = \tan ({\theta _{c0}} ) \; x $ | (18) |
在远场尾流区,Bastankhah等假定横向速度分布与速度亏损分布类似,也呈现出高斯型。应用展向动量方程,可以建立起尾流中心横向速度与尾流宽度之间的关系。进一步积分,即可得到当x≥x0时的尾流偏转量:
| $ \begin{split} \dfrac{{{y_d}}}{{{d_0}}} =& {\theta _{c0}}\dfrac{{{x_0}}}{{{d_0}}} + \dfrac{{{\theta _{c0}}}}{{{d_0}}}\sqrt {\dfrac{{\cos \beta }}{{{k_y}{k_z}{C_T}}}} \Big (2.9 + 1.3\sqrt {1 - {C_T}} - {C_T} \Big ) \cdot \\& { \ln \left[ {\dfrac{{(1.6 + \sqrt {{C_T}} )\left( {1.6\sqrt {\dfrac{{8{\sigma _y}{\sigma _z}}}{{{d_0}^2\cos \beta }}} - \sqrt {{C_T}} } \right)}}{{(1.6 - \sqrt {{C_T}} )\left( {1.6\sqrt {\dfrac{{8{\sigma _y}{\sigma _z}}}{{{d_0}^2\cos \beta }}} + \sqrt {{C_T}} } \right)}}} \right]} \end{split}$ | (19) |
其中,
| $ {\sigma _y} = {k_y}(x - {x_0}) + \frac{{\cos \beta \; {d_0}}}{{\sqrt 8 }} $ | (20) |
| $ {\sigma _z} = {k_z}(x - {x_0}) + \frac{{{d_0}}}{{\sqrt 8 }} $ | (21) |
与Jiménez模型相比,Bastankhah模型考虑了来流湍流度和近场尾流长度等实际因素影响,预测结果更为精确,但表达式较为复杂。
Shapiro模型将处于偏航状态的风轮盘等效为一个升力体,通过求解产生给定“升力”(侧向力)所需要的环量,得出了初始横流速度[59]。基于该初始速度和展向动量方程,推导出横流速度沿流向变化的表达式:
| $ {v_c}(x) = \frac{{{C_T}{U_\infty }{{\cos }^2}\beta \; \sin \beta \; d_0^2}}{{8d_w^2(x)}}\left[ {1{\text{ + erf}}\left( {\frac{x}{{\sqrt 2 r{}_0}}} \right)} \right] $ | (22) |
| $ {d_w} = {d_0} + {k_w}{d_0}\ln (1 + {{\text{e}}^{x/{r_0} - 2}}) $ | (23) |
积分后,即为尾流中心偏转:
| $ {y_d} = \int_0^x { - \frac{{{v_c}(x)}}{{{U_\infty }}}{\text{d}}x} $ | (24) |
该模型表达式较Bastankhah模型简洁,在一定程度上也考虑了近场尾流的影响。
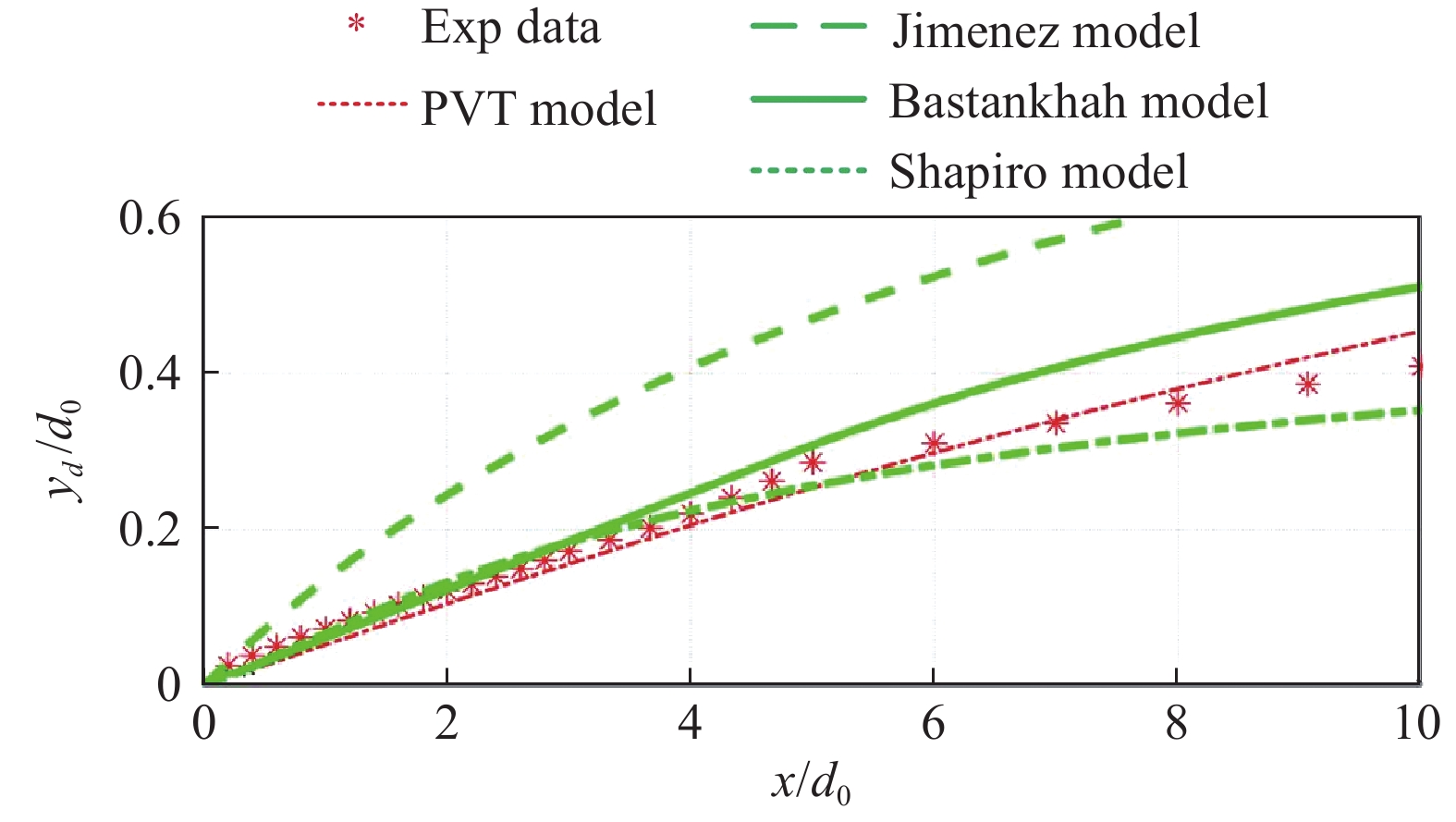
Zong等在β = 30°和CT = 0.82的条件下,对比了以上三种尾流偏转模型的预测结果[53]。如图18所示,Jiménez模型的预测误差明显偏大,比实验值高50%以上。Bastankhah模型和Shapiro模型的预测精度相当,在x<5d0时的最大相对预测误差小于10%。PVT模型的预测精度最高,但该模型需要采用空间推进方法求解,严格意义上来讲并不属于解析模型范畴。
|
图 18 不同尾流偏转模型预测结果对比[53] Fig.18 Comparison of the wake deflections predicated by different analytical models[53] |
尽管Medici[11]、Fleming[25]、Bastankhah[54]以及Howland[55]等研究人员很早就注意到了偏航风力机尾流速度亏损剖面呈现出非对称的肾型,但如何采用简单解析数学表达式去描述这种尾流剖面至今仍是个难题。更为复杂的是,偏航风力机尾流剖面形状还受到大气边界层热稳定性以及湍流度的影响[63]。Martinez等[56-57]和Zong等[53]分别建立了卷曲尾流模型和点涡输运模型,能够很好地重现肾型速度亏损剖面。但这两个模型求解单个尾流所需要的时间在秒量级,比普通解析模型的求解时间(毫秒量级)高出了1000倍。因此,还不能直接用于包含数百个变量的大型风电场产能的在线优化。
目前,工程应用中,普遍假设偏航风力机的尾流剖面为椭圆形,在y和z两个方向上具有不同的特征宽度σy和σz。在此基础上,将第1.2小节中非偏航状态风力机尾流的表达式
| $ \Delta u = f(x)g\left(\sqrt {\frac{{{{[y - {y_d}(x)]}^2}}}{{{\sigma _y}^2(x)}} + \frac{{{{(z - {z_h})}^2}}}{{{\sigma _z}^2(x)}}} \; \right) $ | (25) |
即可得到偏航风力机尾流速度亏损分布。其中,zh代表了轮毂中心距离地面的高度。
以EPFL高斯模型为例(式9),应用至偏航风力机时,尾流速度亏损表达式为[36]:
| $ \frac{{\Delta u}}{{{U_\infty }}} = \left[ {1 - \sqrt {1 - \frac{{{C_T}}}{{8{{\left(\dfrac{{\sigma _y}{\sigma _z}}{d_0}\right)}^2}}}} } \right]{{\text{e}}^{ - \tfrac{{{{(y - {y_d})}^2}}}{{2\sigma _y^2}} - \tfrac{{{{(z - {z_h})}^2}}}{{2\sigma _z^2}}}} $ | (26) |
其中,yd的数学模型可以选用第2.2小节中的任意一个。
3 多风力机尾流叠加方法 3.1 尾流速度亏损叠加大型风电场一般由多排风力机构成。在某些特定风向下,下游风力机会处在上游多个风力机的尾流中。如何根据前两个小节所推导的孤立风力机尾流速度亏损,去估算尾流重叠区域的总速度亏损,是评估整个风电场产能的关键所在。
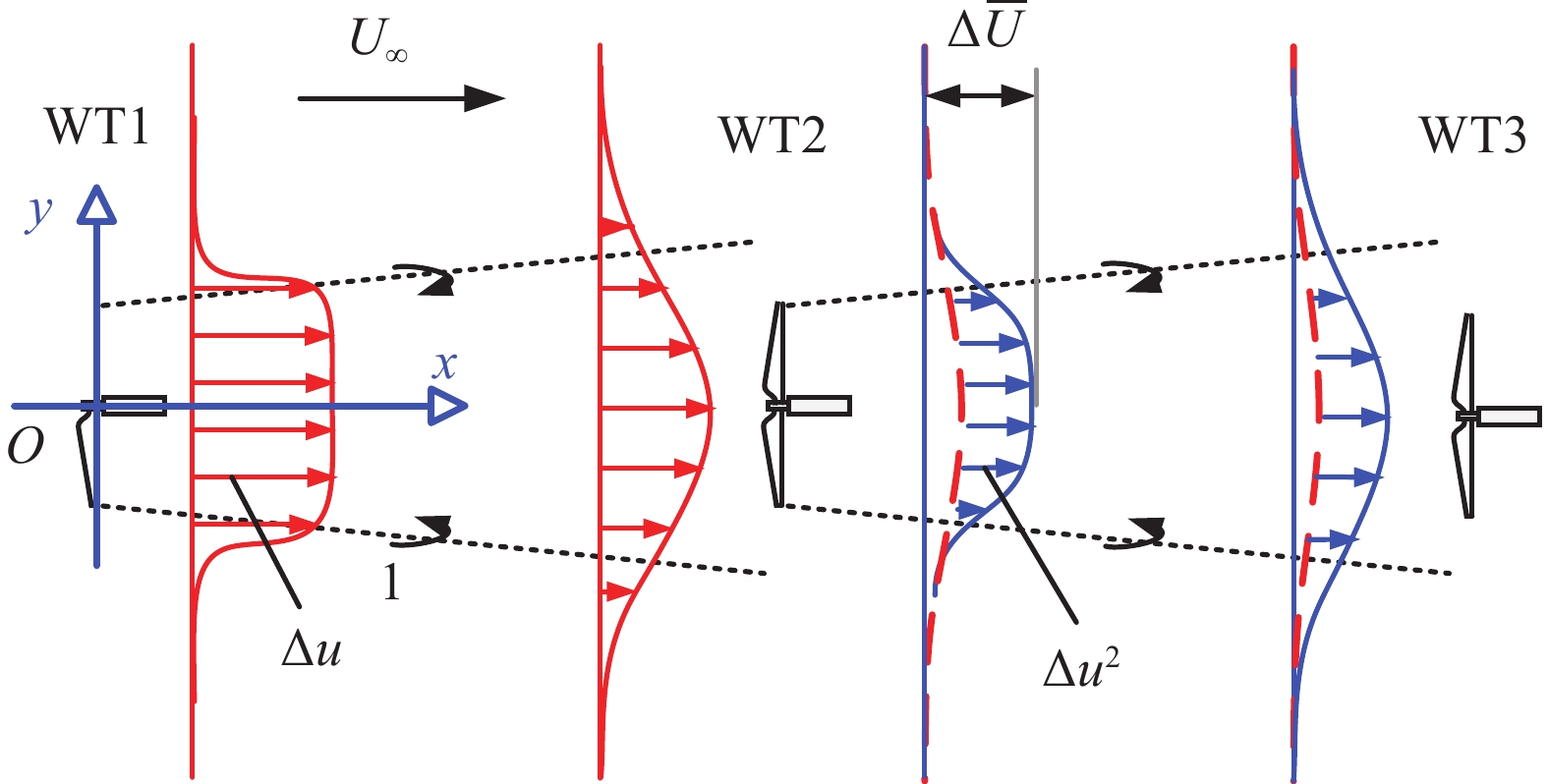
以图19中三个风力机构成的小型风电场为例,P2点处在尾流重叠区域,其风速受到WT1和WT2尾流的共同影响。为了估算WT3的产能,必须将WT1和WT2单独作用下的尾流速度亏损按照某种法则进行叠加,得到WT3风轮处的流向速度分布。

|
图 19 风电场内多风力机尾流干扰 Fig.19 Multiple wind turbine wake interactions in a wind farm |
表3中总结了现有的五种尾流速度亏损叠加方法。其中:
| 表 3 尾流速度亏损叠加方法小结 Table 3 A list of wake deficit superposition methods |
|
|
下面结合图20对各个方法的物理含义进行诠释。在方法A中,Lissaman假定在风电场内,相邻风力机之间的间距大、尾流干扰弱,因此在计算孤立风力机尾流时,每个风力机轮毂处的平均风速都可以近似为自由来流速度,
在方法B中,Katic等在计算孤立风力机尾流时,采用与Lissaman相同的假设,
方法C和方法D与方法A和方法B是一一对应的,在尾流叠加运算上保持一致(线性相加/平方相加)[66-67]。但在计算单个风力机尾流速度亏损时,取消了弱尾流效应假设(
方法E是唯一一种具备动量守恒特性的尾流叠加方法。在推导过程中,首先引入特征传播速度这一参数,实现了尾流动量亏损表达式的线性化。然后,经过一系列的推导,发现满足动量守恒条件的尾流叠加实际上是一种加权线性叠加。在叠加过程中,某一尾流所占的权重等于该尾流特征传播速度
| $ \frac{{u_c^i(x)}}{{u_h^i}} = \frac{1}{2} + \frac{1}{2}\sqrt {1 - \frac{{C_T^i}}{{8{\dfrac{{\sigma _y}{\sigma _z}}{d_0^2}}}}} $ | (27) |
其中,
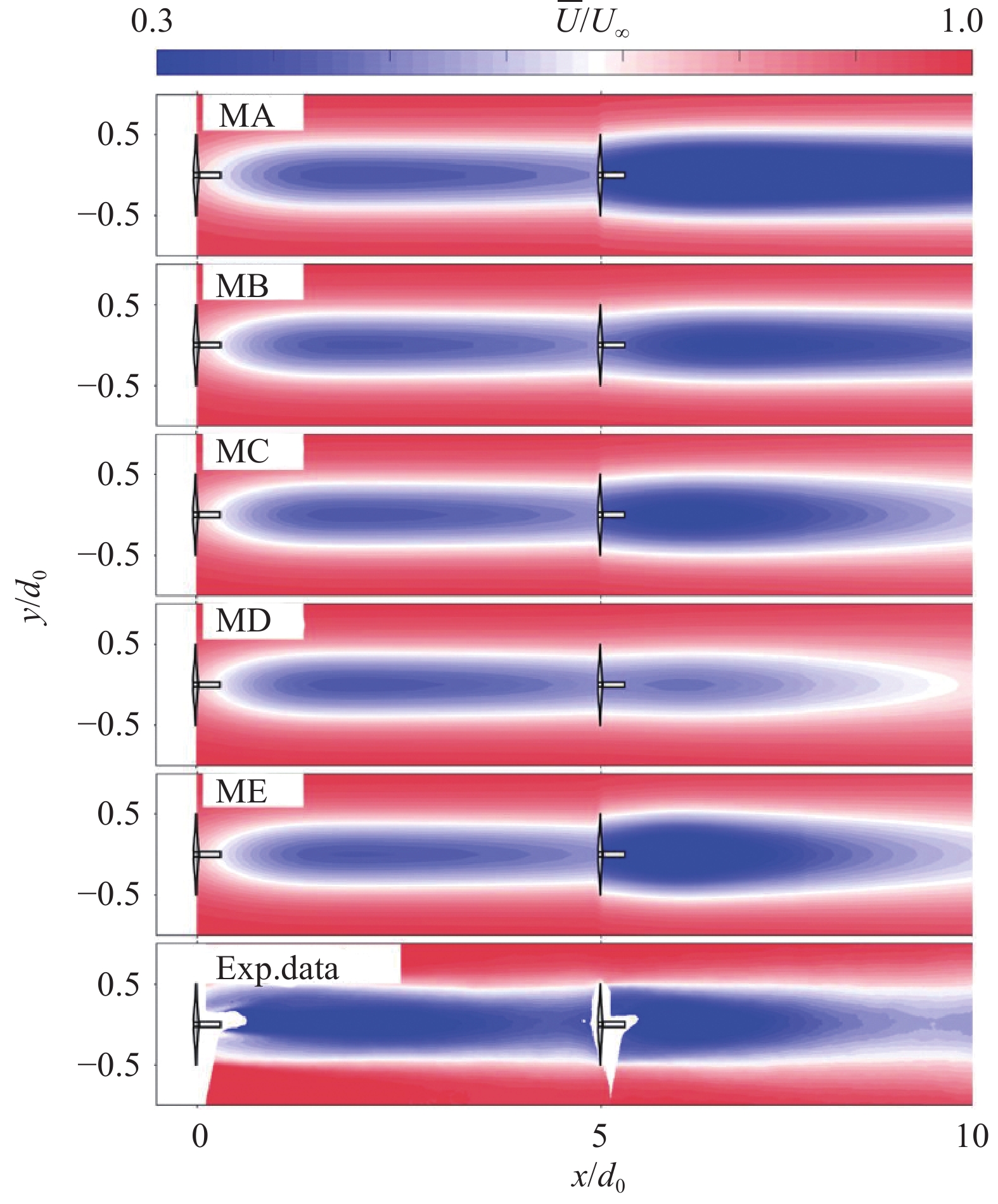
图21定性对比了不同尾流叠加方法所获得两风力机尾流速度云图[24]。其中:MA,MB,···,ME分别是方法A,B,···,E的缩写;风力机模型的英文编号为为WIRE-01,具体几何信息参见文献[69]中。与实验结果相比,方法A和方法B高估了合成后的尾流速度亏损,方法D则低估了合成后尾流速度的亏损。方法C、方法E给出的速度分布云图与实验结果最接近。
|
图 21 基于不同尾流速度亏损叠加方法获得的速度云图[68] Fig.21 Wake velocity contours obtained with different wake deficit superposition methods[68] |
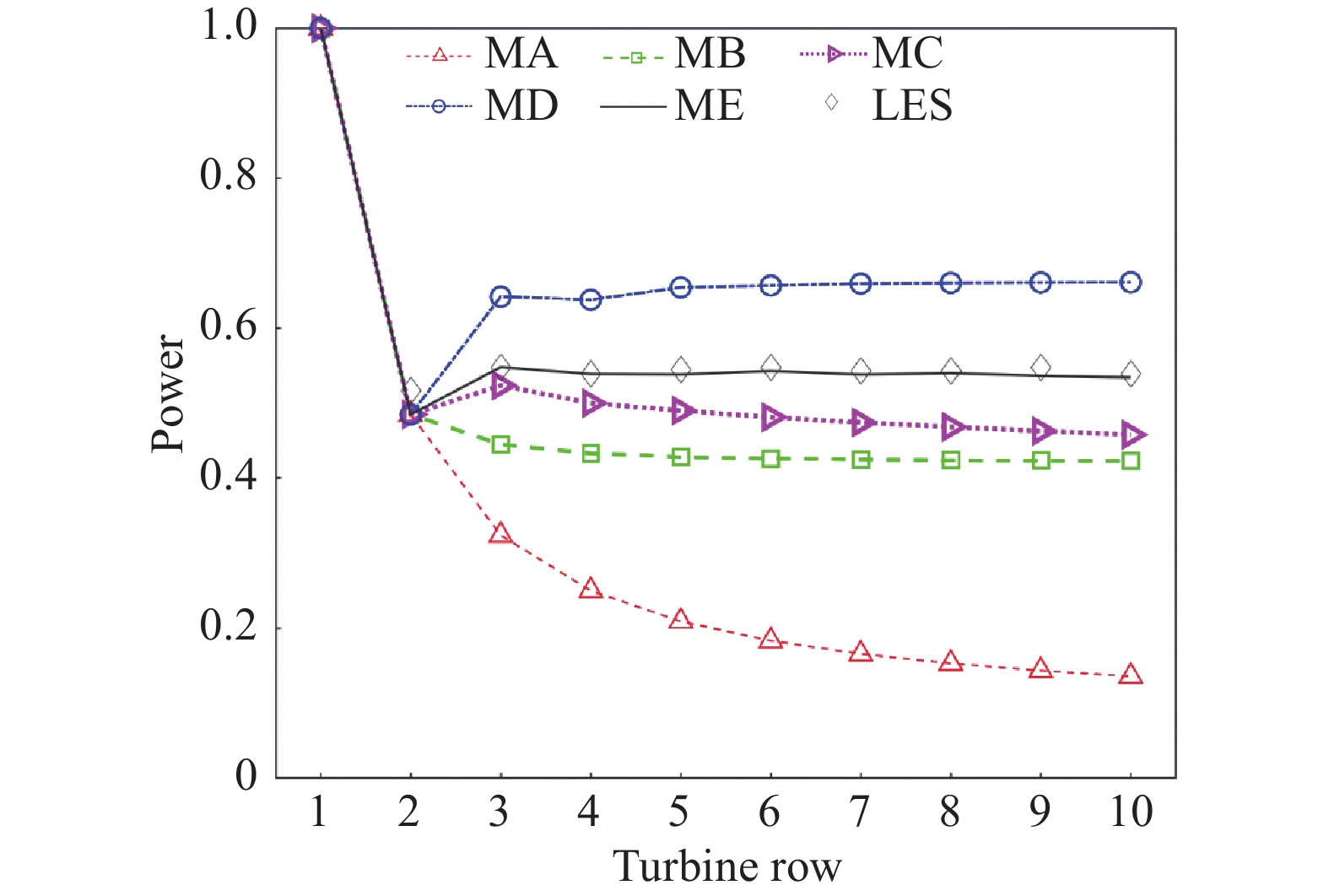
图22给出了不同尾流方法所预测的Horns Rev风电场各排风力机平均产能(风向θ = 270°)。在所有方法中,只有方法E较好地重现了LES结果。基于线性速度亏损叠加的方法A过高地估计了合成后尾流速度亏损,因而预测出的下游风力机产能偏低,给出的风力机产能随叶片排数增加而连续递减的变化趋势也与LES结果严重不符。方法B、C、D预测出来的变化趋势大致合理,但产能偏差较大,达到了10%~20%。
|
图 22 不同尾流叠加方法预测的Horns Rev风电场各排风力机产能[68] Fig.22 Normalized power production of different wind turbine rows in Horns Rev wind farm predicted by the five wake superposition methods[68] |
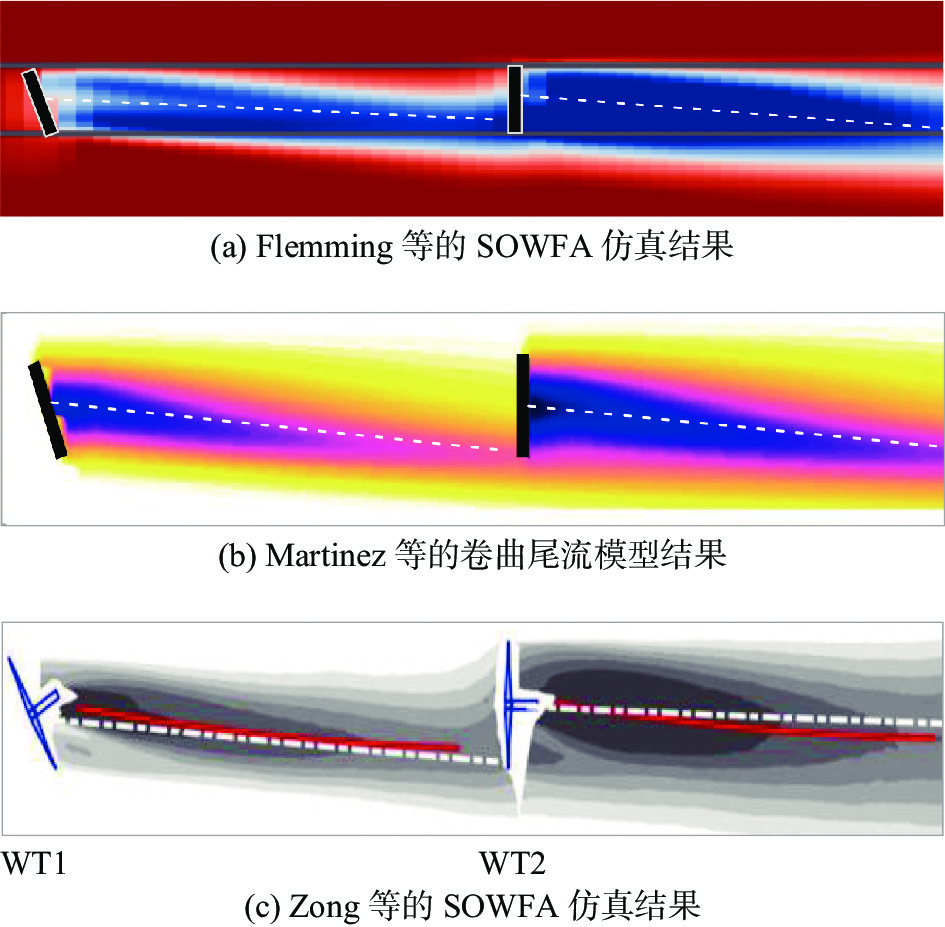
NREL和EPFL等团队在通过LES和风洞实验研究主动尾流控制技术时发现[56,68,70]:当上游风力机偏航时,会诱导一个横向速度;在该横向速度的输运作用下,不仅该风力机的尾流会偏向一侧,其下游非偏航风力机的尾流也会发生偏转(图23)。这种由上游风力机偏航而引起的下游风力机尾流附加偏转现象,被叫做“二次尾流偏转效应”。最近,该效应还得到了外场实验的证实[71-72]。因为该效应的存在,所以下游风力机可以“借力”上游风力机,用较小的偏航角实现更多的尾流偏转。
与尾流速度亏损叠加初衷类似,为了能够重现主动尾流控制技术中的二次尾流偏转现象、提高解析模型预测精度,也需要对不同风力机所诱导的横向速度在尾流重叠区域进行叠加。最终,某个风力机后部的尾流中心偏转量将不仅是受自身偏航所诱导的横向速度影响,而是由叠加后的总横流速度决定。Zong和Porté-Agel[68]从展向动量守恒方程出发,推导出的尾流横向速度叠加公式为:
| $ V_c^j \approx \sum\limits_i {\frac{{u_h^i}}{{u_h^j}}} v_{}^i(x_c^j,y_c^j) $ | (28) |
其中:
|
图 23 上游风力机偏航所诱导的“二次尾流偏转效应”[56,68,70] Fig.23 The secondary wake steering effect induced by an upstream yawed wind turbine[56,68,70] |
King等采取了不同的方法来模化尾流二次偏转效应[73]。首先,将上游偏航风力机背后的涡系等效为“一个尾涡+一个流向对转涡对”;然后,假设每一个旋涡所诱导的横向速度分布都可以用Lamb-Oseen涡描述,进一步采用线性叠加方法获得所有这些上游旋涡在下游风力机处所诱导的合速度;最后,将该诱导速度等效为下游风力机偏航角的增加,通过定义一个有效偏航角来模化尾流的附加偏转。King等还进行了一系列的风场产能优化,发现忽略二次尾流偏转效应会严重低估AWC所带来的风电场产能收益[73]。
4 风电场产能优化研究人员在应用AWC技术对风电场进行优化时,目标有两个:一是最大化产能、二是最小化偏航所带来的叶片疲劳载荷[74-76]。所选取的优化方法包括遍历算法(小型风电场)、梯度下降法、遗传算法、数据驱动方法、对策论方法和神经网络算法等[77-83]。风电场在不同偏航角下产能的估算主要通过解析模型来完成。风洞和外场实验测量局限于小型风电场研究,主要目的在于验证各类模型预测精度和控制方案可行性,为发展新方法提供支撑。下面根据发展脉络对有代表性的结果梳理如下。
4.1 小型风电场的实验/LES结果KTH的Medici早在2003年就对不同偏航角下单个风力机的尾流速度剖面和产能进行了风洞实验测量,发现30°偏航状态下,尾流中的最大动能亏损点可以向一侧偏移0.4d0[11]。若只考虑两个风力机尾流干扰情形,随着上游风力机偏航角度的增加,总产能呈现出一种先增加而后减小的变化趋势。最佳的上游风力机偏航角为20°,AWC可以将产能提升11%。接着,Medici考虑了6个风力机组成的虚拟五边形风电场。由于沿着任何风向上风力机的排数都不超过2,因此整个风电场产能的估算和优化不需要应用任何尾流叠加原理和算法。结果表明AWC技术有望将整个风电场的平均产能增加2%~3%,改变偏航风力机的功率衰减指数对该最佳偏航角和产能增加量影响较大。
挪威科技大学的Adaramola和爱荷华大学的Ozbay先后在风洞中研究了两个模型风力机的全尾流干扰,流向间距分别为3d0和2d0[84]。前者的产能测试结果与Medici基本一致—当上游风力机的偏航角度为30°时,风电场的效率最高可提升12%。后者则进一步表明来流湍流度对AWC技术的能量收益有着至关重要的影响;在湍流度为18%下,上游风力机偏航已经不能给整个风电场带来任何正向能量收益。这与尾流恢复速率加快、整个风电场在基准条件下产能损失较小有关[85]。
NREL的Fleming等也对流向间距为7d0的两个风力机尾流干扰问题进行了研究[26]。通过LES仿真,发现上游风力机正向偏航时,其自身叶片弯曲载荷减小,而下游风力机叶片的弯曲载荷则明显增加。最佳偏航角(25°)下的正能量收益为4.6%,低于Adaramola和Medici等的实验结果。
慕尼黑工业大学的Campagnolo等在风洞中研究了AWC技术在单列三个风力机产能优化中的应用[86]。与Adaramola和Ozbay等团队的全尾流干扰情形不同,实验中各个风力机的流向间距为4d0、展向间距为0.5d0(部分尾流干扰)。该研究团队搭建了闭环控制回路,以总产能最大化为目标,采用基于梯度的优化算法寻找最佳的偏航角序列。获得的净能量收益为15%,上游第一和第二个风力机的偏航角分别为20°和16°。
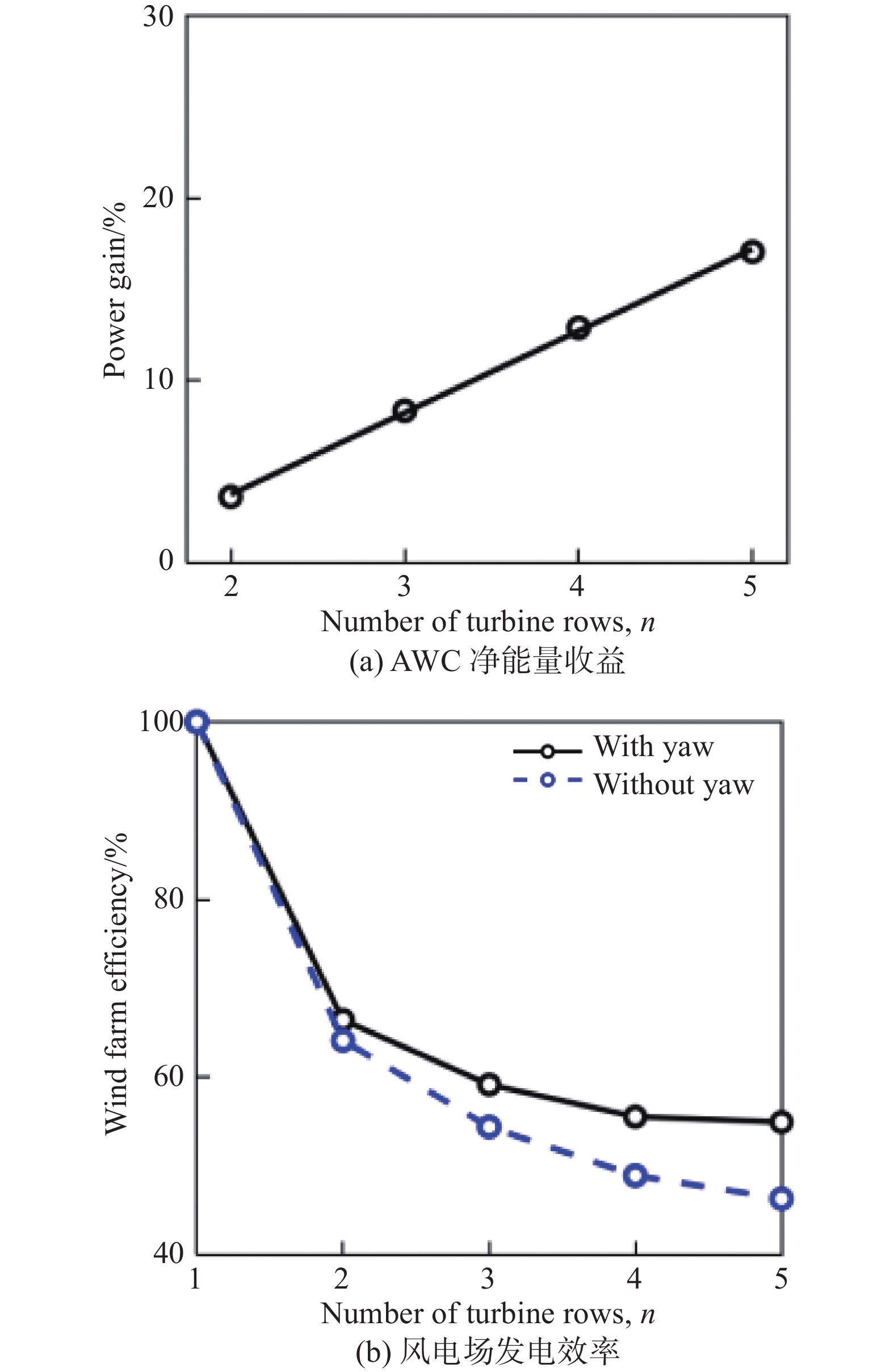
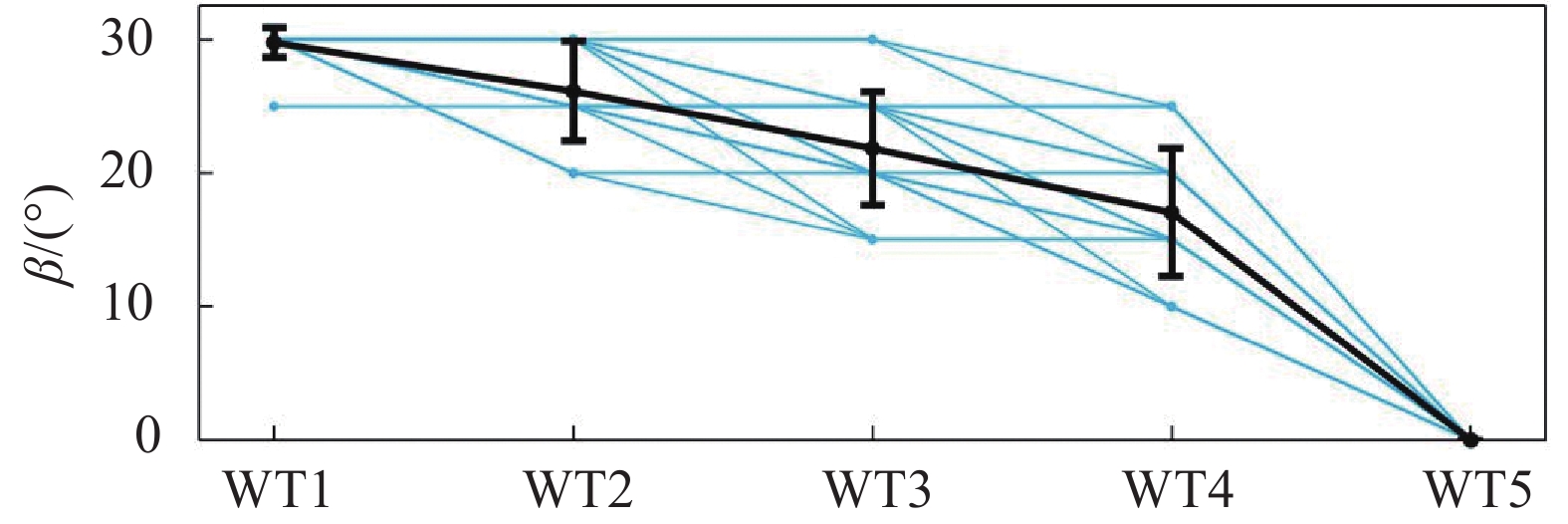
EPFL的Bastankhah和Porte-Agel在风洞中搭建了五个模型风力机所组成的单列风电场[18]。选取的风力机流向间距为5d0、展向间距为0(全尾流干扰),来流湍流度为8%。通过对200多组可能获得正能量收益的所有偏航角组合进行逐一测试,发现最佳的偏航角序列始终呈现出由上游至下游的依次递减趋势,与Campagnolo等的实验结果一致(图24)。另外,风力机排数越多,采用AWC技术获得的相对能量收益就会越大。如图25所示,两风力机时的能量收益仅为3%,而五个风力机时的能量收益则达到了17%。
|
图 24 最大净能量收益所对应的偏航角序列[18] Fig.24 Optimal yaw angle distribution pertaining to the maximum power gain[18] |
Lin对标Bastankhah风洞实验结果,对三个风力机所组成的单列风电场进行了LES建模,获得了样本空间内数百个偏航角组合下的净能量收益以及等效疲劳载荷[87]。以这两个目标参数为坐标轴,做出了非劣最优目标域(即Pareto前沿)。结果表明,非劣最优目标域的整体形状为扁长型,对应的偏航角为中等幅值以上;能量收益越大,对叶片的等效疲劳损伤载荷就越高。
以上风洞实验和LES结果均表明,AWC技术在风电场产能优化方面有着巨大的应用潜力。这进一步驱使研究人员在实际风电场中对主动尾流控制技术进行验证[17,71-72,88]。
2018~2019年之间,NREL选取一个商用大型风电场中的三个风力机作为实验对象,先后开展了两期主动尾流控制实验。控制系统的输入为风向和风速,输出为FLORIS模型(详见文献[89])所预测的上游风力机最佳偏航角。需要说明的是,由于大气边界层内部参数变化剧烈,需要对采集到的传感器信号做低频滤波后再输入到AWC控制系统[90] 。ECN的Mendez Reyes和Kanev等还进一步提出在控制系统中加入滞环回线、引入风力机载荷变化量查询表等,以避免频繁的不必要偏航机动,保护风力机始终处于安全偏航角范围内[91-93]。
NREL外场实验数据表明:在南北两个强尾流干扰风向上,通过AWC技术可以将前两个风力机的总产能提升6%以上,约为静态条件下(不考虑风向动态变化)解析模型所预测的最佳产能提升量的一半;同时,由二次尾流偏转效应所导致的最下游风力机产能变化明显。
2019年,斯坦福大学的Howland等在加拿大Alberta风电场进行了主动尾流控制技术的验证[17]。如图26所示,该风电场由6个Vesta-80 2 MW风力机组成,沿北偏西30°的方向排成一列,流向间距为3.5d0。实验过程中的具体控制策略为:在尾流损失最大的方向上,将前五个风力机的偏航角设置为20°,第6个风力机不偏航。通过不同风速下的数据统计分析,发现应用AWC以后,6个风力机的总产能提升了7%~13%。同时,在特定风向上的风力机产能脉动大幅降低,最高可达72%。
4.2 大型风电场的解析模型预测结果早在2013年,斯坦福大学的Park、Law等就建立了协同控制下风电场总产能预测的解析模型,并以偏航角和轴向诱导系数为变量进行了优化[75,94-96]。其中,单个风力机的诱导尾流速度采用改进的Jensen模型来描述,保证了速度剖面的连续性;偏航风力机尾流的偏转在早期文献中被假定为线性增长,仅由初始尾流轨迹角决定[94];经过改进后,尾流轨迹角为推力系数、偏航角以及尾流宽度的函数,与Shapiro推导出的表达式较为类似[95];尾流速度亏损的叠加方法选用的是Katic等提出的直接平方相加法。
基于以上模型,Park等先后采用最速下降法、序列凸规划法和数据驱动的贝叶斯方法对虚拟矩形风电场的产能进行了优化。结果表明:当风力机间距不变时,协同控制技术(包含主动尾流控制技术)所带来的产能收益会随着风电场规模的增加而不断提升,趋势与Bastankhah的实验结果吻合较好[18]。进一步,Park等还以Horns-Rev为例,预测协同控制技术可将全尾流干扰时(θ = 270°)的风电场产能提高40%,各个风向平均后的风电场效率提升约为7.1%[95]。这些数值与最新理论模型预测结果相比,明显偏高[19,73]。此外,由于该模型忽略了二次偏转效应,在最大产能下,预测的风力机偏航角并没有呈现出沿下游递减的趋势。
2021年,NREL的King等在文献[56]和文献[97]的基础上,建立了包含二次尾流偏转效应的风电场产能预测解析模型(GCH 模型),其目标是服务于实际风电场的主动尾流控制系统设计[73]。该模型采用标准的EPFL高斯表达式来描述单个风力机后的尾流速度亏损;偏航状态下的自身尾流偏转和诱导二次偏转分别通过涡系诱导的横向速度和等效偏航角来估算,详见第3.2小节和原文献;尾流速度亏损的叠加方法仍是Katic提出的平方相加法。
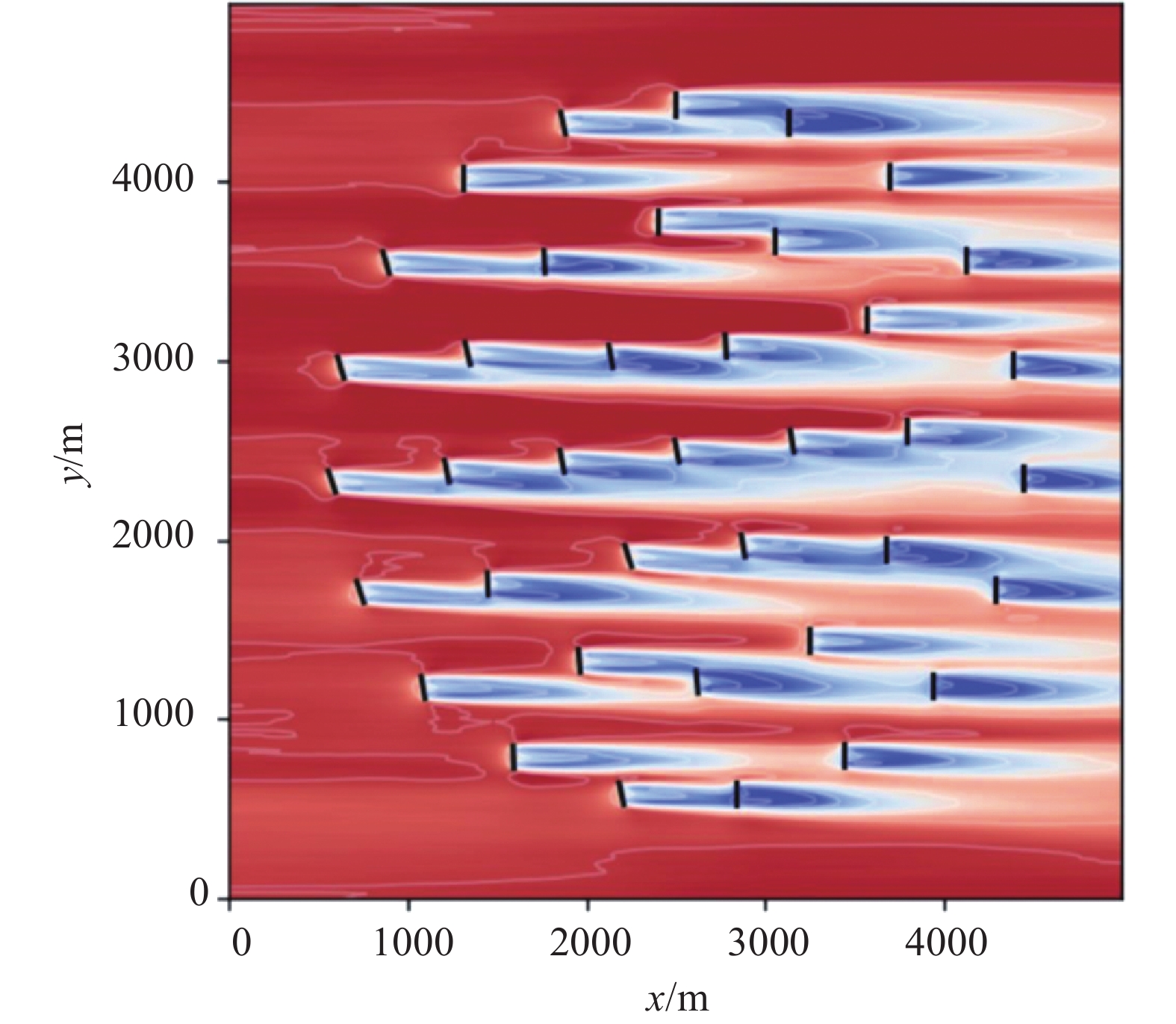
经过与LES结果及传统风电场预测模型对比,King等提出的GCH模型可以很好地重现多排风力机中的二次尾流偏转现象。产能收益预测精度与LES结果吻合较好,远远高于传统模型。如图27所示,以38个风力机均匀排布所构成的圆型风电场为例,偏航控制可以将全年各个风向的总产能提升约1.6%~2.2%[73]。
|
图 27 基于GCH模型对圆形风电场优化后的流场结果[73] Fig.27 Flow field of a circular wind farm after being optimized by GCH model[73] |
EPFL的Zong和Porté-Agel吸纳了最新的AWC研究成果,将高斯尾流速度亏损模型、Shapiro尾流偏转预测方法、具有动量守恒特性的尾流速度亏损叠加原理和横向速度叠加原理整合在一起,建立了用于风电场产能优化的又一解析模型[19]。无论是在全尾流还是部分尾流条件下,该模型所预测的结果与小型风力机阵列在风洞中的实验结果均吻合很好。基于该模型的一系列参数研究表明:风力机排数、来流湍流度、风力机间距和风向是影响AWC能量收益的关键因素;风力机排数越多,基准条件下的风电场效率就越低,由AWC所带来的相对能量收益就越高;当风向从风力机列的方向逐渐偏移至无尾流干扰方向时,由AWC所带来的相对能量收益呈现出一种先增大后减小的变化趋势;增加风力机间距和提高湍流度都会减少AWC所带来的能量收益。
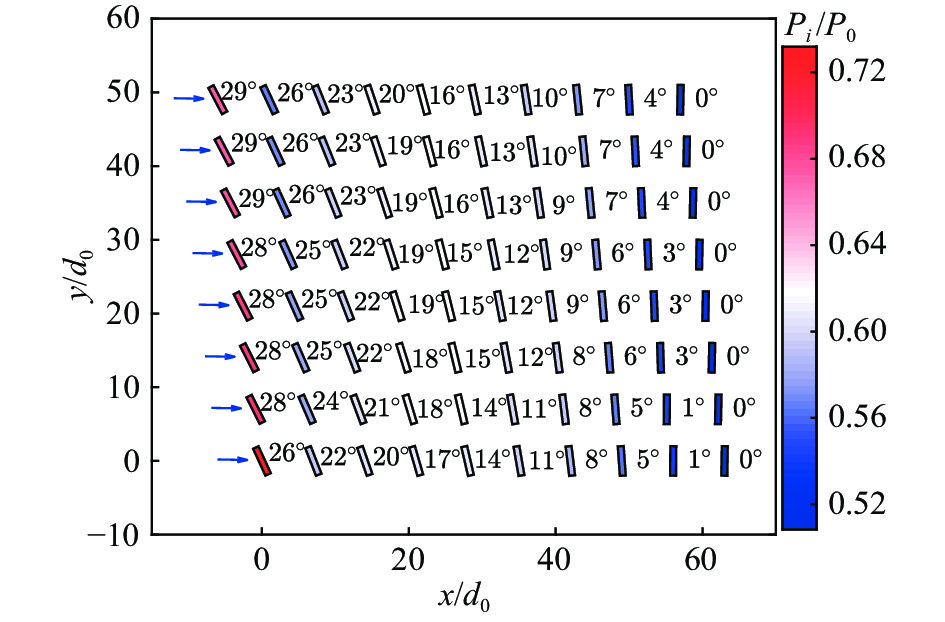
Zong和Porté-Agel进一步对Horns-Rev一期风电场进行了AWC优化[19]。各个方向平均后的净能量收益约为1.8%,特定风向上的最大相对能量收益达到了16%。典型条件下(θ = 274°)的优化结果如图28所示,从上游至下游,各个风力机偏航角依次减小,最上游风力机的偏航角不超过30°,并且顺着叶片排朝下游依次减小,与Bastankhah的实验结果一致[18]。
|
图 28 Horns-Rev风电场在θ = 274°时的最佳偏航角和功率分布[18] Fig.28 Optimal yaw angle and power distributions in Horns-Rev wind farm at a wind direction of θ = 274°[18] |
主动尾流控制技术早在2003年就已经提出来了,但在当时并没有引起太大关注。直到2009至2011年间,Barthelmie团队以实测产能数据说明大型风电场在特殊风向上的尾流损失高达30%~40%以后,AWC技术才成为研究人员关注的焦点。经过十多年的快速发展,该技术已经从实验室内的理论模型研究、风洞实验研究走向了实际风电场的实验验证。未来,建议对以下几个方面开展进一步的研究:
1)现有的风力机尾流模型大部分都是基于远场尾流的自相似速度剖面假设和动量守恒定律推导出来的,并不能准确描述近场尾流的演化。在近场区域,存在着不可忽略的流向压力梯度,速度剖面也受机舱、塔架等风力机部件特性影响较大。建议在未来对近场尾流进行单独建模,满足个别内陆风电场极小流向间距下的产能预测需求。
2)在尾流扩张和偏转模型中,存在着大量的经验参数,如尾流扩张速率和近场尾流区的长度等。目前,这些参数都是依靠经验进行初选,然后根据预测结果偏差进行反向调整,缺乏可靠理论依据。在下一步研究中,可以考虑建立不同地貌、地表、大气稳定性和湍流度下各个模型经验参数取值数据库,指导工程应用。
3)复杂地貌下的逆压梯度和风向顺变对偏航风力机尾流中心偏转和尾流速度剖面的影响至今还未见研究。当在复杂地形应用AWC技术时,需要考虑这些因素的影响。
4)目前现有AWC模型对风电场产能优化时,并没有考虑风向脉动、风速脉动[98]、湍流度变化、风力机极限偏转角度限制、偏航调整频率等实际因素对优化结果的影响。建议对现有的AWC模型做出改进,建立更符合实际风电场运行环境的工程模型。
5)实际风电场应用AWC技术时,研究人员普遍关心的一个问题是偏航到底对风力机寿命的影响有多大。建议建立风力机全寿命产能模型,利用实际风电场的载荷检测和大气数据,评估应用AWC技术所带来的产能提升是否能超过由于风力机寿命缩短和维护频率增多而带来的成本增加。
| [1] |
IEA. Global Energy Review 2021. Internatioanl Energy Agency 2021. Internatioanl Energy Agency 2021[EB/OL]. https://www.iea.org/reports/global-energy-review-2021
|
| [2] |
PORTÉ-AGEL F, BASTANKHAH M, SHAMSODDIN S. Wind-turbine and wind-farm flows: a review[J]. Boundary-Layer Meteorology, 2020, 174(1): 1-59. DOI:10.1007/s10546-019-00473-0 |
| [3] |
RITCHIE H, ROSER M. Energy[EB/OL]. Published online at OurWorldInData. org. , 2021. https://ourworldindata.org/energy
|
| [4] |
JAGANMOHAN M. Installed wind power capacity worldwide 2001-2020[EB/OL]. Published online at www. statista. com, 2021. https://www.statista.com/statistics/268363/installed-wind-power-capacity-worldwide/
|
| [5] |
黎作武, 贺德馨. 风能工程中流体力学问题的研究现状与进展[J]. 力学进展, 2013, 43(5): 472-525. LI Z W, HE D X. Reviews of fluid dynamics researches in wind energy engineering[J]. Advances in Mechanics, 2013, 43(5): 472-525. (in Chinese) |
| [6] |
STEVENS R J A M, MENEVEAU C. Flow structure and turbulence in wind farms[J]. Annual Review of Fluid Mechanics, 2017, 49(1): 311-339. DOI:10.1146/annurev-fluid-010816-060206 |
| [7] |
BARTHELMIE R J, HANSEN K, FRANDSEN S T, et al. Modelling and measuring flow and wind turbine wakes in large wind farms offshore[J]. Wind Energy, 2009, 12(5): 431-444. DOI:10.1002/we.348 |
| [8] |
BARTHELMIE R J, PRYOR S C, FRANDSEN S T, et al. Quantifying the impact of wind turbine wakes on power output at offshore wind farms[J]. Journal of Atmospheric and Oceanic Technology, 2010, 27(8): 1302-1317. DOI:10.1175/2010jtecha1398.1 |
| [9] |
BARTHELMIE R J, JENSEN L E. Evaluation of wind farm efficiency and wind turbine wakes at the Nysted offshore wind farm[J]. Wind Energy, 2010, 13(6): 573-586. DOI:10.1002/we.408 |
| [10] |
HASAGER C, RASMUSSEN L, PEÑA A, et al. Wind farm wake: the horns rev photo case[J]. Energies, 2013, 6(2): 696-716. DOI:10.3390/en6020696 |
| [11] |
MEDICI D. Experimental studies of wind turbine wakes: power optimisation and meandering[D]. KTH, 2005.
|
| [12] |
ADARAMOLA M S, KROGSTAD P Å. Experimental investigation of wake effects on wind turbine performance[J]. Renewable Energy, 2011, 36(8): 2078-2086. DOI:10.1016/j.renene.2011.01.024 |
| [13] |
WAGENAAR J W, MACHIELSE L A H, SCHEPERS J G. Controlling wind in ECN’s scaled wind farm[C]// EWEA 2012. https://www.researchgate.net/publication/264851319_Controlling_Wind_in_ECN's_Scaled_Wind_Farm
|
| [14] |
DAR Z, KAR K, SAHNI O, et al. Windfarm power optimization using yaw angle control[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 104-116. DOI:10.1109/TSTE.2016.2585883 |
| [15] |
WANG J, BOTTASSO C L, CAMPAGNOLO F. Wake redirection: comparison of analytical, numerical and experimental models[C]//Journal of Physics: Conference Series. IOP Publishing, 2016, 753(3): 032064. https://re.public.polimi.it/retrieve/handle/11311/1007400/163974/WANGJ01-16.pdf doi: 10.1088/1742-6596/753/3/032064
|
| [16] |
CAMPAGNOLO F, PETROVIĆ V, BOTTASSO C L, et al. Wind tunnel testing of wake control strategies[C]//2016 American Control Conference (ACC), Boston, MA, USA. IEEE, 2016: 513-518. doi: 10.1109/ACC.2016.7524965
|
| [17] |
HOWLAND M F, LELE S K, DABIRI J O. Wind farm power optimization through wake steering[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(29): 14495-14500. https://www.pnas.org/content/pnas/116/29/14495.full.pdf doi: 10.1073/pnas.1903680116
|
| [18] |
BASTANKHAH M, PORTÉ-AGEL F. Wind farm power optimization via yaw angle control: a wind tunnel study[J]. Journal of Renewable and Sustainable Energy, 2019, 11(2): 023301. DOI:10.1063/1.5077038 |
| [19] |
ZONG H H, PORTÉ-AGEL F. Experimental investigation and analytical modelling of active yaw control for wind farm power optimization[J]. Renewable Energy, 2021, 170: 1228-1244. DOI:10.1016/j.renene.2021.02.059 |
| [20] |
NASH R, NOURI R, VASEL-BE-HAGH A. Wind turbine wake control strategies: a review and concept proposal[J]. Energy Conversion and Management, 2021, 245: 114581. DOI:10.1016/j.enconman.2021.114581 |
| [21] |
NANOS E M, BOTTASSO C L, MANOLAS D I, et al. Vertical wake deflection for floating wind turbines by differential ballast control[J]. Wind Energy Science Discussions, 2021(Accepted). https://www.researchgate.net/publication/354010920_Vertical_wake_deflection_for_floating_wind_turbines_by_differential_ballast_control doi: 10.5194/wes-2021-79
|
| [22] |
NANOS E M, LETIZIA S, CLEMENTE D J B, et al. Vertical wake deflection for offshore floating wind turbines by differential ballast control[J]. Journal of Physics:Conference Series, 2020, 1618: 022047. DOI:10.1088/1742-6596/1618/2/022047 |
| [23] |
KIMURA K, TANABE Y, MATSUO Y, et al. Forced wake meandering for rapid recovery of velocity deficits in a wind turbine wake[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019: 2083. doi: 10.2514/6.2019-2083
|
| [24] |
WANG J, FOLEY S, NANOS E M, et al. Numerical and experimental study of wake redirection techniques in a boundary layer wind tunnel[J]. Journal of Physics:Conference Series, 2017, 854: 012048. DOI:10.1088/1742-6596/854/1/012048 |
| [25] |
FLEMING P A, GEBRAAD P M O, LEE S, et al. Evaluating techniques for redirecting turbine wakes using SOWFA[J]. Renewable Energy, 2014, 70: 211-218. DOI:10.1016/j.renene.2014.02.015 |
| [26] |
FLEMING P, GEBRAAD P M O, LEE S, et al. Simulation comparison of wake mitigation control strategies for a two-turbine case[J]. Wind Energy, 2015, 18(12): 2135-2143. DOI:10.1002/we.1810 |
| [27] |
FLEMING P, ANNONI J, SHAH J J, et al. Field test of wake steering at an offshore wind farm[J]. Wind Energy Science, 2017, 2(1): 229-239. DOI:10.5194/wes-2-229-2017 |
| [28] |
FLEMING P A, NING A, GEBRAAD P M O, et al. Wind plant system engineering through optimization of layout and yaw control[J]. Wind Energy, 2016, 19(2): 329-344. DOI:10.1002/we.1836 |
| [29] |
BENSASON D, SIMLEY E, ROBERTS O, et al. Evaluation of the potential for wake steering for US land-based wind power plants[J]. Journal of Renewable and Sustainable Energy, 2021, 13(3): 033303. DOI:10.1063/5.0039325 |
| [30] |
SONG D R, YANG J, FAN X Y, et al. Maximum power extraction for wind turbines through a novel yaw control solution using predicted wind directions[J]. Energy Conversion and Management, 2018, 157: 587-599. DOI:10.1016/j.enconman.2017.12.019 |
| [31] |
SØRENSEN J N. Aerodynamic aspects of wind energy conversion[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 427-448. DOI:10.1146/annurev-fluid-122109-160801 |
| [32] |
VERMEER L J, SØRENSEN J N, CRESPO A. Wind turbine wake aerodynamics[J]. Progress in Aerospace Sciences, 2003, 39(6-7): 467-510. DOI:10.1016/S0376-0421(03)00078-2 |
| [33] |
MEDICI D, IVANELL S, DAHLBERG J Å, et al. The upstream flow of a wind turbine: blockage effect[J]. Wind Energy, 2011, 14(5): 691-697. DOI:10.1002/we.451 |
| [34] |
BASTANKHAH M, PORTÉ-AGEL F. Wind tunnel study of the wind turbine interaction with a boundary-layer flow: Upwind region, turbine performance, and wake region[J]. Physics of Fluids, 2017, 29(6): 065105. DOI:10.1063/1.4984078 |
| [35] |
DASARI T, WU Y, LIU Y, et al. Near-wake behaviour of a utility-scale wind turbine[J]. Journal of Fluid Mechanics, 2019, 859: 204-246. DOI:10.1017/jfm.2018.779 |
| [36] |
HONG J R, TOLOUI M, CHAMORRO L P, et al. Natural snowfall reveals large-scale flow structures in the wake of a 2.5-MW wind turbine[J]. Nature Communications, 2014, 5: 4216. DOI:10.1038/ncomms5216 |
| [37] |
CHAMORRO L P, PORTÉ-AGEL F. Effects of thermal stability and incoming boundary-layer flow characteristics on wind-turbine wakes: a wind-tunnel study[J]. Boundary-Layer Meteorology, 2010, 136(3): 515-533. DOI:10.1007/s10546-010-9512-1 |
| [38] |
POPE S B. Turbulent flows[J]. Measurement Science and Technology, 2001, 12(11). DOI:10.1088/0957-0233/12/11/705
|
| [39] |
BASTANKHAH M, PORTÉ-AGEL F. A new analytical model for wind-turbine wakes[J]. Renewable Energy, 2014, 70: 116-123. DOI:10.1016/j.renene.2014.01.002 |
| [40] |
AINSLIE J F. Calculating the flowfield in the wake of wind turbines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 27(1-3): 213-224. DOI:10.1016/0167-6105(88)90037-2 |
| [41] |
FANG J N, PORTÉ-AGEL F. Large-eddy simulation of very-large-scale motions in the neutrally stratified atmospheric boundary layer[J]. Boundary-Layer Meteorology, 2015, 155(3): 397-416. DOI:10.1007/s10546-015-0006-z |
| [42] |
LARSEN T J, MADSEN H A, LARSEN G C, et al. Validation of the dynamic wake meander model for loads and power production in the Egmond aan Zee wind farm[J]. Wind Energy, 2013, 16(4): 605-624. DOI:10.1002/we.1563 |
| [43] |
ESPAÑA G, AUBRUN S, LOYER S, et al. Wind tunnel study of the wake meandering downstream of a modelled wind turbine as an effect of large scale turbulent eddies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 101: 24-33. DOI:10.1016/j.jweia.2011.10.011 |
| [44] |
WU Y T, PORTÉ-AGEL F. Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations[J]. Boundary-Layer Meteorology, 2011, 138(3): 345-366. DOI:10.1007/s10546-010-9569-x |
| [45] |
JENSEN N O. A note on wind turbine interaction[R]. Riso-M-2411. Risoe National Laboratory, Roskilde, Denmark, 1983: 16. https://backend.orbit.dtu.dk/ws/portalfiles/portal/55857682/ris_m_2411.pdf
|
| [46] |
FRANDSEN S, BARTHELMIE R, PRYOR S, et al. Analytical modelling of wind speed deficit in large offshore wind farms[J]. Wind Energy, 2006, 9(1‐2): 39-53. DOI:10.1002/we.189 |
| [47] |
HANSEN M. Aerodynamics of wind turbines[M]. Routledge, 2015. DOI:10.4324/9781315769981
|
| [48] |
SHAMSODDIN S, PORTÉ-AGEL F. A model for the effect of pressure gradient on turbulent axisymmetric wakes[J]. Journal of Fluid Mechanics, 2018, 837: R3. DOI:10.1017/jfm.2017.864 |
| [49] |
ABKAR M, SØRENSEN J, PORTÉ-AGEL F. An analytical model for the effect of vertical wind veer on wind turbine wakes[J]. Energies, 2018, 11(7): 1838. DOI:10.3390/en11071838 |
| [50] |
BODINI N, ZARDI D, LUNDQUIST J K. Three-dimensional structure of wind turbine wakes as measured by scanning lidar[J]. Atmospheric Measurement Techniques, 2017, 10(8): 2881-2896. DOI:10.5194/amt-10-2881-2017 |
| [51] |
ARCHER C L, VASEL-BE-HAGH A, YAN C, et al. Review and evaluation of wake loss models for wind energy applications[J]. Applied Energy, 2018, 226: 1187-1207. DOI:10.1016/j.apenergy.2018.05.085 |
| [52] |
FLEMING P A, SCHOLBROCK A K, JEHU A, et al. Field-test results using a nacelle-mounted lidar for improving wind turbine power capture by reducing yaw misalignment[J]. Journal of Physics:Conference Series, 2014, 524: 012002. DOI:10.1088/1742-6596/524/1/012002 |
| [53] |
ZONG H H, PORTÉ-AGEL F. A point vortex transportation model for yawed wind turbine wakes[J]. Journal of Fluid Mechanics, 2020, 890: A8. DOI:10.1017/jfm.2020.123 |
| [54] |
BASTANKHAH M, PORTÉ-AGEL F. Experimental and theoretical study of wind turbine wakes in yawed conditions[J]. Journal of Fluid Mechanics, 2016, 806: 506-541. DOI:10.1017/jfm.2016.595 |
| [55] |
HOWLAND M F, BOSSUYT J, MARTÍNEZ-TOSSAS L A, et al. Wake structure in actuator disk models of wind turbines in yaw under uniform inflow conditions[J]. Journal of Renewable and Sustainable Energy, 2016, 8(4): 043301. DOI:10.1063/1.4955091 |
| [56] |
MARTÍNEZ-TOSSAS L A, ANNONI J, FLEMING P A, et al. The aerodynamics of the curled wake: a simplified model in view of flow control[J]. Wind Energy Science, 2019, 4(1): 127-138. DOI:10.5194/wes-4-127-2019 |
| [57] |
MARTÍNEZ-TOSSAS L A, KING J, QUON E, et al. The curled wake model: a three-dimensional and extremely fast steady-state wake solver for wind plant flows[J]. Wind Energy Science, 2021, 6(2): 555-570. DOI:10.5194/wes-6-555-2021 |
| [58] |
JIMÉNEZ Á, CRESPO A, MIGOYA E. Application of a LES technique to characterize the wake deflection of a wind turbine in yaw[J]. Wind Energy, 2010, 13(6): 559-572. DOI:10.1002/we.380 |
| [59] |
SHAPIRO C R, GAYME D F, MENEVEAU C. Modelling yawed wind turbine wakes: a lifting line approach[J]. Journal of Fluid Mechanics, 2018, 841: R1. DOI:10.1017/jfm.2018.75 |
| [60] |
QIAN G W, ISHIHARA T. A new analytical wake model for yawed wind turbines[J]. Energies, 2018, 11(3): 665. DOI:10.3390/en11030665 |
| [61] |
BRUGGER P, DEBNATH M, SCHOLBROCK A, et al. Lidar measurements of yawed-wind-turbine wakes: characterization and validation of analytical models[J]. Wind Energy Science, 2020, 5(4): 1253-1272. DOI:10.5194/wes-5-1253-2020 |
| [62] |
BRANLARD E, GAUNAA M. Cylindrical vortex wake model: skewed cylinder, application to yawed or tilted rotors[J]. Wind Energy, 2016, 19(2): 345-358. DOI:10.1002/we.1838[LinkOut |
| [63] |
VOLLMER L, STEINFELD G, HEINEMANN D, et al. Estimating the wake deflection downstream of a wind turbine in different atmospheric stabilities: an LES study[J]. Wind Energy Science, 2016, 1(2): 129-141. DOI:10.5194/wes-1-129-2016 |
| [64] |
LISSAMAN P B S. Energy effectiveness of arbitrary arrays of wind turbines[J]. Journal of Energy, 1979, 3(6): 323-328. DOI:10.2514/3.62441 |
| [65] |
KATIC I, HØJSTRUP J, JENSEN N O. A simple model for cluster efficiency[C]//European wind energy association conference and exhibition. 1986, 1: 407-410. https://backend.orbit.dtu.dk/ws/portalfiles/portal/106427419/A_Simple_Model_for_Cluster_Efficiency_EWEC_86_.pdf
|
| [66] |
NIAYIFAR A, PORTÉ-AGEL F. Analytical modeling of wind farms: a new approach for power prediction[J]. Energies, 2016, 9(9): 741. DOI:10.3390/en9090741 |
| [67] |
VOUTSINAS S, RADOS K, ZERVOS A. On the analysis of wake effects in wind parks[J]. Wind Engineering, 1990, 14(4): 204-219. https://www.jstor.org/stable/43749429
|
| [68] |
ZONG H H, PORTÉ-AGEL F. A momentum-conserving wake superposition method for wind farm power prediction[J]. Journal of Fluid Mechanics, 2020, 889: A8. DOI:10.1017/jfm.2020.77 |
| [69] |
BASTANKHAH M, PORTÉ-AGEL F. A new miniature wind turbine for wind tunnel experiments. part I: design and performance[J]. Energies, 2017, 10(7): 908. DOI:10.3390/en10070908 |
| [70] |
FLEMING P, ANNONI J, CHURCHFIELD M, et al. A simulation study demonstrating the importance of large-scale trailing vortices in wake steering[J]. Wind Energy Science, 2018, 3(1): 243-255. DOI:10.5194/wes-3-243-2018 |
| [71] |
FLEMING P, KING J, DYKES K, et al. Initial results from a field campaign of wake steering applied at a commercial wind farm – Part 1[J]. Wind Energy Science, 2019, 4(2): 273-285. DOI:10.5194/wes-4-273-2019 |
| [72] |
FLEMING P, KING J, SIMLEY E, et al. Continued results from a field campaign of wake steering applied at a commercial wind farm – Part 2[J]. Wind Energy Science, 2020, 5(3): 945-958. DOI:10.5194/wes-5-945-2020 |
| [73] |
KING J, FLEMING P, KING R, et al. Control-oriented model for secondary effects of wake steering[J]. Wind Energy Science, 2021, 6(3): 701-714. DOI:10.5194/wes-6-701-2021 |
| [74] |
KNUDSEN T, BAK T, SVENSTRUP M. Survey of wind farm control—power and fatigue optimization[J]. Wind Energy, 2015, 18(8): 1333-1351. DOI:10.1002/we.1760 |
| [75] |
PARK J, LAW K H. A data-driven, cooperative wind farm control to maximize the total power production[J]. Applied Energy, 2016, 165: 151-165. DOI:10.1016/j.apenergy.2015.11.064 |
| [76] |
KIRCHNER-BOSSI N, PORTÉ-AGEL F. Wind farm area shape optimization using newly developed multi-objective evolutionary algorithms[J]. Energies, 2021, 14(14): 4185. DOI:10.3390/en14144185 |
| [77] |
GEBRAAD P M O, VAN WINGERDEN J W. Maximum power‐point tracking control for wind farms[J]. Wind Energy, 2015, 18(3): 429-447. DOI:10.1002/we.1706 |
| [78] |
GEBRAAD P, THOMAS J J, NING A, et al. Maximization of the annual energy production of wind power plants by optimization of layout and yaw-based wake control[J]. Wind Energy, 2017, 20(1): 97-107. DOI:10.1002/we.1993 |
| [79] |
BROGNA R, FENG J, SØRENSEN J N, et al. A new wake model and comparison of eight algorithms for layout optimization of wind farms in complex terrain[J]. Applied Energy, 2020, 259: 114189. DOI:10.1016/j.apenergy.2019.114189 |
| [80] |
KIRCHNER-BOSSI N, PORTÉ-AGEL F. Realistic wind farm layout optimization through genetic algorithms using a Gaussian wake model[J]. Energies, 2018, 11(12): 3268. DOI:10.3390/en11123268 |
| [81] |
STANFEL P, JOHNSON K, BAY C J, et al. Proof-of-concept of a reinforcement learning framework for wind farm energy capture maximization in time-varying wind[J]. Journal of Renewable and Sustainable Energy, 2021, 13(4): 043305. DOI:10.1063/5.0043091 |
| [82] |
SONG D R, FAN X Y, YANG J, et al. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method[J]. Applied Energy, 2018, 224: 267-279. DOI:10.1016/j.apenergy.2018.04.114 |
| [83] |
BERNARDONI F, CIRI U, ROTEA M A, et al. Identification of wind turbine clusters for effective real time yaw control optimization[J]. Journal of Renewable and Sustainable Energy, 2021, 13(4): 043301. DOI:10.1063/5.0036640 |
| [84] |
OZBAY A, TIAN W, YANG Z F, et al. Interference of wind turbines with different yaw angles of the upstream wind turbine[C]//42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, Louisiana. Reston, Virginia: AIAA, 2012. doi: 10.2514/6.2012-2719
|
| [85] |
HANSEN K S, BARTHELMIE R J, JENSEN L E, et al. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm[J]. Wind Energy, 2012, 15(1): 183-196. DOI:10.1002/we.512 |
| [86] |
CAMPAGNOLO F, PETROVIĆ V, SCHREIBER J, et al. Wind tunnel testing of a closed-loop wake deflection controller for wind farm power maximization[J]. Journal of Physics: Conference Series, 2016, 753: 032006. https://iopscience.iop.org/article/10.1088/1742-6596/753/3/032006/pdf doi: 10.1088/1742-6596/753/3/032006
|
| [87] |
LIN M, PORTÉ-AGEL F. Power maximization and fatigue-load mitigation in a wind-turbine array by active yaw control: an LES study[J]. Journal of Physics:Conference Series, 2020, 1618: 042036. DOI:10.1088/1742-6596/1618/4/042036 |
| [88] |
FLEMING P, ANNONI J, SCHOLBROCK A, et al. Full-scale field test of wake steering[J]. Journal of Physics:Conference Series, 2017, 854: 012013. DOI:10.1088/1742-6596/854/1/012013 |
| [89] |
GEBRAAD P M O, TEEUWISSE F W, VAN WINGERDEN J W, et al. Wind plant power optimization through yaw control using a parametric model for wake effects—a CFD simulation study[J]. Wind Energy, 2016, 19(1): 95-114. DOI:10.1002/we.1822 |
| [90] |
ROTT A, DOEKEMEIJER B, SEIFERT J K, et al. Robust active wake control in consideration of wind direction variability and uncertainty[J]. Wind Energy Science, 2018, 3(2): 869-882. DOI:10.5194/wes-3-869-2018 |
| [91] |
MENDEZ REYES H, KANEV S, DOEKEMEIJER B, et al. Validation of a lookup-table approach to modeling turbine fatigue loads in wind farms under active wake control[J]. Wind Energy Science, 2019, 4(4): 549-561. DOI:10.5194/wes-4-549-2019 |
| [92] |
KANEV S. Dynamic wake steering and its impact on wind farm power production and yaw actuator duty[J]. Renewable Energy, 2020, 146: 9-15. DOI:10.1016/j.renene.2019.06.122 |
| [93] |
KANEV S K, SAVENIJE F J, ENGELS W P. Active wake control: an approach to optimize the lifetime operation of wind farms[J]. Wind Energy, 2018, 21(7): 488-501. DOI:10.1002/we.2173 |
| [94] |
PARK J, KWON S, LAW K H. Wind farm power maximization based on a cooperative static game approach[C]//Proceedings of the SPIE, 2013, 8688. http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid = 418924BF2676423839D98C004A37CDB7?doi = 10.1.1.300.3939&rep = rep1&type = pdf doi: 10.1117/12.2009618
|
| [95] |
PARK J, LAW K H. Cooperative wind turbine control for maximizing wind farm power using sequential convex programming[J]. Energy Conversion and Management, 2015, 101: 295-316. DOI:10.1016/j.enconman.2015.05.031 |
| [96] |
PARK J, LAW K H. Bayesian ascent: a data-driven optimization scheme for real-time control with application to wind farm power maximization[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1655-1668. DOI:10.1109/TCST.2015.2508007 |
| [97] |
BAY C J, KING J, FLEMING P, et al. Unlocking the full potential of wake steering: implementation and assessment of a controls-oriented model[J]. Wind Energy Science Discussions, 2019, 1-20. DOI:10.5194/wes-2019-19 |
| [98] |
王浩, 柯世堂, 王同光. 台风过境全过程大型风力机风荷载特性[J]. 空气动力学学报, 2020, 38(5): 915-923. WANG H, KE S, WANG T G. Wind loads characteristic of large wind turbine considering typhoon transit process[J]. Acta Aerodynamica Sinica, 2020, 38(5): 915-923. DOI:10.7638/kqdlxxb-2019.0108 (in Chinese) |
 2022, Vol. 40
2022, Vol. 40