2. 南京航空航天大学 民航学院,南京 210016
2. College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
随着风力机复合材料叶片尺寸的增加,几何非线性效应、截面面内和面外翘曲等非经典的效应,对叶片结构动力学动态响应产生显著影响。然而由于弹性耦合影响,复合材料结构的分析要比各向同性结构的更难[1]。传统的模态叠加法仍然适用于计算小功率风力机的弹性变形。然而对于大型风力机而言,在复杂工况下可能会发生大的变形,在这时,传统的线性方法无法再准确地预测叶片的动态响应。
为带有预扭和弯曲的复合材料叶片开发一种考虑几何非线性的梁模型是风力机领域的一个新的焦点。叶片截面上的应变通常是小应变,因此,几何非线性[2-3]主要是由叶片截面的有限旋转造成的。传统的线性分析方法是将叶片简化为欧拉伯努利梁模型[4],并采用模态叠加法进行求解,但此方法没有考虑扭转自由度,精度不够。文献[5]中采用微分求积单元求解几何非线性,而本文应用了基于Lengendre谱有限元的几何精确梁理论[6-8],这个理论是基于经典铁木辛柯梁理论[9-10]且考虑了截面旋转发展而来。这个结构模型包含了耦合的挥舞、摆振和扭转自由度。目前,气动计算中常用的方法是AL-LES方法和叶素动量理论等。由于AL-LES方法[11-12]计算的复杂性,于是在本文中用几何精确梁理论与叶素动量理论[13-15]耦合来建立风力机叶片气动弹性模型。这个模型能准确计算在气动载荷下的叶片变形并且充分考虑变形对气动弹性稳定性造成的几何非线性影响。
本文主要将几何非线性分析方法应用在两种不同功率的大型风力机中的大柔性叶片,首先采用几何精确梁理论计算悬臂梁变形,并与理论值进行对比,验证结构计算方法的可靠性与准确性。然后通过叶素动量理论与几何精确梁方法耦合计算,实现大型风力机5 MW和15 MW的动态响应计算。
1 理论描述 1.1 叶素动量理论叶素动量方法实际上是叶素理论和动量理论的结合。气流在流管内流动满足动量定理,但是气流在流经叶片时会受到扰动,从而导致了气流的切向和轴向速度发生变化,通常引入切向和轴向诱导因子来反应气流在通过风轮平面时速度的损失。叶素理论将叶片沿展向离散为有限数量的叶素,叶素随着风轮旋转形成了一个圆环,沿展向对升、阻力积分便可求得气动推力和扭矩。叶片一个叶素微元的受力如图1所示。
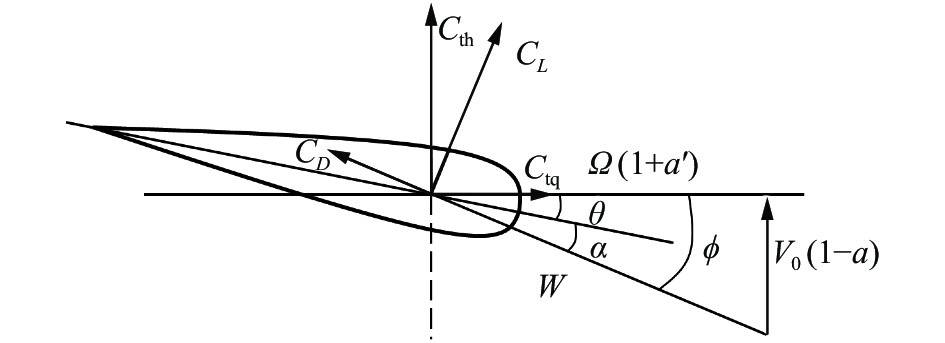
|
图 1 叶素上的来流速度与气动力示意图 Fig.1 Inflow velocity and aerodynamic forces on the blade |
W为入流合速度,速度合成关系为:
| $ W = \sqrt{{V}_{0}^{2}(1-a)^{2}+{\varOmega }^{2}{r}^{2}(1+{a}^{\prime })^{2}} $ | (1) |
| $ \sin \phi = \frac{{{V_0}\left( {1 - a} \right)}}{W} $ | (2) |
| $ \cos \phi = \frac{{\varOmega \left( {1 + a'} \right)}}{W} $ | (3) |
式中
叶素升力、阻力表达式为:
| $ {\text{d}}{F_{\text{l}}} = \frac{1}{2}\; \rho {W^2}C_L\;c\;{\text{d}}r $ | (4) |
| $ {\text{d}}{F_{\text{d}}} = \frac{1}{2}\; \rho {W^2}C_D\;c\;{\text{d}}r $ | (5) |
式中:
通过将叶段升、阻力分解到风轮旋转平面及垂直于风轮旋转平面的方向,得到了切向力
| $ {\text{d}}{F_{{\text{tq}}}} = {\text{d}}{F_{\text{l}}}\sin \phi - {\text{d}}{F_{\text{d}}}\cos \phi $ | (6) |
| $ {\text{d}}{F_{{\rm{th}}}} = {\text{d}}{F_{\text{l}}}\cos \phi + {\text{d}}{F_{\text{d}}}\sin \phi $ | (7) |
叶素的剖面是一系列基本翼型,而基本翼型的气动数据一般作为输入条件来确定不同入流条件下的气动力,输入的气动数据一般为不同攻角α下的升力系数
| $ {C_{{\text{th}}}} = C_L\cos \phi + C_D\sin \phi $ | (8) |
| $ {C_{{\text{tq}}}} = C_L\sin \phi - {C_D}\cos \phi $ | (9) |
考虑叶片数量B,微元上受到的推力和转矩通过叶素理论描述为:
| $ {\text{d}}T = \frac{1}{2} \rho {W^2}{C_N}B c{\text{d}}r $ | (10) |
| $ {\text{d}}Q = \frac{1}{2} \rho {W^2}{C_{\text{t}}}Bcr{\text{d}}r $ | (11) |
根据动量理论和叶素理论下的推力和转矩公式相等,可得轴向诱导因子
| $ a = \dfrac{1}{{\dfrac{{4{{\sin }^2}\phi }}{{\sigma {C_{{\text{th}}}}}} + 1}} $ | (12) |
| $ a'{\text{ = }}\dfrac{1}{{\dfrac{{4\sin \phi \cos \phi }}{{\sigma {C_{{\text{tq}}}}}} - 1}} $ | (13) |
式中,
几何精确梁理论以受初始弯扭的梁能承受大的位移和旋转的能力为特点。通过一个三维横截面分析,六个自由度的所有耦合效应,包括拉伸、剪切、扭转、弯曲、扭转翘曲、面内翘曲等,都能被几何精确梁理论涵盖。“几何精确”指的是在公式中没有对初始几何形状和变形后的几何形状进行近似[16],如图2所示。
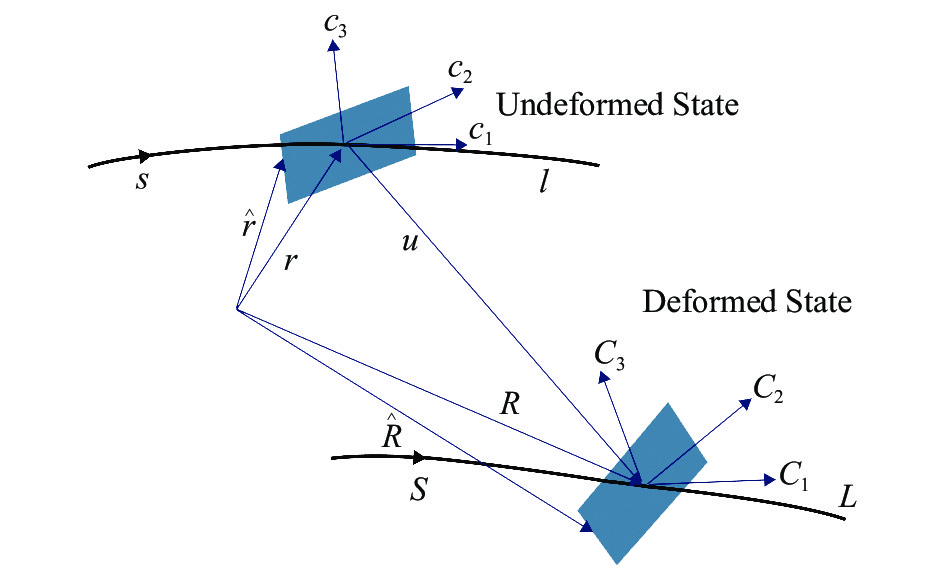
|
图 2 梁变形状态示意图 Fig.2 Schematic of the beam in deformed states |
几何精确梁理论的非线性运动控制方程如下:
| $ \frac{{\partial h}}{{\partial t}} - F' = f $ | (14) |
| $ \frac{{\partial g}}{{\partial t}} + \frac{{\partial u}}{{\partial t}}h - M' - \left( {{{x}'_0} + u'} \right)F = m $ | (15) |
式中
基于小应变假设,动量与速度、应变与截面力之间的关系为:
| $ \Bigg\{ \begin{array}{c} h \\ g \end{array} \Bigg\} = {{\boldsymbol{M}}_1}\Bigg\{ \begin{array}{c} v \\ \omega \end{array} \Bigg\} $ | (16) |
| $ \Bigg\{ \begin{array}{c} F \\ M \end{array} \Bigg\} = {\boldsymbol{K}}\Bigg\{ \begin{array}{c} \varepsilon \\ \kappa \end{array} \Bigg\} $ | (17) |
式中
一维应变与曲率定义为:
| $ \Bigg\{ \begin{array}{c} \varepsilon \\ \kappa \end{array} \Bigg\} = \Bigg\{ \begin{array}{c} {{x}'_0} + u' - \left( {R\left. {{R_0}} \right){l_1}} \right. \\ k \end{array} \Bigg\} $ | (18) |
式中
梁的非线性控制运动方程通过Newton-Raphson方法来求解,并用Lengendre谱有限元方法对增量方程离散化。线性分析中假设位移无穷小,因而物体的位形保持不变,但在大变形下必须建立参考位形为已知位形的方程。想推导由线性化得出的近似解的控制方程,可将应力应变参照于已知位形之上,首先需要线性化处理。非线性运动控制方程的线性化形式如下所示:
| $ {\bar {\boldsymbol{M}}_1}\Delta \bar a + \bar {\boldsymbol{G}} \Delta \bar v + \bar {\boldsymbol{K}} \Delta \bar q = {\bar F_0} - {\bar F_1} $ | (19) |
式中
几何精确梁理论的时间积分采用广义α时间积分器来计算。由非线性控制运动方程定义的广义α时间积分系统需要非线性系统在每个时间步长进行求解,相邻两个步数之间的差别在一定范围内时判定为收敛。几何精确梁理论应用的是能量停止准则,用每一次迭代时的内能增量与初始内能增量相比来判断是否收敛,该准则提供了当位移和力接近其平衡值时的度量:
| $ \begin{split}&\left| {\Delta {U^{\left( i \right)T}}\left( {{}^{t + \Delta t}R - {}^{t + \Delta t}{F^{\left( {i - 1} \right)}}} \right)} \right| \leqslant \left| {{\varepsilon _{_E}}\left[ {\Delta {U^{\left( 1 \right)T}}\left( {{}^{t + \Delta t}R - {}^tF} \right)} \right]} \right|\\\end{split} $ | (20) |
式中:
几何精确梁理论是基于由铁木辛柯梁发展而来的梁理论,也采用了平截面假设,但二者对于截面转动的处理方式不同[17]。一般的线性梁模型通过小变形假设忽略了方程中与截面转动相关的正、余弦项和高次幂项来简化为线性方程,而几何精确梁理论考虑了截面转动和扭转自由度,其中的三维旋转可表示为Wiener-Milenkovic参数,用以下方程来表示:
| $ c = 4\tan \left( {\frac{\varphi }{4}} \right)n $ | (21) |
式中,
将风力机叶片简化为梁单元,输入相应结构参数后,对节点自由度通过Legendre谱有限元进行数值实现,采用梯形求积法 ,用单个单元对风力机叶片进行建模,用Wiener-Milenkovic参数表示三维旋转,得到叶片各个节点的线位移、角位移,其次对非线性运动控制方程采用Newton-Raphson求解,线性化处理后,采用广义α时间积分器判断方程是否收敛。
1.3 气动弹性响应计算输入风模型后,在一个时间步长内,BEM计算叶片的气动载荷,然后计算叶片气动力、重力、离心力合力。通过输入的结构数据构建质量、刚度矩阵,建立叶片动力学方程,通过Newton-Raphson方法求解叶片响应,将叶片当前状态反馈到气动模型中,根据叶片变形后当地的来流条件和攻角确定升、阻力系数,叶片气动外形更新后进行下一个时间步长的计算。气动弹性响应计算流程图见图3。
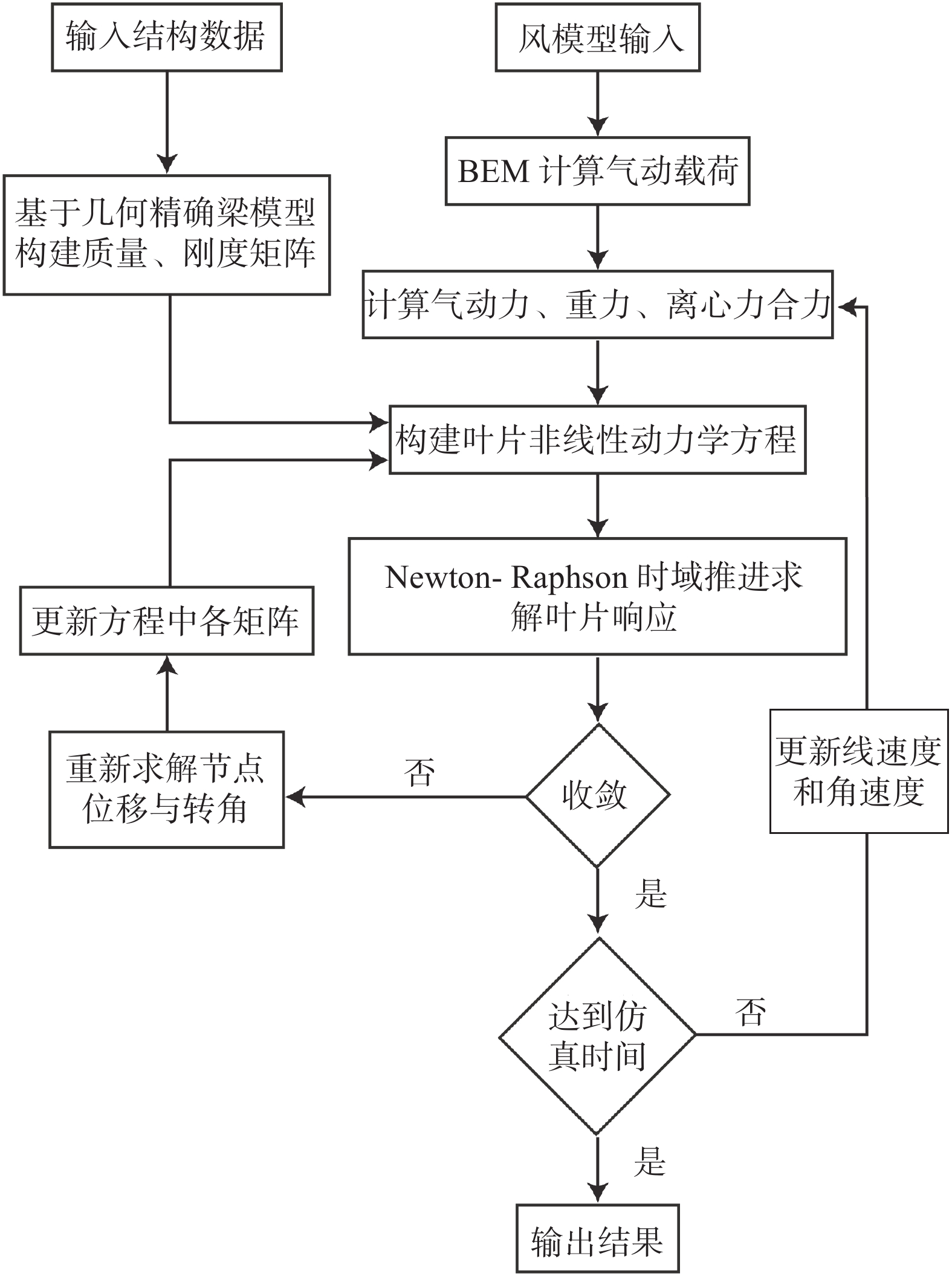
|
图 3 气弹响应计算流程图 Fig.3 Flow chart of the aeroelastic response calculation |
通过与文献[18]中理论值进行对比,来验证本文几何精确梁计算模型的可靠性与准确性。文献[18]中采用的是一个带有预弯的悬臂梁。梁的横截面是正方形,弹性模量为68.9 GPa。悬臂梁变形时的状态如图4所示,预弯梁与x轴夹角为45°,向叶尖分别施加1335 N和2670 N的力。
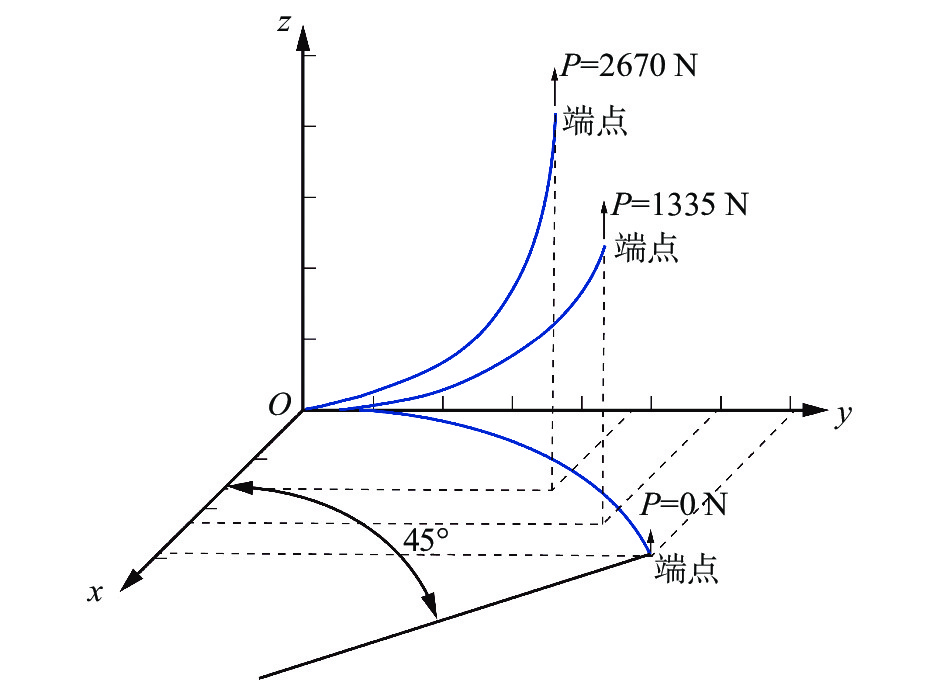
|
图 4 预弯梁的变形示意图 Fig.4 Schematic of the curved beam in deformed states |
表1和表2分别是施加1335 N和2670 N的力时与文献中的叶尖位移结果对比。从表中可以看出,本文采用的几何精确梁算法与文献[18]中的解析解吻合良好,说明几何精确梁理论对于带有预弯的梁位移的预测有较高的精度。对于风力机叶片来说,文献[19]中已经证明了几何精确梁模型的结果与2.3 MW风力机叶片的实验值更加吻合。
| 表 1 施加1335 N时叶尖位移对比 Table 1 Comparison of the blade tip displacements under a force of 1335 N |
|
|
| 表 2 施加2670 N时叶尖位移对比 Table 2 Comparison of the blade tip displacements under a force of 2670 N |
|
|
本文研究大型水平轴风力机柔性叶片,选用NREL 5 MW[20]和IEA 15 MW[21]风力机,风力机的叶片主要参数见表3和表4。
| 表 3 NREL 5 MW叶片主要参数 Table 3 Key parameters of the NREL 5 MW blade |
|
|
| 表 4 IEA 15 MW叶片主要参数 Table 4 Key parameters of the IEA 15 MW blade |
|
|
分别采用线性模态叠加法和几何精确梁方法,对均匀来流条件下的5 MW和15 MW风力机组的功率和推力模拟进行对比分析,在单个风速下的功率值和推力值均采用风力机稳定运行周期的平均值。图5~图12中,Linear代表模态叠加法,Nonlinear代表几何精确梁方法。
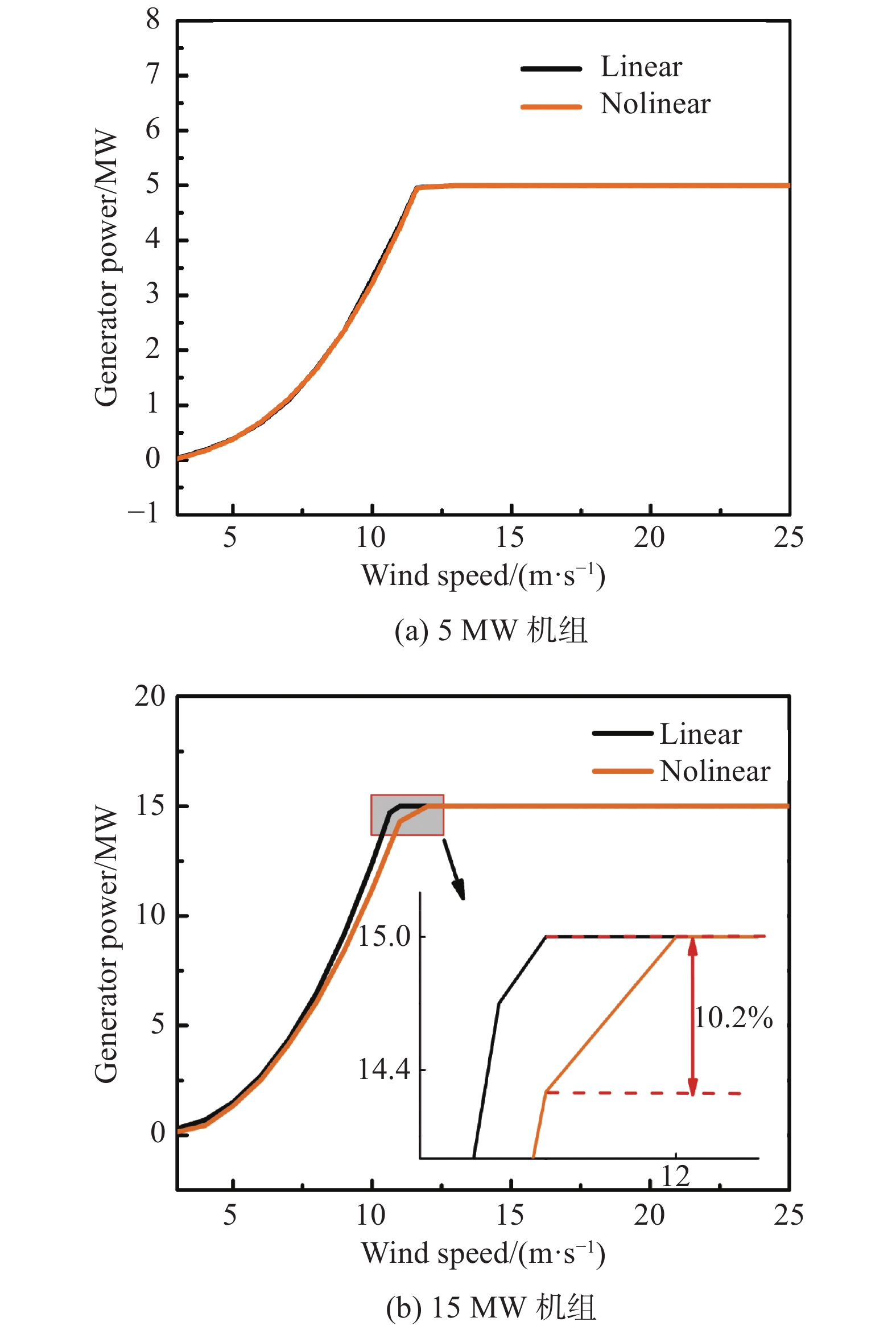
|
图 5 5 MW和15 MW机组在不同风速下的功率曲线 Fig.5 Power performance curves of the 5 MW and 15 MW wind turbines under different wind speeds |
图5给出了5 MW和15 MW机组在不同风速下的功率曲线。从图5(a)中可以看出,对于5 MW风力机,额定风速在11.4 m/s附近。对于功率来说,在低于额定风速下,非线性结果均略小于线性结果,但总体差距不明显。从图5(b)中可以看出,对于15 MW风力机组,额定风速在10.56 m/s附近;非线性方法下的额定风速在11.5 m/s附近,并且对于功率来说,低于额定风速下的结果也均小于线性结果,但其差值比5 MW机组的要大,分析认为这是由于叶片的扭转变形可能会造成输出功率的降低,因为带有扭转变形的模型具有较低的载荷并且发电量也较低。越接近11.5 m/s风速,两种方法的功率差值越大,这说明,模态叠加法和几何精确梁理论两种方法对低风速下小变形叶片的风力机发电功率的预测无明显区别,但在中、高风速下叶片发生了较大变形,尤其对于15 MW这种大柔性叶片,几何精确梁理论与模态叠加法相比,在叶片结构分析中考虑了叶片的扭转变形和弯扭耦合效应,因此更适合于求解带有几何非线性效应的叶片。
图6给出了5 MW和15 MW机组在不同风速下的风轮推力。从图中可以看出:两个机组随着风速增加,风轮推力逐渐增大,均在额定风速下达到最大推力;对于5 MW机组,非线性方法下的风轮推力要略小于线性结果,差距较小,总的来说一致性较好;对于15 MW机组,最大推力出现在风速11.5 m/s附近,与功率曲线完全对应。在额定风速附近,计算结果有明显差异,非线性结果要小于线性计算结果。额定风速之后,线性与非线性结果一致性较好。出现这种差异可能是由于15 MW的117 m叶片大幅度的变形使风力机风轮实际的扫掠面积变小,翼型的气动性能偏离了最优状态。
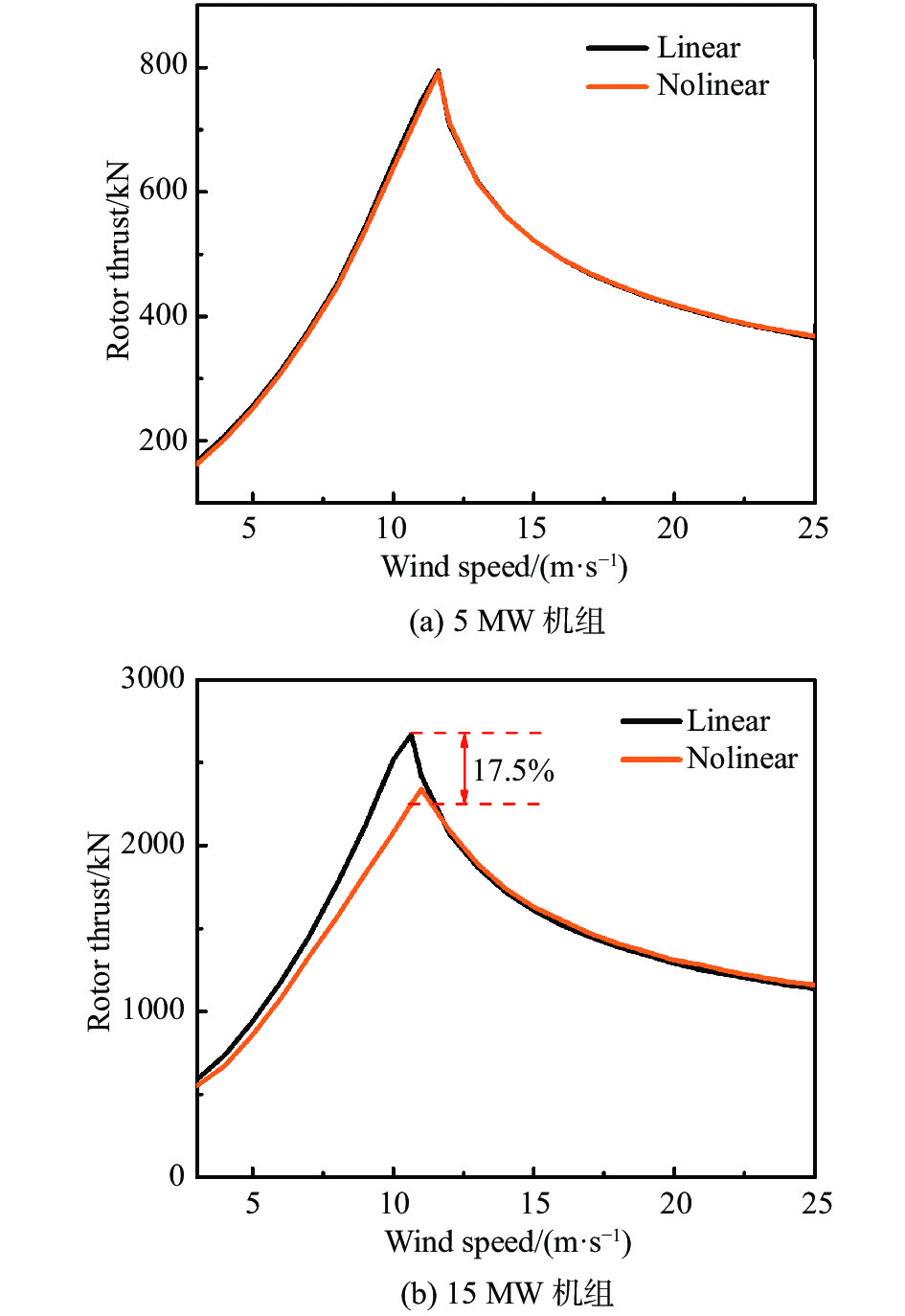
|
图 6 5 MW和15 MW机组在不同风速下的风轮推力 Fig.6 Rotor thrust of the 5 MW and 15 MW wind turbines under different wind speeds |
叶尖挥舞变形量如图7所示。对于5 MW机组,叶尖的最大挥舞变形发生在额定风速下,此时风力机刚达到满发,在额定风速附近线性与非线性结果差值为0.246 m。在低风速范围内,线性与非线性结果吻合良好,而在中高风速下,非线性结果要略小于线性结果,并且随着风速增大差值也越大,出现这种现象的原因是实际变形过程中,由于叶片产生的位移而导致长度减小,从而发生了弯曲方向的刚度强化,可见非线性分析方法更加贴合实际情况。而15 MW机组的变化趋势相同,线性结果与非线性结果在额定风速附近差值最大为3.4 m,非线性结果在低风速内与线性结果吻合较好,而在中高风速下,非线性结果与线性结果差异明显,说明在额定风速附近和高风速下,大功率机组的叶片显示出了强非线性,普通的模态叠加法已经失效,这时对几何非线性的考虑尤为重要。
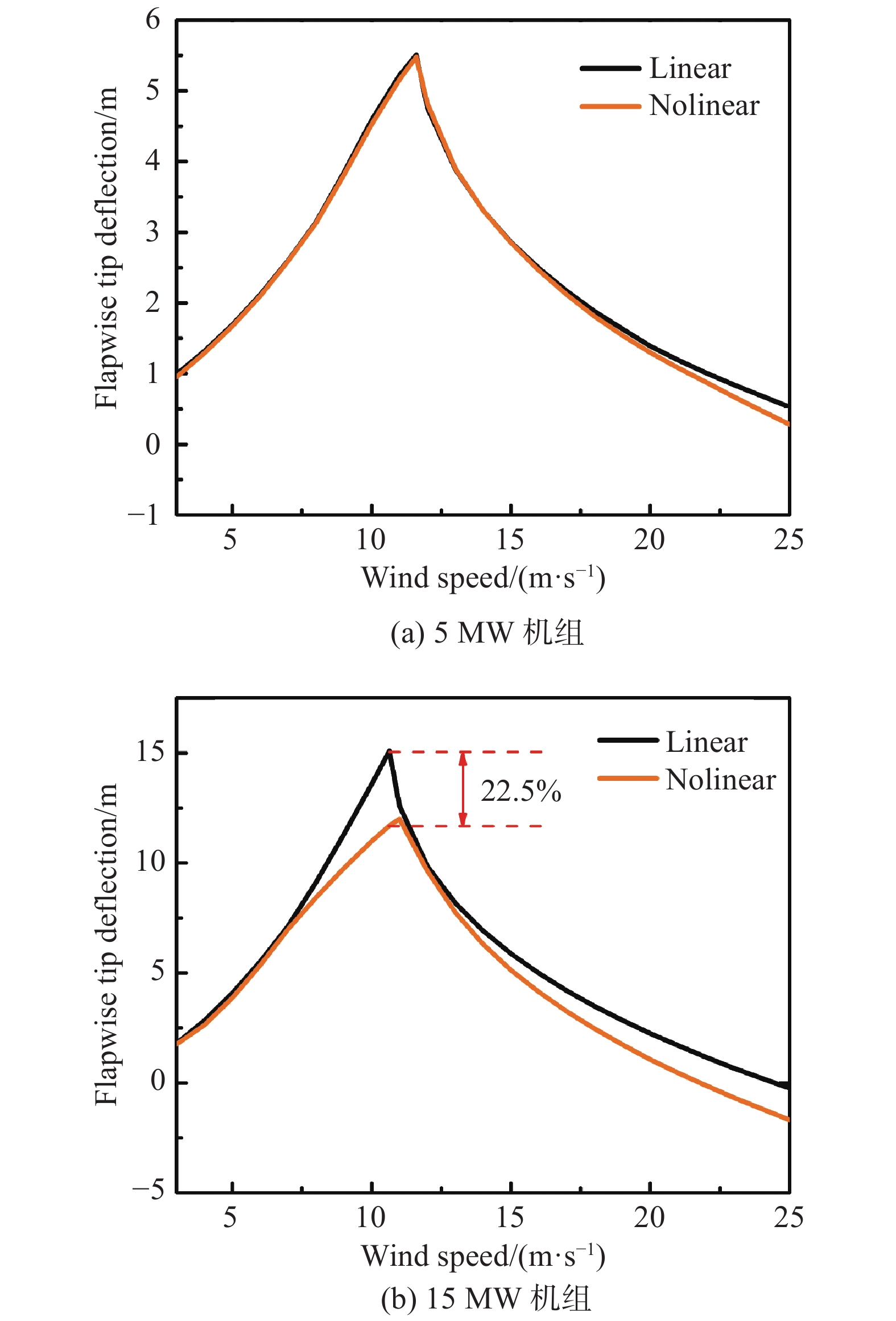
|
图 7 5 MW和15 MW机组在不同风速下的叶尖挥舞位移 Fig.7 Flapwise tip deflection of the 5 MW and 15 MW wind turbines under different wind speeds |
图8给出了5 MW和15 MW机组在不同风速下的叶根挥舞弯矩。由图可见,叶根挥舞弯矩在额定风速附近达到最大值。对于5 MW机组,线性与非线性结果吻合良好,在额定风速附近非线性结果略小于线性结果,差值为0.15 MN;对于15 MW机组,非线性结果在低于额定风速范围内要小于线性结果,差值较大,并在额定风速附近差值达到最大值13.1 MN,其余风速下吻合较好。从5 MW到15 MW,数值偏差增加了21.23%。叶根的挥舞力矩主要由气动载荷决定,而叶片的扭转变形与攻角紧密相关,进而影响了气动载荷,基于欧拉伯努利梁理论的线性模态叠加法仅考虑了叶片的弯曲自由度,对于61.5 m叶片的叶根弯矩具有较高的计算精度,但是针对大功率级风力机组的叶片,没有考虑扭转自由度就会导致在额定风速下产生较大差异。
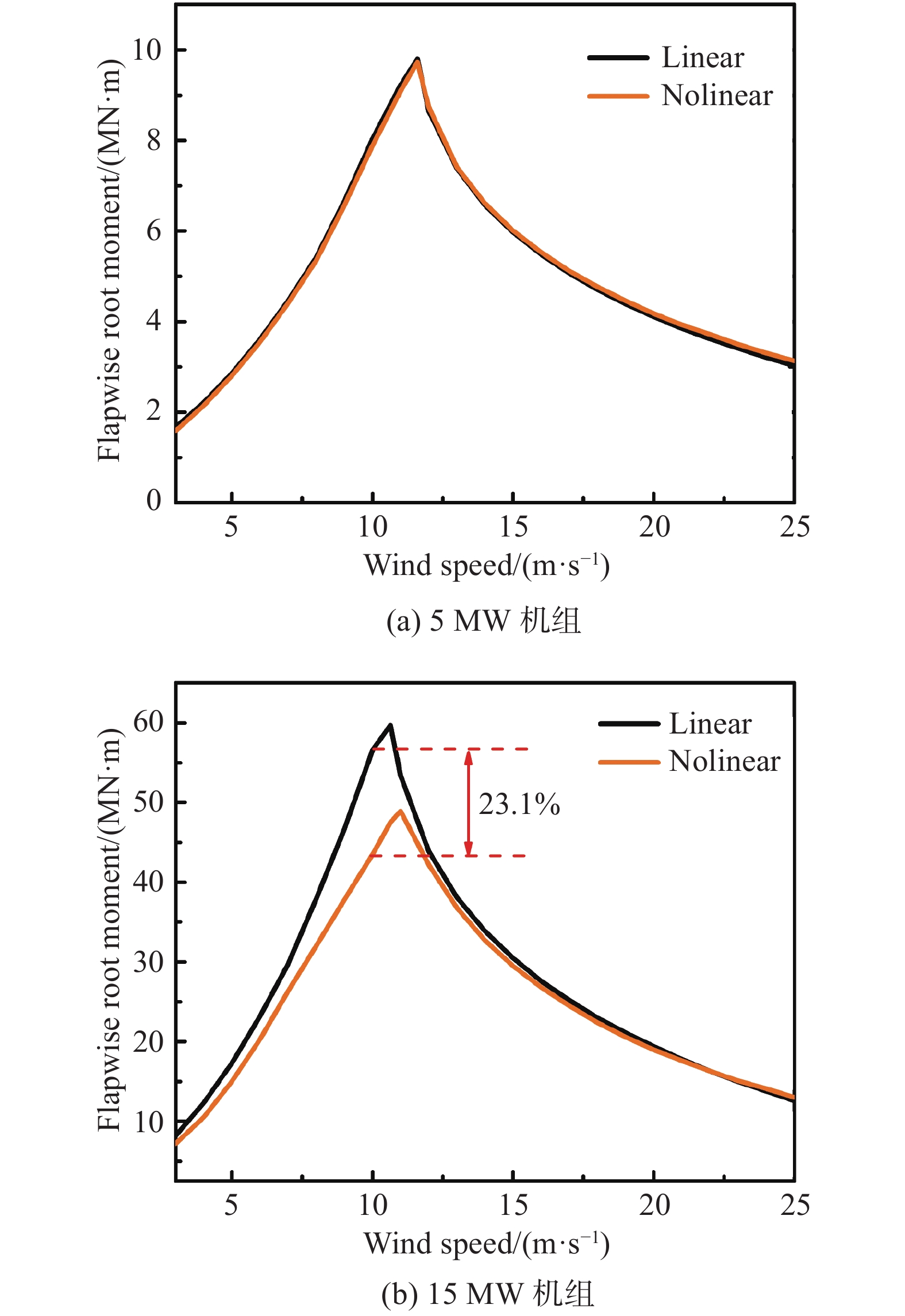
|
图 8 5 MW和15 MW机组在不同风速下的叶根挥舞弯矩 Fig.8 Flapwise root moment of the 5 MW and 15 MW wind turbines under different wind speeds |
图9给出了5 MW和15 MW机组在不同风速下的叶根摆振弯矩。从图中可以看出,对于5 MW机组,叶根摆振力矩在额定风速下达到了最大值,非线性结果在高风速下要大于线性结果,差值随着风速增大而增大;对于15 MW机组,非线性结果在额定风速到切出风速范围内整体明显大于线性结果。叶根摆振弯矩主要由从整体坐标系到叶片局部坐标系的重力分量决定。叶片桨距角和扭转变形的大小直接影响了这两个坐标系中坐标的转换和重力分量的大小,达到额定风速叶片变桨后两种方法得到的桨距角差异较大,所以影响了重力分量的大小,进而影响了中高风速下叶根摆振弯矩的大小。
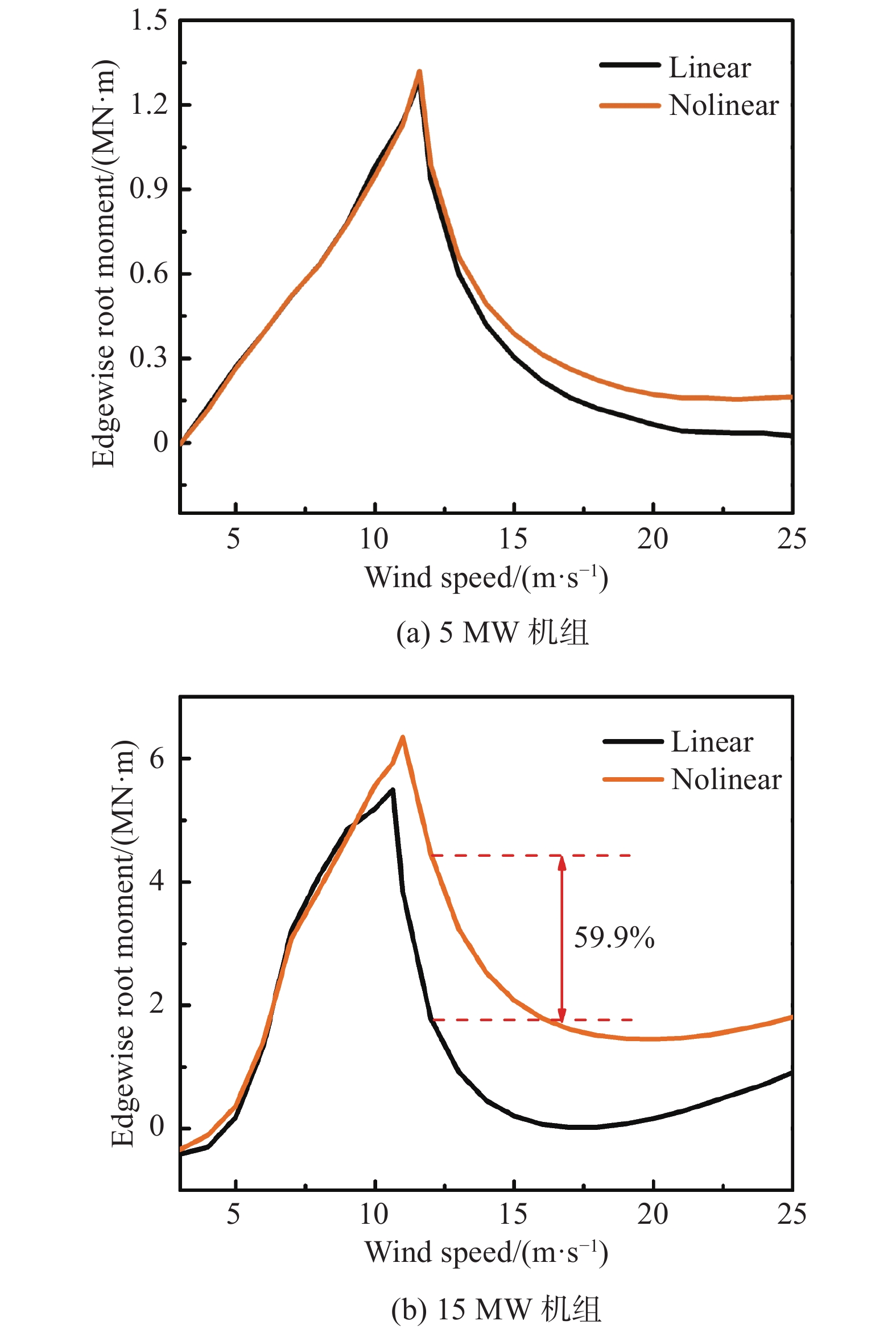
|
图 9 5 MW和15 MW机组在不同风速下的叶根摆振弯矩 Fig.9 Edgewise root moment of the 5 MW and 15 MW wind turbines under different wind speeds |
两个机组的响应在线性方法与非线性方法的最大差值如表5所示,ΔP、ΔT、ΔTx、ΔMx、 ΔMy分别为功率、推力、叶尖挥舞位移、叶根摆振弯矩、叶根挥舞弯矩在不同风速下的最大差值。对于功率、载荷和位移来说,15 MW机组两种方法下的最大差值要比5 MW机组明显偏大,并且对于叶根摆振弯矩来说,非线性计算结果更大。
| 表 5 两个机组的响应在两种方法下的最大差值 Table 5 Maximum difference between the response of the two wind turbines under two methods |
|
|
湍流风场的建立基于IEC标准中给出的Kaimal模型,根据IEC 61400-1,对于中性和稳定大气,功率谱模型定义如下:
| $ \frac{{f{\text{ }}{S_k}\left( f \right)}}{{\sigma _k^2}}{\text{ = }}\frac{{\dfrac{4f {L_k}}{V_{{\text{hub}}}}}}{{{{\left( {1 +\dfrac {6f{L_k}}{V_{{\text{hub}}}}} \right)}^{\frac{5}{3}}}}} $ | (22) |
式中:f为频率;k为速度分量方向的指数;
湍流风的设定采用正常湍流风(NTM)。基于给出的Kaimal速度谱模型,由频域的速度分布来产生时域的风速数据,在二维矩形区域建立一定湍流强度的脉动风速场,并作为气动模型的来流风输入,进行湍流风况的风力机气动弹性仿真。表6对轮毂高度处风速为10 m/s的湍流风场进行了描述,生成了湍流强度为18.34%的剪切湍流风,风速数据分布在二维平面961(31×31)个网格点上,网格平面高度和宽度均为260 m,可覆盖整个风轮及部分塔架。
| 表 6 湍流风场参数 Table 6 Parameters of the turbulent wind field |
|
|
分别采用线性分析与非线性分析方法,计算了湍流风速10 m/s时两个风力机组的动态响应,并进行了对比分析。有效模拟时长为200 s,选取后100 s运行时段的数据进行分析,并将位移和载荷的时域变化进行快速傅立叶变换,得到其频域特征。
图10(a)~图10(d)分别描述了两个机组的叶片在风速10 m/s、湍流度18.34%条件下的叶尖挥舞位移在时域和频域的情况。对于5 MW机组而言,线性与非线性结果差别并不明显,图10(c)中,在频率为0.18 Hz、0.36 Hz处存在一些峰值,并且为该风况下频率0.183 Hz时的值的倍数。根据表3和表4,0.74 Hz处对应的是一阶挥舞模态,在高频区非线性响应运动能量要略大于线性响应。而对于15 MW机组,线性与非线性结果之间的差别要明显大于5 MW机组的,与稳态风况中额定风速附近下的结果较吻合。其对应转频为0.118 Hz,在0.119 Hz处峰值对应此转频,0.579 Hz处对应的是一阶挥舞模态,并且在低频区线性响应能量更高,在高频区非线性响应能量更高。
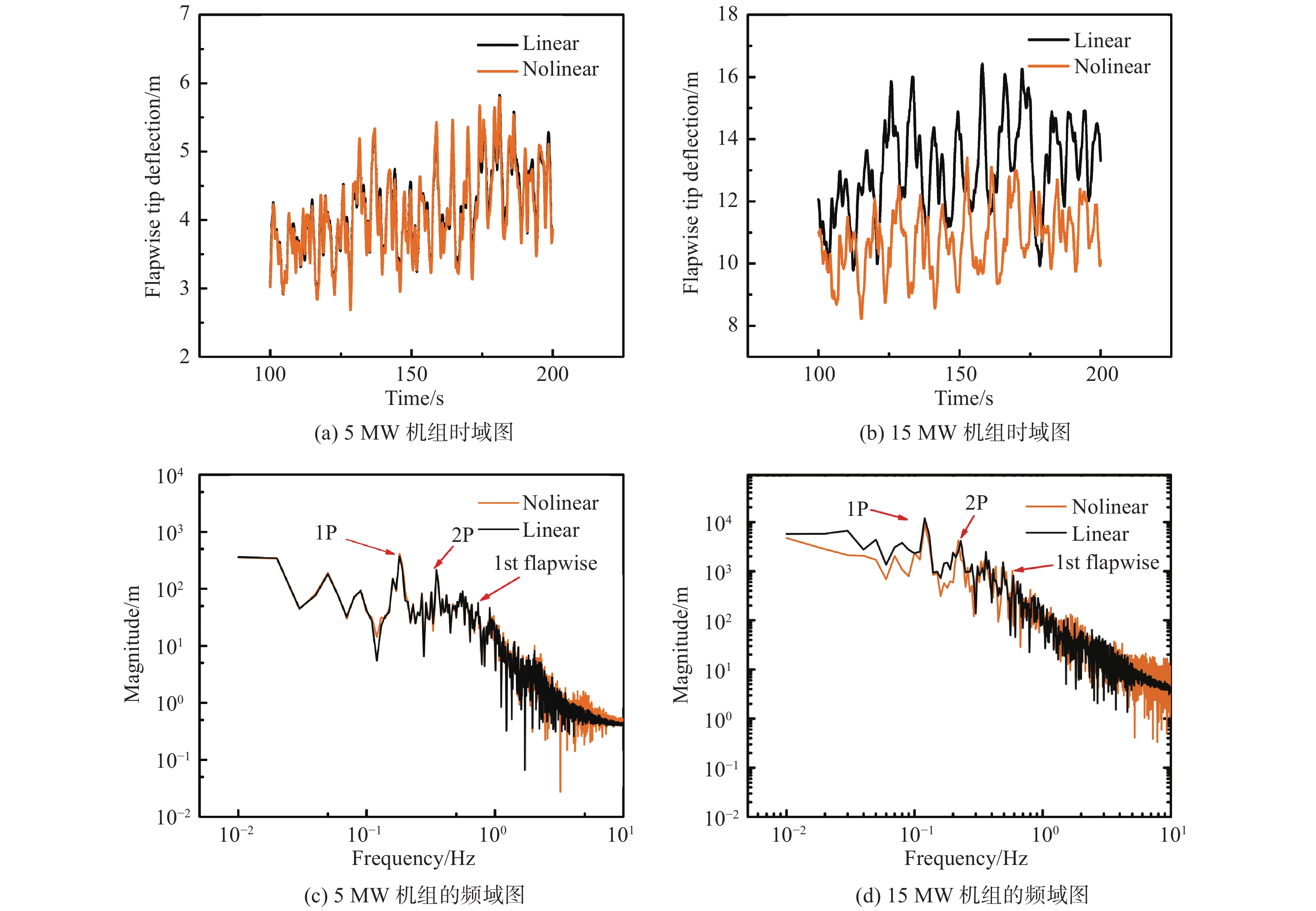
|
图 10 10 m/s湍流风条件下的叶尖挥舞位移 Fig.10 Flapwise tip deflection of the wind turbines under a turbulent inflow of 10 m/s |
图11(a)~图11(d)描述了叶根挥舞弯矩在时域和频域的变化情况,其随时间的变化趋势与叶尖挥舞位移的非常相似。5 MW机组的线性结果与非线性结果差别同样不明显,同样在0.74 Hz处对应的是一阶挥舞模态,在高频区非线性响应略大于线性响应。对于15 MW机组,无论是均值还是振幅,非线性结果都要小于线性结果,差别偏大。在0.579 Hz处对应的是一阶挥舞模态,在低频区同样线性响应能量更高,高频区叶根挥舞弯矩的线性与非线性值吻合较好。
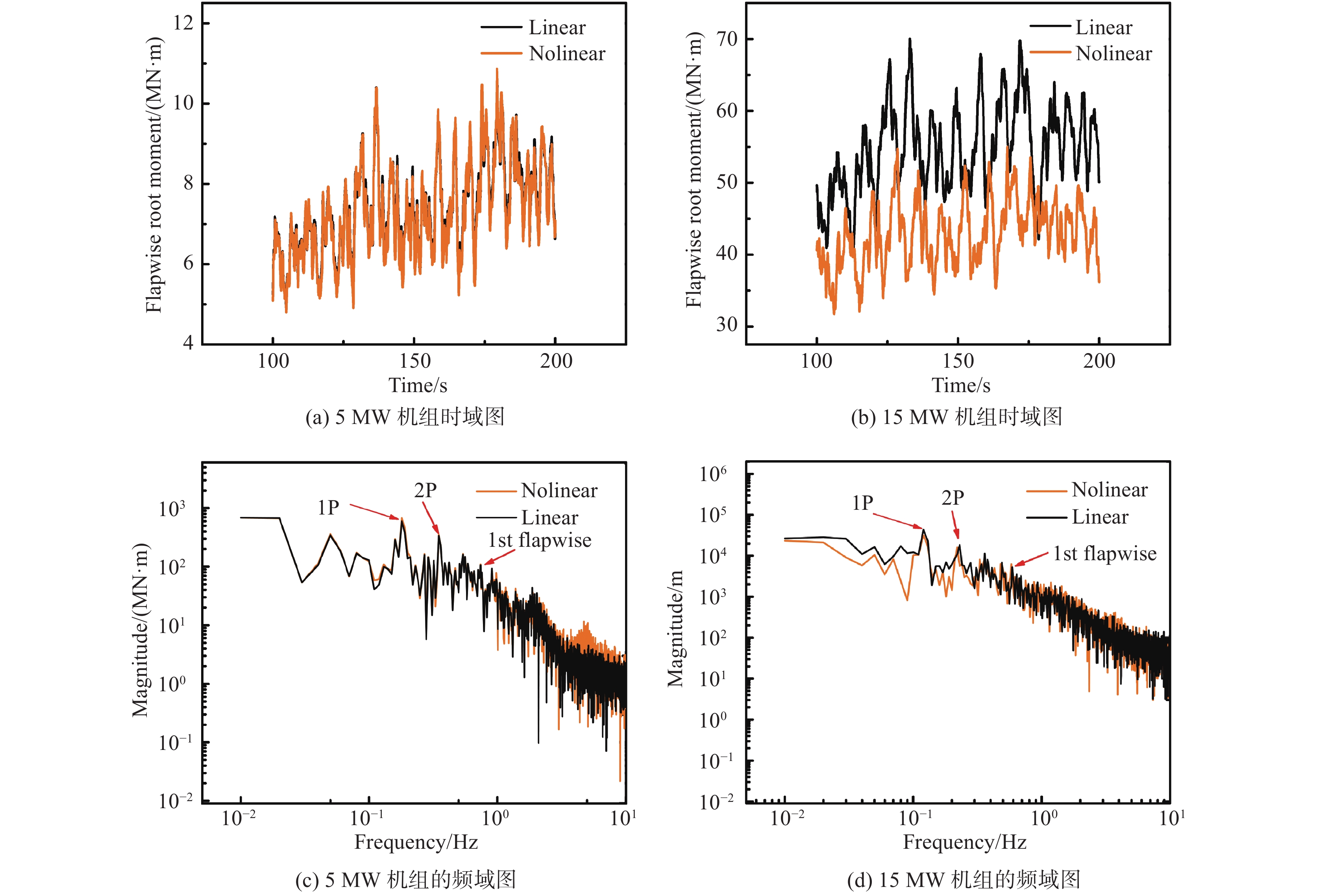
|
图 11 10 m/s湍流风下的叶根挥舞弯矩 Fig.11 Flapwise root moment of the wind turbines under a turbulent inflow of 10 m/s |
从图12(a)~图12(d)看出,叶根摆振弯矩随时间的变化呈明显的周期性,基本围绕均值正负波动。对于5 MW和15 MW风力机,线性与非线性时域结果均差别较小。在频域分析中,5 MW机组在1.09 Hz处对应的是一阶摆振模态,并在两种方法下捕捉到的峰值位置在高频区有明显差异,线性方法在对5 MW机组的峰值预测上在高频区延迟了42.6%,根据文献[22],线性方法在高频区捕捉到的峰值位置有明显延迟,与本文结果相符。而高频区非线性响应的湍流能量大于线性响应;线性方法预测的一阶摆振模态频率在15 MW机组上高估了3.2%,在低频区非线性响应的湍流能量要大于线性响应的,高频区线性响应大于非线性响应。
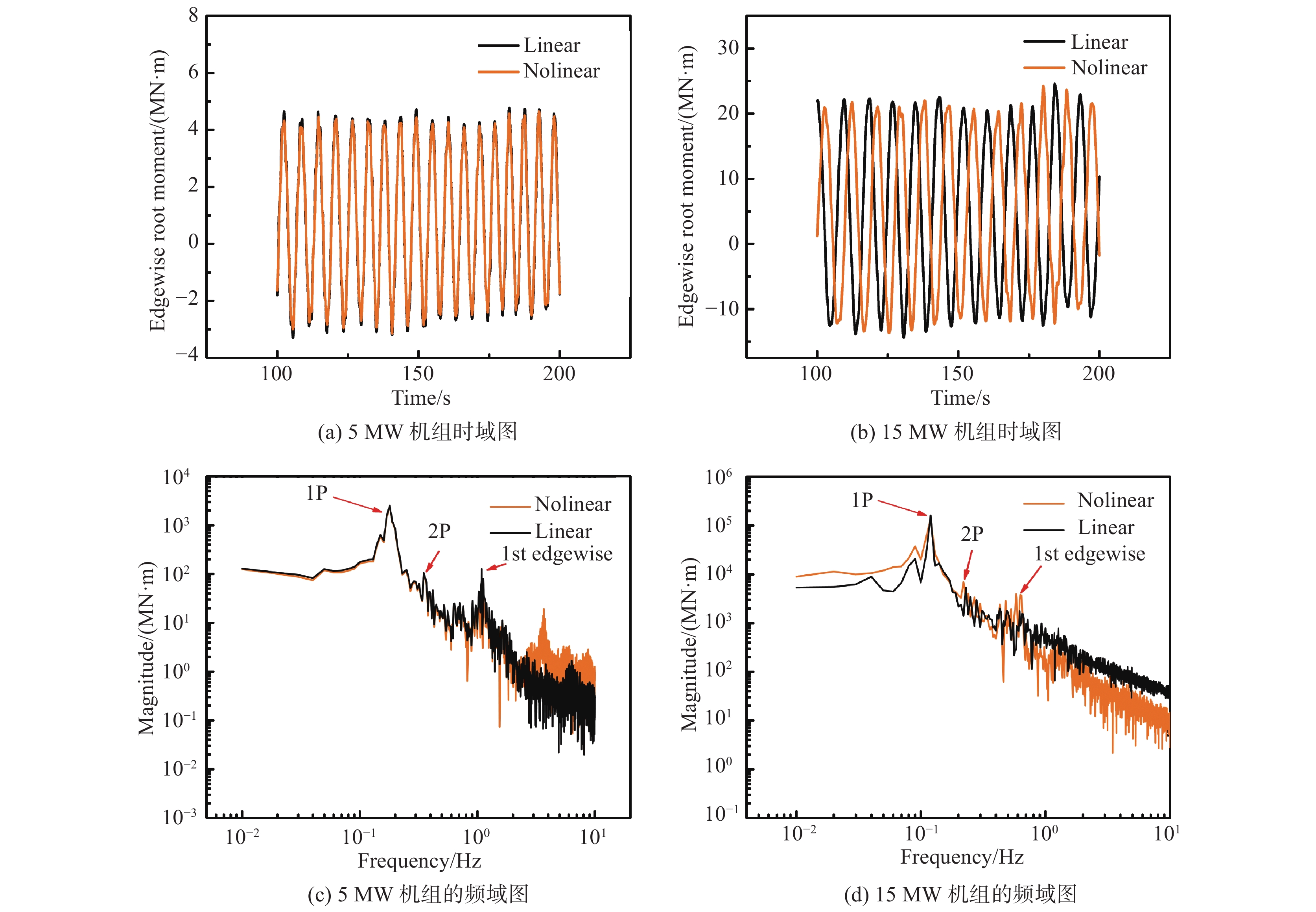
|
图 12 10 m/s湍流风下的叶根摆振弯矩 Fig.12 Edgewise root moment of wind turbines under a turbulent inflow of 10 m/s |
本文计算了悬臂梁的纯弯曲位移,并与文献中的理论值进行对比,验证了几何精确梁理论求解带有几何非线性效应的梁的精度。然后计算了NREL 5 MW与IEA 15 MW风力机在线性与非线性分析下的动态响应,具体研究结论如下:
1)几何精确梁理论考虑了弯扭耦合下叶片产生的额外扭转,减小的桨距角相当于弥补了额外的扭转,从而影响了控制器的设定点。
2)对于挥舞方向的位移与载荷,15 MW风力机线性与非线性计算结果在中高风速下差别明显,叶尖位移最大相差了22.5%,而对于摆振方向的载荷在过高风速下才出现较为明显的差别。
3)在考虑几何非线性后,15 MW风力机叶尖挥舞位移和叶根挥舞弯矩最大减小了22.5%和23.1%。因此对于百米级的大柔性叶片,在保证结构安全的同时,可以进一步降低叶片质量。
4)对于挥舞方向的位移和载荷,与非线性方法相比,线性方法高估了低频区的响应,低估了高频区的响应。
5)对于叶根摆振弯矩,线性方法在对5 MW机组的峰值预测上在高频区大幅度延迟,且15 MW机组中非线性方法下的频率更加贴近一阶摆振模态频率。
综上,对于5 MW机组等刚度较大的风力机叶片而言,基于欧拉梁理论的模态叠加法仍然适用,其叶片质心偏移量很小,不会引起响应发生较大变化,且风激发的最低模态主要是弯曲模态,位移较小,可以被经典梁理论中的线性项准确捕捉;但对于15 MW等大功率机组的百米级叶片,叶片柔性大、变形大,并具有弯扭耦合特征,模态叠加法已不再适用,且功率的变化可能需要优化新的控制策略来改善风力机气动性能。相对于经典梁理论,本文基于几何精确梁理论所建立的非线性叶片气动弹性响应计算方法精度更高,更适用于各向异性复合材料的百米级叶片的数值求解。随着风力机叶片柔性化发展,对于更大功率的风力机和更大的柔性叶片,应考虑几何非线性对风力机叶片气动弹性响应的影响,以准确评估风力机设计的安全性和稳定性。
| [1] |
WANG Q, SPRAGUE M A, JONKMAN J, et al. BeamDyn: a high-fidelity wind turbine blade solver in the FAST modular framework[J]. Wind Energy, 2017, 20(8): 1439-1462. DOI:10.1002/we.2101 |
| [2] |
曹九发, 王同光, 王枭. 大型风力机的几何非线性动态响应研究[J]. 振动与冲击, 2016, 35(14): 182-187,214. CAO J F, WANG T G, WANG X. Geometric nonlinear dynamics response of large-scale wind turbine[J]. Journal of Vibration and Shock, 2016, 35(14): 182-187,214. DOI:10.13465/j.cnki.jvs.2016.14.030 (in Chinese) |
| [3] |
吕计男, 刘子强, 赵玲, 等. 大型风力机气动弹性响应计算研究[J]. 空气动力学学报, 2012, 30(1): 125-129. LYU J N, LIU Z Q, ZHAO L, et al. Large-scale wind turbine aeroelastic responses analysis[J]. Acta Aerodynamica Sinica, 2012, 30(1): 125-129. DOI:10.3969/j.issn.0258-1825.2012.01.022 (in Chinese) |
| [4] |
RINKER J, GAERTNER E, ZAHLE F, et al. Comparison of loads from HAWC2 and OpenFAST for the IEA wind 15 MW reference wind turbine
[J]. Journal of Physics:Conference Series, 2020, 1618: 052052. DOI:10.1088/1742-6596/1618/5/052052 |
| [5] |
ZHOU X D, HUANG K F, LI Z. Geometrically nonlinear beam analysis of composite wind turbine blades based on quadrature element method[J]. International Journal of Non-Linear Mechanics, 2018, 104: 87-99. DOI:10.1016/j.ijnonlinmec.2018.05.007 |
| [6] |
吴坛辉, 洪嘉振, 刘铸永. 非线性几何精确梁理论研究综述[J]. 中国科技论文, 2013, 8(11): 1126-1130. WU T H, HONG J Z, LIU Z Y. Advances of geometrically exact 3D beam theory[J]. China Sciencepaper, 2013, 8(11): 1126-1130. DOI:10.3969/j.issn.2095-2783.2013.11.012 (in Chinese) |
| [7] |
陈进格, 沈昕, 王广, 等. 基于升力面和大变形梁的风力机叶片气弹模型[J]. 工程热物理学报, 2018, 39(7): 1469-1475. CHEN J G, SHEN X, WANG G, et al. Aeroelastic modeling for wind turbine blade based on lifting surface model and nonlinear beam theory[J]. Journal of Engineering Thermophysics, 2018, 39(7): 1469-1475. (in Chinese) |
| [8] |
王珍. 绝对节点坐标梁单元与几何精确梁单元对比研究[D]. 北京: 北京理工大学, 2017.doi: 10.26948/d.cnki.gbjlu.2017.001219
|
| [9] |
YU W B, HODGES D H, VOLOVOI V, et al. On Timoshenko-like modeling of initially curved and twisted composite beams[J]. International Journal of Solids and Structures, 2002, 39(19): 5101-5121. DOI:10.1016/s0020-7683(02)00399-2 |
| [10] |
DOEVA O, MASJEDI P K, WEAVER P M. Static deflection of fully coupled composite Timoshenko beams: an exact analytical solution[J]. European Journal of Mechanics - A/Solids, 2020, 81: 103975. DOI:10.1016/j.euromechsol.2020.103975 |
| [11] |
GAO Z T, LI Y, WANG T G, et al. Modelling the nacelle wake of a horizontal-axis wind turbine under different yaw conditions[J]. Renewable Energy, 2021, 172: 263-275. DOI:10.1016/j.renene.2021.02.140 |
| [12] |
GAO Z T, LI Y, WANG T G, et al. Recent improvements of actuator line-large-eddy simulation method for wind turbine wakes[J]. Applied Mathematics and Mechanics, 2021, 42(4): 511-526. DOI:10.1007/s10483-021-2717-8 |
| [13] |
李义金, 王同光, 钱耀如. 风力机叶片旋转平面内弯曲对动力学响应的影响[J]. 空气动力学学报, 2017, 35(5): 659-664. LI Y J, WANG T G, QIAN Y R. Dynamic response of the wind turbine blade bending in the rotational plane[J]. Acta Aerodynamica Sinica, 2017, 35(5): 659-664. DOI:10.7638/kqdlxxb-2016.0119 (in Chinese) |
| [14] |
GAO Z T, QIAN X H, WANG T G. Spectral partition characteristics of wind turbine load response under different atmospheric stability[J]. Sustainable Energy Technologies and Assessments, 2021, 47: 101421. DOI:10.1016/j.seta.2021.101421 |
| [15] |
张立, 丁勤卫, 李春, 等. 风载荷对不同海上浮式风力机平台运动特性影响对比研究[J]. 太阳能学报, 2021, 42(9): 302-311. ZHANG L, DING Q W, LI C, et al. Comparative study on effects of wind load on motion characteristics of different offshore floating wind turbine platforms[J]. Acta Energiae Solaris Sinica, 2021, 42(9): 302-311. DOI:10.19912/j.0254-0096.tynxb.2019-0918 (in Chinese) |
| [16] |
YU W B, BLAIR M. GEBT: a general-purpose nonlinear analysis tool for composite beams[J]. Composite Structures, 2012, 94(9): 2677-2689. DOI:10.1016/j.compstruct.2012.04.007 |
| [17] |
吕品, 廖明夫, 尹尧杰. 考虑几何非线性的风力机叶片气弹模型[J]. 机械科学与技术, 2015, 34(12): 1805-1812. LYU P, LIAO M F, YIN Y J. An aero-elastic analysis method for wind turbine blades with geometrically nonlinear effect[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(12): 1805-1812. DOI:10.13433/j.cnki.1003-8728.2015.1201 (in Chinese) |
| [18] |
BATHE K J, BOLOURCHI S. Large displacement analysis of three-dimensional beam structures[J]. International Journal for Numerical Methods in Engineering, 1979, 14(7): 961-986. DOI:10.1002/nme.1620140703 |
| [19] |
GUNTUR S, JONKMAN J, SIEVERS R, et al. A validation and code-to-code verification of FAST for a megawatt-scale wind turbine with aeroelastically tailored blades[J]. Wind Energy Science, 2017, (2): 443-468. https://wes.copernicus.org/articles/2/443/2017/wes-2-443-2017.pdf doi: 10.5194/wes-2016-42
|
| [20] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Office of Scientific and Technical Information (OSTI), 2009. doi: 10.2172/947422
|
| [21] |
GAERTNER E, RINKER J, SETHURAMAN L, et al. IEA wind TCP task 37: definition of the IEA 15-Megawatt offshore reference wind turbine[R]. NREL/TP-5000-75698, 2020. doi: 10.2172/1603478
|
| [22] |
QU X Q, LI Y, TANG Y G, et al. Comparative study of short-term extreme responses and fatigue damages of a floating wind turbine using two different blade models[J]. Applied Ocean Research, 2020, 97: 102088. DOI:10.1016/j.apor.2020.102088 |
 2022, Vol. 40
2022, Vol. 40


